2. 武汉大学资源与环境科学学院, 湖北 武汉 430079;
3. 中国资源卫星应用中心, 北京 100094
2. School of Resource and Environment Sciences, Wuhan University, Wuhan 430079, China;
3. China Centre for Resources Satellite Data and Application, Beijing 100094, China
高分四号是世界上第一颗静止轨道高分辨率光学遥感卫星,于2015年12月29号发射成功。静止轨道卫星位于地球赤道上空距地面约36 000 km,轨道平面与赤道平面夹角为零,并且绕地球运行的角速度与地球自转的角速度相同,故相对于地面静止。地球静止轨道卫星具有对地球观测位置相对固定、时间分辨率高、观测范围广等特点,非常适合对地长期连续监视以及快速访问,与低轨遥感卫星形成有益的补充,高分四号旨在获取极高的时间分辨率和中等空间分辨率全国范围内相关区域的多光谱图像信息,能够满足减灾、林业、气象等用户广泛需求[1-4]。
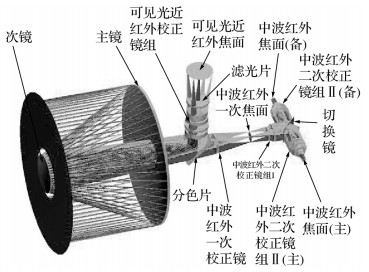
高分四号位于105.6°E, 0°N,采用三轴稳定平台设计[5],对地相机与姿控系统刚性连接,通过整星机动改变对地成像角度,其成像时最大的测摆与俯仰能力为±8.5°,指向控制精度为0.1°。为了保证高分辨率,光学相机按照长焦距、窄视场角的方式进行设计。相机具有两个面阵传感器,可见光近红外传感器与中波红外传感器,它们拥有共同的光学镜头,仅通过滤光片进行波段的分离成像;可见光近红外传感器可以通过旋转滤光片对5个波段进行分时成像。高分四号相机的光学设计如图 1所示,两个感光通道的参数如表 1所示。
|
| 图 1 高分四号相机光学系统构型布局 Fig. 1 The configuration of GF4 optical system |
| 项目 | 可见光近红外通道 | 中波红外通道 |
| 光谱范围 | B1:450-900 nm B2:450-520 nm B3:520-600 nm B4:630-690 nm B5:760-900 nm |
B6:3.5-4.1 um |
| 焦距 | 6600 mm | 1350 mm |
| 像元大小 | 9 um | 15 um |
| 探测器 | 10 240×10 240 CMOS 器件 |
1024×1024中波 红外器件 |
| 地面瞬时视场 | 50 m | 400 m |
| 单景成像区域 | 500 km×500 km | 400 km×400 km |
| 视场角FOV | 0.8°×0.8° | 0.66°×0.66° |
| 积分时间 | 0.5~100 ms | 0.1~10 ms |
高分辨率光学遥感卫星的在轨几何定标是确保其成像几何质量的关键技术[6-7]。高分四号卫星在实验室进行了严格的标定,包括相机的内部畸变标定以及相机相对于姿控系统的安装关系标定。然而,由于发射过程中振动以及周围环境的变化,会使各参数偏离地面的标定值,因此需要重新进行在轨几何定标[8-9]。对于传统的静止轨道气象卫星,如美国的GOES系列卫星,多采用基于地标的方式进行相机的标定[10-13]。传统的低轨光学线阵推扫遥感卫星,则采用基于高精度几何定标场的方式进行标定,通过卫星影像与定标场参考数据匹配得到的高精度控制点,完成相机内外定标系数的解算,从而提高卫星的几何成像质量[14-15]。然而,对于高分辨率静止轨道光学面阵遥感卫星的在轨几何定标的研究却是空白。
本文提出了一种高分辨率静止轨道光学面阵遥感卫星的在轨几何定标方法,通过外定标与内定标两个步骤完成在轨几何定标。针对静止轨道卫星长焦距窄视场角的特点,采用二维指向角模型来描述与补偿相机的内部畸变。试验表明,通过高精度的在轨几何定标,相机的内部精度得到了显著的提升,内部精度优于1个像素。
1 高分四号相机严格几何成像模型 1.1 成像误差分析 1.1.1 外部误差外方位元素描述了本体坐标系到物方坐标系的转换关系,决定了投影中心到物方点在卫星本体坐标系下的光线矢量。卫星的外方位元素可由姿轨量测系统获得,然而量测设备精度和安装工艺的限制以及环境的变化都会给外方位元素引入误差。
1.1.1.1 轨道量测误差对于低轨卫星,通常采用GPS辅助完成高精度定轨,其定轨精度最高可到厘米级,可以忽略不计。然而,由于静止轨道卫星的轨道高度高,难以接收到GPS信号,因此高分四号采用地面观测预报卫星的轨道,轨道观测信息在J2000坐标系下,最高采样频率为1 Hz,理论精度优于200 m。因此,轨道的观测误差将直接影响图像的定位精度。
1.1.1.2 姿态量测误差高分四号的姿态量测系统(ADS)由3组星敏与陀螺组合而成,可以输出观测频率为4 Hz的姿态数据。采用的星敏定姿精度为10 s (均值),且由于静止轨道卫星高度远高于低轨卫星,因此相同的姿态误差会引起更加显著的定位误差,如1 s的姿态误差引起的图像定位精度的偏差可达175 m。
1.1.1.3 相机安装误差高分四号相机与姿态量测系统之间采用刚性连接方式,通过其安装关系可以将相机坐标系下的光线矢量转换到惯性坐标系下。由于高分四号卫星的卫星轨道高度高,在一年中的不同季节、一天中的不同时间,都会引起卫星周围温度剧烈的变化。同时由于高分四号卫星采用三轴稳定平台设计,通过整星机动改变对地成像角度,这样就造成当卫星对不同位置进行成像时,需要调整卫星整体的姿态角度,从而引起卫星的各个面太阳光照角度的变化,导致卫星表面各部分所接收的外热流也在发生变化[16-17]。而热环境的变化会极大地影响相机的相对安装关系,通过地面测试显示,由于温度光照变化以及对不同区域成像时星敏成像天区的变化引起的安装误差和星敏观测误差可达0.02°。因此,与低轨卫星显著不同的是,静止轨道卫星的热变形三轴安装误差具有显著的大幅度的波动性,并且作为最主要的误差源直接影响图像的绝对定位精度[18-19]。尽管该热变形误差具有一定的统计规律,然而美国经历了6颗三轴稳定静止轨道卫星(GOES 8~13)才解决其热变形误差的补偿问题,且高度保密,因此非常具有挑战性。
1.1.2 内部误差内方位元素描述了像平面坐标系到相机坐标系的转换关系,决定了各探元在相机坐标系下的光线矢量。虽然相机的内部参数在地面实验室进行精确的标定,但是任何器件及环境的变化都会改变原有的标定参数,从而造成光线矢量的偏差[20-21]。静止轨道面阵相机主要有3类内部误差:感光面的平移、旋转、缩放;镜头光学畸变;焦距的变化。因此,为了高精度的恢复各探元的光线矢量,这些误差必须要精确标定。
1.1.2.1 感光面误差感光面误差计算公式为
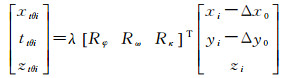 (1)
(1)
式中
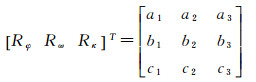
感光面的平移可以描述为主点的偏移,Δx0与Δy0表示主点的偏移量,感光面的旋转可以表示为φ-ω-κ旋转系统的变换,旋转角为Δφ、Δω、Δκ,Rφ、Rω、Rκ为各旋转角对应的旋转矩阵,λ为缩放系数。
1.1.2.2 镜头畸变镜头畸变在光学器件中普遍存在,由于高分四号相机采用长焦距、窄视场角的设计,因此利用一次径向畸变与切向畸变就足以描述其畸变情况,更高阶的畸变形式并没有明显的优势。镜头畸变计算公式为
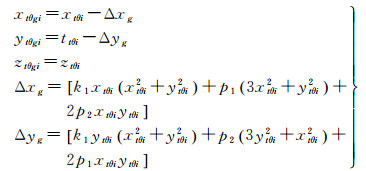 (2)
(2)
式中,k1表示径向畸变系数;p1、p2表示切向畸变系数。
1.1.2.3 焦距误差为了保证最好的成像质量,在轨调焦是不可避免的,焦距误差计算公式为
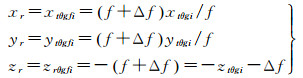 (3)
(3)
式中,f表示地面标定的焦距值; Δf表示焦距的改变量。
通过补偿所有的内部误差,可由相机坐标系下量测的探元坐标P(xi, yi, zi)获得真实的探元坐标P(xr, yr, zr)
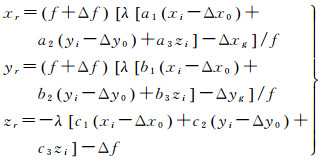 (4)
(4)
通过以上分析,可以获得高分四号卫星严格几何成像模型
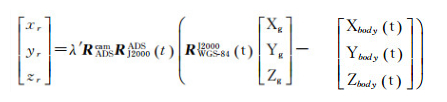 (5)
(5)
式中,t表示成像时刻;λ′为系数尺度因子;RADScam表示相机的安装矩阵;RJ2000ADS(t)为姿控系统的量测矩阵,表示从J2000坐标系到ADS坐标系的旋转关系,可由姿态数据根据时间插值而得;RWGS-84J2000(t)表示WGS-84坐标系到J2000坐标系的旋转矩阵;[Xbody(t)Ybody(t)Zbody(t)]T表示投影中心在J2000坐标系下的坐标,可由轨道数据根据时间插值而得;[Xg Yg Zg]T表示WGS-84坐标系下的物方点坐标,其对应的真实像方坐标[xr yr zr]T可由式(4)求得。
2 高分四号在轨几何定标方法 2.1 在轨几何定标模型本文采用先外定标后内定标的分布式定标方案,完成高分四号卫星的在轨几何定标,即先确定参考相机坐标系,然后在此基础上确定相机的内部畸变曲面。由于高分四号静止轨道卫星相机的长焦距窄视场角的设计,外部的角元素误差与线元素误差具有高度的相关性,同时由于其轨道高度高,因此角元素误差引起的定位误差比低轨卫星具有更高的显著性。卫星的姿态轨道量测值为随机误差,相机的安装关系为规律性未知的系统误差。当利用一景影像进行外定标时,相机的安装矩阵将补偿轨道与姿态误差以及部分的相机内部畸变误差,因此,外定标所确定的相机坐标系并没有真实地反映相机此时的安装关系,仅是为内定标提供了广义的参考坐标系。
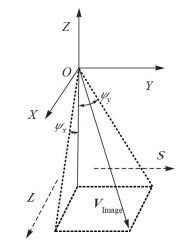
虽然内部误差的严格物理模型公式(4)考虑了绝大部分的误差,但是由于其过度参数化,且部分参数之间具有高度的相关性和低显著性,若直接利用其作为相机的内定标模型会导致方程的病态从而影响定标精度[22-23]。本文采用二维指向角模型作为相机的内定标模型,如图 2所示,VImage是探元指向,ψx和ψy为指向角。通过检校每个探元在由外定标确定的参考相机坐标系下指向角的正切值,来恢复每个探元在相机坐标系下的精确的光线矢量。
|
| 图 2 面阵相机的二维指向角模型 Fig. 2 2-dimensional detector angle model of area-array sensors |
本文用多项式模型对各指向角的正切值进行拟合。由于其视场角较小,且各类内部误差为小量,因此具有高正交性与低相关性的三次多项式模型,可以作为静止轨道卫星面阵相机的内定标模型
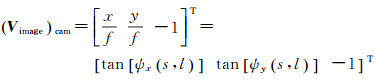 (6)
(6)
式中
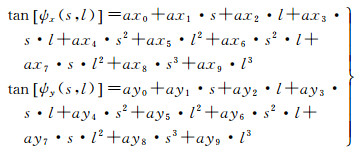
式中,(Vimage)cam是相机坐标系下的探元指向; (s, l)是像平面坐标系下的探元坐标;ax0,ax1, …, ax9和ay0, ay1, …, ay9是内定标参数。
因此,可以构建高分四号在轨几何定标模型
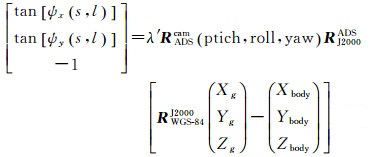 (7)
(7)
式中,XE=(ptich, roll, yaw)是外定标参数,ptich、roll、yaw为相机的安装角,用于确定相机的安装关系,为内定标提供参考相机坐标系。XI=(a0, a1, …, a9, b0, b1, …, b9)是内定标参数,用于描述和补偿相机的内部畸变。
2.2 几何定标参数估计通过将卫星影像与参考数据进行密集匹配,获取K个均匀分布的控制点来进行相机内外定标参数的解算,(s, l)i为控制点的影像像素坐标,(Xg, Yg, Zg)I为控制点对应的WGS-84下的地理坐标,i=1, 2, …, K。
利用地面标定的值XE0和XI0作为定标参数XE和XI的初始值。
(1)为了确定相机的外定标参数,假设内定标的初始值为“真值”,将(XE, XI0)代入式(7)并对每个控制点构建的方程进行线性化处理,可以得到误差方程
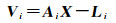 (8)
(8)
式中,Li是当前内外定标参数得到误差向量;Ai是误差方程的系数矩阵;X为当前外定标参数的改正值(Δptich, Δroll, Δyaw),Pi为每个控制点的权值。通过最小二乘解算得
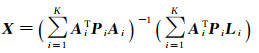 (9)
(9)
对外定标参数进行更新,不断迭代,直到X小于一定阈值
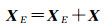 (10)
(10)
(2)为了确定相机的内定标参数,假设所求的外定标参数为“真值”, 将XE代入式(7)并构建方程
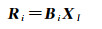 (11)
(11)
式中,Ri是观测向量;Bi是系数矩阵;XI为内定标系数;Pi为每个控制点的权值。通过最小二乘解算得
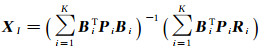 (12)
(12)
为了确保控制点匹配的数量与分布,需要选取没有云覆盖与大片水域覆盖的地区。由于可见光近红外传感器中第1波段为全色波段,与其他波段相比具有更加丰富的纹理信息,因此利用全色波段图像进行可见光近红外传感器的标定,利用中红外波段图像进行中红外传感器的标定。本文选取的定标景数据为依次成像的覆盖中国河南省范围的可见光与中红外影像数据。由于国内可用的高精度几何定标场难以覆盖两个传感器的成像范围(500 km×500 km和400 km×400 km),本文利用Landsat8提供的15 m分辨率全色波段正射影像(200 km×200 km)作为参考影像数据,将其投影方式由UTM投影转换到WGS-84投影,并利用ENVI 5.1将多景影像拼接为整体参考数据以完全覆盖所选定的卫星影像区域。本文利用ASTER GDEM (GDEM2)提供的30 m分辨率高程数据作为定标的参考高程数据。卫星影像与参数数据的详细信息如表 2所示。
| 参数 | 全色图像 | 中红外图像 |
| 地面分辨率/m | 约55 | 约490 |
| 图像大小/像素 | 10 240×10 240 | 1024×1024 |
| 成像时间 | 12:04:08 on 8 February 2016 |
12:05:09 on 8 February 2016 |
| 中心地理坐标 | E111.9, N34.0 | E111.9, N34.0 |
| 成像姿态 | 俯仰角:0.88°;滚转角:5.44°;偏航角:0 | |
| 参数 | 参考正射影像数据 | 参考高程数据 |
| 地面分辨率/m | 15 | 30 |
| 几何精度RMSE/m | 平面精度: 12 | 高程精度: 17 |
| 区域覆盖情况 | 山地与平原 | |
图 3显示了高分四号卫星定标景影像数据与参考影像数据,其中(c)、(d)的方框圈定了参考数据中覆盖的卫星影像数据范围。

|
| 图 3 卫星定标景影像数据与参考影像数据 Fig. 3 The satellite calibration imagery data and reference data |
3.2 试验结果与分析 3.2.1 成像区域分析
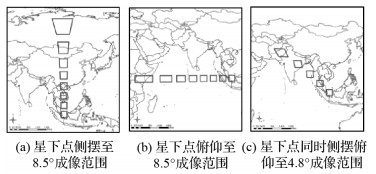
高分四号卫星可以通过地面系统发出的指令通过整星机动来改变相机主光轴的指向,从而改变成像区域,成像测摆角与俯仰角的变化会带来地面成像范围的变化。为了分析静止轨道卫星高分四号的成像区域特性,本文进行了成像范围仿真试验。高分四号卫星位于105.6°E, 0°N,轨道高度约36 000 km,轨道半径约42 000 km,视场角小,当卫星侧摆约8.7°时,卫星的成像范围已接近地球两极。高分四号卫星成像时俯仰角与侧摆角的最大机动能力为±8.5°。以高分四号卫星可见光近红外传感器为例(图 4),对其成像区域进行模拟仿真,可见不同的侧摆角与俯仰角会带来明显的成像范围的变化,同时其地面分辨率也会相应改变。当对星下点成像时,影像的地面分辨率最高,同时成像范围也最小;垂轨方向地面分辨率会随着侧摆角绝对值的增大而降低,沿轨方向地面分辨率会随着俯仰角绝对值的增大而降低,同时相应的成像范围会逐渐变大。因此需要通过在轨几何定标,高精度地恢复静止轨道卫星影像的内部光线矢量,才能确保其内部几何精度。
|
| 图 4 静止轨道卫星单景图像成像范围 Fig. 4 Imaging range of single sence of geostationary satellite |
3.2.2 几何定标精度分析 3.2.2.1 可见光近红外传感器几何定标
将选取的全色波段影像与参考数据进行自动匹配,获得1 118 502个同名点,同名点的坐标与高程值可以由参考数据获得,为了保证控制点的均匀性与准确性,本文剔除误匹配点并筛选出202 386个同名点作为最终的控制点来解算内外定标参数。定标前后可见光近红外传感器的外部安装参数如表 3所示。
| 外定标参数/(°) | 定标前 | 定标后 |
| Pitch | 0.0 | -0.028 753 |
| Roll | 0.0 | 0.105 181 |
| Yaw | 0.0 | 0.379 610 |
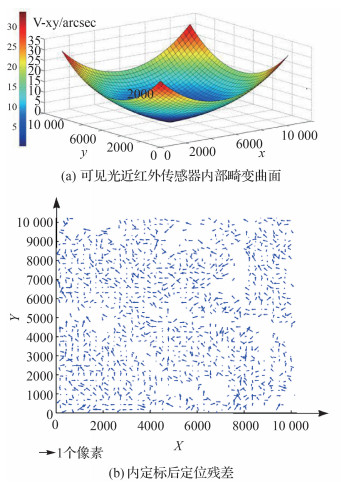
通过严格的外定标,外部误差和部分的内部误差被补偿。为了定性和定量分析外定标后传感器内部残余的内部畸变误差,内定标前各探元的光线矢量偏差如图 5(a)所示。可见,外定标后残余的内部畸变具有高度的中心对称性,越靠近图像的边缘处,由于畸变引起的光线矢量偏差就越大。因此,可推测,相机安装误差、主点偏移及感光面的旋转等引起光线指向非对称的偏差在相机外定标过程中得到了补偿,残余的内部畸变为相机的镜头畸变及感光面的缩放等引起光线指向对称性偏差的误差。这些残余的内部畸变需要通过内定标模型进行补偿,图 5(b)显示内定标后的定位残差分布图,可见,内定标后残差不存在明显的畸变特性,分布具有随机性,因此可知内部畸变得到消除和补偿。几何定位精度提升明显,定标景内定位精度优于1像素。
|
| 图 5 可见光近红外传感器定标效果 Fig. 5 The result of the calibration of panchromatic and near-infrared sensor |
3.2.2.2 中红外传感器几何定标
对于中红外传感器的定标,为了增加其匹配的控制点的数量,本文利用精确标定后的可见光近红外传感器定标景数据作为中外红传感器定标的参考影像。虽然可见光与中红外传感器理论上拥有统一的相机安装关系,但由于可见光传感器的外定标参数中包含了部分内部畸变与外部误差,并不是真实的相机坐标系,因此,中红外传感器需要重新计算其内外定标参数。通过将中红外影像与可见光影像的密集匹配,选取均匀分布的36 302个同名点作为控制点来计算内外定标参数。定标前后中红外传感器的外部安装参数如表 4所示。
| 外定标参数/(°) | 定标前 | 定标后 |
| Pitch | 0.0 | 0.026 994 |
| Roll | 0.0 | 0.086 810 |
| Yaw | 0.0 | 0.171 221 |
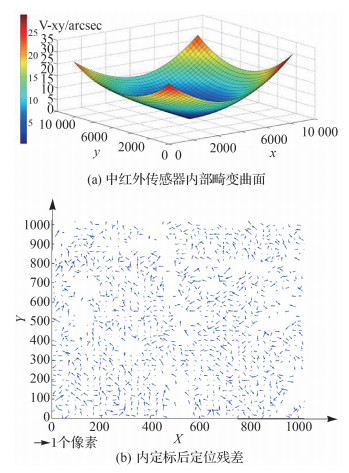
内定标前各探元的光线矢量偏差如图 6(a)所示,图 6(b)显示了内定标后的定位残差分布图,几何定位精度提升明显,定标景内定位精度优于1个像素。由图 6(a)可见中红外传感器的内部畸变曲面误差的最大值略小于可见光传感器,同时由于中红外传感器的视场角较小于可见光传感器,因此同样验证了外定标后残余的内部畸变主要为相机的光学镜头畸变。
|
| 图 6 中红外传感器定标效果图 Fig. 6 The result of the calibration of intermediate infrared sensor |
3.2.2.3 几何定位精度验证
为了验证几何定位的精度,本文选取多组数据进行精度验证。数据A为短时间(半小时)内成像且不同成像区域的数据,数据B、C分别为短时间内成像且同一成像区域的数据,数据B与数据C之间成像区域相同,但成像时间不同(间隔两小时以上)。表 5中的绝对定位精度为无控制点条件下的直接定位精度,内精度为有控定位精度,即通过4个及以上控制点,对影像只进行仿射变换而消除影像的系统性整体偏移后的影像定位中误差,主要反映影像的内部畸变大小及景内的相对精度。由B、C组数据可知,短时间内获得的同一地区全色影像的绝对定位精度具有一致性规律,影像间仅存在较小的定位精度波动, 由于短时间内同一角度成像时,相机所处的热环境可认为恒定不变,因此该波动主要由定姿定轨的随机误差造成;而由A组数据可知,同样短时间内通过改变成像角度获得的不同地区全色影像的绝对定位精度具有显著的波动,由此可知,高分四号影像的绝对定位精度会显著地受到成像角度的影响。通过对比B、C组数据,可见同一地区成像时间间隔较大时获得的全色影像的绝对定位精度也具有明显的偏差,由此可知,高分四号影像的绝对精度同样会显著地受到成像时间的影响。因此,验证了高分四号静止轨道卫星在不同成像时间及不同成像角度成像时,由于光照角度及热环境的影响,会导致相机安装结构的变化,从而影响其姿态确定精度,造成定位精度的下降。如表 5所示的中红外相对于全色的无控定位精度基本在1个像素(中红外)以内,表明了同时成像的中红外影像与全色影像的绝对定位精度具有明显的一致性规律,且通过A、B、C组数据,可见不论成像时间与成像角度的改变,全色与中红外影像的内部精度在x与y方向上均优于1个像素,表明通过在轨几何定标,高精度的恢复了中红外影像与全色影像的内部光线矢量,消除了内部畸变的影响,使其定位精度仅受外部误差的影响。
| 中心经纬度 | 成像时间 | 全色绝对定位 精度(无控制 点)/m |
全色内精度 (有控制点、像方 仿射变换)/像素 |
中红外相对于 全色定位精度 (无控制点)/像素 |
中红外内精度 (有控制点、像方 仿射变换)/像素 |
||||||||
| X方向 | Y方向 | X方向 | Y方向 | X方向 | Y方向 | X方向 | Y方向 | ||||||
| A组 | 95.7°E,32.7°N | 2016-02-02 11:20:43 | 6 144.50 | -5 002.40 | 0.657 | 0.555 | -0.960 | -0.381 | 0.286 | 0.41 | |||
| 99.9°E,32.6°N | 2016-02-02 11:22:37 | 8 043.66 | -7 331.41 | 0.755 | 0.716 | -0.876 | -0.445 | 0.365 | 0.62 | ||||
| 96.5°E,15.7°N | 2016-02-02 11:26:29 | -8 477.84 | -3 961.37 | 0.498 | 0.253 | -0.859 | -0.86 | 0.498 | 0.521 | ||||
| 100.2°E,28.4°N | 2016-02-02 11:32:06 | 7 725.26 | -7 259.48 | 0.906 | 0.758 | 0.119 | 0.246 | 0.309 | 0.485 | ||||
| 118.9°E,32.2°N | 2016-02-02 11:46:19 | 1 726.56 | 3 051.41 | 0.504 | 0.454 | -0.961 | 0.172 | 0.402 | 0.531 | ||||
| 114.7°E,32.1°N | 2016-02-02 11:48:13 | 3 522.18 | 1 713.18 | 0.673 | 0.498 | 0.236 | -0.104 | 0.469 | 0.637 | ||||
| B组 | 103.3°E,33.8°N | 2016-03-06 13:08:48 | -8 240.51 | -2 196.57 | 0.572 | 0.873 | 0.493 | -0.468 | 0.432 | 0.532 | |||
| 103.3°E,33.8°N | 2016-03-06 13:13:02 | -8 549.00 | -2 032.46 | 0.482 | 0.597 | -0.362 | -0.691 | 0.238 | 0.368 | ||||
| 103.3°E,33.8°N | 2016-03-06 13:18:40 | -10 005.6 | -1 548.90 | 0.617 | 0.384 | -0.753 | 0.283 | 0.523 | 0.391 | ||||
| 103.3°E,33.8°N | 2016-03-06 13:24:18 | -9 631.50 | -1 778.96 | 0.786 | 0.853 | 0.645 | 0.474 | 0.442 | 0.404 | ||||
| 103.3°E,33.8°N | 2016-03-06 13:28:31 | -10 405.00 | -1 092.69 | 0.758 | 0.745 | 0.485 | 0.823 | 0.623 | 0.301 | ||||
| C组 | 103.3°E,33.8°N | 2016-03-06 10:29:36 | -1 301.39 | -5 087.42 | 0.637 | 0.594 | 0.623 | 0.734 | 0.353 | 0.402 | |||
| 103.3°E,33.8°N | 2016-03-06 10:35:14 | -726.16 | -5 379.09 | 0.439 | 0.876 | -0.732 | 0.682 | 0.534 | 0.440 | ||||
| 103.3°E,33.8°N | 2016-03-06 10:39:28 | -1 615.84 | -5 137.67 | 0.715 | 0.648 | -0.185 | -0.295 | 0.584 | 0.593 | ||||
| 103.3°E,33.8°N | 2016-03-06 10:45:06 | -2 619.52 | -5 351.63 | 0.562 | 0.431 | 0.591 | -0.975 | 0.489 | 0.301 | ||||
| 103.3°E,33.8°N | 2016-03-06 10:49:19 | -2 135.56 | -5 168.94 | 0.848 | 0.739 | -0.254 | 0.179 | 0.623 | 0.481 | ||||
| 注:A组为短时间内成像且不同成像区域数据几何精度统计;B组、C组为同一地区不同成像时间数据几何精度统计。 | |||||||||||||
4 结语
本文介绍了静止轨道卫星高分四号的相机参数以及成像模式,对其几何定位误差源进行了分类与分析,推导了静止轨道卫星面阵传感器的严密几何成像模型,并在此基础上构建了高精度的在轨几何定标模型,利用安装角来恢复相机的安装关系,确立参考相机坐标系;利用二维指向角模型来描述和补偿面阵相机的内部畸变,提升影像的内部几何精度;同时提出了先外定标后内定标的定标参数估计方案。
本文根据卫星机动能力,对卫星成像区域进行模拟仿真,分析其成像区域特性;通过几何定标试验,可使可见光近红外传感器与中红外传感器影像的内部畸变在沿轨与垂轨方向上稳定优于1个像素;通过对比分析其绝对定位精度,验证了高分四号静止轨道卫星相较于低轨卫星更易受到光照角度及热环境的影响,使其安装关系存在明显的热变形波动,从而在不同成像时间及不同成像角度成像时定位精度具有显著的波动性,因此有待进一步研究分析其热变形的建模及补偿问题。
| [1] | 陶家生, 孙治国, 孙英华, 等. 静止轨道高分辨率光学遥感探索[J]. 光电工程, 2012, 39(6): 1–6. TAO Jiasheng, SUN Zhiguo, SUN Yinghua, et al. Exploration of High Resolution Optical Remote Sensing of the Geostationary Orbit[J]. Opto-electronic Engineering, 2012, 39(6): 1–6. |
| [2] | 吴玮, 秦其明, 杨思全, 等. 面向减灾应用的光学成像静止卫星能力分析[J]. 遥感技术与应用, 2013, 28(6): 984–993. WU Wei, QIN Qiming, YANG Siquan, et al. Capacity Analysis of Optical Geostationary Satellite for Disaster Reduction[J]. Remote Sensing Technology and Application, 2013, 28(6): 984–993. |
| [3] | 崔敦杰. 地球静止轨道卫星有效载荷可优选凝视型光学遥感器[J]. 遥感技术与应用, 1998, 13(3): 30–37. CUI Dunjie. An Optimized Sensor for Geostationary Orbit Satellite Payload[J]. Remote Sensing Technology and Application, 1998, 13(3): 30–37. |
| [4] | 李德仁. 我国第一颗民用三线阵立体测图卫星--资源三号测绘卫星[J]. 测绘学报, 2012, 41(3): 317–322. LI Deren. China's First Civilian Three-line-array Stereo Mapping Satellite:ZY-3[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 317–322. |
| [5] | 刘翔, 张天序, 杨卫东. 三轴稳定卫星图像系统性几何校正研究[J]. 计算机与数字工程, 2005, 33(11): 14–17. LIU Xiang, ZHANG Tianxu, YANG Weidong. Three-axis-stabilized Satellite Image Distortion Simulation and Systemic Geometric Correction[J]. Computer and Digital Engineering, 2005, 33(11): 14–17. |
| [6] | 蒋永华, 张过, 唐新明, 等. 资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报, 2013, 42(4): 523–529, 553. JIANG Yonghua, ZHANG Guo, TANG Xinming, et al. High Accuracy Geometric Calibration of ZY-3 Three-line Image[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 523–529, 553. |
| [7] | 曹金山, 袁修孝, 龚健雅, 等. 资源三号卫星成像在轨几何定标的探元指向角法[J]. 测绘学报, 2014, 43(10): 1039–1045. CAO Jinshan, YUAN Xiuxiao, GONG Jianya, et al. The Look-angle Calibration Method for On-orbit Geometric Calibration of ZY-3 Satellite Imaging Sensors[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1039–1045. DOI:10.13485/j.cnki.11-2089.2014.0147 |
| [8] | WANG Mi, YANG Bo, HU Fen, et al. On-orbit Geometric Calibration Model and Its Applications for High-resolution Optical Satellite Imagery[J]. Remote Sensing, 2014, 6(5): 4391–4408. DOI:10.3390/rs6054391 |
| [9] | ZHANG Yongjun, ZHENG Maoteng, XIONG Jinxin, et al. On-orbit Geometric Calibration of ZY-3 Three-line Array Imagery with Multistrip Data Sets[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 224–234. DOI:10.1109/TGRS.2013.2237781 |
| [10] | 刘良明, 叶沅鑫, 范登科, 等. FY-2卫星S-VISSR数据几何纠正研究[J]. 武汉大学学报(信息科学版), 2012, 37(4): 384–388. LIU Liangming, YE Yuanxin, FAN Dengke, et al. Study on Geometric Rectification for FY-2 S-VISSR Data[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4): 384–388. |
| [11] | LU Feng, ZHANG Xiaohu, XU Jianming. Image Navigation for the FY2 Geosynchronous Meteorological Satellite[J]. Journal of Atmospheric and Oceanic Technology, 2008, 25(7): 1149–1165. DOI:10.1175/2007JTECHA964.1 |
| [12] | YANG Lei, FENG Xiaohu, LÜ Ke, et al. Automated Landmark Matching of FY-2 Visible Imagery with Its Applications to the On-orbit Image Navigation Performance Analysis and Improvements[J]. Chinese Journal of Electronics, 2014, 23(CJE-3): 649–654. |
| [13] | KIM T, LEE T Y, CHOI H J. Landmark Extraction, Matching, and Processing for Automated Image Navigation of Geostationary Weather Satellites[C]//Proceedings of SPIE 5657 Image Processing and Pattern Recognition in Remote Sensing Ⅱ. Honolulu, HI:SPIE, 2004, 5657:30-37. |
| [14] | CHEN Yifu, XIE Zhong, QIU Zhengge, et al. Calibration and Validation of ZY-3 Optical Sensors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(8): 4616–4626. DOI:10.1109/TGRS.2015.2403957 |
| [15] | RADHADEVI P V, MÜLLER R, D'ANGELO P, et al. In-flight Geometric Calibration and Orientation of ALOS/PRISM Imagery with a Generic Sensor Model[J]. Photogrammetric Engineering & Remote Sensing, 2011, 77(5): 531–538. |
| [16] | 李积慧, 韩双丽, 王家骐, 等. 空间相机的热分析与热控制技术[J]. 光学精密工程, 1999, 7(6): 34–41. LI Jihui, HAN Shuangli, WANG Jiaqi, et al. Thermal Analysis and Thermal Control Techniques of Space Camera[J]. Optics and Precision Engineering, 1999, 7(6): 34–41. |
| [17] | 赵振明, 王兵, 高娟. 地球静止轨道凝视型相机热分析与热设计[J]. 航天返回与遥感, 2010, 31(3): 34–40. ZHAO Zhenming, WANG Bing, GAO Juan. Preliminary Research on the Thermal Design Methods of the Geosynchronous Orbit Stating Camera[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(3): 34–40. |
| [18] | 张月, 王超, 苏云, 等. 地球静止轨道甚高分辨率成像系统热控方案[J]. 红外与激光工程, 2014, 43(9): 3116–3121. ZHANG Yue, WANG Chao, SU Yun, et al. Thermal Control Scheme for Ultrahigh Resolution Imaging System on Geosynchronous Orbit[J]. Infrared and Laser Engineering, 2014, 43(9): 3116–3121. |
| [19] | 郭永富. 静止轨道卫星在轨温度参数变化规律研究[J]. 航天器工程, 2011, 20(1): 76–81. GUO Yongfu. Research on the Temperatures of Satellite on Geostationary Orbit[J]. Spacecraft Engineering, 2011, 20(1): 76–81. |
| [20] | 王洪涛, 罗长洲, 王渝, 等. 星敏感器模型参数分析及校准方法研究[J]. 电子科技大学学报, 2010, 39(6): 880–885. WANG Hongtao, LUO Changzhou, WANG Yu, et al. Star Sensor Model Parametric Analysis and Calibration Method Study[J]. Journal of University of Electronic Science and Technology of China, 2010, 39(6): 880–885. |
| [21] | ZHANG Guo, JIANG Yonghua, LI Deren, et al. In-orbit Geometric Calibration and Validation of ZY-3 Linear Array Sensors[J]. The Photogrammetric Record, 2014, 29(145): 68–88. DOI:10.1111/phor.2014.29.issue-145 |
| [22] | 张剑清, 潘励, 王树根. 摄影测量学[M]. 2版. 武汉: 武汉大学出版社, 2010: 20-21. ZHANG Jianqing, PAN Li, WANG Shugen. Photogrammetry[M]. 2nd Ed. Wuhan: Wuhan University Press, 2010: 20-21. |
| [23] | 王金龙. 误差理论与测量平差基础[M]. 2版. 武汉: 武汉大学出版社, 2009: 46-48. WANG Jinlong. Errors Theory and Surveying Adjustment[M]. 2nd Ed. Wuhan: Wuhan University Press, 2009: 46-48. |


