2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西安测绘研究所, 陕西 西安 710054;
4. 信息工程大学军事测绘导航工程军队重点实验室, 河南 郑州 450052
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
4. Military Key Laboratory of Surveying, Mapping and Navigation of Engineering, Information Engineering University, Zhengzhou 450052, China
卫星测高是近30年来探测海洋环境信息最有效的技术手段。它以卫星为平台,以星载高度计为主要有效载荷,辅以精密的定轨系统,高精度、周期性地对海洋环境信息进行探测,通过地面数据处理,可以生成海洋重力场、海洋大地水准面、海底地形和其他海洋测绘产品。
近年来的卫星测高任务按其用途大致可分为两类,一类用于海洋动力环境监测研究,另一类是用于反演海洋重力场的大地测量任务(geodetic mission,GM)[1],后者主要包括Geosat的GM任务、ERS-1的168 d重复周期任务以及Jason-1的GM任务。测高卫星应用需求的深化牵引着其逐渐向高空间和高时间分辨率方向发展,依靠单颗测高卫星的传统GM任务要同时满足全球高精度、高分辨率海洋重力场反演的要求,需要很长时间的高精度海面高观测积累,而在此期间,复杂的海况变化致使升降轨海面高梯度的观测精度已不能满足重力场反演的需要[1]。对应于更高的任务需求,测高技术也进行着革新,如合成孔径雷达测高计技术(已用于Cryosat-2、Sentinel-3)、Ka波段测高技术(已用于SARAL)、Ka波段干涉雷达测高计技术(拟用于SWOT),以及测高卫星星座技术和GNSS信号测高技术等[2-4]。
在测高卫星星座技术的发展方面,文献[1, 5]论证了一种新颖的海洋卫星测高模式,用于获取更高分辨率(如1′×1′)的全球海洋重力场。该种模式的特点为:两颗卫星采用相同的轨道参数,在有效观测期间,经度方向上有固定的距离。其主要优势为可以同时给出星下点海面高东西方向和南北方向上的梯度值,且所计算海面高梯度的精度优于传统单颗卫星得到的结果。根据文献[1, 5],本文所指的双星串飞编队测高模式是指两颗卫星前后相距一定距离(时间间隔约4 s,空间距离约30 km)、同时飞行的工作模式,双星地面瞬时轨间距约1′,单星轨间距为2′。
高度计定标是所有卫星测高应用的基础与前提。传统卫星高度计测距偏差的确定常通过在轨卫星的绝对定标实现,其思路为在卫星经过定标场海域上空时,以定标场设备测得的海面高为基准,将卫星高度计在定标场海域测得的海面高进行比较,得到海面高的偏差作为卫星高度计的测距偏差。长期、连续的多次定标,可以确定由测高卫星系统测得的海面高偏差及其随时间的漂移。通过高度计的定标与验证工作,能够快速向项目组反馈测量数据的质量,在数据产品发布前进行必要的数据质量评估;通过精细的高度计定标工作,还能够发现测高系统中可能存在的系统或误差模型缺陷[6-10]。
重力场反演的主要观测量为海面高差(海面高梯度),因而海面高差是双星串飞编队测高模式中最核心的观测量。获取该观测量的过程中,两颗卫星高度计的测距值相对偏差是不可或缺的重要部分,其误差影响所有海面高差观测量,因而相对偏差的精度直接影响重力场反演的精度。本文将双星串飞编队测高模式下精确确定卫星高度计测距值的相对偏差定义为相对定标。在双星串飞编队测高模式下,绝对定标方法可用于分别确定两颗卫星高度计的测距偏差,对于测高系统的监测具有重要的作用,同时,相对定标对主要用于海洋重力场反演的双星串飞编队测高模式至关重要,高精度的相对定标是任务成功实施的前提,本文主要研究该模式下的相对定标。
多卫星高度计之间测距相对偏差的确定,大致分为两种方法:一种是通过卫星轨道之间全球范围内的交叉点信息进行平差得到[11-12];另一种针对Jason-1与T/P、Jason-2与Jason-1之间的重复周期共同飞行阶段,通过求取全球范围内偏差的均值[13],或通过地面定标场进行直接绝对定标结果的比较[7-8, 14]。然而,前一种方法需要积累大量全球范围内的数据才能较为准确地得出高度计之间的测距偏差,具有信息滞后性;后一种方法对于本文所介绍新型测高模式下的相对定标虽有借鉴意义,但其所研究对象与本文有实质差异,如Jason-2与Jason-1之间的前后时间差约55 s,本文中双星之间的时间差约4 s;又如Jason-2与Jason-1几乎在同一轨道,而本文中双星之间的轨道间距约1′。
由于双星串飞编队测高模式的新颖性与特殊性,现有方法并不适用于该模式下的相对定标。基于此,本文对该模式下高度计的相对定标方法进行研究。
1 双星串飞编队测高模式下相对定标原理获得全球海洋区域2′×2′分辨率及毫伽级精度的海洋重力场模型是现有传统高度计观测模式下反演海洋重力场的极限[1]。双星串飞编队海洋卫星测高模式在较短时间内能够实现高分辨率全球大部分海域的海面高梯度测量,为海洋测高重力场的精确确定提供高分辨率的数据。
星载雷达高度计沿垂线向海面发射微波脉冲,并接收从海面反射回来的信号,利用星上计时系统及信号捕捉系统可以求解获得雷达天线相位中心到瞬时海面的垂直距离。通过轨道确定获得卫星质心相对于参考椭球的高度,经相关的误差改正就可得到瞬时海面的椭球高,即海面高(sea surface height,SSH)。
根据卫星高度计的测高原理[15-17],由卫星高度计得到的海面高SSHAlt可以定义为
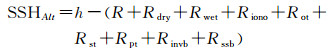 (1)
(1)
式中,h为卫星的轨道高度;R为卫星到海面的高度计测距值;Rdry表示干对流层延迟改正;Rwet表示湿对流层延迟改正;Riono表示电离层延迟改正;Rot表示海洋潮汐改正;Rst表示地球固体潮汐改正;Rpt表示极潮改正;Rinvb表示逆气压改正;Rssb表示海况偏差改正(后文中误差改正项特指以上8项误差改正项)。
对两颗或两颗以上的卫星高度计进行相对定标的目的是确定多卫星高度计之间测距值的相对偏差与漂移,从而联合多代卫星的观测值进行全球海面的持续监测以及其他研究[18-19]。多颗卫星之间的相对定标方法在引言中已进行了概括,针对双星串飞编队测高模式,考虑到对于任一卫星高度计建立专用定标场的必然性,本文研究定标场环境下高度计相对定标的方法。
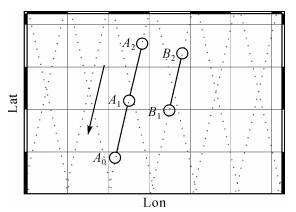
双星串飞编队测高模式下,A、B两颗卫星的地面轨迹如图 1所示。由于两颗卫星几乎同时飞越定标场,且星下点轨迹相距不远(约2 km),因而可将两颗卫星在定标场海域测得的海面高进行比较,得到海面高测量值的相对偏差。设卫星A与卫星B在定标场中的比较点分别为A1点与B1点,两卫星地面轨迹的空间距离约为1′,A1B1距离约2 km (假设定标场位于30°纬度)。将两颗卫星分别在比较点得到的海面高作差,并考虑两点之间的瞬时海面高差异,可得海面高值的相对偏差,亦即高度计之间测距值的相对偏差。基于小范围内海面地形几乎一致的考虑,本文将瞬时海面高差异可近似为水准面高差。
|
| 图 1 双星串飞编队测高模式地面轨迹示意图 Fig. 1 Ground track of dual-satellite formation flying altimetry mode |
记A卫星在A1位置测得的海面高为SSHAltA,B卫星在B1位置测得的海面高为SSHAltB。记A1位置与B1位置水准面高差为Δhgeoid,则海面高相对偏差Biasrelative为
 (2)
(2)
式中,Δ表示A1、B1两点相关量之差。
除确定高度计测距值相对偏差这一核心参数外,相对定标还可以有效地用于评估高度计测量系统的精度与稳定性。如果长时间多次相对定标结果都非常稳定,说明高度计测量系统工作稳定;反之,可以根据相对定标结果中出现的跳变快速地示警,监测系统是否正常运行。将相对定标的结果与单颗卫星高度计绝对定标的结果相结合,有望改善单颗卫星绝对定标的精度。
2 误差改正项特性分析相对偏差计算式中有8项改正项,它们大部分在很小的空间与时间尺度上几乎没有变化。对这些误差改正项进行特性分析,从而根据它们的变化特性对式(2)的求解进行简化。
2.1 试验数据的谱分析对海洋测高卫星数据进行谱分析,来研究各误差改正项的频谱特性,作为相对定标计算模型简化分析的基础与依据。Jason-2卫星的GDR类型数据约延迟60 d左右发布,在发布的所有数据中精度最高,这里以GDR-D版本Jason-2卫星数据作为分析对象,分析过程中电离层延迟与湿对流层延迟均采用实测改正值。
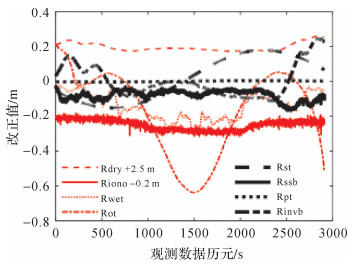
分别选取不同周期穿越太平洋、大西洋、印度洋的上升以及下降弧段进行各误差改正项的谱分析,所得结果颇为一致。篇幅所限,这里给出典型的第56弧段的分析结果。第56弧段穿越太平洋,地面轨迹在50°N与65°S之间的部分全部为海洋,没有陆地对测高数据的污染,数据连续性较好,各误差改正项变化连续。使用Welch功率谱估计方法[20],得到各误差项改正值的功率谱,图 2所示为各误差改正项的时序变化图(为了将所有改正项相对清楚地呈现于一张图中,Rdry在原值上加2.5 m,Riono在原值上减0.2 m),图 3为与其对应的功率谱。
|
| 图 2 各误差改正项时序变化图 Fig. 2 Time series of multiple error corrections |
|
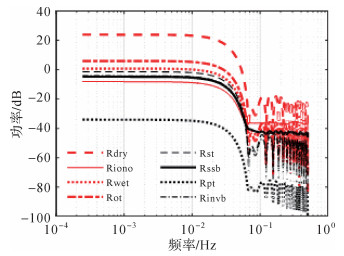
| 图 3 各误差改正项的功率谱(共2911历元数据) Fig. 3 Power spectral density of multiple error corrections (2911 epochs in total) |
由图 3知,所有的8项改正项均呈现出低频特性,信号的主要能量均集中在0.03 Hz以下的频段,对应的误差项波长均在150 km以上。由各误差改正项的功率谱可以推估,在双星串飞编队测高模式两星下比较点相距约2 km、测量时间相差约4 s的条件下,各误差改正项变化不大,从而在海面高测量偏差相对定标中,式(2)中各误差改正项之差的影响很小。
2.2 试验数据的差分统计特性对Jason-2卫星的实测数据产品进行差分结果的统计分析,得到各误差改正项差分值的变化特性与范围,以对式(2)进行简化。Jason-2的重复周期约9.9 d,随机选择2015年中的6个完整周期(周期之间相隔约两个月)的测量数据作为分析对象。
按照Jason-2数据产品手册中推荐的数据选取原则,选择无冰海域(surface_type为0同时ice_flag为0)的全部有效历元数据进行分析。将前后两个历元均为有效的数据作差,得到一帧差分值,将各周期内所有有效差分值作为整体进行统计,一个完整周期所有弧段的测量结果可得约50万帧有效差分数据。
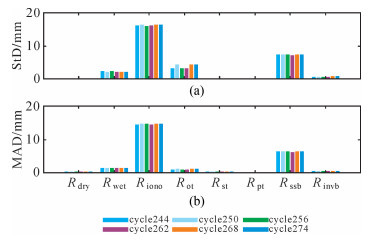
对各个完整周期中不同误差改正项的1 s差分结果进行统计计算,相关结果如图 4所示,其中图 4(a)为各个周期不同误差项差分序列的标准差(standard deviation, StD),图 4(b)为相应的中位数绝对偏差(median absolute deviation, MAD),MAD定义如下[21]
|
| 图 4 各误差改正项差分序列统计结果 Fig. 4 Statistics of 1 s differential value of multiple error corrections |
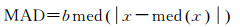 (3)
(3)
式中,med (x)表示序列x的中位数;b=1.482 6。MAD被认为是在高斯分布下,对标准差具有抗差特性的鲁棒估计值[22-23]。
对比图 4(a)与图 4(b),Rwet、Riono、Rot、Rssb 4项的StD相对较大,其中Riono与Rssb两项的StD与MAD较为接近,而Rwet与Rot两项的MAD较StD要大许多。由于MAD的特性,笔者认为这种差异产生的原因是Rwet与Rot的差值序列中存在着较大的粗差,在大粗差的影响下, 整个序列的StD变得较大,从而认为MAD更能代表Rwet与Rot序列的变化特性,其标准差应接近图 4(b)中的结果,即均小于1.2 mm。由此,Riono与Rssb的变化相对剧烈,对应差分序列的标准差分别在16 mm与7.5 mm;其他误差项变化较为平缓,差分序列标准差均小于1.2 mm,相对于厘米级期望定标精度,可忽略它们的影响。由以上分析,在式(2)中需要考虑电离层延迟与海况偏差两差值项的影响,其他项的影响可忽略。
3 相对定标模式及误差分析由上文可知电离层延迟与海况偏差两项的变化幅值相对较大,然而,电离层的总电子含量具有的大尺度变化特性,与此结果有一定出入,电离层延迟对卫星高度计的影响需要进一步考虑。首先对电离层延迟改正进行再分析,然后对式(2)进行简化推导并进行误差估计。
3.1 电离层延迟影响再分析根据图 4中源于GDR文件原始数据的分析结果,电离层延迟改正值在空间尺度上变化较大,1 s差分值的标准差达到1.6 cm。若按此结果,显然在相对偏差的求取中需要着重考虑该项;然而从另一个角度进行分析却有不同的结果。
考虑单个频率载波信号的电离层延迟模型[16]
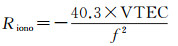 (4)
(4)
式中,f为载波频率(Hz);VTEC为垂直传播路径上的总电子含量(electrons/m2);Riono为电离层延迟(单位为m)。对于测高卫星Ku波段的载波信号(13.575 GHz),1 TECu (1 TECu=1016electrons/m2)的VTEC变化量约引起2.186 mm的延迟变化。然而,TECu是很大的TEC计量单位,在小的空间尺度上(2 km)与小的时间间隔内(4 s),VTEC的变化量很难达到1 TECu。
通过GPS双频载波相位观测数据,可以计算电离层TEC的变化率(rate of TEC,ROT)[24-26]。借鉴ROT的计算方法[24],采用1 s采样率的GPS双频载波相位观测数据,分析了中纬地区(假设定标场位于中纬地区)的VTEC变化率,结果表明一般空间环境条件下,VTEC变化率小于0.05 TECu/s,这意味着前后1 s VTEC的变化量对于Ku波段的载波信号产生的延迟变化量应小于0.11 mm,该结果远不能达到图 4中电离层延迟改正值的变化程度。
通过GDR文件计算出的电离层延迟改正值变化幅度与TEC变化情况具有较大偏离,其原因值得探究。式(5)为Ku波段电离层延迟改正值的双频改正计算式[27-28]
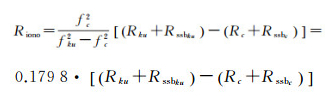 (5)
(5)
式中,fku=13.575 GHz是Ku波段载波频率;fc=5.3 GHz是C波段载波频率;Rku、Rc分别为Ku、C波段测距值(单位为m);Rssbku是Ku波段海况偏差改正值(单位为m);Rssbc是C波段海况偏差改正值(单位为m)。在计算Riono时,将两个波段经海况偏差改正后的测距值相减,带入了距离测量中的误差,同时,海况偏差等不确定项也对测距值产生影响[28],因而Riono计算结果中包含了许多不确定误差。在实际使用GDR文件中的电离层延迟时,数据发布机构建议使用通过平滑处理后的改正值[16],为提供可追溯的改正值,GDR文件中的电离层改正值并未进行平滑[16]。因此,通过GDR文件中的原始数据计算得到1 s电离层改正项差分值序列的标准差相比真实情况误差较大。文献[27]认为由双频高度计测量得到的电离层延迟受到高度计测距噪声的污染,其在分析电离层延迟的功率谱时,对原始电离层延迟序列首先进行了Wiener滤波,以减小以上污染的影响。
仍然采用ROT的计算方法[24],对式(2)中ΔRiono项的影响进行估算。利用30 s采样率的GPS双频载波相位观测数据,可以得到30 s前后TEC的变化量,由于此处关注的是TEC变化范围,因而记其绝对值为ΔTEC如式(6)[24]
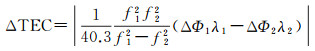 (6)
(6)
式中,f与λ分别为载波信号的频率(单位为Hz)与波长(单位为m);ΔΦ为前后30 s的载波相位变化量(周);下标1、2分别代表两种载波信号(L1与L2)。
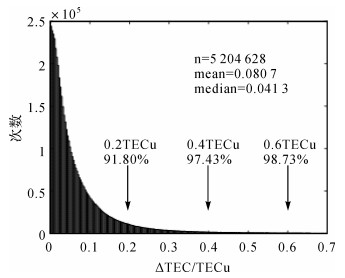
基于电离层单层模型假设,设单层电离层的高度为350 km,根据GPS的轨道参数可推求得相隔1 s前后两穿刺点间的距离约为67.159 2 m,则30 s前后对GPS卫星观测的电离层穿刺点相距约2 km,从而可通过ΔTEC估算相距2 km、相隔4 s条件下VTEC的变化量级,进一步估计ΔRiono项的大小。IGS的JFNG测站位于北纬30.5°,通过该站2015年全年对30°以上仰角GPS卫星的观测数据,计算得到约520万个有效的ΔTEC,其统计直方图如图 5所示(另有0.95%的ΔTEC大于0.7 TECu)。
|
| 图 5 JFNG测站2015年ΔTEC的直方图 Fig. 5 Histogram of ΔTEC of Station JFNG during 2015 |
由图 5知,ΔTEC的变化基本上都在0.6 TECu以下(98.73%),全年ΔTEC的均值为0.080 7 TECu,中位数为0.041 3 TECu,ΔTEC以0.997的置信水平小于1.15 TECu。ΔTEC反映的是TEC在相距2 km、相隔30 s前后的变化量,感兴趣的相距2 km、相隔4 s前后的VTEC变化量可认为不大于ΔTEC。由此,在中纬地区,与ΔRiono项相关的VTEC变化量小于1.15 TECu,相对应的Ku波段延迟量之差ΔRiono小于2.51 mm。
SARAL是世界上首颗搭载Ka波段雷达高度计(AltiKa)的卫星,于2013年2月25日成功发射,至今,SARAL/AltiKa已全部实现了初期预设的科学目标[29]。AltiKa的工作频率为35.75 GHz,相比传统的雷达高度计(如Jason-2)采用的13.575 GHz (Ku波段)、5.3 GHz (C波段)频率更高,相应的优势包括更高的工作频率降低了电离层变化对测量的影响[30]。假设双星串飞编队测高模式中的两颗卫星采用类似于AltiKa的Ka波段高度计,则电离层延迟项之差的影响更小,其原因是电离层延迟量与载波频率的平方成反正,而Ka波段频率是Ku波段频率的2.6倍余。当VTEC变化量小于1.15 TECu时,在Ka波段测距技术条件下,ΔRiono项不超过0.36 mm。
综上,通过GDR文件反映出的电离层延迟的变化情况包含许多由其他因素引入的误差。对于式(2)中相对偏差的计算,在中纬地区,ΔRiono项不超过2.51 mm (Ku波段)或0.36 mm (Ka波段),相对于厘米级的相对定标精度,ΔRiono项应可忽略。
3.2 相对偏差计算公式的简化Jason-2卫星的地面轨迹速率约为5.8 km/s,图 4中所示海况偏差改正值1 s差分序列的标准差在7.5 mm左右的意义可理解为:相距约5.8 km的海面因海况不同而造成的高度计测距值之差约为7.5 mm。双星串飞编队测高模式下两颗卫星的轨间距为2 km左右,进行粗略估计,此模式下相距2 km左右的海面因海况不同而造成的高度计测距值之差应小于7.5 mm的一半即3.75 mm;类似地,对于电离层延迟与海况偏差之外的其他误差项(差分序列标准差小于1.2 mm),在测量区域相距2 km左右时对高度计测距值之差的影响应小于0.6 mm。
综上,在相对定标的计算中,对于厘米级的期望定标精度,认为各误差改正项中海况偏差的影响需要进行考虑,而海况偏差之外各误差改正项的影响可忽略,在式(2)可将它们直接消去。因而,海面高相对偏差主要与两颗星的相对径向轨道误差、测距误差、海况偏差及两星下比较点间的水准面高差相关,双星串飞编队测高模式下海面高相对偏差计算式(2)可简化为
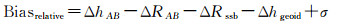 (7)
(7)
式中,σ表示由消去的误差项造成的误差,由海况偏差之外的7项误差项构成,误差估计为0.3 cm。
式(7)即双星串飞编队测高模式下高度计相对定标的计算式,该模式下,相对偏差的单次定标结果可以通过4项参数作差得到,而其他的误差改正项对相对偏差计算的影响不大。现有文献中也有类似求取相对偏差的方法,但这些文献中相对偏差的求取不是研究的重点,所采用方法也与上述方法不同。以Jason-2与Jason-1卫星搭载的高度计为例,文献[7-8]通过绝对定标的方法分别得到了两高度计的测量偏差,然后将所得到的测量偏差相减得到了两高度计之间测距值的相对偏差;文献[14]将两高度计分别对相同海面测得的SSH直接相减得到测距值的相对偏差。归纳起来,现有文献求取相对偏差的过程中都至少求取了两颗卫星分别测得的海面高,文献[7-8]的方法中另外引入了传统绝对定标方法中海面高参考基准SSHin situ的误差。在双星串飞编队测高模式下,两颗卫星前后相隔时间很短(仅约4 s)且地面轨迹距离很近(约2 km),许多求取海面高过程中的误差改正项几乎没有变化,因而在相对定标的过程中都可以直接忽略,从而在求解高度计测距相对偏差时简化了参与求解的参数项,且避免了各误差改正项求取中的模型误差,因此,通过式(7)求取高度计测量值的相对偏差具有更高的精度。
值得注意的是,由于Jason-2与Jason-1之间相隔时间约55 s,在近1 min时间内海况变化、大气环境变化使得两颗卫星测距值的误差改正项变化幅度增大(如Jason-1与T/P对相同星下点观测的湿对流层与电离层差值均值约1 cm,标准差也近1 cm[6]),因而用式(7)求取类似于Jason-2与Jason-1卫星高度计之间测距值相对偏差的适用性变差。
3.3 相对定标误差预估根据式(7),对相对定标结果进行误差预估。首先考虑式中各项单独的误差,然后通过误差传播定律来评估相对定标结果的整体精度。
式(7)中ΔhAB为两颗卫星的相对径向轨道差,其精度可参照TanDEM-X任务[31]中双星的相对定轨精度。TanDEM-X任务将2010年发射的TanDEM-X卫星与2007年发射的TerraSAR-X卫星组成星间距为2 km的紧密编队,构成双站合成孔径干涉测量手段,获取全球范围内的高分辨率、高精度DEM数据。在2011年1月实施的为期一个月的双频基线测试试验中,由德国地学研究中心(GFZ)等3家机构分别给出的相对定轨结果表明双星之间相对轨道精度达到或优于5 mm,相对径向轨道精度达到或优于3 mm[32],本文将0.5 cm作为两颗卫星的相对径向定轨精度。
Jason-2卫星搭载的Poseidon-3高度计1 s平均测距噪声的需求精度是1.7 cm,目标精度为1.5 cm,实际GDR产品中的噪声水平为1.8 cm[16, 33]。SARAL卫星搭载的AltiKa高度计1 s平均测距噪声的需求精度为1.5 cm (RMS,有效波高为2 m),目标精度为1 cm,实际数据处理结果表明AltiKa高度计1 s平均测距结果的噪声水平在有效波高为2 m时为1 cm (中值误差为0.9 cm)[30]。国内中科院微波遥感技术重点实验室已研制出合成孔径雷达高度计样机,并进行了机载校飞试验,其2 km分辨率的理论测距精度在有效波高为2 m时为1.45 cm[34]。根据卫星高度计未来的发展趋势(采用干涉雷达测量技术、Ka波段测量技术等),本文将1 cm设为单个高度计测距噪声,则根据误差传播定律,ΔRAB=RA-RB的精度可设为1 cm的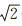
对于水准面高差(或瞬时海面高差)的确定,有两种可参考的方法:①通过高阶次的重力场位系数模型求取两星下点处的水准面高,进而得到水准面高差;或通过平均海面高模型(如DTU13),首先求取星下点海域的平均海面梯度,进而根据两星下点之间的相对位置求取海面高差。②通过在星下点布设两个或多个GNSS浮标[35-36]来求取瞬时海面高差,即在编队卫星通过定标场前后,通过两个布设在星下点海域的GNSS浮标直接求取两点之间的瞬时海面高差(利用短基线之间的较高相对精度),或通过在星下点海域布设多个GNSS浮标,通过内插的方法分别推估得到两星下点之间的瞬时海面高[36],作差得瞬时海面高差。这两种方法虽没有直接的精度评估结果,但可以期望的是,在水准面变化相对平缓的离岸(约20 km左右)定标场海域,可以获取精度优于1 cm的水准面高差或瞬时海面高差。
根据图 4,海况偏差1 s差分序列的标准差约0.8 cm,所反映的是相距约5.8 km海面对高度计脉冲信号反射的平均差异,根据该值,将海况偏差改正差值的精度设为0.8 cm。
将以上各项误差以表格列出见表 1。通过误差传播定律,可得两颗卫星测得海面高相对偏差的精度σbias估计为
| cm | |
| 误差项 | 精度 |
| 轨道误差σΔhAB | 0.5 |
| 测距误差σΔRAB | 1.41 |
| 海况偏差σΔRssb | 0.8 |
| 水准面高差σΔhgeoid | 1.0 |
| 其他误差σ | 0.3 |
| 相对偏差σbias | 1.99 |
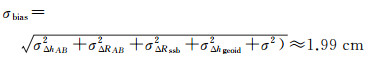 (8)
(8)
在卫星测高应用中,高度计定标是任务实施的基础与前提,传统单颗测高卫星采用绝对定标方法得到高度计的测量偏差。对于本文所讨论的特殊双星串飞编队测高模式,绝对定标对于监测测高系统的状态与性能仍然具有重要作用,然而对于该种以高精度、高分辨率地球重力场反演为主要目标的测高模式,绝对定标方法不能精确确定两颗高度计测量值之间的相对偏差,而该相对偏差是影响重力场反演精度的重要参数。本文以精确求定该相对偏差为目标,研究了双星串飞编队测高模式下高度计的相对定标方法。
提出了通过海面高作差求取相对偏差的卫星高度计相对定标方法,介绍了该方法的基本原理,进而采用Jason-2卫星的实测数据分析了海面高求取过程各误差改正项的功率谱特性以及1 s差分序列的统计特性,针对电离层延迟改正项的特殊性重新评估了它对相对偏差求解的影响,确定了相对偏差的计算式并对相对偏差的求解误差进行了预估,得出的主要结论包括:
(1)对试验数据的功率谱分析表明,计算海面高过程中的各误差改正项均呈现出低频特性;差分序列的统计结果表明,电离层延迟与海况偏差之外的6项误差改正项的1 s差分序列标准差均小于1.2 mm,以厘米级定标精度为前提时可忽略其影响。
(2) GDR文件中电离层延迟包含了海况偏差等因素引入的误差,所反映出的电离层延迟变化幅度大于其真实变化情况,中纬地区相距2 km、相隔4 s的条件下VTEC变化量小于1.15 TECu,在相对偏差计算中电离层延迟之差应可忽略。
(3)以厘米级定标精度为目标,简化推导了高度计相对偏差的计算式,认为相对偏差主要与两颗卫星的相对径向轨道误差、测距误差、海况偏差及两星下比较点间的水准面高差相关。
(4)以在轨海洋测高卫星的性能为参考,结合未来测高系统及相关领域技术的发展,预估得到双星串飞编队测高模式下高度计测距值相对偏差的单次定标精度约为1.99 cm。
| [1] | 鲍李峰, 许厚泽. 双星伴飞卫星测高模式及其轨道设计[J]. 测绘学报, 2014, 43(7): 661–667. BAO Lifeng, XU Houze. Twin-satellites Altimetry Mode and Its Orbit Design[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 661–667. DOI:10.13485/j.cnki.11-2089.2014.0109 |
| [2] | 李建成, 金涛勇. 卫星测高技术及应用若干进展[J]. 测绘地理信息, 2013, 38(4): 1–8. LI Jiancheng, JIN Taoyong. On the Main Progress of Satellite Altimetry and Its Applications[J]. Journal of Geomatics, 2013, 38(4): 1–8. |
| [3] | BENVENISTE J. Radar Altimetry:Past, Present and Future[M]//VIGNUDELLI S, KOSTIANOY A G, CIPOLLINI P, et al. Coastal Altimetry. Berlin Heidelberg:Springer, 2011:1-17. |
| [4] | PITZ I, OTTO A, SCHMIDT M. Ocean Surface Topography Constellation:The Next 15 Years in Satellite altimetry[J]. Kybernetika Praha, 2012, 2(2): 490–493. |
| [5] | BAO Lifeng, XU Houze, LI Zhicai. Towards a 1 mGal Accuracy and 1 Min Resolution Altimetry Gravity Field[J]. Journal of Geodesy, 2013, 87(10-12): 961–969. DOI:10.1007/s00190-013-0660-1 |
| [6] | BONNEFOND P, EXERTIER P, LAURAIN O, et al. Absolute Calibration of Jason-1 and TOPEX/Poseidon Altimeters in Corsica[J]. Marine Geodesy, 2003, 26(3-4): 261–284. |
| [7] | BONNEFOND P, EXERTIER P, LAURAIN O, et al. Absolute Calibration of Jason-1 and Jason-2 Altimeters in Corsica during the Formation Flight Phase[J]. Marine Geodesy, 2010, 33(S1): 80–90. |
| [8] | HAINES B J, DESAI S D, BORN G H. The Harvest Experiment:Calibration of the Climate Data Record from TOPEX/Poseidon, Jason-1 and the Ocean Surface Topography Mission[J]. Marine Geodesy, 2010, 33(S1): 91–113. |
| [9] | BONNEFOND P, HAINES B J, WATSON C. In Situ Absolute Calibration and Validation:A Link from Open-Ocean to Coastal Altimetry[M]//VIGNUDELLI S, KOSTIANOY A G, CIPOLLINI P, et al. Coastal Altimetry. Berlin Heidelberg:Springer, 2011:259-296. |
| [10] | WAN Junzhi, GUO Wei, ZHAO Fei, et al. HY-2A Altimeter Time Tag Bias Estimation Using Reconstructive Transponder[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(7): 1431–1435. DOI:10.1109/LGRS.2015.2406535 |
| [11] | DETTMERING D, BOSCH W. Global Calibration of Jason-2 by Multi-mission Crossover Analysis[J]. Marine Geodesy, 2010, 33(S1): 150–161. |
| [12] | BOSCH W, DETTMERING D, SCHWATKE C. Multi-mission Cross-calibration of Satellite Altimeters:Constructing a Long-term Data Record for Global and Regional Sea Level Change Studies[J]. Remote Sensing, 2014, 6(3): 2255–2281. DOI:10.3390/rs6032255 |
| [13] | ABLAIN M, PHILIPPS S, PICOT N, et al. Jason-2 Global Statistical Assessment and Cross-calibration with Jason-1[J]. Marine Geodesy, 2010, 33(S1): 162–185. |
| [14] | WATSON C, WHITE N, CHURCH J, et al. Absolute Calibration in Bass Strait, Australia:TOPEX, Jason-1 and OSTM/Jason-2[J]. Marine Geodesy, 2011, 34(3-4): 242–260. DOI:10.1080/01490419.2011.584834 |
| [15] | WATSON C S. Satellite Altimeter Calibration and Validation Using GPS Buoy Technology[D]. Tasmania:University of Tasmania, 2005. |
| [16] | DUMONT J P, ROSMORDUC V, PICOT N, et al. OSTM/Jason-2 Products Handbook (Issue:1 rev 8)[M].[S.l.]:NCAA/NESDIS, 2011. |
| [17] | WATSON C, WHITE N, COLEMAN R, et al. TOPEX/Poseidon and Jason-1:Absolute Calibration in Bass Strait, Australia[J]. Marine Geodesy, 2004, 27(1-2): 107–131. DOI:10.1080/01490410490465373 |
| [18] | NEREM R S, CHAMBERS D P, CHOE C, et al. Estimating Mean Sea Level Change from the TOPEX and Jason Altimeter Missions[J]. Marine Geodesy, 2010, 33(S1): 435–446. |
| [19] | LEULIETTE E W, SCHARROO R. Integrating Jason-2 into a Multiple-Altimeter Climate Data Record[J]. Marine Geodesy, 2010, 33(S1): 504–517. |
| [20] | WELCH P. The Use of Fast Fourier Transform for the Estimation of Power Spectra:A Method Based on Time Averaging over Short, Modified Periodograms[J]. IEEE Transactions on Audio and Electroacoustics, 1967, 15: 70–73. DOI:10.1109/TAU.1967.1161901 |
| [21] | ROUSSEEUW P J, CROUX C. Alternatives to the Median Absolute Deviation[J]. Journal of the American Statistical Association, 1993, 88(424): 1273–1283. DOI:10.1080/01621459.1993.10476408 |
| [22] | YANG Y, CHENG M K, SHUM C K, et al. Robust Estimation of Systematic Errors of Satellite Laser Range[J]. Journal of Geodesy, 1999, 73(7): 345–349. DOI:10.1007/s001900050252 |
| [23] | SMITH W H F. Resolution of Seamount Geoid Anomalies Achieved by the SARAL/AltiKa and Envisat RA2 Satellite Radar Altimeters[J]. Marine Geodesy, 2015, 38(S1): 644–671. |
| [24] | WANNINGER L. The Occurrence of Ionospheric Disturbances above Japan and Their Effects on Precise GPS Positioning[C]//Proceedings of the CRCM 93. Kobe:[s.n.], 1993. |
| [25] | PI X, MANNUCCI A J, LINDQWISTER U J, et al. Monitoring of Global Ionospheric Irregularities Using the Worldwide GPS Network[J]. Geophysical Research Letters, 1997, 24(18): 2283–2286. DOI:10.1029/97GL02273 |
| [26] | TANNA H J, PATHAK K N. Longitude Dependent Response of the GPS Derived Ionospheric ROTI to Geomagnetic Storms[J]. Astrophysics and Space Science, 2014, 352(2): 373–384. DOI:10.1007/s10509-014-1938-3 |
| [27] | IMEL D A. Evaluation of the TOPEX/POSEIDON Dual-frequency Ionosphere Correction[J]. Journal of Geophysical Research, 1994, 99(C12): 24895–24906. DOI:10.1029/94JC01869 |
| [28] | DECARVALHO R, HAINES B J, DESAI S D. Sensitivity Analysis Techniques Applied to Jason-1 and Jason-2/OSTM Cross Calibration[J]. Marine Geodesy, 2011, 34(3-4): 364–381. DOI:10.1080/01490419.2011.584836 |
| [29] | VERRON J, SENGENES P, LAMBIN J, et al. The SARAL/AltiKa Altimetry Satellite Mission[J]. Marine Geodesy, 2015, 38(S1): 2–21. |
| [30] | STEUNOU N, DESJONQUÈRES J D, PICOT N, et al. AltiKa Altimeter:Instrument Description and In Flight Performance[J]. Marine Geodesy, 2015, 38(S1): 22–42. |
| [31] | 杜亚男, 冯光财, 李志伟, 等. TerraSAR-X/TanDEM-X获取高精度数字高程模型技术研究[J]. 地球物理学报, 2015, 58(9): 3089–3102. DU Yanan, FENG Guangcai, LI Zhiwei, et al. Generation of High Precision DEM from TerraSAR-X/TanDEM-X[J]. Chinese Journal of Geophysics, 2015, 58(9): 3089–3102. |
| [32] | JAGGI A, MONTENBRUCK O, MOON Y, et al. Inter-agency Comparison of TanDEM-X Baseline Solutions[J]. Advances in Space Research, 2012, 50(2): 260–271. DOI:10.1016/j.asr.2012.03.027 |
| [33] | LAMBIN J, MORROW R, FU L L, et al. The OSTM/Jason-2 Mission[J]. Marine Geodesy, 2010, 33(S1): 4–25. |
| [34] | 王磊.高精度卫星雷达高度计数据处理技术研究[D].北京:中国科学院大学, 2015. WANG Lei. Study on the Data Processing for High Precision Satellite Radar Altimeter[D]. Beijing:University of Chinese Academy of Sciences, 2015. |
| [35] | WATSON C, COLEMAN R, HANDSWORTH R. Coastal Tide Gauge Calibration:A Case Study at Macquarie Island Using GPS Buoy Techniques[J]. Journal of Coastal Research, 2008, 24(4): 1071–1079. |
| [36] | FRAPPART F, ROUSSEL N, BIANCALE R, et al. The 2013 Ibiza Calibration Campaign of Jason-2 and SARAL Altimeters[J]. Marine Geodesy, 2015, 38(S1): 219–232. |


