目前,非差精密单点定位技术(precise point positioning, PPP)[1]得到了广泛的应用[2-3],然而未校准硬件延迟(uncalibrated phase delays, UPD)的小数部分(fractional cycle bias, FCB)破坏了非差模糊度的整数特性,导致非差模糊度无法直接固定,非差的各类估值均为模糊度浮点解。若能有效利用非差模糊度的整数特性,PPP的待估参数精度和收敛特性将有进一步改善的空间[4-11]。采用区域或全球范围内的GNSS观测网,通过有效的估计或分离方法,将FCB与模糊度分离,恢复非差模糊度的整数特性,搜索并固定模糊度,是近年来GNSS领域的研究热点之一[12-13]。
FCB分为接收机端和卫星端两部分,接收机端FCB随时间变化较大,一般在服务端采取星间单差的方法消除接收机端FCB的影响,然后将卫星端无电离层组合FCB分解为宽巷FCB和窄巷FCB,分别进行估计[4]。其中,宽巷FCB采用与几何距离无关的MW组合[14-15]进行估计,MW组合波长(86.2 cm)较长,因此卫星端宽巷FCB具有较好的稳定性,使用不少于90个历元(45 min)的数据进行平滑后,宽巷FCB可收敛到0.1周以内,并且精度保持稳定[16],因此每天估计一组卫星端宽巷FCB即可满足非差宽巷模糊度固定的要求。窄巷FCB估计时,首先对当前历元的每个参考站,利用无电离组合浮点模糊度和固定后的整数宽巷模糊度计算窄巷模糊度,估计其小数部分,即确定当前历元该参考站的窄巷FCB估值;其次对当前历元所有参考站的窄巷FCB估值取平均,得到该历元的窄巷FCB[4, 7, 9-10]。无电离组合浮点模糊度收敛后,各个参考站计算的窄巷FCB估值稳定性较好。然而受观测数据质量和未精化模型误差的影响,参考站之间窄巷FCB估值的互差较大,直接取平均会造成一天内窄巷FCB的时间序列稳定性较差。目前主要采用分段函数的方式,每10~15 min[4, 9]或每个连续观测弧段(大约2 h)[7]估计出一组该时段内有效的窄巷FCB。
本文改进了窄巷FCB估计的策略,该策略取当前历元所有参考站窄巷FCB估值的中位数作为抗差初值,采用IGGⅢ方案降低有偏差的窄巷FCB估值的权比,提高了窄巷FCB的精度和稳定性。试验利用IGS (International GNSS Service)全球网的数据,分析了抗差估计方法估计的窄巷FCB的时变特性,并对估计的窄巷FCB进行了窄巷模糊度残差分析、用户端静态小时解和仿动态单天解的精度验证。
1 基于星间单差的卫星端窄巷FCB估计 1.1 星间单差宽巷FCB估计对卫星s1(参考星)和s2,参考站r1,星间单差宽巷模糊度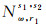
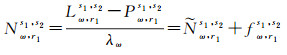 (1)
(1)
式中,Lω=(f1L1-f2L2)/(f1-f2);Pω=(f1P1+f2P2)/(f1+f2);f1和f2代表载波频率;L1和L2代表载波观测值;P1和P2代表伪距观测值;λω=86.2 cm;Nω为实数宽巷模糊度;
受伪距精度和观测噪声的影响,MW值抖动较大,对无周跳发生的弧段内的数据进行平滑[16],平滑方式有直接取平均[16]和加权平均[4]两种。
采用直接取平均的方法,平滑后的星间单差宽巷模糊度及标准差为
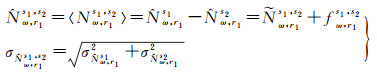 (2)
(2)
式中,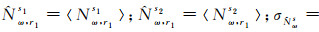
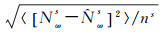
采用加权平均的方法时,按卫星高度角E定权,定权公式为
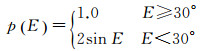 (3)
(3)
对服务端所有参考站计算的星间单差宽巷FCB估值求平均,得到星间单差宽巷FCB及标准差
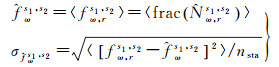 (4)
(4)
式中,frac (·)为小数部分求取函数;nsta为参考站个数。
1.2 星间单差窄巷FCB估计窄巷FCB估计前,首先需要固定每个参考站的宽巷模糊度,按式(5)计算宽巷模糊度的固定率[4]
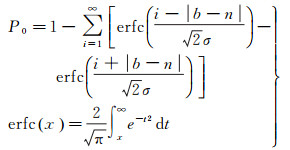 (5)
(5)
式中,b和n分别是改正了宽巷FCB的宽巷模糊度及其最近的整数;σ是其标准差。当P0≤α时,将模糊度固定为其最近的整数,否则保持模糊度的浮点解。一般情况下,取α=0.001。
其次,按照传统PPP无电离层组合模型,逐历元解算无电离层组合浮点模糊度,为增强方程的强度,加快无电离层组合模糊度参数与对流层参数、接收机钟差的分离,即加快浮点模糊度收敛,通常将参考站的坐标固定为已知值,已知值可选非差浮点解[7, 11]或静态网解结果[17]。
对参考站r1,卫星s1和s2,宽巷模糊度固定后为整数
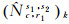
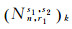
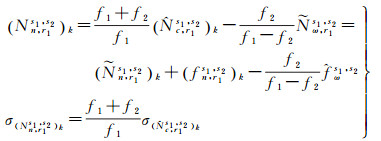 (6)
(6)
式(6)求得的窄巷模糊度含有宽巷UPD整数部分的影响,也未改正宽巷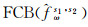
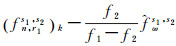
对第k个历元服务端所有参考站计算的星间单差窄巷FCB估值求平均,得到第k个历元星间单差窄巷FCB及标准差
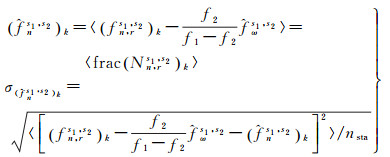 (7)
(7)
首先,分析上述星间单差窄巷FCB估计算法(以下称直接取平均方法)估计的窄巷FCB的稳定性。选择2013年1月1日全球IGS跟踪站网的数据,G01号卫星作为参考星,参考站坐标固定为非差单天解。采用已有算法,以G08、G19、G20、G32为例,服务端估计的窄巷FCB随时间的变化如图 1所示,图中不同颜色的实线代表不同参考站计算的窄巷FCB估值。

|
| 图 1 星间单差窄巷FCB估值时间序列 Fig. 1 Time series of single-difference narrow-lane FCB |
从图 1中可以看出,非差无电离层组合模糊度收敛后,各个参考站求得的窄巷FCB估值稳定性较好,但由于窄巷的波长相对较短,受观测数据质量和未模型化误差的影响较大,参考站之间窄巷FCB估值的互差较大,最大超过了0.3周。采用直接取平均法估计当前历元的窄巷FCB,窄巷FCB估值出现较大偏差的参考站会严重影响窄巷FCB的精度和稳定性。
针对当前历元星间单差窄巷FCB估值出现较大偏差的参考站,引入抗差估计[18-25]的理论,取当前历元所有参考站求得的窄巷FCB估值的中位数作为抗差初值,采用IGGⅢ方案,降低有偏差的参考站的窄巷FCB估值的权比。
对卫星s1和s2,服务端估计第k个历元的星间单差窄巷FCB的误差方程为
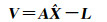 (8)
(8)
式中,A=[1 1 … 1]T;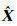
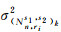
基于抗差初值的抗差估计分两个阶段,第1阶段为第1步,基于中位数初值计算抗差解:
(1)取历元k全部参考站星间单差窄巷FCB估值的中位数
 (9)
(9)
式中,median (·)为中位数算子。
(2)求历元k各个参考站星间单差窄巷FCB估值与中位数之差,即初始残差
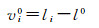 (10)
(10)
(3)计算均方差因子估值
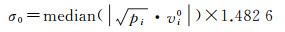 (11)
(11)
(4)采用IGGⅢ方案计算等价权因子及等价权
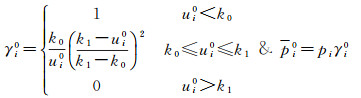 (12)
(12)
式中,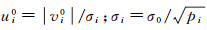
(5)计算历元k窄巷FCB的抗差解及残差
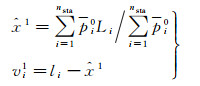 (13)
(13)
第2阶段为第2次迭代至迭代终止,第m次迭代的计算流程为:
(1)按式(11)更新均方差因子估值σ0m。
(2)按式(12)计算等价权因子,更新等价权,按式(13)迭代计算抗差解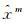
(3)如果两次计算的窄巷FCB改正数之差绝对值均小于限差(eps),则计算结束,输出结果;否则继续迭代。
精度估计时,单位权中误差μ的计算公式为
 (14)
(14)
式中,n′为淘汰的参考站的窄巷FCB估值个数,即pi=0。
3 试验分析试验采用2012年12月30日-2013年1月5日(GPS周1721周)、IGS全球网的观测数据,采样间隔为30 s,服务端估计宽巷、窄巷FCB时,选择全球分布的200个跟踪站,将G01作为参考星,非差解算时的参数设置如表 1所示。经过多次试算,本文取k0=1.2,k1=5.0,迭代终止的限差eps=0.005周。
| 类型 | 处理方法 | |
| 观测模型 | 观测值 | 无电离层组合,消除电离层低阶项影响 |
| 数据定权 | 高度角定权,截止角:10° | |
| 钟跳、周跳探测 | 历元间差分、TurboEdit算法(不修复) | |
| 卫星轨道及钟差 | IGS 15 min精密轨道+30 s精密钟差 | |
| 天线相位中心改正 | igs08.atx模型 | |
| 潮汐改正 | 固体潮、极潮改正(IERS2010)、海潮改正(FES2004) | |
| 相对论效应 | 卫星钟相对论、引力延迟、地球自转效应 | |
| 对流层延迟 | VMF1格网模型内插 | |
| 参数估计 | 位置参数、模糊度参数 | 每个历元估计一次 |
| 接收机钟差 | 采用白噪声过程建模,每个历元估计一次 | |
| 对流层延迟 | 采用随机游走过程建模,每个历元估计一次 |
3.1 宽巷FCB时变特性分析
为减弱伪距噪声的影响,剔除连续观测时间少于20 min和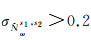
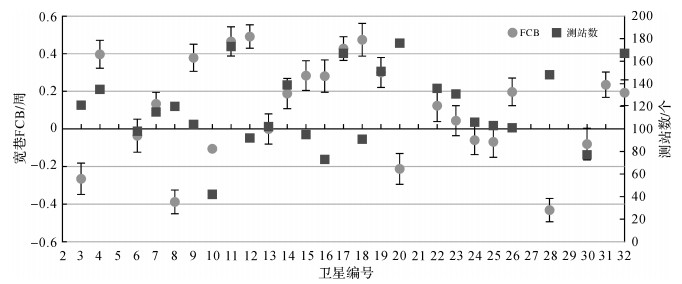
|
| 图 2 2013年1月1日星间单差宽巷FCB及标准差 Fig. 2 Single-difference wide-lane FCB and standard error of Jan 1st, 2013 |
1721周的宽巷FCB如图 3所示,星间单差宽巷FCB是一个很稳定的时间序列,连续一周的变化范围小于0.05周,这与文献[4]得出的结论是一致的。
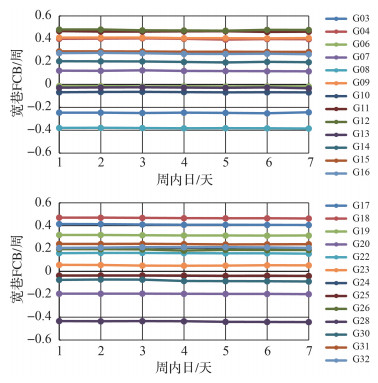
|
| 图 3 1721周星间单差宽巷FCB Fig. 3 Single-difference wide-lane FCB of GPS 1721 week |
3.2 窄巷FCB时变特性分析 3.2.1 窄巷FCB单天序列对比分析
无电离层组合模糊度求解时,将参考站的坐标固定为非差单天解。2013年1月1日,抗差估计方法估计的26颗卫星每个历元的窄巷FCB如图 4所示,横坐标为当天2850个历元(从23:45分后的30个历元没有精密星历和钟差,故不参与计算)。从图 4中可以看出,每颗卫星的星间单差窄巷FCB不为0,不同卫星对的窄巷FCB在一天内的变化幅度(最大值与最小值的差值)不同,G11、G12、G13和G30相对参考星G01的窄巷FCB的稳定性较好,单天变化幅度小于0.04周;G04、G08、G15、G17、G19和G28相对参考星G01的窄巷FCB的稳定性稍差,单天变化幅度大于0.08周,但所有卫星的变化幅度均小于0.1周;所有卫星窄巷FCB变化幅度的均值为0.065周,窄巷FCB时间序列的稳定性较强。
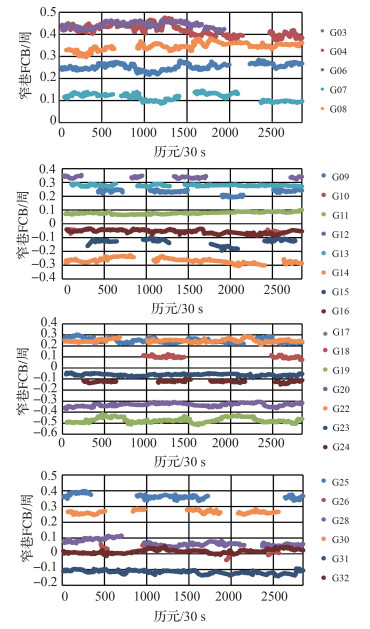
|
| 图 4 抗差估计方法估计的2013年1月1日星间单差窄巷FCB时间序列 Fig. 4 Single-difference narrow-lane FCB of Jan 1st, 2013 based on robust estimation |
抗差估计方法估计的每颗卫星的窄巷FCB及其极限误差(3倍中误差)如图 5所示,不同卫星的极限误差差异较大,但所有卫星极限误差的最大值不超过0.08周,均值为0.050周。

|
| 图 5 抗差估计方法估计的2013年1月1日星间单差窄巷FCB及其极限误差 Fig. 5 Single-difference narrow-lane FCB and its limiting error of Jan 1st, 2013 based on robust estimation |
为了对比直接取平均方法和抗差估计方法估计的窄巷FCB的差异,以G08、G09、G19、G20、G23和G32为例,2013年1月1日,两种方法估计的窄巷FCB的差值如图 6所示。从图中可以看出,两种方法估计的窄巷FCB的差值最大达到了0.1周。
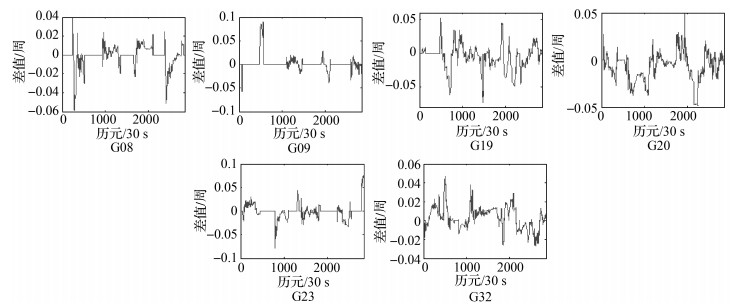
|
| 图 6 直接取平均方法与抗差估计方法估计的窄巷FCB差值 Fig. 6 Differences of narrow-lane FCB between the method of mean and robust estimation |
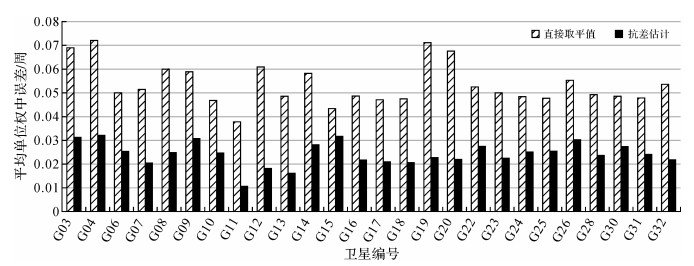
分别计算两种方法估计的窄巷FCB的平均单位权中误差,结果如图 7所示。平均单位权中误差是指先计算每个历元窄巷FCB的单位权中误差,再取所有历元单位权中误差的均值。从图 7可以看出,针对部分参考站计算的窄巷FCB估值存在较大的偏差,通过中位数法选取可靠的抗差初值,并采用IGGⅢ方案降低偏差较大的窄巷FCB估值的权比,每颗卫星窄巷FCB的平均单位权中误差大大降低,所有卫星窄巷FCB的平均单位权中误差平均降低了54.6%。
|
| 图 7 窄巷FCB平均单位权中误差 Fig. 7 Average mean square error of unit weight of narrow-lane FCB |
3.2.2 窄巷FCB多天序列对比分析
计算1721周连续7 d的窄巷FCB,两种方法估计的星间单差窄巷FCB的稳定性对比见表 2。通过中位数初值辅以IGGⅢ方案迭代解算的混合算法,降低了偏差较大的参考站的窄巷FCB估值的影响,有效地剔除了异常干扰,窄巷FCB每天变化幅度的最大值和均值、极限误差的最大值和均值都比直接取平均方法分别降低了0.12、0.066、0.07和0.043周,降低幅度分别达到54.6%、52.4%、46.7%和48.9%。
| 参数 | 窄巷FCB估值性质/周 | |||
| 变化幅度的 最大值 |
变化幅度 的均值 |
极限误差 最大值 |
极限误差 均值 |
|
| 直接取平均 | 0.22 | 0.126 | 0.15 | 0.088 |
| 抗差估计 | 0.10 | 0.060 | 0.08 | 0.045 |
由表 2可知,通过采用基于抗差初值的窄巷FCB抗差估计方法,卫星端窄巷FCB时间序列的稳定性大大提高。为进一步分析采用分段函数形式表示窄巷FCB时的分段间隔设置问题,本文与最早提出采用分段函数估计窄巷FCB,根据经验和用户端试验验证每10~15 min估计一组窄巷FCB的文献[4]以及采用更为精化的非差解算误差改正模型,每个连续观测弧段(大约2 h)估计一组窄巷FCB的文献[7]进行了详细的对比,结果见表 3。
(1)与文献[4]相比,文献[7]采用IGS08天线模型,每个历元估计一次对流层天顶湿延迟,误差改正模型更为精化,区域网每个连续时段内大多数卫星端窄巷FCB的极限误差小于0.1周,因此每个连续观测弧段(大约2 h)估计出一组窄巷FCB。
(2)与文献[7]相比,本文采用了基于抗差初值的窄巷FCB抗差估计方法,保证了窄巷FCB估值的抗差性,获得了具有较高精度、稳定性较强的窄巷FCB,窄巷FCB极限误差的最大值低于文献[7],因此本文取每颗卫星所有历元窄巷FCB的均值作为该卫星当天的窄巷FCB,即采用分段函数的形式表示窄巷FCB时,将间隔设置为24 h。
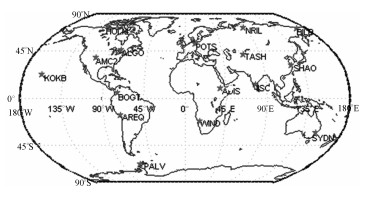
3.3 用户端验证为了验证上述计算的卫星端宽巷和窄巷FCB的准确性(图 8),采用1721周全球分布的16个跟踪站作为用户端,数据采样间隔为30 s。
|
| 图 8 16个全球分布的用户站 Fig. 8 Sixteen globally-distributed user stations |
3.3.1 窄巷模糊度残差分析
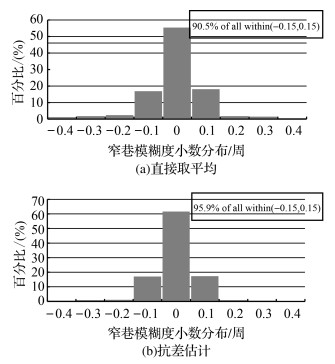
在服务端提供高精度FCB的条件下,用户端收敛后的窄巷模糊度改正窄巷FCB后,理论上应接近整数值。分别采用直接取平均方法和抗差估计方法估计的窄巷FCB改正实数窄巷模糊度,对其小数部分进行统计分析,图 9给出了窄巷模糊小数部分的频率分布,从中可以得出,与采用直接取平均方法估计的窄巷FCB相比,采用抗差估计方法估计的窄巷FCB改正实数窄巷模糊度后,窄巷模糊度的残差落在0.15周以内的频率提高了5.4%。
|
| 图 9 窄巷模糊度小数部分频率分布 Fig. 9 Distribution of narrow-lane ambiguity fraction part |
3.3.2 静态小时解分析
将16个跟踪站的原始观测文件分割成7×24段1 h长度的数据,按表 1的参数设置计算固定解。用户端利用FCB固定模糊度时,按式(5)固定宽巷模糊度,取整成功率设为0.999;采用LAMBDA算法[27]固定窄巷模糊度,Ratio阈值设为3.0。宽、窄巷模糊度固定成功后反求出无电离层组合模糊度,将其代入观测方程进行约束,进而获得固定解。
将每小时的解算结果与IGS日解坐标值作差得到偏差,再将每个测站所有时段的偏差绝对值取平均,作为该站的统计结果偏差。表 4给出了浮点解和固定解1 h的静态定位精度。
| cm | |||||||||
| 测站 | 模糊度浮点解 | 模糊度固定解 | |||||||
| U | E | N | 三维位置偏差 | U | E | N | 三维位置偏差 | ||
| ADIS | 3.16 | 3.44 | 0.88 | 4.75 | 1.50 | 0.80 | 0.21 | 1.71 | |
| ALGO | 2.24 | 2.95 | 1.13 | 3.87 | 0.97 | 0.69 | 0.31 | 1.23 | |
| AMC2 | 2.75 | 2.84 | 1.29 | 4.16 | 1.52 | 1.01 | 0.97 | 2.07 | |
| AREQ | 1.76 | 2.63 | 0.77 | 3.26 | 1.60 | 1.10 | 0.96 | 2.17 | |
| BILB | 2.71 | 2.61 | 1.24 | 3.96 | 1.68 | 0.48 | 0.55 | 1.83 | |
| BOGT | 3.67 | 3.95 | 0.95 | 5.47 | 1.10 | 0.80 | 0.61 | 1.49 | |
| HOLM | 1.87 | 2.74 | 1.48 | 3.63 | 1.41 | 0.70 | 0.60 | 1.68 | |
| IISC | 2.23 | 2.65 | 0.78 | 3.55 | 0.70 | 0.81 | 0.56 | 1.21 | |
| KOKB | 2.77 | 3.77 | 0.92 | 4.77 | 0.78 | 0.33 | 0.68 | 1.09 | |
| NRIL | 1.62 | 2.57 | 0.87 | 3.16 | 0.60 | 0.71 | 0.46 | 1.03 | |
| PALV | 2.02 | 2.97 | 0.66 | 3.65 | 1.70 | 1.07 | 1.03 | 2.26 | |
| POTS | 1.75 | 2.89 | 0.77 | 3.47 | 1.35 | 0.71 | 0.32 | 1.56 | |
| SHAO | 2.48 | 4.06 | 1.39 | 4.96 | 1.64 | 0.88 | 1.07 | 2.15 | |
| SYDN | 3.57 | 3.91 | 1.42 | 5.48 | 1.21 | 0.85 | 0.65 | 1.62 | |
| TASH | 2.71 | 3.54 | 0.89 | 4.55 | 1.47 | 0.69 | 0.57 | 1.72 | |
| WIND | 3.59 | 4.17 | 0.97 | 5.59 | 1.26 | 0.44 | 0.34 | 1.38 | |
| 平均值 | 2.56 | 3.23 | 1.03 | 4.27 | 1.28 | 0.75 | 0.62 | 1.64 | |
分析表中静态小时解的精度可知,利用每天发布的一组卫星端的宽巷和窄巷FCB,16个跟踪站U、E、N 3个方向的定位精度分别提高了49.9%、76.6%、39.7%,E方向的精度改善最为明显。非差模糊度固定后,载波相位观测值成为类似于伪距的绝对观测值,但测距精度高达毫米级,减少了待估参数的维度,加快了位置参数的分离,显著提高了短时间的定位精度。
3.3.3 仿动态单天解分析为了对比直接取平均方法和本文抗差估计方法估计的窄巷FCB,对16个跟踪站的原始观测数据进行仿动态解算,将坐标当成方差为10 000 m2的白噪声进行估计,坐标真值为IGS日解坐标值。表 5统计了两种方法估计的窄巷FCB对应的定位结果和窄巷模糊度固定率。
| 测站 | 模糊度固定解(直接取平均) | 模糊度固定解(抗差估计) | |||||||
| U/cm | E/cm | N/cm | 固定率/(%) | U/cm | E/cm | N/cm | 固定率/(%) | ||
| ADIS | 3.48 | 2.56 | 1.58 | 80.65 | 3.18 | 2.05 | 1.25 | 86.27 | |
| ALGO | 3.89 | 2.46 | 2.09 | 80.14 | 3.56 | 2.13 | 1.72 | 83.54 | |
| AMC2 | 3.45 | 1.56 | 1.59 | 73.08 | 3.08 | 1.05 | 1.28 | 80.39 | |
| AREQ | 4.56 | 2.64 | 2.33 | 75.25 | 4.01 | 1.87 | 2.03 | 81.67 | |
| BILB | 4.19 | 2.99 | 1.96 | 64.14 | 3.18 | 1.75 | 1.56 | 79.91 | |
| BOGT | 4.59 | 1.59 | 2.51 | 66.24 | 4.09 | 1.05 | 2.51 | 71.94 | |
| HOLM | 2.69 | 1.66 | 1.59 | 80.01 | 2.15 | 0.91 | 0.97 | 90.08 | |
| IISC | 3.69 | 2.19 | 0.96 | 71.60 | 3.01 | 1.98 | 1.63 | 79.14 | |
| KOKB | 2.97 | 2.58 | 2.19 | 71.19 | 2.49 | 2.04 | 1.86 | 80.64 | |
| NRIL | 3.46 | 1.99 | 1.26 | 74.05 | 3.16 | 1.23 | 0.98 | 81.59 | |
| PALV | 2.16 | 2.39 | 1.53 | 80.39 | 1.99 | 1.71 | 1.08 | 86.12 | |
| POTS | 2.33 | 1.95 | 3.07 | 76.40 | 2.09 | 1.11 | 2.18 | 83.08 | |
| SHAO | 4.76 | 2.46 | 3.69 | 70.29 | 3.95 | 1.59 | 2.73 | 79.69 | |
| SYDN | 4.59 | 2.79 | 2.84 | 69.14 | 3.87 | 2.03 | 2.14 | 77.60 | |
| TASH | 3.99 | 1.79 | 1.76 | 67.41 | 3.45 | 1.00 | 1.05 | 79.96 | |
| WIND | 3.28 | 2.28 | 1.55 | 78.30 | 2.43 | 1.49 | 1.02 | 91.43 | |
| 平均值 | 3.63 | 2.24 | 2.03 | 73.64 | 3.11 | 1.56 | 1.62 | 82.07 | |
从表 5中可以得出,采用抗差估计方法估计窄巷FCB,窄巷FCB的精度和稳定性得到提高,用户端仿动态解算采用LAMBDA算法固定窄巷模糊度时,平均窄巷模糊度固定率从73.64%提高到82.07%;U、E、N 3个方向的平均定位偏差分别减少了0.52 cm、0.68 cm和0.41 cm。
4 结论本文论述了基于星间单差的窄巷FCB估计方法,针对窄巷FCB估值出现较大偏差的参考站,提出了基于抗差初值的窄巷FCB抗差估计方法,该方法取当前历元所有参考站窄巷FCB估值的中位数作为抗差初值,采用IGGⅢ方案降低了有偏差的窄巷FCB估值的影响,试验采用IGS全球网1721周的观测数据,得出:
(1)与直接取平均方法相比,抗差估计方法估计的窄巷FCB 24 h内变化幅度的最大值和均值、极限误差的最大值和均值降低了0.12、0.066、0.07和0.043周,卫星端窄巷FCB的精度和稳定性得到提高;与文献[4]和文献[7]相比,采用分段函数的形式表示窄巷FCB时,可将分段间隔设置为24 h,即每天估计一组卫星端的窄巷FCB就可满足非差窄巷模糊度固定的要求。
(2)与采用直接取平均方法估计的窄巷FCB改正实数窄巷模糊度相比,采用抗差估计方法估计的窄巷FCB改正实数窄巷模糊度后,窄巷模糊度的残差落在0.15周以内的频率更高。
(3)采用本文估计的一组卫星端的窄巷FCB,用户端U、E、N 3个方向的仿动态模糊度固定单天解平均偏差分别减少了0.52 cm、0.68 cm和0.41 cm,平均窄巷模糊度固定率提高了8.43%。
| [1] | ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005–5017. DOI:10.1029/96JB03860 |
| [2] | 袁修孝, 付建红, 楼益栋. 基于精密单点定位技术的GPS辅助空中三角测量[J]. 测绘学报, 2007, 36(3): 251–255. YUAN Xiuxiao, FU Jianhong, LOU Yidong. GPS-supported Aerotriangulation Based on GPS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 251–255. |
| [3] | 张宝成, 欧吉坤, 袁运斌, 等. 基于GPS双频原始观测值的精密单点定位算法及应用[J]. 测绘学报, 2010, 39(5): 478–483. ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Precise Point Positioning Algorithm Based on Original Dual-frequency GPS Code and Carrier-phase Observations and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 478–483. |
| [4] | GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389–399. DOI:10.1007/s00190-007-0187-4 |
| [5] | BERTIGER W, DESAI S D, HAINES B, et al. Single Receiver Phase Ambiguity Resolution with GPS Data[J]. Journal of Geodesy, 2010, 84(5): 327–337. DOI:10.1007/s00190-010-0371-9 |
| [6] | LAURICHESSE D, MERCIER F, BERTHIAS J P, et al. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination[J]. Navigation, 2009, 56(2): 135–149. DOI:10.1002/navi.2009.56.issue-2 |
| [7] | GENG Jianghui, TEFERLE F N, SHI C, et al. Ambiguity Resolution in Precise Point Positioning with Hourly Data[J]. GPS Solutions, 2009, 13(4): 263–270. DOI:10.1007/s10291-009-0119-2 |
| [8] | 李星星, 张小红, 李盼. 固定非差整数模糊度的PPP快速精密定位定轨[J]. 地球物理学报, 2012, 55(3): 833–840. LI Xingxing, ZHANG Xiaohong, LI Pan. PPP for Rapid Precise Positioning and Orbit Determination with Zero-difference Integer Ambiguity Fixing[J]. Chinese Journal of Geophysics, 2012, 55(3): 833–840. |
| [9] | 姚宜斌, 彭文飞, 孔建, 等. 精密单点定位模糊度固定效果分析[J]. 武汉大学学报(信息科学版), 2013, 38(11): 1281–1285. YAO Yibin, PENG Wenfei, KONG Jian, et al. Analysis of Ambiguity Fixing in Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2013, 38(11): 1281–1285. |
| [10] | CHEN Hua, JIANG Weiping, GE Maorong, et al. An Enhanced Strategy for GNSS Data Processing of Massive Networks[J]. Journal of Geodesy, 2014, 88(9): 857–867. DOI:10.1007/s00190-014-0727-7 |
| [11] | 潘宗鹏, 柴洪洲, 刘军, 等. 基于部分整周模糊度固定的非差GPS精密单点定位方法[J]. 测绘学报, 2015, 44(11): 1210–1218. PAN Zongpeng, CHAI Hongzhou, LIU Jun, et al. GPS Partial Ambiguity Resolution Method for Zero-difference Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1210–1218. DOI:10.11947/j.AGCS.2015.20150056 |
| [12] | GENG Jianghui, MENG Xiaolin, DODSON A H, et al. Integer Ambiguity Resolution in Precise Point Positioning:Method Comparison[J]. Journal of Geodesy, 2010, 84(9): 569–581. DOI:10.1007/s00190-010-0399-x |
| [13] | 张宝成, 欧吉坤. 论精密单点定位整周模糊度解算的不同策略[J]. 测绘学报, 2011, 40(6): 710–716. ZHANG Baocheng, OU Jikun. On the Different Strategies for Integer Ambiguity Resolution in Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 710–716. |
| [14] | MELBOURNE W G. The Case for Ranging in GPS-based Geodetic Systems[C]//Proceedings of First International Symposium on Precise Positioning with the Global Positioning System. Rockville:[s.n.], 1985:373-386. |
| [15] | WUBBENA G. Software Developments for Geodetic Positioning with GPS Using TI-4100 Code and Carrier Measurements[C]//Proceedings of First International Symposium on Precise Positioning with the Global Positioning System. Rockville:[s.n.], 1985:403-412. |
| [16] | 张小红, 李盼, 李星星, 等. 宽巷载波相位模糊度小数偏差时变特性分析[J]. 测绘学报, 2013, 42(6): 798–803, 809. ZHANG Xiaohong, LI Pan, LI Xingxing, et al. An Analysis of Time-varying Property of Widelane Carrier Phase Ambiguity Fractional Bias[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 798–803, 809. |
| [17] | 郑艳丽. GPS非差精密单点定位模糊度固定理论与方法研究[D].武汉:武汉大学, 2013. ZHENG Yanli. Research on Integer Ambiguity Resolution in GPS Precise Point Positioning[J]. Wuhan:Wuhan University, 2013. |
| [18] | 周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989, 18(2): 115–120. ZHOU Jiangwen. Classical Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1989, 18(2): 115–120. |
| [19] | 杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社, 1993. YANG Yuanxi. Robust Estimation Theoery and Its Applications[M]. Beijing: Bayi Publishing House, 1993. |
| [20] | YANG Yuanxi. Robust Estimation for Dependent Observations[J]. Manuscripta Geodaetica, 1994, 19(1): 10–17. |
| [21] | 杨元喜. 测量平差模型的抗差最小二乘解及其影响函数[J]. 测绘学院学报, 1994, 11(2): 77–82. YANG Yuanxi. Robust Estimation and Its Influence Function of Surveying Adjustment Model[J]. Journal of the Institute of Surveying and Mapping, 1994, 11(2): 77–82. |
| [22] | 杨元喜. 自适应抗差最小二乘估计[J]. 测绘学报, 1996, 25(3): 206–211. YANG Yuanxi. Adaptive Robust Least Square Estimate[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(3): 206–211. |
| [23] | YANG Y. Robust Estimation of Geodetic Datum Transformation[J]. Journal of Geodesy, 1999, 73(5): 268–274. DOI:10.1007/s001900050243 |
| [24] | YANG Y, HE H, XU G. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 75(2-3): 109–116. DOI:10.1007/s001900000157 |
| [25] | YANG Y, SONG L, XU T. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights[J]. Journal of Geodesy, 2002, 76(6-7): 353–358. DOI:10.1007/s00190-002-0256-7 |
| [26] | 蒋庆仙, 王成宾, 马小辉, 等. 利用中位数进行光纤陀螺信号抗差估计[J]. 武汉大学学报(信息科学版), 2011, 36(6): 656–659. JIANG Qingxian, WANG Chengbin, MA Xiaohui, et al. Robust Estimation for FOG Signal Based on Median Method[J]. Geomatics and Information Science of Wuhan University, 2011, 36(6): 656–659. |
| [27] | TEUNISSEN P J G. The Least-squares Ambiguity Decorrelation Adjustment:A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65–82. DOI:10.1007/BF00863419 |



