2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西安测绘研究所, 陕西 西安 710054;
4. 信息工程大学导航与空天目标工程学院, 河南 郑州 450052;
5. 长安大学地质工程与测绘学院, 陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
4. College of Navigation and Aerospace Engineering, Information Engineering University, Zhengzhou 450052, China;
5. School of Geological Engineering and Geomatics, Chang'an University, Xi'an 710054, China
通过重力归算量化地形质量对地表重力的引力作用,是离散重力数据格网化以及局部大地水准面精化的重要基础工作[1-7]。重力归算具体包括空间改正、层间改正[8-9]、地形改正(有的文献称为局部地形改正)[10-17]3个部分。本文重点对层间改正展开研究。传统层间改正的布格层分平面层和球面层[18]两种类型。文献[19-20]给出了球面布格层层间改正与平面布格层层间改正相差约2倍的结论。布格层是高度为计算点高程的等高度地形层,无论是无限延伸的平面层还是覆盖全球的球壳的形式,由于其区域范围与地形改正的范围不一致,因此两种类型的层间改正中均含有远区虚拟地形引入的误差。
基于此,本文提出使用布格层的区域范围与地形改正的范围一致的层间改正的方法,推导了有限范围层间改正的简便计算公式,该公式与由地形改正严密积分算法演化的公式具有一致性,并且在数学上具有一定的创新意义和理论价值。最后通过试验得出球面布格层不适宜内插,计算点地形超过1000 m时,应使用基于有限范围层间改正的重力归算进行内插的结论。
1 传统层间改正算法--平面层、球面层传统层间改正所使用的布格层有平面和球面两种类型。
平面布格层是计算点所在的平面与该点在大地水准面上对应点所在平面之间的无限延伸的地形层。当地面计算点位于大地水准面上方时,平面布格层位于计算点之下,若除去这部分地形质量的引力作用,重力值将比实测重力值小,因此此时层间改正符号为负。在以计算点为原点的柱空间坐标系下,积分半径为a、高度为Δh(计算点位于大地水准面之上时,Δh符号取正)的平面布格地形层对计算点的地形改正公式的近似结果为[17]
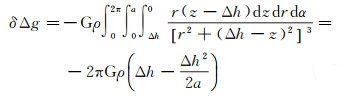 (1)
(1)
式中,G为地球引力常数;ρ为地壳密度。实际计算时通常假设平面布格层是一个无限延伸的地形层,即a取无限大,因此平面无限布格层层间改正的实用公式为
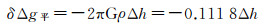 (2)
(2)
球面布格层是计算点所在的球面与该点在大地水准面上对应点所在的球面之间的球壳状的地形层。球面布格层的层间改正计算公式为[12]
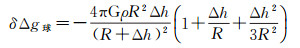 (3)
(3)
式中,R为地球平均半径。比较式(2)、式(3)可知,球面布格层改正在量级上约为平面布格层的2倍。
重力归算中的地形影响包含层间改正与地形改正两部分,由于实际计算时,地形改正仅采用有限区域范围,这使层间改正与地形改正计算范围不一致,即平面布格层和球面布格层层间改正均包含未进行地形改正的远区虚拟地形产生的误差。由于布格层的高度为计算点的高程,因此该误差对不同高度的计算点也不相同:计算点高度越大,其层间改正中远区虚拟地形产生的误差也越大。
为消除层间改正中远区虚拟地形产生的误差,本文提出使用有限范围的层间改正进行重力归算,令布格层的范围与归算时地形改正的经纬度范围一致。虽然式(1)将布格层限定为圆柱也是有限区域范围,但由于实际地形数据都是经纬度划分的网格形式,因而使用圆柱计算层间改正不能完全与地形改正的范围吻合,存在近似误差。本文将层间改正的区域设定为以经纬度网格划定的区域,较圆柱形式的布格层层间改正更为严密。
2 有限范围的层间改正算法推导本文对有限范围的层间改正算法的推导是在地形改正算法的基础上进行的。不顾及地形改正符号时,空间直角坐标系下的地面点地形改正δΔg的计算公式为
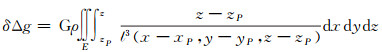 (4)
(4)
式中,(xP, yP, zP)、(x, y, z)分别为计算点和流动点的三维直角坐标;
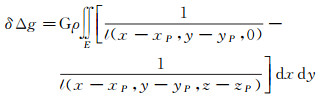 (5)
(5)
对于地形改正而言,不同流动点的z坐标是不同的,而层间改正可视作流动点高程均等于计算点高程的一种特殊的地形改正,因此当式(5)用于计算层间改正时,则需将流动点与计算点之差zP-z固定为常数Δh。考虑到层间改正的符号,有限范围的层间改正δΔglimit的算法公式为
 (6)
(6)
式中,Ω′表示有限布格层的区域范围,不是任意指定的,需与重力归算中地形改正的范围保持一致,即式(5)中E与式(6)中的Ω′范围相同,均可表达为式(7)
 (7)
(7)
式(6)的计算可直接由地形改正中的严格积分公式[8, 16]转化而来
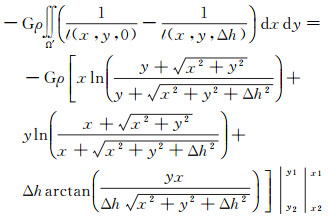 (8)
(8)
为进一步简化有限范围的层间改正的计算,本文推导了一种更为简便的计算公式。推导的基本原理是有限范围的层间改正等于无限平面层层间改正减去远区平面虚拟地形(有限范围以外的地形)产生的层间改正,推导过程中多次运用了极限的数学方法。
首先将无限平面布格层分为有限区域和远区两部分,顾及式(2),得到式(9)
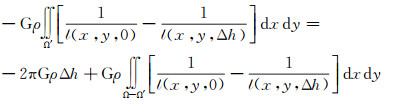 (9)
(9)
式中,Ω-Ω′表示远区范围;Ω′表示有限区域范围,根据式(7),Ω-Ω′的坐标范围为式(10)
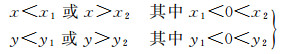 (10)
(10)
将式(9)右端第2项远区层间改正标记为δΔgΩ-Ω′,标明y轴积分域为式(11)的形式
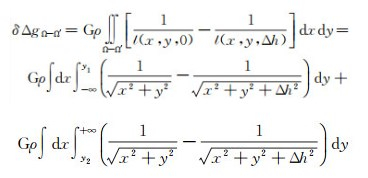 (11)
(11)
根据积分关系式(12)
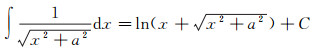 (12)
(12)
得到式(11)的积分核对y轴的不定积分
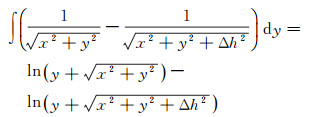 (13)
(13)
当取负极限时,式(13)简化为式(14)
 (14)
(14)
当取正极限时,式(13)简化为式(15)
 (15)
(15)
将式(14)、式(15)代入式(11),得
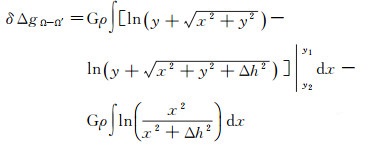 (16)
(16)
利用积分关系式(17)
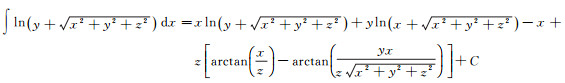 (17)
(17)
及关系式(18)
 (18)
(18)
对式(16)进一步简化
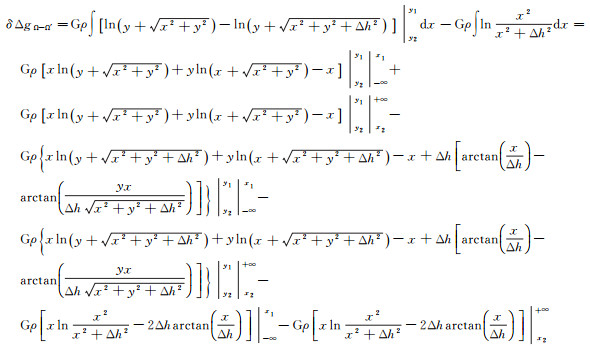
然后利用下列几项极限等式
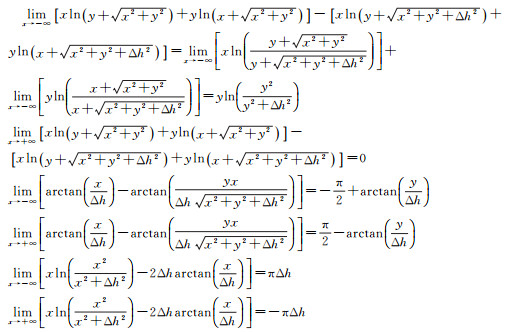
得到δΔgΩ-Ω′的计算结果为式(19)
 (19)
(19)
综合式(9)、式(19),得到有限范围的层间改正δΔglimit的计算公式为
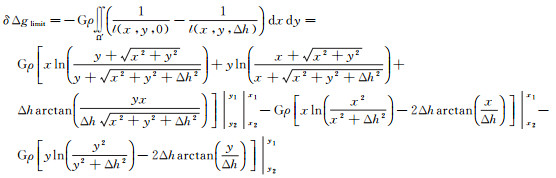 (20)
(20)
对比式(8)、式(20),得下列等式
 (21)
(21)
将式(21)代入式(8),得到有限范围的层间改正的简单算式(22)
 (22)
(22)
一旦给定计算区域的范围,利用式(22)即可快速、严格地计算有限范围的层间改正。
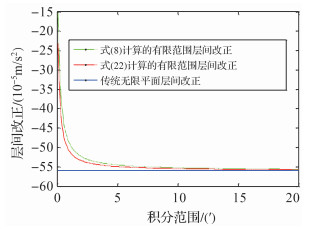
3 试验与分析 3.1 算法分析为了验证式(8)与式(22)的等效性,令计算点的纬度为30°,高度为500 m,并且积分范围(近似为平面)是经纬度等度数的矩形区域。将两种算法计算的有限范围层间改正及式(2)计算的无限平面层层间改正随积分范围的变化表示于图 1,其中横坐标为计算点距离积分区域边缘的度数。
|
| 图 1 计算点高度500 m的层间改正比较 Fig. 1 Comparision of Bouger correction with calculation point at 500 m |
从图 1可以看出,利用地形改正严格积分算法直接演化而来的式(8)与本文推导的简便公式(22)计算的有限范围的层间改正结果的一致性较好,两者的差异随着积分范围的越大而越小,当积分区域范围为20′时,两算法计算的层间改正相差0.11×10-5 m/s2(即0.11 mGal)。同时,积分范围越大,有限范围的层间改正与传统的无限范围平面层层间改正的差异越小,当积分区域范围为20′时,两算法计算的层间改正与平面层层间改正分别相差0.37×10-5 m/s2、0.26×10-5 m/s2。
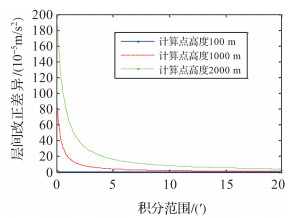
上文的分析中曾指出传统无限布格层的层间改正中远区虚拟地形产生的误差随计算点高度的增加而增大,为了说明这一误差的大小,下面令计算点的纬度为30°,高度分别取100 m、1000 m、2000 m,将式(22)计算的有限范围的层间改正与式(2)的传统无限范围平面层层间改正的差值表示于图 2。
|
| 图 2 不同高度的有限范围与无限范围层间改正之差 Fig. 2 The difference of Bouger correction of limited and unlimited range with different heights |
从图 2可以分析出,有限范围与无限范围层间改正的差异随着计算点高度的增加而增大。当积分区域范围为20′时,对于100 m、1000 m、2000 m高度的计算点,该差异分别为0.01×10-5 m/s2、1.03×10-5 m/s2、4.14×10-5 m/s2。当计算点高程超过1000 m时,有限范围层间改正与传统平面层层间改正相差超过1.0×10-5 m/s2,此时将有限范围层间改正代替传统的无限范围层间改正是非常有必要的。
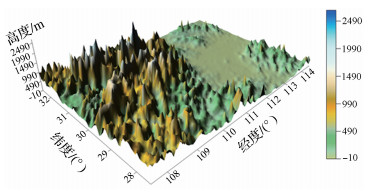
3.2 基于重力归算的内插试验层间改正是重力归算的一项重要内容,而重力归算的一个重要应用方向是离散重力数据内插,因此下面通过分析采用不同层间改正方法的重力归算的内插精度,说明有限范围层间改正的实用意义。试验区范围为107.5°-114.5°E、27.5°-32.5°N,通过地面重力测量获得的地表重力离散点48 390个,重力实测数据的特点是分布不均匀,地势平坦的区域重力点较为密集,精度相对较高,地势起伏较大的区域重力点较为稀疏,精度相对较低。重力离散点高程最大2870 m、最小-34 m,试验区地形分辨率为5″×5″,分布如图 3所示。
|
| 图 3 试验区地形图 Fig. 3 Topographic map of experimental area |
首先分别计算球面布格层、平面布格层、有限范围布格层(1.5°、1°,此为实践中通常采用的地形改正的区域范围)的层间改正,将结果统计于表 1。
| 10-5 m/s2 | ||||
| 布格层 | 最小值 | 最大值 | 平均值 | 均方根 |
| 球面布格层 | -642.27 | 7.60 | -50.37 | 86.07 |
| 平面布格层 | -320.88 | 3.79 | -25.16 | 42.99 |
| 有限范围布格层 (1.5°) |
-319.37 | 3.80 | -25.16 | 42.95 |
| 有限范围布格层 (1°) |
-318.42 | 3.80 | -25.14 | 42.91 |
从表 1可以看出,球面层层间改正的量级约为平面层的2倍,有限范围层间改正与平面层层间改正的数值相差较小,且计算区域的范围越大,差值越小。进一步将有限范围层间改正与传统无限范围平面层层间改正的差值示于表 2。
| 10-5m/s2 | ||||
| 区域范围 | 最小值 | 最大值 | 平均值 | 均方根 |
| 1.5° | -0.022 | 1.508 | 0.252E-2 | 5.357E-2 |
| 1° | -0.014 | 2.463 | 1.952E-2 | 9.888E-2 |
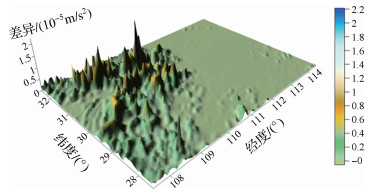
表 2中1.5°区域范围时二者差异最大值为1.5×10-5 m/s2,均方根为0.05×10-5 m/s2。为了说明两者差值大小的具体分布情况,将1°区域范围下的差值分布显示于图 4。
|
| 图 4 1°范围布格层与平面层层间改正差异 Fig. 4 The correction difference between the limited Bouguer layer (1°) and the plane layer (10-5 m/s2) |
图 4体现了有限范围层间改正与传统平面层层间改正的差异与数据点的高程有关,高程越大该差异也越大。这与前文的分析一致。综合表 2、图 4可以得出,有限范围层间改正与平面层层间改正的差值与重力点的高程、计算范围有关,高度越大、范围越小,此项差异越大。
下面开始内插试验,以通过内插精度的提高说明有限范围层间改正的有效性。首先将试验区48 390个离散重力点筛选出3229个点作为检验点,其余点作为内插点,以检验点内插结果与原数据的差值作为评价内插精度的指标。内插算法为Shepard反距离内插法,重力归算时分别采用不同种层间改正方法,特别强调的是有限范围层间改正的区域范围与地形改正的区域范围一致。表 3为插值统计结果。
| 10-5m/s2 | |||||
| 地形改 正范围 |
层间改正 | 最大值 | 最小值 | 平均值 | 均方根 |
| 1.5° | 球面层 | 135.06 | -121.79 | 1.18 | 18.188 9 |
| 平面层 | 25.18 | -20.31 | 4.93E-2 | 2.348 5 | |
| 1.5°有限层 | 25.22 | -20.08 | 4.64E-2 | 2.348 2 | |
| 1° | 球面层 | 135.06 | -121.88 | 1.18 | 18.201 9 |
| 平面层 | 25.14 | -20.45 | 5.03E-2 | 2.349 1 | |
| 1°有限层 | 25.21 | -20.10 | 4.52E-2 | 2.348 8 | |
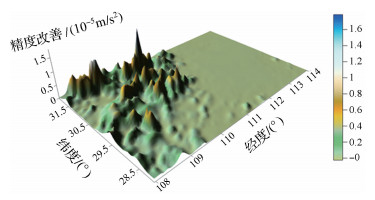
由表 3可以看出,球面布格层的插值效果很差,不宜内插。表中平面层与有限范围布格层插值均方根相差较小,这是因为3229个检测点多数位于平坦的海拔低的区域,高程低的数据处的平面层层间改正与有限范围层间改正本身的差异较小。当计算范围为1°、1.5°时,有限范围层间改正的内插精度较平面层均方差均提升了3×10-4×10-5 m/s2。对于平面层而言,当地形改正范围从1°扩充到1.5°时,均方根提升了6×10-4×10-5 m/s2,参照此量级,说明此时有限范围层间改正对内插精度的提高作用不应该被忽略。为了说明有限范围层间改正相对于传统平面层间改正内插的改善效果,将1°区域范围下两者差异显示于图 5。
|
| 图 5 有限范围(1°)层间改正与平面层间改正内插精度的改善效果 Fig. 5 Improvement of interpolation accuracy of the limited Bouguer layer (1°) compared to the plane layer |
图 5说明了有限范围层间改正较传统无限范围平面层层间改正对内插精度的提高主要在海拔较高的计算点上,对于地形高度为2000 m的计算点而言,1°区域范围下有限范围层间改正内插精度将提高约1.5×10-5 m/s2。结合上文的分析,在计算点地形高度超过1000 m时,应使用基于有限范围层间改正的重力归算进行内插。
4 结论本文在传统平面层、球面层层间改正的基础上,提出了使用有限范围层间改正进行重力归算的方法,其范围与重力归算中地形改正的范围一致。然后通过推导给出了有限范围层间改正的简便计算方法,该式具有一定的数学理论价值。通过试验证明该算法与通过地形改正严密积分法演化来的算法具有一致性。最后通过基于重力归算的内插试验,说明球面层层间改正不适宜内插;当计算点地形高大于1000 m时,应使用基于有限范围层间改正的重力归算进行内插。
| [1] | 管泽霖, 管铮, 黄谟涛, 等. 局部重力场逼近理论和方法[M]. 北京: 测绘出版社, 1997. GUAN Zelin, GUAN Zheng, HUANG Motao, et al. Theory and Method of Regional Gravity Field Approximation[M]. Beijing: Surveying and Mapping Press, 1997. |
| [2] | 郭俊义. 物理大地测量学基础[M]. 武汉: 武汉测绘科技大学出版社, 1994. GUO Junyi. Foundation of Physical Geodesy[M]. Wuhan: Wuhan Technical University of Surveying and Mapping Press, 1994. |
| [3] | 罗志才, 陈永奇, 宁津生. 地形对确定高精度局部大地水准面的影响[J]. 武汉大学学报(信息科学版), 2003, 28(3): 340–344. LUO Zhicai, CHEN Yongqi, NING Jinsheng. Effect of Terrain on the Determination of High Precise Local Gravimetric Geoid[J]. Geomatics and Information Science of Wuhan University, 2003, 28(3): 340–344. |
| [4] | 章传银, 晁定波, 丁剑, 等. 球近似下地球外空间任意类型场元的地形影响[J]. 测绘学报, 2009, 38(1): 28–34. ZHANG Chuanyin, CHAO Dingbo, DING Jian, et al. Precision Topographical Effects for Any Kind of Field Quantities for Any Altitude[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 28–34. |
| [5] | NAHAVANDCHI H. The Direct Topographical Correction in Gravimetric Geoid Determination by the Stokes-Helmert Method[J]. Journal of Geodesy, 2000, 74(6): 488–496. DOI:10.1007/s001900000110 |
| [6] | 庞振兴.平均空间重力异常精细构制方法研究[D].郑州:信息工程大学, 2008. PANG Zhenxing. Research on the Refining Methods of Gravity Anomaly[D].Zhengzhou:Information Engineering University, 2008. |
| [7] | 孙文.我国高分辨率三维重力场与似大地水准面研究[D].郑州:信息工程大学, 2014. SUN Wen. Determination of High Resolution of 3D Gravity Field and Quasi-geoid of China[D]. Zhengzhou:Information Engineering University, 2014. |
| [8] | VANÍČEK P, NOVÁK P, MARTINEC Z. Geoid, Topography and the Bouguer Plate or Shell[J]. Journal of Geodesy, 2001, 75(4): 210–215. DOI:10.1007/s001900100165 |
| [9] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. San Francisco: W H Freeman and Company, 1967. |
| [10] | SMITH D A, ROBERTSON D S, MILBERT D G. Gravitational Attraction of Local Crustal Masses in Spherical Coordinates[J]. Journal of Geodesy, 2001, 74(11-12): 783–795. DOI:10.1007/s001900000142 |
| [11] | NAHAVANDCHI H. Terrain Correction Computations by Spherical Harmonics and Integral Formulas[J]. Physics and Chemistry of the Earth, Part A:Solid Earth and Geodesy, 1999, 24(1): 73–78. DOI:10.1016/S1464-1895(98)00013-1 |
| [12] | 郭春喜, 王惠民, 王斌. 全国高分辨率格网地形和均衡改正的确定[J]. 测绘学报, 2002, 31(3): 201–205. GUO Chunxi, WANG Huimin, WANG Bin. Determination of High Resolution Grid Terrain and Isostatic Corrections in All China Area[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 201–205. |
| [13] | 章传银, 晁定波, 丁剑, 等. 厘米级高程异常地形影响的算法及特征分析[J]. 测绘学报, 2006, 35(4): 308–314. ZHANG Chuanyin, CHAO Dingbo, DING Jian, et al. Arithmetic and Characters Analysis of Terrain Effects for CM-order Precision Height Anomaly[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 308–314. |
| [14] | 郭东美, 许厚泽. 局部地形改正的奇异积分研究[J]. 地球物理学报, 2011, 54(4): 977–983. GUO Dongmei, XU Houze. Research on the Singular Integral of Local Terrain Correction Computation[J]. Chinese Journal of Geophysics, 2011, 54(4): 977–983. |
| [15] | 郑增记.基于GOCE重力场模型与地形改正的似大地水准面精化[D].西安:长安大学, 2013. ZHENG Zengji. Refining of Quasi-geoid Based the GOCE Gravitational Model and Terrain Correction[D]. Xi'an:Chang'an University, 2013. |
| [16] | 江丽.球坐标系下基于扇形柱体的地形改正研究与实现[D].北京:中国地质大学, 2014. JIANG Li. Research and Implementation of Terrain Correction Using Sector Cylinder Models in Spherical Coordinate[D]. Beijing:China University of Geosciences, 2014. |
| [17] | 王增利, 文琳. 一种地形改正新算法[J]. 大地测量与地球动力学, 2011, 31(3): 115–119. WANG Zengli, WEN Lin. A New Terrain Correction Method[J]. Journal of Geodesy and Geodynamics, 2011, 31(3): 115–119. |
| [18] | 李姗姗, 吴晓平, 张传定, 等. 顾及地形与完全球面布格异常梯度项改正的区域似大地水准面精化[J]. 测绘学报, 2012, 41(4): 510–516. LI Shanshan, WU Xiaoping, ZHANG Chuanding, et al. Regional Quasi-geoid Refining Considering Corrections of Terrain and Complete Spherical Bouguer Anomaly's Gradient Term[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 510–516. |
| [19] | 荣敏, 周巍. 球近似地形改正的研究分析[J]. 大地测量学与地形动力学, 2015, 35(1): 58–61. RONG Min, ZHOU Wei. Study on Topography Correction Based on Spherical Approximation[J]. Journal of Geodesy and Geodynamics, 2015, 35(1): 58–61. |
| [20] | 荣敏. Stokes-Helmert方法确定大地水准面的理论与实践[D].郑州:信息工程大学, 2015. RONG Min. Stokes-Helmert Method for Geoid Determination[D]. Zhengzhou:Information Engineering University, 2015. |


