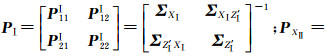2. 信息工程大学地理空间信息学院, 河南 郑州 450001
2. Institute of Geospatial Information, Information Engineering University, Zhengzhou 450001, China
三维坐标转换是大地测量最基本的问题, 为了进行不同框架间的坐标转换,目前常采用相似变换模型,如Bursa模型、Molodensky模型等[1]。传统的三维坐标转换模型通常只考虑公共点在原框架下的坐标误差,即首先利用公共点在原框架和目标框架下的坐标采用最小二乘解得转换参数,然后利用所求得的转换参数转换非公共点得到其在目标框架下的新坐标。当观测误差服从正态分布时,相似变换模型的解可认为是最优的。如公共点的坐标存在异常误差,可采用抗差估计算法抑制其异常误差的影响[2]。如异常观测数据较多时可采用高崩溃率的转换参数抗差解法[3]。相似变换模型应用于局部区域的坐标转换时可能存在病态问题,利用正则化算法可解决其病态性[4]。传统的三维坐标变换通常是针对小旋转角的,对大旋转角并不适用,于是有学者研究了以方向余弦为参数、适用于大旋转角的三维基准转换模型[5],扩大了坐标转换模型的应用范围。由于受地壳板块运动、局部变形等的影响,坐标存在局部系统误差,相似变换模型不能很好地顾及这些局部效应,有学者提出了可变参数的坐标转换法[6-7]、坐标系综合变换法[8]和组合变换法[9],通过合理增加模型参数来吸收这种局部系统性参数,从而改善坐标转换效果。仅通过改进函数模型很难完全消除局部变形误差的影响,于是有学者把函数模型变换后的残差看成随机场,采用拟合推估进行坐标转换[10-11],其本质是拟合推估两步解法[12-13]的实际应用。拟合推估应用的关键是合理确定信号的协方差矩阵,若信号与观测量间的协方差不协调,可通过方差分量估计[14]或自适应估计[15-18]来调整,以便较合理地确定拟合推估的信号与观测量间的权比。
测站坐标是对观测数据进行数据处理获得的,不可避免地受到测量误差的污染,由此构造的坐标转换系数矩阵自然也会存在误差,于是有学者研究了三维坐标变换中同时顾及系数矩阵误差和观测向量误差的整体最小二乘法[19];同时考虑系数阵误差且适用于大旋转角的坐标转换通用整体算法[20]以及控制异常误差影响的稳健整体最小二乘方法[21]。通常,整体最小二乘假设系数矩阵的所有元素都是有误差的,但实践中系数矩阵并不是所有元素都有误差,于是,有学者研究了仅考虑坐标转换系统矩阵部分元素有误差的整体最小二乘法[22-23]。这种考虑系数阵元素误差的转换模型通常是非线性的,进行总体最小二乘解算常采用迭代解法[24-26]。
事实上,坐标转换中公共点与非公共点的误差对坐标转换结果都有影响[27],于是有学者提出了顾及两套坐标误差的坐标转换方法[28],考虑系数矩阵所有元素都有误差的无缝坐标转换模型[29-30]。上述算法的核心是利用原框架下公共点与非公共点间的协方差建立拟合推估模型,对非公共点的坐标转换值进行改进,采用牛顿迭代法进行计算。然而由前文所述,系数矩阵中并不是所有元素都有误差,这种认为系数矩阵所有元素都有误差是不合实际的;此外,系数矩阵中相同元素的改正数也应该相同。
为此,本文针对原框架和目标框架下的坐标均存在误差、非公共点与公共点间存在相关性,以及坐标转换系数矩阵中仅部分元素存在误差的实际情况,提出了一种三维基准转换严密模型,推导了严密的坐标转换公式。该模型同时考虑框架点误差和转换点间协方差关系,对系数矩阵仅考虑有误差的元素,将公共点和非公共点联合处理,同时计算坐标转换参数、公共点和非公共点的转换值;进一步,借鉴自适应思想[15-18],推导了原框架和目标框架坐标的方差不一致情况下的坐标转换自适应解法;最后,利用“陆态网络工程”2000个区域站的实测坐标向CGCS2000的转换进行试验验证。
1 坐标转换联合模型描述两个地球参考架的转换关系常采用相似变换模型[1],原框架到目标框架的三维坐标转换模型为
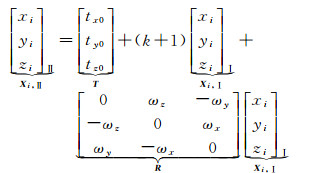 (1)
(1)
式中,Xi, Ⅱ为目标框架下的坐标;Xi, Ⅰ为原框架下的坐标;T=[tx0 ty0 tz0]T为平移参数;k为尺度参数;ζ=[ωx ωy ωz]T为旋转参数。
由于坐标都是由观测数据通过平差得到的,不可避免地受到观测误差的影响,公共点在两框架下的坐标也都可能存在误差。通常,整体最小二乘认为由式(1)构造的误差方程的系数矩阵所有元素都有误差[19],但其中部分元素为常数1和0,并不包含误差,仅部分元素有误差。如此,只对有误差的元素进行改正
 (2)
(2)
式中,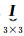
联合m个公共点求解坐标转换参数,则有
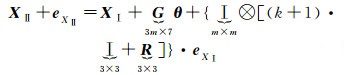 (3)
(3)
式中,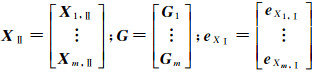
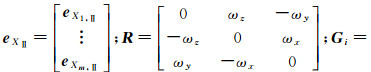

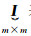
假设原框架另有n个非公共点坐标Z′Ⅰ,则转换到目标框架下的坐标为
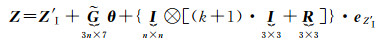 (4)
(4)
式中,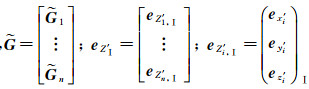
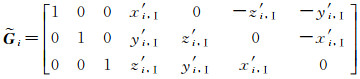
由于坐标转换的旋转参数和尺度参数都是小量,坐标误差也是小量,忽略其二阶小量,同时考虑到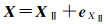
 (5)
(5)
假定原框架与目标框架是独立的,则公共点与非公共点协方差矩阵为
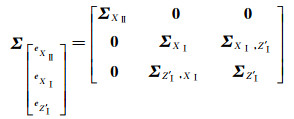 (6)
(6)
式(5)也可写为
 (7)
(7)
相应的协方差矩阵为
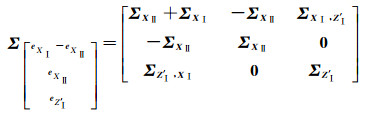 (8)
(8)
可以看出,仅考虑系数矩阵中有误差的元素的坐标转模型式(5)、式(7),确保了系数矩阵中原框架坐标具有相同的改正数,这与传统的认为系数矩阵中所有元素都有误差的整体最小二乘法误差矩阵不同。
2 坐标转换联合模型解算由于式(5)与式(7)是等价的,可以采用任一式进行计算,对式(5)构造误差方程[27],并写成紧凑模式
 (9)
(9)
式中,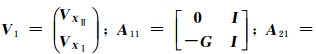
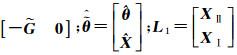
相应的权阵为
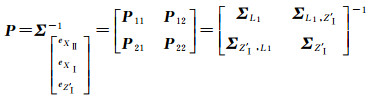 (10)
(10)
式中,
由矩阵分块求逆公式有
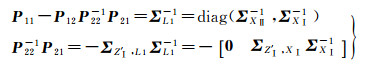 (11)
(11)
依据最小二乘原理求解式(9)
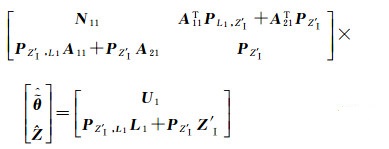 (12)
(12)
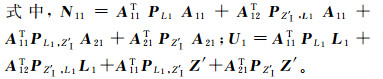
整理有
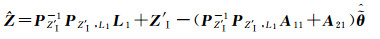 (13)
(13)
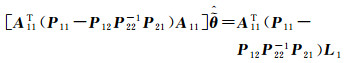 (14)
(14)
把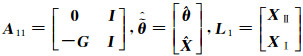
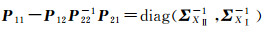
 (15)
(15)
则有
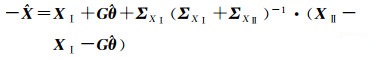 (16)
(16)
 (17)
(17)
把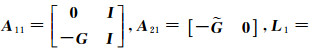
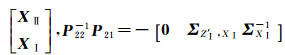
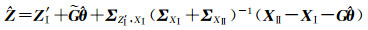 (18)
(18)
其相应的协方差矩阵为
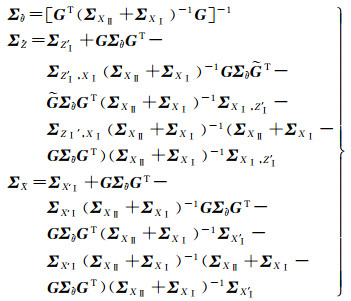 (19)
(19)
可以看出:
(1)转换参数的求解仅与公共点在原框架和目标框架的坐标值和协方差有关,与原框架中公共点与非公共点间的协方差无关,即非公共点对转换参数没有贡献。
(2)原框架内的公共点与非公共点转换到目标框架的解的形式为标准坐标转换值加上一改正量的形式,对公共点的改正量dX、非公点的改正量dZ分别为
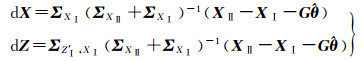 (20)
(20)
(3)顾及框架间误差的坐标转换较标准坐标转换的公共点和非公共点的协方差是变小的,其协方差改正量分别为
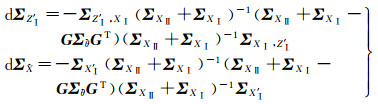 (21)
(21)
(4)顾及框架间误差的坐标转换解与拟合推估解[11]的形式非常相似,如果把原框架的坐标协方差看成拟合推估信号的协方差,则二者的解是一样的,如此,避免了拟合推估中构造合适的信号协方差函数的问题。但需要明确的是二者的物理意义并不相同。
3 方差不一致的自适应求解通常情况下,由于在数据处理中很难确定可靠的坐标框架的先验方差,原框架(或目标框架)的坐标所对应的协方差矩阵仅反映框架内的相互关系,且估计的精度往往偏高[31]。通常,不同框架间其方差因子并不一致,势必影响转换精度[14]。考虑不同框架间方差因子不一致情况下的自适应解的目标函数为
 (22)
(22)
对式(22)求极值后,整理有
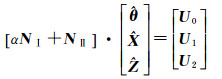 (23)
(23)
式中,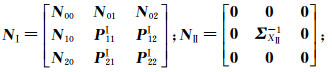
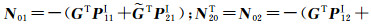

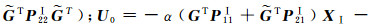


仿照式(12)-式(18)的推导,其分步解为
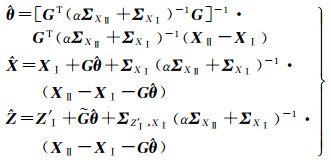 (24)
(24)
式(24)与式(16)、式(17)、式(18)形式非常相近,但若自适应因子α≠1,解的数值就会不同。自适应因子α起着平衡原框架和目标框架坐标误差影响的作用。
采用不同统计方法可以构造不同的自适应因子,可以采用极大似然估计法和Helmert方差分量估计法确定自适应因子[17, 30]。两类观测量的Helmert方差分量公式[16]为
 (25)
(25)
式中
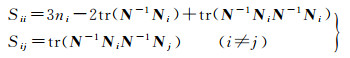 (26)
(26)
式中,ni为原框架和目标框架坐标点个数;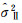

解得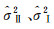
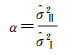 (27)
(27)
即可按式(23)、式(24)重新估算转换参数和坐标转换值。
4 计算与分析利用“陆态网络工程”2000个区域站观测数据,计算了它们在2009、2011年的坐标及其协方差,作为试验分析数据。这两期数据的联测时间分别为2009-04-31-2009-10-31、2011-02-22-2011-10-14,每个测站观测4 d,1 d为一个观测时段,数据采样率为30 s, 基线解算采用GAMIT软件,平差处理采用CGCS2000联合平差开发的基线网平差软件,处理结果站坐标三分量的精度均优于1 cm。为了验证顾及框架误差的坐标转换联合模型的效果,取“陆态网络工程”一期的1000个点作为公共点,其余1000点作为非公共点,分别采用经典转换模型和本文提出的联合转换模型进行坐标转换。在联合转换模型中计算非公共点坐标转换值时,非公共点与公共点间的协方差是必不可少的,计算中采用前述平差所得到的协方差作为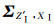
一般来说,坐标值及其精度是最容易获得的,可按坐标各分量的实际精度定权,记为方案1;当认为目标框架坐标精度较高,即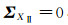
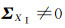
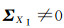

由前所述可知,考虑公共点与非公共点间的协方差与否对转换参数的计算是没有影响的,表 1给出了不同方案下计算的转换参数及其精度。可以看出,考虑公共点坐标的协方差的不同方案(按坐标各分量的方差、仅考虑原框架的坐标协方差和同时考虑原框架和目标框架的坐标协方差),所估计的转换参数差异不太大,且数值较小,平移参数最大差值也不超过0.5 mm,除了方案2 X方向的旋转参数为2.17 mas外,其余方案的旋转参数几乎为零,并且转换参数估值与其均方差的量级基本一致,说明这些参数并不明显。
| 方案 | tx0/cm | ty0/cm | tz0/cm | k/ppb | ωx/mas | ωy/mas | ωz/mas |
| 方案1 | 0.002 | 0.008 | 0.010 | 0.002 | 0.000 | 0.000 | 0.000 |
| ±0.011 | ±0.013 | ±0.016 | ±0.00 | ±0.000 | ±0.000 | ±0.000 | |
| 方案2 | 0.012 | -0.003 | -0.049 | 0.010 | 2.127 | 0.000 | 0.000 |
| ±0.041 | ±0.049 | ±0.063 | ±0.00 | ±0.000 | ±0.000 | ±0.000 | |
| 方案3 | 0.002 | -0.003 | 0.006 | 0.001 | 0.000 | 0.000 | 0.000 |
| ±0.027 | ±0.033 | ±0.043 | ±0.000 | ±0.000 | ±0.000 | ±0.000 |
为了分析不同定权方式对联合转换模型与经典转换模型计算的坐标转换值差值的影响,表 2给出了联合转换模型与经典转换模型的计算结果差值统计(左边为公共点坐标的差值,右边为非公共点的差值)。不考虑各点各分量间的协方差,仅考虑点位坐标各分量的方差,经典转换模型与新的联合模型计算的坐标转换值的差值在X、Y、Z方向的标准差,公共点为5 mm、9 mm、8 mm,非公共点为8 mm、30 mm、20 mm;仅考虑原框架坐标协方差所计算的坐标转换值差值在X、Y、Z方向的标准差,公共点为13 mm、23 mm、19 mm,非公共点为4 mm、12 mm、10 mm;同时考虑原框架和目标框架坐标协方差的不同转换模型所计算坐标转换值差值在X、Y、Z方向的标准差,公共点为5 mm、8 mm、7 mm,非公共点为2 mm、3 mm、3 mm。
| cm | ||||||||||
| 方案 | 公共点 | 非公共点 | ||||||||
| max | min | mean | std | max | min | mean | std | |||
| 方案1 | X | 4.01 | -1.27 | 0.08 | 0.49 | 6.23 | -2.24 | 0.29 | 0.88 | |
| Y | 4.53 | -7.58 | -0.14 | 0.93 | 4.87 | -17.57 | -1.53 | 3.06 | ||
| Z | 1.60 | -5.06 | -0.27 | 0.76 | 6.05 | -8.91 | -0.95 | 2.06 | ||
| 方案2 | X | 10.88 | -4.20 | 0.23 | 1.28 | 1.94 | -1.38 | 0.05 | 0.36 | |
| Y | 11.40 | -10.18 | -0.39 | 2.27 | 6.37 | -2.64 | 0.20 | 1.22 | ||
| Z | 6.64 | -8.96 | -0.74 | 1.87 | 5.14 | -2.87 | -0.21 | 1.00 | ||
| 方案3 | X | 4.02 | -1.26 | 0.07 | 0.53 | 1.22 | -0.43 | 0.01 | 0.15 | |
| Y | 6.26 | -6.09 | -0.21 | 0.82 | 1.67 | -1.07 | -0.01 | 0.28 | ||
| Z | 3.44 | -3.73 | -0.17 | 0.73 | 1.52 | -1.30 | -0.01 | 0.30 | ||
图 1给出了非公共点两种模型计算的转换值差异。仅考虑点位坐标各分量方差情况下,经典转换模型计算的坐标转换值与联合转换模型的坐标标转换值的差值变化较大,在X、Y、Z方向最大差值分别为6 cm、17 cm、9 cm;忽略目标框架误差仅考虑原框架误差时,这两种转换模型计算的坐标转换值的差值变化变小,在X、Y、Z方向最大差值分别为2 cm、6 cm、5 cm;同时考虑目标框架和原框架误差时,这两种转换模型计算的坐标转换值的差值变化更加平稳,在X、Y、Z方向最大差值分别为1 cm、2 cm、2 cm。
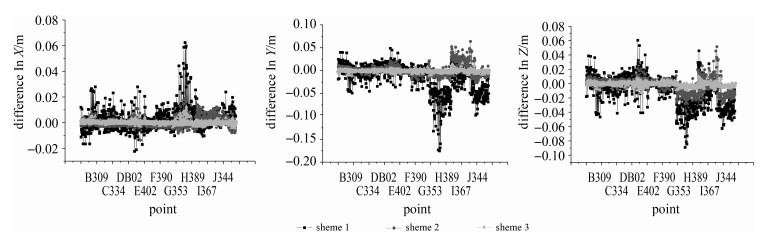
|
| 图 1 联合转换模型与经典转换模型计算的非公共点坐标转换值的差异 Fig. 1 Corrections vectors between result by using classical method and ones using combined method |
综合图 1、表 2的分析,说明联合转换模型与经典转换模型中不同定权方式对计算的坐标转换值有着不同的影响,同时考虑考虑目标框架和原框架误差时,坐标转换值的差异相对较平稳。
4.2 计算结果精度分析为了说明不同定权方案下坐标转换模型的精度情况,表 3给出了经典转换模型与联合转换模型所计算的公共点残差统计情况,表 4给出了非公共点即外部检查点的精度统计情况。
| cm | ||||||||||
| 方案 | 联合转换模型 | 经典转换模型 | ||||||||
| max | min | mean | std | max | min | mean | std | |||
| 方案1 | X | 4.14 | -06.87 | -0.15 | 0.84 | 4.20 | -10.88 | -0.23 | 1.28 | |
| Y | 6.79 | -11.16 | 0.24 | 1.45 | 10.18 | -11.41 | 0.39 | 2.27 | ||
| Z | 5.99 | -6.52 | 0.46 | 1.20 | 8.95 | -6.64 | 0.73 | 1.87 | ||
| 方案2 | X | 0.00 | 0.00 | 0.00 | 0.00 | 4.20 | -10.88 | -0.23 | 1.28 | |
| Y | 0.00 | 0.00 | 0.00 | 0.00 | 10.18 | -11.40 | 0.39 | 2.27 | ||
| Z | 0.00 | 0.00 | 0.00 | 0.00 | 8.96 | -6.64 | 0.74 | 1.87 | ||
| 方案3 | X | 3.91 | -6.87 | -0.16 | 0.83 | 4.20 | -10.88 | -0.23 | 1.29 | |
| Y | 6.64 | -10.37 | 0.18 | 1.62 | 10.18 | -11.41 | 0.39 | 2.27 | ||
| Z | 5.85 | -6.10 | 0.57 | 1.30 | 8.95 | -6.64 | 0.73 | 1.87 | ||
| cm | |||||||||||
| 方案 | 联合转换模型 | 经典转换模型 | |||||||||
| max | min | mean | std | max | min | mean | std | ||||
| 方案1 | X | 10.02 | -9.75 | -0.16 | 1.24 | 9.84 | -9.75 | -0.22 | 1.32 | ||
| Y | 19.35 | -13.37 | 0.09 | 2.23 | 19.31 | -8.67 | 0.41 | 2.50 | |||
| Z | 18.36 | -5.24 | 0.42 | 1.76 | 18.47 | -4.20 | 0.59 | 2.03 | |||
| 方案2 | X | 09.86 | -9.89 | -0.19 | 1.24 | 9.84 | -9.75 | -0.22 | 1.32 | ||
| Y | 19.77 | -10.07 | 0.64 | 2.03 | 19.31 | -8.67 | 0.41 | 2.50 | |||
| Z | 18.77 | -5.75 | 0.42 | 1.85 | 18.47 | -4.20 | 0.59 | 2.02 | |||
| 方案3 | X | 9.92 | -9.82 | 0.22 | 1.28 | 9.84 | -9.75 | -0.22 | 1.32 | ||
| Y | 19.40 | -8.88 | 0.34 | 2.45 | 19.31 | -8.67 | 0.41 | 2.50 | |||
| Z | 18.48 | -4.48 | 0.52 | 1.96 | 18.47 | -4.20 | 0.59 | 2.03 | |||
从公共点残差看,按方差定权的联合模型所得到差值的标准差,在X、Y、Z方向分别为0.8 cm、1.5 cm、1.2 cm;当认为目标框架坐标精度非常高时,即ΣXⅡ=0,从式(16)可知,联合转换模型确定的坐标转换值应为目标框架点坐标值,即其残差为零;当认为目标框架和原框架均有误差时,联合模型在X、Y、Z方向标准差分别为0.8 cm、1.6 cm、1.3 cm。在这3种精度情况下,经典模型的标准差均为1.3 cm、2.2 cm、1.8 cm,明显大于联合模型。
从外部检查点看,按方差定权的联合模型所计算得到的差值的标准差,在X、Y、Z方向分别为1.2 cm、2.2 cm、1.7 cm;当认为目标框架坐标精度非常高ΣXⅡ=0时,联合模型在X、Y、Z方向的标准差分别为1.2 cm、2.0 cm、1.8 cm;当认为目标框架和原框架误差时,联合模型所得到的残差在X、Y、Z方向标准差分别为1.3 cm、2.4 cm、1.9 cm。在这3种模型下经典模型的标准差均为1.3 cm、2.5 cm、2.0 cm。可以发现无论哪种情况,联合转换模型均比经典模型精度高。
从内外部精度看,在这3种情况下经典模型的标准差基本一致,但联合转换模型的标准差并不相同,均比经典模型精度高。由于经典模型仅受转换参数影响,由表 1可知,不同方案下的坐标转换参数差异非常小,由此计算的坐标转换值差异也会小;但联合模型不仅受转换参数影响,而且也受公共点残差的影响,其影响通过协方差进行体现,自然各种定权模式下的精度统计并不一致。
4.3 不同先验方差对结果的影响分析坐标转换涉及原框架和目标框架两类坐标,这两类坐标通常对应不同的方差因子,从数据处理角度看,这两类坐标方差因子的比值决定了坐标转换中原框架和目标框架坐标对解的贡献大小,方差因子的不同比值必然对坐标转换结果有所影响。
为了分析先验方差对基准变换的影响,进行了不同先验精度下的试算(比值分别为0.01、1、100)。表 5给出了不同先验精度下坐标转换的统计精度。可以看出,在不同的方差因子比值情况下,标准联合转换模型所确定的外部检查点有不同精度。在方差因子比值为0.01时,X、Y、Z方向标准差分别为1.2 cm、1.9 cm、1.8 cm;在方差因子比值为1时,X、Y、Z方向标准差分别为1.3 cm、2.4 cm、1.9 cm;在方差因子比值为100时,X、Y、Z方向标准差分别为1.9 cm、1.9 cm、2.1 cm。
| cm | ||||||||||
| 先验方差 | 自适应联合转换模型 | 标准联合转换模型 | ||||||||
| max | min | mean | std | max | min | mean | std | |||
| 0.01 | X | 9.86 | -5.55 | -0.18 | 1.40 | 9.86 | -5.55 | -0.18 | 1.20 | |
| Y | 19.51 | -10.06 | 0.62 | 1.84 | 19.51 | -10.06 | 0.62 | 1.94 | ||
| Z | 18.77 | -5.74 | 0.40 | 1.75 | 18.77 | -5.74 | 0.40 | 1.76 | ||
| 1 | X | 9.86 | -5.55 | -0.18 | 1.40 | 9.92 | -9.82 | 0.22 | 1.28 | |
| Y | 19.51 | -10.06 | 0.62 | 1.84 | 19.40 | -8.88 | 0.34 | 2.45 | ||
| Z | 18.77 | -5.74 | 0.41 | 1.76 | 18.48 | -4.48 | 0.52 | 1.96 | ||
| 100 | X | 9.86 | -5.55 | -0.18 | 1.40 | 11.89 | -4.98 | 0.23 | 1.92 | |
| Y | 19.51 | -10.06 | 0.62 | 1.84 | 19.88 | -9.48 | 0.49 | 1.90 | ||
| Z | 18.77 | -5.74 | 0.40 | 1.76 | 18.31 | -4.52 | 0.42 | 2.15 | ||
通过方差分量估计构造的自适应因子调整目标框架和原框架随机模型后,自适应联合转换模型所确定的外部检查点的统计精度基本一致,其标准差在X、Y、Z方向为1.4 cm、1.8 cm、1.8 cm。自适应因子调整目标框架与原框架间的方差因子间比值,起到了平衡目标框架与原框架对结果贡献的作用。
图 2给出了先验精度比值为100情况下的联合转换模型经自适应调整过程中的方差因子的变化,经过10次调整方差因子比值逐步趋近于1,保证了他们的方差因子基本相同,使其贡献更加合理。
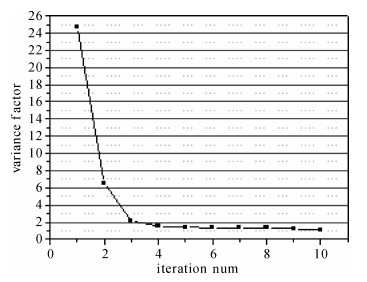
|
| 图 2 方差因子的迭代变化 Fig. 2 Iterative adaptive factor |
5 结论
坐标转换中公共点、非公共点坐标都存在误差,本文从更一般的情况出发,提出了一种严密的坐标转换联合模型,利用2000点规模的GNSS控制网实测数据,分析了这种联合模型在不同误差情况下的效果,主要结论如下。
(1)该模型同时考虑了公共点在目标框架和原框架中的误差、原框架的非公共点与公共点间相关性,以及转换系数矩阵的误差,理论严密。在忽略二阶小量基础上,推导的转换公式更具一般性,兼容了传统的坐标转换模型。
(2)理论分析和实际计算均表明,转换参数的求解仅与公共点在原框架和目标框架的坐标值和协方差有关,与原框架内的公共点与非公共点间的协方差无关,即非公共点对转换参数没有贡献。
(3)通常情况下,原框架与目标框架的方差因子不一致,坐标转换联合模型的自适应解法采用方差分量估计构造的自适应因子调整了原框架与目标框架坐标的贡献,保证了它们的方差因子基本一致。
(4)利用2000点的实测数据,按等权、点位坐标各分量的方差定权、仅按需转换框架定权以及同时考虑两套框架协方差定权,联合转换模型较传统坐标转换模型具有更高的坐标转换精度。
| [1] | 朱华统, 杨元喜, 吕志平. GPS坐标系统的变换[M]. 北京: 测绘出版社, 1994. ZHU Huatong, YANG Yuanxi, LV Zhiping. Transformation of GPS Datum[M]. Beijing: Press of Surveying and Mapping, 1994. |
| [2] | YANG Y, SONG L, XU T. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights[J]. Journal of Geodesy, 2002, 76(6-7): 353–358. DOI:10.1007/s00190-002-0256-7 |
| [3] | YANG Y. Robust Estimation of Geodetic Datum Transformation[J]. Journal of Geodesy, 1999, 73(5): 268–274. DOI:10.1007/s001900050243 |
| [4] | 沈云中, 胡雷鸣, 李博峰. Bursa模型用于局部区域坐标变换的病态问题及其解法[J]. 测绘学报, 2006, 35(2): 95–98. SHEN Yunzhong, HU Leiming, LI Bofeng. Ill-posed Problem in Determination of Coordinate Transformation Parameters with Small Area's Data Based on Bursa Model[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2): 95–98. |
| [5] | 陈义, 沈云中, 刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报(信息科学版), 2004, 29(2): 1101–1105. CHEN Yi, SHEN Yunzhong, LIU Dajie. A Simplified Model of Three Dimensional-datum Transformation Adapted to Big Rotation Angle[J]. Geomatics and Information Science of Wuhan University, 2004, 29(2): 1101–1105. |
| [6] | ABOU-BEIH O M, AL-GARNI A M. Precise Geodetic Positioning Based on the Concept of Variable Datum Transformation Parameters[J]. Australian Surveyor, 1996, 41(3): 214–220. DOI:10.1080/00050338.1996.10558629 |
| [7] | 熊介, 杨元喜. 三维大地网的转换与变形[J]. 测绘学报, 1988, 17(1): 1–8. XIONG Jie, YANG Yuanxi. On the Transformation and Deformation of Three-dimensional Geodetic Network[J]. Acta Geodaetica et Cartographica Sinica, 1988, 17(1): 1–8. |
| [8] | 杨元喜, 徐天河. 不同坐标系综合变换法[J]. 武汉大学学报(信息科学版), 2001, 26(6): 509–513. YANG Yuanxi, XU Tianhe. The Combined Method of Datum Transformation between Different Coordinate Systems[J]. Geomatics and Information Science of Wuhan University, 2001, 26(6): 509–513. |
| [9] | 曾安敏, 张丽萍. 顾及随机误差和局部变形误差的坐标组合转换法[J]. 大地测量与地球动力学, 2012, 32(2): 120–123, 127. ZENG Anmin, ZHANG Liping. Combined Method for Datum Transformation Considering Stochastic Error and Local Deformation[J]. Journal of Geodesy and Geodynamics, 2012, 32(2): 120–123, 127. |
| [10] | YOU R J, HWANG H W. Coordinate Transformation Between Two Geodetic Datums of Taiwan by Least-squares Collocation[J]. Journal of Surveying Engineering, 2006, 132(2): 64–70. DOI:10.1061/(ASCE)0733-9453(2006)132:2(64) |
| [11] | 曾安敏. 基于拟合推估的1980西安坐标系到2000国家坐标系的变换[J]. 大地测量与地球动力学, 2008, 28(5): 157–160. ZENG Anmin. Transformation from 1980 Xi'an Coordinate System to 2000 Chinese Coordinate System Based on Collocation[J]. Journal of Geodesy and Geodynamics, 2008, 28(5): 157–160. |
| [12] | 周江文. 拟合推估新解之一--两步解法[J]. 测绘学报, 2002, 31(3): 189–191. ZHOU Jiangwen. A Two Steps Solution of Collocation[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 189–191. |
| [13] | 杨元喜, 刘念. 拟合推估两步极小解法[J]. 测绘学报, 2002, 31(3): 192–195. YANG Yuanxi, LIU Nian. A New Resolution of Collocation by Two Minimization Steps[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 192–195. |
| [14] | 杨元喜, 张菊清, 张亮. 基于方差分量估计的拟合推估及其在GIS误差纠正的应用[J]. 测绘学报, 2008, 37(1): 152–157. YANG Yuanxi, ZHANG Juqing, ZHANG Liang. Variance Component Estimation Based Collocation and Its Application in GIS Error Fitting[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 152–157. |
| [15] | YANG Y, HE H, XU T. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 75(2-3): 109–116. DOI:10.1007/s001900000157 |
| [16] | YANG Yuanxi, XU Tianhe. An Adaptive Kalman Filter Based on Sage Windowing Weights and Variance Components[J]. The Journal of Navigation, 2003, 56(2): 231–240. DOI:10.1017/S0373463303002248 |
| [17] | YANG Y, ZENG A, ZHANG J. Adaptive Collocation with Application in Height System Transformation[J]. Journal of Geodesy, 2009, 83(5): 403–410. DOI:10.1007/s00190-008-0226-9 |
| [18] | 曾安敏, 张丽萍, 吴富梅, 等. XAS80到CGCS2000坐标转换的自适应拟合推估算法[J]. 武汉大学学报(信息科学版), 2012, 37(12): 1434–1437. ZENG Anmin, ZHANG Liping, WU Fumei, et al. Adaptive Collocation Method to Coordinate Transformation from XAS80 to CGCS2000[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12): 1434–1437. |
| [19] | 袁庆, 楼立志, 陈玮娴. 加权总体最小二乘在三维基准转换中的应用[J]. 测绘学报, 2011, 40(S): 115–119. YUAN Qing, LOU Lizhi, CHEN Weixian. The Application of the Weighted Total Least-squares to Three Dimensional-datum Transformation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S): 115–119. |
| [20] | 方兴, 曾文宪, 刘经南, 等. 三维坐标转换的通用整体最小二乘算法[J]. 测绘学报, 2014, 43(11): 1139–1143. FANG Xing, ZENG Wenxian, LIU Jingnan, et al. A General Total Least Squares Algorithm for Three Dimensional Coordinate Transformations[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1139–1143. DOI:10.13485/j.cnki.11-2089.2014.0193 |
| [21] | 陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5): 715–722. CHEN Yi, LU Jue. Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 715–722. |
| [22] | 姚宜斌, 孔建. 顾及设计矩阵随机误差的最小二乘组合新解法[J]. 武汉大学学报(信息科学版), 2014, 39(9): 1028–1032. YAO Yibin, KONG Jian. A New Combined LS Method Considering Random Errors of Design Matrix[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9): 1028–1032. |
| [23] | 姚宜斌, 黄书华, 张良, 等. 求解三维坐标转换参数的整体最小二乘新方法[J]. 武汉大学学报(信息科学版), 2015, 40(7): 853–857. YAO Yibin, HUANG Shuhua, ZHANG Liang, et al. A New Method of TLS for Solving the Parameters of Three-dimensional Coordinate transformation[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 853–857. |
| [24] | 孔建, 姚宜斌, 吴寒. 整体最小二乘的迭代解法[J]. 武汉大学学报(信息科学版), 2010, 35(6): 711–714. KONG Jian, YAO Yibin, WU Han. Iterative Method for Total Least-squares[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 711–714. |
| [25] | SHEN Yunzhong, LI Bofeng, CHEN Yi. An Iterative Solution of Weighted Total Least-squares Adjustment[J]. Journal of Geodesy, 2011, 85(4): 229–238. DOI:10.1007/s00190-010-0431-1 |
| [26] | SHEN Y Z, CHEN Y, ZHANG D H. A Quaternion-based Geodetic Datum Transformation Algorithm[J]. Journal of Geodesy, 2006, 80(5): 233–239. DOI:10.1007/s00190-006-0054-8 |
| [27] | KOTSAKIS C, VATALIS A, SANSò F. On the Importance of Intra-frame and Inter-frame Covariances in Frame Transformation Theory[J]. Journal of Geodesy, 2014, 88(12): 1187–1201. DOI:10.1007/s00190-014-0753-5 |
| [28] | 李微晓, 沈云中, 李博峰. 顾及2套坐标误差的三维坐标变换方法[J]. 同济大学学报(自然科学版), 2011, 39(8): 1243–1246. LI Weixiao, SHEN Yunzhong, LI Bofeng. Three-dimensional Coordinate Transformation with Consideration of Coordinate Errors in Two Coordinate Systems[J]. Journal of Tongji University (Natural Science), 2011, 39(8): 1243–1246. |
| [29] | 李博峰, 沈云中, 李微晓. 无缝三维基准转换模型[J]. 中国科学:地球科学, 2012, 55(12): 2099–2108. LI Bofeng, SHEN Yunzhong, LI Weixiao. The Seamless Model for Three-dimensional Datum Transformation[J]. Science China Earth Science, 2012, 55(12): 2099–2108. DOI:10.1007/s11430-012-4418-z |
| [30] | 李博峰. 无缝仿射基准转换模型的方差分量估计[J]. 测绘学报, 2016, 45(1): 30–35. LI Bofeng. Variance Component Estimation in the Seamless Affine Transformation Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 30–35. DOI:10.11947/j.AGCS.2016.20140676 |
| [31] | BLEWITT G.GPS Data Processing Methodology[C]//TEUNISSEN P J G, KLEUSBERG A.GPS for Geodesy.2nd ed.Berlin:Springer, 1998:231-270. |