2. 中国测绘科学研究院政府地理信息系统研究中心, 北京 100830
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China
空间分析能很好地反映地理要素的局部空间特征,准确地探索自然地理要素和社会人文要素空间特征的变化情况[1-3]。地理加权回归(geographically weighted regression,GWR)是一种有效探测空间非平稳特征的分析方法。它的思路是:将空间位置属性嵌入到回归系数中[4-5],建立因变量和自变量之间的函数关系,利用有标记(labeled)样本代入函数关系,算出回归系数,从而建立回归模型,进行分析或预测。这里有标记样本是指含有自变量和因变量的样本数据[6]。对应的,只含自变量、不含因变量的样本数据称为未标记(unlabeled)样本[6]。在GWR建模过程中,有标记样本的数量关系到模型的精度,当有标记样本较少时,往往难以建立可靠的模型[7]。而实际应用中,有时难以获得大量的有标记样本,如PM2.5浓度观测数据,受空气质量监测站数量的限制,一个城市同一个时间内,只能获取十几条甚至几条观测数据。但多数情况下,可以方便地收集大量的未标记样本。因此,如何在少量有标记样本情况下,充分利用未标记样本提升GWR模型精度是一个值得研究的问题。
半监督协同训练可以利用未标记样本辅助训练,提升少量有标记样本的学习性能[8-11]。本质上,半监督协同训练是一种半监督学习方法,它是在大量未标记样本和少量有标记样本的基础上,采用迭代的方式,让不同的学习器训练未标记样本,通过吸收训练结果提升学习性能[12]。文献[13]将半监督学习方法和k近邻回归方法相结合,提出了协同回归法(co-training regression,COREG)。文献[14]用支持向量机建立回归器,实现了基于支持向量机的半监督回归训练方法(Semi-SVM)。上述研究表明,基于半监督学习的回归方法可以充分利用大量未标记样本,提升少量有标记样本的回归精度。然而,受回归器的限制,这些方法还不能有效地分析空间非平稳特性,因此,在空间分析中存在一定的局限性。
综上所述,有两个问题需要解决:①少量有标记样本下,GWR回归精度不高;②当前基于半监督学习的回归方法无法分析空间非平稳特征。为解决上述问题,本文提出一种基于半监督学习的地理加权回归方法(semi-supervised-learning geographically weighted regression,SSLGWR)。该方法充分利用半监督学习的优势,通过未标记样本辅助,提升小样本数据下GWR的回归精度。同时,SSLGWR以GWR为回归器,可以研究空间非平稳特征,更适用于空间领域分析应用。
1 基于半监督学习的地理加权回归方法 1.1 方法原理SSLGWR的原理是:采用有标记样本建立两个差异化的回归器,利用两个回归器训练未标记样本,在每个回归器上选择训练结果最好的未标记样本,加入另一个回归器的有标记样本中,重新建立回归器,不断重复训练过程,直到满足特定条件为止。它实质上是利用两个回归器的“分歧”训练未标记样本,以提升回归模型的泛化能力。研究发现,当两个回归器存在显著的差异时,可以提升学习性能[15]。事实上,SSLGWR的差异性不仅体现在回归器上,还包括未标记样本,而未标记样本训练结果的质量也关系到回归器的性能。因此,本节重点阐述地理加权回归器、未标记样本和置信度方法3个关键内容。
1.1.1 地理加权回归器原理地理加权回归的回归系数与样本空间位置有关,即自变量对因变量的影响随空间位置的变化而变化[16-17]。影响的程度可以用一个距离函数表示,该距离称为带宽,影响程度称为空间权重,距离函数称为空间核函数,简称核函数[4]。常用的核函数有距离阈值法、距离反比法、高斯(Gauss)核函数和近高斯(Bi-square)核函数等[4, 13]。当确定核函数后,存在一个带宽,使回归模型的误差最小,此时的带宽称为最优带宽[18]。地理加权回归模型的关键是选择核函数,确定最优带宽。研究发现,不同核函数的带宽敏感度不同,而带宽的变化会对结果产生大幅度影响。因此,核函数和带宽可以用来区分回归器。设回归器为
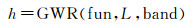 (1)
(1)
式中,fun表示核函数;L表示有标记样本,记作L={(xi,ui,vi,yi)| i=1,2,…,n};band表示最优带宽。
带宽过大回归参数的估计偏大,带宽过小回归参数的估计方差会偏大[18]。为了减小带宽造成的误差,当重建回归器时,需要重新计算带宽。本文最优带宽采用Cleveland提出的CV交叉验证法来计算[19]
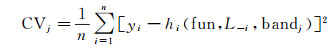 (2)
(2)
式中,CVj表示带宽为bandj时的CV值,j=1,2,…,m表示m个备选带宽;yi为因变量y在(xi,ui,vi)处的观测值;L-i表示去掉(xi,ui,vi,yi)后的有标记样本。选择bandk使CV值最小
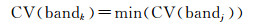 (3)
(3)
式中,bandk即为最优带宽。
1.1.2 未标记样本为了提升泛化能力,除了保持回归器的差异性外,训练的未标记样本也应保持显著差异。因此,未标记样本的选择应遵循下述命题。
设U为未标记样本,记作U={(xi,ui,vi)|i=1,2, …,m},设U1、U2分别为回归器1和2在某次训练时选择的未标记数据,记作U1={(xi,ui,vi)|i=1,2,…,l},U2={(xi,ui,vi)|i=1,2,…,l},U1⊂U,U2⊂U。那么,对任意(xi,ui,vi)∈U1,则(xi,ui,vi)∉U2,且对任意(xi,ui,vi)∈U2,则(xi,ui,vi)∉U1。
U1、U2数据量(即l值)的设置要考虑未标记样本U总量、训练次数和训练时间等因素。如果l值太大,不仅会增加每次的训练时间,而且在U一定的情况下,训练次数会减少,可能会因训练不够充分,导致学习效果不明显。如果l值太小,备选的训练数据就很少,可能无法挑出满足条件的训练结果,造成回归性能无法优化。
1.1.3 置信度方法置信度方法用于从若干未标记训练数据中选择优质的训练结果。它满足预测一致性原则,即具有真实标记的样本应能较一致地体现出回归的内在规律,因此,被回归器以高置信度选择的样本应是使该回归器与有标记样本更一致的样本[15]。本文采用均方误差(mean squared error,MSE)作为置信度判断的指标,当选择置信度高的未标记数据时可描述为如下命题:如果在未标记样本中存在一条数据,当其加入有标记样本后,使回归器的MSE变小且减小的幅度最大,那么这条数据即为置信度最高的未标记样本[7, 13]。在训练过程中,采用有标记样本来检测回归器训练前后性能的改变情况。设yL为有标记样本的真实值,ŷL为有标记样本在原回归器上的预测值,ŷ′L为有标记样本在新回归器上的预测值,新回归器是指吸收了未标记样本后重新建立的回归器。那么置信度可记为
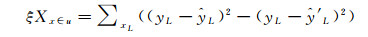 (4)
(4)
那么,当存在ξXx∈u>0时,令
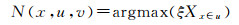 (5)
(5)
式中,N(x,u,v)即为置信度最高的未标记样本。这里,置信度大于零说明存在未标记样本使回归器性能提升,置信度最大说明性能提升幅度最大,即选中的数据是参与训练的未标记样本中置信度最高的数据。
1.2 算法流程SSLGWR的过程可概括为:首先利用不同核函数和有标记样本建立两个回归器。然后从未标记样本池中选择两份未标记数据,分别在两个回归器上进行回归训练。再利用置信度方法选择最优的未标记数据,加入到另一个回归器的有标记样本中,重新建立回归器模型。重复训练过程直到循环结束为止,最终模型的预测结果为两个回归器预测结果的平均数。
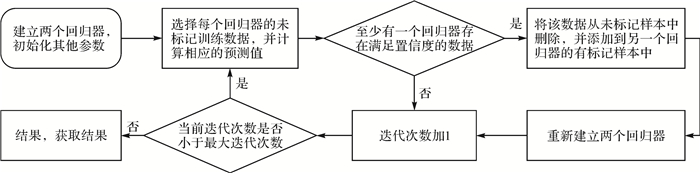
SSLGWR流程如图 1所示,对应步骤描述如下。
|
| 图 1 SSLGWR流程 Fig. 1 Flow chart of SSLGWR |
(1)获取有标记样本、未标记样本;计算不同核函数下有标记样本的最优带宽,建立两个回归器;初始化参数,设置训练最大迭代次数、未标记训练样本的数量。
(2)对每一个回归器,从未标记样本中选择未标记训练数据,并计算其在对应回归器上的预测值。
(3)对每个回归器上的未标记训练数据进行置信度判断,当至少有一个回归器存在置信度高的数据时执行步骤(4),否则执行步骤(6)。
(4)将选中的未标记样本和预测值作为有标记样本,加入另一个回归器中,同时,从未标记样本中删除该数据。
(5)当有标记样本发生变化时,计算带宽,重新建立回归器模型。
(6)迭代次数增加1。
(7)判断当前迭代次数是否小于最大迭代次数,是则执行步骤(2),否则执行步骤(8)。
(8)循环结束,获取两个回归器有标记样本和回归器模型。输出结果为两个回归器预测值的平均数。
2 试验本文基于Matlab实现了SSLGWR方法。设置最大迭代次数为50次,每次训练的未标记数据量为100。程序将有标记样本之间的距离分为11等份,取中间10个节点作为备选带宽。试验以MSE作为性能评价指标,性能提升比率是训练前后的MSE之差与训练前MSE的比值[7, 13]。此外,结果用成对T检验来评价显著性水平。本文分别用模拟数据和真实数据进行测试,并采用GWR、COREG方法进行对比。
2.1 模拟数据试验 2.1.1 试验数据模拟数据共8套,公式如表 1所示。其中,x表示自变量,u、v表示位置变量,y表示因变量,U表示服从均匀分布,为了模拟真实性,数据中增加高斯白噪声。模拟数据的数据量在1000到3000之间。模拟数据1-6来自文献[18]研究地理加权回归方法的试验数据,模拟数据7、8是文献[7, 13]测试COREG方法性能的试验数据。参考文献[7, 13]COREG的试验配置,每套数据按照70%和30%的比例分为试验数据和测试数据,试验数据按不同比例分为有标记样本和未标记样本,每个试验都采用10%:90%、30%:70%、50%:50% 3种比例配置,每组试验重复30次。
| 编号 | 公式 | 变量取值范围 | 数量 |
| 1 | y=(u+v)+ 3ln (1+u)x/5+ε |
x~U(0, 1),u, v~U[0, 20] |
1000 |
| 2 | y=6+ux1+ vx2+ε |
x1, x2~U(0, 1),u, v~U[0, 20] |
1000 |
| 3 | y=sin (u)+5x1+ vx2+ε |
x1, x2~U(0, 1)u, v~U[0, 20] |
2000 |
| 4 | y=sin (u)+5x1+ x2+ε |
x1, x2~U(0, 1),u, v~U[0, 20] |
1000 |
| 5 | y=uv+10x1+ 5x2+(u+v)x3+ε |
x1, x2, x3~U(0, 1),u, v~U[0, 20] |
3000 |
| 6 | y=10sin (πx1x2)+ 20(x3-0.5)2+ 10u+5v+ε |
x1, x2, x3~U(0, 1),u, v~U[0, 1] |
2000 |
| 7 | y=0.79+1.27x1x2+ 1.56ux1+ 3.42vx2+2.06uvx3+ε |
x1, x2, x3~U(0, 1),u, v~U[0, 1] |
1000 |
| 8 | y=0.6x+0.3u+ε | x1, x2, x3~U(0, 1),u, v~U[0, 1] |
2000 |
2.1.2 结果分析
表 2记录了某一次试验的结果。首先,对比SSLGWR与GWR在相同配置下的MSE,除了模拟数据1在50%标记数据下GWR略优于SSLGWR外,其余配置参数下SSLGWR的MSE均小于GWR,说明半监督训练,可以有效地利用未标记样本,提升回归模型的整体性能。其次,对比SSLGWR与COREG,在10%有标记样本下,COREG方法性能最优,在30%和50%的有标记样本下,COREG性能最差。说明当有标记样本增加时,空间非平稳特征成为影响回归性能的主要因素,由于COREG无法探测空间非平稳特征,回归精度最差。最后,对比SSLGWR在不同配置参数下的MSE,发现10%标记样本的MSE最大,50%标记样本下的MSE最小,30%标记样本下的MSE与50%的相差不大,说明有标记样本数据量对回归模型性能影响很大,当训练数据达到一定数量时,回归模型的性能趋于稳定。
| 编号 | 10%有标记样本 | 30%有标记样本 | 50%有标记样本 | ||||||||
| GWR | COREG | SSLGWR | GWR | COREG | SSLGWR | GWR | COREG | SSLGWR | |||
| 1 | 13.32 | 2.75 | 10.83** | 1.97 | 2.50 | 1.91* | 1.39 | 2.12 | 1.39 | ||
| 2 | 10.44 | 3.21 | 9.68** | 1.64 | 2.99 | 1.61* | 1.41 | 3.01 | 1.36* | ||
| 3 | 9.67 | 10.38 | 5.70** | 1.48 | 6.89 | 1.49* | 1.29 | 5.72 | 1.29* | ||
| 4 | 26.05 | 4.47 | 9.94** | 3.71 | 3.04 | 2.49** | 1.37 | 2.94 | 1.36* | ||
| 5 | 61.08 | 30.03 | 21.35** | 2.11 | 16.66 | 2.09* | 1.89 | 15.70 | 1.88* | ||
| 6 | 18.9 | 6.84 | 16.29** | 10.11 | 5.02 | 9.52** | 8.71 | 5.06 | 8.69* | ||
| 7 | 287.29 | 21.61 | 64.87*** | 2.27 | 1.85 | 1.99** | 1.39 | 1.88 | 1.36* | ||
| 8 | 2.75 | 1.42 | 1.86*** | 1.06 | 1.63 | 1.05** | 1.01 | 1.68 | 1.01* | ||
| 注:*表示0.1的显著度;**表示0.05的显著度;***表示0.01的显著度。 | |||||||||||
表 3记录了SSLGWR方法30次试验性能提升比率的平均值。除了模拟数据1在50%下的性能没有提升,其他性能均有提升,大部分数据提升效果显著。说明SSLGWR在半监督学习辅助下,显著地提升了少量有标记样本的回归性能,且在少量有标记样本下作用最显著。此外,10%、30%、50%标记样本下SSLGWR性能分别平均提升39.66%、11.92%、0.94%,说明SSLGWR性能提升比率随着有标记样本量的增加,呈减小趋势。这是因为随着有标记样本量的增加,回归模型逐渐趋于稳定,性能提升的空间变小。
| (%) | |||||||||
| 标记样本 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 平均值 |
| 10 | 18.68 | 7.3 | 41.04 | 61.85 | 65.04 | 13.8 | 77.42 | 32.14 | 39.66 |
| 30 | 5.12 | 2.5 | 11.3 | 32.88 | 1.11 | 6.26 | 15.7 | 12.23 | 11.92 |
| 50 | -0.13 | 4.06 | 0.21 | 0.43 | 0.33 | 0.25 | 2.03 | 0.34 | 0.94 |
2.2 真实数据试验 2.2.1 数据准备与预处理
本文以京津冀地区人口分布与影响因素作为真实数据进行试验。人口分布与社会经济发展、自然条件、交通等因素密切相关[20-21]。本文以京津冀2897个乡镇为统计单元,以乡镇人口总数为因变量,以乡镇质心的平面投影坐标为空间位置变量,选择GDP、道路网密度、气温、降雨、DEM、土地利用、地形地貌等17个指标作为备选自变量,其中人口数据来源第6次人口普查,GDP、气温、降雨、DEM、地形地貌数据来源于中国科学院资源环境科学数据中心,道路网数据和土地利用数据来源于中国地图出版社。经过多重共线性分析和逐步回归分析[22],选择地均GDP、道路网密度、DEM、居民地面积和林地面积5个因素建模。真实数据采用全部数据作为试验数据,采用10折交叉验证法进行验证。试验按10%:90%、30%:70%、50%:50% 3种比例配置有标记样本和未标记样本,每组试验重复30次。
2.2.2 结果分析试验记录了性能提升比率最优的MSE、RMSE、R2、Rj2和成对T检验的P-值,计算了30次试验性能提升的平均值,如表 4所示。首先,从性能平均提升比率看,3种配置下SSLGWR性能均有提升,并在10%配置下性能提升比率最高,说明半监督学习能帮助GWR提升回归性能,且在小样本数据下SSLGWR方法的优势最显著。其次,COREG在10%配置下,性能优于GWR和SSLGWR,而在30%和50%配置下,性能比GWR和SSLGWR差。说明有标记样本的数据量和空间非平稳特征是制约回归精度的重要因素,有标记样本量增加后,空间非平稳特征成为主要影响因素。第三,真实数据试验的性能提升比率没有呈现递减规律,这是因为相对京津冀研究区,50%的数据量仍然属于小样本数据。
| 方法 | MSE | RMSE | R2 | Rj2 | P-值 | 性能平均提升/% | |
| 10% | GWR | 0.007 4 | 0.086 0 | 0.738 8 | 0.737 4 | - | - |
| COREG | 0.006 3 | 0.079 4 | 0.793 4 | 0.792 1 | |||
| SSLGWR | 0.006 7 | 0.081 9 | 0.788 | 0.787 3 | 0.036 1 | 8.94 | |
| 30% | GWR | 0.003 4 | 0.058 3 | 0.641 0 | 0.639 7 | - | - |
| COREG | 0.007 3 | 0.085 4 | 0.611 3 | 0.612 5 | |||
| SSLGWR | 0.003 1 | 0.055 7 | 0.662 0 | 0.659 8 | 0.009 8 | 3.36 | |
| 50% | GWR | 0.003 | 0.054 8 | 0.853 4 | 0.850 9 | - | - |
| COREG | 0.006 1 | 0.078 1 | 0.805 5 | 0.802 7 | |||
| SSLGWR | 0.002 2 | 0.046 9 | 0.873 7 | 0.871 3 | 0.004 8 | 5.87 |
图 2绘制了真实值和不同配置下SSLGWR模型预测值的空间分布情况。从宏观角度观察,4幅图中人口分布空间趋势基本保持一致,都集中在“北京-天津-邯郸-石家庄”形成的区域内,说明3个回归模型在全局趋势预测上接近真实情况。从微观角度观察,4幅图中人口都集中分布在北京、天津,但图(b)的范围比图(a)的范围大,而图(c)、图(d)的情况优于图(b),这是由于预测结果偏大造成的。另外图(d)探测出承德市人口较多的区域符合真实情况,结果优于图(b)、图(c),说明50%配置试验结果在局部分析上要优于其他配置结果。

|
| 图 2 京津冀人口与预测分布 Fig. 2 The distribution of population in Beijing, Tianjin and Hebei |
3 结论
本文提出了一种基于半监督学习的地理加权回归方法,它能充分利用未标记样本,在有标记样本数据量小的情况下,显著地提升回归性能。同时,利用地理加权回归方法作为回归器,能有效地分析回归模型中的非平稳因素,从而让半监督回归方法适用于空间分析。本文通过模拟数据和真实数据对SSLGWR进行测试,模拟数据性能提升比率明显,真实数据性能有所提升。试验结果说明,在少量有标记样本回归分析中,SSLGWR能有效地利用未标记样本提升回归模型的泛化能力。希望SSLGWR能在房价预测、PM2.5预测等方面得到推广应用。但是,SSLGWR方法也存在一定的不足。在训练过程中,由于训练未标记样本和检验未标记样本都是利用有标记样本进行,尽管本文采用了置信度方法筛选未标记样本,尽量控制过拟合问题,但仍然不可避免,未来可进一步解决。
| [1] | 杨康, 李满春, 刘永学, 等. 基于累积相似度表面的空间权重矩阵构建方法[J]. 测绘学报, 2012, 41(2): 259–265, 272. YANG Kang, LI Manchun, LIU Yongxue, et al. Accumulated Similarity Surface for Spatial Weights Matrix Construction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 259–265, 272. |
| [2] | 朱长明, 张新, 路明, 等. 湖盆数据未知的湖泊动态库容遥感监测方法[J]. 测绘学报, 2015, 44(3): 309–315. ZHU Changming, ZHANG Xin, LU Ming, et al. Lake Storage Change Automatic Detection by Multi-source Remote Sensing without Underwater Terrain Data[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 309–315. DOI:10.11947/j.AGCS.2015.20130438 |
| [3] | 禹文豪, 艾廷华, 刘鹏程, 等. 设施POI分布热点分析的网络核密度估计方法[J]. 测绘学报, 2015, 44(12): 1378–1383, 1400. YU Wenhao, AI Tinghua, LIU Pengcheng, et al. Network Kernel Density Estimation for the Analysis of Facility POI Hotspots[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1378–1383, 1400. DOI:10.11947/j.AGCS.2015.20140538 |
| [4] | FOTHERINGHAM A S, CHARLTON M, BRUNSDON C. Measuring Spatial Variations in Relationships with Geographically Weighted Regression[M]//FISCHER M M, GETIS A. Recent Developments in Spatial Analysis. Berlin Heidelberg:Springer, 1997:60-82. |
| [5] | HUANG Bo, WU B, BARRY M. Geographically and Temporally Weighted Regression for Modeling Spatio-temporal Variation in House Prices[J]. International Journal of Geographical Information Science, 2010, 24(3): 383–401. DOI:10.1080/13658810802672469 |
| [6] | 张晨光, 张燕. 半监督学习[M]. 北京: 中国农业科学技术出版社, 2013: 26-29. ZHANG Chenguang, ZHANG Yan. Semi-supervised Learning[M]. Beijing: China Agricultural Sciences and Technology Press, 2013: 26-29. |
| [7] | 黎铭.单视图协同训练方法的研究[D].南京:南京大学, 2008. LI Ming. Research on Single-view Co-training Approaches[D]. Nanjing:Nanjing University, 2008. |
| [8] | ZHOU Zhihua, LI Ming. Semi-supervised Learning by Dis-agreement[J]. Knowledge and Information Systems, 2010, 24(3): 415–439. DOI:10.1007/s10115-009-0209-z |
| [9] | 周志华, 王珏. 机器学习及其应用2007[M]. 北京: 清华大学出版社, 2007: 259-275. ZHOU Zhihua, WANG Jue. Machine Learning and Applications 2007[M]. Beijing: Tsinghua University Press, 2007: 259-275. |
| [10] | WANG Wei, ZHOU Zhihua. A New Analysis of Co-training[C]//Proceedings of the 27th International Conference on Machine Learning. Haifa, Israel:[s.n.], 2010. |
| [11] | YANG Yi, LIU Jiping, XU Shenghua, et al. An Extended Semi-supervised Regression Approach with Co-training and Geographical Weighted Regression:A Case Study of Housing Prices in Beijing[J]. ISPRS International Journal of Geo-Information, 2016, 5(1): 4. DOI:10.3390/ijgi5010004 |
| [12] | GOLDMAN S A, ZHOU Yan. Enhancing Supervised Learning with Unlabeled Data[C]//Proceedings of the Seventeenth International Conference on Machine Learning. San Francisco, CA:ACM, 2000:327-334. |
| [13] | ZHOU Zhihua, LI Ming. Semisupervised Regression with Cotraining-style Algorithms[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(11): 1479–1493. DOI:10.1109/TKDE.2007.190644 |
| [14] | 马蕾, 汪西莉. 基于支持向量机协同训练的半监督回归[J]. 计算机工程与应用, 2011, 47(3): 177–180. MA Lei, WANG Xili. Semi-supervised Regression Based on Support Vector Machine Co-training[J]. Computer Engineering and Applacation, 2011, 47(3): 177–180. |
| [15] | 周志华. 基于分歧的半监督学习[J]. 自动化学报, 2013, 39(11): 1871–1878. ZHOU Zhihua. Disagreement-based Semi-supervised Learning[J]. Acta Automatica Sinica, 2013, 39(11): 1871–1878. DOI:10.3724/SP.J.1004.2013.01871 |
| [16] | WU Bo, LI Rongrong, HUANG Bo. A Geographically and Temporally Weighted Autoregressive Model with Application to Housing Prices[J]. International Journal of Geographical Information Science, 2014, 28(5): 1186–1204. DOI:10.1080/13658816.2013.878463 |
| [17] | ROBINSON D P, LLOYD C D, MCKINLEY J M. Increasing the Accuracy of Nitrogen Dioxide (NO2) Pollution Mapping Using Geographically Weighted Regression (GWR) and Geostatistics[J]. International Journal of Applied Earth Observation and Geoinformation, 2013, 21: 374–383. DOI:10.1016/j.jag.2011.11.001 |
| [18] | 覃文忠.地理加权回归基本理论与应用研究[D].上海:同济大学, 2007. QIN Wenzhong. The Basic Theoretics and Application Research on Geographically Weighted Regression[D]. Shanghai:Tongji University, 2007. http://www.oalib.com/references/17553961 |
| [19] | CLEVELAND W S. Robust Locally Weighted Regression and Smoothing Scatterplots[J]. Journal of the American Statistical Association, 1979, 74(368): 829–836. DOI:10.1080/01621459.1979.10481038 |
| [20] | 柏中强, 王卷乐, 杨雅萍, 等. 基于乡镇尺度的中国25省区人口分布特征及影响因素[J]. 地理学报, 2015, 70(8): 1229–1242. BAI Zhongqiang, WANG Juanle, YANG Yaping, et al. Characterizing Spatial Patterns of Population Distribution at Township Level across the 25 Provinces in China[J]. Acta Geographica Scinica, 2015, 70(8): 1229–1242. |
| [21] | 戚伟, 李颖, 刘盛和, 等. 城市昼夜人口空间分布的估算及其特征--以北京市海淀区为例[J]. 地理学报, 2013, 68(10): 1344–1356. QI Wei, LI Ying, LIU Shenghe, et al. Estimation of Urban Population at Daytime and Nighttime and Analyses of Their Spatial Pattern:A case Study of Haidian District, Beijing[J]. Acta Geographica Scinica, 2013, 68(10): 1344–1356. |
| [22] | GOLDSTEIN R. Conditioning Diagnostics:Collinearity and Weak Data in Regression[J]. Technometrics, 1993, 35(1): 85–86. DOI:10.1080/00401706.1993.10484997 |



