高精度轨道数值积分算法是导航卫星动力学精密定轨的基础。现阶段常用的高精度数值积分算法有单步法(如Runge-Kutta-Fehlberg算法,RKF)和多步法(如Admas预估校正算法)两种[1-2]。为了充分利用这两种积分方法的优势,实际应用中常常先通过RKF计算出Admas起始状态点,再进行Admas积分(RKF-Admas方法),有效提高单颗卫星长弧段轨道数值积分效率[3-5]。
随着我国北斗导航卫星区域系统(BDS)建成运行[6]以及其他GNSS(global navigation satellite system)系统(美国GPS、俄罗斯GLONASS、欧洲Galileo)的快速发展[7],多GNSS系统兼容应用是卫星导航领域的发展趋势,其中包括多系统GNSS卫星联合精密定轨[8-11]。在可预见的未来,空间中将有多达90余颗GNSS卫星投入使用[12],而传统RKF-Admas方法将会显著影响多系统GNSS卫星数值积分效率,具体表现在:一方面,由于各颗卫星积分过程较为独立,传统方法采用逐颗卫星依次积分,这种方式导致了同一时刻各颗卫星摄动公共计算部分的过多冗余计算,并会随着卫星数的增加显著降低多卫星积分效率,这在效率要求较高的实时滤波定轨中尤为明显[13-14];另一方面,在长弧段轨道积分中,为了保证所有卫星的积分精度,传统方法在实际应用中通常采用较为保守的固定积分步长(如90 s),从而限制了计算效率。这是由于数值积分方法易受动力学模型异常扰动的影响(如卫星地影机动[15-17]),大步长会严重损害积分精度,并且步长对GNSS卫星的影响有待进行研究。鉴于此,文献[18—20]研究了变步长Admas积分算法,通过计算不同阶公式实时估计每一步的误差,并自适应确定每步积分所需步长。这种方法需要增加不同阶的计算量,适用于一般轨道类型卫星的变步长数值积分。然而GNSS卫星轨道类型较单一,均采用近圆形轨道[21](偏心率e≤0.01),运行速度和摄动力影响都较稳定,无需频繁变更积分步长。
综上所述,研究一种适用于多系统GNSS卫星的快速积分方法具有重要的意义。本文在RKF-Admas方法基础上,利用Admas预估校正算法特点,提出在大步长积分过程中通过预估值与校正值的差异探测动力学模型异常扰动,自适应降低Admas积分步长以保证积分精度,同时充分利用各颗卫星积分过程中的相同计算部分实现多卫星联合同步积分,从而达到快速积分目的。
1 多系统GNSS卫星快速积分算法 1.1 自适应变换Admas积分步长Admas预估校正算法使用被积函数值的线型多项式代替被积函数,在一步积分过程中只需计算两次动力学右函数,并且可以选取较大的步长,因此效率较单步法RKF高,常用于卫星长弧段轨道数值积分。该算法由两步构成,首先利用Adams-Bashforth显式公式通过历史存储的同阶数状态点对下一个状态点的值进行预报,然后利用Admas-Moulton隐式公式计算出下一个状态点的改进值[2, 22]。
假定卫星运动方程可表示为一阶微分方程
 (1)
(1)
式中,
n阶Adams-Bashforth显性公式由式(2) 给出
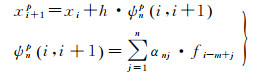 (2)
(2)
式中,xi+1p表示下一个状态点的预估值;h表示积分步长;ψnp(i, i+1)表示由被积函数值组成的n阶线型多项式,其多项式系数αnj可通过查表获得。
n阶Adams-Moulton隐性公式由式(3) 给出
 (3)
(3)
式中,xi+1表示下一个状态点的校正值;ψn(i, i+1)包含了由式(2) 给出的预估值计算得到的被积函数组成的n阶线性多项式,其系数βnj亦可通过查表获得。
由式(2) 与式(3) 可以看出,Adams-Bashforth显式公式计算得到的预估值只受历史状态被积函数值的影响,而Adams-Moulton隐式公式则受下一状态被积函数的影响。当被积函数受动力学模型异常扰动影响时(如进出地影或轨道机动),将会通过校正值与预估值之间差异反映出来。
n阶Adams-Moulton隐式公式截断误差可表示为
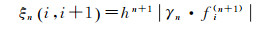 (4)
(4)
式中,γn表示后向差分系数[2]。由此可见,当被积函数受动力学模型异常扰动影响时,被积函数的n+1阶导数fi(n+1)将变得不连续,若步长h选取较大时,则会放大被积函数的不连续导致的误差,破坏了数值稳定性,导致长弧段积分误差积累不可忍受。
因此,可以通过构造预估值与校正值的差异探测动力学模型异常扰动,自适应降低Admas积分步长以保证积分精度。判断条件式如下
 (5)
(5)
式中,
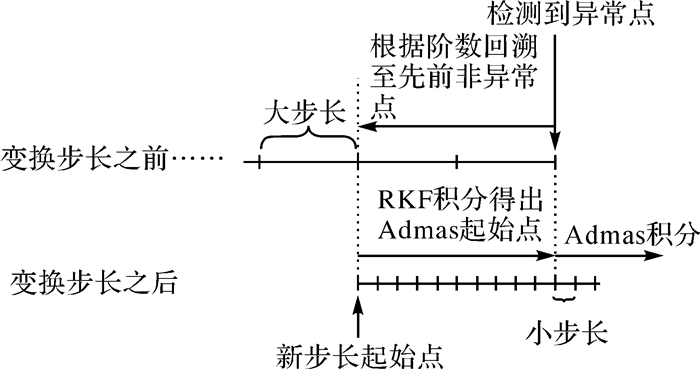
当Δxi+1满足式(5) 时,可认为动力学模型有异常发生。为保证积分精度,此时终止原先的积分过程,根据Admas阶数选取先前某个未发生异常的状态点,利用RKF积分得出较小步长Admas起始点后再继续积分过程,由此可以完成自适应Admas变换步长积分算法。值得说明的是,由于被积函数fi与积分步长无关,因此积分步长的调整不会影响积分轨道的连续性。以11阶Admas算法为例,其变换步长过程如图 1所示。
|
| 图 1 自适应变换Admas积分步长方法示意 Fig. 1 Diagram of the adaptive step-changed Admas integration method |
1.2 多系统GNSS卫星快速积分算法
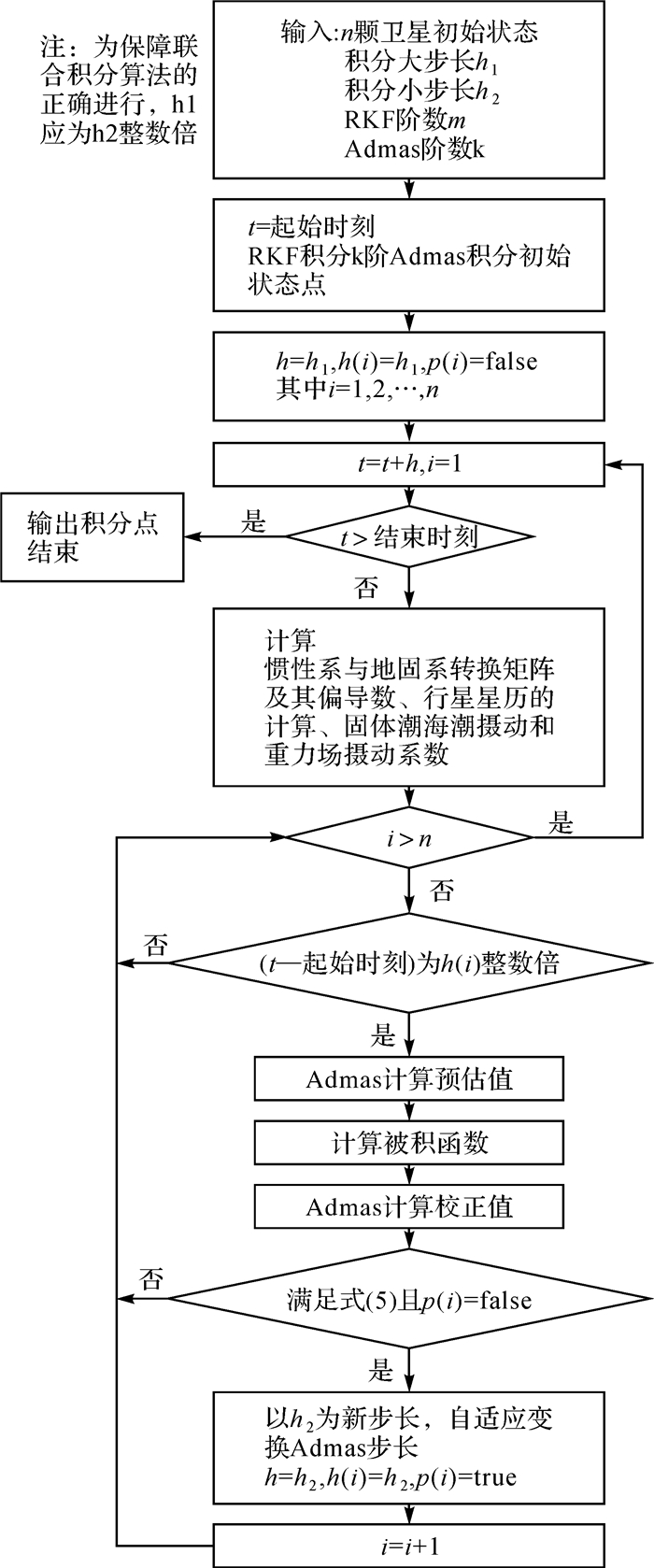
多系统GNSS卫星精密定轨对联合数据处理效率要求较高,其中就包括需要在较短时间内完成几十颗卫星的数值积分工作。由于各颗卫星积分过程较为独立,现阶段通常采用逐卫星依次积分,而同一时刻惯性系与地固系转换矩阵及其偏导数、行星星历的计算、固体潮海潮摄动和重力场摄动系数等对所有卫星影响相同,因此逐颗卫星依次积分存在过多的冗余计算。由于导航卫星轨道类型较单一,积分策略基本一致,这为多卫星同步积分的实现提供了便利。鉴于此,结合自适应变换Admas步长和多卫星联合同步积分两方面,提出一种多系统GNSS卫星快速积分算法:以RKF-Admas算法为基础,充分利用大步长及多卫星联合同步积分的效率优势,通过自适应变换Admas步长控制动力学模型扰动对卫星积分精度的损害,以达到快速精确完成多卫星积分目的。多系统GNSS卫星快速积分算法流程如图 2所示。
|
| 图 2 多系统GNSS卫星快速积分算法流程 Fig. 2 The flow chart of the rapid orbit integration algorithm for multi-GNSS satellites |
2 试验与分析 2.1 积分步长对轨道动力学拟合精度影响分析
为了提高积分效率,需要选取较大的积分步长。然而大步长会影响积分精度,因此需要分析不同积分步长(尤其是大步长)对导航卫星积分精度的影响。由于积分产生的误差会最终反映至轨道动力学拟合RMS中,因此轨道拟合可以用来评估不同步长对积分精度的影响。
利用武汉大学(Wuhan University, WHU)发布的GNSS卫星精密轨道产品[8],通过设置60 s、90 s、300 s和450 s 4种积分步长对GPS、GLONASS、BDS和Galileo卫星进行RKF-Admas(分别选取RKF8(9) 阶和11阶Admas)固定步长的单天数值积分与拟合计算(2014年,年积日275),其三维RMS由图 3给出。其中动力学模型选用IGS推荐的策略(http://acc.igs.org/reprocess2.html)。图中G03与G25两颗卫星因在精密星历中缺失未参与统计。从图中可以看出,有7颗GPS卫星(G05、G10、G12、G18、G20、G22和G32)、5颗BDS的GEO卫星(C01至C05) 以及1颗BDS的MEO卫星(C14) 对不同积分步长较敏感,其轨道拟合精度在不同步长间差异较大,尤其是当步长增加到450 s时,轨道拟合精度最大衰减至分米级别;而当步长在90 s以内时,积分仍能反映出较好的稳定性,其差异在2 mm以内。除去这13颗卫星,其余卫星轨道拟合精度对这4种积分步长不敏感,这说明即使将积分步长增加到450 s,大部分卫星的积分精度也并无损害(差异小于0.5 mm)。

|
| 图 3 不同积分步长GPS、GLONASS、BDS和Galileo卫星轨道拟合三维RMS Fig. 3 The 3D-RMS of 1-day orbit fitting applied for GPS, GLONASS, BDS and Galileo satellites based on different intergration step |
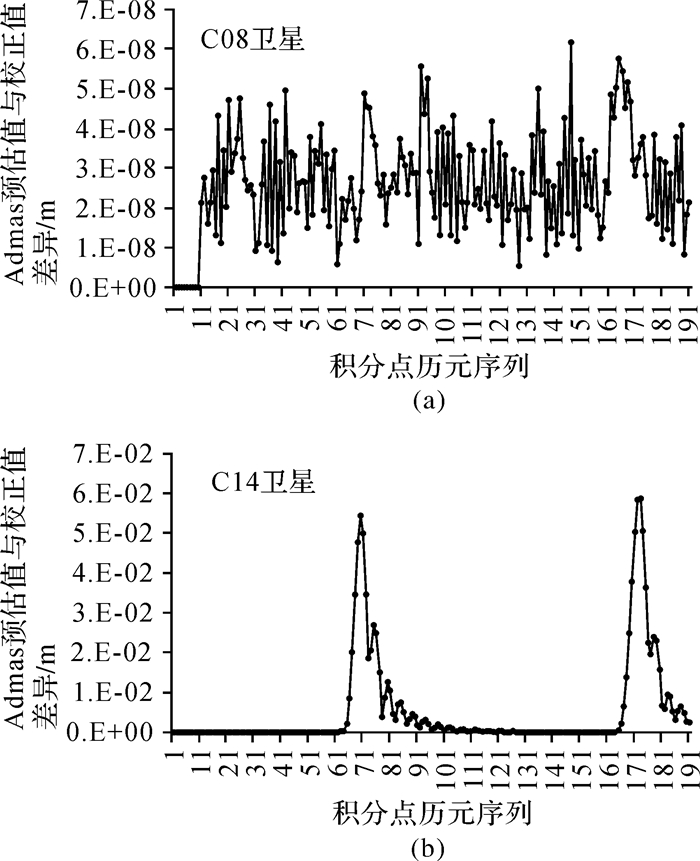
图 4给出了450 s积分步长时BDS的C08卫星与C14卫星在Admas积分过程中三维坐标位置预估值与校正值差异的单天时间序列(总共192个积分点)。由于Admas阶数为11,其起始的11个积分点由RKF计算获得,因此差异数值为零。从图中可以看出,C08卫星预估值与校正值差异的时间序列稳定(STD约为1×10-8 m),并且其值接近于零;而C14卫星的时间序列产生了两次明显的扰动,并且扰动幅度呈数量级增大,远远超过平稳数据点的变化范围。
|
| 图 4 Admas积分(450 s步长)卫星三维坐标位置预估值与校正值差异 Fig. 4 The difference of Admas (450 s step) prediction and correction for the satellite's position |
为了进一步探究扰动的原因,利用双锥体地影模型[15]统计当天各颗蚀卫星通过地影的起止时刻,其结果列于表 1中,单位为秒。从表 1中可以看出,C08卫星未受地影影响,被积函数光滑连续,因此Admas积分预报值与估计值差异时间序列较稳定且数值接近于零;C14卫星两次通过地影区间,并且进入地影时刻与图 4中的两次波动的起始时刻吻合,这是由于卫星进入地影时破坏了被积函数的连续性,采用大积分步长时在半影期间未被积分算法所采样,因此导致产生了明显的波动[2],从而影响积分精度。另一方面,所有检测到通过地影的卫星与图 3中不同积分步长结果差异较大的卫星一致,并且通过试验得知这些卫星具有与C14卫星相似的变化规律(GEO卫星略有不同,其时间序列只有一次波动,这与进出地影次数相符,由于篇幅有限,结果不再给出),而未通过地影的卫星具有与C08卫星相似的稳定性,因此进出地影为导致GNSS卫星被积函数不连续的主要原因。本文基于以上GNSS卫星Admas积分预报值与估计值差异变化特征,假定差异数值上两个数量级的跳跃即有可能发生了动力学异常扰动,即k取值100,则地影机动通过式(5) 同时结合双锥体地影模型可以准确检测出来。
| s | ||
| 卫星 | 起始时刻 | 结束时刻 |
| G05 | 660 | 3420 |
| 43 620 | 46 560 | |
| G12 | 7320 | 7980 |
| 50 280 | 51 240 | |
| G20 | 28 620 | 31 860 |
| 71 700 | 74 940 | |
| G32 | 24 900 | 27 000 |
| 67 920 | 70 140 | |
| C03 | 57 480 | 61 200 |
| C05 | 69 780 | 73 680 |
| G10 | 38 160 | 41 040 |
| 81 240 | 84 180 | |
| G18 | 12 120 | 15 060 |
| 55 200 | 58 200 | |
| G22 | 16 020 | 19 020 |
| 59 100 | 62 100 | |
| C01 | 50 280 | 54 240 |
| C02 | 64 620 | 68 580 |
| C04 | 45 540 | 49 320 |
| C14 | 26 940 | 27 960 |
| 73 140 | 74 520 | |
2.2 自适应变换Admas积分步长算法效果分析
由于大步长会导致蚀卫星积分精度的极大衰减,因此可以利用本文提出的自适应变换Admas积分步长算法来控制这种精度的衰减。为了验证自适应变换Admas积分步长算法效果,分别用固定步长Admas积分算法和自适应变换步长Admas积分算法对年积日275当天蚀卫星进行轨道拟合,其三维RMS由图 5给出。其中自适应算法中小步长和大步长分别设置为90 s和450 s。从图中可以看出,自适应变换步长算法可以有效避免大步长对蚀卫星积分精度的损害,其轨道拟合精度与固定为小步长的Admas积分算法精度相同,证明了本文提出的自适应变换Admas积分步长算法的有效性。

|
| 图 5 不同积分策略的蚀卫星轨道拟合三维RMS Fig. 5 The 3D-RMS of 1-day orbit fitting applied for satellites across eclipse based on different integration strategies |
2.3 多系统GNSS卫星快速积分算法精度及效率分析
为了充分验证多系统GNSS卫星快速积分方法的精度,分别利用IGS多模GNSS试验跟踪网(multi-GNSS experiment, MGEX)[7]的两个分析中心武汉大学(WHU)[8]和欧洲定轨中心(Center for Orbit Determination in Europe, CODE)[23]发布的GNSS精密轨道产品进行一个月的单天轨道拟合试验(2014年,年积日245至275),统计平均三维RMS。结合上节的分析,小步长选取90 s,大步长选取450 s,通过自适应变换Admas步长算法保证蚀卫星的积分精度。
图 6给出了一个月内四系统GNSS卫星单天轨道拟合平均三维RMS。从图中可以看出,算法具有较高的精度,其中WHU拟合三维RMS的平均值:GPS为11 mm,GLONASS为14 mm,BDS为16 mm,Galileo为12 mm;CODE拟合三维RMS的平均值:GPS为17 mm,GLONASS为18 mm,BDS为18 mm,Galileo为14 mm。由于本文采用的动力学模型与WHU产品一致,因此拟合精度略优于CODE产品。两个分析中心产品的平均三维拟合精度均优于20 mm,说明本文提出的快速积分算法能够满足精密定轨的需求。

|
| 图 6 4系统GNSS卫星单天轨道拟合平均三维RMS Fig. 6 The average 3D-RMS of 1-day orbit fitting for GNSS satellites |
表 2给出了本文快速积分算法与传统逐卫星固定步长算法在一个月内单天轨道拟合RMS差异的相关统计数据。为了保证包括蚀卫星在内的所有卫星的积分精度,传统积分方法固定积分步长选取为90 s。从表中可以看出,采用两种方法计算得到的差异均值均小于0.5 mm,最大值小于2 mm,说明本文提出的算法与传统方法具有相同的积分精度。由于快速积分算法中非蚀卫星实质上采用的是450 s大步长,因此这种积分差异主要是由两种方法积分步长不同导致的。此外,蚀卫星拟合RMS差异较非蚀卫星稍大,这是由于蚀卫星动力学模型的不连续性对积分步长变化的影响稍大,不过其值本身依然与非蚀卫星差异较小(0.1 mm左右),说明新算法能够有效处理大步长对蚀卫星的影响。
| mm | |||
| WHU | CODE | ||
| 非蚀卫星 | 平均值 | 0.4 | 0.3 |
| 最大值 | 1.3 | 1.2 | |
| 蚀卫星 | 平均值 | 0.5 | 0.4 |
| 最大值 | 1.8 | 1.4 | |
为了进一步验证多系统GNSS卫星快速积分方法对计算效率的提升作用,分别利用传统逐卫星固定步长积分、多卫星联合固定步长积分和多卫星联合自适应变换步长积分(即本文提出的快速积分方法)3种积分策略进行试验,统计平均单颗卫星的耗时以及总耗时随卫星数的变化(CPU主频2.60 GHz,内存容量2 GB)。图 7给出了以上3种积分策略下平均单颗卫星耗时。从图中可以看出,同时采用固定步长时,多卫星联合积分算法较逐卫星积分算法效率有明显的提高,其平均单颗卫星耗时均值分别为0.21 s和1.38 s,提高了约6倍,这是由于不同卫星共用计算部分在同一时刻只计算一次,大幅度提高了计算效率;同时采用多卫星联合积分时,自适应变换步长较固定步长算法效率也有所提高,其平均单颗卫星耗时均值为0.09 s,提高了约1倍,这是由于大部分未受地影影响的卫星有效利用了大步长的效率优势,减少了动力学模型计算次数。与传统逐卫星固定步长积分算法相比,自适应变换步长多卫星联合快速积分算法效率提升了14倍,说明本文提出的新算法具有较高的效率。

|
| 图 7 不同积分策略平均单颗卫星耗时 Fig. 7 The average computing time of a single satellite based on different integration strategies |
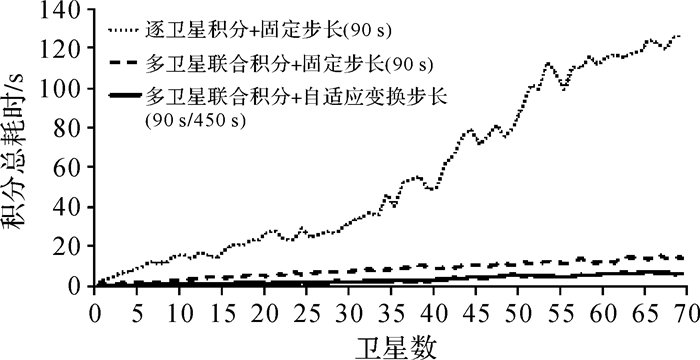
图 8给出了3种积分策略下计算总耗时与卫星数的关系。从图中可以看出随着卫星数的增加,3种积分策略的计算总耗时也增加,并且呈线性相关。然而,在线性变化趋势上不同积分策略具有不同的斜率,其中采用自适应变换步长的多卫星联合积分算法的斜率明显小于采用传统逐卫星固定步长积分算法的斜率,这说明参与积分计算卫星数目越多,效率提升越明显。可以预计在多达100颗卫星同时参与计算情况下,新算法仍能在10 s内完成单天轨道积分与拟合。
|
| 图 8 不同积分策略总耗时与卫星数的关系 Fig. 8 The relationship between the computing time and the number of satellites based on different integration strategies |
3 结论
随着多系统GNSS在轨卫星数的不断增加,传统逐卫星固定步长积分算法成为制约多系统GNSS卫星数值积分效率的重要因素。本文结合自适应变换Admas积分步长和多卫星联合同步积分两个方面实现了多系统GNSS卫星快速积分方法,并研究了不同积分步长对GNSS卫星积分精度的影响。试验结果表明:① 对于未受地影影响的卫星,积分步长增大到450 s时也不损失轨道拟合精度,而对于受地影影响的卫星,积分步长在90 s以内时轨道拟合精度差异小于2 mm;② 自适应变换Admas积分步长可以在充分利用大步长效率优势的同时,避免了大步长对蚀卫星积分精度的损害;③ 利用WHU和CODE发布的精密轨道产品,GPS/GLONASS/BDS/Galileo 4个系统轨道拟合平均三维RMS均优于20 mm,说明多系统GNSS卫星快速积分算法满足精密定轨的需求;④ 相比传统逐卫星固定步长积分算法,新算法在不损失传统算法积分精度前提下能显著提高计算效率,可用于精密定轨中变分方程的计算,其平均单颗卫星计算速度提升14倍,并且随着卫星数的增加,提升效果越明显。
致谢: 感谢武汉大学和欧洲定轨中心提供的GPS、GLONASS、BDS和Galileo卫星精密轨道产品。
| [1] | 刘林. 人造地球卫星轨道力学[M]. 北京: 高等教育出版社, 1992. LIU Lin. Orbit Dynamics of the Artificial Earth Satellite[M]. Beijing: Higher Education Press, 1992. |
| [2] | MONTENBRUCK O, GILL E. Satellite Orbits:Models, Methods and Applications[M]. New York: Springer, 2000. |
| [3] | 李敏. 多模GNSS融合精密定轨理论及其应用研究[D]. 武汉: 武汉大学, 2011. LI Min. Research on Multi-GNSS Precise Orbit Determination Theory and Application[D]. Wuhan:Wuhan University, 2011. |
| [4] | 赵齐乐. GPS导航星座及低轨卫星的精密定轨理论和软件研究[D]. 武汉: 武汉大学, 2004. ZHAO Qile. Research on Precision Orbit Determination Theory and Software of Both GPS Navigation Constellation and LEO Satellites[D]. Wuhan:Wuhan University, 2004. |
| [5] | 祝楚恒, 费景高. 联合应用Runge-Kutta公式与Adams公式的积分方法[J]. 电子计算机动态, 1963(2): 31–35. ZHU Chuheng, FEI Jinggao. Joint Application of Runge-Kutta and Admas Method[J]. Journal of Computer Research and Development, 1963(2): 31–35. |
| [6] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [7] | MONTENBRUCK O, STEIGENBERGER P, KHACHIKYAN R, et al. IGS-MGEX:Preparing the Ground for Multi-Constellation GNSS Science[C]//Proceedings of the 4th International Colloquium on Scientific and Fundamental Aspects of the Galileo System. Prague:ESA, 2013. |
| [8] | GUO Jing, XU Xiaolong, ZHAO Qile, et al. Precise Orbit Determination for Quad-Constellation Satellites at Wuhan University:Strategy, Result Validation, and Comparison[J]. Journal of Geodesy, 2016, 90(2): 143–159. DOI:10.1007/s00190-015-0862-9 |
| [9] | TEGEDOR J, ØVSTEDAL O, VIGEN E. Precise Orbit Determination and Point Positioning Using GPS, GLONASS, Galileo and BeiDou[J]. Journal of Geodetic Science, 2014, 4(1): 65–73. |
| [10] | 李敏, 施闯, 赵齐乐, 等. 多模全球导航卫星系统融合精密定轨[J]. 测绘学报, 2011, 40(S1): 26–30. LI Min, SHI Chuang, ZHAO Qile, et al. Multi-GNSS Precision Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 26–30. |
| [11] | 刘伟平, 郝金明, 李建文, 等. 多GNSS融合的北斗卫星精密定轨[J]. 测绘学报, 2014, 43(11): 1132–1138. LIU Weiping, HAO Jinming, LI Jianwen, et al. Multi-GNSS Joint Precise Orbit Determination of BeiDou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1132–1138. DOI:10.13485/j.cnki.11-2089.2014.0186 |
| [12] | 陈俊勇. 全球导航卫星系统进展及其对导航定位的改善[J]. 大地测量与地球动力学, 2009, 29(2): 1–3. CHEN Junyong. Progress in GNSS and Its Influence on Navigation and Positioning[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 1–3. |
| [13] | LAURICHESSE D, CERRI L, BERTHIAS J P, et al. Real Time Precise GPS Constellation and Clocks Estimation by Means of a Kalman Filter[C]//Proceedings of the 26th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+2013). Nashville, Tennessee:Nashville Convention Center, 2013. |
| [14] | ZHANG Q, MOORE P, HANLEY J, et al. Auto-Bahn:Software for Near Real-time GPS Orbit and Clock Computations[J]. Advances in Space Research, 2007, 39(10): 1531–1538. DOI:10.1016/j.asr.2007.02.062 |
| [15] | WOODBURN J. Mitigation of the Effects of Eclipse Boundary Crossings on the Numerical Integation of Orbit Trajectories Using an Encke Type Correction Algorithm (AAS 01-223)[C]//Proceedings of the 11th Annual Space Flight Mechanics Meeting. Santa Barbara, CA:The American Astronautical Society, 2001. |
| [16] | 陈刘成. 地影模型对导航卫星轨道数值积分的影响及改进[J]. 武汉大学学报(信息科学版), 2007, 32(5): 450–453. CHEN Liucheng. How Navigation Satellite Orbit Numerical Integration Affected by Shadow Model and Its Correcting Methods[J]. Geomatics and Information Science of Wuhan University, 2007, 32(5): 450–453. |
| [17] | RODRIGUEZ-SOLANO C J, HUGENTOBLER U, STEIGENBERGER P, et al. Improving the Orbits of GPS Block ⅡA Satellites during Eclipse Seasons[J]. Advances in Space Research, 2013, 52(8): 1511–1529. DOI:10.1016/j.asr.2013.07.013 |
| [18] | BERRY M M. A Variable-Step Double-Integration Multi-Step Integrator[D]. Virginia:Virginia Polytechnic Institute and State University, 2004. |
| [19] | KROGH F T. Changing Stepsize in the Integration of Differential Equations Using Modified Divided Differences[C]//BETTIS D G. Proceedings of the Conference on the Numerical Solution of Ordinary Differential Equations. Berlin Heidelberg:Springer, 1974. |
| [20] | SHAMPINE L F, GORDON M K. Computer Solution of Ordinary Differential Equations[M]. . |
| [21] | 李征航, 黄劲松. GPS测量与数据处理[M]. 2010. LI Zhenghang, HUANG Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2010. |
| [22] | DIETHELM K, FORD N J, FREED A D. A Predictor-Corrector Approach for the Numerical Solution of Fractional Differential Equations[J]. Nonlinear Dynamics, 2002, 29(1-4): 3–22. |
| [23] | PRANGE L, ORLIAC E, DACH R, et al. CODE's Multi-GNSS Orbit and Clock Solution[C]//EGU General Assembly Conference. Vienna, Austria:EGU, 2015. |



