2. 中国测绘科学研究院, 北京 100830;
3. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079;
4. 长安大学地质工程与测绘学院, 陕西 西安 710054
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China;
3. GNSS Research Center, Wuhan University, Wuhan 430079, China;
4. College of Geology Engineering and Geomantics, Chang'an University, Xi'an 710054, ChinaAbstract
中国北斗卫星导航系统是我国自行研制、独立运行的全球卫星定位与通信系统,其空间部分采用地球静止轨道(geostationary Earth orbit, GEO)、倾斜地球同步轨道(inclined geosynchronous satellite orbit, IGSO)及中地球轨道(medium Earth orbit, MEO)混合星座设计[1]。2012年10月,第16颗北斗卫星成功发射,标志着我国北斗导航工程区域组网顺利完成,2020年前后,我国共将发射约40颗北斗导航卫星,完成覆盖全球的系统建设目标。无论是全球星座还是区域星座,卫星轨道和钟差的确定精度直接影响其位置服务能力。
导航卫星高精度轨道确定通常采用简化动力学方法,其定轨精度主要取决于卫星动力学模型和几何观测信息。由于GEO卫星高轨及静地特性,制约了卫星动力学模型的定轨。目前GEO卫星的跟踪站分布不均匀,决定了动力学模型的约束远远不及几何观测对轨道确定的贡献大,尤其体现在卫星运动方向(切向)和轨道面法向。随着测站数量和分布不同,测距偏差可以8~20倍放大到轨道切向和法向上[3];IGSO卫星同样是高轨,其星下点轨迹为“8”字形,站星几何结构变化与较为明显,但其覆盖范围内的测站分布较差,导致大部分观测弧段定轨几何构型较弱,同样会影响轨道的三维精度;MEO卫星理论上站星几何结构变化最为显著,定轨构型对轨道精度影响最弱,但难以在短时间内全球布站,目前其几何构型对定轨精度也有一定限制,因此BDS卫星定轨地面站构型分析及优化方法还需深入研究。
目前众多学者已经开展了GNSS星座构型对地面定位性能的影响分析[4]以及各类动力学参数模型对卫星精密定轨影响分析[5-6]的研究,而关于地面站构型对卫星定轨和地球自转参数估计影响的探讨还相对较少[7]。其中文献[8]分别采用非差和双差模型,综合对比了全球地面站分布对GPS和GLONASS卫星定轨的影响;文献[9]根据定轨中法方程条件数,针对区域卫星导航系统定轨的测控站布局,进行一系列仿真试验;文献[10—11]提出了动力学精度因子,衡量卫星定轨的几何构型强度,并通过实例验证了其有效性。研究表明,卫星定轨精度与地面站分布息息相关,本文在简化动力学定轨模型基础上,探讨了多历元几何观测信息累积的轨道改进;研究了北斗导航卫星定轨理想几何构型条件;利用离散概率密度法研究地面站分布构型,并分析了GEO/IGSO/MEO卫星轨道改进机理和优化方法。
1 卫星多历元轨道改进机理 1.1 卫星简化动力学定轨模型导航卫星GNSS精密定轨中,状态向量x包含卫星轨道参数(位置、速度)和力模型参数(光压模型等物理参数)及其他待估参数(钟差、相位模糊度等)等。对于动力学模型,满足如下方程

式中,x0为初始状态;F为n维非线性函数,将上式线性化为[12]
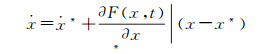
式中,x*为基于某时刻的参考轨道初值,令X=x-x*,A=∂F(x, t)/∂x,可得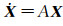
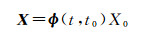 (1)
(1)
式中,φ(t, t0)为状态转移矩阵,可根据数值积分求得。同时,地面站GNSS观测为定轨提供了几何信息。设地面跟踪站的观测量为Y,第i历元的观测数据yi与其真值G(xi, ti)和测量误差εi的观测方程为[13]
 (2)
(2)
因此将上式非线性方程展开后,结合式(1),可得
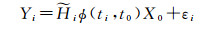 (3)
(3)
式中,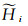
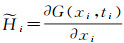
因为文本关心卫星和地面站几何构型对定轨的影响,为此忽略除卫星位置外的其他力模型参数及GNSS观测方程附加参数,根据式(2),在观测历元tk,几何观测方程为[11]
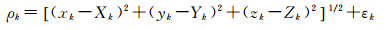 (4)
(4)
式中,εk为各类观测误差;ρk是第tk历元距离观测值或伪距观测值;(Xk, Yk, Zk)为第tk历元测站的位置向量;(xk, yk, zk)为第tk历元卫星的位置向量[13-14]。
为了讨论问题方便,假设卫星在任意时刻的运动速度矢量V(t),则将任意时刻位置表示为初始位置的函数,即
 (5)
(5)
式中,(x0, y0, z0)为卫星初始时刻位置;(vx, vy, vz)为卫星速度,因为卫星存在加速度,其随时间变化,由卫星运动动力学方程或解微分方程给出。
将式(5) 代入式(4) 后,可得改造后的观测方程
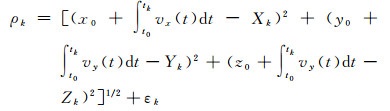 (6)
(6)
将式(6) 线性化后,可得

式中,[x′0 y′0 z′0]为卫星初始位置的初值;[dx0 dy0 dz0]为其几何观测信息对初值的改正量。式(6) 中,为了揭示多历元几何观测综合确定初始位置的作用机理,将卫星运动相对于初始位置产生的位移可与测站坐标合并(即假设卫星是静止的,而测站发生了相对运动),每个历元的几何观测值则转换为一组虚拟跟踪站相对于初始时刻卫星位置的定位问题,即
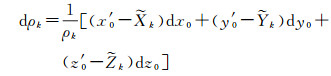 (7)
(7)
式中,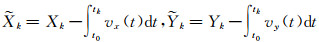
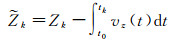
V=HΔx-L
式中,V是观测值改正数;Δx为初始时刻轨道位置改正;L是含有各种误差的常数项;H为系数阵,可以表示[16]为
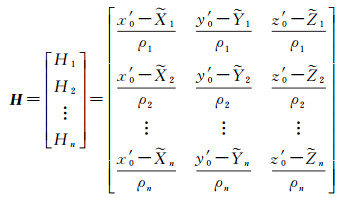 (8)
(8)
式中,n为观测历元,此时可定义评价定轨精度的指标如下
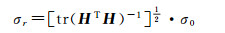
式中,σ0是距离测量中误差;tr是矩阵的迹,据此可定义反映几何观测结构优劣的动力学几何精度因子(ODOP)
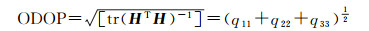
式中,q11、q22、q33是权系数阵的主对角线元素,ODOP越大,则精度越低,
 (9)
(9)
代表权系数阵,k=1, 2,…,n。
经过式(7) 改造,形成了不同历元对初始时刻观测的虚拟跟踪站,由式(9) 可知,卫星定轨就是各历元虚拟跟踪站与初始时刻卫星位置组成的观测方程叠加解算,反映了由各历元虚拟跟踪站定轨构型的叠加。随着卫星与跟踪站的相对运动,叠加构型会不断优化(例如IGSO/MEO卫星),定轨精度越高;理论上,同等地面构型条件下观测弧长越长,HkTHk累加越大,定轨精度也会越高。
2 卫星定轨理想几何构型条件为了研究几何构型条件,仅考虑卫星位置参数,根据式(8),引入单位向量矩阵,将H矩阵参数化。
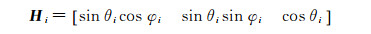 (10)
(10)
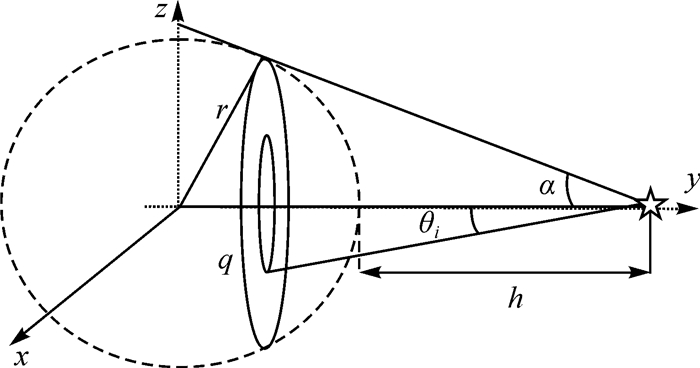
研究表明当HTH对角化且元素相等时,ODOP达到最小,但当考虑钟差时,还要求构型具有一定的对称性,否则会导致钟差和位置参数相关[17]。文献[18]研究给出了满足上述条件的许多构型解,下面仅仅以嵌套圆锥构型为例,讨论地面站最佳分布。如图 1所示,α为卫星至地球切线方向与卫星至地心方向的夹角;g为观地面站分布圆;r为地球半径;h为地心至地面距离;θi为卫星与测站分布面构成的圆锥角。
|
| 图 1 定轨几何构型示意 Fig. 1 Schematic diagram of geometric configuration with satellite orbit determination |
假设地面站分布在T个圆上,每个圆上测站都是均匀的,分布面为g1、g2、g3、…、gT,对应圆锥角为θ1、θ2、θ3、…、θT∈(0, a),可得[19-21]
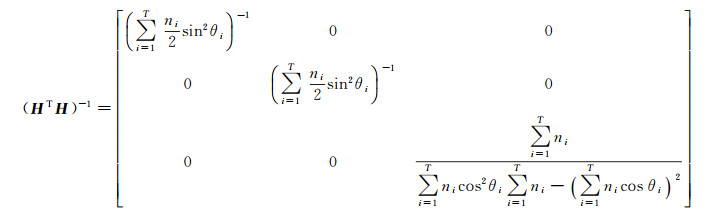
得到GNSS导航卫星定轨几何构型精度指标模型
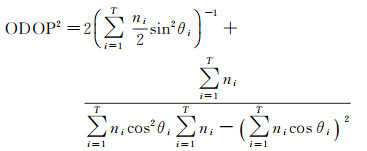 (11)
(11)
若令
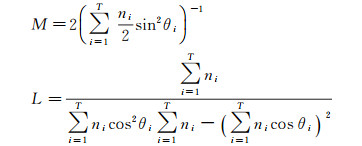
则测站数量相等情况下,根据M式可知,当测站覆盖范围小时,即θi变小时,ODOP模型函数值会变大,定轨精度降低。根据上述L可知,当测站分布密集(T接近)时,即θi趋于相等,L式分母接近于零,ODOP模型函数值会变大,定轨精度降低。
由于每个历元最优几何构型的叠加也是最优的,因此几何信息中决定北斗卫星定轨精度的3个影响因子为测站数量,测站覆盖范围和分布密度。理想几何构型条件就是测站数量越多,覆盖范围越广,分布密度越均匀,则式(11) 越小,定轨精度越高。
3 卫星定轨地面测站的离散概率密度对于特定的地面站分布(例如目前给定的北斗地面站,其分布可能还不尽合理),以该地面站分布作为初始条件,需要讨论站点选取或新建站点位置选择。下面通过引入站点离散概率密度,便于分析地面站的分布特征(覆盖范围和分布密度),并在此基础上,讨论如何进行选站,以期用于改善站点分布密度和地面站最优分布的目的。式(4) 中每个观测方程都是基于测站和卫星连线方向,即定轨时测站对卫星实际作用力方向,为了更好地描述1.2节得到的各虚拟跟踪站构型叠加及对卫星有效作用,建立以卫星为原点,10 km为半径的球(半径仅作为比例因子,跟绝对精度无关),每个跟踪站跟卫星连线方向是该测站对该卫星轨道精度改进的主方向。球的空间方程为
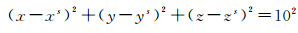 (12)
(12)
而每个跟踪站跟卫星连线方程为
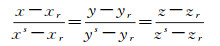 (13)
(13)
则联立式(12) 和式(13),可以得到所有跟踪站与卫星连线和球的交点点集,即测站对卫星在轨道积分时间内,形成了离散投影点集{(x1, y1, z1), (x2, y2, z2), (x3, y3, z3),…,(xn, yn, zn)}。上述点集实际上构成了整个积分弧段上累积的(虚拟)地面站几何分布特征,在此基础上,可以绘制其空间点集概率密度图,用于研究地面站分布的均匀程度及覆盖范围。
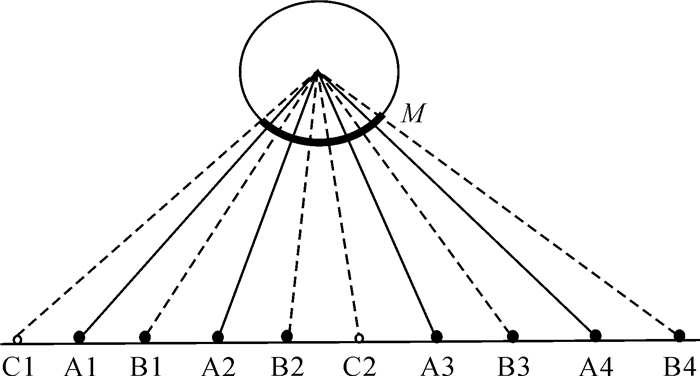
图 2中A1、A2、A3、A4为初始时刻4个跟踪站。根据第2节,当卫星运动到某一时刻后,形成了B1、B2、B3、B4 4个虚拟跟踪站(相当于卫星没动,而测站运动),M弧段相当于跟踪站对卫星实际作用投影点组成的区域(包括范围和密度)。GEO卫星静地特性,整个弧段内不会形成新的虚拟跟踪站,覆盖范围和密度基本不会变化。而IGSO和MEO卫星随着运动,产生与初始时刻对应的虚拟跟踪站,并有新的跟踪站加入(C1, C2);同时也会丢失低高度角的虚拟跟踪站,但会使整个弧段对卫星作用范围不断增大或投影点密度不断变化,即对初始时刻叠加后的构型越优化。因此静地的GEO卫星定轨精度是最低的;IGSO卫星在赤道上空作“8”字形运动,而MEO卫星全球周期运动,造成MEO卫星的作用投影点范围(叠加的构型)大于IGSO卫星,其定轨精度也要高于IGSO卫星。
|
| 图 2 虚拟跟踪站定轨示意 Fig. 2 Schematic diagram of satellite orbit determination with virtual monitoring stations |
根据式(14) 求解所有投影点集的几何中心,几何中心方向是所有测站对卫星作用的“合力”方向,即卫星精度最高的方向。中心至各投影点的距离代表了测站覆盖范围,该距离内投影点出现的概率代表了卫星受力密度。因此绘制一维的离散概率密度图,能够直观展现构型叠加对定轨的影响。该概率密度总和为1,当测站数量一定情况下,其区间范围(宽度)、对称性和均匀性则构成了影响卫星定轨的地面构型特征指标(正对应于第2节的几何因子),通过增大覆盖范围,改善离散投影点分布密度来优化定轨构型。
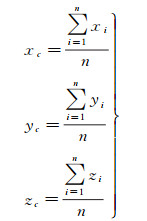 (14)
(14)
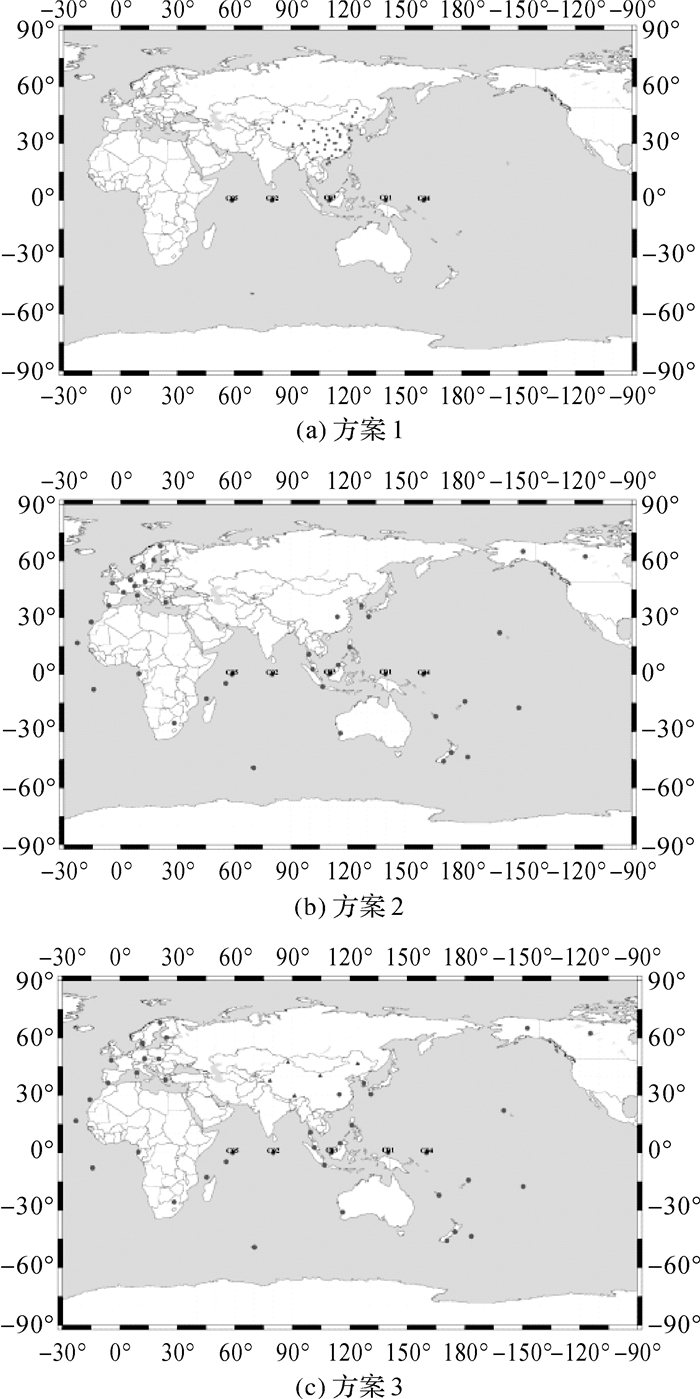
图 3依次表示试验的3个方案(自左到右,同以下图),其中方案1:均匀选取国家测绘地理信息局在全国布设的210个兼容BDS连续运行基准站[22]中50个站(代表狭小区域测站分布);方案2:选取IGS多模GNSS试验网络(MGEX)50个测站(全球测站分布),方案3:均匀选取IGS多模GNSS试验网络(MGEX)45个测站,并优化增加5个国家连续运行基准站(图 3蓝色点)。3种方案数据均为2016年年积日第335天,测站数量相等,其离散投影点分布如图 4、图 6、图 8、图 10所示,图中点集为整个弧段各测站对卫星的实际作用离散投影点;投影点的概率密度如图 5、图 7、图 9、图 11所示,其横轴表示球几何中心至投影点集的距离,纵轴表示整个弧段该距离范围内离散投影点的概率,图中空白区域指该距离内没有测站布设。
|
| 图 3 BDS卫星跟踪站分布 Fig. 3 Distribution of BDS monitoring stations |

|
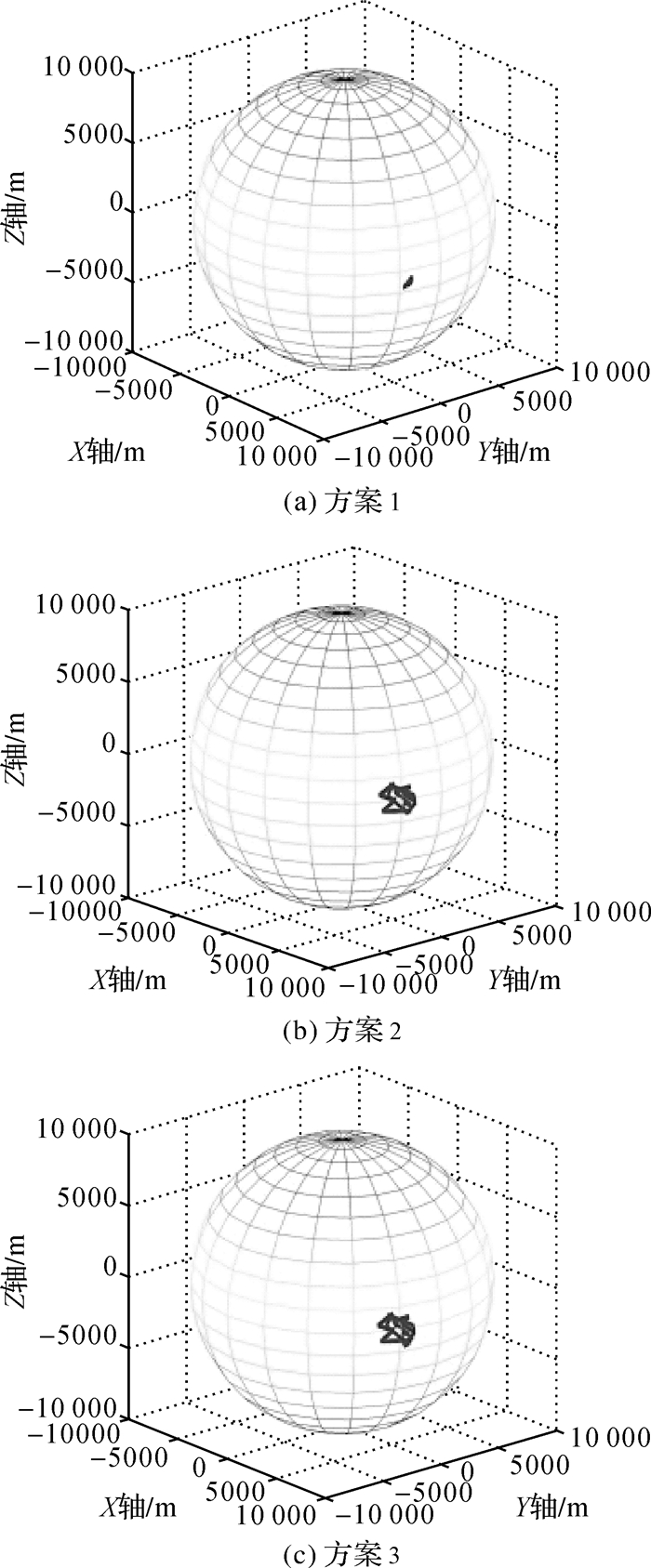
| 图 4 C01投影点分布 Fig. 4 Distribution of projective points with C01 |
|
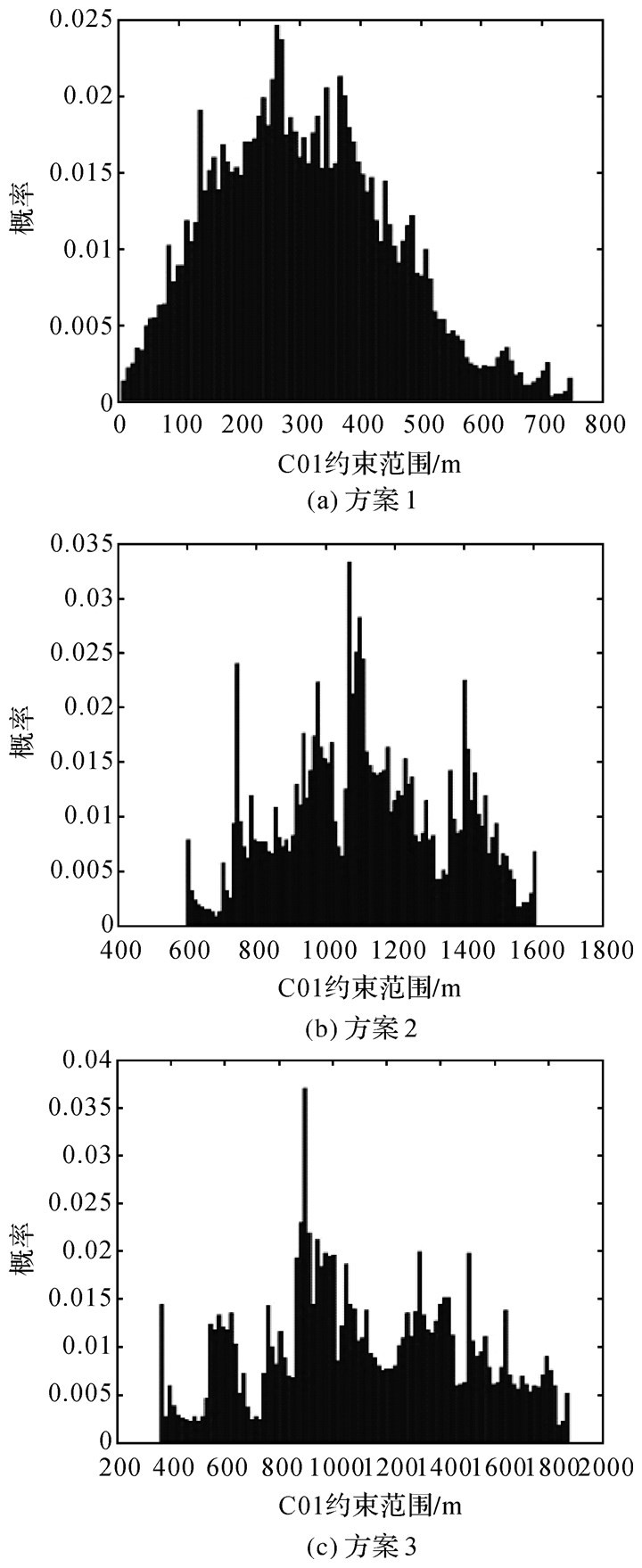
| 图 5 C01离散概率密度 Fig. 5 Probability density of discrete points with C01 |
|
| 图 6 C04投影点分布 Fig. 6 Distribution of projective points with C04 |

|
| 图 7 C04离散概率密度 Fig. 7 Probability density of discrete points with C04 |
|
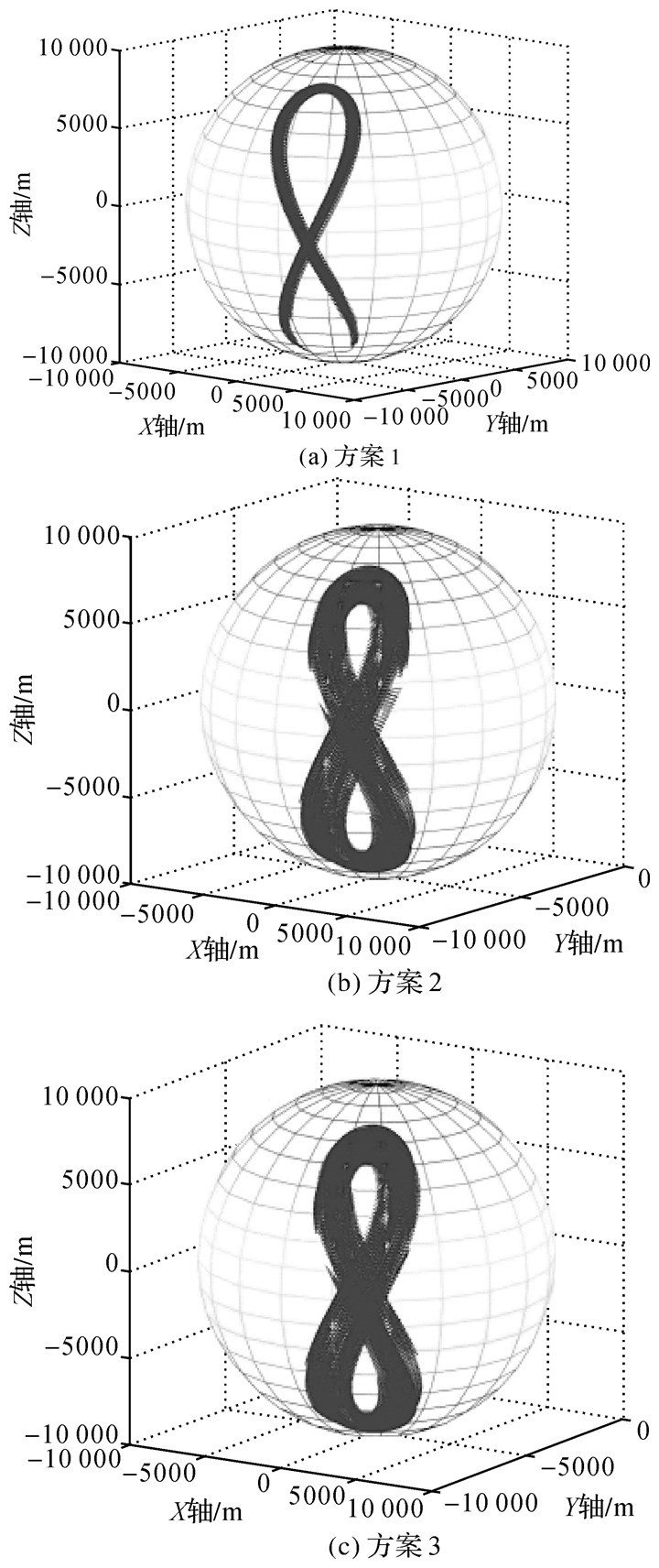
| 图 8 C06投影点分布 Fig. 8 Distribution of projective points with C06 |
|
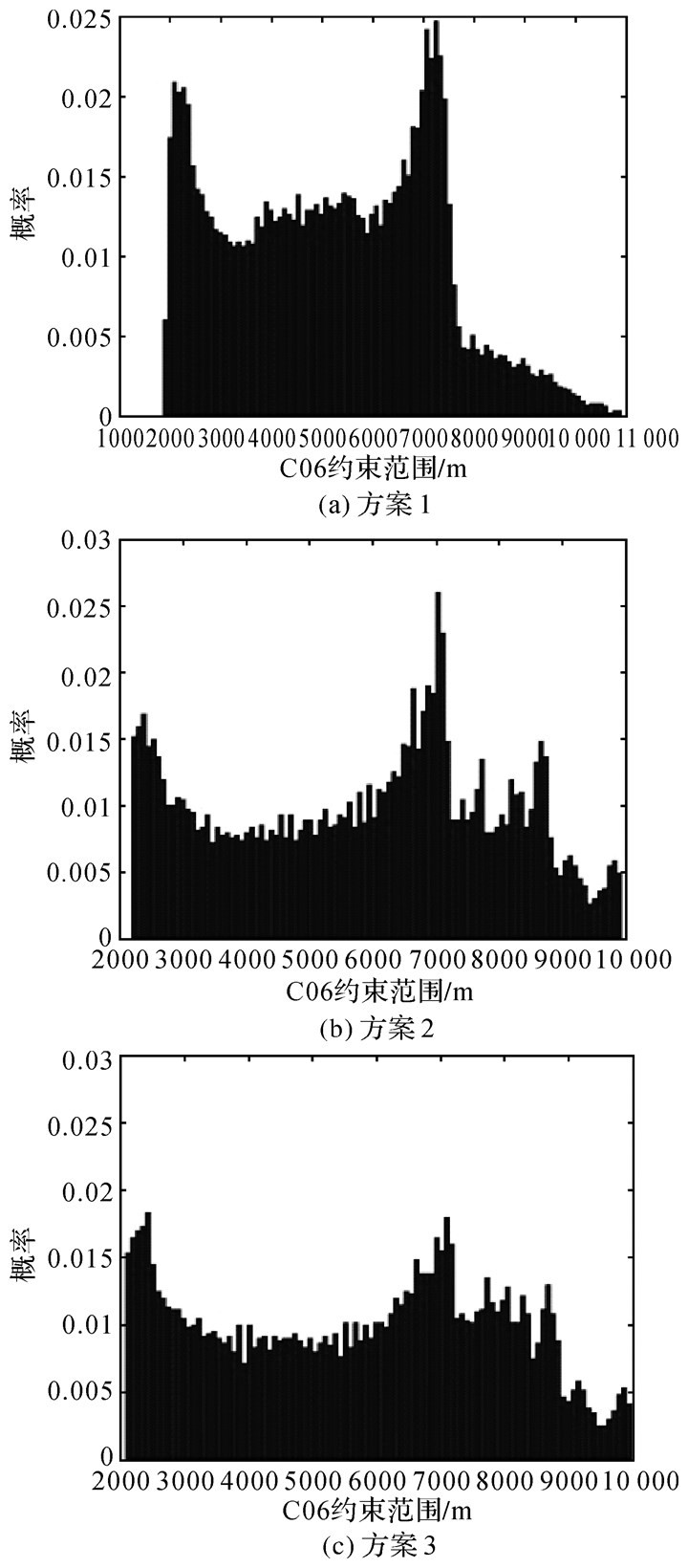
| 图 9 C06离散概率密度 Fig. 9 Probability density of discrete points with C06 |
|
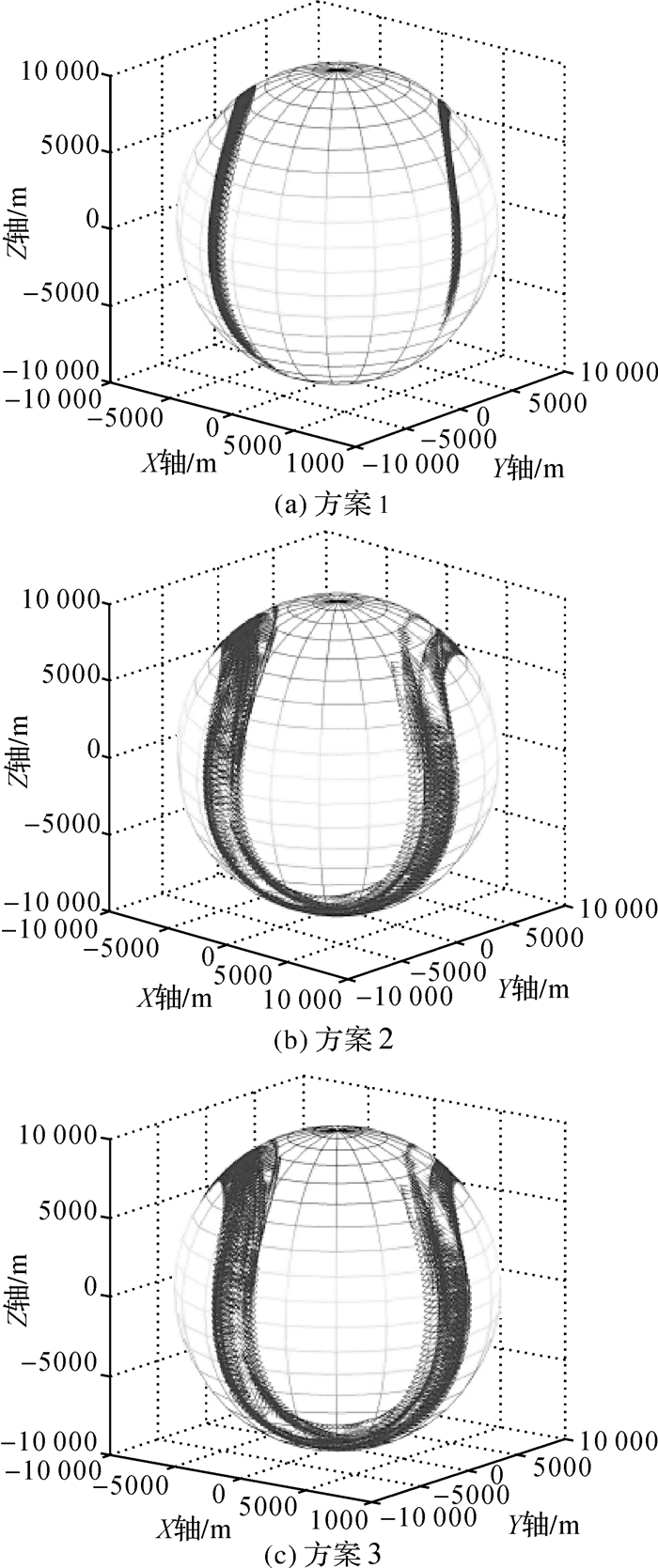
| 图 10 C11投影点分布 Fig. 10 Distribution of projective points with C11 |

|
| 图 11 C11离散概率密度 Fig. 11 Probability density of discrete points with C11 |
限于篇幅,文章没有展现所有卫星,其GEO卫星以C01、C04卫星为例,IGSO以C06为例,MEO以C11为例。3种方案,GEO卫星投影点(测站对卫星作用点)分布区域最狭小,其覆盖范围最大为2000 m,IGSO卫星投影点分布在球的一侧,成“8”字形,最大覆盖范围为10 000 m,MEO卫星投影点环绕球分布,成空间对称状,覆盖范围可以达到13 000 m。因此地面跟踪站对MEO卫星叠加构型最优,精度最高,IGSO卫星构型略弱,精度次之,而GEO卫星构型最差,精度最低,验证了第3节结论。
C01卫星,由图 5可知,方案1测站分布在中国境内,较为密集,覆盖范围小,方案2采用全球站,分布更均匀,作用范围更广,方案3采用优化后的测站分布,测站几何信息覆盖范围增加到1800 m,离散概率密度更均匀。
C04卫星,3种方案分布变化类似C01卫星,方案3测站几何信息约束范围增加到1800 m,但因为C04位于太平洋上空,周围是岛屿,东侧是大洋,优化后测站控制不够,依然会出现覆盖不到的距离(图 7中方案2和方案3空白区域)。
C06和C11卫星,图 8及图 10中方案1的投影点集条带较细,叠加构型差,图 9及图 10中投影点概率密度非常不均匀;方案2和方案3,投影点分布条带变宽,优化了定轨构型;方案3优化后的测站概率密度分布最均匀。因为C06和C11卫星相对跟踪站运动,构型优化后基本不会对覆盖范围造成影响,但会明显改善分布密度。
采用相同数据进行BDS卫星定轨试验,3DRMS重复弧段精度如表 2所示,可以看出MEO卫星精度高于IGSO卫星,GEO卫星精度最低。3种方案中,方案1仅采用国家站定轨,构型最差,卫星精度最低;方案3优化后的测站分布,定轨精度最高,其与离散概率密度变化符合。与方案2的全球站定轨相比,方案3定轨精度GEO卫星提高了10%;C06卫星提高了16%;C10卫星提高了4%,提高幅度最小。
| mm | |||
| 卫星号 | 方案1 | 方案2 | 方案3 |
| C01 | 804 | 436 | 381 |
| C04 | 953 | 448 | 408 |
| C06 | 212 | 100 | 84 |
| C11 | 180 | 48 | 46 |
5 结论
定轨精度主要取决于卫星动力学模型精度及GNSS几何观测信息,由于北斗卫星跟踪站分布现状,造成地面几何观测信息的约束对轨道确定贡献较大。本文基于卫星定轨基本原理,讨论了定轨构型对BDS卫星轨道确定的影响机理和几何因子,并采用离散概率密度法对定轨构型进行了分析和优化,结论如下:
(1) 采用多历元几何观测信息累加的轨道改进,得出定轨精度是由各历元虚拟跟踪站对初始轨道的定轨构型的叠加来体现,弧段越长(如GEO)或累积构型(如IGSO/MEO)越优,其定轨精度越高,然而,该结论的假设是动力学信息足够精确,确保不同历元卫星位置的动力学连接信息精确。
(2) 从建立的理想定轨几何构型条件,得出地面站数量,覆盖范围和分布密度是测站信息中决定北斗卫星定轨精度的3个几何因子。
(3) 当测站数量一定时,采用宽度(覆盖范围)、对称性和均匀性(分布密度)指标描述并展示了几何因子对3类卫星叠加构型的影响机理,MEO卫星精度最高,IGSO其次,GEO卫星精度最低;并依此方法进行了定轨构型的优化。
(4) 本文中仅采用中国区域地面站定轨时,3类卫星的离散概率密度指标最差,定轨精度最低;相对于全球站BDS卫星定轨,采用中国境内跟踪站优化后能够明显改善GEO和IGSO卫星定轨的离散概率密度,提高其定轨精度,但MEO卫星精度改善较小,该方法可为全球BDS跟踪站优化和布设提供参考。
| [1] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [2] | SHI Chuang, ZHAO Qile, LI Min, et al. Precise Orbit Determination of BeiDou Satellites with Precise Positioning[J]. Science China:Earth Sciences, 2012, 55(7): 1079–1086. DOI:10.1007/s11430-012-4446-8 |
| [3] | 杜兰. GEO卫星精密定轨技术研究[D]. 郑州: 信息工程大学, 2006. DU Lan. A Study on the Precise Orbit Determination of Geostationary Satellites[D]. Zhengzhou:Information Engineering University, 2006. |
| [4] | 薛树强, 杨元喜. 最小GDOP组合Walker星座构型[J]. 武汉大学学报(信息科学版), 2016, 41(3): 380–387. XUE Shuqiang, YANG Yuanxi. Combined Walker Configurations with Minimal GDOP[J]. Geomatics and Information Science of Wuhan University, 2016, 41(3): 380–387. |
| [5] | 韩保民. 动力学模型对简化动力学定轨精度影响仿真[J]. 系统仿真学, 2006, 18(10): 2722–2724. HAN Baomin. Simulation of Impact of Force Models on Orbiting Accuracy of Reduced-dynamic Orbit Determination[J]. Journal of System Simulation, 2006, 18(10): 2722–2724. DOI:10.3969/j.issn.1004-731X.2006.10.006 |
| [6] | 郭靖. 姿态、光压和函数模型对导航卫星精密定轨影响的研究[D]. 武汉: 武汉大学, 2014. GUO Jing. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites[D]. Wuhan:Wuhan University, 2014. |
| [7] | WANG Qianxin, DANG Yamin, XU Tianhe. The Method of Earth Rotation Parameter Determination Using GNSS Observations and Precision Analysis[M]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2013 Proceedings:BeiDou/GNSS Navigation Applications·Test & Assessment Technology·User Terminal Technology. Berlin:Springer, 2013:247-256. |
| [8] | GEIST E O, DACH R, SCHÖNEMANN E, et al. Influence of Station Distribution on GNSS Satellite Orbits[C]//International GNSS Service (IGS) Workshop. Sydney, Australia:[s.n.], 2016. |
| [9] | 文援兰, 柳其许, 朱俊, 等. 测控站布局对区域卫星导航系统的影响[J]. 国防科技大学学报, 2007, 29(1): 1–6. WEN Yuanlan, LIU Qixu, ZHU Jun, et al. The Effect of TT&C Deployment on the Regional Satellite Navigation System[J]. Journal of National University of Defense Technology, 2007, 29(1): 1–6. |
| [10] | ZHANG Rui, ZHANG Qin, HUANG Guanwen, et al. Impact of Tracking Station Distribution Structure on BeiDou Satellite Orbit Determination[J]. Advances in Space Research, 2015, 56(10): 2177–2187. DOI:10.1016/j.asr.2015.07.045 |
| [11] | 张睿, 杨元喜, 张勤, 等. BDS卫星动力学参数最优解与定轨跟踪站最优分布[J]. 大地测量与地球动力学, 2016, 36(3): 216–220. ZHANG Rui, YANG Yuanxi, ZHANG Qin, et al. Optimal Estimation of Dynamic Parameters of BDS Orbit for Optimal Selection of Tracking Stations[J]. Journal of Geodesy and Geodynamic, 2016, 36(3): 216–220. |
| [12] | 赵齐乐. GPS导航星座及低轨卫星的精密定轨理论和软件研究[D]. 武汉: 武汉大学, 2004. ZHAO Qile. Research on Precise Orbit Determination Theory and Software of both GPS Navigation Constellation and LEO Satellites[D]. Wuhan:Wuhan University, 2004. |
| [13] | 李敏. 多模GNSS融合精密定轨理论及其应用研究[D]. 武汉: 武汉大学, 2011. LI Min. Research on Multi-GNSS Precise Orbit Determination Theory and Application[D]. Wuhan:Wuhan University, 2011. |
| [14] | 党亚民, 秘金钟, 成英燕. 全球导航卫星系统原理与应用[M]. 北京: 测绘出版社, 2007. DANG Yamin, BEI Jinzhong, CHENG Yingyan. Principles and Applications of Global Navigation Satellites System[M]. Beijing: Surveying and Mapping Press, 2007. |
| [15] | 薛树强, 杨元喜, 党亚民. 测距定位方程非线性平差的封闭牛顿迭代公式[J]. 测绘学报, 2014, 43(8): 771–777. XUE Shuqiang, YANG Yuanxi, DANG Yamin. A Closed-form of Newton Iterative Formula for Nonlinear Adjustment of Distance Equations[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 771–777. DOI:10.13485/j.cnki.11-2089.2014.0127 |
| [16] | 耿涛. 基于区域基准站的导航卫星实时精密定轨理论及试验应用[D]. 武汉: 武汉大学, 2009. GENG Tao. Real-time Precise Orbit Determination Theory for Navigation Satellites and Its Experimental Application Based on Regional Reference Stations[D]. Wuhan:Wuhan University, 2009. |
| [17] | 徐天河, 贺凯飞. 顾及系统误差的GEO卫星几何法定轨[J]. 大地测量与地球动力学, 2009, 29(1): 64–69. XU Tianhe, HE Kaifei. Geometry Orbit Determination of GEO Satellite Attending to Systematic Errors[J]. Journal of Geodesy and Geodynamics, 2009, 29(1): 64–69. |
| [18] | XUE Shuqiang, YANG Yuanxi. Positioning Configurations with the Lowest GDOP and Their Classification[J]. Journal of Geodesy, 2015, 89(1): 49–71. DOI:10.1007/s00190-014-0760-6 |
| [19] | ZHANG Longping, DANG Yamin, XUE Shuqiang, et al. The Optimal Distribution Strategy of BeiDou Monitoring Stations for GEO Precise Orbit Determination[M]//SUN Jiadong, LIU Jingnan, FAN Shiwei, et al. China Satellite Navigation Conference (CSNC) 2015 Proceedings:Volume Ⅰ. Berlin:Springer, 2015:153-161. |
| [20] | 薛树强, 杨元喜, 陈武, 等. 正交三角函数导出的最小GDOP定位构型解集[J]. 武汉大学学报(信息科学版), 2014, 39(7): 820–825. XUE Shuqiang, YANG Yuanxi, CHEN Wu, et al. Positioning Configurations with Minimum GDOP from Orthogonal Trigonometric Functions[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 820–825. |
| [21] | 薛树强, 杨元喜. 最小GDOP定位构型的一种嵌套圆锥结构[J]. 武汉大学学报(信息科学版), 2014, 39(11): 1369–1374. XUE Shuqiang, YANG Yuanxi. Nested Cones for Single-point-positioning Configuration with Minimal GDOP[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11): 1369–1374. |
| [22] | 陈明, 武军郦, 李志才. 北斗精密定轨及广播星历轨道精度评估[J]. 测绘工程, 2016, 25(11): 1–6. CHEN Ming, WU Junli, LI Zhicai. Precise Orbit Determination and Broadcast Ephemeris Accuracy Assessment and Analysis for BDS[J]. Engineering of Surveying and Mapping, 2016, 25(11): 1–6. |



