2. 北京市测绘设计研究院城市空间信息工程北京市重点实验室, 北京 100038;
3. 青海省交通科学研究院, 青海 西宁 810001;
4. 北京建筑大学测绘与城市空间信息学院, 北京 100044
2. Beijing Key Laboratory of Urban Spatial Information Engineering, Beijing Institute of Surveying and Mapping, Beijing 100038, China;
3. Qinghai Research Institute of Transportation, Xining 810001, China;
4. School of Surveying and Urban Spatial Information, Beijing University of Civil Engineering and Architecture, Beijing 100044, ChinaAbstract
目前BDS可在亚太地区提供导航、授时和短报文信息服务,其服务区域为55°E~180°E,55°S~55°N之间的大部分区域;重点区域为东经70°E~145°E,5°N~55°N。截止到2016年6月12日,共发射23颗北斗导航卫星,其中可用卫星包括5颗MEO(medium earth orbit)卫星、8颗IGSO(inclined geosynchronous satellite orbit)卫星和6颗GEO(geosynchronous earth orbit)卫星。
与GPS、GLONASS卫星系统不同,为了增强亚太地区的导航性能,BDS增加了IGSO和GEO两种卫星,但因IGSO和GEO卫星运行角速度较慢及MEO卫星较少,易造成BDS定位模型结构的病态性,模糊度初始化需要较长时间,甚至可造成模糊度搜索失败。文献[1—2]提出通过构建多星座定位模型,减弱北斗定位模型的病态性,提高模糊度搜索速度和可靠性。由于BDS星座结构特点,BDS水平方向观测精度不均匀,通常南北方向的精度略低于东西方向的精度[3],而融入GPS、GLONASS和Galileo等卫星系统可有效地提高水平方向观测精度及可靠性,因此应用于变形监测领域的北斗高精度定位算法大部分融合GPS等卫星系统进行组合定位[4-6]。
组合定位时,需要确定不同类型观测值权比。文献[7]利用方差分量估计理论合理地顾及各传感器观测信息在融合导航中的权比,提出了自适应融合导航模型,利用模拟数据验证其有效性;文献[8]根据一个时段的所有观测数据进行方差分量估计,精密确定GPS和GLONASS观测值之间的权比,验证了组合定位的优越性。
为了减弱粗差、大气延迟误差、多路径效应等偏差影响,实现GNSS高精度的单历元定位,文献[9]设计了基于移动开窗法协方差估计和方差分量估计的自适应Kalman滤波方法,文献[10]建立一套实时的动态导航随机估计模型,可有效地控制观测异常和载体状态扰动异常对动态系统参数估值的影响[9-10]。上述研究主要应用于导航定位领域,而在蠕变观测环境中如何确定不同观测值当前历元最优权比、移动窗口长度和位移收敛速率的关系并未进行研究。
采用GNSS精度最高的静态相对定位技术,对灾害体进行周期性观测,精度可达毫米级,但不能实现实时掌握灾害体的形变过程。一般商用GNSS RTK(real-time kinematic)的测量标称精度一般为平面1 cm,高程2 cm,在实际监测环境中,由于多路径效应以及大气衍射等多种误差因素的影响,使GNSS不易达到其标称精度,难以满足大坝、滑坡等蠕变体更高精度的要求[11-12]。
滑坡等地质灾害监测一般采用高精度大地测量型多频接收机,且一次性使用,当滑坡发生时,无法回收重新利用。为了降低监测成本,文献[13]利用多天线接收机技术进行相关研究,该技术并不是真正意义上的多天线共用时钟技术,其在监测过程中需微波开关不断切换天线,易引起相位周跳误差,每切换一次需要重新初始化,不能实现单历元定位[13]。对于滑坡地质灾害监测,文献[14]使用低成本单频接收机构建高精度算法模型,进行三维模拟试验,使位移探测精度达到毫米级水平。
为了进一步提高位移探测精度及降低监测成本,本文提出BDS/GPS抗差精密定权Kalman方法,使用时钟同步双天线BDS/GPS接收机,构建BDS/GPS单频单差定位模型,采用动态快速求解单频模糊度方法,实现模糊度单历元固定,分别对GPS和BDS观测值进行等价权的抗差估计,利用引入时间遗忘因子的Helmert方差估计方法,精确确定GPS和BDS权比,实时更新观测值方差,实现扩展Kalman滤波的逐历元定位。通过相关试验,重点研究BDS/GPS观测值等价权抗差及移动窗口参数对初始坐标收敛时间和定位精度的影响,分析移动窗口参数与位移探测精度及位移收敛速率的关系。
1 BDS/GPS单频单差定位模型通常GNSS高精度定位采用传统的载波相位双差模型,该模型可消除短基线大部分电离层、对流层误差。相对于单差模型,双差模型冗余度较小,且观测值间具有较强的相关性,观测方程的随机模型复杂,而单差观测值之间不相关,BDS/GPS单差载波相位方程为
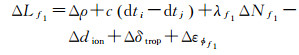 (1)
(1)
式中,Δ为单差因子,λf1为频率f1(L1或B1) 的载波相位波长;ΔLf1为测站i、j与卫星k之间的单差载波相位观测值,单位为m;Δρ为测站i、j与卫星k之间的距离差值;dti和dtj分别为接收机i、j的钟差;ΔNf1为单差模糊度;Δdion、Δδtrop分别为单差电离层、对流层延迟误差;Δεφf1为载波相位观测噪声和多路径误差。
对于短基线( < 20 km),经过差分后的大气延迟误差可忽略不计[15]。采用时钟同步双天线接收机N71JN,单差可消除接收机钟差,式(1) 可线性化为
 (2)
(2)
式中,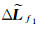
由式(2) 可知,假设基准站和测站共视n颗卫星,未知数为n+3,方程秩亏数为3,无法进行单历元解算,一般常用的方法是结合伪距方程进行计算,由于伪距精度较低,通常需要增加历元数进行搜索固定[16]。为实现单历元模糊度固定,本文采用如下方法:首先采用SVD分解变换构造左零空间矩阵消除坐标参数,进而利用卡尔曼滤波方法获得整周模糊度的浮点解,然后对模糊度协方差进行排序和多次(逆)双乔里斯基分解的降相关处理,采用Cholesky分解来调整对角元素的顺序,最后利用LAMBDA固定模糊度的整数解[17]。
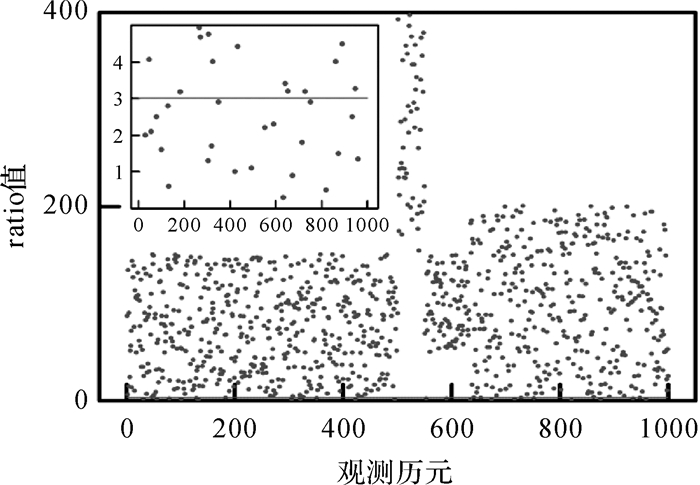
选取连续1000个历元,通过Ratio值来判断该方法单历元固定模糊度的有效性,如图 1所示,部分历元由于观测卫星多路径效应和残余大气误差较大,造成模糊度固定失败,因此模糊度固定成功率(ratio>3) 为98%,基本满足单历元模糊度固定要求[18]。
|
| 图 1 Ratio值散点图 Fig. 1 Ratio's scatter diagram |
1.1 等价权抗差定权
式(2) 经误差改正和模糊度代入后,可得卡尔曼滤波测量方程[19]
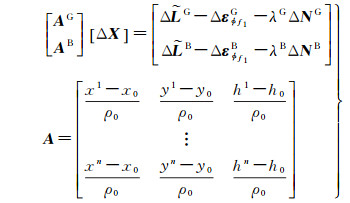 (3)
(3)
式中,ΔX是三维坐标向量改正;(x0, y0, h0)为监测点坐标初始值(采用单点定位获取);(xn, yn, hn)为卫星坐标(可通过卫星星历计算);ρ0为卫星和接收机间的几何距离初值;上标G和B分别表示GPS和BDS卫星。试验区域可共视GPS卫星数约为7颗,BDS卫星数约为11颗,根据稳健加权最小二乘法可分别进行定位[20]。
由于模糊度中存在异常值,测点坐标严重偏离真实值坐标,对异常历元可采取等价权抗差方法抑制存在较大误差的观测值对初始定权结果的影响。观测噪声和多路径效应的大小与高度角密切相关,采用式(4) 和式(5) 对当前历元的GPS和BDS观测值按卫星高度角模型分别进行定权Pk[21]
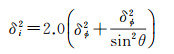 (4)
(4)
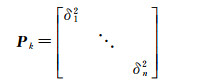 (5)
(5)
式中,k=1,2,分别代表GPS和BDS;n为卫星数。
根据卫星的载波相位观测值的观测精度(波长的百分之一),可以确定其在天顶时的观测误差的标准差δφ,θ为卫星高度截止角,由误差传播定律求出观测误差标准差δi2
根据IGG Ⅲ抗差估计理论迭代定权获取GPS和BDS的初始权值[22-25]。由于单差观测值之间不相关,等价权
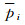
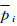
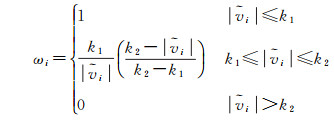 (6)
(6)
式中,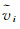
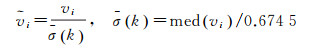
式(6) 中,k1=1.5~2.0;k2=3.0~8.5;
由于单频单历元定位模型冗余度较低及部分历元卫星信号质量较差,经过上述抗差处理,GPS和BDS观测值间的权比精度仍然较低,可采用基于移动窗口Helmert方差估计方法,利用历史窗口数据来平滑当前历元权比,引入时间相关因子可降低历史信息对当前历元信息的影响,提高权值估计的精度和可靠性[10, 26]。
(1) 利用1.1节的等价权抗差定权方法确定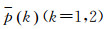
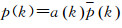
(2) 利用Helmert方差估计GPS和BDS观测值单位权方差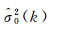
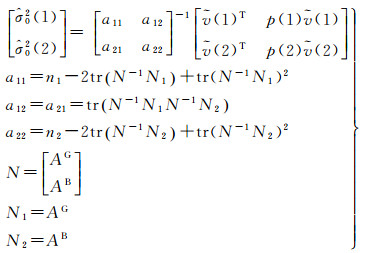 (7)
(7)
式中,n1、n2分别为GPS、BDS卫星数;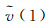
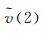
(3) 根据单位权方差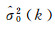

(4) 将步骤(1) 中的a(k)替换为
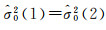
最后可精确确定当前历元i载波相位L1和B1观测值的权比为
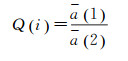
当GPS和BDS共视卫星数较少或信号质量较差,单历元定位权比解算精度可能不高,可引入时间相关因子采用移动窗口平滑滤波方法提高当前历元权比精度[8]。
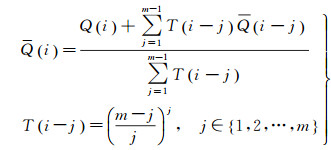 (8)
(8)
利用历史窗口存储的m个历元的权比、时间相关遗忘因子T及历元i的权比,根据式(8) 计算多历元平滑处理的权比
(5) 用
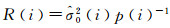


(6) 将当前观测向量协方差阵与状态向量信息按照离散形式的EKF(extended Kalman filter)算法进行逐历元递推[27-29]。
针对观测向量含有较大多路径误差和单历元方程冗余度较差的问题,本文首先利用等价权抗差处理抑制观测向量中的较大误差,并利用多历元平滑权比的方法,提高当前历元GPS和BDS观测值权比的精确度,进而实时更新观测向量方差,采用扩展卡尔曼滤波进行定位。
2 试验及数据分析本文采用N71JN接收机作为试验的硬件设备,N71JN可搜索到BDS B1/B2和GPS L1/L2信号,可实现单系统独立定位和双系统联合定位。为了验证BDS/GPS抗差精密定权Kalman方法的有效性,选取B1和L1载波信号进行组合定位,并利用三维位移装置进行位移加载[14]。
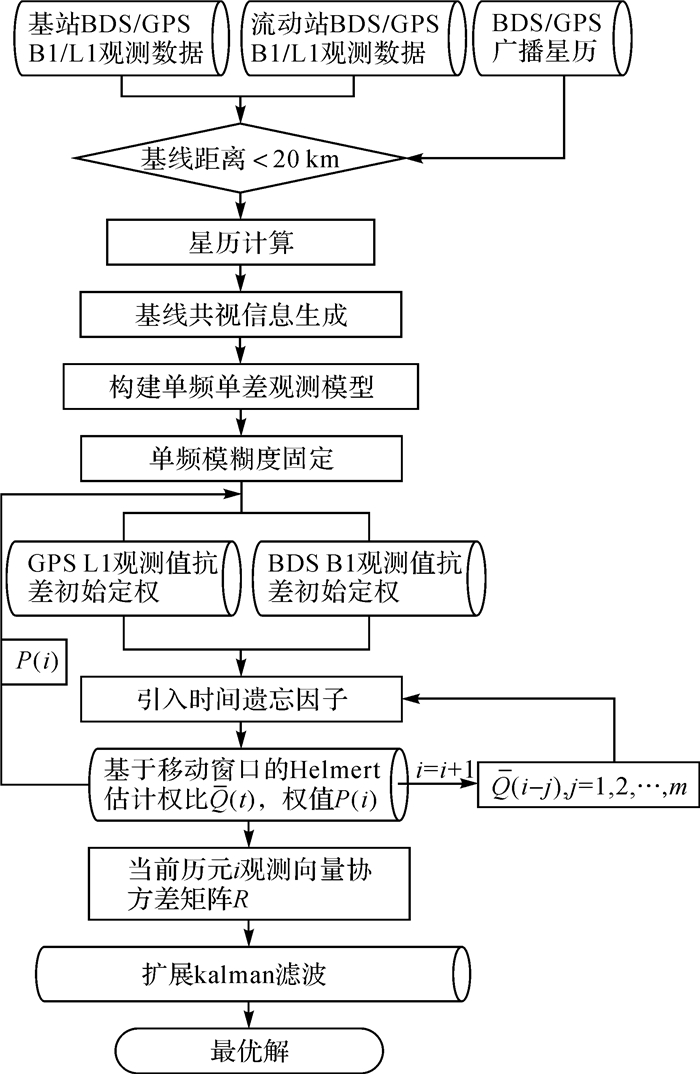
试验场设在北京交通大学学生公寓22号楼和学苑公寓4号楼楼顶,如图 2所示。两个天线(A220GR3D)连接到同一接收机,传输电缆较长时GNSS信号衰减严重,采用低噪声信号放大器,可使天线与接收机的距离达到2 km,基线长度约为1 km[30]。以基站为坐标原点建立局部独立坐标系,正东、正北方向和CGCS2000大地高方向分别为X、Y、H坐标轴。软件采用自主编制的BJMonitor,核心算法流程如图 3所示。

|
| 图 2 基线布置示意 Fig. 2 Baseline arrangement schematic diagram |
|
| 图 3 算法流程 Fig. 3 Algorithm flowchart |
接收机卫星高度截止角设置为10°,数据采集时间为2015年10月10日14:10—12月22日14:10(北京时间),采样间隔为5 s,移动窗口参数分别为0.2 h(144个历元)、1 h(720个历元)和2 h(1440个历元)。在静态和加载位移情况下,使用以下方案进行比较分析。
2.1 静态试验方案1:未采用等价权抗差模型(BDS+GPS)。
方案2:采用等价权抗差模型(BDS+GPS)。
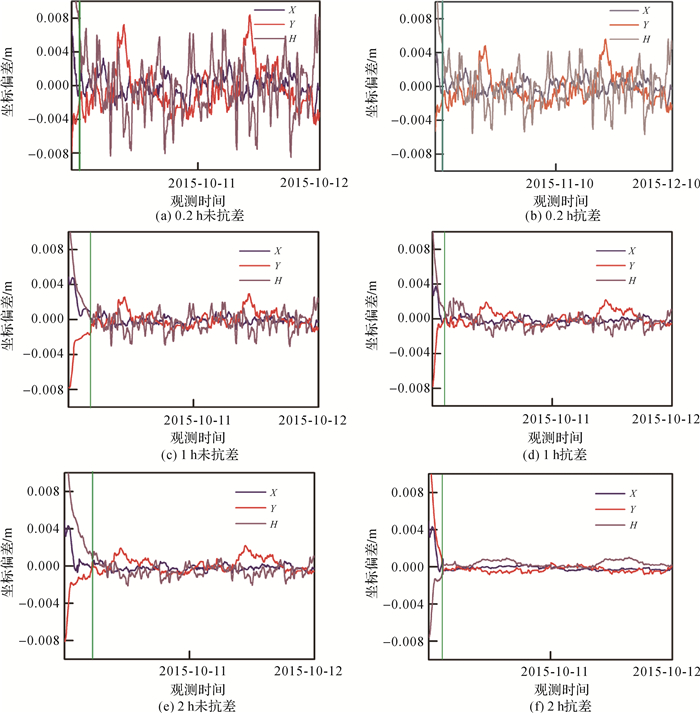
如图 4所示,相对于真实坐标的坐标偏差,由于多路径及残余大气误差的影响,不同移动窗口参数的坐标偏差在±8 mm范围内周期性波动。不采用等价权抗差的卡尔曼滤波模型,移动窗口由0.2 h增大为1 h以及1 h增大为2 h,显著减小坐标偏差,而移动窗口为1 h,采用等价权抗差也可提高坐标精度,与方案1移动窗口参数为2 h坐标偏差基本一致;由左半部分及右半部分两幅图对比发现,随着移动窗口参数的增大,坐标收敛时间也随之增加,而相同移动窗口,采用等价权抗差初始坐标收敛时间显著减小,约为方案1的1/2。由图 5(a)可看出,对于方案1和方案2,移动窗口参数为1 h和2 h的坐标偏差RMS值基本在1 mm内,定位精度达到亚毫米水平,而移动窗口参数为0.2 h的坐标偏差RMS值约为0.5~3.5 mm,由于移动窗口历元较少,经过抗差处理后,Y和H方向仍未达到亚毫米级定位精度;同一移动窗口参数,方案2的RMS值小于方案1,说明采用等价权抗差可提高坐标精度;BDS系统卫星几何分布不均匀,可视卫星主要为GEO和IGSO卫星(分布在东西方向),故Y坐标偏差RMS大于X方向,且H坐标易受多路径效应影响,其偏差RMS值最大。GPS卫星的加入可改善BDS定位模型的病态性,图 5(b)中相对于单BDS,BDS/GPS X坐标偏差RMS值明显减小,其中H坐标精度提高最为显著,X坐标有所提高,而Y坐标精度提高有限,与共视可用卫星数BDS大于GPS和GPS卫星星座构型有关。
|
| 图 4 X、Y、H坐标偏差曲线图,左半部分两幅图对应方案1,右半部分两幅图对应方案2(移动窗口参数分别为0.2 h、1 h及2 h,绿线代表坐标收敛完成的时间) Fig. 4 Time series of coordinate bias in X, Y and H, two figures in the left section corresponding to scheme 1, two figures in the right section corresponding to scheme 2(Moving window is 0.5 hour, 1 hour and 2 hours respectively, the green line represents the time at which the initial coordinates complete convergence) |

|
| 图 5 监测点在7种模式下坐标偏差RMS值 Fig. 5 RMS of coordinate bias at monitoring station in X, Y and H in seven situations (after the initial coordinates complete convergence) |
2.2 位移加载试验
由2.1部分可知,移动窗口参数一定时,等价权抗差模型可显著提高坐标精度,故以下方案全部使用等价权抗差方法,来分析移动窗口参数和加载位移探测精度、位移收敛速率的关系。为了获取探测位移,以下方案采用人工加载位移收敛前后100个历元的平均值作为位移收敛初始值和结束值,移动窗口参数为0.2 h、1 h和2 h,坐标波动范围分别约为4 mm、2 mm及1 mm时,位移收敛结束。通过位移收敛时间,判断不同移动窗口参数可探测的位移速率,为不同的蠕变体提供移动窗口参数选择标准。
2.2.1 方案1:X方向加载位移本次试验在X方向(正东方向)于北京时间2015-12-20 14:51:50和2015-12-21 10:39:40分别加载位移6 mm和3 mm。图 6中,红色线时间间隔为第1次加载位移收敛时间,紫色线时间间隔为第2次加载位移收敛时间,移动窗口2 h的抗差模型比移动窗口1 h的位移收敛较慢,移动窗口0.2 h的位移收敛时间小于1 h,同时由收敛前后100个历元平均值的差值可知,移动窗口2 h的探测位移为6.3 mm、3.4 mm,移动窗口1 h的探测位移为6.5 mm、3.6 mm,而移动窗口0.2 h的探测位移为6.9 mm、3.8 mm,与真实位移6 mm和3 mm相比,可得移动窗口2 h的位移探测精度为0.3 mm、0.4 mm,移动窗口1 h的位移探测精度为0.5 mm、0.6 mm,而移动窗口0.2 h的位移探测精度为0.9 mm、0.8 mm;对于位移的收敛速度,移动窗口2 h、1 h和0.2 h实时探测位移变化速率约为1 mm/h、2 mm/h和12 mm/h。

|
| 图 6 X方向加载位移曲线图(移动窗口分别为0.2 h、1 h和2 h) Fig. 6 Time series of loading displacement in X (moving window is 0.2 hour, 1 hour and 2 hours respectively) |
2.2.2 方案2:Y方向加载位移
对于Y方向(正北方向),于北京时间2015-10-25 12:12:30和2015-10-28 9:00:40分别人工加载位移10 mm,由图 7可知移动窗口2 h的探测位移为10.5 mm、10.6 mm,移动窗口1 h的探测位移为10.8 mm、10.9 mm,而移动窗口0.2 h的探测位移为11.6 mm、11.7 mm,可得移动窗口2 h的位移探测精度为0.5 mm、0.6 mm,移动窗口1 h的位移探测精度为0.8 mm、0.9 mm,而移动窗口0.2 h的位移探测精度为1.6 mm、1.7 mm;移动窗口2 h、1 h和0.2 h实时探测位移变化速率约为0.8 mm/h、1.8 mm/h和12.5 mm/h。
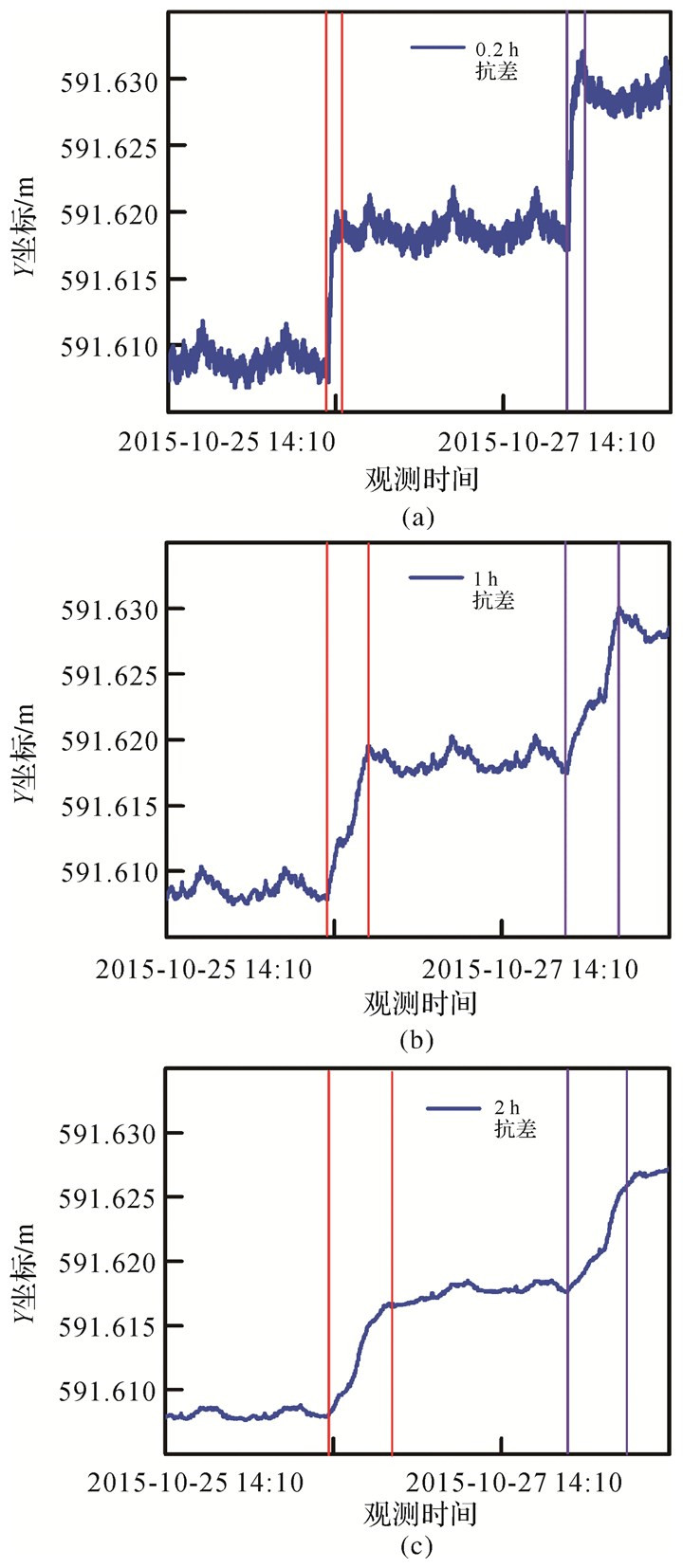
|
| 图 7 Y方向加载位移曲线图(移动窗口分别为0.5 h、1 h和2 h) Fig. 7 Time series of loading displacement in Y (moving window is 0.5 hour, 1 hour and 2 hours respectively) |
2.2.3 方案3:H方向加载位移
H方向(CGCS2000大地高方向)于北京时间2015-11-20 11:05:20人工加载位移5 mm,分析方法同方案1、2,图 8中移动窗口2 h、1 h及0.2 h探测位移精度分别为0.8 mm、1.3 mm和1.9 mm,实时探测位移变化速率约为0.9 mm/h、2.2 mm/h和11.8 mm/h。
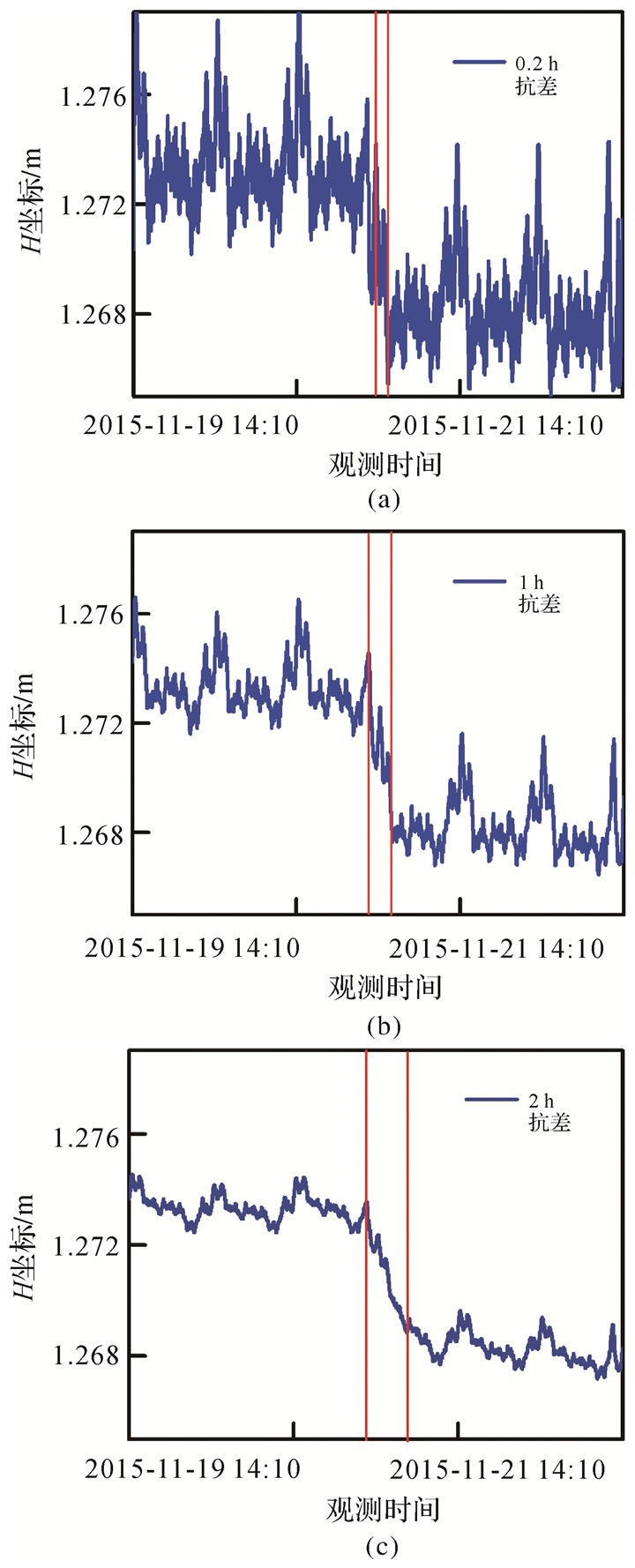
|
| 图 8 H方向加载位移曲线图(移动窗口分别为0.5 h、1 h和2 h) Fig. 8 Time series of loading displacement in H (moving window is 0.5 hour, 1 hour and 2 hours respectively) |
由以上分析可知,历史窗口历元平滑抗差随参数的增大可显著提高位移探测精度,相同窗口参数,位移探测精度H方向最低,Y方向次之,X方向最高,与2.1节精度分析基本一致,而移动窗口历史信息会掩盖当前历元权比信息特征,位移收敛时间将相应增加。为了确定移动窗口和位移变化速率的关系,对移动窗口参数0.2 h、1 h、2 h、3 h、4 h、5 h、6 h和7 h进行分析,由图 9可知移动窗口参数和位移变化速率基本成反比关系,移动窗口的增大会降低位移的收敛速率,当窗口参数增大到3 h,位移探测速率近似为零,故本次试验只选取移动窗口参数为0.2 h、1 h和2 h进行了比较分析。
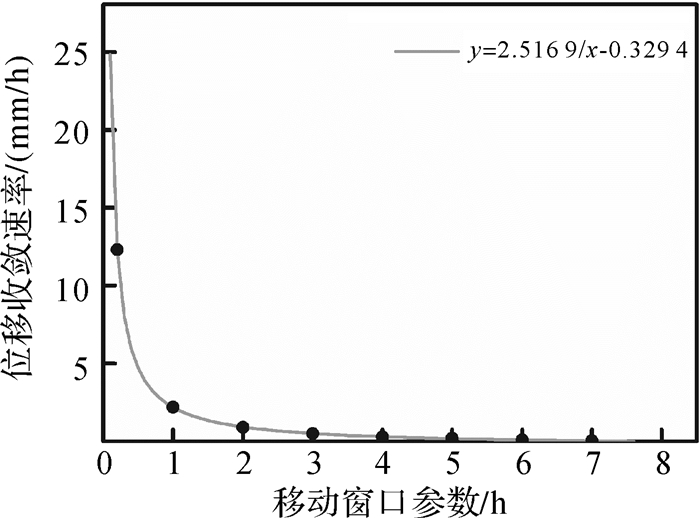
|
| 图 9 移动窗口参数和位移收敛速率关系 Fig. 9 Relation between moving window and displacement convergence rate |
3 结论
本文利用时钟同步双天线接收机N71JN,提出BDS/GPS抗差精密定权Kalman方法,构建BDS/GPS单频单差组合定位模型,实现模糊度的单历元固定,并利用等价权抗差,进一步减弱多路径及残余大气误差对单差观测值权的影响,引入时间相关因子,采用基于移动窗口的Helmert方差估计扩展Kalman滤波,实现了实时位移亚毫米的探测精度,并得出以下有益结论:
(1) 采用时钟同步双天线接收机,可显著降低监测成本,相对于双差模型,简化的单差单频方程可进一步提高模型冗余度。
(2) 使用等价权抗差方法,可减少扩展卡尔曼滤波收敛时间,加速概略坐标固定到准确坐标,可提高坐标的精度;
(3) 随着窗口的增大,位移探测精度将显著提高,移动窗口参数为1 h和2 h的外符合精度基本可达到亚毫米水平。
(4) 移动窗口参数与可探测位移收敛速率基本成反比关系,随着移动窗口参数增大,可实时探测位移速率显著下降。
以上结论将在大坝、滑坡等变形监测领域采用BDS/GPS抗差精密定权Kalman方法,为硬件设备及移动窗口参数的选取提供依据。本文针对长度为1 km的基线,验证了该算法的有效性,适用于具有蠕变特征的变形体;而当基线较长(> 1 km)时,需进一步研究如何有效避免GNSS信号的衰减,提高信噪比。随着计算机信息技术的发展,核心信息处理器运算能力的提高,可同时处理两个甚至更多的接收机板卡位置信息,实现GNSS多天线时钟同步定位,进一步降低成本,使该方法广泛应用于高精度蠕变监测领域。
| [1] | PAN S G, GAO W, WANG S L, et al. Analysis of Ill Posedness in Double Differential Ambiguity Resolution of BDS[J]. Survey Review, 2014, 46(339): 411–416. DOI:10.1179/1752270614Y.0000000121 |
| [2] | 王胜利, 王庆, 杨徉, 等. 北斗IGSO/GEO/MEO卫星联合高精度定位方法[J]. 中国惯性技术学报, 2013, 21(6): 792–796. WANG Shengli, WANG Qing, YANG Yang, et al. Method of High-precision Joint Positioning of Satellite IGSO/GEO/MEO[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 792–796. |
| [3] | 肖玉钢, 姜卫平, 陈华, 等. 北斗卫星导航系统的毫米级精度变形监测算法与实现[J]. 测绘学报, 2016, 45(1): 16–21. XIAO Yugang, JIANG Weiping, CHEN Hua, et al. Research and Realization of Deformation Monitoring Algorithm with Millimeter Level Precision Based on BeiDou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 16–21. DOI:10.11947/j.AGCS.2016.20140649 |
| [4] | 姚宜斌, 胡明贤, 许超钤. 基于DREAMNET的GPS/BDS/GLONASS多系统网络RTK定位性能分析[J]. 测绘学报, 2016, 45(9): 1009–1018. YAO Yibin, HU Mingxian, XU Chaoqian. Positioning Accuracy Analysis of GPS/BDS/GLONASS Network RTK Based on DREAMNET[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1009–1018. DOI:10.11947/j.AGCS.2016.20160133 |
| [5] | 高星伟, 过静珺, 程鹏飞, 等. 基于时空系统统一的北斗与GPS融合定位[J]. 测绘学报, 2012, 41(5): 743–748. GAO Xingwei, GUO Jingjun, CHENG Pengfei, et al. Fusion Positioning of BeiDou/GPS Based on Spatio Temporal System Unification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 743–748. |
| [6] | 王光鼎, 张升康, 杨汝良. 基于北斗无源与GLONASS导航系统的卫星组合导航用户位置计算[J]. 测绘学报, 2007, 36(4): 377–382. WANG Guangding, ZHANG Shengkang, YANG Ruliang. User Position Computation Based on Passive BeiDou and GLONASS Navigation System Combination[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 377–382. DOI:10.3321/j.issn:1001-1595.2007.04.004 |
| [7] | 杨元喜, 高为广. 基于方差分量估计的自适应融合导航[J]. 测绘学报, 2004, 33(1): 22–26. YANG Yuanxi, GAO Weiguang. Integrated Navigation by Using Variance Component Estimates of Multi-sensor Measurements and Adaptive Weights of Dynamic Model Information[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1): 22–26. |
| [8] | 段举举, 沈云中. GPS/GLONASS组合静态相位相对定位算法[J]. 测绘学报, 2012, 41(6): 825–830. DUAN Juju, SHEN Yunzhong. An Algorithm of Combined GPS/GLONASS Static Relative Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 825–830. |
| [9] | 杨元喜, 徐天河. 基于移动开窗法协方差估计和方差分量估计的自适应滤波[J]. 武汉大学学报(信息科学版), 2003, 28(6): 714–718. YANG Yuanxi, XU Tianhe. An Adaptive Kalman Filter Combining Variance Component Estimation with Covariance Matrix Estimation Based on Moving Window[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 714–718. |
| [10] | 周泽波, 沈云中, 李博峰. GPS/Doppler导航随机模型的移动窗口实时估计算法[J]. 测绘学报, 2011, 40(2): 220–225. ZHOU Zebo, SHEN Yunzhong, LI Bofeng. Moving Time-window Based Real-time Estimation Algorithm for the Stochastic Model of GPS/Doppler Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 220–225. |
| [11] | 王利. 地质灾害高精度GPS监测关键技术研究[D]. 西安: 长安大学, 2014. WANG Li. A Study on Key Technology of High Precision GPS Monitoring for Geological Hazard[D]. Xi'an:Chang'an University, 2014. |
| [12] | 高旺, 高成发, 潘树国, 等. 北斗三频宽巷组合网络RTK单历元定位方法[J]. 测绘学报, 2015, 44(6): 641–648. GAO Wang, GAO Chengfa, PAN Shuguo, et al. Single-epoch Positioning Method in Network RTK with BDS Triple-frequency Widelane Combinations[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 641–648. DOI:10.11947/j.AGCS.2015.20140308 |
| [13] | HE Xiufeng, SANG Wengang, CHEN Yongqi, et al. Steep-slope Monitoring:GPS Multiple-antenna System at Xiaowan Dam[J]. GPS World, 2005, 16(11): 20–25. |
| [14] | CINA A, PIRAS M. Performance of Low-cost GNSS Receiver for Landslides Monitoring:Test and Results[J]. Geomatics, Natural Hazards and Risk, 2015, 6(5-7): 497–514. DOI:10.1080/19475705.2014.889046 |
| [15] | CHANG Xiaowen, PAIGE C C, YIN Lan. Code and Carrier Phase Based Short Baseline GPS Positioning:Computational Aspects[J]. GPS Solutions, 2004, 7(4): 230–240. DOI:10.1007/s10291-003-0077-z |
| [16] | 任光辉. 基线约束的GPS单历元定向技术研究与实现[D]. 上海: 上海交通大学, 2013. REN Guanghui. Single Epoch GPS Orientation Determination Method and Realization with Baseline Constraint[D]. Shanghai:Shanghai Jiao Tong University, 2013. |
| [17] | 段荣, 赵修斌, 庞春雷, 等. 改进的GPS整周模糊度动态快速解算[J]. 华中科技大学学报(自然科学版), 2014, 42(9): 54–58. DUAN Rong, ZHAO Xiubin, PANG Chunlei, et al. Modified Algorithm for GPS Rapid Integer Ambiguity Resolution[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2014, 42(9): 54–58. |
| [18] | KUBO N. Advantage of Velocity Measurements on Instantaneous RTK Positioning[J]. GPS Solutions, 2009, 13(4): 271–280. DOI:10.1007/s10291-009-0120-9 |
| [19] | 王世进, 秘金钟, 李得海, 等. GPS/BDS的RTK定位算法研究[J]. 武汉大学学报(信息科学版), 2014, 39(5): 621–625. WANG Shijin, BEI Jinzhong, LI Dehai, et al. Real-time Kinematic Positioning Algorithm of GPS/BDS[J]. Geomatics and Information Science of Wuhan University, 2014, 39(5): 621–625. |
| [20] | 龚循强, 李志林. 稳健加权总体最小二乘法[J]. 测绘学报, 2014, 43(9): 888–894. GONG Xunqiang, LI Zhilin. A Robust Weighted Total Least Squares Method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 888–894. DOI:10.13485/j.cnki.11-2089.2014.0140 |
| [21] | 蔡艳辉, 程鹏飞, 李夕银. 用卡尔曼滤波进行GPS动态定位[J]. 测绘通报, 2006(7): 6–8. CAI Yanhui, CHENG Pengfei, LI Xiyin. Kinematic Point Positioning with Kalman Filtering[J]. Bulletin of Surveying and Mapping, 2006(7): 6–8. |
| [22] | YANG Yuanxi, SONG Lijie, XU Tianhe. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights[J]. Journal of Geodesy, 2002, 76(6-7): 353–358. DOI:10.1007/s00190-002-0256-7 |
| [23] | 王彬, 李建成, 高井祥, 等. 抗差加权整体最小二乘模型的牛顿-高斯算法[J]. 测绘学报, 2015, 44(6): 602–608. WANG Bin, LI Jiancheng, GAO Jingxiang, et al. Newton-Gauss Algorithm of Robust Weighted Total Least Squares Model[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 602–608. DOI:10.11947/j.AGCS.2015.20130704 |
| [24] | 周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989, 18(2): 115–120. ZHOU Jiangwen. Classic Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1989, 18(2): 115–120. |
| [25] | 陶叶青, 高井祥, 姚一飞. 基于中位数法的抗差总体最小二乘估计[J]. 测绘学报, 2016, 45(3): 297–301. TAO Yeqing, GAO Jingxiang, YAO Yifei. Solution for Robust Total Least Squares Estimation Based on Median Method[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 297–301. DOI:10.11947/j.AGCS.2016.20150234 |
| [26] | 高晓, 戴吾蛟. 抗差Helmert方差分量估计在GPS/BDS组合定位中的应用[J]. 大地测量与地球动力学, 2014, 34(1): 173–176. GAO Xiao, DAI Wujiao. Application of Robust Helmert Variance Component Estimation to Position in Combination of GPS and BDS[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 173–176. |
| [27] | GROVES P D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems[M]. 2nd ed.[S.l.]:Artech House, 2013. |
| [28] | KALMAN R E. A New Approach to Linear Filtering and Prediction Problems[J]. Journal of Basic Engineering, 1960, 82(1): 35–45. DOI:10.1115/1.3662552 |
| [29] | ZHAO Sihao, CUI Xiaowei, GUAN Feng, et al. A Kalman Filter-based Short Baseline RTK Algorithm for Single-frequency Combination of GPS and BDS[J]. Sensors, 2014, 14(8): 15415–15433. DOI:10.3390/s140815415 |
| [30] | 何秀凤, 桑文刚, 贾东振. 基于GPS的高边坡形变监测方法[J]. 水利学报, 2006, 37(6): 746–750. HE Xiufeng, SANG Wengang, JIA Dongzhen. Deformation Monitoring of Steep Rock Slopes by Means of GPS[J]. Journal of Hydraulic Engineering, 2006, 37(6): 746–750. |


