2. 中国科学院上海天文台, 上海 200092;
3. 中国科学院大学, 北京 100049;
4. 北京卫星导航中心, 北京 100094
2. Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200092, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. Beijing Satellite Navigation Center, Beijing 100094, ChinaAbstract
受混合星座区域网定轨和钟差预报精度的限制[1],北斗广播星历的精度还不如GPS,国内外许多学者也对北斗广播星历精度进行了评估[2-8]。文献[2]分析了2013年全年的北斗广播星历精度,认为北斗广播星历精度与GPS Block IIA卫星相当,均好于GLONASS和Galileo卫星。文献[3]对2012年的北斗广播星历轨道进行分析,表明GEO卫星径向精度优于1.5 m,IGSO/MEO卫星径向精度优于1.0 m,但没有考虑钟差误差的影响。文献[4]的结果表明北斗广播星历所有卫星平均精度为1.5 m,且主要受钟差误差的影响。文献[5]与文献[4]结论类似,但所采用数据的时间较短。文献[6]在此基础上研究了北斗广播星历的单点定位精度。文献[7]基于2013年至2015年的结果,得出所有卫星的广播星历精度平均为1.85 m,认为广播星历轨道和钟差误差呈现出与其轨道周期一致的周期变化特性。文献[8]通过激光检核结果比较表明与事后精密定轨比较结果一致。文献[9]基于事后精密星历分析了北斗空间信号误差的预报和改正。我国也建立了iGMAS(international GNSS monitoring and assessment)分析中心,对包括北斗系统在内的多GNSS系统的空间信号参数进行监测和评估。
北斗广播电文播发的信息包含了卫星基本轨道、钟差参数(基本导航电文)以及广域差分、完好性参数。其中,卫星轨道参数利用区域监测网的观测数据进行精密定轨(precise orbit determination,POD),经广播星历拟合后得到;卫星钟差参数则是基于星地双向时间比对(two-way satellite time transfer,TWTT),并进行参数拟合得到。POD与TWTT是两种独立的体制,两者融合成基本广播电文的过程中存在复杂的系统差归算[10],而系统差归算的误差则会造成基本导航电文的偏差。广域差分参数是在以上轨道、钟差参数的基础上,利用区域监测网的数据进一步进行空间信号的实时修正,理论上经过广域差分修正后,广播星历应该不存在偏差。本文利用北斗广播星历和IGS提供的精密星历,对北斗广播星历误差和空间信号参数进行深入分析。同时利用MGEX监测站数据和北斗广域差分信息,从伪距定位残差对北斗广播星历偏差进行研究。
1 北斗广播星历误差及空间信号精度计算 1.1 计算策略IGS于2012年提出MGEX(Multi GNSS EXperi-ment)计划,致力于提供多GNSS系统服务。目前共有CODE、GFZ、WHU 3个分析中心持续提供北斗事后精密产品,其中GFZ从2014年1月28日至今,提供包含GPS+GLONASSS+Galileo+BDS+QZSS在内的精密轨道和钟差(http://www.gfz-potsdam.de/en/section/space-geodetic-techniques/projects/mgex-beidou-analysis/),其GEO轨道精度约为50 cm,IGSO和MEO轨道精度约为10 cm和5 cm[11]。本文以gbm精密轨道和钟差作为参考,通过比较北斗广播星历和gbm精密星历的差异来反映北斗广播星历误差。
在进行广播星历轨道和钟差比较时,需要考虑以下几点:
(1) 坐标系统:gbm精密星历是基于WGS-84坐标系,而北斗广播星历则基于CGCS2000坐标系。许多文献都表明[12],这两个坐标系之间的差异在厘米级,这样的量级在进行广播星历比较时可以忽略。
(2) 时间系统:gbm精密星历是基于GPST(GPS Time),北斗广播星历基于BDT(BeiDou time),二者间存在14 s的差异,在比较时需要进行时间系统基准差异修正[13]。
(3) 群延迟(time group delay, TGD)改正:gbm精密钟差是基于B1B2无电离层组合,而北斗广播星历则基于B3频点[14],因此在比较卫星钟差时需要进行TGD改正。将B3钟差改正到B1B2无电离层组合钟差的公式为
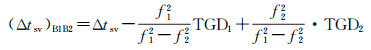 (1)
(1)
式中,(Δtsv)B1B2为B1B2无电离层组合钟差;Δtsv为广播星历计算得到的B3频点的钟差;TGD1和TGD2分别为广播星历中的B1、B2频点相对于B3频点的TGD延迟;f1、f2为B1、B2频点的频率。
(4) 卫星钟差基准统一:广播星历与精密星历的时间基准并不一样,在进行钟差比较时,需要扣除卫星钟差基准差异的影响。部分文献在进行基准统一时,选择扣除该历元所有卫星广播星历与精密星历钟差差异的均值[2-8]。这种方法的缺陷是当个别卫星存在粗差时,会使均值偏离真实的基准差异而无法反映真实的卫星钟差误差。本文选择所有卫星广播星历与精密星历钟差差异的中位数作为基准进行扣除,这样能有效避免卫星粗差的影响。
(5) 相位中心偏差(phase center offset, PCO):北斗广播星历轨道名义上定义为基于相位中心,但激光检核(satellite laser ranging, SLR)表明其实际上是基于质量中心[2]。由于精密星历轨道也基于质量中心,因此轨道比较时无需进行相位中心改正。而钟差比较时必须扣除二者相位中心的差异,对于gbm精密星历,其2014年年积日197之前使用的PCO改正为IGS默认值(0.6, 0.0, 1.1),其后使用的PCO改正值为欧空局(European Space Agency, ESA)给出的值[15]。因此在处理2014年年积日197之前的数据时,北斗广播星历与gbm精密星历相位中心差异改正为0,2014年年积日197之后的相位中心差异改正为PCOESA-PCOIGS。
空间信号测距误差(signal-in-space user range error, SISURE)是卫星位置与钟差的实际值与卫星广播星历之间的差异,它反映了卫星轨道和钟差的整体误差,可用于评价广播星历综合精度,其计算公式为
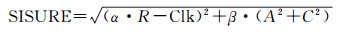 (2)
(2)
式中,R、C、A、Clk分别指卫星径向(radial)、法向(cross-track)、切向(along-track)和钟差误差(clock);α和β分别是各方向的投影系数,对于GEO和IGSO,其值分别为0.99和1/126;对于MEO,其值分别为0.98和1/154[2]。同时定义R-Clk为轨道径向与钟差误差的合成。由公式可以看出, R-Clk占了SISURE的大部分。
1.2 北斗广播星历误差及空间信号精度分析为了进行北斗广播星历误差长期分析,选择2014年2月1日至2016年10月26日共约3年的数据,按照30 min间隔的采样率计算北斗广播星历的误差,同时计算SISURE与R-Clk。在计算中,粗差剔除策略按照式(3) 进行处理[2]
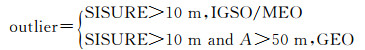 (3)
(3)
表 1列出了2014年2月至2016年10月间北斗广播星历误差及空间信号精度RMS统计结果。需要注意的是,C15(IGSO)卫星从2016年5月开始工作至2016年10月11日,其后C15编号改为C13(IGSO),替代原来一直处于不健康状态的C13(MEO),因此C13和C15实际上是同一颗卫星,在计算时将两者合并,统一归为现在的C13(IGSO)。如未特别说明,后文中的C13既是现在的C13,也指原来的C15。
| m | ||||||
| PRN | C | A | R | Clk | R-Clk | SISURE |
| 1 | 3.22 | 15.69 | 0.79 | 1.78 | 1.94 | 2.40 |
| 2 | 4.29 | 11.25 | 0.82 | 2.84 | 2.70 | 2.91 |
| 3 | 2.91 | 5.39 | 0.86 | 1.12 | 1.21 | 1.33 |
| 4 | 4.02 | 8.10 | 0.98 | 1.94 | 2.23 | 2.37 |
| 5 | 3.43 | 5.72 | 0.79 | 0.90 | 1.13 | 1.27 |
| 6 | 1.65 | 2.72 | 0.68 | 1.74 | 1.83 | 1.85 |
| 7 | 1.93 | 2.96 | 0.70 | 0.68 | 0.90 | 0.95 |
| 8 | 2.19 | 2.89 | 0.70 | 0.68 | 0.94 | 0.99 |
| 9 | 1.54 | 2.56 | 0.62 | 0.77 | 0.97 | 1.00 |
| 10 | 1.68 | 2.69 | 0.66 | 0.68 | 0.91 | 0.95 |
| 13 | 1.51 | 2.44 | 0.60 | 0.87 | 1.08 | 1.11 |
| 11 | 1.18 | 3.00 | 0.56 | 1.21 | 1.30 | 1.37 |
| 12 | 1.17 | 2.85 | 0.54 | 1.54 | 1.59 | 1.64 |
| 14 | 0.94 | 2.83 | 0.50 | 1.51 | 1.54 | 1.59 |
| Avg(GEO) | 3.57 | 9.23 | 0.85 | 1.71 | 1.84 | 2.05 |
| Avg(IGSO) | 1.75 | 2.71 | 0.66 | 0.90 | 1.11 | 1.14 |
| Avg(MEO) | 1.10 | 2.89 | 0.53 | 1.42 | 1.48 | 1.53 |
| Avg(All) | 2.26 | 5.08 | 0.70 | 1.30 | 1.45 | 1.55 |
为了观察不同类型卫星的轨道和钟差误差,按照卫星类型,将所有卫星近3年的轨道钟差误差及SISURE变化情况列于图 1。
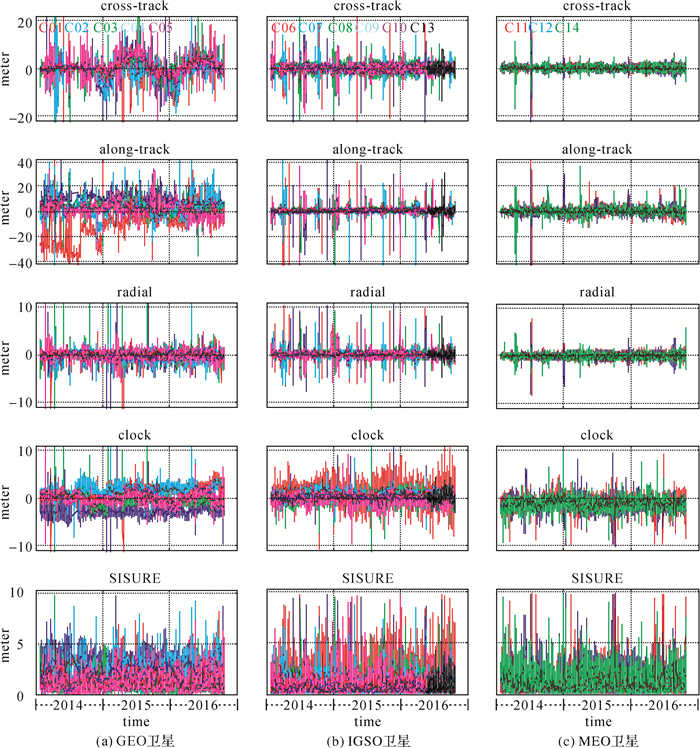
|
| 图 1 北斗广播星历误差及空间信号精度变化 Fig. 1 BDS broadcast ephemeris error and SISURE |
结合表 1和图 1可以看出,GEO卫星轨道误差最大,IGSO和MEO误差相当。总体来说,各卫星切向误差最大,C01卫星在2014年2月至8月的切向误差甚至超过20 m,而径向误差最小,这符合北斗卫星区域定轨的特性。与文献[2]相比,轨道切向误差变小了,其他误差则比较接近,这可能是二者数据样本不一样的原因。不论何种类型卫星,钟差误差都明显大于径向误差,因而可以推断北斗钟差误差是影响用户定位精度的主要因素。同时,从图中可以看出,部分卫星钟差误差存在系统性偏差,后文将对这个偏差进行进一步分析。
GEO、IGSO、MEO不同类型卫星空间信号精度RMS统计值分别为2.05 m、1.14 m、1.53 m,GEO卫星空间信号精度较差是由于其为静止卫星,几何构型不变,导致GEO卫星区域定轨精度较低。MEO较IGSO差一些是因为目前北斗监测网仍然是区域监测网,监测站在中国境内一天对MEO卫星可见性仅为几个小时,不可见时段的星历依赖于轨道和钟差的预报,当时钟数据龄期(AODC)[14]过长时,可能会导致卫星钟差预报误差增大。
SISURE反映了卫星空间测距误差的大小,而卫星径向和钟差误差的合成(R-Clk)能反映卫星空间测距误差的方向。为了观察R-Clk的长期变化,按照一个月进行划分,统计每个月的R-Clk均值。表 2给出了所有月份R-Clk的均值和标准差。图 2是不同类型的卫星R-Clk的每个月均值及标准差变化趋势,图中标准差用误差棒表示。
| sat | mean±STD/m |
| 1 | -1.31±1.37 |
| 2 | 2.52±1.03 |
| 3 | 0.19±1.20 |
| 4 | -1.86±1.17 |
| 5 | -0.14±1.11 |
| 6 | -1.25±1.32 |
| 7 | -0.19±0.82 |
| 8 | 0.19±0.92 |
| 9 | -0.42±0.83 |
| 10 | 0.20±0.88 |
| 11 | 0.69±1.11 |
| 12 | 1.12±1.15 |
| 13 | -0.75±0.85 |
| 14 | 1.13±1.09 |
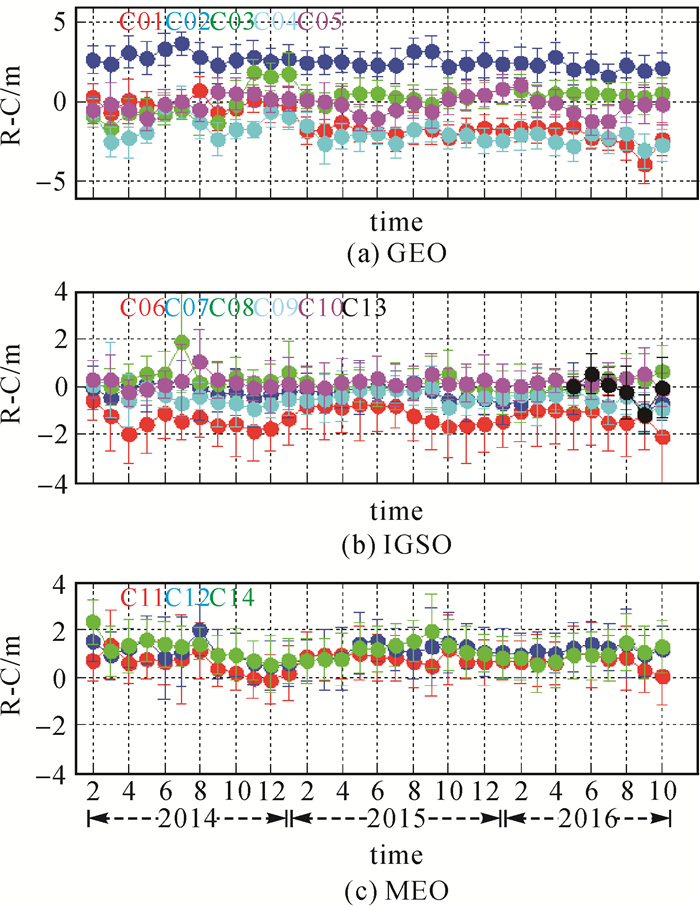
|
| 图 2 北斗卫星R-Clk每月均值变化趋势 Fig. 2 Mean value of monthly R-C statistics for different BeiDou satellites |
从表 2和图 2可以看出,C01、C02、C04、C06卫星的R-Clk均值明显大于其他同类型卫星,同时C02卫星的误差方向与C04相反,MEO卫星中C12、C14的均值也较大。从图中变化趋势可以看出,各卫星的R-Clk均值除了噪声,还存在大小各异的系统性偏差。
2 北斗广播星历偏差计算从第1节结果可以看出,北斗广播星历存在均值偏差。北斗广域增强系统在广播星历轨道和钟差参数的基础上,利用区域监测网的数据计算等效钟差改正数,能够实时消除广播星历轨道和钟差所产生的系统性误差,经改正后的用户差分距离误差(user differential range error, UDRE)优于0.5 m[16]。理论上经过广域差分修正后,广播星历应该不存在大的偏差。
为了研究北斗广播星历是否还存在一些固定偏差,本节利用北斗广域差分改正数进行进一步分析。选取了对北斗卫星可视性较好的一共18个MGEX监测站,对2016年年积日从200到296共97 d的数据进行单点定位,定位时固定站坐标,计算各个频点定位后的伪距观测值残差。计算时北斗轨道和钟差利用北斗广域差分改正数进行修正,由于北斗卫星轨道实际上是基于质心,因此未作PCO改正。不同频点的电离层误差用IGS电离层格网模型改正,对流层延迟采用模型改正,数据采样率为150 s,卫星截止高度角为10°,其余各项误差改正采用常规模型进行改正。监测站分布见图 3,图中红色圆形点位用于伪距残差计算,蓝色三角形点位用于后面的验证。
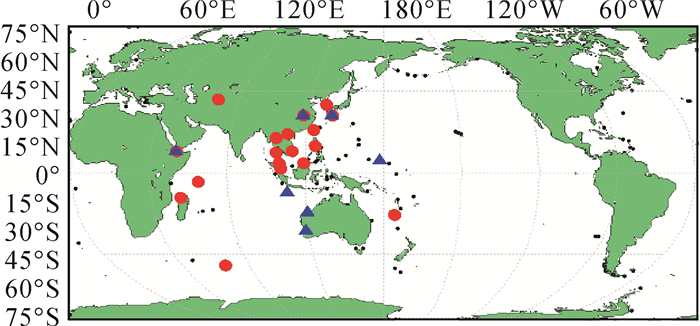
|
| 图 3 MGEX监测站(红色:估计广播星历偏差;蓝色:定位验证) Fig. 3 MGEX station used (red: for estimating, blue: for positioning validation) |
对2016年年积日200至296的数据进行处理,获取定位后的伪距残差,将各站的伪距残差按照每天进行统计,计算每天各卫星对所有观测站的伪距残差的均值及标准差。图 4是B1频点不同卫星的伪距残差随时间的变化趋势,其中误差棒表示每天的标准差。
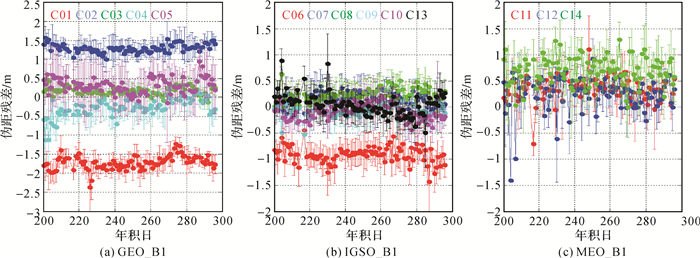
|
| 图 4 B1频点伪距残差变化单天均值及其标准差(2016年) Fig. 4 Mean value and STD of daily code residual variation at B1 frequency(2016年) |
从图 4可以看出,基于北斗广播星历和广域差分改正数精密定位的伪距残差均值存在系统偏差,且该偏差变化较为平稳,将这种偏差称为广播星历偏差(broadcast ephemeris bias, BEB)。
基于以上结果,统计了所有卫星不同频点的广播星历偏差及其标准差,见表 3。结合图 4可以看到,C01、C02、C06的BEB值较大,其他卫星都在0.5 m内。
| m | |||
| sat | bias±STD | ||
| B1 | B2 | B3 | |
| 1 | -1.72±0.31 | -1.19±0.42 | -1.19±0.22 |
| 2 | 1.30±0.28 | 0.56±0.38 | 0.77±0.34 |
| 3 | 0.18±0.19 | -0.02±0.29 | 0.19±0.28 |
| 4 | -0.25±0.43 | 0.11±0.62 | 0.10±0.34 |
| 5 | 0.31±0.59 | 0.40±0.75 | 0.16±0.80 |
| 6 | -0.92±0.31 | -0.59±0.42 | -0.80±0.32 |
| 7 | 0.17±0.30 | 0.09±0.40 | -0.15±0.43 |
| 8 | 0.22±0.29 | 0.16±0.40 | -0.08±0.32 |
| 9 | -0.08±0.29 | 0.24±0.36 | -0.02±0.31 |
| 10 | -0.10±0.32 | -0.20±0.43 | 0.01±0.42 |
| 11 | 0.36±0.41 | 0.42±0.55 | 0.01±0.49 |
| 12 | 0.29±0.43 | 0.26±0.54 | 0.02±0.52 |
| 13 | 0.04±0.36 | 0.17±0.45 | 0.36±0.28 |
| 14 | 0.71±0.47 | 0.42±0.61 | 0.23±0.62 |
另外,从表 3中可以看到不同频点的BEB值并不一样,推测其可能与卫星TGD有关。IGS基于全球MGEX观测网数据,计算了北斗广播星历不同频点的TGD改正[17-18]。该值与广播星历中的TGD并不一致,可将二者进行相减得到的dTGD(differential TGD)与本文中获取的BEB进行比较,为了统一基准,将二者所有卫星的均值扣除。图 5显示了B1B2无电离层组合的差异BEB和dTGD的比较结果。从图中可以看出,大部分卫星的差异较为接近。采用线性回归分析,计算其相关系数[19],二者达到0.89,这说明BEB和dTGD之间相关性很大,推测可能是由于北斗监测站接收机与IGS监测站接收机对相同卫星的通道时延标定不一致,导致北斗广播星历TGD用于IGS监测站接收机时存在偏差,但仍需进一步深入研究。
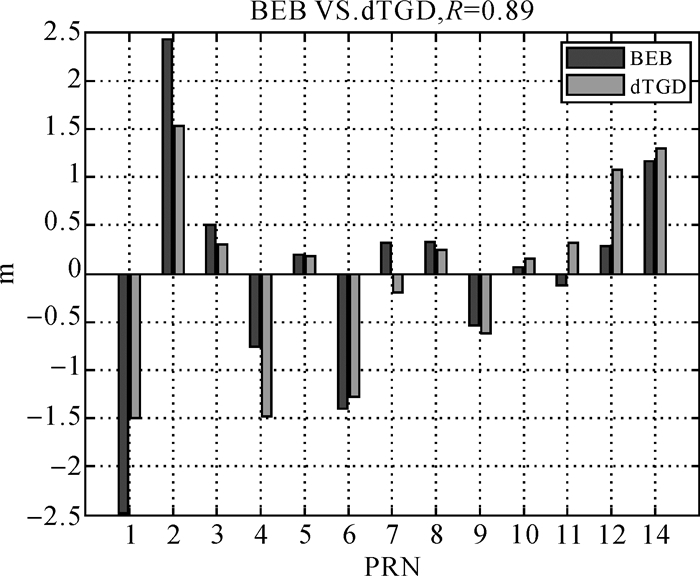
|
| 图 5 BEB与dTGD比较 Fig. 5 Comparison of BEB and dTGD |
3 北斗广播星历偏差在定位中的应用
为了验证本文给出的BEB的定位效果,采用不同时间、不同站的数据进行单点定位验证。选取2015-12-27—2016-01-09共14 d的7个MGEX站数据,测站分布见图 3蓝色点位。其中KARR、NNOR、POHN、XMIS 4个站在计算伪距偏差时并没有用到。NNOR接收机类型为SEPT POLARX4,其他均为Trimble NETR9。定位时采用北斗广播星历,将各频点的BEB改正到广播星历TGD参数上,对这些站进行伪距单点定位,观测值采用B1B2无电离层组合,对流层延迟采用模型改正,数据采样率为30 s,卫星截止高度角为10°,将IGS给出的精密坐标作为真实坐标,比较BEB改正前后的定位结果差异。
图 6是GMSD测站在2016年1月1日这一天的单点定位结果比较。其中图 6(a)为常规定位的结果,图 6(b)为增加BEB改正后的定位结果。表 4给出了各个站14 d的动态定位RMS比较。
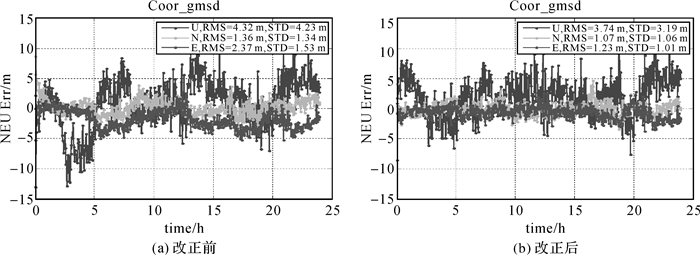
|
| 图 6 广播星历偏差改正前后定位精度比较(GMSD) Fig. 6 Positioning error comparison before (a) and after (b) BEB correction (GMSD) |
| sta | without BEB correction/m | with BEB correction/m | improvement/(%) | ||||||||
| N | E | U | N | E | U | N | E | U | |||
| DJIG | 3.37 | 8.46 | 9.65 | 2.65 | 5.65 | 6.44 | 21.3 | 33.2 | 33.3 | ||
| GMSD | 1.76 | 2.44 | 4.23 | 1.23 | 1.48 | 3.71 | 30.2 | 39.4 | 12.4 | ||
| JFNG | 1.73 | 2.33 | 4.03 | 1.24 | 1.36 | 3.38 | 28.1 | 41.7 | 16.1 | ||
| KARR | 2.01 | 2.39 | 3.50 | 2.01 | 1.82 | 3.17 | 0.0 | 23.9 | 9.3 | ||
| NNOR | 2.24 | 2.41 | 3.54 | 2.01 | 1.52 | 3.28 | 10.3 | 37.1 | 7.4 | ||
| POHN | 2.65 | 5.45 | 6.13 | 2.42 | 4.85 | 6.07 | 8.5 | 10.9 | 1.0 | ||
| XMIS | 1.70 | 2.32 | 3.49 | 1.59 | 1.78 | 3.16 | 6.6 | 23.3 | 9.5 | ||
| mean | 2.21 | 3.68 | 4.94 | 1.88 | 2.64 | 4.17 | 14.9 | 28.4 | 15.5 | ||
从以上定位结果可以看出,北斗广播星历偏差能改善定位精度,在南北(N)、东西(E)、高程(U)方向定位提高程度分别为14.9%、28.4%和15.5%,东西方向改善最明显,这可能是由于GEO卫星BEB改正值比其他卫星大,且GEO卫星纬度相同,因而对东西方向改善最大。同时,北斗广播星历偏差对于不同时间,不同观测站,不同接收机,都能改进其定位效果,这说明BEB与时间、接收机无关,更有可能是北斗广播星历不同卫星的系统性偏差造成的(如卫星TGD或者系统监测站的通道时延误差)。
为了进一步分析BEB对定位的影响,图 7给出了2016年1月1日GMSD站BEB改正前后不同卫星的伪距单点定位残差的RMS及STD比较。可以看到个别卫星(C01, C02, C04, C08, C14) 原始伪距残差较大,这主要就是广播星历偏差造成的。而改正后的各颗卫星定位残差RMS相近,约为1 m左右。从STD来看,二者没有太大区别,这也验证了改正的广播星历偏差是系统性的。
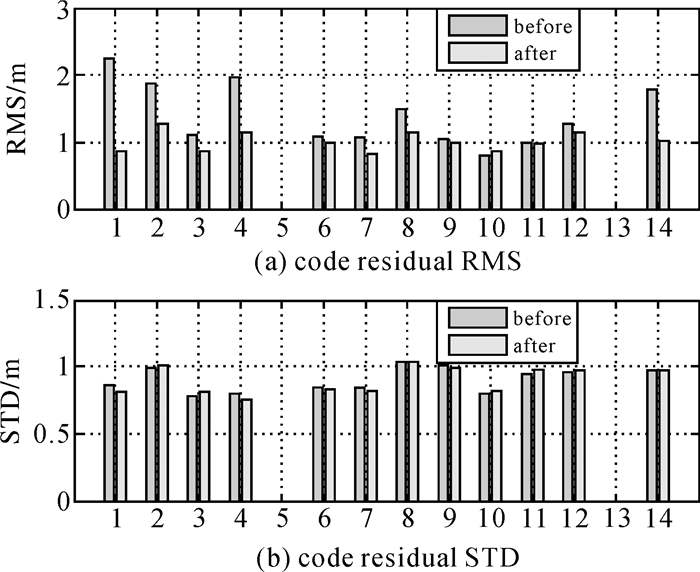
|
| 图 7 BEB改正前后各卫星定位残差的RMS和STD统计 Fig. 7 RMS and STD of code residual comparison after BEB correction |
4 结论
本文对近三年的北斗广播星历误差进行分析,证明了北斗广播星历存在偏差。从精密定位中发现了伪距定位残差具有系统性偏差,从中发现广播星历具有长期系统性的偏差。根据多天多站的解算给出了广播星历偏差的改正值,并对其定位效果进行了验证,得出以下结论:
(1) 北斗广播星历GEO卫星轨道误差最大,IGSO和MEO误差相当,各卫星切向误差最大,钟差误差大于径向误差。GEO、IGSO、MEO卫星空间信号精度统计结果分别约2.05 m、1.14 m、1.53 m。各卫星的R-Clk均值除了噪声,还存在大小各异的系统性偏差。
(2) 经广域差分改正数修正的北斗广播星历存在系统性偏差,且这个偏差变化较为平稳。相同卫星不同频点不一致,且与IGS和北斗广播星历TGD差异的相关性很大。
(3) 广播星历偏差改正能改善用户基本导航定位精度,且对不同时间和用户接收机类型都有提高,总体来说,在N、E、U 3个方向分别提高14.9%、28.4%、15.5%。伪距定位残差RMS也有改善。但由于本文中计算偏差所采用的数据只有96 d,且验证数据与计算结果相距只有200 d左右。从长期来看,这个偏差是否仍是固定的,有待基于长期大量数据的进一步研究。
致谢: 感谢IGS提供的观测数据和gbm提供的MGEX精密星历。
| [1] | ZHOU Shanshi, CAO Yueling, ZHOU Jianhua, et al. Positioning Accuracy Assessment for the 4GEO/5IGSO/2MEO Constellation of COMPASS[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(12): 2290–2299. DOI:10.1007/s11433-012-4942-z |
| [2] | MONTENBRUCK O, STEIGENBERGER P, HAUSCHILD A. Broadcast Versus Precise Ephemerides:A Multi-GNSS Perspective[J]. GPS Solutions, 2015, 19(2): 321–333. DOI:10.1007/s10291-014-0390-8 |
| [3] | CHEN Liang, JIAO Wenhai, HUANG Xiaorui, et al. Study on Signal-in-space Errors Calculation Method and Statistical Characterization of BeiDou Navigation Satellite System[C]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin:Springer, 2013:423-434. |
| [4] | HU Zhigang, CHEN Guo, ZHANG Qiang, et al. An Initial Evaluation about BDS Navigation Message Accuracy[C]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin:Springer, 2013:479-491. |
| [5] | 张清华, 隋立芬, 贾小林, 等. 北斗卫星导航系统空间信号误差统计分析[J]. 武汉大学学报(信息科学版), 2014, 39(3): 271–274. ZHANG Qinghua, SUI Lifen, JIA Xiaolin, et al. SIS Error Statistical Analysis of BeiDou Satellite Navigation System[J]. Geomatics and Information Science of Wuhan University, 2014, 39(3): 271–274. |
| [6] | CHEN Gucang, HU Zhicang, WANG Guangxing, et al. Assessment of BDS Signal-in-space Accuracy and Standard Positioning Performance during 2013 and 2014[C]//SUN Jiadong, LIU Jingnan, FAN Shiwei, et al. China Satellite Navigation Conference (CSNC) 2015 Proceedings. Berlin:Springer, 2015:437-453. |
| [7] | 刘万科, 任杰, 曾琪, 等. 2013-2015年BDS空间信号测距误差的精度评估[J]. 国防科技大学学报, 2016, 38(3): 1–6. LIU Wanke, REN Jie, ZENG Qi, et al. Accuracy Assessment of BDS Signal-in-space Range Errors in 2013-2015[J]. Journal of National University of Defense Technology, 2016, 38(3): 1–6. DOI:10.11887/j.cn.201603001 |
| [8] | 耿涛, 苏醒, 许小龙, 等. 北斗卫星导航系统精密定轨和广播星历轨道精度分析[J]. 中国科技论文, 2015, 10(9): 1023–1026. GENG Tao, SU Xing, XU Xiaolong, et al. Research on Precise and Broadcast Ephemeris Orbit of BeiDou Navigation Satellite System[J]. China Science paper, 2015, 10(9): 1023–1026. |
| [9] | ZHANG Yize, CHEN Junping, GONG Xiuqiang, et al. Modeling and Application of Compass Satellite Orbits and Clocks Predicted Correction[C]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2014 Proceedings. Berlin:Springer, 2014:181-191. |
| [10] | HE Feng, ZHOU Shanshi, HU Xiaogong, et al. Satellite-Station Time Synchronization Information Based Real-time Orbit Error Monitoring and Correction of Navigation Satellite in BeiDou System[J]. Science China Physics, Mechanics & Astronomy, 2014, 57(7): 1395–1403. |
| [11] | DENG Zhiguo, GE Maorong, UHLEMANN M, et al. Precise Orbit Determination of BeiDou Satellites at GFZ[R]. Pasadena:IGS Workshop, 2014. |
| [12] | 高星伟, 过静珺, 程鹏飞, 等. 基于时空系统统一的北斗与GPS融合定位[J]. 测绘学报, 2012, 41(5): 743–748. GAO Xingwei, GUO Jingjun, CHENG Pengfei, et al. Fusion Positioning of Compass/GPS Based on Spatio Temporal System Unification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 743–748. |
| [13] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [14] | 中国卫星导航管理办公室. 北斗卫星导航系统空间信号接口控制文件公开服务信号(2. 0版)[ Z]. 2013. China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal (Version 2.0)[Z]. 2013. |
| [15] | DILSSNER F, SPRINGER T, SCHÖNEMANN E, et al. Estimation of Satellite Antenna Phase Center Corrections for BeiDou[R]. Pasadena:IGS Workshop, 2014. |
| [16] | CAO Yueling, Hu Xiaogong, WU Bin, et al. The Wide-area Difference System for the Regional Satellite Navigation System of Compass[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(7): 1307–1315. DOI:10.1007/s11433-012-4746-1 |
| [17] | WANG Ningbo, YUAN Yunbin, LI Zishen, et al. Determination of Differential Code Biases with Multi-GNSS Observations[J]. Journal of Geodesy, 2016, 90(3): 209–228. DOI:10.1007/s00190-015-0867-4 |
| [18] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P. Differential Code Bias Estimation Using Multi-GNSS Observations and Global Ionosphere Maps[J]. Journal of the Institute of Navigation, 2014, 61(3): 191–201. DOI:10.1002/navi.v61.3 |
| [19] | 曹俊忠. 一元线性回归显著性检验方法分析[J]. 西北纺织工学院学报, 1988(3-4): 78–82. CAO Junzhong. The Analysis on the Significant Testing Ways of the Simple Linear Regression[J]. Journal of Northwest Institute of Textile Science and Technology, 1988(3-4): 78–82. |



