电离层延迟误差变化从几米到几十米不等,是卫星导航数据处理中主要的误差源之一。目前在导航定位中应用最广泛的是Klobuchar模型,该模型简单,电离层延迟修正率一般在50%~60%[1-2]。为了满足日益增长的导航定位精度的需求,不同的Klobuchar模型的精化方案被提出,均在不同程度上提升了模型的修正率。
电离层的模型精化方案分为参数精化和模型精化,一般涉及夜间常值和初始相位的固定、区域参数拟合最佳等方面。文献[3—8]通过一定的数学方法修正电离层模型参数,使之更加符合局域电离层的变化情况,但并未考虑电离层夜间延迟和初始相位值固定所引入的模型误差。文献[9—17]通过改变模型的表达形式,试图从根本上改变由电离层夜间延迟和初始相位值固定所引入的模型误差,但因考虑得不够全面或者在某个尺度上的改进函数的阶数较低[18],难以达到较好的精化效果。
一个合适的电离层模型应当能在一定程度上描述电离层在时间和空间上的宏观变化规律。在时间上,电离层日变化有很好的单峰结构[1, 19],且峰值出现时间一般都在午后,据文献[20]等大量文献研究表明峰值主要集中分布在地方时的12时至16时,其中14时附近分布最为集中;夜间电离层电子含量普遍要低于白天的,易出现当天的电子含量的最小值,但数值上并非固定不变。在空间上,由于不同的纬度区域受到的太阳辐射有所不同,电离层会随纬度的变化而有所变化[21-22];除了低纬的赤道异常区域在经度上存在四峰纵向结构[23]外,电离层随经度变化较小,可忽略不计。
针对电离层模型精化的现状和电离层TEC(total electron content)的时空变化规律,本文提出了一个适用于不同区域的Klobuchar-like模型,该模型可根据区域大小调节参数数目以适应于不同尺度区域的电离层延迟修正。
1 Klobuchar模型及其精化 1.1 经典Klobuchar模型Klobuchar电离层模型[1]是根据中纬度地区大量实验资料拟合得到的经验模型。该模型将夜间的VTEC(vertical TEC)视作一个9.23TECU(TEC Unit)的常量(电离层延时为5 ns),该常量为全球夜间平均VTEC在一个太阳活动周期的平均值[24];每天电离层TEC最大时刻固定为地方时的14:00;并将白天的时延变化用一个余弦函数进行拟合,基本上反映了电离层日变化特性,从大尺度上保证了电离层的可预报性与可靠性。该模型现已被GPS和BDS两大系统采用,除了在坐标系统、参数定义等细节上有区别[18]外,两大系统所采用的Klobuchar模型在形式上具有统一性,具体形式为
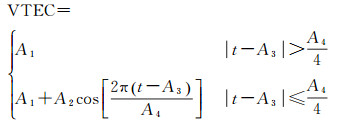 (1)
(1)
式中,VTEC是以秒为单位的垂直延迟;A1为夜间垂直延迟常数,取值为5 ns;A2为白天余弦函数振幅;A3为电子总数峰值的地方时时刻,取值为50 400 s;A4为大于20 h的余弦函数周期。
1.2 14参数Klobuchar模型文献[13—15]将Klobuchar模型由8参数扩充到14参数,并采用实测GPS双频观测资料,在最小二乘的基础上,估计并校验其参数设置,建立了符合中国地区电离层实际变化情况的14参数Klobuchar模型
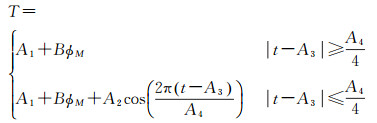 (2)
(2)
式中
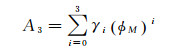 (3)
(3)
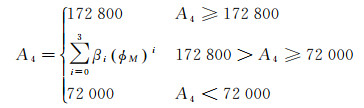 (4)
(4)
式中,夜间延迟用A1+BφM来代替,即随纬度变化的一阶函数;A3为初始相位,随磁纬而变化。A4为余弦曲线的周期,在经典Klobuchar模型的基础上增加了172 800的周期上限。该模型考虑到了夜间值、相位初始值固定的影响,并对其加以修正,使得模型的精度有所提高,但是该模型并未考虑到夜间值随时间变化的情况[18]。
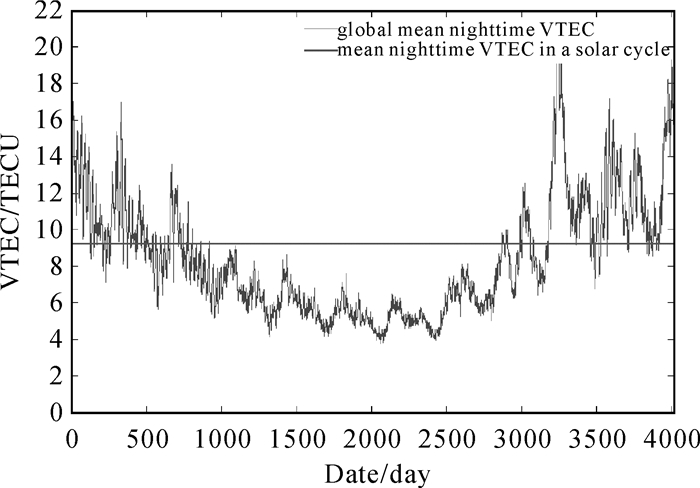
1.3 Klobuchar-like电离层模型由文献[24]所给出的一个太阳活动周期内的全球夜间电离层变化趋势(图 1)可知,夜间全球平均VTEC的值与太阳活动有关,最大值约为最小值的5倍;该文同时指出,一个太阳活动周期内的全球电离层夜间平均VTEC值与Klobuchar的夜间常值相近,验证了夜间常值在一定程度上的合理性,但也表明了Klobuchar的夜间常值存在很大的改进空间。
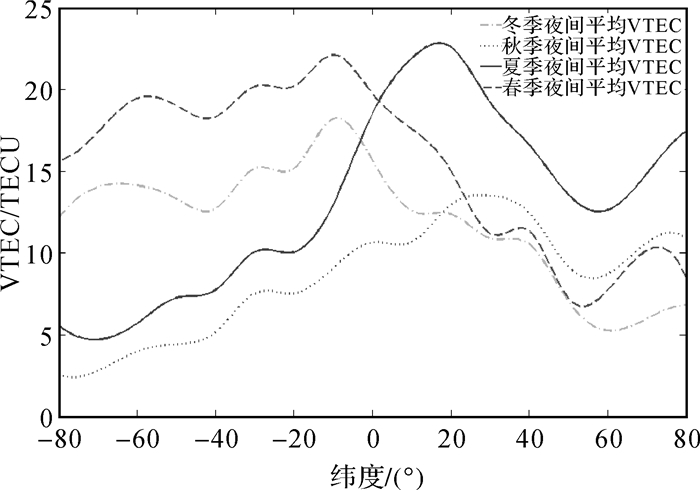
图 2给出了不同季节某一天的夜间电离层平均VTEC随着纬度的变化趋势,每个纬度上的数值是该纬度上6个等间距经度位置上的夜间电离层平均VTEC的平均值。从图中可以看出,不同季节的夜间平均VTEC变化趋势存在较大差异,量级差异也较大;同季节(同一天)的夜间平均VTEC,同半球的低纬度要高于中高纬度,但南北具有不对称性。因此,夜间VTEC随着纬度变化比较明显,Klobuchar模型中夜间VTEC值应当随着纬度变化而变化。
|
| 图 2 不同季节夜间平均VTEC随纬度的变化 Fig. 2 Variations of mean nighttime VTEC with latitude in different seasons |
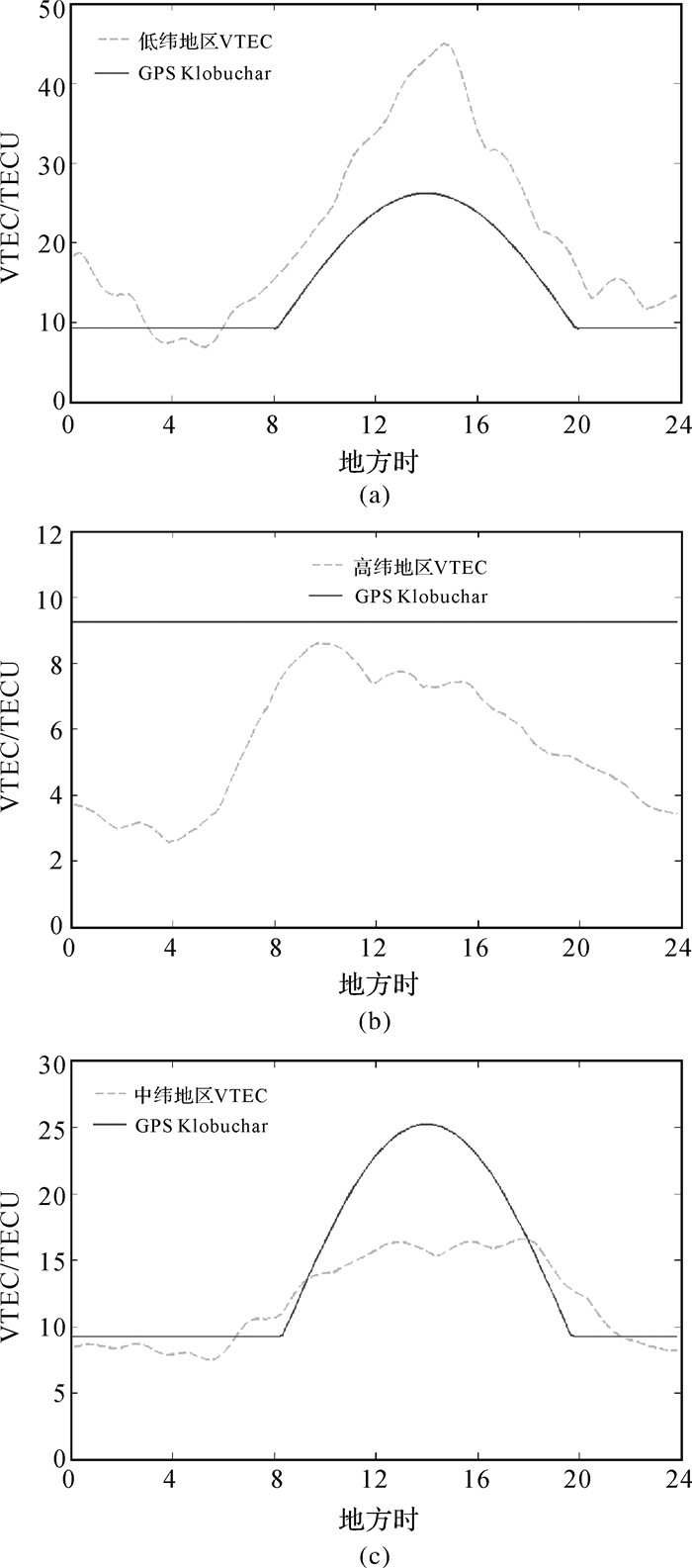
图 3给出了2016年9月22日低纬地区(KOUR站,5.25°N,52.81°W)、高纬地区(VESL站,71.67°S,2.84°W)、中纬地区(CHAN站,43.79°S,125.44°E)的VTEC日变化情况与GPS Klobuchar修正量,VTEC日变化数据来源于GIMs数据(下同)。从图中可以发现,电离层夜间VTEC随着时间变化而变化,并非固定常值,且VTEC日最大值并非均在地方时14:00;GPS Klobuchar的模型参数由370组常数中选取后编入导航电文播发给用户,导致了GPS Klobuchar对各个纬度的电离层修正均未达到较好的效果。因此,Klobuchar模型的电离层精化应当顾及夜间VTEC随地方时变化以及初始相位变化等情况,同时模型的参数应该如BDS系统一样根据实测数据拟合,而非从顾及整个太阳活动周期内电离层变化的370组常数中选取。
|
| 图 3 不同纬度地区的VTEC日变化与GPS Klobuchar修正量 Fig. 3 Daily variations of VTEC and GPS Klobuchar corrections at different latitudes |
综上所述,夜间VTEC与太阳活动有关,太阳活动周期的不同阶段,夜间VTEC变化很大[24];不同纬度的夜间VTEC值不同;夜间VTEC还随着地方时的变化而变化,因此经典的Klobuchar模型固定夜间VTEC会引入20%~30%的误差[5, 14]。经典Klobuchar模型中将余弦的初始相位固定,其实际意义是VTEC达到最大时为地方时14时,而实际情况表明这并不准确,穿刺点处的峰值时间在12~16时,固定初始相位通常可能带来3%~10%的误差[5, 10, 14]。因此,文献[3—17]对经典Klobuchar模型从参数精化和模型精化两个方面进行精化,取得了一定的改进效果,但依然存在上文所提及的问题。在对各种适用范围较广的模型精化方案进行归纳总结的基础上,本文提出了一个适用于不同区域大小的Klobuchar-like模型,如式(5) 所示
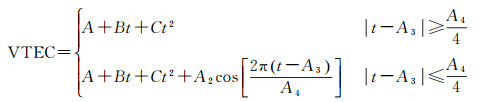 (5)
(5)
式中
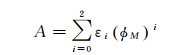 (6)
(6)
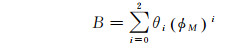 (7)
(7)
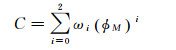 (8)
(8)
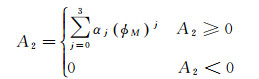 (9)
(9)
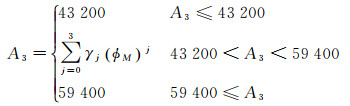 (10)
(10)
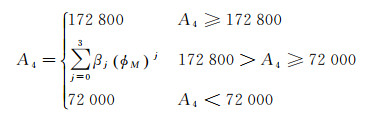 (11)
(11)
式中,εi、θi、ωi(i=0, 1, 2) 分别为夜间延迟关于时间的常数项、一阶项、二阶项系数的修正系数;φM为纬度,包括地理纬度和地磁纬度,即不同的定位系统可以选择不同的纬度模式。A2为白天余弦函数振幅,A3为电子总数目峰值的地方时时刻,A4为余弦函数周期, 它们的取值方法参照式(9)、式(10) 和式(11)。
该模型为全球精化模型,将夜间电离层延迟值作为纬度和地方时的二元二次函数,初始相位是纬度的一元三次函数,可通过实测数据(如BDS-TEC、GPS-TEC)和GIMs预测产品对广播星历的参数进行实时更新。该模型也可适用于区域的电离层修正,即根据区域的大小选取i、j的上限m、n,如当区域较小时可取m=0、n=0;当区域较大时可取m=1、n=2。
2 试验与分析为了验证Klobuchar-like模型的有效性和实用性,本文通过不同太阳活动时期不同季节的单站建模、区域建模和全球建模对Klobuchar-like模型进行评估。数据日期分别是2008年5月1日、2008年10月1日、2013年6月21日、2013年12月22日、2016年3月20日和2016年9月22日。
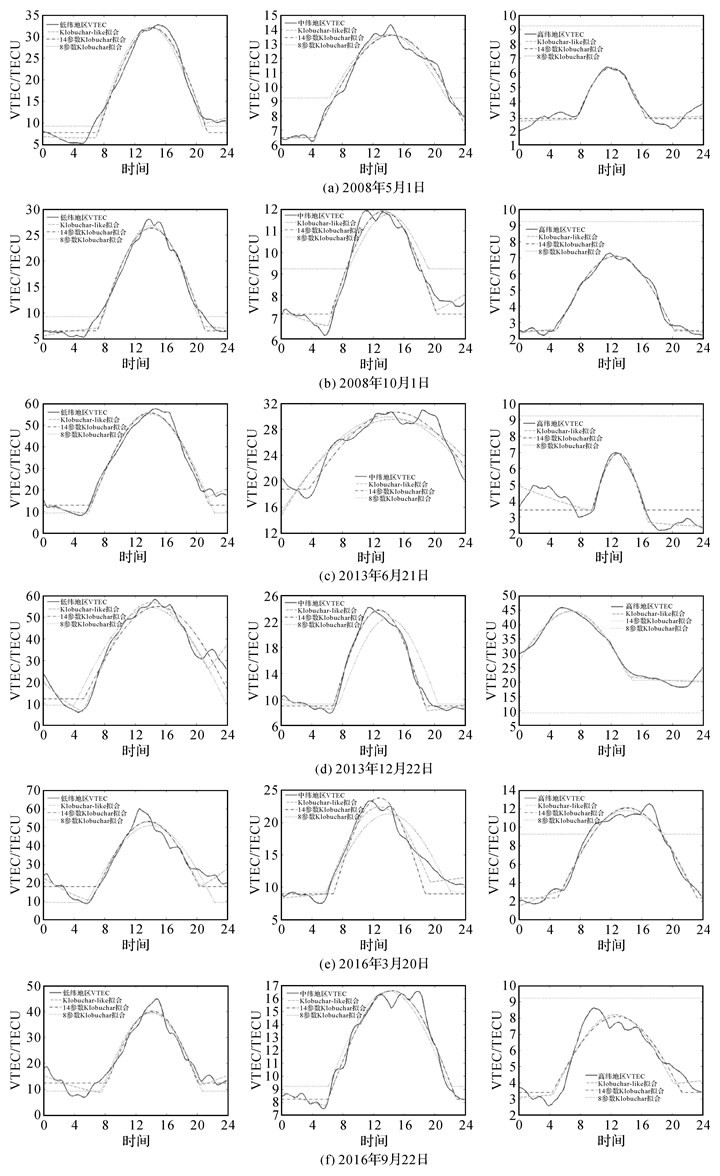
2.1 单站电离层建模在单站建模时选取了图 3中涉及的高、中、低纬度区域的3个站点的VTEC对Klobuchar-like、14参数Klobuchar、8参数Klobuchar 3种模型进行了建模,建模结果如图 4所示。
|
| 图 4 VTEC日变化与Klobuchar-like、14参数Klobuchar、8参数Klobuchar拟合的VTEC Fig. 4 Daily variations of VTEC, Klobuchar-like 14-paramaters Klobuchar and 8-paramaters Klobuchar corrections |
从图中可以发现,Klobuchar-like模型顾及了夜间电离层VTEC随地方时变化和初相位不固定等情况,能够较好地反映不同时期各个纬度区域的变化情况,优于14参数Klobuchar模型和8参数Klobuchar模型;14参数模型能够较好地顾及初始相位不稳定的情况,虽在单站建模时将电离层夜间变化视作一个常值,但较经典的8参数Klobuchar模型仍有较大的提高,基本能反映不同时期各个纬度区域的变化情况,优于8参数Klobuchar模型,但对夜间电离层变化较大的情况(如2013年12月22日、2016年3月20日和2016年9月22日低纬度地区以及2013年6月21日高纬度地区)建模结果并不理想;8参数Klobuchar模型仅能大致反映电离层的变化趋势,其夜间常值的固定导致电子含量较低的高纬地区的拟合结果大多为一条直线,初始相位的固定会导致最值不在14:00的电离层变化的拟合结果偏差较大,且偏差很大时会造成函数拟合不收敛的情况,如2013年12月22日的高纬地区(当天VESL站此时处于极昼状态)其峰值在5:00左右,8参数Klobuchar模型拟合时不收敛,在作图和统计修正率将其视作常值处理。
表 1给出了不同时期不同纬度区域单站建模的Klobuchar-like、14参数Klobuchar、8参数Klobuchar的修正率。分析表 1可知,在单站建模中,不同时期的单天平均电离层修正率和整体修正率从高到低依次为Klobuchar-like模型、14参数Klobuchar模型、8参数Klobuchar模型。各时段的整体平均修正率依次为92.96%、89.90%、47.22%。Klobuchar-like模型和14参数Klobuchar模型的修正率相较于8参数Klobuchar模型在高纬度地区的提升最大,分别提升了97.29%、94.79%;在低纬度地区提升次之,分别提升了33.02%、27.25%;在中纬地区提升最小,分别达到了6.90%、5.99%。
| (%) | |||||
| 日期 | 模型 | 修正率 | |||
| 高纬地区 | 中纬地区 | 低纬地区 | 平均值 | ||
| 2008-05-01 | 8参数Klobuchar | -84.73 | 87.02 | 81.27 | 27.85 |
| 14参数Klobuchar | 90.13 | 97.23 | 86.04 | 91.13 | |
| Klobuchar-like | 89.99 | 97.33 | 90.95 | 92.76 | |
| 2008-10-01 | 8参数Klobuchar | 78.74 | 82.89 | -54.23 | 35.80 |
| 14参数Klobuchar | 92.04 | 95.78 | 95.67 | 94.50 | |
| Klobuchar-like | 91.73 | 97.10 | 95.68 | 94.84 | |
| 2013-06-21 | 8参数Klobuchar | -57.35 | 93.93 | 87.52 | 41.37 |
| 14参数Klobuchar | 80.33 | 96.07 | 86.43 | 87.61 | |
| Klobuchar-like | 91.90 | 93.84 | 92.85 | 92.86 | |
| 2013-12-22 | 8参数Klobuchar | *33.26 | 87.03 | 73.37 | 64.55 |
| 14参数Klobuchar | 95.70 | 94.85 | 79.56 | 90.04 | |
| Klobuchar-like | 96.20 | 95.90 | 91.74 | 94.61 | |
| 2016-03-20 | 8参数Klobuchar | -9.81 | 89.84 | 78.39 | 52.81 |
| 14参数Klobuchar | 88.83 | 89.22 | 80.55 | 86.20 | |
| Klobuchar-like | 91.08 | 93.86 | 89.78 | 91.57 | |
| 2016-09-22 | 8参数Klobuchar | 7.41 | 93.00 | 82.41 | 60.94 |
| 14参数Klobuchar | 89.27 | 96.50 | 83.99 | 89.92 | |
| Klobuchar-like | 90.36 | 97.05 | 85.86 | 91.09 | |
| 各时段平均值 | 8参数Klobuchar | -5.41 | 88.95 | 58.12 | 47.22 |
| 14参数Klobuchar | 89.38 | 94.94 | 85.37 | 89.90 | |
| Klobuchar-like | 91.88 | 95.85 | 91.14 | 92.96 | |
| 注:修正率=(VTEC-VTECreference)/VTECreference,其中,VTECreference为参考VTEC;*表示8参数Klobuchar模型拟合时不收敛,在统计修正率时将其视作常值处理。 | |||||
2.2 区域电离层建模
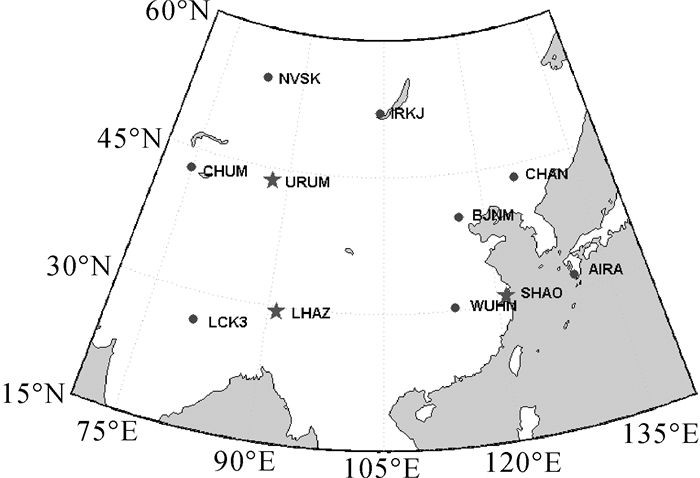
根据图 5选取的中国大陆及周边的试验站点的GIMs电离层数据,建立了中国大陆的区域的Klobuchar-like模型、14参数Klobuchar模型、8参数Klobuchar模型。图 5中,圆点标示的站点为获取模型参数拟合的数据的站点(简称数据站点),五角星标注的为计算外符合精度的检核站点。由于夜间电离层变化与太阳光照无关,与地磁有关;而日间变化与太阳光照强度有关。所以,为了同时兼顾地磁对电离层的影响和保持与时间、电离层日变化的一致性,Klobuchar-like模型在夜间变化的参数A、B、C中采用地磁纬度,在日变化的参数A2、A3、A4中采用地理纬度,且参数m、n设置为m=2、n=2。
|
| 图 5 中国大陆及周边的实验站点 Fig. 5 Stations at Chinese mainland and its ambitus |
表 2给出了所建立的中国大陆及周边区域的Klobuchar-like模型、14参数Klobuchar模型、8参数Klobuchar模型的修正率。其中,“内符合精度”、“外符合精度”、“整体精度”的修正率分别表示使用各模型对数据站点、检核站点、所有站点的VTEC修正率。
| (%) | |||||
| 日期 | 模型 | 修正率 | |||
| 内符合精度 | 外符合精度 | 整体精度 | |||
| 2008-05-01 | 8参数Klobuchar | 83.59 | 85.50 | 84.17 | |
| 14参数Klobuchar | 91.93 | 91.42 | 91.79 | ||
| Klobuchar-like | 93.93 | 92.67 | 93.59 | ||
| 2008-10-01 | 8参数Klobuchar | 73.29 | 78.48 | 74.71 | |
| 14参数Klobuchar | 90.18 | 90.59 | 90.29 | ||
| Klobuchar-like | 93.73 | 92.60 | 93.42 | ||
| 2013-06-21 | 8参数Klobuchar | 87.74 | 85.75 | 87.07 | |
| 14参数Klobuchar | 93.17 | 93.14 | 93.16 | ||
| Klobuchar-like | 93.76 | 93.15 | 93.56 | ||
| 2013-12-22 | 8参数Klobuchar | 75.96 | 85.58 | 78.58 | |
| 14参数Klobuchar | 89.53 | 91.82 | 90.16 | ||
| Klobuchar-like | 89.91 | 90.94 | 90.19 | ||
| 2016-03-20 | 8参数Klobuchar | 80.98 | 85.39 | 82.18 | |
| 14参数Klobuchar | 86.87 | 88.29 | 87.26 | ||
| Klobuchar-like | 89.33 | 89.56 | 89.39 | ||
| 2016-09-22 | 8参数Klobuchar | 84.88 | 90.96 | 86.54 | |
| 14参数Klobuchar | 89.11 | 89.11 | 89.11 | ||
| Klobuchar-like | 89.59 | 88.06 | 89.17 | ||
| 各时段平均值 | 8参数Klobuchar | 81.07 | 85.28 | 82.21 | |
| 14参数Klobuchar | 90.13 | 90.73 | 90.30 | ||
| Klobuchar-like | 91.71 | 91.16 | 91.55 | ||
由表 2可知,在同一模型中,各时段的平均内符合精度、外符合精度、整体符合精度差异不大;所建立的中国大陆及周边区域模型的修正率从高到低依次是Klobuchar-like模型、14参数Klobuchar模型、8参数Klobuchar模型,各时段的整体平均修正率依次为91.55%、90.30%和82.21%。由于所选区域位于中纬度,相对于单站建模,8参数Klobuchar模型修正率提升较大,14参数Klobuchar模型的修正率略有提升。
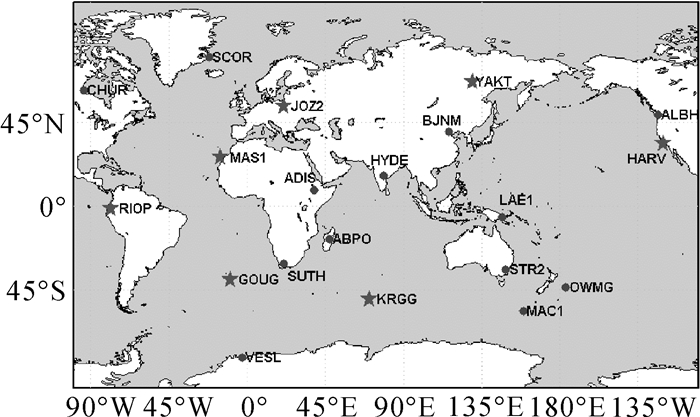
2.3 全球电离层建模本文利用13个数据站点的VTEC建立了全球的Klobuchar-like模型、14参数Klobuchar模型、8参数Klobuchar模型,并与由GPS播发的电离层参数所计算的GPS Klobuchar进行对比。建模精度评估中所采用的数据站点及检核站点如图 6所示。Klobuchar-like模型中,参数m、n设置为m=2、n=3,纬度采用的模式与区域电离层建模的纬度模式相同。
|
| 图 6 全球电离层建模试验站点 Fig. 6 Stations in global ionosphere modeling |
表 3给出了本文所建立的全球的Klobuchar-like模型、14参数Klobuchar模型、8参数Klobuchar模型、GPS Klobuchar模型的修正率。
| (%) | |||||
| 日期 | 模型 | 修正率 | |||
| 内符合精度 | 外符合精度 | 整体精度 | |||
| 2008-05-01 | GPS Klobuchar | — | — | 24.92 | |
| 8参数Klobuchar | 35.28 | 33.81 | 34.71 | ||
| 14参数Klobuchar | 72.75 | 61.19 | 68.26 | ||
| Klobuchar-like | 77.16 | 70.56 | 74.59 | ||
| 2008-10-01 | GPS Klobuchar | — | — | 36.77 | |
| 8参数Klobuchar | 61.00 | 32.40 | 53.08 | ||
| 14参数Klobuchar | 75.30 | 69.56 | 72.79 | ||
| Klobuchar-like | 77.63 | 78.57 | 78.04 | ||
| 2013-06-21 | GPS Klobuchar | — | — | 56.77 | |
| 8参数Klobuchar | 59.87 | 54.07 | 57.84 | ||
| 14参数Klobuchar | 73.09 | 68.58 | 71.51 | ||
| Klobuchar-like | 75.73 | 69.59 | 73.58 | ||
| 2013-12-22 | GPS Klobuchar | — | — | 38.91 | |
| 8参数Klobuchar | 55.24 | 61.75 | 57.92 | ||
| 14参数Klobuchar | 71.20 | 59.11 | 66.22 | ||
| Klobuchar-like | 77.65 | 61.06 | 70.82 | ||
| 2016-03-20 | GPS Klobuchar | — | — | 54.45 | |
| 8参数Klobuchar | 57.62 | 44.58 | 52.55 | ||
| 14参数Klobuchar | 63.28 | 52.54 | 59.10 | ||
| Klobuchar-like | 71.19 | 60.39 | 66.99 | ||
| 2016-09-22 | GPS Klobuchar | — | — | 48.03 | |
| 8参数Klobuchar | 50.44 | 43.72 | 48.09 | ||
| 14参数Klobuchar | 68.27 | 59.75 | 65.29 | ||
| Klobuchar-like | 72.79 | 70.44 | 71.97 | ||
| GPS Klobuchar | — | — | 43.31 | ||
| 各时段平均值 | 8参数Klobuchar | 53.24 | 45.06 | 50.70 | |
| 14参数Klobuchar | 70.65 | 61.79 | 67.20 | ||
| Klobuchar-like | 75.36 | 68.44 | 72.67 | ||
由表 3可知,全球电离层建模时,Klobuchar-like模型、14参数Klobuchar模型、8参数Klobuchar模型的各时段平均外符合精度均比内符合精度低约8%,各时段平均整体符合精度介于两者之间;各时段平均整体符合精度、内符合精度、外符合精度从高至低依次为Klobuchar-like模型、14参数Klobuchar模型、8参数Klobuchar模型;各模型各时段平均整体符合精度均高于GPS Klobuchar模型;Klobuchar-like模型、14参数Klobuchar模型各时段的整体符合精度均高于8参数Klobuchar模型与GPS Klobuchar模型;除部分(2016年3月20日)8参数Klobuchar模型修正率略低于GPS Klobuchar模型修正率外,8参数Klobuchar模型修正率远高于GPS Klobuchar模型修正率,因此,建议模型的参数如BDS系统一样根据实测数据拟合,以期获得较高的修正精度。某些时候部分模型(如2008年10月1日的Klobuchar-like模型、2013年12月22日的8参数Klobuchar模型)的外符合精度要略高于内符合精度,其原因可能在于选取的检核点多分布在中纬度区域且没有外推点。
另外,文献[10]所提出的10参数Klobuchar精化模型也是一种全球电离层Klobuchar精化模型,该模型以TOPEX/Poseidon和JASON-1 TEC为参考数据时的修正率为62.70%,以GPS-TEC参考数据时的修正率为65.75%。本文所提出的Klobuchar-like模型以GIMs数据为参考,修正率达到72.67%, 取得了较好的修正效果。
3 结语本文利用IGS提供的GIMs数据分析了电离层夜间VTEC变化和电离层日变化的时空特点,着重分析了经典Klobuchar模型在描述这些时空特点时存在的不足。针对这些不足和Klobuchar模型精化的现状,总结提出了Klobuchar-like模型,并通过单站建模、区域建模、全球建模与14参数Klobuchar模型、8参数Klobuchar模型、GPS Klobuchar模型相比较验证了本文提出的模型的有效性和实用性。
Klobuchar-like模型可用于不同区域尺度的电离层建模,可以通过BDS-TEC、GPS-TEC和GIMs预测产品等电离层实测或预测数据拟合参数,并通过广播星历播发用于导航定位。该模型存在模型参数略多的缺点,不利于星上数据存储,后续研究中将会进一步优化完善。
| [1] | KLOBUCHAR J A. Ionospheric Time-delay Algorithm for Single-frequency GPS Users[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, AES-23(3): 325–331. DOI:10.1109/TAES.1987.310829 |
| [2] | 吴雨航, 陈秀万, 吴才聪, 等. 电离层延迟修正方法评述[J]. 全球定位系统, 2008, 33(2): 1–5. WU Yuhang, CHEN Xiuwan, WU Caicong, et al. Review of the Ionospheric Delay Correction Methods[J]. GNSS World of China, 2008, 33(2): 1–5. |
| [3] | 何玉晶. GPS电离层延迟改正及其扰动监测的分析研究[D]. 郑州: 信息工程大学, 2006. HE Yujing. Study on GPS Ionospheric Delay Correction and Analysis of Disturbance Monitoring[D]. Zhengzhou: Information Engineering University, 2006. |
| [4] | YUAN Yunbin, HUO Xingliang, OU Jikun, et al. Refining the Klobuchar Ionospheric Coefficients Based on GPS Observations[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(4): 1498–1510. DOI:10.1109/TAES.2008.4667725 |
| [5] | 李维鹏, 李建文, 戴伟. Klobuchar电离层延迟改正模型精化方法的研究[J]. 测绘科学, 2009, 34(5): 49–51. LI Weipeng, LI Jianwen, DAI Wei. Study on the Methods of Updating Klobuchar Ionospheric Delay Correction Model[J]. Science of Surveying and Mapping, 2009, 34(5): 49–51. |
| [6] | FILJAR R, KOS T, KOS S. Klobuchar-like Local Model of Quiet Space Weather GPS Ionospheric Delay for Northern Adriatic[J]. Journal of Navigation, 2009, 62(3): 543–554. DOI:10.1017/S0373463309005281 |
| [7] | SHUKLA A K, DAS S, SHUKLA A P, et al. Approach for Near-Real-time Prediction of Ionospheric Delay Using Klobuchar-like Coefficients for Indian Region[J]. IET Radar, Sonar & Navigation, 2013, 7(1): 67–74. |
| [8] | 高杨, 焦诚, 刘萧, 等. 利用中国区域电离层数据拟合Klobuchar参数[J]. 全球定位系统, 2014, 39(5): 37–40. GAO Yang, JIAO Cheng, LIU Xiao, et al. Fitting Klobuchar Coefficients Using Ionospheric Data in Chinese Area[J]. GNSS World of China, 2014, 39(5): 37–40. |
| [9] | 朱进. 天文和测地VLBI物理模型的研究[D]. 南京: 南京大学, 1991. ZHU Jin. Research of Astronomy and Geodetic VLBI Physical Model[D]. Nanjing: Nanjing University, 1991. |
| [10] | WANG Ningbo, YUAN Yunbin, LI Zishen, et al. Improvement of Klobuchar Model for GNSS Single-frequency Ionospheric Delay Corrections[J]. Advances in Space Research, 2016, 57(7): 1555–1569. DOI:10.1016/j.asr.2016.01.010 |
| [11] | 蔡成辉, 刘立龙, 黎峻宇, 等. 基于改进的Klobuchar模型建立南宁市区域电离层延迟模型[J]. 大地测量与地球动力学, 2015, 35(5): 797–800. CAI Chenghui, LIU Lilong, LI Junyu, et al. Establishment of Region Ionospheric Delay Model in Nanning Based on Improved Klobuchar Model[J]. Journal of Geodesy and Geodynamics, 2015, 35(5): 797–800. |
| [12] | 徐李冰, 蔡成林, 陈光喜, 等. 一种新的北斗Klobuchar模型及其精度分析[J]. 大地测量与地球动力学, 2015, 35(5): 788–792. XU Libing, CAI Chenglin, CHEN Guangxi, et al. A New Klobuchar Model and Its Precision Analysis for Beidou Navigation Satellite System[J]. Journal of Geodesy and Geodynamics, 2015, 35(5): 788–792. |
| [13] | 章红平. 基于地基GPS的中国区域电离层监测与延迟改正研究[D]. 上海: 中国科学院上海天文台, 2006. ZHANG Hongping. Research on Regional Ionospheric Monitoring and Delay Correction in China Based on Ground-based GPS[D]. Shanghai: Shanghai Astronomical Observatory, Chinese Academy of Sciences, 2006. |
| [14] | 章红平, 平劲松, 朱文耀, 等. 电离层延迟改正模型综述[J]. 天文学进展, 2006, 24(1): 16–26. ZHANG Hongping, PING Jinsong, ZHU Wenyao, et al. Brief Review of the Ionospheric Delay Models[J]. Progress in Astronomy, 2006, 24(1): 16–26. |
| [15] | 黄逸丹, 王明远, 韩玲, 等. 基于中国电离层资料对Klobuchar模型的改进[C]//中国空间科学学会空间探测专业委员会第十九次学术会议论文集(下册). 宁波: 中国空间科学学会, 2007. HUANG Yidan, WANG Mingyuan, HAN Ling, et al. Improvement of Klobuchar Ionospheric Model Based on the Chinese Material[C]//Proceedings of the 19th Academic Communication of Professional Committee of China's Space Science Society Space Detection. Ningbo: Chinese Society of Space Research, 2007. |
| [16] | 李猛, 廖瑛, 梁加红, 等. 电离层延迟模型改进研究[J]. 计算机仿真, 2009, 26(10): 21–24. LI Meng, LIAO Ying, LIANG Jiahong, et al. Improvement of Ionosphere Delay Model[J]. Computer Simulation, 2009, 26(10): 21–24. |
| [17] | 吴风波, 张小红. 利用澳洲北斗GEO数据改进Klobuchar模型[J]. 大地测量与地球动力学, 2015, 35(6): 1012–1016. WU Fengbo, ZHANG Xiaohong. Improving the Klobuchar Model Based on Beidou GEO Observations in Australia[J]. Journal of Geodesy and Geodynamics, 2015, 35(6): 1012–1016. |
| [18] | 刘宸, 刘长建, 冯绪, 等. Klobuchar电离层模型精化进展[J]. (in Press). LIU Chen, LIU Changjian, FENG Xu, et al. Advances in Refinements of Klobuchar Ionospheric Model[J]. (in Press). |
| [19] | 武业文, 刘瑞源, 张北辰, 等. 中国地区电离层TEC的变化特性[C]//第十三届全国日地空间物理学术讨论会论文集. 银川: [s. n. ], 2009. WU Yewen, LIU Ruiyuan, ZHANG Beichen, et al. Variation Characteristic of Ionosphere TEC in China[C]//Proceedings of the 13th National Space Physics Symposium. Yinchuan:[s.n.], 2009. |
| [20] | 冯建迪, 王正涛, 赵珍珍. 卫星导航服务的全球电离层时变特性分析[J]. 测绘科学, 2015, 40(2): 13–17. FENG Jiandi, WANG Zhengtao, ZHAO Zhenzhen. Analysis of Temporal Variation of Global Ionosphere Based on IGS[J]. Science of Surveying and Mapping, 2015, 40(2): 13–17. |
| [21] | 张笑凡, 何宏, 陈键锋. TEC浓度误差变化分析[J]. 测绘与空间地理信息, 2014, 37(5): 176–179. ZHANG Xiaofan, HE Hong, CHEN Jianfeng. TEC Concentration Error Change Analysis[J]. Geomatics & Spatial Information Technology, 2014, 37(5): 176–179. |
| [22] | HOMAM M J. Latitudinal Effect on Total Electron Content Variations[C]//International Symposium on Antennas and Propagation (ISAP). Kaohsiung: IEEE, 2014: 127-128. |
| [23] | NOGUEIRA P A B, ABDU M A, SOUZA J R, et al. Longitudinal Variation in Global Navigation Satellite Systems TEC and Topside Ion Density over South American Sector Associated with the Four-peaked Wave Structures[J]. Journal of Geophysical Research: Space Physics, 2013, 118(12): 7940–7953. DOI:10.1002/2013JA019266 |
| [24] | LIU Chen, LIU Changjian, DU Ying, et al.The Quantitative Analysis of the Mean Nighttime VTEC Based on EMD[M]//SUN Jiadong, LIU Jingnan, FAN Shiwei, et al. China Satellite Navigation Conference (CSNC) 2016 Proceedings: Volume Ⅲ. Singapore: Springer, 2016: 285-295. |