2. 中国测绘科学研究院, 北京 100830;
3. 山东科技大学测绘科学与工程学院, 山东 青岛 266590;
4. 长安大学地质工程与测绘学院, 陕西 西安 710054
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China;
3. College of Geomatics, Shandong University of Science and Technology, Qingdao 266590, China;
4. College of Geology Engineering and Geomantics, Chang'an University, Xi'an 710054, ChinaAbstract
北斗卫星导航系统(BeiDou navigation satellite system,BDS)是中国自主研发、独立运行的全球卫星导航系统[1]。自2012年底BDS系统正式向亚太大部分地区提供正式运行服务以来,BDS已广泛应用于交通运输、海洋渔业、水文监测、大地测量、车载导航等领域。随着实时高精度定位用户的不断增长,如何满足实时高精度定位需求成为当前研究的热点[2]。精密轨道与钟差是卫星导航定位系统实现高精度定位的前提条件,目前IGS和我国全球连续监测评估系统(international GNSS monitoring & assessment system,iGMAS)网站可提供GNSS(BDS/GPS/GLONASS/GALILEO)事后精密轨道和钟差产品[3-6]。但事后产品不能满足用户实时高精度(如:厘米级)定位需求,因此需开展实时轨道和实时钟差的估计算法研究[7-10]。文献[3]指出实时轨道可利用超快速精密轨道进行预报得到,由于导航卫星原子钟易受外界及本身因素的影响,变化极为复杂,很难利用数学模型进行准确预报,必须进行实时估计。
多频多模GNSS数据融合已成为GNSS发展的必然趋势[11]。文献[12]提出了基于GPS/北斗数据融合钟差实时估计模型,显著提高了北斗钟实时估计的精度。在多GNSS钟差融合估计随机模型方面,目前主要考虑GNSS空间信号传播误差,采用高度角权函数对不同的GNSS观测进行配权,然而,卫星轨道误差也是GNSS钟差估计的重要误差源,由于测站分布、卫星星座构型等原因导致BDS/GPS轨道精度存在差异[13-16],因此在进行实时钟差估计中若采用常规的将卫星轨道精度采取等权处理策略,将影响卫星钟差的估计精度。
本文针对BDS/GPS轨道精度差异,介绍了基于非差观测量的实时钟差估计方法,开展了顾及轨道精度差异的观测权函数设计,优化了实时钟差估计的随机模型,利用根据该方法实现的软件,基于多模试验跟踪网(multi-GNSS experiment,MGEX)数据和两个iGMAS跟踪站实时观测数据,基于原有随机模型和本文优化后的随机模型采用单GPS、单BDS和BDS/GPS组合等方式进行实时钟差解算,将iGMAS事后精密钟差产品作为基准对两种随机模型的实时钟差精度开展对比分析,验证了算法的有效性。
1 基于非差观测值的实时钟差估计方法 1.1 观测模型文献[14—15]指出在GNSS组合定位与定轨中,由于时空基准、信号体制等因素的差异导致卫星信号在接收机内部会产生相应的不同的硬件延迟,称为系统间偏差(inter-system bias,ISB)。文献[17]指出在常规的GNSS组合定位时,如BDS/GPS组合,需选取一个系统作为基准,如选取GPS系统,然后对每个接收机增加一个BDS相对于GPS的系统间偏差参数进行估计。文献[12]指出在基于双频观测值进行实时钟差估计中,一般采用消去电离层一阶项的非差消电离层组合观测值进行计算,BDS/GPS联合估计时需引入一个BDS ISB偏差参数,其观测方程可表示为
 (1)
(1)
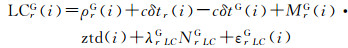 (2)
(2)
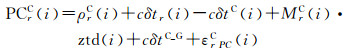 (3)
(3)
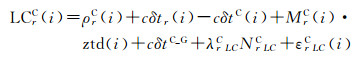 (4)
(4)
式中,r和i分别表示测站和历元编号;G和C分别表示GPS和BDS卫星;PC、LC为分别表示伪距和载波相位的无电离层组合观测值;P1、P2、L1、L2分别表示两个频率上的伪距和载波相位观测值;f1、f2分别表示两个频率的波长;c为光速;δtr为接收机钟差;δts为卫星钟差;M表示测站与卫星间的对流层投影函数;ztd为测站的天顶对流层延迟值;NLC为无电离层线性组合模糊度,非整数;λLC为无电离层组合波长;cδtC_G表示BDS相对于GPS的ISB;εPC和εLC分别表示伪距和载波相位的多路径、观测噪声等未模型化的其他误差。
如果以式(1)—(4) 为观测方程求解卫星钟差参数,法方程是奇异的。为了能够求解钟差参数,必须引入一个基准钟,求解其他接收机钟差和卫星钟钟差相对于该基准钟的钟差。文献[19]已证明只要保证基准钟的钟差精度优于10-6 s,相对钟差和绝对钟差对用户定位结果是等价的。
1.2 基于设计权函数的随机模型在观测模型中,不同观测值的权可设计为
 (5)
(5)
式中,σ02为单位权中误差;σi, j2为j(G/GPS或C/北斗)卫星的i(相位/伪距)观测值的方差。若忽略卫星轨道影响误差,σPC.G2表示GPS PC观测观测值的方差,即
 (6)
(6)
通常情况下,观测方差随着卫星高度角会变大,为此常采用高度角加权模型,同样以GPS PC观测值为例,可设计如下观测方差函数
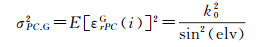 (7)
(7)
式中,k02为天顶方向观测值的方差;elv为卫星高度角。然而,GPS轨道和北斗轨道的精度不同,即使同一GNSS系统,在不同区域轨道误差也可能存在差异,为此需要在观测噪声的基础上,进一步考虑轨道误差对观测值定权的影响。
实时钟差是基于预报轨道的,因此定轨的精度决定了预报轨道的精度。在定轨时,可以获取中间时刻的卫星轨道精度信息,而该信息在一定程度上代表了预报轨道的误差大小。轨道中间时刻的位置状态方差协方差矩阵为
 (8)
(8)
基于上述信息,可采用非线性误差传播方法研究轨道误差所引起的卫星和测站距离可模型化为
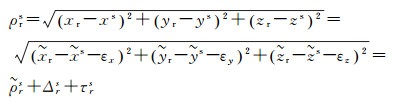 (9)
(9)
式中,

 (10)
(10)
式中,ε=[εx εy εz]表示轨道误差向量;θ为误差向量,为方向余弦和误差向量的夹角。显然,对于GNSS这样的长距离问题,一般情况下线性化残余项很小,这意味着,线性化误差传播引起的系统性偏差Δrs可以忽略不计。然而对于短距离问题,这一误差却往往不能忽略不计。文献[21—22]在这一基础上分别得到了系统偏差估计的二阶项公式和任意阶次逼近公式,并指出对于长距离问题,二阶近似可精确得到距离统计量的方差信息
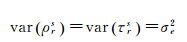 (11)
(11)
式中,σe2=eTDje为误差椭圆给出的方向方差;e即为卫星和地面站连线的方向余弦。相关推导可参考文献[21—22]。显然,当方差协方差矩阵对角线元素的数值大小和观测噪声的方差大小相当时,甚至大于观测噪声的方差时,由于轨道误差引起的误差应该联合用于确定观测值的权,即结合误差传播,可得以为更为合理的权设计方案
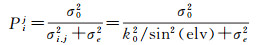 (12)
(12)
上述配权原理综合考虑了观测噪声和轨道误差对钟差确定的影响。就目前而言,由于北斗的卫星轨道精度相对较差,意味着北斗卫星观测值对地面站的钟差估计所占权重会降低,而对于同一北斗卫星,由于地面站分布影响轨道误差椭圆形状和大小,也会引起不同测站对同一卫星的钟差估计分配不同的权。
1.3 实时钟差估计算法文献[23]指出均方根滤波是一种改进的卡尔曼滤波算法,其算法简单、数据稳定性高,特别适用于进行实时数据处理。本文非差实时钟差估计方法采用均方根滤波方法。假定有一先验信息,设具有先验方差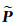
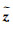
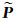
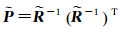
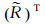

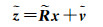 (13)
(13)
式中,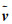

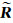

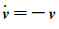
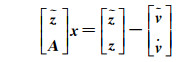 (14)
(14)
两侧乘以正交变换矩阵T,得下式
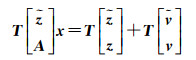 (15)
(15)
根据Householder变换,式(15) 可变化为
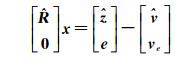 (16)
(16)
式中,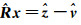
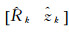
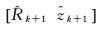
本文在中国测绘科学研究院现有的实时钟差解算软件的基础上,对上述算法进行了软件实现。为验证上述分析的实时钟差的解算性能,本文选取了2016年12月1日全球78个MGEX站和两个iGMAS基准站的实时观测数据(数据采样率1 s),设计单GPS、单BDS和BDS/GPS组合3种方案,分别采用原有未顾及卫星轨道精度差异的随机模型和本文提出的随机模型进行实时钟差解算,对生成的钟差产品进行统计分析。80个用于实时钟差估计的测站分布见图 1。

|
| 图 1 用于实时钟差估计的80个测站分布图 Fig. 1 The distribution of 80 sites in real-time clock error estimation |
本文用于实时钟差估计的观测值先验信息、各项误差改正模型及参数处理策略见表 1。
| 参数 | 处理方法 | |
| 观测量 | 观测值 | 伪距载波无电离层组合观测值 |
| 先验约束 | GPS L1:伪距:0.6 m,载波:0.01周BDS B1:伪距:1.5 m,载波:0.01周 | |
| 截止高度角 | 10° | |
| 观测值加权 | p=1, e>30°; p=4sin2e, e≤30°或本文提出的随机模型 | |
| 误差改正 | 天线相位缠绕 | 模型改正 |
| 相位中心变化 | GPS: IGS08模型BDS: iGMAS推荐值 | |
| 潮汐改正 | 模型改正(固体潮、海洋潮汐等) | |
| 卫星相位中心 | 绝对相位中心 | |
| 相对论改正 | 模型改正 | |
| 参数估计 | 参考钟 | 固定一个接收机钟 |
| 卫星轨道 | iGMAS分析中心(中国测绘科学研究院)产品,3 h更新 | |
| 测站坐标 | 固定已知值 | |
| 对流层 | Saastmoine模型+随机游走 | |
| 卫星钟差 | 估计 | |
| 接收机钟差 | 估计 | |
| 模糊度 | 估计 | |
| ISB | 估计 |
2.2 实时钟差评估方法
实时钟差精度评估选取iGMAS事后精密钟差产品作为参考,由于两套钟差产品所选的基准钟不同,会导致钟差值之间存在一定的系统性偏差,但是这种系统性偏差在定位中被模糊度和接收机钟差吸收,不影响最终定位结果。因此,在分析实时钟差产品与事后精密产品的符合程度时,需首先将两套钟差产品的基准钟统一,消除系统偏差影响,具体方法为采用二次差方法消除基准偏差后进行钟差精度评定,见下式
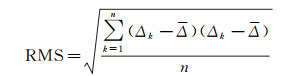 (17)
(17)
式中,Δi第k个历元两套卫星钟差之差; 
利用中国测绘科学研究院承建的iGMAS分析中心的钟差精度分析软件,对比分析了两种策略下单GPS、单BDS和BDS/GPS联合的实时钟差精度差异。
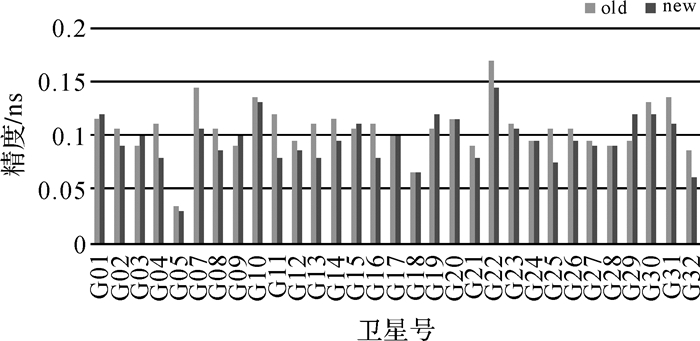
2.3.1 单BDS利用iGMAS事后精密钟差文件,为实现两类产品的基准统一,选取GPS PRN06卫星作为基准星,对两种计算策略下的实时钟差产品进行精度统计,统计结果见图 2及图 3。
|
| 图 2 两种策略下GPS实时钟差精度对比 Fig. 2 The comparison of GPS real time clock error accuracy with two strategies |
|
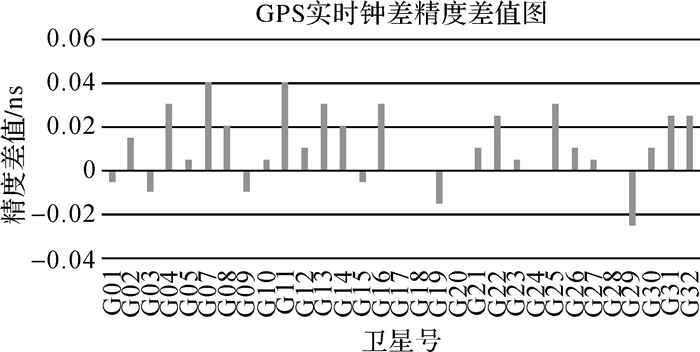
| 图 3 两种策略下的GPS精度差值 Fig. 3 The difference of GPS real time clock error accuracy with two strategies |
由图 2、图 3可知,从精度来看,两种策略计算的GPS实时钟差都优于0.2 ns。具体从精度数值分析,两种策略下的精度差异基本在20 ps左右,最大值接近40 ps;除去基准星,其余GPS 31颗卫星有20颗卫星的精度得到提高,6颗卫星的精度变差,5颗卫星精度相当;基于各卫星精度统计结果,求取两种策略下31颗卫星的精度均值分别为105.6 ps和95.3 ps,精度整体提高了9%。
2.3.2 单BDS利用iGMAS事后精密钟差文件,为实现两类产品的基准统一,选取BDS PRN14卫星作为基准星,对两种计算策略下的实时钟差产品进行精度统计,统计结果见图 4、图 5。
|
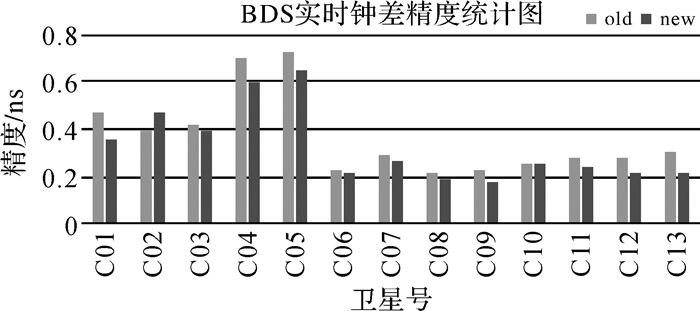
| 图 4 两种策略下BDS实时钟差精度对比 Fig. 4 The comparison of BDS real time clock error accuracy with two strategies |
|
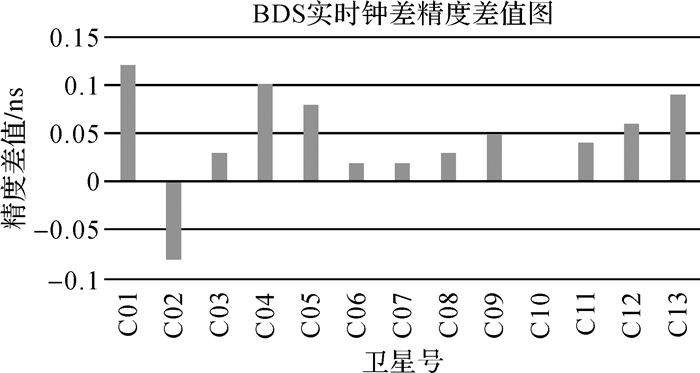
| 图 5 两种策略下的BDS精度差值 Fig. 5 The difference of BDS real time clock error accuracy with two strategies |
从精度来看,两种策略计算的BDS实时钟差都在一个量级,GEO钟差精度都在0.5 ns左右,MEO/IGSO的钟差精度在0.2 ns左右。从具体数据分析,两种策略下GEO卫星精度差异在0.1 ns左右,IGSO/MEO精度差异在50 ps左右,除去个别卫星精度降低外,大多数卫星精度都有所改善。
利用各不同轨道卫星精度均值来整体来统计,两种策略的GEO钟差精度分别为0.542 ns和0.492 ns,精度提高9.3%,IGSO的精度分别为0.246 ns和0.222 ns,精度提高10%,MEO的精度分布为0.287 ns和0.223 ns,精度提高22.1%。对整个BDS卫星精度总体统计,两种策略的精度分别为0.369 ns和0.326 ns,整体精度提高11.7%。
2.3.3 BDS/GPS利用iGMAS事后精密钟差文件,为实现两类产品的基准统一,分别选取GPS PRN06和BDS PRN14卫星作为基准星, 对两种计算策略下的BDS/GPS实时钟差产品进行精度统计,统计结果见图 6、图 7。
|
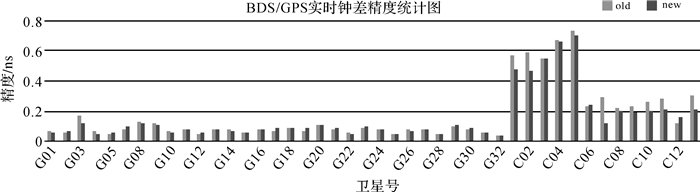
| 图 6 两种策略下BDS/GPS实时钟差精度对比图 Fig. 6 The comparison of BDS/GPS real time clock error accuracy with two strategies |
|
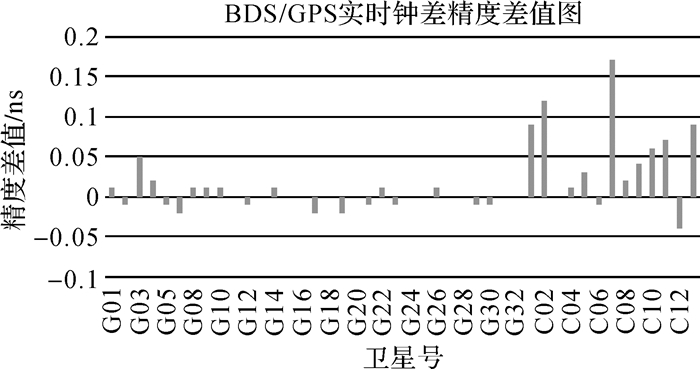
| 图 7 两种策略下的BDS/GPS精度差值 Fig. 7 The difference of BDS/GPS real time clock error accuracy with two strategies |
由图 6、图 7可知,基于新的随机模型的BDS/GPS精度都有提高,其中BDS精度提高尤为明显。从具体数据来看,两种策略下的GPS钟差精度差异基本都在20 ps以内,其均值分别为0.078 9 ns和0.078 3 ns,精度基本没有变化,较单GPS提高幅度降低,BDS钟差精度均值分别为0.363 ns和0.316 ns,精度整体提高12.8%,其中GEO、IGSO和MEO的提高幅度分别为9.1%、21.8%和17.2%。
3 结论本文在BDS/GPS融合的实时钟差估计的观测模型和基于均方根滤波的实时钟差估计的基础上,针对BDS/GPS卫星轨道精度差异,顾及轨道精度差异设计了GNSS/北斗数据融合观测权函数,优化了实时钟差估计的随机模型,利用MGEX站和iGMAS站的观测数据开展了原有随机模型和本文提出的随机模型的对比分析。从结果来看:本文方法对单GPS、单BDS和BDS/GPS融合的实时钟差产品精度都有提高,其中BDS钟差精度整体较GPS更为显著,提高幅度约12.8%,其中IGSO/MEO更为突出,提高幅度约20%。本文提出顾及卫星轨道差异的权函数设计,从理论上进行了推理证明,完善了实时钟差估计模型,对单GNSS系统和多模GNSS融合实时钟差估计都有一定的参考意义。
| [1] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [2] | 杨元喜. 北斗卫星导航系统与测绘学科发展[J]. 测绘科学技术学报, 2015, 32(1): F0002. YANG Yuanxi. BeiDou Navigation Satellite System and the Development of Surveying and Mapping[J]. Journal of Geomatics Science and Technology, 2015, 32(1): F0002. |
| [3] | 赵齐乐, 戴志强, 王广兴, 等. 利用非差观测量估计北斗卫星实时精密钟差[J]. 武汉大学学报(信息科学版), 2016, 41(5): 686–691. ZHAO Qile, DAI Zhiqiang, WANG Guangxing, et al. Real-time Precise BDS Clock Estimation with the Undifferenced Observation[J]. Geomatics and Information Science of Wuhan University, 2016, 41(5): 686–691. |
| [4] | LOU Yidong, LIU Yang, SHI Chuang, et al. Precise Orbit Determination of BeiDou Constellation Based on BETS and MGEX Network[J]. Scientific Reports, 2014(4): 4692. |
| [5] | ZHAO Qile, GUO Jing, LI Min, et al. Initial Results of Precise Orbit and Clock Determination for Compass Navigation Satellite System[J]. Journal of Geodesy, 2013, 87(5): 475–486. DOI:10.1007/s00190-013-0622-7 |
| [6] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Initial Assessment of the Compass/BeiDou-2 Regional Navigation Satellite System[J]. GPS Solutions, 2013, 17(2): 211–222. DOI:10.1007/s10291-012-0272-x |
| [7] | ZHANG Weixing, LOU Yidong, GU Shengfeng, et al. Joint Estimation of GPS/BDS Real-time Clocks and Initial Results[J]. GPS Solutions, 2016, 20(4): 665–676. DOI:10.1007/s10291-015-0476-y |
| [8] | LI Xingxing, GE Maorong, DAI Xiaole, et al. Accuracy and Reliability of Multi-GNSS Real-time Precise Positioning:GPS, GLONASS, BeiDou, and Galileo[J]. Journal of Geodesy, 2015, 89(6): 607–635. DOI:10.1007/s00190-015-0802-8 |
| [9] | GE Maorong, CHEN Junping, DOUŠA J, et al. A Computationally Efficient Approach for Estimating High-rate Satellite Clock Corrections in Realtime[J]. GPS Solutions, 2012, 16(1): 9–17. DOI:10.1007/s10291-011-0206-z |
| [10] | HUANG Guanwen, ZHANG Qin, XU Guochang. Real-time Clock Offset Prediction with an Improved Model[J]. GPS Solutions, 2014, 18(1): 95–104. DOI:10.1007/s10291-013-0313-0 |
| [11] | 杨元喜, 陆明泉, 韩春好. GNSS互操作若干问题[J]. 测绘学报, 2016, 45(3): 253–259. YANG Yuanxi, LU Mingquan, HAN Chunhao. Some Notes on Interoperability of GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 253–259. DOI:10.11947/j.AGCS.2016.20150653 |
| [12] | 陈良, 耿长江, 周泉. 北斗/GPS实时精密卫星钟差融合解算模型及精度分析[J]. 测绘学报, 2016, 45(9): 1028–1034. CHEN Liang, GENG Changjiang, ZHOU Quan. Estimation Model and Accuracy Analysis of BeiDou/GPS Real-time Precise Satellite Clock Error Integrated Resolving[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1028–1034. DOI:10.11947/j.AGCS.2016.20150296 |
| [13] | ZHANG Longping, DANG Yamin, XUE Shuqiang, et al. The Optimal Distribution Strategy of BeiDou Monitoring Stations for GEO Precise Orbit Determination[C]//SUN Jiadong, LIU Jingnan, FAN Shiwei, et al. China Satellite Navigation Conference (CSNC) 2015 Proceedings:Volume Ⅰ. Lecture Notes in Electrical Engineering. Berlin:Springer, 2015:153-161. |
| [14] | LOU Yidong, LIU Yang, SHI Chuang, et al. Precise Orbit Determination of BeiDou Constellation:Method Comparison[J]. GPS Solutions, 2016, 20(2): 259–268. DOI:10.1007/s10291-014-0436-y |
| [15] | 韩保民. 基于星载GPS的低轨卫星几何法定轨理论研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2003. HAN Baomin. GPS-based Kinematic Orbit Determination for Low Earth Satellites[D]. Wuhan:Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2003. |
| [16] | 徐龙威, 刘晖, 刘玉洁, 等. 一种顾及GNSS系统间偏差的伪距单点定位方法[J]. 大地测量与地球动力学, 2016, 36(9): 813–816. XU Longwei, LIU Hui, LIU Yujie, et al. A Multi-GNSS Pseudorange Positioning Method with Inter System Bias[J]. Journal of Geodesy and Geodynamics, 2016, 36(9): 813–816. |
| [17] | 刘志强, 王解先, 段兵兵. 单站多参数GLONASS码频间偏差估计及其对组合精密单点定位的影响[J]. 测绘学报, 2015, 44(2): 150–159. LIU Zhiqiang, WANG Jiexian, DUAN Bingbing. Estimation of GLONASS Code Inter-frequency Biases with Multiple Parameters Based on a Single Station and Its Impact on Combined Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 150–159. DOI:10.11947/j.AGCS.2015.20130800 |
| [18] | 蔡华, 赵齐乐, 楼益栋. 精密卫星钟差确定系统的实现与精度分析[J]. 武汉大学学报(信息科学版), 2009, 34(11): 1293–1296. CAI Hua, ZHAO Qile, LOU Yidong. Implementation and Precision Analysis of GPS Precise Clock Estimation System[J]. Geomatics and Information Science of Wuhan University, 2009, 34(11): 1293–1296. |
| [19] | 叶世榕. GPS非差相位精密单点定位理论与实现[D]. 武汉: 武汉大学, 2002. YE Shirong. Theory and Its Realization of GPS Precise Point Positioning Using Un-differenced Phase Observation[D]. Wuhan:Wuhan University, 2002. |
| [20] | 薛树强, 杨元喜, 党亚民. 测距定位方程非线性平差的封闭牛顿迭代公式[J]. 测绘学报, 2014, 43(8): 771–777. XUE Shuqiang, YANG Yuanxi, DANG Yamin. A Closed-form of Newton Iterative Formula for Nonlinear Adjustment of Distance Equations[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 771–777. |
| [21] | XUE Shuqiang, DANG Yamin, LIU Jiping, et al. Bias Estimation and Correction for Triangle-based Surface Area Calculations[J]. International Journal of Geographical Information Science, 2016, 30(11): 2155–2170. DOI:10.1080/13658816.2016.1162795 |
| [22] | XUE Shuqiang, YANG Yuanxi, DANG Yamin. Formulas for Precisely and Efficiently Estimating the Bias and Variance of the Length Measurements[J]. Journal of Geographical Systems, 2016, 18(4): 399–415. DOI:10.1007/s10109-016-0235-9 |
| [23] | BIERMAN G J. Factorization Methods for Discrete Sequential Estimation[M]. Mineola: Dover Publications, 1977. |



