近几年来GNSS系统发展迅速,多系统多频率是将来的发展趋势[1-2]。BDS系统于2012年正式投入运行,服务范围覆盖亚太地区,在2015年中期开始了第三阶段的建设,预计将于2020年完成全球组网,最终形成5颗同步卫星和30颗非同步卫星的星座构成[3-4]。GPS系统正在实施现代化计划,主要内容包括使用新的民用信号、发射新型号的卫星以及对地面控制部分进行更新,目前已有12颗BLOCK-IIF卫星支持L5频率信号。
随着多个全球和区域卫星导航系统的建成,多系统PPP能够有效提高定位的精确性、可用性和可靠性[5-8]。然而不同系统的信号在同一台接收机中的硬件延迟并不相同,导致了硬件延迟偏差的出现[9-13]。系统间偏差ISB包括了系统时间偏差和硬件延迟偏差[14]。在进行多系统PPP数据处理时必须要考虑ISB的影响[15]。ISB建模有助于深入了解ISB的误差特性,对多系统PPP研究具有一定的参考价值。通过对ISB进行精确建模和预报,采用ISB预报值进行先验约束能够提高多系统PPP的定位精度。因此有必要对ISB建模和预报方法进行研究。
文献[16]指出系统间偏差与接收机内部的信号时延有关。文献[17]发现在多系统PPP中Galileo、BDS与GPS的ISB同接收机类型相关,不同类型接收机之间GPS/BDS的ISB差异最大超过了100 ns。文献[18]对GPS/Galileo紧组合当中的差分ISB进行了研究,利用双差组合分析了差分ISB的稳定性及其对定位结果的影响,试验结果表明差分ISB的长期稳定性较好,大小与接收机类型有关。文献[19]研究了IRNSS相对GPS、Galileo、QZSS在L5/E5a频率上的差分ISB及其应用。文献[20]采用谱分析和LS拟合的方法对ISB进行了短期预报,取得了良好的成果。需要注意的是,参考文献[1, 18, 19]中提到的系统间偏差为差分ISB,与PPP中的ISB在定义上存在本质的差别。
文献[20]中LS方法对拟合数据是等权处理的,而在实际情况中随着时间的推移早期数据与预报时刻的时空相关性会逐渐减弱,近期数据对ISB预报更有价值。因此本文提出一种改进的ISB建模方法,采用Kalman滤波估计模型参数,并根据时空相关性对ISB拟合数据的方差进行调整。试验结果表明该方法可以有效提高ISB的预报精度。
1 ISB估计和建模 1.1 ISB估计方法采用消电离层组合消去电离层延迟误差一阶项,PPP的观测方程为[21-22]
 (1)
(1)
式中,上标G和C分别表示GPS和BDS系统;P和L分别表示伪距观测量和载波相位观测量,单位为m;ρS为在信号发射和接收时刻卫星与接收机天线相位中心的几何距离;c为光在真空中的速度;dtr为接收机钟差;dtS为卫星钟差;τC为BDS系统时相对GPS系统时的时间偏差;drS、dS和brS、bS分别为接收机、卫星的码硬件延迟和相位硬件延迟;TS为对流层延迟误差;NS为相位模糊度,单位为m;εPS和εLS分别为伪距和载波相位观测误差包括观测噪声和多路径误差。
采用精密轨道和钟差产品后,消去了卫星钟差和卫星码硬件延迟,观测方程为
 (2)
(2)
对式(2) 进行整理得到
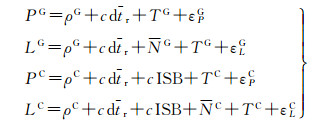 (3)
(3)
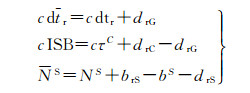 (4)
(4)
式中,
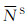
| 类别 | 模型 |
| 估计函数 | 扩展卡尔曼滤波 |
| 观测量 | 非差分消电离层码和载波相位组合 |
| 信号选择 | GPS:L1/L2;BDS:B1/B2 |
| 观测值采样率/s | 30 |
| 卫星高度截止角/(°) | 7 |
| 观测值加权 | 高度角加权 |
| 精密轨道及钟差 | MGEX精密产品WUM 15 min精密轨道和5 min精密钟差 |
| 对流层延迟 | Saastamoinen模型和随机游走过程 |
| 电离层延迟 | 消电离层组合消去一阶项影响 |
| 相位缠绕效应 | 改正 |
| 地球自转 | IGS ESP产品 |
| 卫星天线PCO和PCV | GPS改正;BDS仅改正PCO |
| 接收机天线PCO和PCV | GPS改正;BDS未改正 |
| 相对论效应 | 改正 |
| 地球固体潮 | IERS 2010 |
| 极潮 | IERS 2010 |
| 海洋潮汐 | IERS 2010 |
| 接收机钟差 | 每个历元作为白噪声估计 |
| 相位模糊度 | 连续弧段作为常数估计 |
| 地球参考框架 | ITRF2008 |
| ISB | 每30 min估计一次 |
1.2 ISB建模方法
分析中心在计算精密钟差产品时,天与天之间基准钟的调整会导致卫星钟差发生跳变,并引起ISB序列的跳变。该跳变会影响ISB模型的拟合程度,因此在进行建模之前需要对拟合数据进行预处理。如果一段ISB序列超出了正常的阈值范围,则判断此处发生了跳变,并将该段ISB序列减去跳变的幅度。跳变修复的公式为
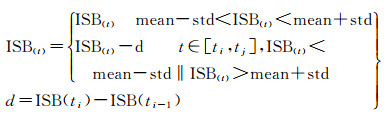 (5)
(5)
式中,ISB(t)为t时刻的ISB值;ti和tj分别为ISB序列超出阈值的起始和结束时刻;ti-1为ISB序列超出阈值起始时刻的前一历元;mean和std分别为ISB拟合数据的平均值和标准差;d为跳变的幅度。
ISB拟合数据可以看作是由趋势项和周期项两部分组成的。首先利用FFT(fast fourier transform)分析ISB序列并确定拟合数据的周期,然后分别使用二次曲线和三角函数对拟合数据的趋势项和周期项进行拟合,建模的数学模型为
 (6)
(6)
式中,t=ti-t0,t0为起始历元,ti为第i个历元;n为周期项的个数;Pi为已知的周期;A、B、C、Di和Ei为待估参数。
在实际情况中,随着时间的推移早期数据与预报时刻的时空相关性会逐渐减弱,近期数据对ISB预报更有价值。因此提出一种改进的ISB建模方法,采用Kalman滤波方法估计模型参数,并根据时空相关性对ISB拟合数据的方差进行调整。Kalman滤波的增益矩阵为[22-23]
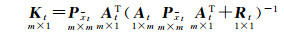 (7)
(7)
式中,下标t为t时刻;m为待估参数的个数;Kt为增益矩阵;
为了增加靠近预测时刻的拟合数据对模型参数的贡献,用ISB序列末端多个拟合数据的平均值作为确定拟合数据方差的标准,考虑到在ISB波动较大的情况下采用多天数据的平均值能够增强预测的稳定性,因此选择使用拟合数据最后3 d的平均值为标准。确定ISB拟合数据方差的具体方法为
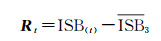 (8)
(8)
式中,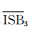
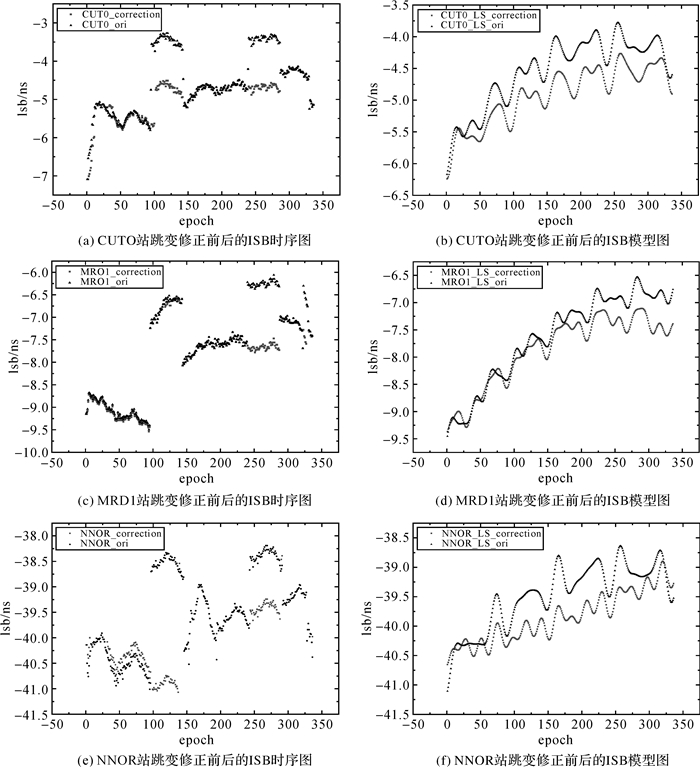
考虑到BDS和GPS系统均要有足够的可用卫星,选择MGEX(multi-GNSS experiment)网中观测条件较好的CUT0、MAYG、MRO1和NNOR 4个测站2015年年积日87—93天共7 d的数据进行建模。首先利用PPP估计ISB序列,在修正ISB跳变后分别采用Kalman滤波和等权LS方法进行ISB建模,根据所建模型预报年积日94天的ISB值,最后利用当天的ISB估计值来验证预报结果的精度,并对Kalman滤波和等权LS方法进行了对比分析。为了验证ISB序列跳变修正的效果,ISB跳变修正前和修正后均采用等权LS方法进行建模,并对ISB模型的拟合程度进行了比较。表 2给出了测站在E、N、U方向的定位误差。4个测站7 d静态PPP的定位精度在东向和高程方向均为厘米级,北向定位精度为毫米级,较高的定位精度保证了ISB的估计质量。图 1给出了跳变修正前后的ISB估计值和模型值。图 2给出了年积日88—89天精密卫星钟差的历元差。
| cm | |||
| stations | E | N | U |
| CUT0 | 0.97 | 0.50 | 1.74 |
| MAYG | 0.67 | 0.64 | 0.30 |
| MRO1 | 0.83 | 0.56 | 3.15 |
| NNOR | 1.35 | 0.39 | 2.22 |
|
| 图 1 跳变修正前后的ISB时序图和模型图 Fig. 1 ISB time series and ISB models before and after the slip correction |

|
| 图 2 年积日第88天23:50至第89天00:05共4个历元精密卫星钟差的历元差 Fig. 2 Ordinal epoch difference of precise satellite clock from 23:50 in the day of year 88 to 00:05 in the day of year 89 |
由图 1可以看出,ISB跳变发生在年积日第88—89天和第91—92天,跳变是由于分析中心在计算精密钟差产品时天与天之间基准钟的调整导致的。以年积日第88—89天为例,将年积日第88天23:50至第89天00:05共4个历元的精密卫星钟差依次做差。由图 2可知,第88天23:50至23:55之差和第89天00:00至00:05之差接近于0 ns,而第88天23:55和第89天00:00之差约为-20 ns,发生了很大的跳变。
根据图 1可知,在跳变修正之前,跳变的幅度干扰了LS拟合模型对ISB序列振幅的拟合,导致拟合模型的振幅过大,不利于对ISB的预报。在修正跳变之后,效果最为明显的是NNOR站,LS拟合模型的振幅变小,周期性也更加明显,模型的拟合精度得到了提高。CUT0、MRO1和NNOR 3个站,跳变修正前模型与原始ISB序列的拟合精度分别为0.62 ns、0.63 ns、0.60 ns,跳变修正后模型与修正ISB序列的拟合精度分别为0.28 ns、0.58 ns、044 ns,拟合精度均有较大提高。
为了对Kalman滤波和等权LS方法进行比较,试验均采用跳变修正后的ISB数据,其中MAYG站ISB序列没有超过跳变阈值,未作跳变修正。使用LS方法估计模型参数时,对ISB拟合数据采用等权处理的方式。采用Kalman滤波方法估计模型参数时,以拟合数据最后3 d的ISB平均值为标准确定拟合数据的方差,如式(8) 所示。在确定模型参数后利用ISB模型预报年积日94天的ISB值,并用当天的ISB估计值对预报结果进行验证。Kalman滤波方法的ISB模型参数和周期项见表 3。此外,对ISB模型参数估值进行了显著性检验。给定显著水平α=0.05,自由度为326,对应的检验临界值为tα/2=1.967。周期Pi采用FFT方法确定为已知量,对A、B、C、Di、Ei等参数构造t统计量。参数估值的显著性检验结果见表 4。
| stations | parameters | |||||
| A | B | C | Di | Ei | P | |
| CUT0 | -0.000 010 4 | 0.005 59 | -5.335 | -0.110 | 0.019 | 47.8 |
| -0.014 | -0.045 | 30.5 | ||||
| -0.045 | -0.023 | 24.0 | ||||
| MAYG | -0.000 029 6 | 0.011 58 | -4.330 | 0.748 | 0.370 | 48.0 |
| -0.062 | 0.108 | 33.6 | ||||
| -0.080 | -0.240 | 24.0 | ||||
| MRO1 | -0.000 017 4 | 0.009 73 | -8.771 | 0.018 | 0.029 | 55.8 |
| -0.033 | 0.015 | 30.5 | ||||
| 0.037 | 0.002 | 19.7 | ||||
| NNOR | -0.000 006 1 | 0.005 45 | -40.421 | -0.092 | -0.042 | 47.8 |
| -0.003 | -0.007 | 30.5 | ||||
| 0.023 | 0.061 | 22.3 | ||||
| stations | t-values | ||||||||
| A | B | C | D1 | D2 | D3 | E1 | E2 | E3 | |
| CUT0 | -4.300 | 6.506 | -85.746 | -3.792 | -0.482 | -1.549 | 0.615 | -1.544 | -0.791 |
| MAYG | -2.354 | 2.644 | -13.510 | 5.005 | -0.434 | -0.548 | 2.464 | 0.713 | -1.615 |
| MRO1 | -4.183 | 6.717 | -82.721 | 0.364 | -0.668 | 0.749 | 0.580 | 0.302 | 0.040 |
| NNOR | -1.929 | 4.949 | -501.672 | -2.449 | -0.080 | 0.612 | -1.108 | -0.186 | 1.617 |
随着时间的推移,早期数据与预报时刻的时空相关性会逐渐减弱,近期数据对ISB预报更有价值。Kalman滤波能够根据拟合数据的方差调整增益矩阵,而等权LS模型无法利用该特点。图 3给出了Kalman滤波和等权LS方法估计的ISB模型及其ISB预报值。由图 3可知,使用Kalman滤波方法估计模型参数时,由于最后3 d拟合数据的方差较小,第5—7天的数据对模型参数的贡献更大,避免了模型参数特别是振幅参数受到早期数据大幅波动的影响,使得拟合曲线在时序末端与ISB序列更吻合。
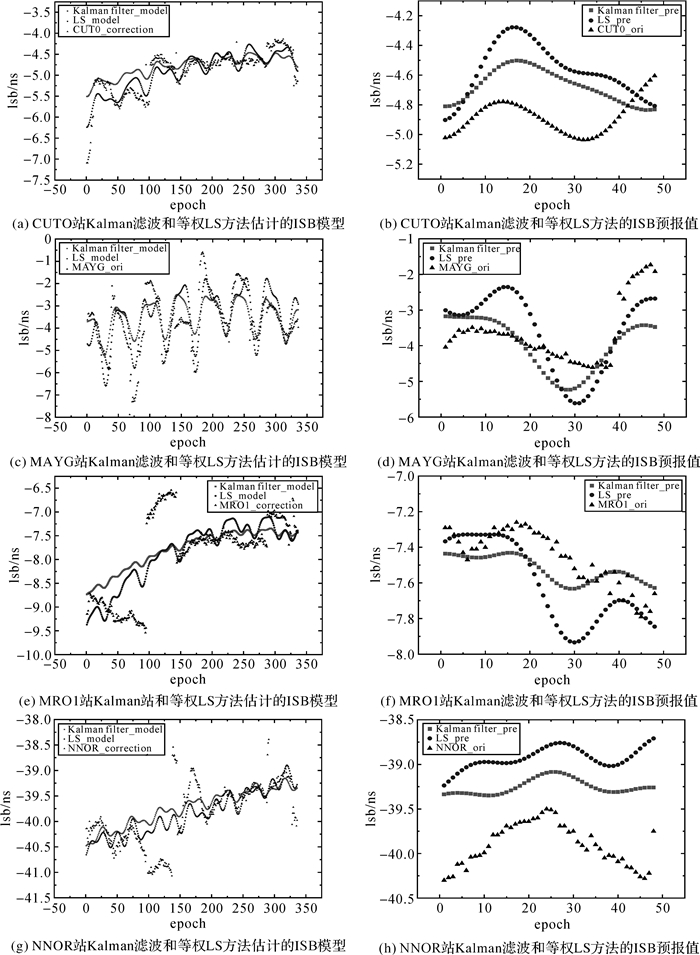
|
| 图 3 Kalman滤波和等权LS方法估计的ISB模型及其ISB预报值 Fig. 3 ISB models established by Kalman filter and LS as well as the ISB predictions of the two models |
由于Kalman滤波方法估计的ISB模型更侧重于ISB时序末端(第5—7天)的拟合程度,因此比较两种ISB模型在最后3天的拟合精度比较客观。表 5给出了Kalman滤波和等权LS方法ISB模型的预报精度和最后3 d的建模精度。由表 5可知,CUT0、MAYG、MRO1、NNOR 4个站使用LS方法第5—7天的拟合精度分别为0.22 ns、2.25 ns、0.31 ns、0.24 ns,使用Kalman滤波方法的拟合精度分别为0.22 ns、2.34 ns、0.24 ns、0.22 ns。只有MAYG站Kalman滤波方法的拟合精度有所降低,从图 3中可以看出,这是MAYG站第5天ISB波动较大所导致的。因为本文拟合数据方差的确定方法能够降低ISB模型对于大幅波动的敏感性,因此MAYG站在第5天的拟合精度较低,而在第6天和第7天Kalman方法的拟合程度依然较好。
| ns | |||||
| stations | modelling accuracy | prediction accuracy | |||
| LS_model | Kalman_model | LS_pre | Kalman_pre | ||
| CUT0 | 0.22 | 0.22 | 0.37 | 0.26 | |
| MAYG | 2.25 | 2.34 | 0.87 | 0.77 | |
| MRO1 | 0.31 | 0.24 | 0.23 | 0.13 | |
| NNOR | 0.24 | 0.22 | 1.00 | 0.68 | |
从ISB预报精度来看,由表 5可知CUT0、MAYG、MRO1、NNOR 4个站等权LS模型的预报精度分别为0.37 ns、0.87 ns、0.23 ns、1.00 ns,Kalman滤波模型的预报精度分别为0.26 ns、0.77 ns、0.13 ns、0.68 ns,预报精度分别提高了29.7%、11.5%、43.5%、32.0%。图 4给出了Kalman滤波和等权LS方法ISB模型的预报精度。

|
| 图 4 Kalman滤波和等权LS方法ISB模型的预报精度 Fig. 4 The RMS values of ISB prediction by Kalman filter and LS models |
2.2 PPP定位精度分析
为了验证ISB预报值的可用性,采用第8天的数据进行静态PPP试验。分别将Kalman滤波和等权LS两种模型的ISB预报值作为先验约束,当ISB模型第5—7天的拟合精度小于1 ns时,先验精度取1 ns,当拟合精度大于1 ns时,先验精度取拟合精度。图 5给出了不加ISB先验约束和使用ISB先验约束PPP的定位误差,表 6给出了相应的定位误差统计结果。

|
| 图 5 不加ISB先验约束和分别采用两种模型ISB预测值先验约束的静态PPP在E、N、U方向的定位误差RMS Fig. 5 The RMS values for static PPP solutions in East, North and Up components without and with ISB priori constraints by LS and Kalman models |
| cm | |||||||||||
| stations | positioning accuracy | ||||||||||
| without | LS_pre | Kalman filter_pre | |||||||||
| E | N | U | E | N | U | E | N | U | |||
| CUT0 | 0.87 | 1.29 | 1.8 | 0.58 | 0.84 | 1.82 | 0.65 | 0.82 | 1.81 | ||
| MAYG | 2.33 | 0.88 | 1.85 | 1.83 | 0.84 | 1.59 | 1.83 | 0.84 | 1.60 | ||
| MRO1 | 0.95 | 0.96 | 2.83 | 1.15 | 0.75 | 2.98 | 1.08 | 0.75 | 2.97 | ||
| NNOR | 1.87 | 1.44 | 3.04 | 2.01 | 0.92 | 2.90 | 1.84 | 0.93 | 2.83 | ||
| mean | 1.51 | 1.14 | 2.38 | 1.39 | 0.84 | 2.32 | 1.35 | 0.84 | 2.30 | ||
| percentage | 7.9% | 26.3% | 2.5% | 10.6% | 26.3% | 3.4% | |||||
根据表 6可知CUT0、MAYG、MRO1、NNOR 4个站静态PPP在E、N、U方向的定位误差RMS值,不加ISB先验约束时为1.51 cm、1.14 cm、2.38 cm,使用等权LS模型ISB先验约束时为1.39 cm、0.84 cm、2.32 cm,分别提高了7.9%、26.3%、2.5%,使用Kalman滤波模型ISB先验约束时为1.35 cm、0.84 cm、2.30 cm,分别提高了10.6%、26.3%、3.4%。与等权LS方法相比,Kalman滤波方法在E和U方向上分别多提高了2.7%和0.9%,在N方向上表现相同。
3 结论针对等权LS方法估计ISB模型参数时忽略了拟合数据时空相关性的问题,提出采用Kalman滤波方法估计模型参数,并根据时空相关性调整拟合数据的方差。分别使用上述两种方法进行ISB建模和预报,对ISB预报精度和附加ISB先验约束的PPP定位结果进行了验证分析。试验结果表明,4个测站Kalman拟合模型的ISB预报精度比等权LS模型分别提高了29.7%、11.5%、43.5%、32.0%;采用Kalman拟合模型ISB先验约束的定位精度与不加先验约束相比在E、N、U方向分别提高了10.6%、26.3%、3.4%,比使用等权LS模型ISB先验约束在E和U方向上分别多提高了2.7%和0.9%,在N方向上表现相同。
| [1] | ODOLINSKI R, TEUNISSEN P J, ODIJK D. Combined BDS, Galileo, QZSS and GPS Single-frequency RTK[J]. GPS Solutions, 2015, 19(1): 151–163. DOI:10.1007/s10291-014-0376-6 |
| [2] | GU Shengfeng, LOU Yidong, SHI Chuang, et al. BeiDou Phase Bias Estimation and Its Application in Precise Point Positioning with Triple-frequency Observable[J]. Journal of Geodesy, 2015, 89(10): 979–992. DOI:10.1007/s00190-015-0827-z |
| [3] | 张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250–256. ZHANG Xiaohong, ZUO Xiang, LI Pan, et al. Convergence Time and Positioning Accuracy Comparison between BDS and GPS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 250–256. DOI:10.11947/j.AGCS.2015.20130771 |
| [4] | 朱永兴, 冯来平, 贾小林, 等. 北斗区域导航系统的PPP精度分析[J]. 测绘学报, 2015, 44(4): 377–383. ZHU Yongxing, FENG Laiping, JIA Xiaolin, et al. The PPP Precision Analysis Based on BDS Regional Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 377–383. DOI:10.11947/j.AGCS.2015.20140082 |
| [5] | ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research:Solid Earth, 1997, 102(B3): 5005–5017. DOI:10.1029/96JB03860 |
| [6] | CHOY S, BISNATH S, RIZOS C. Uncovering Common Misconceptions in GNSS Precise Point Positioning and Its Future Prospect[J]. GPS Solutions, 2017, 21(1): 13–22. DOI:10.1007/s10291-016-0545-x |
| [7] | LOU Yidong, ZHENG Fu, GU Shengfeng, et al. Multi-GNSS Precise Point Positioning with Raw Single-frequency and Dual-frequency Measurement Models[J]. GPS Solutions, 2016, 20(4): 849–862. DOI:10.1007/s10291-015-0495-8 |
| [8] | LI Haojun, XU Tianhe, LI Bofeng, et al. A New Differential Code Bias (C1-P1) Estimation Method and Its Performance Evaluation[J]. GPS Solutions, 2016, 20(3): 321–329. DOI:10.1007/s10291-015-0438-4 |
| [9] | ZHANG Baocheng, TEUNISSEN P J G. Characterization of Multi-GNSS Between-receiver Differential Code Biases Using Zero and Short Baselines[J]. Science Bulletin, 2015, 60(21): 1840–1849. DOI:10.1007/S11434-015-0911-Z |
| [10] | LIU Yinhua, LI Xiaohui, ZHANG Huijun, et al. Calculation and Accuracy Evaluation of TGD from IFB for BDS[J]. GPS Solutions, 2016, 20(3): 461–471. DOI:10.1007/s10291-015-0454-4 |
| [11] | XUE Junchen, SONG Shuli, ZHU Wenyao. Estimation of Differential Code Biases for Beidou Navigation System Using Multi-GNSS Observations:How Stable are the Differential Satellite and Receiver Code Biases?[J]. Journal of Geodesy, 2016, 90(4): 309–321. DOI:10.1007/s00190-015-0874-5 |
| [12] | WANG Ningbo, YUAN Yunbin, LI Zishen, et al. Determination of Differential Code Biases with Multi-GNSS Observations[J]. Journal of Geodesy, 2016, 90(3): 209–228. DOI:10.1007/s00190-015-0867-4 |
| [13] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P. Differential Code Bias Estimation Using Multi-GNSS Observations and Global Ionosphere Maps[J]. Navigation, 2014, 61(3): 191–201. DOI:10.1002/navi.v61.3 |
| [14] | TORRE A D, CAPORALI A. An Analysis of Intersystem Biases for Multi-GNSS Positioning[J]. GPS Solutions, 2015, 19(2): 297–307. DOI:10.1007/s10291-014-0388-2 |
| [15] | LI Xingxing, ZHANG Xiaohong, REN Xiaodong, et al. Precise Positioning with Current Multi-constellation Global Navigation Satellite Systems:GPS, GLONASS, Galileo and BeiDou[J]. Scientific Reports, 2015(5): 8328. |
| [16] | MONTENBRUCK O, HAUSCHILD A, HESSELS U. Characterization of GPS/GIOVE Sensor Stations in the CONGO Network[J]. GPS Solutions, 2011, 15(3): 193–205. DOI:10.1007/s10291-010-0182-8 |
| [17] | TEGEDOR J, φVSTEDAL O, VIGEN E. Precise Orbit Determination and Point Positioning Using GPS, GLONASS, Galileo and BeiDou[J]. Journal of Geodetic Science, 2014, 4(1): 65–73. |
| [18] | PAZIEWSKI J, WIELGOSZ P. Accounting for Galileo-GPS Inter-system Biases in Precise Satellite Positioning[J]. Journal of Geodesy, 2015, 89(1): 81–93. DOI:10.1007/s00190-014-0763-3 |
| [19] | ODIJK D, NADARAJAH N, ZAMINPARDAZ S, et al. GPS, Galileo, QZSS and IRNSS Differential ISBs:Estimation and Application[J]. GPS Solutions, 2016. DOI:10.1007/s10291-016-0536-y |
| [20] | JIANG Nan, XU Yan, XU Tianhe, et al. GPS/BDS Short-term ISB Modelling and Prediction[J]. GPS Solutions, 2017, 21(1): 163–175. DOI:10.1007/s10291-015-0513-x |
| [21] | LI Xingxing, GE Maorong, DAI Xiaolei, et al. Accuracy and Reliability of Multi-GNSS Real-time Precise Positioning:GPS, GLONASS, BeiDou, and Galileo[J]. Journal of Geodesy, 2015, 89(6): 607–635. DOI:10.1007/s00190-015-0802-8 |
| [22] | YANG Yuanxi, HE Haibo, XU Guochang. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 75(2-3): 109–116. DOI:10.1007/s001900000157 |
| [23] | YANG Yuanxi, GAO Weiguang. An Optimal Adaptive Kalman Filter[J]. Journal of Geodesy, 2006, 80(4): 177–183. DOI:10.1007/s00190-006-0041-0 |


