2. 武汉大学测绘学院, 湖北 武汉 430079;
3. 香港理工大学土地测量与地理资讯学系, 香港 999077
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. Department of Land Surveying and Geo-Informatics, Hong Kong Polytechnic University, Hong Kong 999077, ChinaAbstract
随着我国BDS、俄罗斯GLONASS和欧洲Galileo等卫星定位系统迅速发展,基于全球导航卫星定位系统的位置服务已经从单一GPS模式发展到多模GNSS模式阶段[1]。相对于单一的GPS,GNSS各个卫星定位系统在卫星定轨和信号质量等方面具有一定的差异性,导致了GNSS时间序列中的误差特性更加复杂[2],已经成为制约GNSS深入应用的瓶颈问题。特别是对于大坝变形、桥梁振动、边坡滑移和板块运动等长周期高精度的变形监测用户来说,GNSS时间序列的误差在时间轴线上还存在着一定积累的效应,造成的影响不可低估。
早期研究普遍认为GNSS时间序列的噪声主要包括白噪声和闪烁噪声[3]。随着卫星导航定位技术的应用研究深入,人们逐渐认识到GNSS时间序列中还含有显著的随机漫步噪声[4-5]。文献[6—7]分别采用谱指数估计方法,证明了GNSS时间序列中存在着以随机漫步特征为主的噪声。文献[8]利用极大似然估计法来探索坐标时间序列的噪声成分,也同样发现了部分GNSS时间序列中含有随机漫步噪声。文献[9]通过艾伦方差分析法,进一步证实了GNSS时间序列中随机漫步噪声的存在。文献[10]运用误差分析的方法,发现了美国中东部连续GNSS时间序列水平分量中含有较大随机漫步噪声。因此,有必要对GNSS时间序列中的随机漫步噪声开展系统的消噪研究,才能对它加以有效地控制[11]。
时间序列的消噪方法一直都是GNSS研究的热点领域,已经涌现出卡尔曼滤波法、模极大值法和小波阈值法等一批经典的理论[12],其中小波阈值消噪法因简捷有效,最具有代表性[13]。文献[14—15]较早地基于小波理论提出了硬阈值和软阈值两种消除白噪声的方法。针对硬阈值的消噪结果方差较大与软阈值有固定偏差的双重问题,文献[16]对阈值函数进行改进而提出了半软阈值法,较好地降低了消噪结果失真情况。21世纪以来,小波阈值消噪法有了新的进展。文献[17]基于小波理论与模糊数学相结合的方法,对半软阈值法的阈值计算过程进行优化,减少了阈值计算量,进一步扩大了半软阈值法的应用范围。文献[18]提出了一种基于二次曲线的半软阈值函数,大大缩减了阈值计算工作量。文献[19]对小于阈值部分采用缓变到零的消噪策略代替了直接置零方法,确保了有用信号在消噪过程中得到保留。上述半软阈值法的相关研究,其阈值函数主要以线性收缩策略为主,虽然对于以白噪声和闪烁噪声为主的GNSS时间序列具有较好的适应性[20],而对于具有量级小、频率低、敏感性差等复杂特征的随机漫步噪声,直接使用它们容易造成阈值计算量大,且存在着消噪效果不佳等问题。因此,有必要对现有半软阈值函数进行有效的改进,以提高对随机漫步噪声的适应性。
本文提出一种改进的半软阈值算法,重点解决阈值函数的连续性处理和平滑性的参数率定两个关键问题,形成了一套统一的半软阈值函数体系,提高常规半软阈值对随机漫步噪声的适应性。
1 改进半软阈值算法的基本原理 1.1 常规半软阈值法半软阈值法是经典的一种小波阈值消噪方法,小波阈值消噪的过程是对分解后的小波系数进行阈值处理,然后将处理后的小波系数进行小波重构从而得到消噪后的信号。常规半软阈值法对小波系数进行分段处理,一般需要确定两个阈值,其表达式为
 (1)
(1)
式中,ωi, j为原始信号经小波分解后的小波系数; 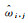
针对阈值函数的改进,主要是将文献[18]中阈值函数二次曲线的优势和文献[19]中阈值函数缓变置零的处理策略进行有效结合,然后从阈值函数的连续性和平滑性两个角度进行处理以达到改进目的。
文献[18]在ωi, j>T的函数部分采用二次曲线形式,符合小波系数中噪声的分布特点,消噪效果明显。该阈值函数其中ωi, j>T的函数部分为
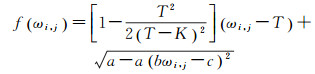 (2)
(2)
式中,T为阈值;a、b、c、K的计算方法为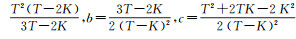
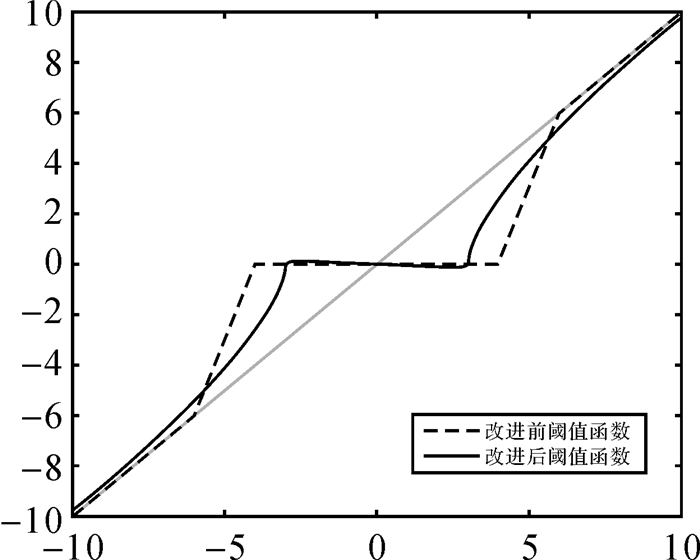
|
| 图 1 改进前后阈值函数曲线 Fig. 1 Comparison of traditional and improved threshold function curves |
文献[19]在|ωi, j|≤T的函数部分没有将小波系数置零,而是缓变到零,这样有利于保留部分信号的小波系数。该阈值函数其中|ωi, j|≤T的函数部分为
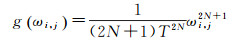 (3)
(3)
式中,T为阈值;N为调节因子(取正整数)。当N取值较小时,经阈值函数处理后的小波系数会偏大,考虑到随机漫步噪声的量级较小特点,往往会导致随机漫步噪声的消除不彻底。因此,在图 1中的|ωi, j|≤T函数部分,改进策略是减去参量h(ωi, j),达到降低该部分函数曲线波动幅度,从而实现对随机漫步噪声的有效控制。
综合上述两点改进策略,初步构建出改进后的阈值函数
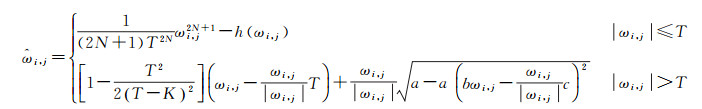 (4)
(4)
式中,T为阈值。
1.2.2 阈值函数的连续性处理由于改进的半软阈值法还是采用分段阈值函数,其在临界点处并不连续;考虑到随机漫步噪声一般都比较小,而且阈值函数连续时,对于经过阈值函数处理后得到的信号,可以更多地保留原始信号的连续的形态性质,最大限度地保留信号质量,所以有必要将分段函数连接成一个连续的函数曲线。这就要求分段阈值函数在彼此相邻的临界点处的函数值相等,也就是要求在临界点处的阈值函数值的差值为零。记两段函数在阈值处的差值为Δ,即
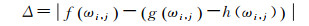 (5)
(5)
如果两段函数在阈值处连续,则在ωi, j=T时,ΔT=0。现在令ΔT=0,得h(ωi, j)=T/(2N+1);同理令Δ-T=0,得到h(ωi, j)=-T/(2N+1)。由此可得,当|ωi, j|≤T时,h(ωi, j)=ωi, j/(2N+1)。
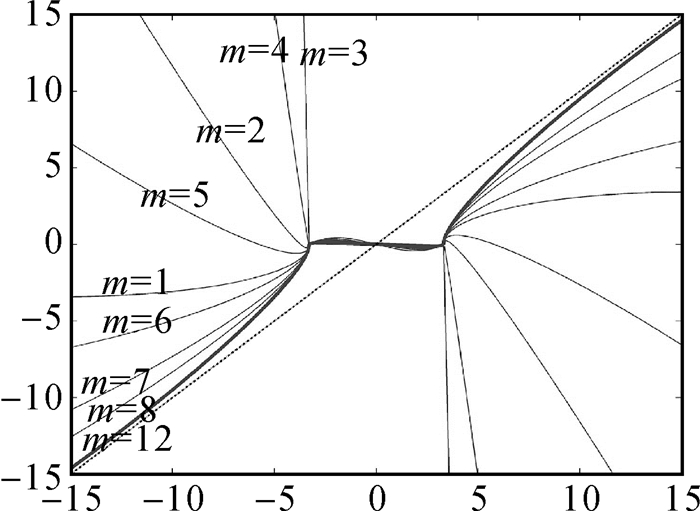
1.2.3 平滑性参数的确定平滑性用于描述每一段函数曲线的重要特征。改进的半软阈值法不仅要求各个临界点是连续的,而且还要确保整个阈值函数的平滑性,因此需要将|ωi, j|≥T和|ωi, j|≤T的两部分函数中的参数进行统一。将式(2) 中[1-T2/[2T-K2]]的参数K与式(3) 中的参数N统一为一个可变因子m,形成一个完整的半软阈值函数算法体系。虽然式(2) 中的参数K与式(3) 中的参数N在各自阈值函数中分别是独立的变量,但是将它们统一为一个可变因子并不会影响其阈值函数,只是为了增加改进阈值函数的适应性,从而确定出最佳的消噪效果。由于式(3) 中参数N的取值为正整数,为了继承该阈值函数的优势,将可变因子的取值范围也确定为正整数。在具体计算过程中,采用消噪后信号的信噪比达到最大或者均方根误差达到最小作为评价标准,此时所对应的m值为最佳平滑性参数,如图 2所示。
|
| 图 2 改进半软阈值函数可变因子的收敛过程 Fig. 2 The convergence process of the improved soft threshold function variable factor |
综上所述,最终改进后的阈值函数表达式为
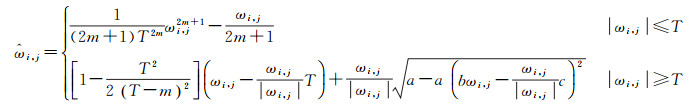 (6)
(6)
式中,m为可变因子(取正整数)。
1.3 评估方法为了进一步验证本文所提出方法的可靠性,采用3种方法对改进算法的实际效果进行评估。第1种方法是利用最为常用的信噪比与均方根误差两个指标作为改进效果的评价标准。第2种方法采用时间序列的自相关系数进行评价,通过时间序列时域自相关计算结果可以判别出噪声的时间相关性,从而定性判断噪声成分[21-22]。第3种方法是采取谱指数估计的分析方法,噪声序列谱指数K的分布范围一般在-3~1之间,当K=-2时,表现为随机漫步噪声;K=0时为白噪声,K=-1时为闪烁噪声,因此噪声序列的谱指数可以定量验证噪声成分[23-24]
2 试验 2.1 数据为了验证改进算法的消噪效果,采用文献[25]中GNSS日解算坐标时间序列模型来生成模拟仿真数据。其表达式为
 (7)
(7)
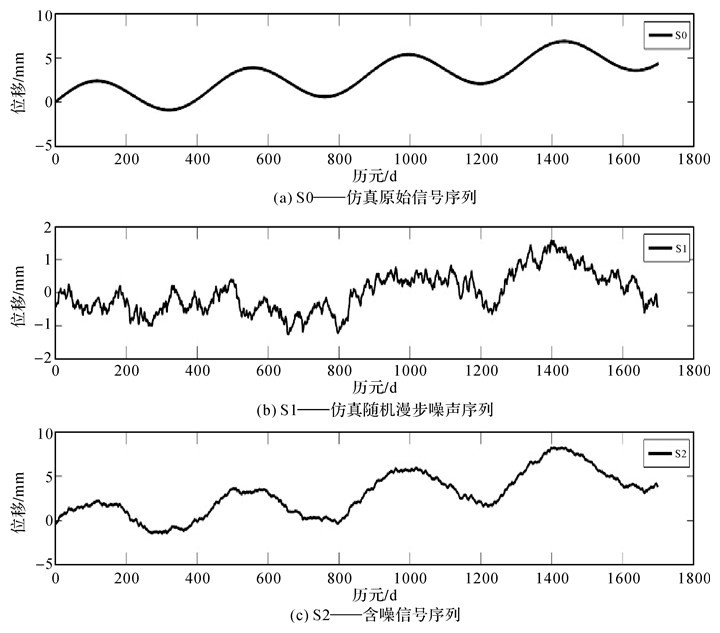
式中,a为初始位置常数项;b为线性速率;c、d、e和f分别为年、半年周期项系数;ti为时间;gi为阶跃;H为阶梯函数;vi为残差。从简化试验角度考虑,没有考虑半年周期项系数e和f,试验数据全部由Matlab平台生成,共1700个历元,如图 3所示。其中,图 3(a)中S0是GNSS时间序列,不含任何误差,坐标时间序列的参数取值依次为a=0、b=0.003 4和c =2。图 3(b)中S1是基于时间相关性特征来生成与S0同步的随机漫步噪声序列,并通过了相应谱指数指标的检验。图 3(c)中S2则是将上述GNSS时间序列S0和随机漫步噪声序列S1相叠加而成。
|
| 图 3 试验数据 Fig. 3 Experimental data |
2.2 结果 2.2.1 常规半软阈值法的消噪结果
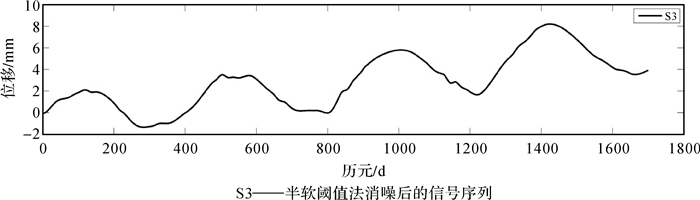
小波消噪过程中常用的阈值确定准则有混合准则(heursure)、无偏风险估计准则(rigrsure)、固定阈值准则(sqtwolog)和极大极小准则(minimaxi)。对于常规半软阈值法,采用无偏风险估计和固定阈值准则分别确定两个阈值 T1和T2,分别为0.674 3和3.872 1,其消噪结果如图 4中S3所示。
|
| 图 4 常规半软阈值法的消噪结果 Fig. 4 Denoising results of traditional semisoft thresholding method |
2.2.2 改进半软阈值的消噪结果
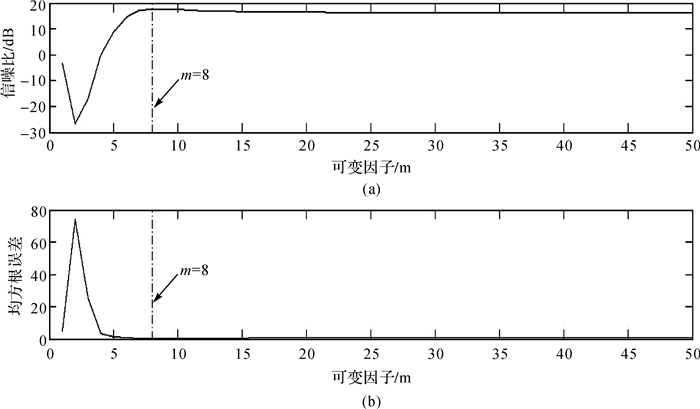
由于改进后的半软阈值只需确定一个阈值,本文采用产生均方误差较小的极大极小阈值选取准则来进行计算,其阈值T =2.371 7。然后,采用信噪比达到最大和均方根误差达到最小作为评价标准,分别计算m从1至50过程中两个指标的具体数值,整体上看两个评价指标结果较为一致,如图 5所示。当m=2时,信噪比最低,均方根误差最大,两者结果都表明此时消噪效果最差;当m=8时,信噪比最大,均方根误差最小,消噪效果最好;而且从8至50过程中,信噪比和均方根误差都保持稳定,消噪效果具有一定持续性。因此,可变因子取值为m=8。其实,这个结果同图 2可变因子的理论收敛过程是十分吻合的:当m取值较小时,函数曲线偏离原始信号比较远,从而导致信噪比与均方根误差偏差较大,当m取值较大时,函数曲线趋于稳定,所对应的信噪比与均方根误差趋于稳定。
|
| 图 5 可变因子m的取值 Fig. 5 The value of variable factor m |
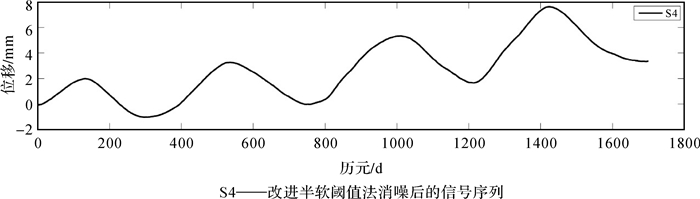
此时,利用式(6) 进行消噪处理,得到改进半软阈值法的结果S4,如图 6所示。
|
| 图 6 改进半软阈值法的消噪结果 Fig. 6 Denoising results of improved semisoft threshold method |
3 分析与讨论 3.1 改进前后的信噪比/均方根误差变化分析
信噪比和均方根误差是最为常用的消噪效果评价指标。信噪比越大、均方根误差越小,则表明消噪后的信号中残留的噪声越少,消噪的效果越好;反之则效果越差。从图 4和图 6可以初步看出,改进后方法得到的消噪结果比改进前更加平滑,其信号特征保留更多。从表 1中可以进一步看出,改进半软阈值法相对于常规半软阈值法,信噪比从15.846提高到17.672 9,均方根误差从0.57下降到0.46,这都说明改进策略是有一定效果的。相对于现有成果中的白噪声或者闪烁噪声的消噪效果来说,虽然两个具体指标提升的绝对值并不大,但是考虑到随机漫步噪声自身数量级并不大这一实际情况,本文提出的改进算法效果是完全可以接受的。
| 参数 | 常规半软阈值法的消噪结果(S3) | 改进半软阈值法的消噪结果(S4) |
| 信噪比 | 15.846 | 17.672 9 |
| 均方根误差 | 0.57 | 0.46 |
3.2 改进前后消除噪声的形态特征讨论
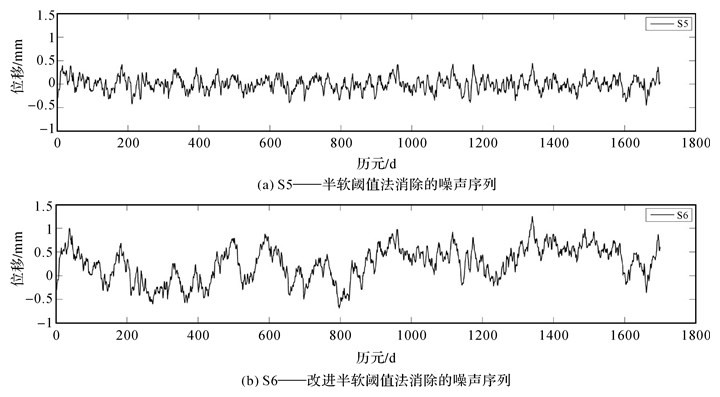
为了从定性角度探索所消除噪声类型,采用时间域自相关函数分析其消除噪声的形态特征。分别利用上述常规半软阈值法的消噪结果S3和改进半软阈值法的消噪结果S4,同原始含噪信号S2进行求差运算处理,得到两种方法所对应消除的噪声序列分别为S5和S6,如图 7所示。从所消除噪声序列的波形对比角度来看,图 7的S6和图 3的S1并不是完全吻合的,在局部区间存在着一定的差异,这主要是噪声仿真的试验过程中对随机漫步噪声特征只能在整体上进行控制、而局部区间内并不能绝对控制所造成的。但是,从整体上看,它们在整体上还是具有类似的趋势。为了量化说明这个趋势,下面进一步开展了它们的自相关分析,结果如图 8所示。
|
| 图 7 改进前后方法所消除的噪声序列 Fig. 7 Noise sequence eliminated before and after improvement |
|
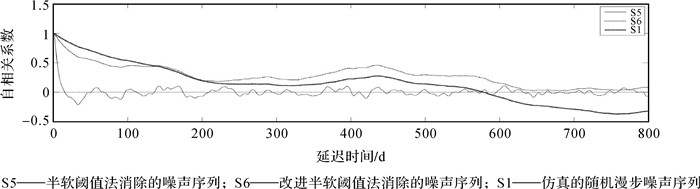
| 图 8 3个噪声序列的自相关函数 Fig. 8 Autocorrelation function of three noise sequences |
图 8所示是利用改进前后方法消除的噪声序列和仿真随机漫步噪声序列所求得自相关系数。从图 8可知,改进前的常规半软阈值法所消除的噪声序列S5的自相关系数中,当延迟时间较小时( < 10 d),噪声时间序列的自相关系数迅速下降至0;其后,随着延迟时间的不断增大,自相关系数函数始终在0附近波动,上述特征说明其中主要含有时域不相关的白噪声成分。改进后的半软阈值法所消除的噪声序列S6的自相关系数中,可以看出其主要含有与时域相关的有色噪声成分。进一步将改进后的方法消除的噪声S6与仿真的随机漫步噪声S1进行对比分析,可以看出在500 d以内这种相关性是非常显著的,这说明了S6跟S1在整体上具有类似的趋势。虽然随着延迟时间的加大,超过500 d以后(接近试验数据时间跨度的1/3),相关性的确会减弱,主要是由于自相关分析方法所采用有限的时间序列造成的,并不说明数据整体的差异大。因此,可以初步确定该有色噪声的主要成分是随机漫步噪声。
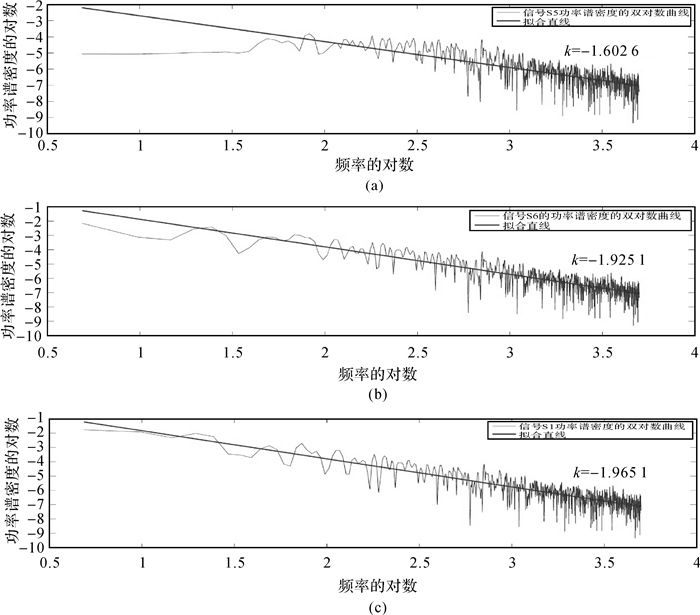
3.3 改进前后消除噪声类型的定量识别上述内容从定性的角度说明了改进方法的消噪效果,下面从定量角度来验证所消除噪声是否为随机漫步类型,为此分别计算改进前后消除噪声的谱指数大小。功率谱密度与频率的对数已经被证明服从反比的关系,当信号功率谱密度对数与对应频率对数的离散点回归直线斜率近似为-2时,就可以认为该信号是随机漫步噪声。图 9所示为改进前后方法消除的噪声序列和仿真随机漫步噪声序列的功率谱密度曲线以及计算拟合直线,其谱指数k依次为改进前-1.602 6、改进后-1.925 1和仿真的随机漫步噪声-1.965 1。对比来看,改进后方法所消除噪声,较改进前的更加接近于仿真的随机漫步噪声,这表明改进方法可以更好地消除随机漫步噪声。
|
| 图 9 噪声序列的功率谱密度及其谱指数 Fig. 9 Power spectral density and spectral index of noise sequence |
4 结论
本文围绕GNSS时间序列中随机漫步噪声消除问题,提出了一种改进的半软阈值算法及其评估,通过验证分析,得到以下结论:
(1) 通过解决阈值函数的连续性处理和平滑性的参数确定两个关键问题,对常规半软阈值函数进行有效改进,在随机漫步消噪方面表现出优异性能;
(2) 从信噪比与均方根误差两个消噪指标、自相关系数和谱指数等多方评估结果来看,改进方法所消除掉的噪声类型属于随机漫步噪声;
(3) 通过引入的可变因子m ,形成了统一的针对随机漫步的半软阈值消噪方法体系,具有更广泛的潜在应用范围。
本文主要是从随机漫步噪声的特征角度入手提出相应的消除噪声方法,由于GNSS时间序列的噪声与其观测环境有相当大的关系,特别是随着GNSS系统更为深入应用的背景下,今后仍需要从噪声产生机理角度来研究GNSS时间序列消噪方法。
| [1] | 刘基余. GNSS全球导航卫星系统的新发展[J]. 遥测遥控, 2007, 28(4): 1–6. LIU Jiyu. Recent Development of the Global Navigation Satellite System[J]. Journal of Telemetry, Tracking, and Command, 2007, 28(4): 1–6. |
| [2] | 杨元喜. 卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报, 2012, 41(5): 646–650. YANG Yuanxi. Some Notes on Uncertainty, Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646–650. |
| [3] | MAO Ailin, HARRISON C G A, DIXON T H. Noise in GPS Coordinate Time Series[J]. Journal of Geophysical Research:Solid Earth, 1999, 104(B2): 2797–2816. DOI:10.1029/1998JB900033 |
| [4] | WILLIAMS S D P, BOCK Y, FANG Peng, et al. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research:Solid Earth, 2004, 109(B3): B03412. |
| [5] | LANGBEIN J, JOHNSON H. Correlated Errors in Geodetic Time Series:Implications for Time-dependent Deformation[J]. Journal of Geophysical Research:Solid Earth, 1997, 102(B1): 591–603. DOI:10.1029/96JB02945 |
| [6] | 黄立人, 符养. GPS连续观测站的噪声分析[J]. 地震学报, 2007, 29(2): 197–202. HUANG Liren, FU Yang. Analysis on the Noises from Continuously Monitoring GPS Sites[J]. Acta Seismologica Sinica, 2007, 29(2): 197–202. |
| [7] | 苏利娜, 丁晓光, 张彦芬, 等. 陕西连续GPS基准站坐标时间序列分析[J]. 大地测量与地球动力学, 2014, 34(5): 106–109. SU Li'na, DING Xiaoguang, ZHANG Yanfen, et al. Study on Coordinate Time Series of Shaanxi Continuous GPS Refrence Stations[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 106–109. |
| [8] | 李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496–503. LI Zhao, JIANG Weiping, LIU Hongfei, et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series inside China[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 496–503. |
| [9] | KAIVOSOJA J, LINKOLEHTO R. GNSS Error Simulator for Farm Machinery Navigation Development[J]. Computers and Electronics in Agriculture, 2015(119): 166–177. |
| [10] | DMITRIEVA K, SEGALL P, DEMETS C. Network-based Estimation of Time-dependent Noise in GPS Position Time Series[J]. Journal of Geodesy, 2015, 89(6): 591–606. DOI:10.1007/s00190-015-0801-9 |
| [11] | 杨元喜, 崔先强. 动态定位有色噪声影响函数——以一阶AR模型为例[J]. 测绘学报, 2003, 32(1): 6–10. YANG Yuanxi, Cui Xianqiang. Influence Functions of Colored Noises on Kinematic Positioning——Taking the AR Model of First Class as an Example[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(1): 6–10. |
| [12] | 吴富梅, 杨元喜. 基于小波阈值消噪自适应滤波的GPS/INS组合导航[J]. 测绘学报, 2007, 36(2): 124–128. WU Fumei, YANG Yuanxi. GPS/INS Integrated Navigation by Adaptive Filtering Based on Wavelet Threshold De-noising[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 124–128. |
| [13] | 黄声享, 刘经南. GPS变形监测系统中消除噪声的一种有效方法[J]. 测绘学报, 2002, 31(2): 104–107. HUANG Shengxiang, LIU Jingnan. A Novel Method for Reducing Noises in GPS Deformation Monitoring System[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 104–107. |
| [14] | DONOHO D L. De-noising by Soft-Thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 613–627. DOI:10.1109/18.382009 |
| [15] | DONOHO D L, JOHNSTONE I M. Ideal Spatial Adaptation by Wavelet Shrinkage[J]. Biometrika, 1994, 81(3): 425–455. DOI:10.1093/biomet/81.3.425 |
| [16] | BRUCE A G, GAO Hongye. WaveShrink:Shrinkage Functions and Thresholds[C]//Proceedings of the SPIE SPIE 2569, Wavelet Applications in Signal and Image Processing Ⅲ. San Diego, CA:SPIE, 1995(2569):270. |
| [17] | 魏文畅, 杨俊杰, 蔡建立. 基于小波变换的半软阈值参数算法研究[J]. 计算机工程与应用, 2009, 45(1): 73–76. WEI Wenchang, YANG Junjie, CAI Jianli. Parameters' Algorithm of Semisoft Shrinkage Based on Wavelet Transforms[J]. Computer Engineering and Applications, 2009, 45(1): 73–76. |
| [18] | 李昊. 新阈值函数及其小波去噪研究[J]. 合肥工业大学学报(自然科学版), 2008, 31(10): 1672–1675. LI Hao. A New Shrinkage Function and Wavelet Shrinkage Denoising[J]. Journal of Hefei University of Technology, 2008, 31(10): 1672–1675. DOI:10.3969/j.issn.1003-5060.2008.10.034 |
| [19] | 王京港, 黄雨青. 基于一种新阈值函数的小波阈值去噪方法研究[J]. 数字技术与应用, 2012(9): 43–45. WANG Jinggang, HUANG Yuqing. A De-noising Algorithm of Wavelet Threshold Based on a New Threshold Function[J]. Digital Technology & Application, 2012(9): 43–45. |
| [20] | WU Hao, LI Kui, SHI Wenzhong, et al. A Wavelet-based Hybrid Approach to Remove the Flicker Noise and the White Noise from GPS Coordinate Time Series[J]. GPS Solutions, 2015, 19(4): 511–523. DOI:10.1007/s10291-014-0412-6 |
| [21] | ZHANG Jie, BOCK Y, JOHNSON H, et al. Southern California Permanent GPS Geodetic Array:Error Analysis of Daily Position Estimates and Site Velocities[J]. Journal of Geophysical Research:Solid Earth, 1997, 102(B8): 18035–18055. DOI:10.1029/97JB01380 |
| [22] | AMIRI-SIMKOOEI A R, TIBERIUS C C J M. Assessing Receiver Noise Using GPS Short Baseline Time Series[J]. GPS Solutions, 2007, 11(1): 21–35. |
| [23] | TEFERLE F N, WILLIAMS S D P, KIERULF H P, et al. A Continuous GPS Coordinate Time Series Analysis Strategy for High-accuracy Vertical Land Movements[J]. Physics and Chemistry of the Earth, Parts A/B/C, 2008, 33(3-4): 205–216. DOI:10.1016/j.pce.2006.11.002 |
| [24] | 黄立人. GPS基准站坐标分量时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2): 31–33. HUANG Liren. Noise Properties in Time Series of Coordinate Component at GPS Fiducial Stations[J]. Journal of Geodesy and Geodynamics, 2006, 26(2): 31–33. |
| [25] | NIKOLAIDIS R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D]. San Diego, CA:University of California, 2002. |


