2. 北京卫星导航中心, 北京 100094
2. Beijing Satellite Navigation Center, Beijing 100094, ChinaAbstract
北斗卫星导航系统是我国空间信息领域重要基础设施,从2012年底正式对外提供定位、导航和授时服务。目前北斗系统已经进入加速发展和应用推广阶段,北斗与其他信息源融合定位成为北斗应用领域的研究热点[1]。但在高楼林立的“城市峡谷”地带,卫星导航信号易受周边建筑物及地形遮挡,因此邻近建筑物的区域成为卫星导航盲区。同时,由于北斗系统采用了GEO+IGSO+MEO的混合卫星星座[2],在特定区域用户可用卫星数量明显减少,导致系统服务连续性降低。在特殊情况下,北斗卫星有可能被电子对抗或受到强烈干扰,也会导致部分地区的系统服务性能降低。因此,为了提高北斗卫星导航系统服务连续性和可靠性,本文引入伪卫星定位技术[3],通过北斗卫星和地面伪卫星协同定位,提高系统服务的定位精度和连续性。
伪距多路径误差是影响北斗卫星导航系统定位精度的重要误差源[4],对于伪卫星也是一样,甚至由于传播路径和周边环境的影响,伪卫星伪距受到的多路径影响更为严重。伪卫星伪距多路径误差属于非随机误差量,难以通过直接的差分改正解算进行消除。通过对伪卫星监测站的数据分析发现,伪卫星伪距数据中含有较大的多路径误差,该误差项与伪卫星的组网布设工作有较强的相关性。当接收机可见的北斗卫星数量小于4颗时,伪卫星成为完成定位解算的必选信号源。因此,如何有效地减弱伪距多路径误差,成为北斗/伪卫星协同定位中的关键问题。
目前国内外对于抑制和消除多路径的研究主要集中于硬件方法和数据后处理方法,其中硬件方法主要分为两类:一类是通过改进天线设计和选址减少多路径信号的接收[5],另一类是通过信号跟踪环路设计以及多径估计技术来对接收机内部数字信号进行处理[6]。硬件方法对导航信号的多路径抑制效果较好,但需要使用昂贵的抗多径天线及专门的数字信号电路设计。数据后处理方法更容易实施,常见方法有以下几种:载波相位平滑伪距[7]、小波方法[8]、数字滤波器[9]、恒星时滤波[10]、信噪比方法[11]和天线阵列数据处理[12]等。其中,CNMC方法对伪距多路径和噪声的消除效果较好且易于实现。文献[13]提出的CNMC方法能有效地削弱北斗卫星的伪距多路径影响,文献[14-15]通过试验验证了CNMC方法在平滑北斗卫星伪距中的效果优于经典的双频Hatch滤波方法。文献[16]研究表明,在GNSS三系统组合定位中,可以应用CNMC平滑北斗数据来提升定位性能。以上几篇文献证明CNMC对北斗卫星伪距处理的可行性和优势。但是如何将CNMC方法应用于伪卫星的伪距多路径处理中,相关研究却很少,而且绝大多数研究是基于仿真数据的。
本文首先研究了应用于北斗卫星的CNMC方法,然后考虑到伪卫星伪距观测值不再受电离层延迟影响这一特点,推导了适用于伪卫星的CNMC方法,给出了具体公式。本文最后使用实际的伪卫星试验场数据,对CNMC方法改进北斗/伪卫星协同定位精度进行了验证和分析。
1 北斗卫星CNMC方法对于北斗卫星,B1频率上的伪距和相位观测方程可以分别表示为
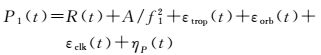 (1)
(1)
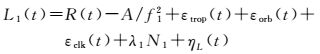 (2)
(2)
式中,P1为B1频率上的伪距观测值;R为几何距离;A/f12为B1频率上的电离层延迟;εtrop为对流层延迟;εorb为卫星轨道误差;εclk为钟差等效距离;ηP为伪距上的多路径和噪声误差;L1为B1频率上的相位观测值;λ1为B1频率波长;N1为B1频率整周模糊度;ηL为相位上的多路径和噪声误差。
伪距与相位观测值之差可以表示为
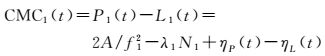 (3)
(3)
若能通过式(3) 求出ηP,进而在伪距中扣除该项,就能提升伪距观测值精度。如何从式(3) 中解算出ηP就是CNMC方法需要解决的核心问题。由于相位多路径不会超过1/4波长且相位观测噪声通常在毫米量级,远小于的数米至几十米的ηP,因此先将ηL忽略。因此,解决问题的关键在于用合适的方法求取或处理电离层延迟项A/f12和模糊度项λ1N1。
根据双频相位观测值可以计算电离层延迟
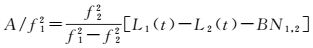 (4)
(4)
式中,BN1, 2为B1、B2两个频率上的整周模糊度组合,若无周跳发生,该项为常数。令k=f22/(f12-f22),将式(4) 代入式(3) 可得
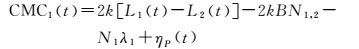 (5)
(5)
再记
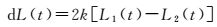 (6)
(6)
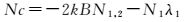 (7)
(7)
则式(5) 又可以表示为
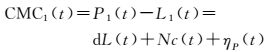 (8)
(8)
式中,dL值可由式(6) 计算,如果能估计出模糊度常数偏差Nc,就可求得伪距多路径和噪声误差ηP。对于Nc,使用式(9) 和式(10) 计算
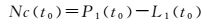 (9)
(9)
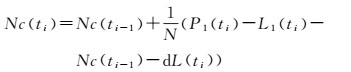 (10)
(10)
式中, N表示累积的历元数目,下标i表示历元序号。首先使用式(9) 对Nc进行初始化,然后使用式(10) 对其逐历元解算,随着时间延长,解算准确性会越来越高。式(10) 实际起到了求平均值的作用,随着历元数目增加,Nc所对应的方差值σNc2会逐渐减小
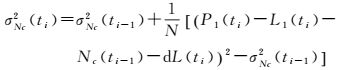 (11)
(11)
则根据式(8) 就可求得伪距多路径和噪声误差为
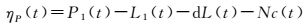 (12)
(12)
在北斗卫星的原始伪距观测值中,扣除由式(12) 计算出的ηP,即可削弱伪距多路径和噪声误差影响。需要注意的是,当相位观测值发生周跳时,需要对Nc解算过程重新初始化。
2 伪卫星CNMC方法多路径误差是由于信号传播过程中路径不同引起的信号干涉时延,定位终端不仅收到直接传播的导航信号,同时接收到周围各种可反射物质反射来信号,此类反射信号与直接接收到的导航信号产生干涉时延,使得测量值与真实值之间产生偏差。地基固定伪卫星信号多路径与在轨的北斗卫星的多路径有一定的差异性,相比之下伪卫星的误差主要具备如下特性:
(1) 在北斗卫星定位时,可以进行选星处理,卫星高度角过低的卫星一般不参与定位解算,这种方法可以削弱多路径的影响;而在北斗/伪卫星协同定位时,伪卫星必然是高度角较低的,因此该多路径误差难以通过选星进行处理;
(2) 北斗卫星的多路径误差主要来源于信号末端的反射物,而伪卫星除了信号末端反射造成的多路径外,由于距离较近且信号发射基站置于地面,因此同时还会受到信号发射端产生的多路径影响;
(3) 北斗卫星的多路径可以通过周期观测后进行统计分析处理,从而得到平均和削弱,而伪卫星通常安装在精确坐标已知的固定点,因此在静态测量时,这种多路径误差很难通过周期观测得到消除和减弱。
以B1频率为例,伪卫星B1频率的伪距和相位观测方程可以分别表示为
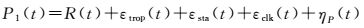 (13)
(13)
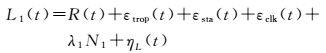 (14)
(14)
式中,εsta表示测站坐标误差,其余项含义与式(1) 和式(2) 类似。显然,伪卫星的伪距和相位观测值不再受电离层延迟影响,因此上一节中相关公式无法直接应用于伪卫星伪距多路径处理中。伪卫星的伪距与相位观测值之差可以表示为
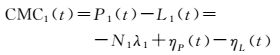 (15)
(15)
与式(3) 类似,ηL可以被忽略。若要求得ηP,就要先求取-N1λ1,将该项记为Nc,使用式(16) 和式(17) 进行计算
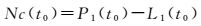 (16)
(16)
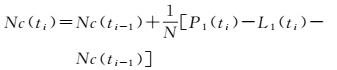 (17)
(17)
首先使用式(16) 对Nc进行初始化,然后使用式(17) 对其逐历元解算,随着时间延长,解算准确性会越来越高。
根据式(15) 就可求得伪距多路径和噪声误差为
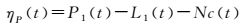 (18)
(18)
在伪卫星的原始伪距观测值中,消除由式(18) 计算出的ηP,即可得到较高精度的伪距观测值。仍然需要注意,当发现周跳时,需要对Nc的解算进行初始化。比较伪卫星和北斗卫星的CNMC方法及相关公式可以发现,伪卫星CNMC方法更为简洁,只需单频数据即可实现。
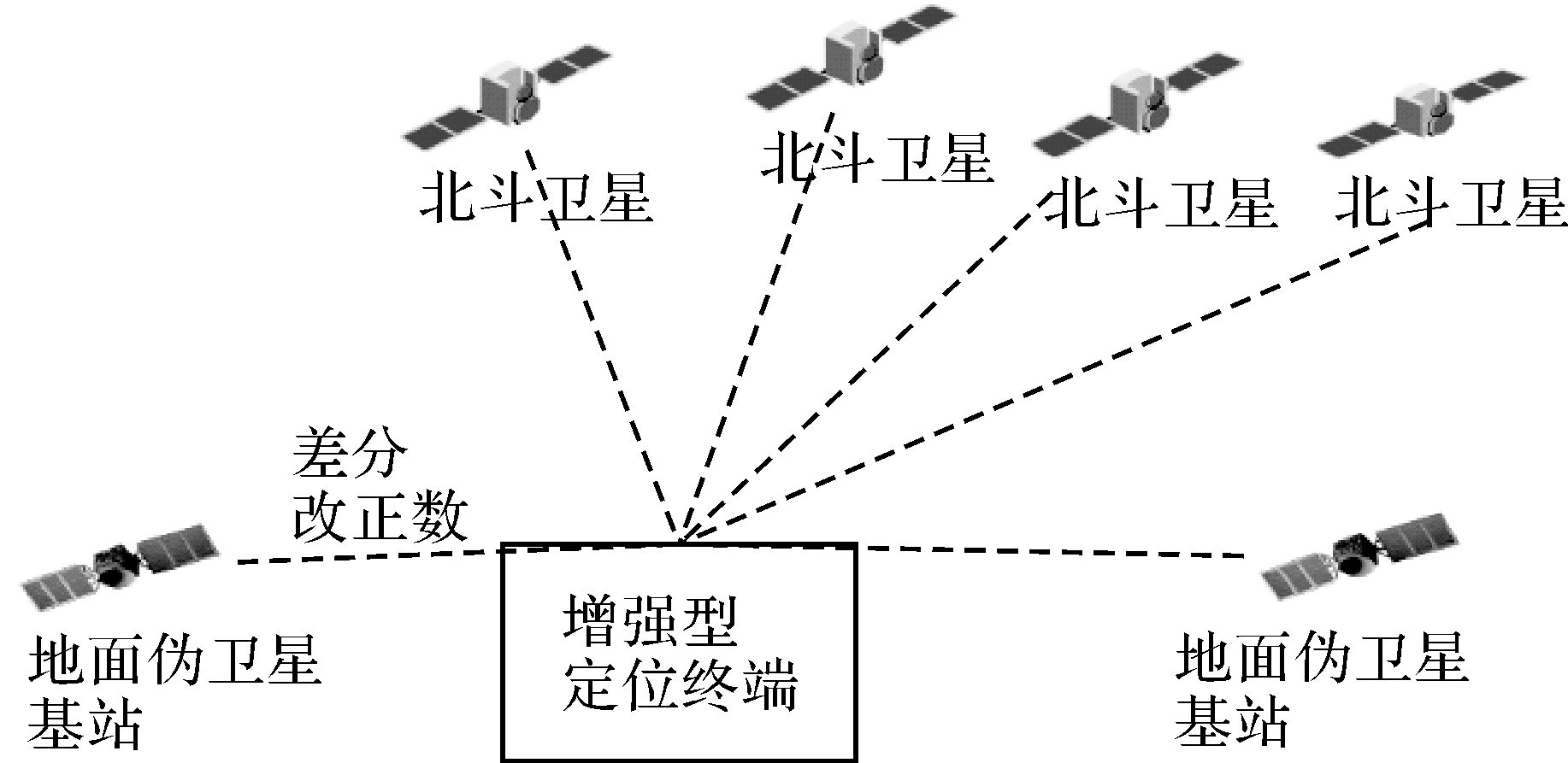
3 试验验证与分析伪卫星试验场位于成都东郊龙泉驿地区,试验场内共架设5座伪卫星基站(图 1),站间距离在5 km内。采用光纤时频传递技术实现了伪卫星时间基准的建立与保持,时间同步精度优于0.5 ns[17]。采用增强型定位终端(图 2)同时采集北斗卫星和地面伪卫星的观测数据,然后进行协同定位解算。增强型定位终端还可以接收伪卫星基站播发的伪距差分改正数,以提高定位精度。

|
| 图 1 伪卫星基站设备 Fig. 1 Pseudolite base station equipment |
|
| 图 2 增强型定位终端示意 Fig. 2 Enhanced positioning terminal |
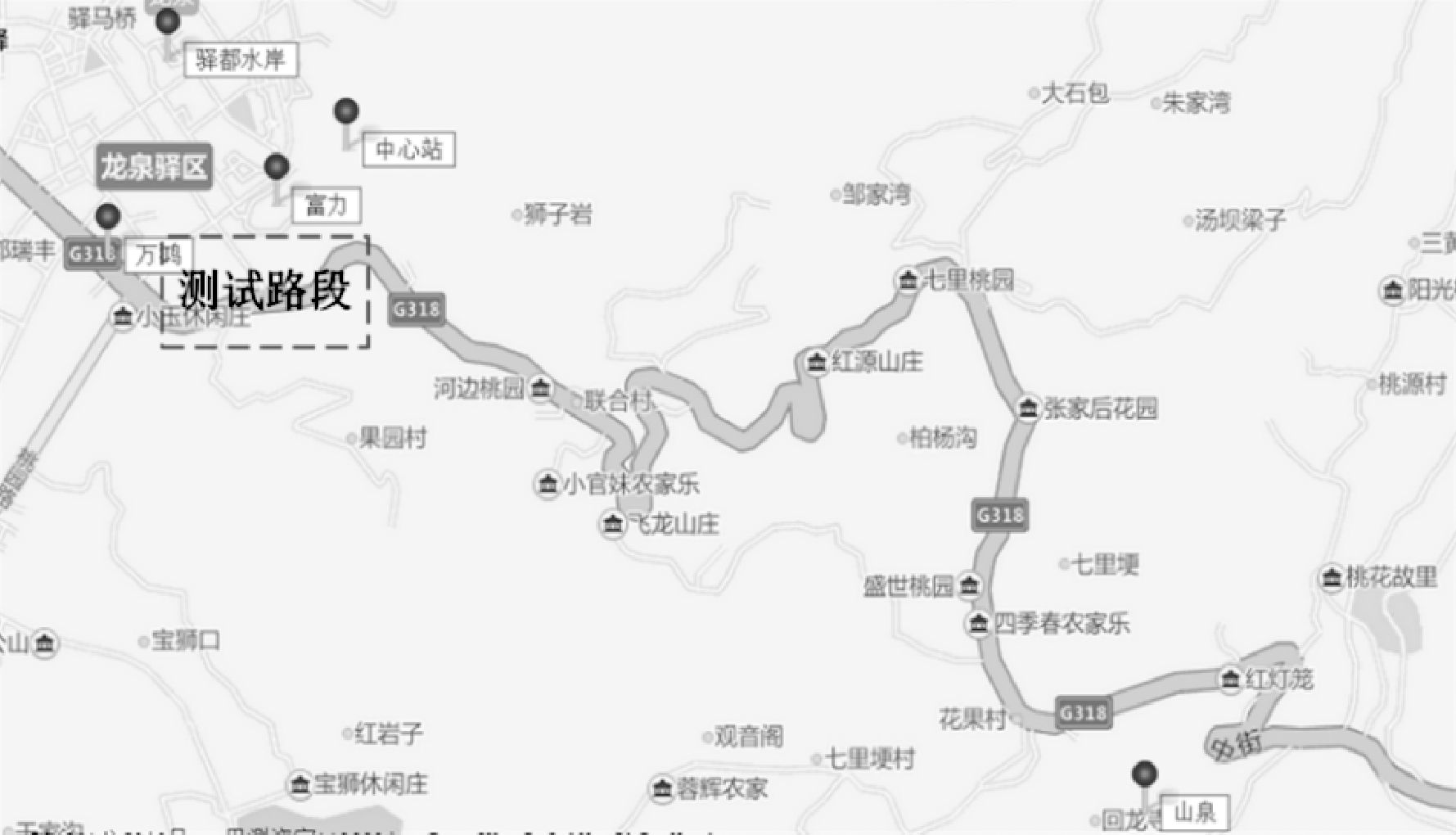
为了验证CNMC方法对于北斗/伪卫星协同定位精度的改进,依托伪卫星试验场进行了车载动态试验,试验时间为2016年4月23日。试验时,在基准站架设双频GPS接收机,在试验车上分别架设流动站GPS接收机和增强型定位终端,均按1 Hz频率采集数据,所采集数据包括伪距、相位、导航电文等以及伪距差分改正数。根据选定的路线进行跑车试验,路线如图 3所示。
|
| 图 3 动态定位试验跑车路线 Fig. 3 Dynamic positioning experiment trajectory |
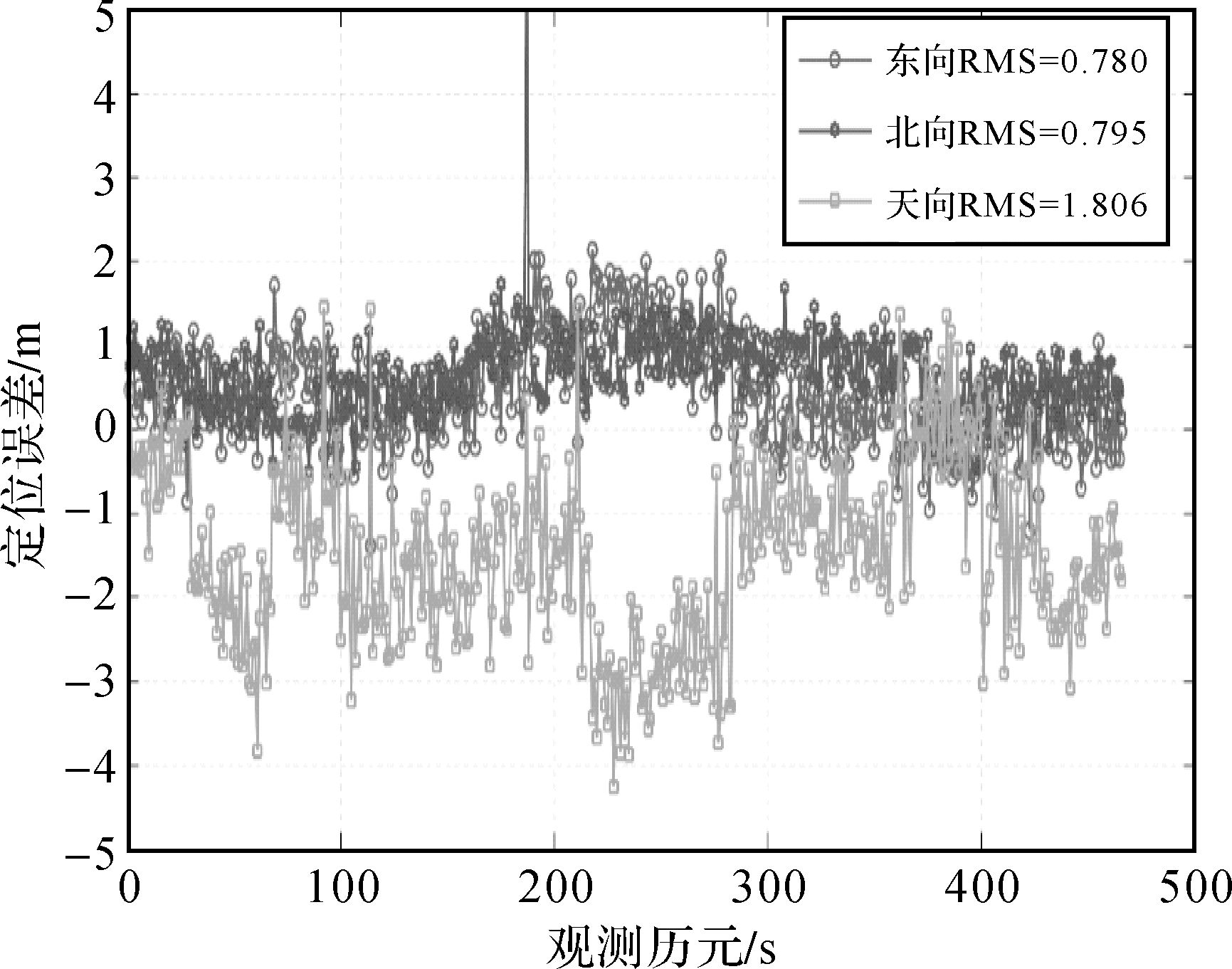
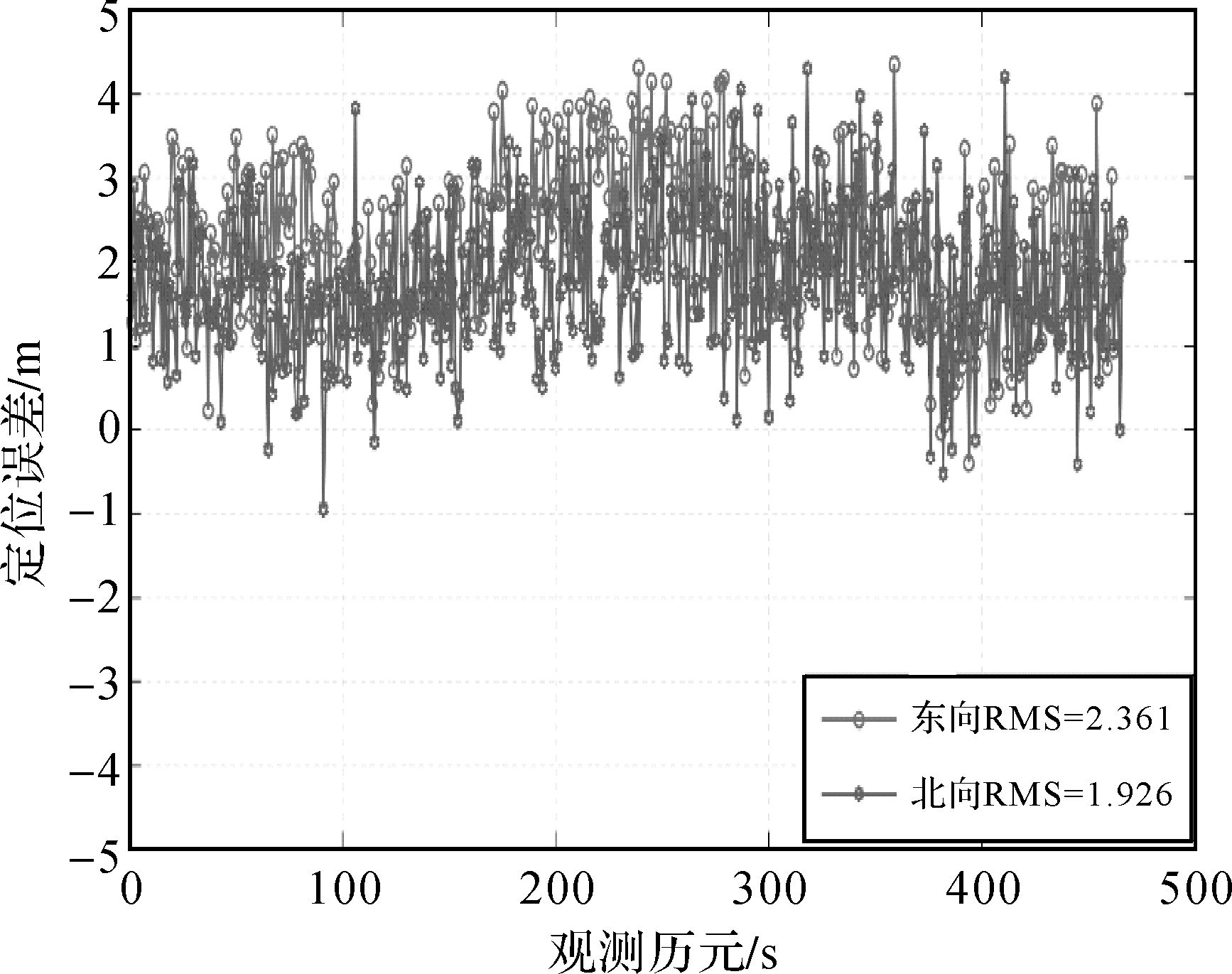
对基准站和流动站GPS接收机数据以载波相位相对定位模式进行解算,顾及时间归算和坐标归算后,得到一条高精度参考轨迹。首先进行单独北斗和单独伪卫星定位解算,将解算结果与参考轨迹比较,得到定位误差图,如图 4和图 5所示,此处解算未对伪距进行CNMC处理。需要说明的是,由于伪卫星基站均架设在地面上,这种几何构型导致了单独伪卫星定位模式下高度方向的误差会很大[18],因此图 5中不再给出高度方向误差。由于单独北斗定位中使用了北斗伪距差分改正数,因此北斗定位精度较好,水平方向RMS在1 m以内。对于单独伪卫星定位结果,其水平方向的定位误差要更大些且不稳定,这主要是由于伪卫星伪距观测值更容易受噪声和多路径误差影响。
|
| 图 4 北斗定位误差 Fig. 4 BeiDou positioning error |
|
| 图 5 伪卫星定位误差 Fig. 5 Pseudolites positioning error |
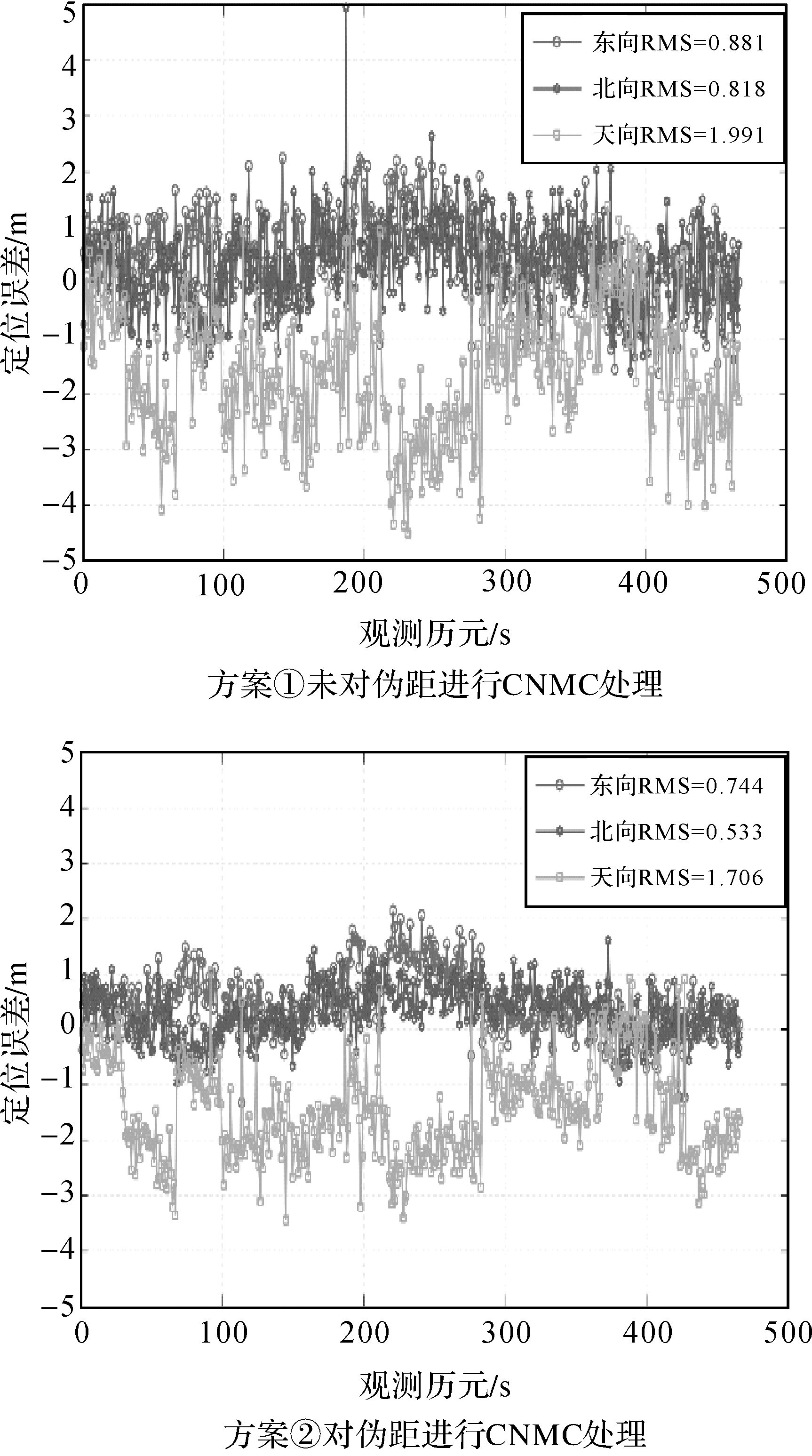
为了验证CNMC方法的效果,对增强型定位终端数据按照如下两种方案进行北斗/伪卫星协同定位解算:① 未对北斗卫星、伪卫星伪距进行CNMC处理;② 按照第2、3节公式,对北斗卫星、伪卫星伪距分别进行CNMC处理。使用最小二乘法作为估计方法,逐历元对北斗和伪卫星的伪距观测值进行联合解算,根据解算经验将二者的权比设为2.5:1。将解算结果与参考轨迹比较,得到协同定位误差图,如图 6所示。
|
| 图 6 北斗/伪卫星协同定位误差 Fig. 6 BeiDou/Pseudolites collaborative positioning error |
观察图 6和表 1可知,经过CNMC处理后,削弱了多路径和噪声影响,北斗卫星和伪卫星的伪距精度因此得到提升,进而改进了北斗/伪卫星协同定位精度和稳定性。经统计分析,三维定位精度由2.326 m改进到了1.936 m。
| m | ||||
| MEAN | STD | RMS | ||
| 方案① 未对伪距进行 CNMC处理 | 东向 | 0.491 | 0.751 | 0.881 |
| 北向 | 0.335 | 0.747 | 0.818 | |
| 天向 | -1.608 | 1.175 | 1.991 | |
| 方案② 对伪距进行 CNMC处理 | 东向 | 0.479 | 0.570 | 0.744 |
| 北向 | 0.301 | 0.439 | 0.533 | |
| 天向 | -1.458 | 0.886 | 1.706 | |
4 结论
(1) 与北斗卫星伪距观测方程相比,地面伪卫星观测值不受电离层延迟影响,因此北斗卫星使用的CNMC方法及相关公式并不能直接适用于伪卫星,因此本文推导出了伪卫星CNMC方法及具体公式。
(2) 实现北斗卫星CNMC方法至少需要双频观测数据;对于伪卫星,只需单频数据即可实现CNMC方法。
(3) 在实际的伪卫星试验场中进行了动态跑车试验,结果表明:对北斗卫星、伪卫星伪距进行CNMC方法处理后,能够改进北斗/伪卫星协同定位精度并提升定位稳定性。
| [1] | 杨元喜. 综合PNT体系及其关键技术[J]. 测绘学报, 2016, 45(5): 505–510. YANG Yuanxi. Concepts of Comprehensive PNT and Related Key Technologies[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 505–510. DOI:10.11947/j.AGCS.2016.20160127 |
| [2] | 王胜利, 王庆, 杨徉, 等. 北斗IGSO/GEO/MEO卫星联合高精度定位方法[J]. 中国惯性技术学报, 2013, 21(6): 792–796. WANG Shengli, WANG Qing, YANG Yang, et al. Method of High-precision Joint Positioning of Satellite IGSO/GEO/MEO[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 792–796. |
| [3] | WANG Jinling, TSUJⅡ T, RIZOS C, et al. GPS and Pseudo-Satellites Integration for Precise Positioning[J]. Geomatics Research Australasia, 2001: 103–117. |
| [4] | 周巍. 北斗卫星导航系统精密定位理论方法研究与实现[D]. 郑州: 信息工程大学, 2013. ZHOU Wei. Research and Realization on Theories and Methods of Precise Positioning Based on BeiDou Navigation Satellite System[D]. Zhengzhou:Information Engineering University, 2013. |
| [5] | COBB H S. GPS Pseudolites:Theory, Design, and Applications[D]. Palo Alto, CA:Stanford University, 1997. |
| [6] | SEO S, PARK J, SUK J Y, et al. A Design of Dual Frequency Bands Time Synchronization System for Synchronized-Pseudolite Navigation System[J]. Journal of Positioning, Navigation, and Timing, 2014, 3(2): 71–81. DOI:10.11003/JPNT.2014.3.2.071 |
| [7] | HATCH R. The Synergism of GPS Code and Carrier Measurements[C]//Proceedings of International Geodetic Symposium on Satellite Doppler Positioning. Las Cruces, NM:New Mexico State University, 1983(2):1213-1231. |
| [8] | 王敏, 柴洪洲, 刘鸣, 等. 一种顾及GEO卫星多路径效应影响的BDS长距离相对定位方法[J]. 测绘科学技术学报, 2016, 33(2): 121–126. WANG Min, CHAI Hongzhou, LIU Ming, et al. A Method of BDS Relative Positioning over Long Baseline Considering the Influence of Multipath Effect from GEO Satellite[J]. Journal of Geomatics Science and Technology, 2016, 33(2): 121–126. |
| [9] | ZHENG D W, ZHONG P, DING X L, et al. Filtering GPS Time-Series Using A Vondrak Filter and Cross-Validation[J]. Journal of Geodesy, 2005, 79(6-7): 363–369. DOI:10.1007/s00190-005-0474-x |
| [10] | 吴雨航, 陈秀万, 吴才聪. 利用信噪比削弱多路径误差的方法研究[J]. 武汉大学学报(信息科学版), 2008, 33(8): 842–845. WU Yuhang, CHEN Xiuwan, WU Caicong. Mitigation of Multi-path Effect Using SNR Values[J]. Geomatics and Information Science of Wuhan University, 2008, 33(8): 842–845. |
| [11] | 聂俊伟. GNSS天线阵抗干扰算法及性能评估技术研究[D]. 长沙: 国防科学技术大学, 2012. NIE Junwei. Study on GNSS Antenna Array Anti-Jamming Algorithm and Performance Evaluation Key Techniques[D]. Changsha:National University of Defense Technology, 2012. |
| [12] | WU X L, ZHOU J H, WANG G, et al. Multipath Error Detection and Correction for GEO/IGSO Satellites[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(7): 1297–1306. DOI:10.1007/s11433-012-4741-6 |
| [13] | 常志巧, 胡小工, 郭睿, 等. CNMC与Hatch滤波方法比较及其在北斗相对定位中的精度分析[J]. 中国科学:物理学力学天文学, 2015, 45(7): 079508. CHANG Zhiqiao, HU Xiaogong, GUO Rui, et al. Comparison between CNMC and Hatch Filter and Its Precision Analysis for BDS Precise Relative Positioning[J]. Scientia Sinica:Physica, Mechanica & Astronomica, 2015, 45(7): 079508. |
| [14] | CAO Yueling, HU Xiaogong, WU Bin, et al. The Wide-Area Difference System for the Regional Satellite Navigation System of COMPASS[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(7): 1307–1315. DOI:10.1007/s11433-012-4746-1 |
| [15] | ZHANG Yize, CHEN Junping C, WU Bin, et al. GPS/GLONASS/COMPASS Combined Positioning Based on CNMC[M]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2014 Proceedings:Volume Ⅲ. Berlin Heidelberg:Springer, 2014:523-532. |
| [16] | CHEN Xing, ZHANG Jian, LU Jinlong, et al. Feed-forward Digital Phase Compensation for Long-distance Precise Frequency Dissemination via Fiber Network[J]. Optics Letters, 2015, 40(3): 371–374. DOI:10.1364/OL.40.000371 |
| [17] | JANG J, AHN W G, SEO S, et al. Flight Test Result for the Ground-based Radio Navigation System Sensor with an Unmanned Air Vehicle[J]. Sensors, 2015, 15(11): 28472–28489. DOI:10.3390/s151128472 |


