2. 中国矿业大学环境与测绘学院, 江苏 徐州 221116
2. School of Environment Science and Spatial Information, China University of Mining and Technology, Xuzhou 221116, ChinaAbstract
周跳的准确探测和修复是保证北斗卫星导航系统数据可用性的前提,但北斗GEO卫星的固有特性导致其伪距多路径误差相比MEO卫星要大,使得伪距差分定位精度低于GPS[1]。在水面、高楼遮蔽等复杂环境中,多路径效应明显增大,卫星观测值包含了较大粗差,严重时甚至导致卫星整周跳变或失锁,降低北斗系统的定位精度。
目前在高精度GNSS导航定位中,对于多频周跳探测方法主要有历元间高次差法[2-3]、伪距/载波相位组合法[3-7]、Geometry Free组合法[8-9]等。文献[4]分析了伪距噪声对周跳估值的影响,给出了最优伪距相位组合法的选取标准,但由于未考虑电离层影响,并且周跳估值取整成功率易受采样间隔和伪距质量影响;文献[6]利用无几何相位组合和弱电离层伪距相位组合探测周跳,但探测的结果受伪距噪声影响较大。文献[7]对伪距相位组合法进行了相应改进,利用电离层残差估计了模糊度残差。文献[8]利用3个无几何相位组合探测周跳,通过筛选较优组合降低了无几何相位组合周跳不敏感特性并简化了搜索算法,但单凭GF组合,只能探测位置,其修复仍依赖三频伪距相位组合,修复能力同样受伪距观测值影响。文献[9]对比了伪距相位组合法和无几何相位组合法,指出了无几何相位周跳修复搜索算法的复杂性以及需要联合两种组合避免不敏感周跳。
总之,上述方法对周跳估值的计算都归结为历元间的探测量差异,强多路径环境中,即使采样频率较高,也不能通过历元间差分完全消除多路径效应,尤其是伪距多路径的残差仍将严重影响伪距相位组合的周跳探测及修复能力。目前,针对伪距受强多路径环境影响的周跳探测方法的研究还不多。GNSS/INS组合系统中,利用惯性系统短时间能保持高精度位置信息的优势,可以修正多路径效应引起的接收机位置误差,将反算的星地距替代包含多路径误差的伪距观测值,能有效克服强多路径环境中定位作业难题。文献[10]给出了惯性辅助紧组合的双差周跳探测模型,探测精度较高,但算法复杂,实现紧组合实时探测也有一定难度。文献[11]基于TDCP(time-differenced carrier phase)方法且顾及卫星几何构型提出了惯性辅助的方法,但仅限于单频接收机,实际应用范围有限。
本文提出了INS定位辅助的北斗三频组合法,利用计算难度小且实时性更好的松组合模式,构建了INS辅助的周跳决策量,优选了强多路径环境中的决策量组合,分析了INS定位误差对周跳探测能力的影响,提高了探测精度。最后以多路径误差较大的GEO卫星为例,利用一组高频采样的受强多路径干扰的水面实测北斗三频动态数据进行验证。
1 BDS/INS松组合模型基于扩展Kalman滤波的BDS/INS松组合滤波中,建立导航系统的状态误差模型,本文选取INS姿态角误差模型,同时顾及状态增量误差、杆臂效应误差。顾及了24个误差项描述系统状态[10, 12]
 (1)
(1)
式中,Xnav为9个导航误差;Xacc为3个加速度偏心误差和3个尺度因子误差;Xgyro为3个陀螺仪偏心误差;Xant为3个天线偏心误差;Xgrav为3个重力异常误差。
以此建立当地地理坐标系下的位置速度松组合的BDS/INS系统误差方程
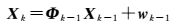 (2)
(2)
展开有如下形式
 (3)
(3)

式中,Φ为系统的状态转移矩阵;wnav、wacc、wgyro、wgrav为动力学高斯白噪声向量;N、E、D为导航坐标系(n系);bx、by、bz为载体坐标系(b系);g为重力加速度常量;Re为载体高度与地球半径之和;δr为INS位置误差向量;δv为INS速度误差向量;δψ为姿态误差向量;
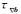
考虑天线相位中心与INS器件参考中心的偏差,在地球坐标系(e系)下,天线相位中心可表示为
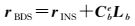 (4)
(4)
式中,Cbn为b系至e系的旋转矩阵。
2 惯性辅助北斗三频周跳探测与修复 2.1 周跳探测模型定义观测历元t时刻,北斗三频载波相位观测方程和伪距观测方程分别为
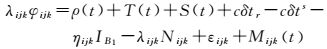 (5)
(5)
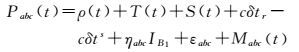 (6)
(6)
式中,i, j, k和a, b, c表示相应组合系数;φijk、Pabc分别为组合频率上的载波相位观测值和伪距观测值;ρ、T、S、δtr、δts分别为卫地距、对流层延迟、轨道误差、接收机和卫星钟差;ηijkIB1为B1频点的相位电离层延迟误差;ηabcIB1为B1频点的伪距电离层延迟误差;Nijk为Bijk频率的载波相位模糊度;εijk、εabc分别为组合频率上的载波和伪距白噪声;Mijk和Mabc为组合载波和伪距多路径效应误差。
由此可知,组合后的频率、波长、电离层延迟系数、噪声放大因子(单位,周)分别为[4-6]
 (7)
(7)
忽略影响较小的载波多路径效应,仅考虑历元间变化剧烈的伪距多路径效应,将式(5) 和式(6) 相减并在历元间做差,可得伪距相位周跳估值为
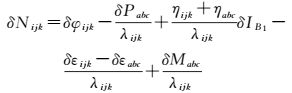 (8)
(8)
历元间伪距的多路径残差以及残余噪声被引入周跳估值中。为此,以BDS/INS松组合估计的接收机天线相位中心与卫星位置的几何距离替代卫地距,一方面消除了载波距项,另一方面也极大削弱了伪距多路径效应残差以及白噪声。此时[10]
 (9)
(9)
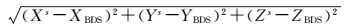 (10)
(10)
式中,rs(Xs, Ys, Zs)为卫星坐标;rBDS(XBDS, YBDS, ZBDS)为北斗天线相位中心位置。
由于INS估计的卫地距不受伪距多路径效应的影响,在高频率采样非差情况下,历元间差分得到的对流层残差可忽略不计,采用精密星历改正卫星轨道误差和卫星钟差,在顾及地球自转效应的基础上,选取卫星高度角较高的卫星作为基准星进行星间单差以消除接收机钟差,因此得到INS辅助的伪距相位组合周跳探测估值为
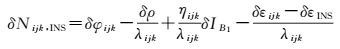 (11)
(11)
假设载波相位各观测值之间互不相关,且精度相等。则INS辅助的伪距相位组合周跳估值的标准差为
 (12)
(12)
式中,σφ为载波相位观测噪声误差;σINS为INS预测的卫星到接收机几何距离误差。σINS的大小取决于INS器件性能以及BDS信号失锁后的独立定位时间。
一般而言,在已知陀螺和加速度计零偏的情况下,可用如下经验公式来估算INS预测误差[13]
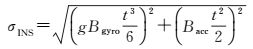 (13)
(13)
式中, g为重力加速度;Bgyro为陀螺零偏;Bacc为加速度计零偏;t为卫星信号失锁时间。
2.2 周跳检验量的选取传统伪距相位组合要保持较高的探测灵敏度,其系数选取应使得载波相位具有较长的波长且保持组合模糊度的整数特性,惯性辅助的伪距相位组合可不考虑伪距噪声影响,除此之外仅需满足[4]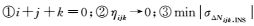
| 序号 | i | j | k | λijk/m | ηijk |
| 1 | 0 | -1 | 1 | 4.884 | -0.040 |
| 2 | -1 | -5 | 6 | 20.932 | -0.362 |
| 3 | 1 | 4 | -5 | 6.371 | 0.321 |
| 4 | 1 | 3 | -4 | 2.765 | 0.281 |
| 5 | 1 | 1 | -2 | 1.297 | 0.201 |
| 6 | 1 | 2 | -3 | 1.765 | 0.241 |
模拟INS器件的陀螺零偏Bgyro=1.5°/h,加速度计零偏Bacc=120 μg,图 1给出了北斗信号失锁后,INS独立定位时间长短各类伪距相位组合的周跳估值误差的影响。

|
| 图 1 INS独立定位时间对周跳估值的影响 Fig. 1 The impact of INS independence positioning time on the cycle-slip estimated value |
分析可知,系数组合(-1,-5,6) 在信号失锁30 s内,仍能保持0.83周的探测精度,且具有较长的探测波长,可作为首选的探测量系数组合。其次,超宽巷(0,-1,1) 和(1,4,-5) 在信号失锁15 s内,分别能保持0.45周和0.35周的探测精度,但是超宽巷组合具有优势明显的电离层延迟系数,仍是较优选择之一。当采样频率为1 s时,INS预测位置误差极小,对于惯性辅助的伪距相位组合,通过对周跳估值直接取整来进行周跳确定,成功率可达99.99%以上[12]。
然而,从表 1可以看出,最多能够选取两个线性无关的周跳探测量,为了有利于周跳修复和减少不敏感周跳,还需选取第3个线性无关的探测量。北斗IGSO和GEO卫星的运动速度比GPS的MEO卫星慢,使得历元间电离层变化量影响较小,无几何相位组合更适用于北斗系统,故本文采用无几何相位组合作为第三探测量,使观测噪声和电离层影响尽量最小。
较优的GF系数组合应在消除几何距离的前提下(即i+j+k=0) 具有较小周跳估值标准差和较小的电离层延迟系数。本文依据最优系数选取标准在[-5, 5]范围内进行系数搜索[6]。表 2列出了较好的系数组合以及相关参数。强多路径环境下,电离层延迟已不是主要影响因素,应尽量选择周跳估值较小的探测量防止漏探,(1,0,-1) 作为第三探测量。
| 序列 | i | j | k | ηijk | δΔNabc/m |
| 1 | 1 | -2 | 1 | -0.159 | 0.008 |
| 2 | 1 | 2 | -3 | -0.038 | 0.013 |
| 3 | 2 | 1 | -3 | -0.167 | 0.012 |
| 4 | 1 | 1 | -2 | -0.068 | 0.008 |
| 5 | 1 | 3 | -4 | -0.008 | 0.017 |
| 6 | 0 | -1 | 1 | 0.030 | 0.005 |
| 7 | 1 | 0 | -1 | -0.099 | 0.004 |
无几何相位组合周跳探测阈值可定义为
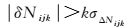 (14)
(14)
式中,取k=3, 4分别以99.73%、99.99%的置信水平进行周跳辨识[9]。
根据本文选取的系数构成线性无关周跳探测组合[14]
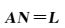 (15)
(15)
式中,

为验证本文的惯性辅助的周跳探测模型,选取徐州市云龙湖水面作为强多路径效应影响的环境,试验数据采集日期为2016年4月20日,采样间隔为1 s,绕湖心一周采集共约40 min。采用的导航设备为中国矿业大学研制的高精度GNSS/INS组合导航平台,基于FPGA(field-programmable gate array)进行1 PPS精确时间同步,试验区域和场景如图 2所示。

|
| 图 2 试验区域与场景 Fig. 2 The test area and scene |
试验设备如下:
(1) IMU:HZ325-1型船用罗经,光纤陀螺(0.02°/s,0.5 mg),如图 3所示。

|
| 图 3 HZ325-1型IMU Fig. 3 HZ325-1 IMU |
(2) 试验板卡:和芯星通UB380三系统高精度板卡。
(3) 航向辅助设备:南方灵锐S86接收机*3。
试验当天风浪较大,将组合导航平台在岸上进行约10 min初始对准后移至试验船,惯导载体Y轴与船体中线保持一致,为防止水面晃动导致的惯导航向角解算异常,利用多天线解算航向角初值。
3.1 强多路径环境对周跳探测的影响分析图 4和图 5分析了采集的北斗GEO PRN01卫星动态观测共2368个历元的三频数据的多路径效应,天线距离水面0.5 m高度,采样间隔为1 s。采用文献[18]中的方法计算多路径效应及其历元间变化量如图 4和图 5所示。

|
| 图 4 北斗PRN01卫星多路径效应 Fig. 4 BDS PRN01 multipath effects |
|
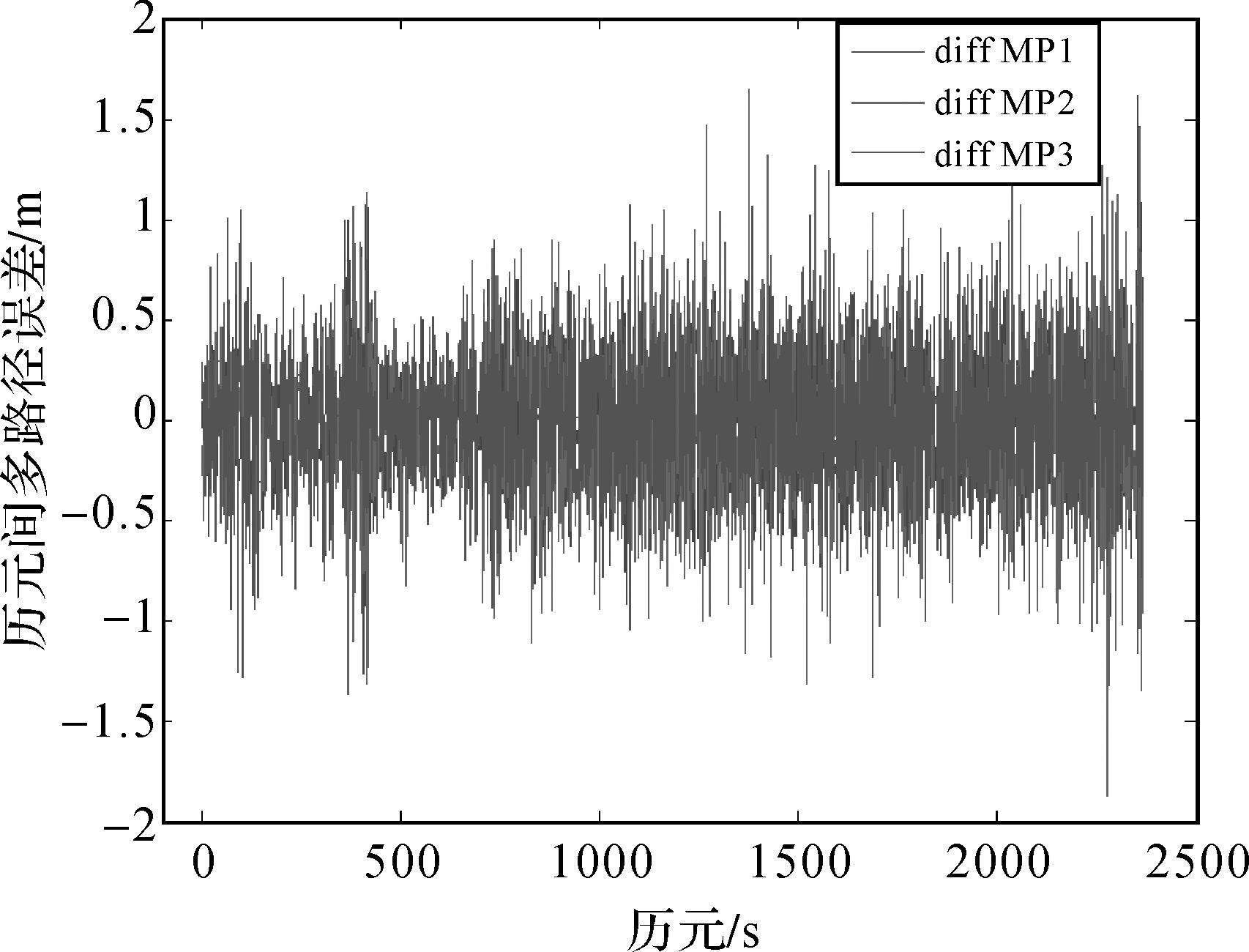
| 图 5 北斗PRN01卫星多路径历元间残差 Fig. 5 BDS PRN01 multipath effects between epoch |
在水面环境中,3个频点的伪距多路径效应(包含伪距噪声)均达到了米级,B2频点多路径效应最为明显,B1、B2、B3频点历元间多路径变化量最大值分别为1.616 m、1.646 m和1.071 m。当多路径效应严重时,将历元间多路径残差看作白噪声,则伪距相位组合周跳估值的标准差可近似为
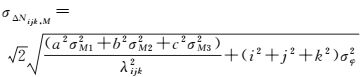 (16)
(16)
式中,可设估值σM1=1.5 m,σM2=1.5 m,σM3=1.0 m,σφ=0.01周进行分析,对于表 1中的伪距相位组合而言,忽略伪距多路径误差导致周跳探测的不准确周跳估值标准差如表 3所示。
| 伪距相位 组合 | σΔNijk/周 (忽略多路径) | σM/周 | σΔNijk, INS/周 |
| (0,-1,1) | 0.054 | 0.226 | 0.020 |
| (-1,-5,6) | 0.112 | 0.053 | 0.111 |
| (1,4,-5) | 0.099 | 0.174 | 0.092 |
| (1,3,-4) | 0.114 | 0.401 | 0.072 |
| (1,1,-2) | 0.192 | 0.852 | 0.035 |
| (1,2,-3) | 0.148 | 0.626 | 0.053 |
此环境下,历元间伪距多路径残差对波长较短的超宽巷(0,-1,1) 组合和(1,4,-5) 组合影响最大,被忽略的多路径误差对周跳探测估值的影响分别是其两倍和一倍,取整成功率明显降低。对于波长较长的(-1,-5,6) 组合影响较小,但仍不可忽略。惯性辅助的伪距相位组合,其周跳估值的标准差小于常用的伪距相位组合,且不受多路径影响,使得其取整成功率更高,探测效果更为明显。为此,引入周跳探测的误探率PF和漏探率PM进行进一步分析
 (17)
(17)
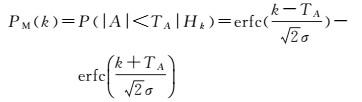 (18)
(18)
式中,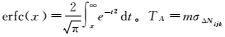
取m=3(99.73%置信水平),得到较优组合受多路径误差影响的误探率和漏探率如表 4所示。
| 伪距相位 组合 | PF(无/有 多路径误差) | PM(无/有 多路径误差) | σΔNijk, M /周 |
| (0,-1,1) | 0.27%/47.5% | 0/0.02% | 0.227 |
| (-1,-5,6) | 0.27%/0.6% | 0/0 | 0.123 |
| (1,4,-5) | 0.27%/13.0% | 0/0.03% | 0.196 |
| (1,3,-4) | 0.27%/40.0% | 0/10.4% | 0.406 |
| (1,1,-2) | 0.27%/49.9% | 2.72%/55.44% | 0.853 |
| (1,2,-3) | 0.27%/48.0% | 0.02%/35.50% | 0.629 |
当伪距多路径影响严重的情况下,除(-1,-5,6) 组合外,几乎无法找到同时满足低误探率和低漏探率的其他组合,超宽巷组合的误探率也已经达到了无法应用的程度,易将伪距多路径效应误探为发生周跳。对于波长较短的组合,其漏探误探情况更为严重。随着采样间隔的变大,多路径影响理论上仍会变大,(-1,-5,6) 组合的探测能力也将随之降低。
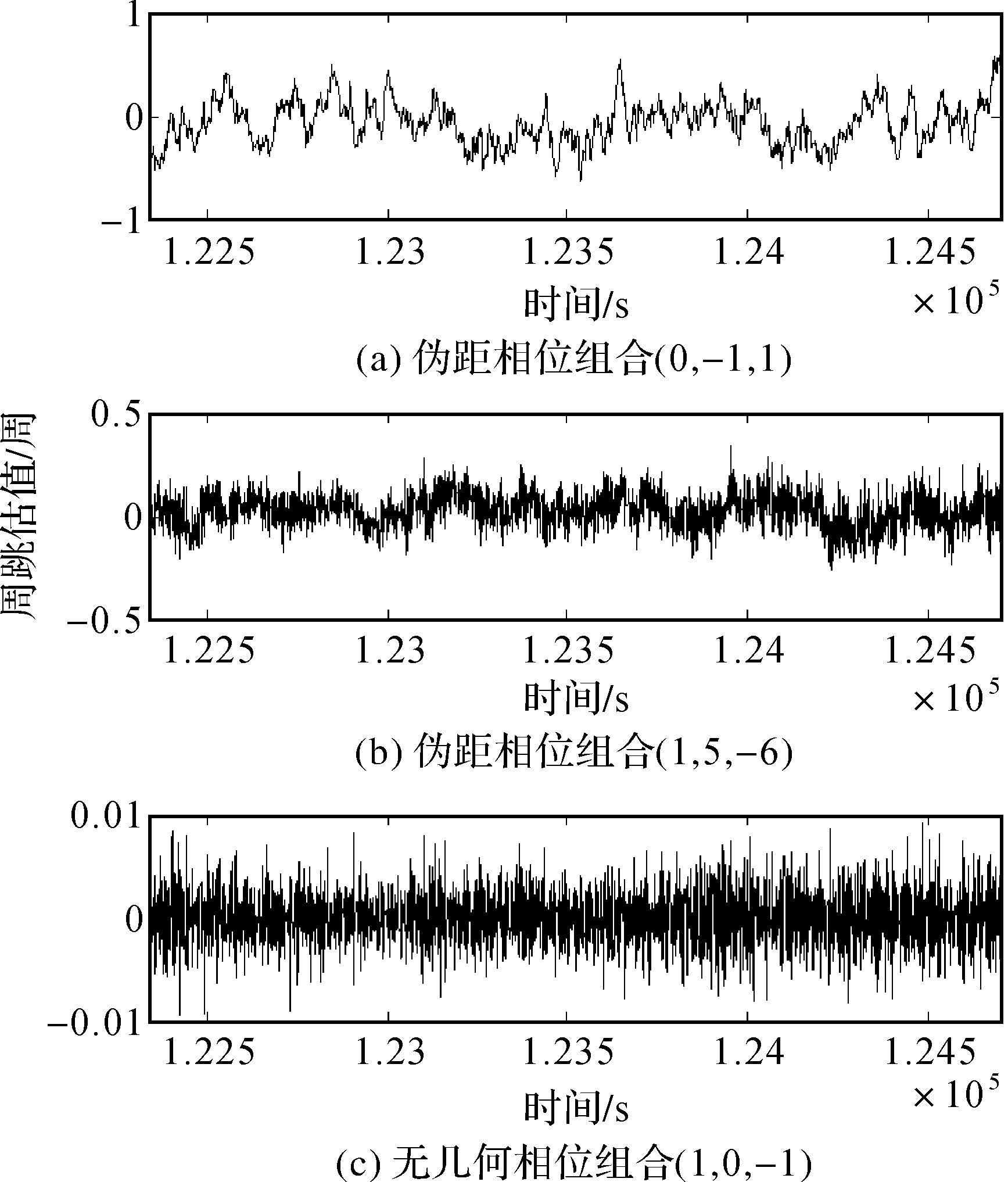
图 6给出试验中利用传统三频伪距相位组合法得到的水面北斗GEO PRN02卫星动态观测数据的周跳估值,采用伪距相位组合(0,-1,1)、(-1,-5,6) 和GF组合(1,0,-1)。波长较短的超宽巷组合呈现了明显的受强多路径影响的趋势项,多个历元周跳估值超过0.5,误探严重;(-1,-5,6) 组合由于波长较长,周跳估值较小,但估值可靠度也有所降低。无几何相位组合不受伪距多路径影响,依然保持良好的探测能力。结果表明,传统探测模型在强多路径环境下失效。
|
| 图 6 受多路径误差影响的PRN02周跳估值 Fig. 6 BDS PRN02 cycle-slip estimated value under multipath effects |
3.2 惯性辅助周跳探测的结果分析
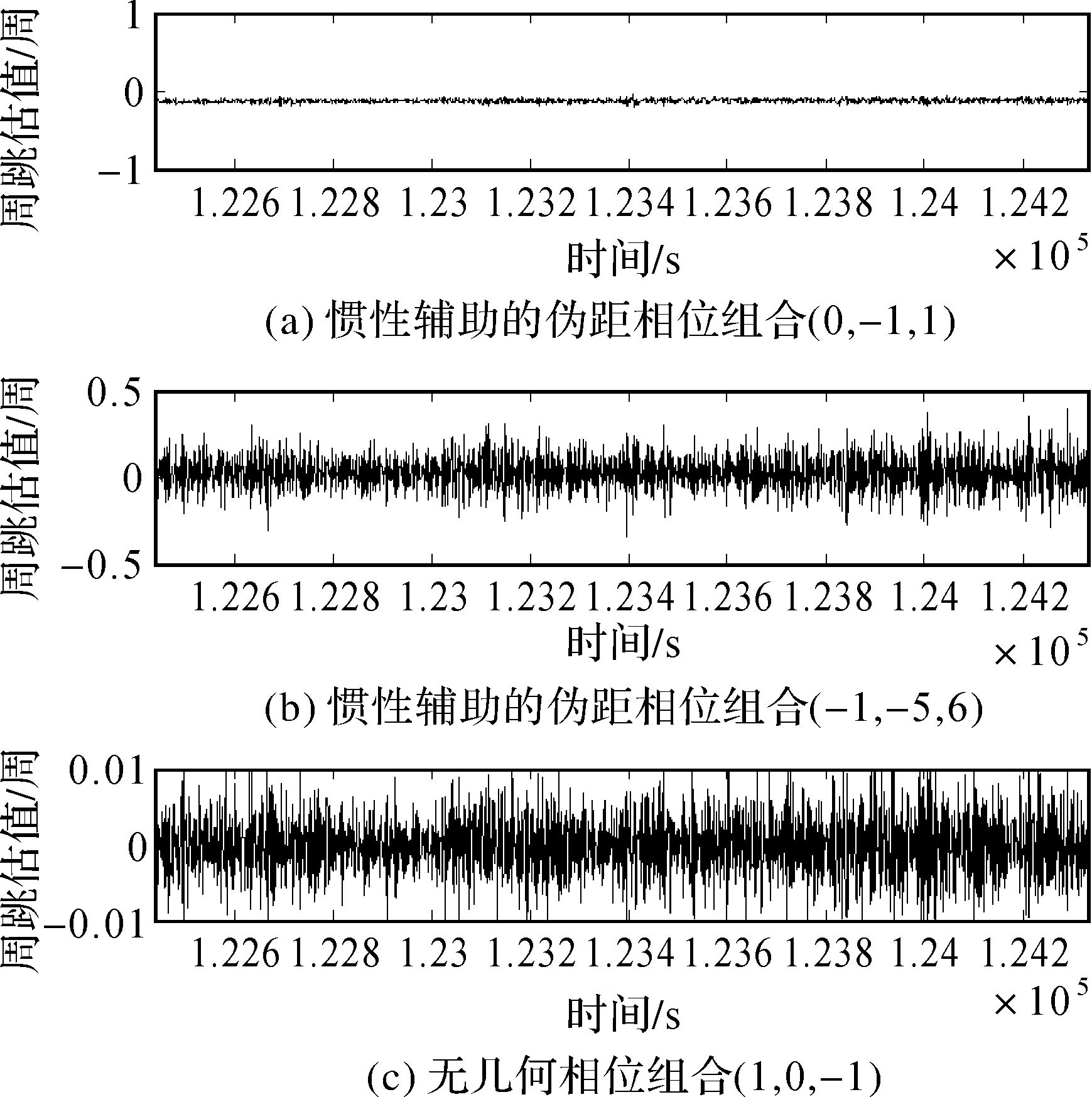
对3.1节中相同数据进行惯性辅助的伪距相位组合法周跳探测与修复作为对比来验证本文方法的有效性和可靠性。以高度角最高的GEO PRN01卫星作为基准星,惯性辅助的伪距相位组合(0,-1,1)、(-1,-5,6) 和GF组合(1,0,-1) 周跳探测估值如图 7所示。对比图 6发现,本文所采用方法的多路径效应历元间残差得到了明显抑制和消除。探测估值明显减小,意味着探测精度明显提高[9]。由于惯性辅助的(0,-1,1)、(-1,-5,6) 组合探测量的σΔNijk, INS分别为0.02和0.111,两个探测量的取整成功率可达到99.99%[4]。
|
| 图 7 惯性辅助的PRN02周跳估值 Fig. 7 BDS PRN02 cycle-slip estimated value with inertial aided |
由于卫星、系统硬件偏差的累加效应和接收机位置误差等可能的存在,波长较短的超宽巷组合周跳估值存在较小的系统性偏移,但由于前期消除了绝大部分误差,此类偏移不会对周跳的确认和修复产生影响。
多路径主要影响小周跳的探测,由于原数据中不存在周跳,为了检验该方法对强多路径环境下的小周跳探测能力,对不同GEO卫星3个频点加入1~5周的分散小周跳,所加入周跳组合如表 5所示。其探测结果如图 8所示,修复结果如表 6所示。由于选取的伪距相位组合对周跳组合(1,1,1) 不敏感,需联合其他探测量进行修复。结果表明,对于模拟的多个小周跳,模型修复率成功率达到了100%。
| 历元位置 | 200 | 500 | 800 | 1100 | 1400 | 1700 |
| 周跳数 | +1 | +2 | +1 | +5 | +3 | +1 |
| -1 | +3 | +1 | -2 | -4 | 0 | |
| +3 | -1 | +1 | +1 | +5 | -1 |

|
| 图 8 惯性辅助的GEO卫星周跳探测结果 Fig. 8 Inertial aided BDS GEO satellites cycle-slip detection |
| PRN | 历元 | 周跳 | 周跳计算值/周 | 周跳修复值/周 |
| C01 | 200 | (1, -1, 3) | (0.951, -1.049, 2.951) | (1, -1, 3) |
| C01 | 500 | (2, 3, -1) | (1.935, 2.935, -1.065) | (2, 3, -1) |
| C01 | 800 | (1, 1, 1) | (0.937, 0.937, 0.937) | (1, 1, 1) |
| C01 | 1100 | (5, -2, 1) | (4.959, -2.041, 0.959) | (5, -2, 1) |
| C01 | 1400 | (3, -4, 5) | (2.888, -4.112, 4.888) | (3, -4, 5) |
| C01 | 1700 | (1, 0, 1) | (1.127, 0.127, -0.873) | (1, 0, 1) |
| C02 | 200 | (1, -1, 3) | (0.951, -1.049, 2.951) | (1, -1, 3) |
| C02 | 500 | (2, 3, -1) | (1.935, 2.935, -1.065) | (2, 3, -1) |
| C02 | 800 | (1, 1, 1) | (0.937, 0.937, 0.937) | (1, 1, 1) |
| C02 | 1100 | (5, -2, 1) | (4.959, -2.041, 0.959) | (5, -2, 1) |
| C02 | 1400 | (3, -4, 5) | (2.888, -4.112, 4.888) | (3, -4, 5) |
| C02 | 1700 | (1, 0, 1) | (1.127, 0.127, -0.873) | (1, 0, 1) |
| C03 | 200 | (1, -1, 3) | (0.965, -1.035, 2.964) | (1, -1, 3) |
| C03 | 500 | (2, 3, -1) | (1.952, 2.952, -1.048) | (2, 3, -1) |
| C03 | 800 | (1, 1, 1) | (0.926, 0.926, 0.926) | (1, 1, 1) |
| C03 | 1100 | (5, -2, 1) | (5.105, -1.900, 1.105) | (5, -2, 1) |
| C03 | 1400 | (3, -4, 5) | (2.977, -4.023, 4.977) | (3, -4, 5) |
| C03 | 1700 | (1, 0, 1) | (1.095, 0.095, -0.905) | (1, 0, 1) |
3.3 组合模型周跳探测能力分析
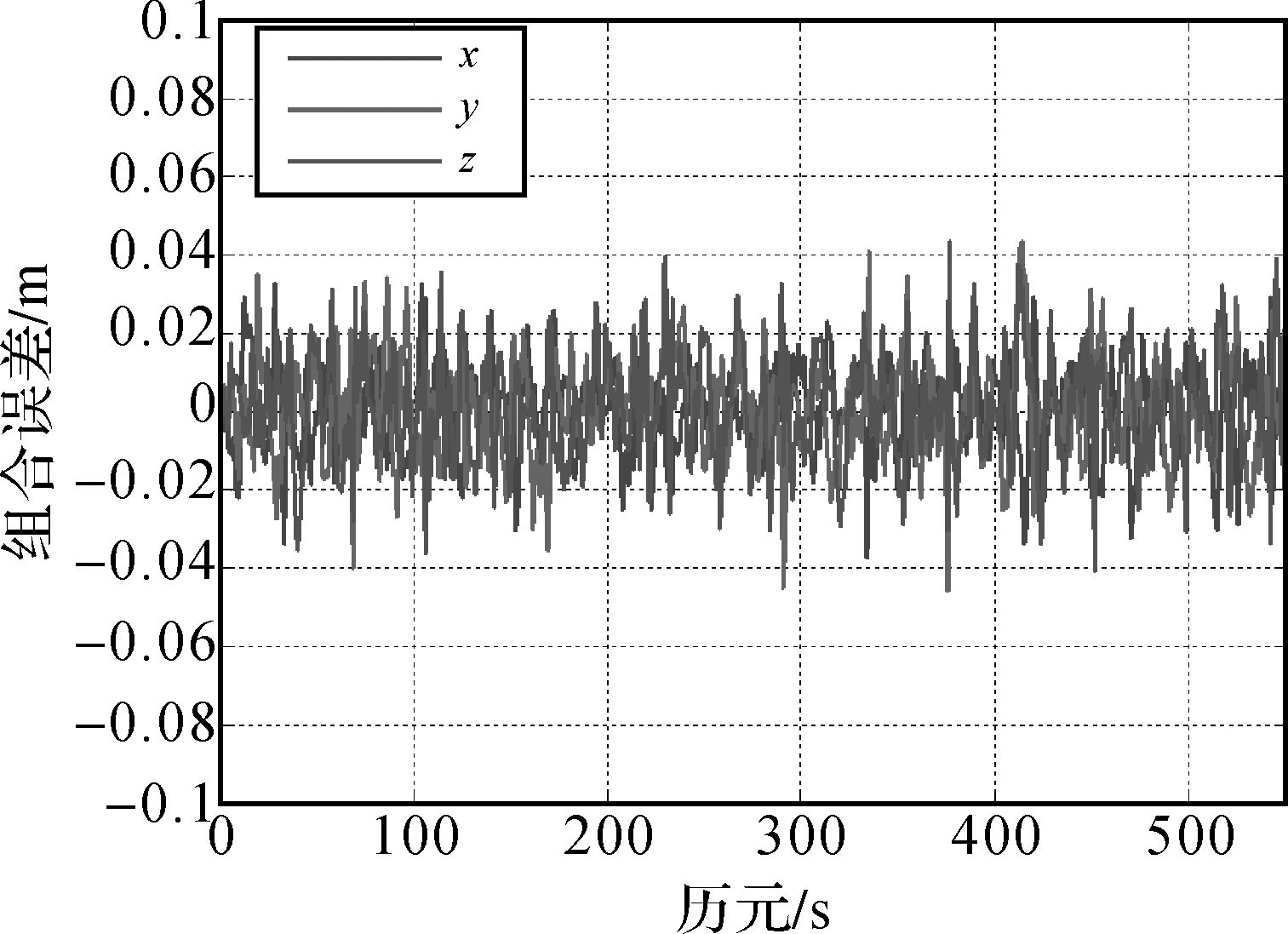
BDS/INS组合结果的优劣将直接影响周跳探测能力的强弱。为了说明松组合结果对周跳探测结果的影响,试验选取BDS信号完整时500 s左右的观测数据进行BDS/INS松组合处理,分别得到X、Y、Z 3个方向组合误差如图 9所示。为了评估卫星信号失锁后,系统独立预测卫地距的能力,在观测值中模拟了BDS信号的完全失锁,得到了信号失锁后30 s内系统预测卫地距误差随时间的变化情况如图 10所示。
|
| 图 9 BDS/INS组合误差 Fig. 9 BDS/INS integrated navigation error |

|
| 图 10 卫星信号失锁后模型星地距预测误差 Fig. 10 INS-predicted range error during BDS outage |
试验时间内,BDS/INS松组合模型在信号卫星信号完整时,3个方向的位置误差均在2~3 cm之间,历元间差分后,对周跳探测影响微弱。当卫星信号失锁后的15 s之内,对于各类型的北斗卫星,组合模型的伪距预测模型均能保持厘米级预测精度。证明该方法对15 s内采样频率数据的周跳探测与修复同样适用。
4 结论本文通过构造惯性辅助的BDS/INS松组合导航模型,引入惯性信息辅助三频周跳探测与修复,试解决强多路径环境下的周跳探测难题,得到以下结论:
(1) 本文方法的价值。惯性辅助的周跳探测方法有效解决了多路径误差影响严重情况下的周跳探测,相比传统伪距相位组合探测量的优势是:该方法极少发生误探,周跳估值不受多路径残差影响,且信号连续情况下周跳估值的标准差更小,取整成功率更高。相比无伪距的3个GF组合探测量的优势是:修复时不依赖伪距,修复更为简便,计算量更小。
(2) 本文方法的有效性。基于两个惯性辅助的伪距相位组合和一个GF组合针对BDS系统易受伪距多路径影响的GEO卫星进行周跳探测与修复,优选了组合观测值,周跳估值得到明显改善,减少了强多路径环境中的误探概率,对连续小周跳的探测与修复不受多路径效应残差影响,能够准确探测观测值中仅1周的小周跳,达到实用化水平。对模拟的2270历元的间断性小周跳,探测成功率为100%,正确修复率为100%。当卫星信号发生失锁后的15 s内,模型依旧能准确预测卫地距。
(3) 本文方法仍未消除惯性辅助后的周跳估值中的残余误差,对低成本IMU/BDS组合的周跳探测与修复中仍需进一步研究。
| [1] | 杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 44(1): 72–81. YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary Assessment of the Navigation and Positioning Performance of BeiDou Regional Navigation Satellite System[J]. Science China Earth Sciences, 2014, 44(1): 72–81. |
| [2] | XU Guochang. GPS:Theory, Algorithms and Applications[M]. 2nd ed.. Berlin, Heidelberg: Springer, 2007. |
| [3] | 李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009. LI Zhenghang, ZHANG Xiaohong. New Techniques and Precise Data Processing Methods of Satellite Navigation and Positioning[M]. Wuhan: Wuhan University Press, 2009. |
| [4] | 李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717–722. LI Jinlong, YANG Yuanxi, XU Junyi, et al. Real-time Cycle-slip Detection and Repair Based on Code-phase Combinations for GNSS Triple-frequency Un-differenced Observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 717–722. |
| [5] | ZHANG Xiaohong, HE Xiyang. BDS Triple-Frequency Carrier-Phase Linear Combination Models and Their Characteristics[J]. Science China Earth Sciences, 2015, 58(6): 896–905. DOI:10.1007/s11430-014-5027-9 |
| [6] | YAO Yifei, GAO Jingxiang, WANG Jian, et al. Real-time Cycle-slip Detection and Repair for BeiDou Triple-Frequency Undifferenced Observations[J]. Survey Review, 2016, 48(350): 367–375. DOI:10.1080/00396265.2015.1133518 |
| [7] | 张成军, 许其凤, 李作虎. 对伪距/相位组合量探测与修复周跳算法的改进[J]. 测绘学报, 2009, 38(5): 402–407. ZHANG Chengjun, XU Qifeng, LI Zuohu. Improving Method of Cycle Slip Detection and Correction Based on Combination of GPS Pseudo Range and Carrier Phase Observations[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 402–407. DOI:10.3321/j.issn:1001-1595.2009.05.005 |
| [8] | 黄令勇, 宋力杰, 王琰, 等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报, 2012, 41(5): 763–768. HUANG Lingyong, SONG Lijie, WAND Yan, et al. BeiDou Triple-frequency Geometry-free Phase Combination for Cycle-slip Detection and Correction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 763–768. |
| [9] | 李林阳, 吕志平, 崔阳, 等. 伪距相位和无几何相位组合探测与修复多频周跳的比较[J]. 大地测量与地球动力学, 2015, 35(3): 396–400. LI Linyang, LV Zhiping, CUI Yang, et al. Comparison of Cycle Slip Detection and Repair of Multiple-frequency Based on Code-phase and Geometry-free Combination[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 396–400. |
| [10] | 韩厚增, 王坚, 李增科. GPS/INS紧组合的INS辅助周跳探测与修复[J]. 测绘学报, 2015, 44(8): 848–857. HAN Houzeng, WANG Jian, LI Zengke. Inertial Aided Kinematic GPS Cycle Slip Detection and Correction for GPS/INS Tightly Coupled System[J]. Acta Geodaetica et Cartographica Sinica,, 2015, 44(8): 848–857. DOI:10.11947/j.AGCS.2015.20140350 |
| [11] | KIM Y, SONG J, KEE C, et al. GPS Cycle Slip Detection Considering Satellite Geometry Based on TDCP/INS Integrated Navigation[J]. Sensors, 2015, 15(10): 25336–25365. DOI:10.3390/s151025336 |
| [12] | DING Weidong. Optimal Integration of GPS with Inertial Sensors:Modelling and Implementation[D]. Sydney, Australia:The University of New South Wales, 2008. |
| [13] | CHIANU K W, DUONG T T, LIAO J K. The Performance Analysis of a Real-time Integrated INS/GPS Vehicle Navigation System with Abnormal GPS Measurement Elimination[J]. Sensors, 2013, 13(8): 10599–10622. DOI:10.3390/s130810599 |
| [14] | HUANG Lingyong, LU Zhiping, ZHAI Guojun, et al. A New Triple-frequency Cycle Slip Detecting Algorithm Validated with BDS Data[J]. GPS Solutions, 2016, 20(4): 761–769. DOI:10.1007/s10291-015-0487-8 |
| [15] | ALTMAYER C. Enhancing the Integrity of Integrated GPS/INS Systems by Cycle Slip Detection and Correction[C]//Proceedings of the IEEE Intelligent Vehicles Symposium 2000. Dearborn, MI:IEEE, 2000:174-179. |
| [16] | ZHAO Qile, SUN Binzi, DAI Zhiqiang, et al. Real-time Detection and Repair of Cycle Slips in Triple-frequency GNSS Measurements[J]. GPS Solutions, 2015, 19(3): 381–391. DOI:10.1007/s10291-014-0396-2 |
| [17] | TANG Weiming, DENG Chenlong, SHI Chuang, et al. Triple-frequency Carrier Ambiguity Resolution for Beidou Navigation Satellite System[J]. GPS Solutions, 2014, 18(3): 335–344. DOI:10.1007/s10291-013-0333-9 |
| [18] | 程鹏飞, 李玮, 秘金钟. 北斗导航卫星系统测距信号的精度分析[J]. 测绘学报, 2012, 41(5): 690–695. CHENG Pengfei, LI Wei, BEI Jinzhong. Precision Analysis of BeiDou Range Measurement Signals[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 690–695. |



