2. 中国科学院上海天文台, 上海 200030;
3. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 湖北 武汉 430077;
4. 三峡大学土木与建筑学院, 湖北 宜昌 443002
2. Shanghai Astronomical Observatory, CAS, Shanghai 200030, China;
3. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, CAS, Wuhan 430077, China;
4. College of Civil Engineering and Architecture, China Three Gorges University, Hubei Yichang 443002, ChinaAbstract
准周期信号在卫星导航系统中普遍存在[1],例如GPS卫星钟差中普遍存在周期约为3 h、4 h、6 h和12 h的准周期信号[2],GLONASS卫星钟显著存在着8 h、12 h和24 h的周期信号[3];北斗卫星钟也存在着显著的周期项[4],这些卫星钟信号中显著存在的周期项的精确提取有利于钟差模型的高精度建立,对钟差预报精度的改善也有着积极意义[2-5]。
当前提取准周期信号常用的方法有最小二乘拟合法[6]、傅里叶带通滤波器(Fourier band pass filtering, FBPF)[7]、奇异谱分析(singular spectrum analysis, SSA)等方法[6],这些方法都在大地测量领域中得到了广泛的使用。其中SSA[8-10]是一种基于Karhumen-Loeve分解理论发展起来的,对一维时间序列进行主成分分析的方法。该方法从时间序列的动力重构出发,并与经验正交函数相联系。SSA方法提取信号不需要先验信息,不受正弦波假定的约束,可以较好地从含噪声的时间序列中提取趋势项信息和周期项信息[11-12],特别适合于时变周期信息的提取[6, 13]。目前SSA方法已经被广泛用于时间序列分析中,例如:GPS坐标时间序列[6, 14-15]、GRACE(gravity recovery and climate experiment)时间序列[16]、地球极移数据[17]、消除GPS多路径效应[10-11]等。傅里叶带通滤波器是常用的准周期提取工具,当前已被广泛用于地学信号准周期项的提取[7]。
当前,SSA方法重建信号依赖于嵌入位数Z(又称滞后窗口),若Z太大,则会导致奇异值分解得到不同的部分产生混叠,若Z太小,又无法使信号从弱到强渐进划分,从而使得部分信号无法获取[6, 10];FBPF提取准周期信号时,其边界值极易受到噪声或者未扣除干净的趋势项的影响[18],导致边界值提取精度不高,而信号的边界信息对于信号的预报有着重要意义。针对SSA和FBPF各自的优点和缺点,本文提出了SSA+FBPF的方法。仿真试验说明,在信噪比很低的情况下,SSA方法重建准周期信号时存在信号与噪声频率混叠的现象,FBPF提取准周期信号其边界值受到了残留趋势项的影响,SSA+FBPF方法较好地克服了这些问题,其提取信号的精度比SSA方法提高了35%,比FBPF提高了26%。将SSA方法、FBPF方法和SSA+FBPF方法用于提取北斗卫星钟PC06和PC07的周期项,经比较发现,SSA+FBPF提取的周期项幅值存在明显起伏,且起伏光滑,说明SSA+FBPF方法较好地克服了残留趋势项和噪声的影响,其提取的24 h准周期项结果相对更可信。试验还表明从北斗卫星钟PC06和PC07提取的24 h准周期项幅值存在明显变化。
1 奇异谱分解(SSA)+傅里叶带通滤波器(FBPF) 1.1 奇异谱分解(SSA)奇异谱分析(SSA)的研究对象是经过中心化后的一维时间序列x1、x2、…、xN,其分析过程主要有3个步骤[6, 10]。
首先,计算轨迹矩阵及其协方差矩阵,假定窗口长度为L,然后根据L计算出大小为L×M阶的轨迹矩阵Y,其中M=N-L+1,(1<L≤N/2), N为数据长度
 (1)
(1)
式中,轨迹矩阵Y的(i, j)处的元素xij=xi+j-1,即所有反对角线上的元素相等。
求轨迹矩阵协方差矩阵的方法有BK法和VG法[6, 19-20],VG算法得到的协方差矩阵具有减少噪声干扰的功效,因此一般采用这种方法构造协方差矩阵,建立方法如下
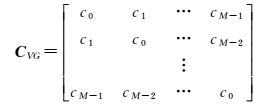 (2)
(2)
式中
 (3)
(3)
然后,通过计算得到协方差矩阵CVG的特征值λk和特征向量Ek,按照特征值大小将特征值排序,其特征值依次为λ1、λ2、…、λM且λ1≥λ2≥…≥λM≥0,对应的特征向量为E1、E2、…、EM。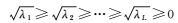
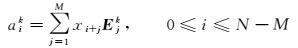 (4)
(4)
 (5)
(5)
SSA分析将信号分解成了M层信号,针对准周期信号,按照SSA原理,可以得到一对近似相等的特征值,以及与其对应的一对正交经验分解和一对正交主成分。一般情况下,假定这对特征成分序号分别为m和m+1。如果满足上述条件,那么第m和m+1层信号之和就是准周期成分。本文顾及信号的傅里叶谱特征,按照SSA方法分解得到的每层信号对应的傅里叶变换谱特征来重构准周期信号。
1.2 傅里叶带通滤波器(FBPF)傅里叶带通滤波器是基于傅里叶变换理论的最简单最常用的滤波器之一,并且已经得到了广泛的应用[7]。
对于离散信号f(j),其离散傅里叶变换为
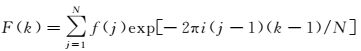 (6)
(6)
式中, N为信号f(j)长度;k=1, 2, …, N;F(k)值为角频率wk对应的傅里叶谱值。
若需要得到频率范围在[ω1, ω2]范围内的值,那么利用对应范围的傅里叶反变换得到
 (7)
(7)
式中,Kω1、Kω2分别为角频率ω1和ω2对应的值。
通过式(6) 和式(7) 分解和重构,可以得到任意选取的频率范围内准周期信号。
1.3 奇异谱分解+傅里叶带通滤波器(SSA+FBPF)SSA方法在有效去除趋势项的基础上[22],能有效提取准周期信号,但容易存在频率混叠的现象,因此会影响准周期信号的重构精度;FBPF能有效提取指定周期范围内的准周期信号,但其提取信号的边界值易受到残留趋势项的影响。针对SSA和FBPF各自在重建或提取准周期信号的优缺点,本文提出SSA+FBPF方法,即首先对利用SSA分解和重建得到的准周期信号进行一定周期范围内的傅里叶带通滤波,然后将SSA重构得到多余成分(频率混叠引入的噪声信号)通过FBPF进行滤出,从而得到指定周期范围内的准周期信号。因此SSA+FBPF方法能确保所提取的振荡信号在指定周期范围内,这样即可以防止振荡信号之间的混叠,又能有效改善噪声对SSA提取信号的干扰,另外,由于SSA方法具有良好的去趋势项能力,SSA+FBPF方法还能减少趋势项对边界值的影响,提高准周期信号的提取精度。
2 仿真试验为了比较验证SSA+FBPF方法与SSA方法和FBPF重建准周期信号的能力,这里在仿真信号里调制一个准周期信号,一个调频白噪声和一个调频随机游走噪声,仿真信号信噪比为0.017。仿真信号见式(8)
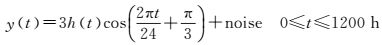 (8)
(8)
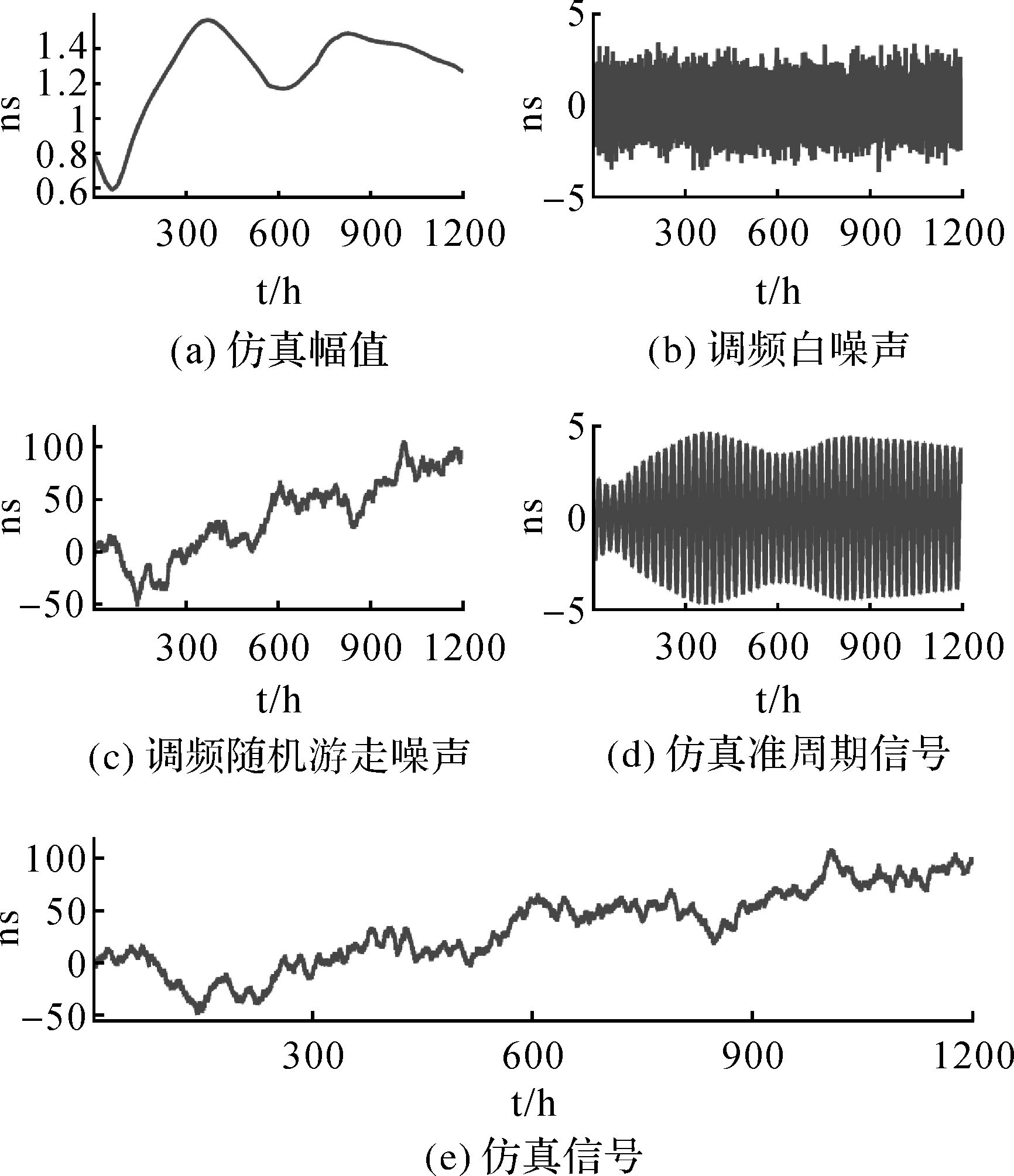
式中,准周期信号的幅值见图 1(a),调频白噪声、调频随机游走噪声和仿真准周期信号分别见图 1(b)、(c)和(d),将这3个信号叠加在一起得到仿真信号y(t),见图 1(e)。
|
| 图 1 仿真信号及其子信号 Fig. 1 Simulation signal and its sub-signals |
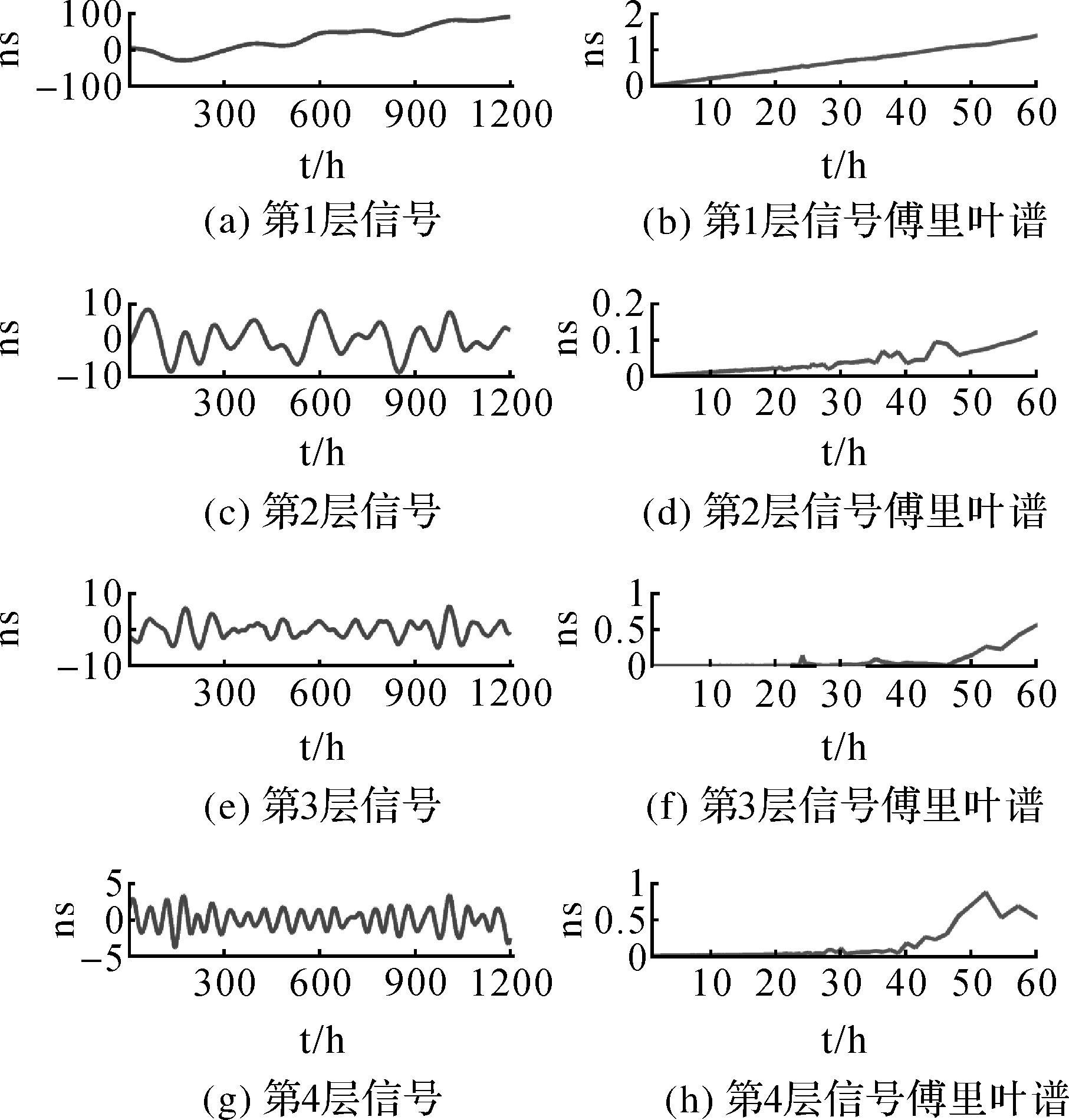
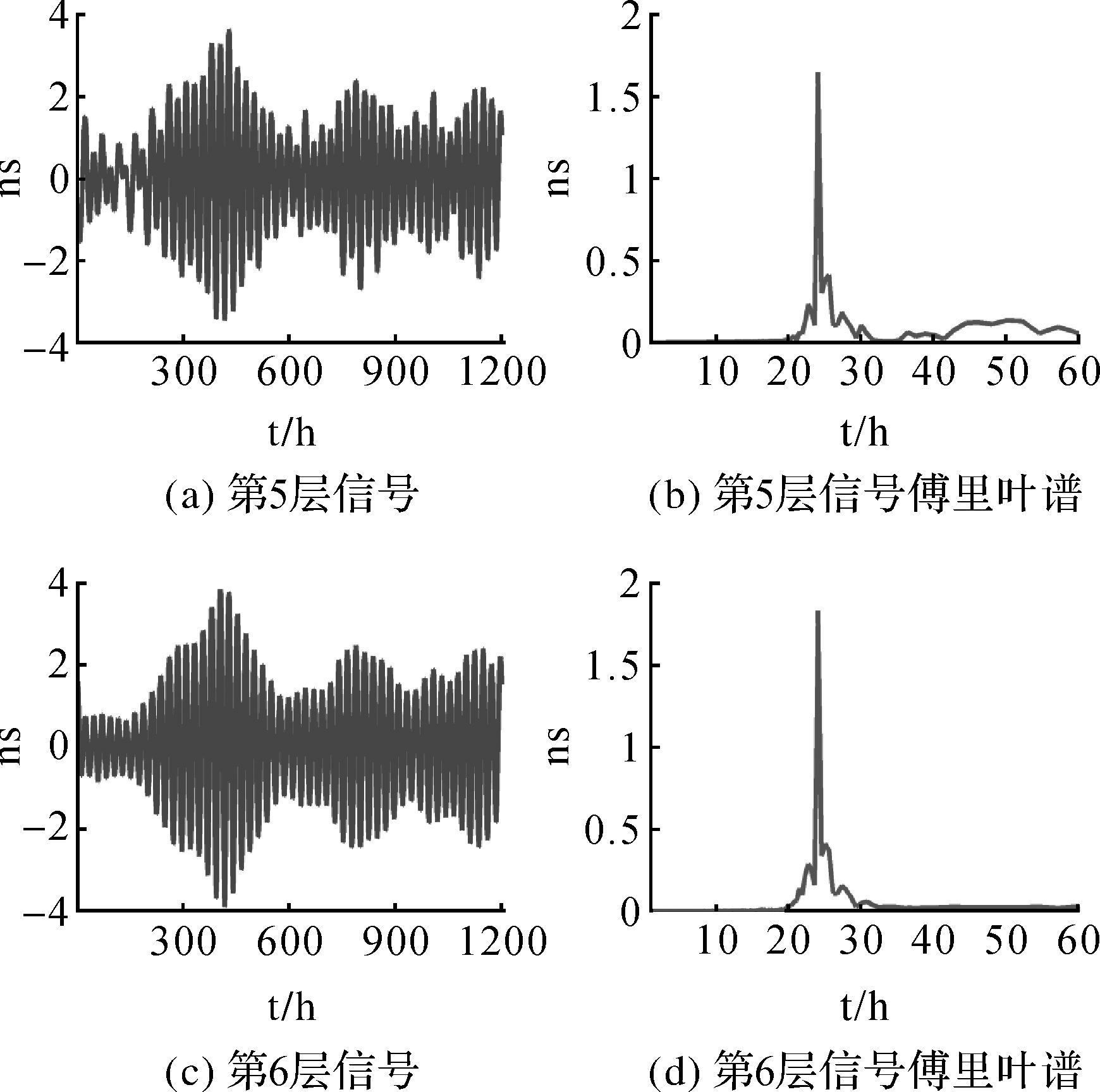
利用SSA方法将仿真信号y(t)分解为6层,得到每层信号及每层信号对应的傅里叶谱,分别见图 2和图 3。
|
| 图 2 SSA分层信号及其谱图(第1层至第4层) Fig. 2 The layer signals of SSA and their Fourier spectrums (the first to forth layer) |
|
| 图 3 SSA分层信号及其谱图(第5层至第6层) Fig. 3 The layer signals of SSA and their Fourier spectrums (the fifth to sixth layer) |
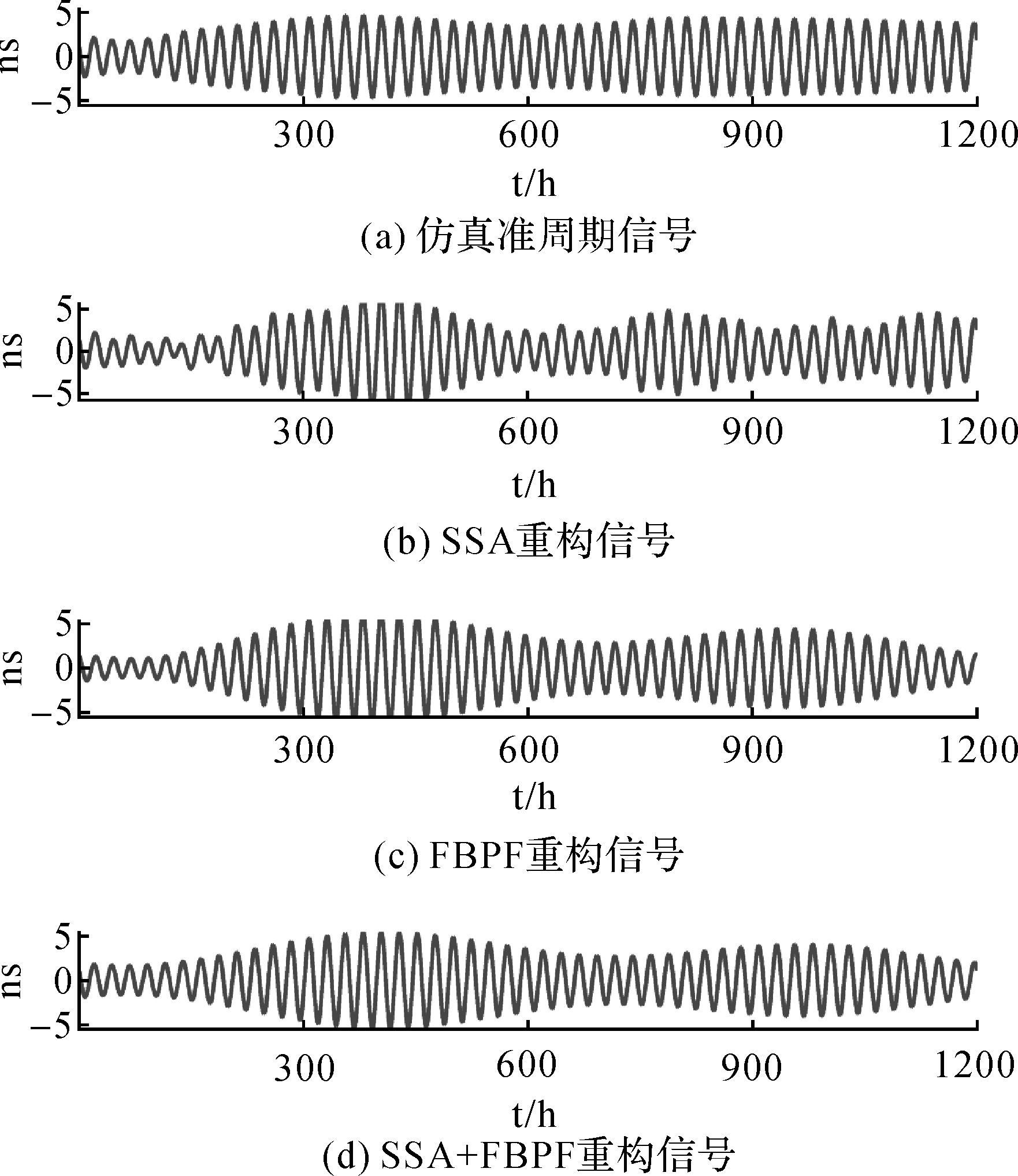
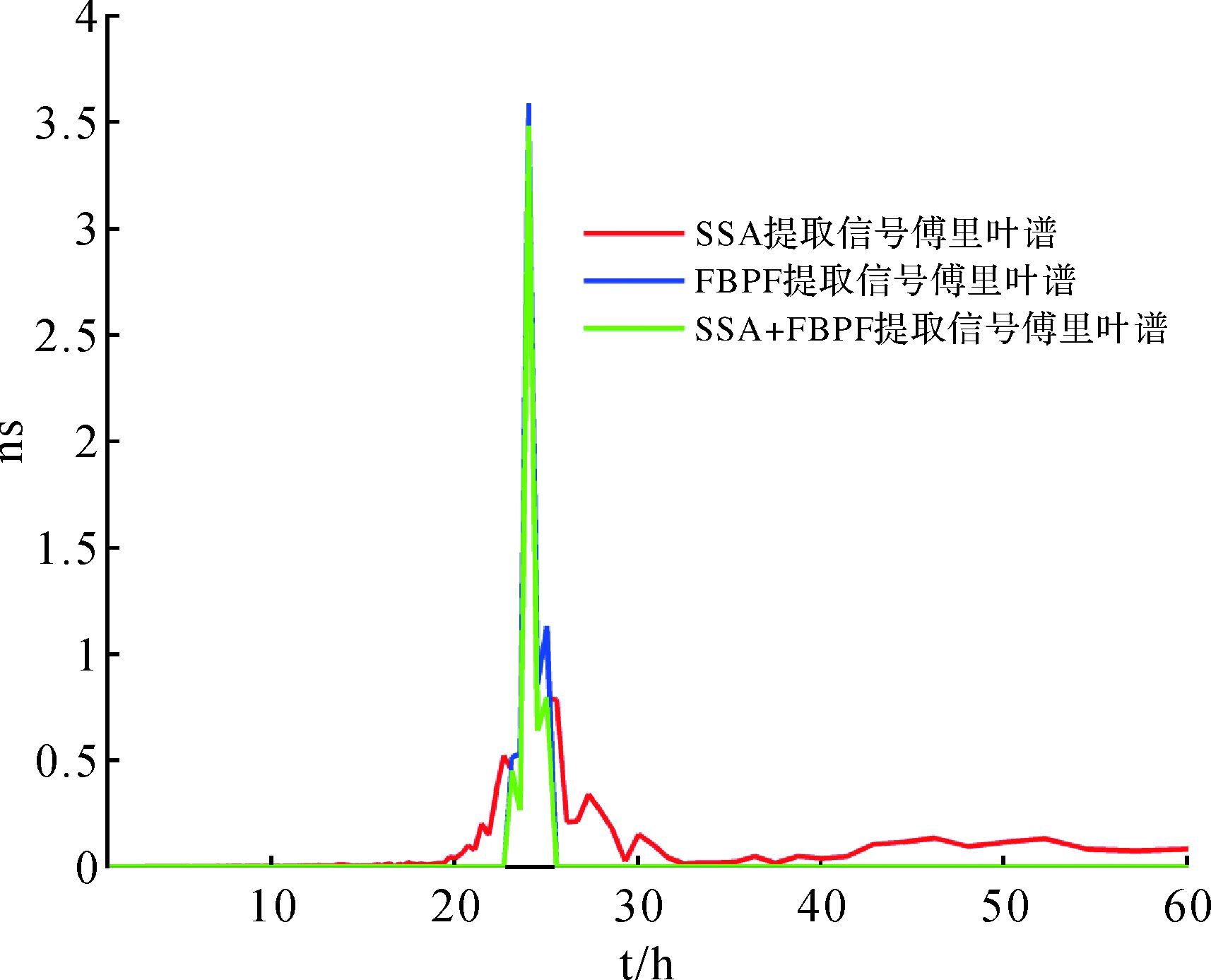
根据每层信号的傅里叶谱图和SSA重构信号原理,选择第5层和第6层子信号进行重构,得到SSA重构信号(见图 4(b))及其傅里叶谱(见图 5中红线部分),对仿真信号通过拟合去线性项后,按照FBPF方法选择周期范围[23, 25]提取得到准周期信号(见图 4(c))及其傅里叶谱(见图 5中蓝线部分),对图SSA得到信号按照式(6) 和式(7) 进行傅里叶带通滤波,选择周期范围为[23, 25],得到新的重建信号(见图 4(d))及其傅里叶谱(见图 5中绿线部分)。SSA重构信号、FBPF提取信号和SSA+FBPF重构信号见图 4,其傅里叶谱见图 5。
|
| 图 4 仿真周期信号、SSA重建信号、FBPF提取信号和SSA+FBPF重建信号比较 Fig. 4 The comparison of the simulation signal and the signals reconstructed by SSA, FBPF and SSA+FBPF |
|
| 图 5 重构信号傅里叶谱比较 Fig. 5 The Fourier spectrums comparison of the reconstructed signals |
从图 5中可以看出,SSA方法提取的信号的谱中出现了明显的多余信号,即在提取周期信号的频段外还包含其他信号,SSA+FBPF方法由于增加了带通滤波功能,显著克服了该问题。
对SSA方法、FBPF方法和SSA+FBPF方法重建信号进行均方根误差计算,得到表 1。
从图 4中可以看出,SSA+FBPF方法重建的信号比SSA方法重建信号具有更好的光滑性,SSA+FBPF重建信号边界值精度比FBPF边界值精度有一定的改善。从表 1中可以看出,SSA+FBPF方法重建信号精度比SSA方法提高了约35%,比FBPF方法提高了26%,说明SSA+FBPF方法比SSA方法具有更好的抗干扰的能力。从图 1(e)中可以看出,仿真信号的趋势项较为复杂,而SSA方法有较好的去趋势项的能力,因此SSA+FBPF取得了比FBPF更好的精度,因此SSA+FBPF方法比FBPF方法具有更好的克服残留趋势项影响的能力。
3 北斗卫星钟差分析和周期项提取北斗卫星导航系统建设当前取得了重要发展,已经陆续发射了18颗北斗二代和4颗北斗三代卫星,这些北斗卫星上的原子钟对整个导航系统的正常运转有着重要作用,因此对这些北斗卫星钟信号特征进行准确评价具有重要意义。
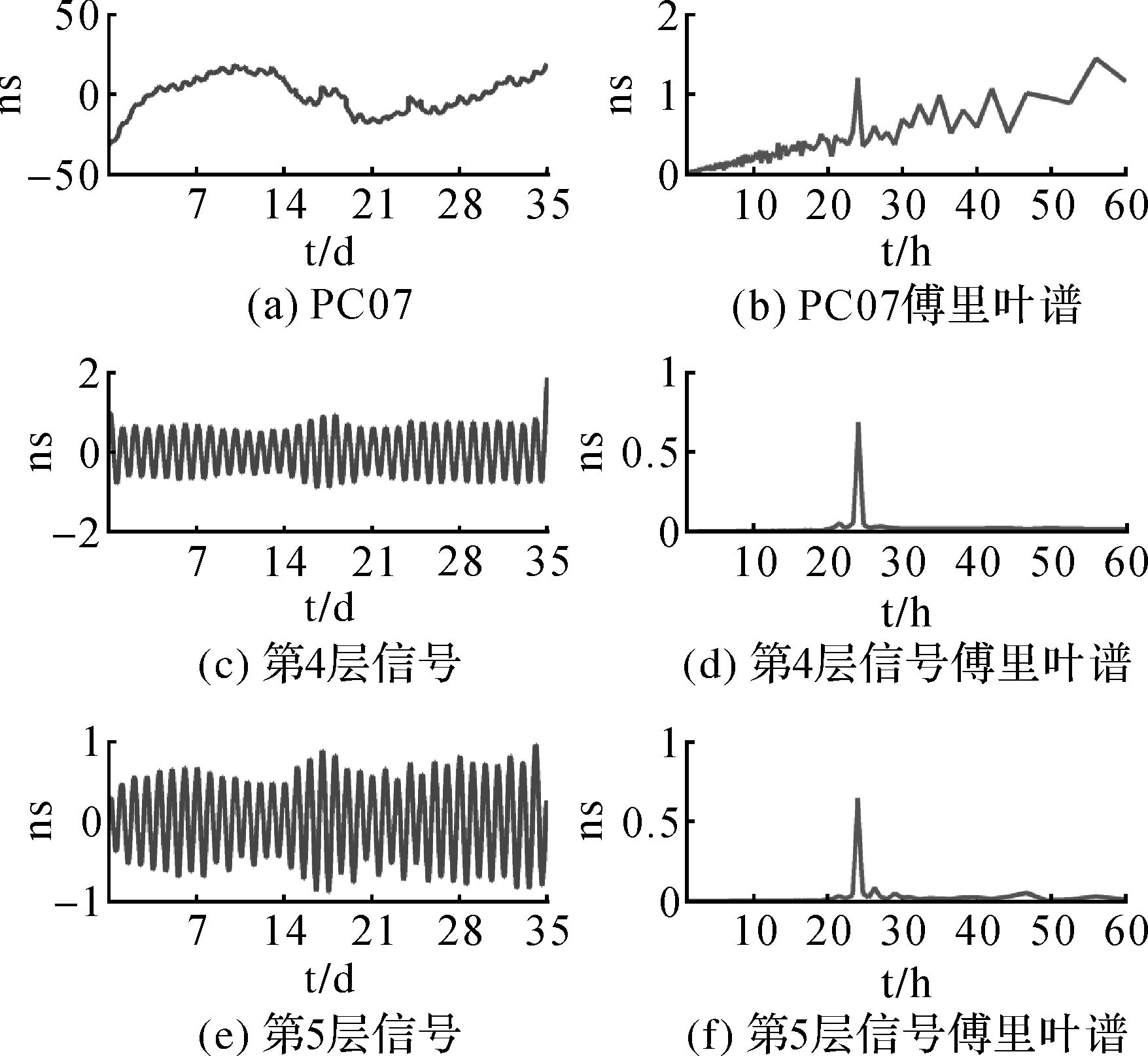
本文选取具有明显周期项特征的PC06和PC07卫星钟进行试验,数据来源于慕尼黑大学(ftp://cddis.gsfc.nasa.gov/gps/products/mgex/)发布的GFZ中心解算的北斗卫星钟差数据,其间隔为5 min,时间范围为2016-08-14—2016-09-17,时间长度为35 d,对其去二次项后得到残差见图 6和图 8,SSA方法、FBPF方法和SSA+FBPF方法分别得到PC06和PC07的周期信号,见图 7和图 9。从图 6和图 8可以看出,PC06和PC07钟差数据边界处仍然含有极为明显的趋势项。分别对PC06和PC07去二次项后残差进行傅里叶谱分析,可以发现PC06和PC07均含有的24 h的周期信号,对二次项后的残差分别进行SSA分层后,根据每层的傅里叶谱,选取含有24 h信号的分解层进行重构。从图 6中可以看出,SSA方法选择第5层和第6层信号重建PC06卫星钟含有的24 h信号,从图 8中可以看出,SSA方法选择第4层和第5层信号重建PC07卫星钟含有的24 h信号。
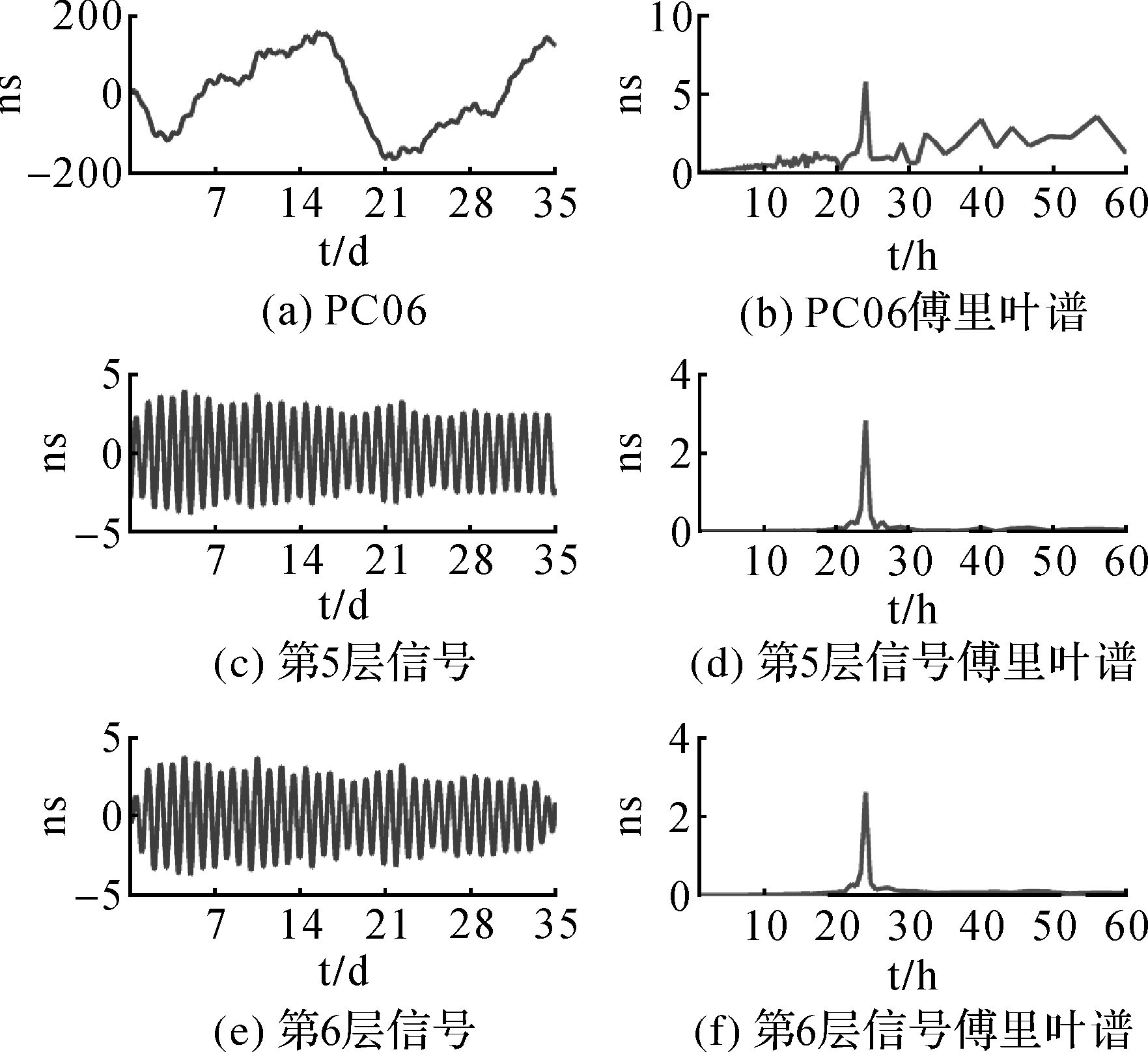
|
| 图 6 PC06去二次项残差、SSA分解第5层和第6层信号及其傅里叶谱 Fig. 6 The residual signal of PC06 removed quadratic term, the fifth to sixth layer signals of SSA and their Fourier spectrums |
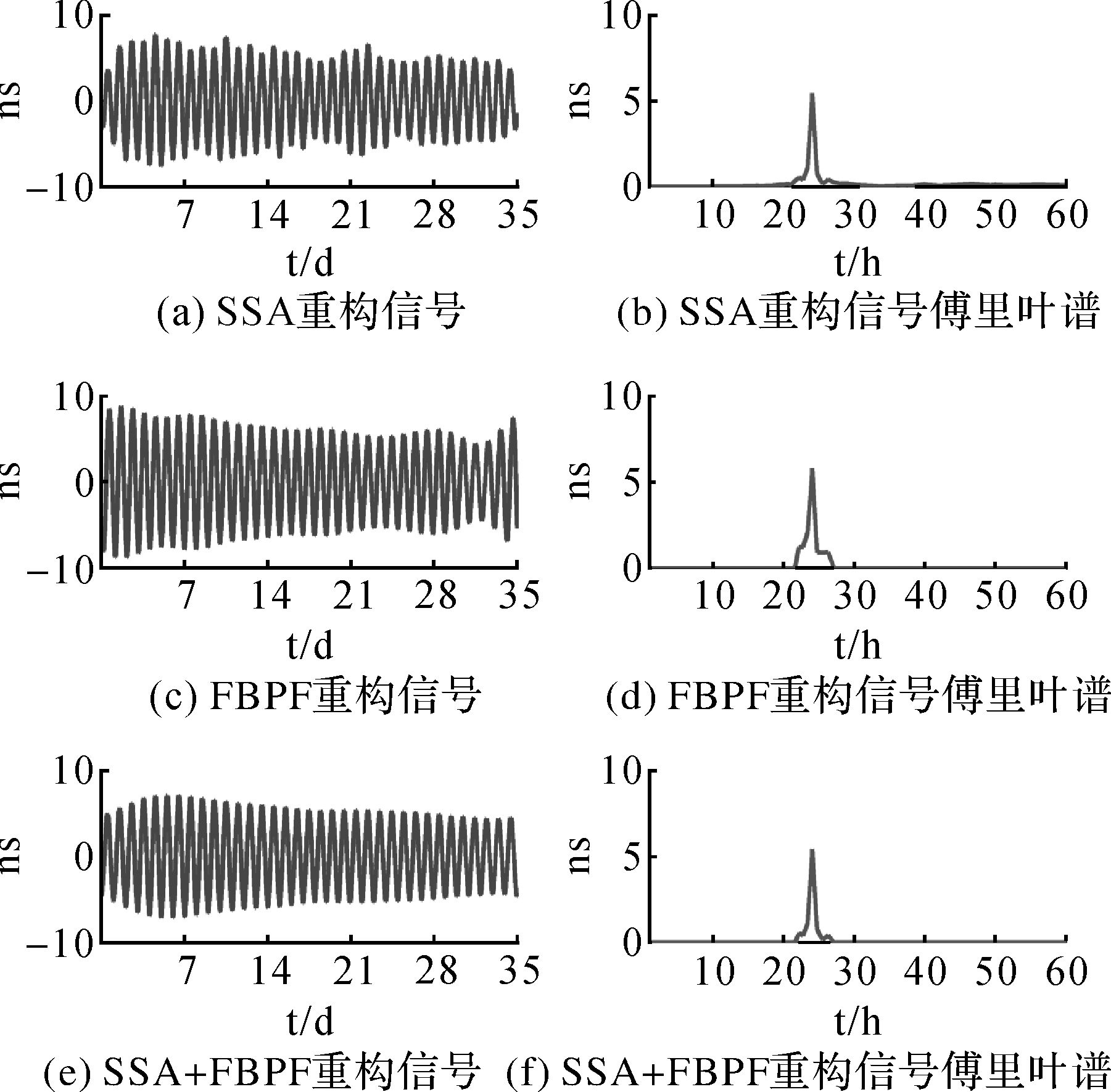
|
| 图 7 SSA、FBPF和SSA+FBPF方法重建PC06的周期项及周期项傅里叶谱比较 Fig. 7 The signals of PC06 reconstructed by SSA, FBPF and SSA+FBPF, and their Fourier spectrums |
|
| 图 8 PC07去二次项后残差、SSA分解第4层和第5层信号及其傅里叶谱 Fig. 8 The residual signal of PC07 removed quadratic term, the fourth to fifth layer signals of SSA and their Fourier spectrums |
|
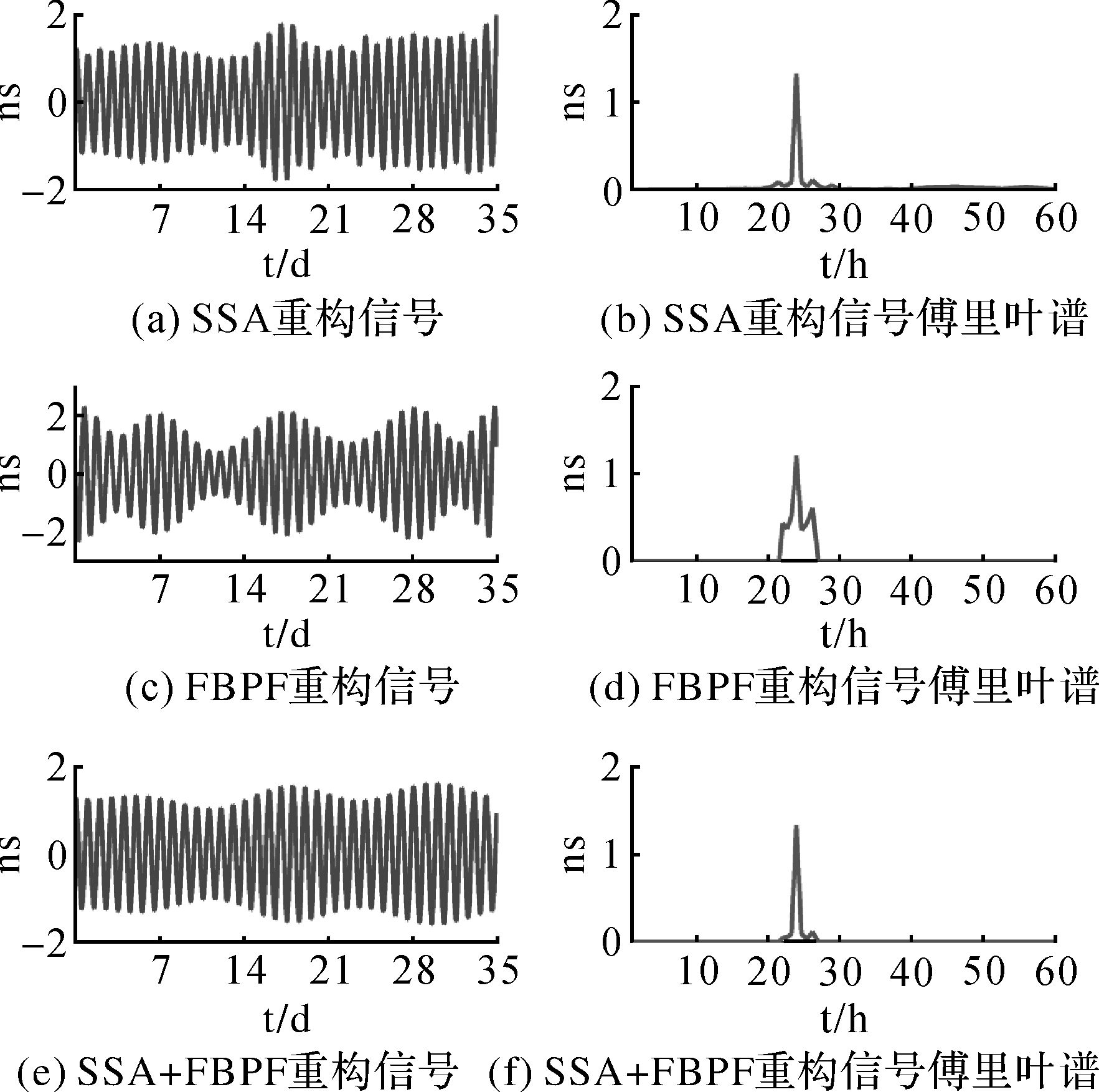
| 图 9 SSA、FBPF和SSA+FBPF方法重建PC07的周期项及周期项傅里叶谱比较 Fig. 9 The signals of PC07 reconstructed by SSA, FBPF and SSA+FBPF, and their Fourier spectrums |
从图 7和图 9中可以看出,SSA重构的周期信号呈现出杂乱现象,明显受到了噪声干扰,FBPF方法重建信号右端边界值存在明显异常,只有SSA+FBPF重构的信号呈现出明显的光滑性,说明SSA+FBPF方法较好地克服了噪声的干扰,得到的准周期信号更具有真实性。
从图 7和图 9中SSA+FBPF重建的24 h周期项可以看出,北斗卫星钟PC06含有的24 h周期项幅值大约为PC07含有的24 h周期项幅值的3倍,它们的幅值均存在明显的变化。
4 结论针对SSA分解信号存在频率混叠的情况,FBPF提取准周期信号存在易被残留趋势项影响的现象,本文采用SSA+FBPF方法,即充分利用SSA分解信号有较好的去趋势项能力的特点,又利用FBPF方法能有效消除指定周期范围外噪声影响的能力。仿真数据试验证明SSA+FBPF方法既克服了SSA分解信号存在频率混叠的情况,又减少了残留趋势项对提取准周期信号边界值精度的影响。利用该方法分析慕尼黑大学发布的北斗卫星钟PC06和PC07,有效提取了其存在的24 h的周期项,并且分析发现其幅值存在着明显的变化,这对下一步提高北斗卫星钟差的预报和实时应用有着重要的意义。
| [1] | GONZALEZ MARTINEZ F J. Performance of New GNSS Satellite Clocks[M]. Karlsruhe: KIT Scientific Publishing, 2013. |
| [2] | SENIOR K L, RAY J R, BEARD R L. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solutions, 2008, 12(3): 211–225. DOI:10.1007/s10291-008-0089-9 |
| [3] | 黄观文. GNSS星载原子钟质量评价及精密钟差算法研究[D]. 西安: 长安大学, 2012. HUANG Guanwen. Research on Algorithms of Precise Clock Offset and Quality Evaluation of GNSS Satellite Clock[D]. Xi'an:Chang'an University, 2012. |
| [4] | 周佩元, 杜兰, 路余, 等. 多星定轨条件下北斗卫星钟差的周期性变化[J]. 测绘学报, 2015, 44(12): 1299–1306. ZHOU Peiyuan, DU Lan, LU Yu, et al. Periodic Variations of BeiDou Satellite Clock Offsets Derived from Multi-satellite Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1299–1306. DOI:10.11947/j.AGCS.2015.20150183 |
| [5] | 张杰, 周渭, 宣宗强, 等. 卫星钟差预报模型中周期项的选取方法及性能分析[J]. 天文学报, 2013, 54(3): 282–290. ZHANG Jie, ZHOU Wei, XUAN Zongqiang, et al. Selection of Periodic Items and Its Performance in the Forcasting Model of Satellite Clock Bias[J]. Acta Astronomica Sinica, 2013, 54(3): 282–290. |
| [6] | CHEN Q, VAN DAM T, SNEEUW N, et al. Singular Spectrum Analysis for Modeling Seasonal Signals from GPS Time Series[J]. Journal of Geodynamics, 2013(72): 25–35. |
| [7] | POPIИSKI W, KOSEK W. The Fourier Transform Band Pass Filter and Its Application for Polar Motion Analysis[J]. Artificial Satellites, Planetary Geodesy No 24, 1995, 30(1): 9–25. |
| [8] | VAUTARD R, YIOU P, GHIL M. Singular-Spectrum Analysis:A Toolkit for Short, Noisy Chaotic Signals[J]. Physica D:Nonlinear Phenomena, 1992, 58(1-4): 95–126. DOI:10.1016/0167-2789(92)90103-T |
| [9] | 王解先, 连丽珍, 沈云中. 奇异谱分析在GPS站坐标监测序列分析中的应用[J]. 同济大学学报(自然科学版), 2013, 4(2): 282–288. WANG Jiexian, LIAN Lizhen, SHEN Yunzhong. Application of Singular Spectral Analysis to GPS Station Coordinate Monitoring Series[J]. Journal of Tongji University (Natural Science), 2013, 4(2): 282–288. |
| [10] | 卢辰龙. 奇异谱分析在大地测量时间序列分析中的应用研究[D]. 长沙: 中南大学, 2014. LU Chenlong. Research on Application of Singular Spectrum Analysis in Geodetic Survey Time Series[D]. Changsha:Central South University, 2014. |
| [11] | 卢辰龙, 匡翠林, 易重海, 等. 奇异谱分析滤波法在消除GPS多路径中的应用[J]. 武汉大学学报(信息科学版), 2015, 40(7): 924–931. LU Chenlong, KUANG Cuilin, YI Zhonghai, et al. Singular Spectrum Analysis Filter Method for Mitigation of GPS Multipath Error[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 924–931. |
| [12] | ALEXANDROV T. A Method of Trend Extraction Using Singular Spectrum Analysis[J]. arXiv:preprint arXiv:0804.3367, 2008. |
| [13] | 徐克红, 程鹏飞, 文汉江. 太阳黑子数时间序列的奇异谱分析和小波分析[J]. 测绘科学, 2007, 32(6): 35–38. XU Kehong, CHENG Pengfei, WEN Hanjiang. Singular Spectrum Analysis and Wavelet Analysis on Time Series of Sunspot[J]. Science of Surveying and Mapping, 2007, 32(6): 35–38. |
| [14] | 罗勇, 匡翠林, 卢辰龙, 等. 基于SSA的GPS坐标序列去噪及季节信号提取[J]. 大地测量与地球动力学, 2015, 35(3): 391–395. LUO Yong, KUANG Cuilin, LU Chenlong, et al. GPS Coordinate Series Denoising and Seasonal Signal Extraction Based on SSA[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 391–395. |
| [15] | XU Chang, YUE Dongjie. Monte Carlo SSA to Detect Time-variable Seasonal Oscillations from GPS-derived Site Position Time Series[J]. Tectonophysics, 2015(665): 118–126. |
| [16] | RANGELOVA E, SIDERIS M G, KIM J W. On the Capabilities of the Multi-Channel Singular Spectrum Method for Extracting the Main Periodic and Non-Periodic Variability from Weekly GRACE Data[J]. Journal of Geodynamics, 2012(54): 64–78. |
| [17] | MALKIN Z, MILLER N. Chandler Wobble:Two More Large Phase Jumps Revealed[J]. Earth, Planets and Space, 2010, 62(12): 943–947. DOI:10.5047/eps.2010.11.002 |
| [18] | CHRISTIANO L J, FITZGERALD T J. The Band Pass Filter[J]. International Economic Review, 2003, 44(2): 435–465. DOI:10.1111/iere.2003.44.issue-2 |
| [19] | BROOMHEAD D S, KING G P. Extracting Qualitative Dynamics from Experimental Data[J]. Physica D:Nonlinear Phenomena, 1986, 20(2-3): 217–236. DOI:10.1016/0167-2789(86)90031-X |
| [20] | VAUTARD R, GHIL M. Singular Spectrum Analysis in Nonlinear Dynamics, with Applications to Paleoclimatic Time Series[J]. Physica D:Nonlinear Phenomena, 1989, 35(3): 395–424. DOI:10.1016/0167-2789(89)90077-8 |
| [21] | VAUTARD R, YIOU P, GHIL M. Singular-Spectrum Analysis:A Toolkit for Short, Noisy Chaotic Signals[J]. Physica D:Nonlinear Phenomena, 1992, 58(1-4): 95–126. DOI:10.1016/0167-2789(92)90103-T |
| [22] | ALEXANDROV T. A Method of Trend Extraction Using Singular Spectrum Analysis[J]. arXiv preprint arXiv:0804.3367, 2008. |



