2. 中国天绘卫星中心, 北京 102102;
3. 信息工程大学地理信息学院, 河南 郑州 450002;
4. 31002部队, 北京 100195
2. China Aerospace Surveying and Mapping Satellite Center, Beijing 102102, China;
3. Institute of Surveying and Mapping, Information Engineering University, Zhengzhou 450002, China;
4. The 31002 Troops, Beijing 100695, ChinaAbstract
卫星导航定位过程中,因导航系统、接收机型号、卫星高度角、测量模式和环境等观测条件不同,导致难以找到一个普遍适用的随机模型进行平差解算[1]。目前较常用随机模型建模方法主要有等权法、卫星高度角函数法和基于验后残差法[2]。等权法较简单,往往不能真实反映测量情况,故高精度定位应用较少;基于卫星高度角越高,信号传播过程中受到的电离层延迟、对流层延迟以及多路径误差越小的反比关系,文献[3-5]针对基于卫星高度角函数确定随机模型的方法进行了深入系统研究; 文献[6-7]基于验后残差分析法对GPS观测值精度进行了估计。除以上静态观测随机模型估计外,文献[2, 8]提出了实时估计动态观测量先验方差-协方差矩阵的方法。以上随机模型,多由基线差分解算得到,是多颗卫星随机特性的统计结果,无法反映单星观测误差特性。为此文献[9]基于单频伪距/载波无几何组合观测对单站单星伪距观测噪声进行了估计。为分析观测值随机模型的相关性,文献[10—12]提出基于三频无几何无电离层组合的方法,实现了对GNSS三频非差观测量协方差矩阵的估计。
为充分发挥目前北斗作为唯一可用三频导航系统的优势,本文旨在研究能够为标准伪距定位(SPS)提供更准确随机模型的目的,通过构建三频伪距/载波无几何无电离层组合特性尽可能消除电离层延迟、与几何相关项对伪距观测精度估计的影响,然后借鉴多元线性回归模型进一步削弱多路径、电离层残差等非观测噪声误差,并通过建立三频伪距/载波GIF组合随机模型,最后实现非差北斗三频伪距相关随机模型的单站估计,以为北斗伪距导航定位提供更精确随机模型。
1 北斗三频伪距/载波GIF组合首先,给出原始伪距、载波观测方程
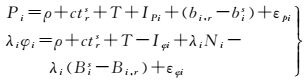 (1)
(1)
式中,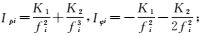
要估计非差三频伪距观测精度,应尽可能消除电离层、对流层、钟差、硬件延迟等对伪距精度估计的影响。根据三频组合理论,构建三频伪距/载波无几何无电离层组合,可消除与几何距离有关误差项,也能消除电离层延迟一阶项[13-14],通用GIF组合表达式为
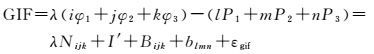 (2)
(2)
式中
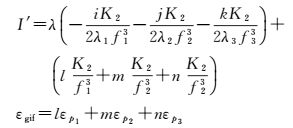
式中,λ和Nijk分别为GIF组合波长和组合模糊度;blmn和Bijk为组合后伪距和载波相位硬件延迟,I′为电离层延迟高阶项残差,εgif为忽略载波观测噪声后的组合伪距观测噪声。
为保证无几何无电离层条件,GIF组合系数必须满足以下条件
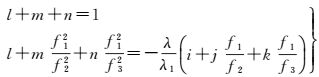 (3)
(3)
若利用式(2) 构造3个线性无关的GIF组合,并分别求解各自组合的观测噪声εgif,即可通下式解算得到每个频点伪距观测噪声
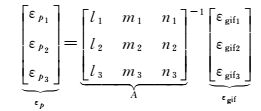 (4)
(4)
由此,原始三频伪距观测噪声估计即可转化为3个GIF组合的伪距噪声解算问题。由式(2) 可知,未发生周跳情况下,三频GIF组合除伪距观测噪声以外,仍然存在整周模糊度、硬件延迟、电离层残差以及多路径误差等。若能采用一定方法进一步改正或消除3个线性无关GIF组合剩余的非噪声观测误差,则可实现非差伪距观测精度估计。
双频MW组合既可以消除电离层延迟又可以消除与几何相关误差项影响,为此可将MW组合看作特殊的三频伪距/载波GIF组合,其表达式为
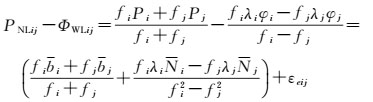 (5)
(5)
式中,i, j∈(1, 2, 3) 且i≠j;b和N为组合后硬件延迟和整周模糊度。
式(5) 得到的伪距/载波GIF组合最多只能保证两个线性无关,还需构造另外一个三频伪距/载波GIF组合。若对载波无电离层组合与伪距无电离层组合进行差分,同样可实现无几何无电离层组合
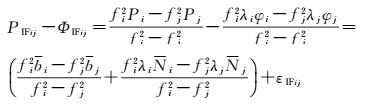 (6)
(6)
下面给出利用式(5) 和式(6) 得到的伪距/载波GIF组合,具体如表 1所示。
| 编号 | 观测组合 | 伪距组合系数 | 以周为单位的载波相位组合系数 |
| 1 | PNL12-ΦWL12 | [f1/(f1+f2) f2/(f1+f2) 0] | [-f1λ1/(f1-f2) f2λ2/(f1-f2) 0] |
| 2 | PNL13-ΦWL13 | [f1/(f1+f3) 0 f3/(f1+f3)] | [-f1λ1/(f1-f3) 0 f3λ3/(f1-f3)] |
| 3 | PNL23-ΦWL23 | [0 f2/(f2+f3) f3/(f2+f3)] | [0 -f2λ2/(f2-f3) f3λ3/(f2-f3)] |
| 4 | PIF12-ΦIF12 | [f12/(f12-f22) -f22/(f12-f22) 0] | [-f12λ1/(f12-f22) f22λ2/(f12-f22) 0] |
| 5 | PIF13-ΦIF13 | [f12/(f12-f22) 0 -f32/(f12-f32)] | [-f12λ1/(f12-f32) 0 f32λ3/(f12-f32)] |
| 6 | PIF23-ΦIF23 | [0 f22/(f22-f32) -f32/(f22-f32)] | [0 -f22λ2/(f22-f32) f32λ3/(f32-f32)] |
从表 1选择3个线性无关的三频伪距/载波GIF组合即可通过式(4) 单站解算顾及各频点观测值相关性的伪距观测值的随机模型。
2 基于多元回归分析建模根据研究,短时间电离层延迟残差、硬件延迟变化缓慢[15-16],多路径误差则是一个长周期零均值正弦变化信号,若GNSS持续观测过程中,未发生周跳和钟跳,可采用多项式拟合法对硬件延迟、多路径效应低阶项误差和电离层延迟误差和整周模糊度进行拟合建模,以消除其对观测噪声估计的影响。针对三频GIF组合除单个组合采用多项式分别拟合以外,还可采用多元线性回归分析的方法同时对三频GIF组合进行拟合解算。具体多元线性回归拟合模型如下
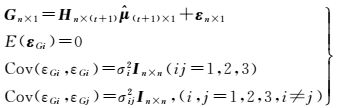 (7)
(7)
式中

式中,gifin(i=1, 2, 3) 为第n历元第i个GIF组合;μi0为第i个GIF组合回归系数;x代表观测历元差值, t为拟合阶数,为保证满秩要求n>t。
利用最小二乘估计上式回归系数
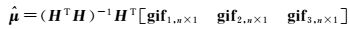 (8)
(8)
此时,残差矩阵
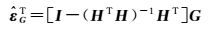 (9)
(9)
对式(9) 残差统计得到方差-协方差阵∑G
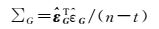 (10)
(10)
此时原始伪距方差-协方差∑εP为
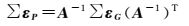 (11)
(11)
由式(11) 可知利用3个伪距/载波GIF组合得到的原始频点观测噪声存在数学相关性。利用以上算法即可得到一段观测历元的伪距观测随机模型。
通常情况下,数据样本越多越能真实反映样本总体统计特性,但随着拟合数据的增多,历元间电离层延迟以及硬件延迟等误差变化逐渐增大,导致拟合效果变差。为此针对不同的观测条件需要选择合适的样本历元。由于不同接收机所处的观测环境不同、所观测的各卫星高度角不同,会造成每颗卫星观测信号的电离层延迟误差和多路径效应不同,因而式(7) 中拟合阶数难以设置为固定值。若拟合阶数较低则难以反映GIF组合变化趋势,若拟合阶数过多可能会出现龙格现象。根据拟合应能最佳反映式(2) 中变化趋势的拟合原理,在拟合样本数目n确定情况下,最佳拟合阶数应使拟合值与实际观测值误差最小,即
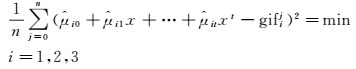 (12)
(12)
实际观测中,随着观测时间的推移电离层延迟、多路径、观测噪声等虽变化缓慢但仍在不断变化,为能准确反映观测噪声实时变化,可采用滑动窗口方法计算每个历元的伪距观测方差-协方差矩阵
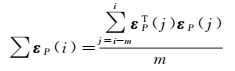 (13)
(13)
式中, m为滑动窗口历元数。
以上基于三频伪距/载波GIF组合得到的三频伪距随机模型,无需基线差分,能尽可能消除非观测误差对伪距观测精度估计的影响,多元回归分析建模顾及了观测值间相关性,可实现非差伪距相关随机模型的单站估计。
3 数据分析采用IGS BYHN站点TRIMBLE NETR9接收机观测到的BDS三频数据进行伪距观测噪声分析,采样间隔30 s,卫星截止高度角10°,设定滑动窗口计算单历元观测噪声时拟合历元数为60。首先针对表 1中不同三频伪距/载波GIF组合得到的伪距噪声随机模型进行比较分析,验证多元回归分析有效性;然后通过计算单历元伪距噪声随机模型,比较相同观测条件下同颗卫星不同频点伪距观测值精度以及相关性,并通过与信噪比SNR指标进行对比分析,验证快速伪距随机模型的有效性。
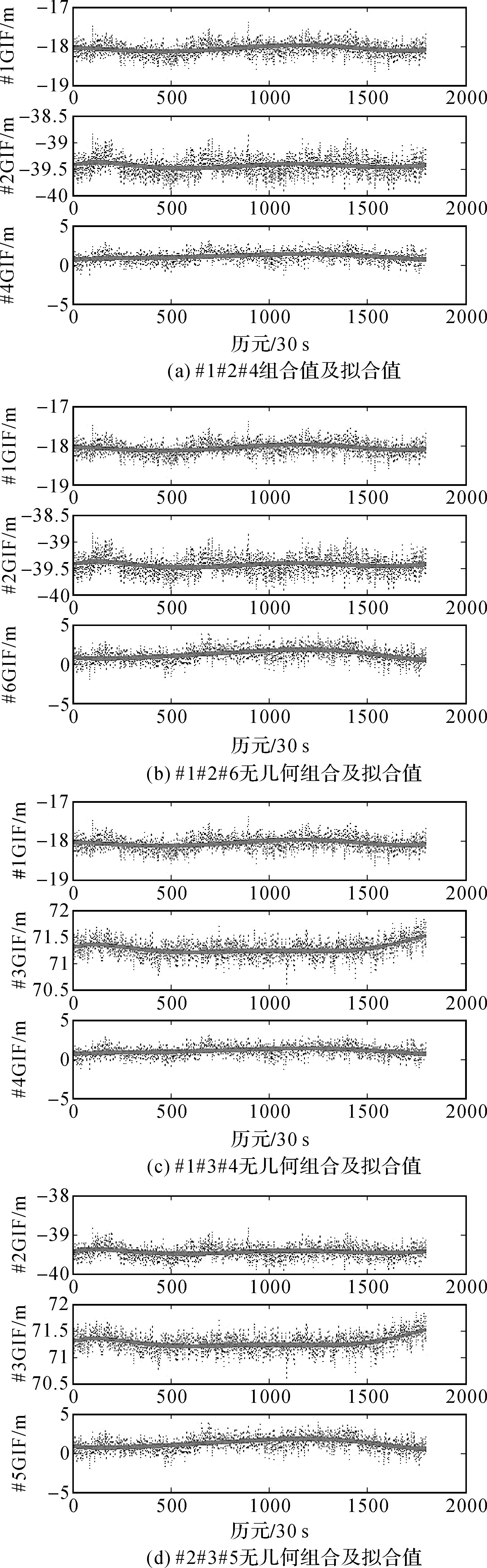
3.1 多元回归分析有效性采用表 1中#1#2#4、#1#2#5、#1#3#4和#2#3#5 4种三频伪距/载波GIF组合对BYHN站点观测到的C02卫星1800历元的伪距噪声进行总体随机模型建模。图 1为利用4种不同算法得到的原始伪距/载波GIF组合值(虚线所示)和多元回归拟合值(实线所示),计算得到的原始伪距噪声方差-协方差阵如表 2所示。
| GIF组合 | 伪距协方差阵 | ||
| #1#2#4 | 0.081 | 0.003 | 0.004 |
| 0.003 | 0.029 | 0.017 | |
| 0.004 | 0.017 | 0.022 | |
| #1#2#5 | 0.081 | 0.003 | 0.004 |
| 0.003 | 0.029 | 0.017 | |
| 0.004 | 0.017 | 0.022 | |
| #1#3#4 | 0.081 | 0.003 | 0.005 |
| 0.003 | 0.029 | 0.017 | |
| 0.005 | 0.017 | 0.032 | |
| #2#3#5 | 0.081 | 0.003 | 0.004 |
| 0.003 | 0.043 | 0.015 | |
| 0.004 | 0.015 | 0.022 | |
|
| 图 1 不同组合解算C02伪距随机模型 Fig. 1 C02 pseudo-range sochastic model computing by different GIF combinations |
从图 1中三频伪距/载波GIF组合观测值相对于拟合值的波动来看,各伪距/载波GIF组合的观测误差不同,但解算求得原始频点伪距方差-协方差矩阵基本一致,见表 2。除#1#2#4组合得到的B3伪距方差稍外,其他伪距噪声方差基本相同,并且不同组合算法得到的伪距间相关系数也基本一致,由此可见多元回归分析对三频伪距/载波GIF组合剩余模糊度、电离层延迟高阶项以及硬件延迟等误差建模较好。以上基于三频伪距/载波GIF组合的伪距观测随机模型建模方法,无需基线解算便可实现单站单星伪距观测随机模型的快速建模,并且能够顾及各频率间伪距观测值的相关性。
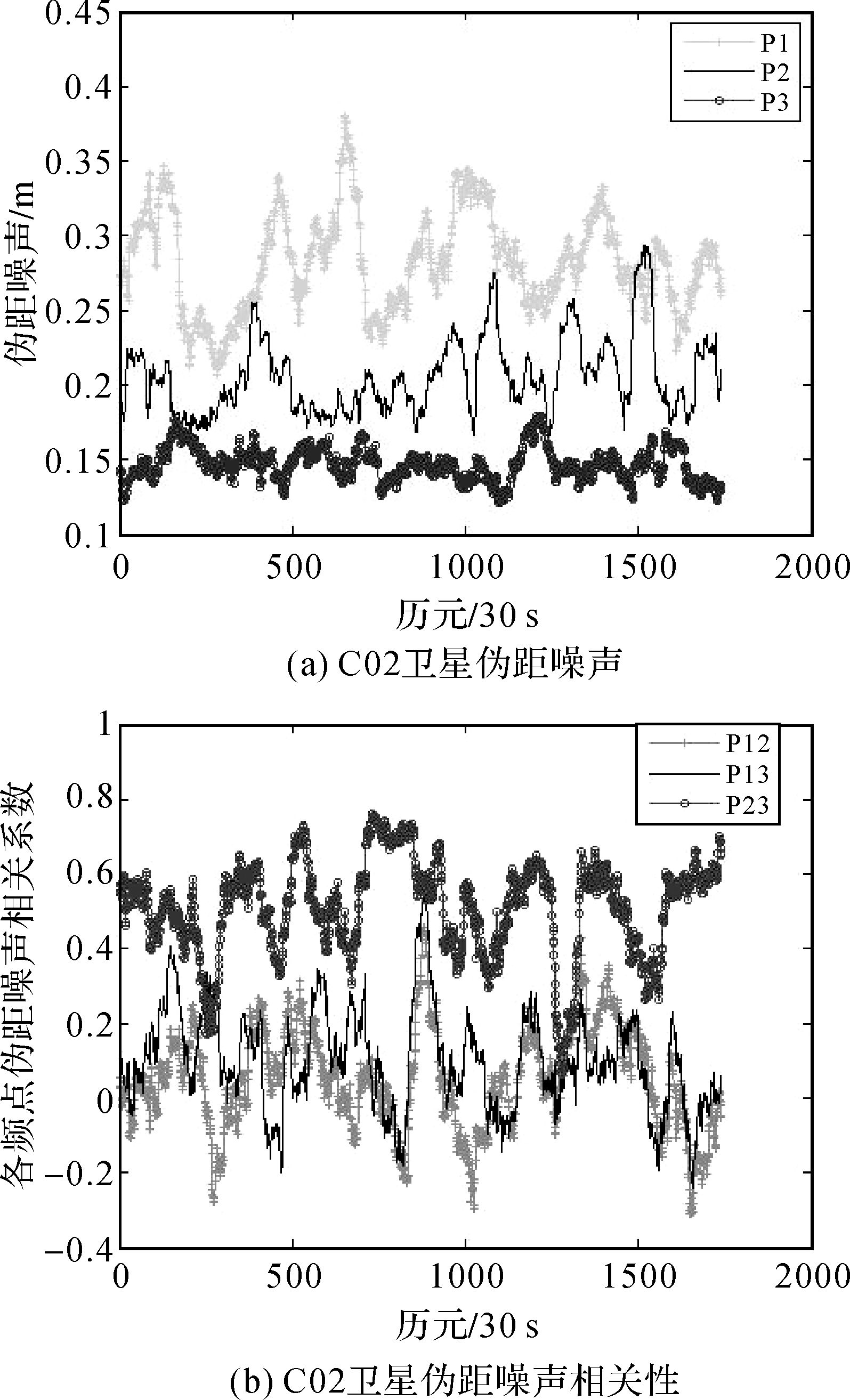
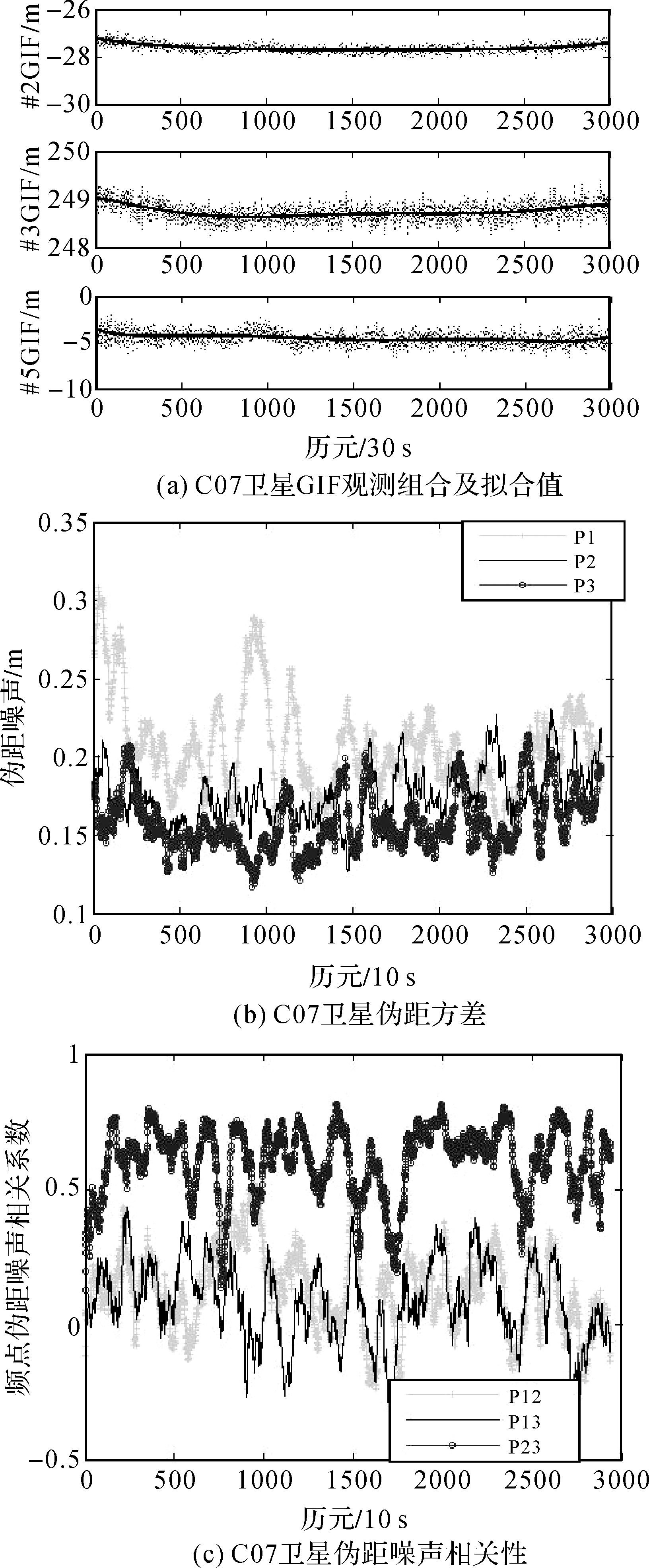
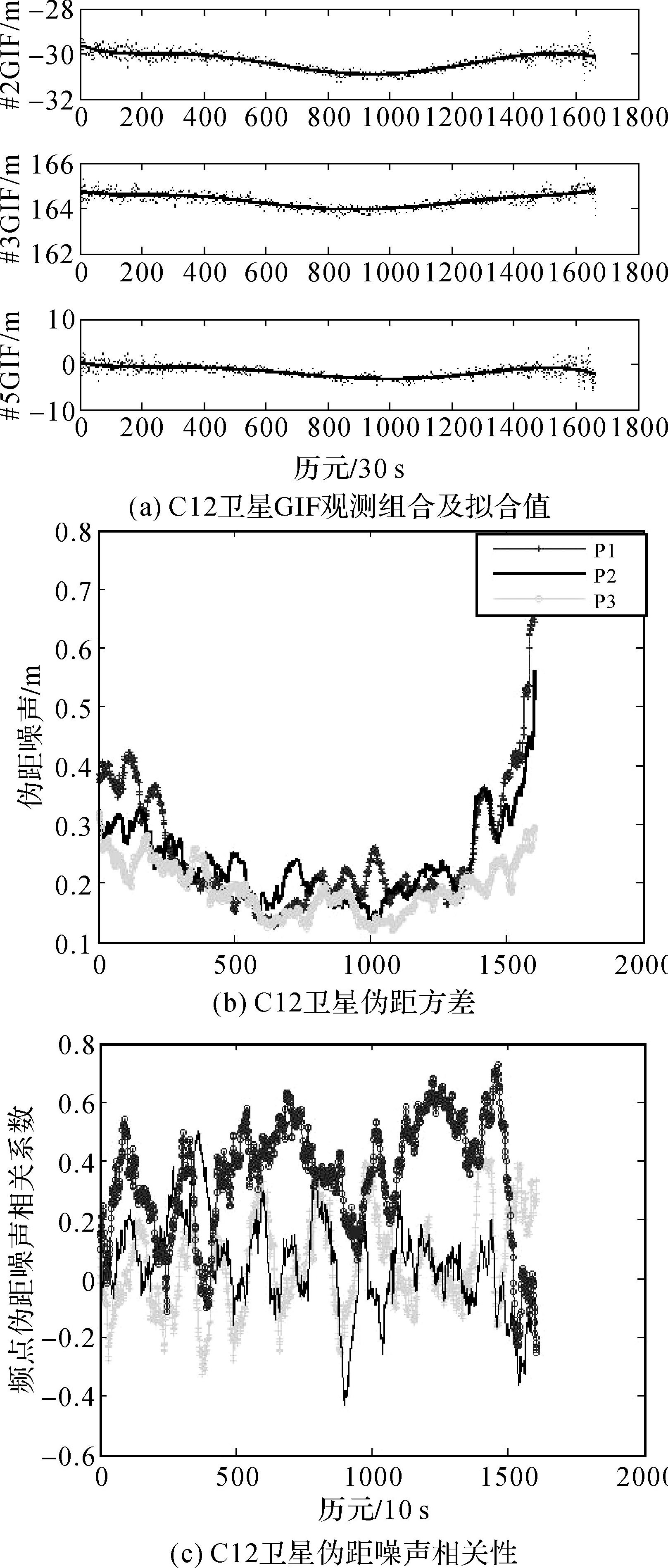
3.2 单历元伪距随机模型解算以#2#3#5组合为例,进一步对北斗GEO卫星C02、IGSO卫星C07和MEO卫星C12基于三频伪距/载波GIF组合求解伪距观测随机模型算法进行分析,对应解算结果分别如图 2—4所示。
|
| 图 2 C02卫星观测精度分析 Fig. 2 Precision analysis of C02 satellite observation |
|
| 图 3 C07卫星观测精度分析 Fig. 3 Precision analysis of C07 satellite observations |
|
| 图 4 C12卫星观测精度分析 Fig. 4 Precision analysis of C12 satellite observations |
对图 2至图 4同一颗卫星3个频点的伪距噪声对比分析可知,本试验中BDS卫星中GEO-C02、IGSO-C07和MEO-C12卫星中B3频点伪距精度最高,B2频点伪距次之,B1频点最差。在相同观测环境下各频点伪距精度不同主要是由于各频点采用的调制解调方式及卫星信号通道不同,下面给出实验数据中的各类观测值类型,具体如下表 3所示。
| 频点 | B1 | B2 | B3 |
| 观测值类型 | C2X & L2X | C7X & L7X | C6X & L6X |
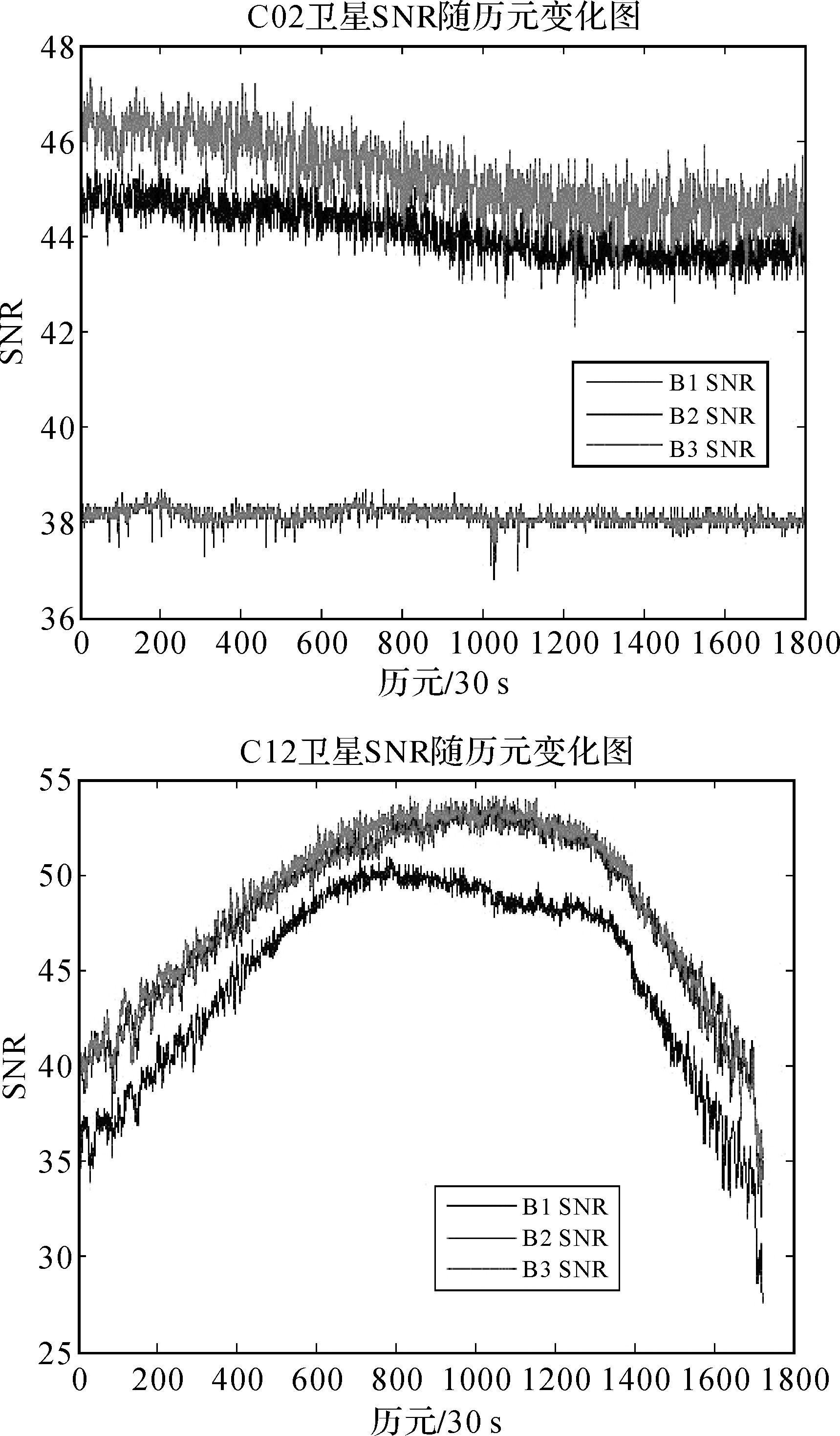
由图 2和图 3可以看出,C02与C07卫星各频点伪距噪声趋势大致相同,而C12卫星噪声明显存在较大趋势性变化。为验证该算法能够反映伪距精度实时变化,特给出C02和C12卫星SNR值变化值,具体如图 5所示。
|
| 图 5 C02和C12卫星SNR变化图 Fig. 5 The SNR variations of C02 and C12 satellites |
C02星中最上方曲线B3频点SNR最大,中间曲线B2频点SNR次之,而最下方的B1频点SNR最小,而基于三频伪距/载波GIF组合得到的各频点观测噪声恰好是B3频点噪声最小,B2次之,B1频点最差,由此证明了基于三频GIF组合的伪距观测噪声分析方法能够真实地反映信号观测质量。此外,C02卫星三个频点观测噪声不同也说明仅仅利用卫星高度角函数反映观测噪声的方法无法区分各频点观测噪声差异。同样C12卫星最上方曲线B3频点SNR最大与B3伪距噪声最小,而最小方曲线B2频点SNR最小与B2伪距噪声相对偏大相对应,而伪距噪声先减小后增大与SNC变化曲线正好成反比,B1频点曲线在B3频点下方几乎与B3频点重合。由此,可见基于3个线性无关的三频伪距/载波GIF组合可对单站单星的伪距观测随机模型进行实时建模,且其解算结果变化趋势与信号SNR变化趋势保持一致。
4 结论通过滑动窗口多元回归分析对3个线性无关的三频伪距/载波GIF组合残差拟合的方法,可实现顾及伪距观测值间相关性的随机模型实时建模。基于三频伪距/载波GIF组合的观测值精度分析算法无需基线差分,通过单站组合观测即可实现观测质量的估计,使得为导航定位、接收机完好性实时监测等应用提供实时准确的随机误差模型成为可能。
| [1] | 李博峰. 混合整数GNSS函数模型及随机模型参数估计理论与方法[D]. 上海: 同济大学, 2010. LI Bofeng. Theory and Method of Parameter Estimation for Mixed Integer GNSS Function and Stochastic Models[D]. Shanghai:Tongji University, 2010. |
| [2] | 何海波, 杨元喜. GPS观测量先验方差-协方差矩阵实时估计[J]. 测绘学报, 2001, 30(1): 42–47. HE Haibo, YANG Yuanxi. Real-time Estimation of a Prior Variance-Covariance for GPS Observations[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 42–47. DOI:10.3321/j.issn:1001-1595.2001.01.009 |
| [3] | EUELER H J, GOAD C C. On Optimal Filtering of GPS Dual Frequency Observations without Using Orbit Information[J]. Bulletin Géodésique, 1991, 65(2): 130–143. DOI:10.1007/BF00806368 |
| [4] | SHEN Yunzhong, LI Bofeng, XU Guochang. Simplified Equivalent Multiple Baseline Solutions with Elevation-dependent Weights[J]. GPS Solutions, 2009, 13(3): 165–171. DOI:10.1007/s10291-008-0109-9 |
| [5] | 张小红, 丁乐乐. 北斗二代观测值质量分析及随机模型精化[J]. 武汉大学学报(信息科学版), 2013, 38(7): 832–836. ZHANG Xiaohong, DING Lele. Quality Analysis of the Second Generation Compass Observables and Stochastic Model Refining[J]. Geomatics and Information Science of Wuhan University, 2013, 38(7): 832–836. |
| [6] | WANG J, SATIRAPOD C, RIZOS C. Stochastic Assessment of GPS Carrier Phase Measurements for Precise Static Relative Positioning[J]. Journal of Geodesy, 2002, 76(2): 95–104. DOI:10.1007/s00190-001-0225-6 |
| [7] | 张小红, 朱锋, 薛学铭, 等. 利用Allan方差分析GPS非差随机模型特性[J]. 测绘学报, 2015, 44(2): 119–127. ZHANG Xiaohong, ZHU Feng, XUE Xueming, et al. Using Allan Variance to Analyze the Zero-differenced Stochastic Model Characteristics of GPS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 119–127. DOI:10.11947/j.AGCS.2015.20130513. |
| [8] | 杨元喜, 徐天河. 基于移动开窗法协方差估计和方差分量估计的自适应滤波[J]. 武汉大学学报(信息科学版), 2003, 28(6): 714–718. YANG Yuanxi, XU Tianhe. An Adaptive Kalman Filter Combining Variance Component Estimation with Covariance Matrix Estimation Based on Moving Window[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 714–718. |
| [9] | 程鹏飞, 李玮, 秘金钟. 北斗导航卫星系统测距信号的精度分析[J]. 测绘学报, 2012, 41(5): 690–695. CHENG Pengfei, LI Wei, BEI Jinzhong. Precision Analysis of BeiDou Range Measurement Signals[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 690–695. |
| [10] | FENG Yanming, WANG Yongchao, WANG Charles, et al. Analyses of Signal-in-space Integrity with Undifferenced Triple Frequency Code and Phase Measurements[R]. Nanjing:CSNC2014, 2014. |
| [11] | FENG Yanming. Computing Covariance Matrices of Line-of-Sight GNSS Triple Frequency Signals[R]. Wuhan:GNSS Summer School, Wuhan University, 2016. |
| [12] | WANG Yongchao, FENG Yanming, ZHENG Fu. Geometry-Free Stochastic Analysis of BDS Triple Frequency Signals[C]//Proceedings of the 2016 International Technical Meeting of the Institute of Navigation. Monterey, California:The Institute of Navigation, 2016:956-969. |
| [13] | 黄令勇, 翟国君, 欧阳永忠, 等. 削弱电离层影响的三频TurboEdit周跳处理方法[J]. 测绘学报, 2015, 44(8): 840–847. HUANG Lingyong, ZHAI Guojun, OUYANG Yongzhong, et al. Triple-Frequency TurboEdit Cycle-Slip Processing Method of Weakening Ionospheric Activity[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 840–847. DOI:10.11947/j.AGCS.2015.20140380 |
| [14] | 黄令勇, 翟国君, 欧阳永忠, 等. 三频GNSS电离层周跳处理[J]. 测绘学报, 2015, 44(7): 717–725. HUANG Lingyong, ZHAI Guojun, OUYANG Yongzhong, et al. onospheric Cycle Slip Processing in Triple-Frequency GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 717–725. DOI:10.11947/j.AGCS.2015.20140348 |
| [15] | LIU Xianglin, TIBERIUS C, DE JONG K. Modelling of Differential Single Difference Receiver Clock Bias for Precise Positioning[J]. GPS Solutions, 2004, 7(4): 209–221. DOI:10.1007/s10291-003-0079-x |
| [16] | GAO Y, HEROUX P, KOUBA J. Estimation of GPS Receiver and Satellite L1/L2 Signal Delay Biases Using Data from CACS[C]//Proceedings of the KIS-94. Banff, Canada:[s.n.], 1994:109-117. |


