2. 山东大学, 山东 威海 264209;
3. 地理信息工程国家重点实验室, 陕西 西安 710054;
4. 青岛农业大学, 山东 青岛 266109
2. Shandong University, Weihai 264209, China;
3. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
4. Qingdao Agricultural university, Qingdao 266109, ChinaAbstract
高精度的卫星钟是导航定位系统的基础,卫星钟参数的预报精度直接影响导航系统的服务性能。现阶段的研究表明,星载原子钟相当敏感,极易受到外界或自身物理性能的影响,从而很难了解其细致的变化规律,使得卫星钟差的高精度预报变得极为困难[1-2]。为了提高卫星钟差预报精度,国内外学者做了大量的研究工作,提出了多种卫星钟差预报模型和方法。常规的预报模型是利用已有的较长时间的历史数据拟合得到模型参数,但往往会受到各天之间钟差的起点偏差这一系统性误差影响,以及精密定轨解算卫星钟差的过程中,轨道和钟差相互耦合导致解算的钟差序列存在着周期性的波动现象[3],从而难以获得相对较高的钟差拟合和预报精度。本文结合卫星钟差的周期特性,同时考虑起点偏差对预报精度的影响,对北斗卫星钟差进行了预报和精度分析。
1 数据预处理与钟跳识别 1.1 钟差序列的数据预处理由于当前北斗导航系统处于全球组网的建设阶段,全球监测站点相对较少,而且分布的不均匀,基于精密定轨与时间同步法解算的北斗卫星钟差数据存在较大程度的缺失。同时北斗卫星钟差数据含有一定量的钟差跳变和粗差,在分析北斗卫星钟差的特性之前,应当对这些影响因素进行数据预处理。其预处理的具体流程如下。
(1) 从钟差文件中获取钟差序列,以单天钟差序列为单元,标记钟差序列的缺失历元;当整天数据缺失相对较少时,对缺失项进行内插处理。
(2) 对内插处理后的完整的钟差序列进行差分处理,转化为频率数据,采用中位数法(MAD)和Baarda数据探测法[4]探测粗差。
(3) 进一步对粗差历元,采用相邻频率求和法[5]识别粗差和钟跳。若存在钟跳,需要将钟差数据进行分段处理。
(4) 整合粗差历元,采用线性插值法补齐。
以单天钟差序列为数据单元进行数据预处理,能提高粗差探测和钟跳的执行效率和准确率,为分析北斗钟差的数据特性提供了重要的保障。
1.2 频率求和法识别粗差和钟跳卫星钟差数据不可避免地存在粗差,常规的处理方法是基于中位数法进行探测,然而实际的处理过程中;当钟差跳变不十分明显时(通过钟差序列成图直观比较,无法发现钟跳),钟差跳变会掩盖在粗差中。如果没有细致的分离粗差和跳变,而统一将其视为粗差,必然会使得钟差的拟合精度大大降低,进而对卫星钟的周期性分析和钟差预报精度造成极大的影响。
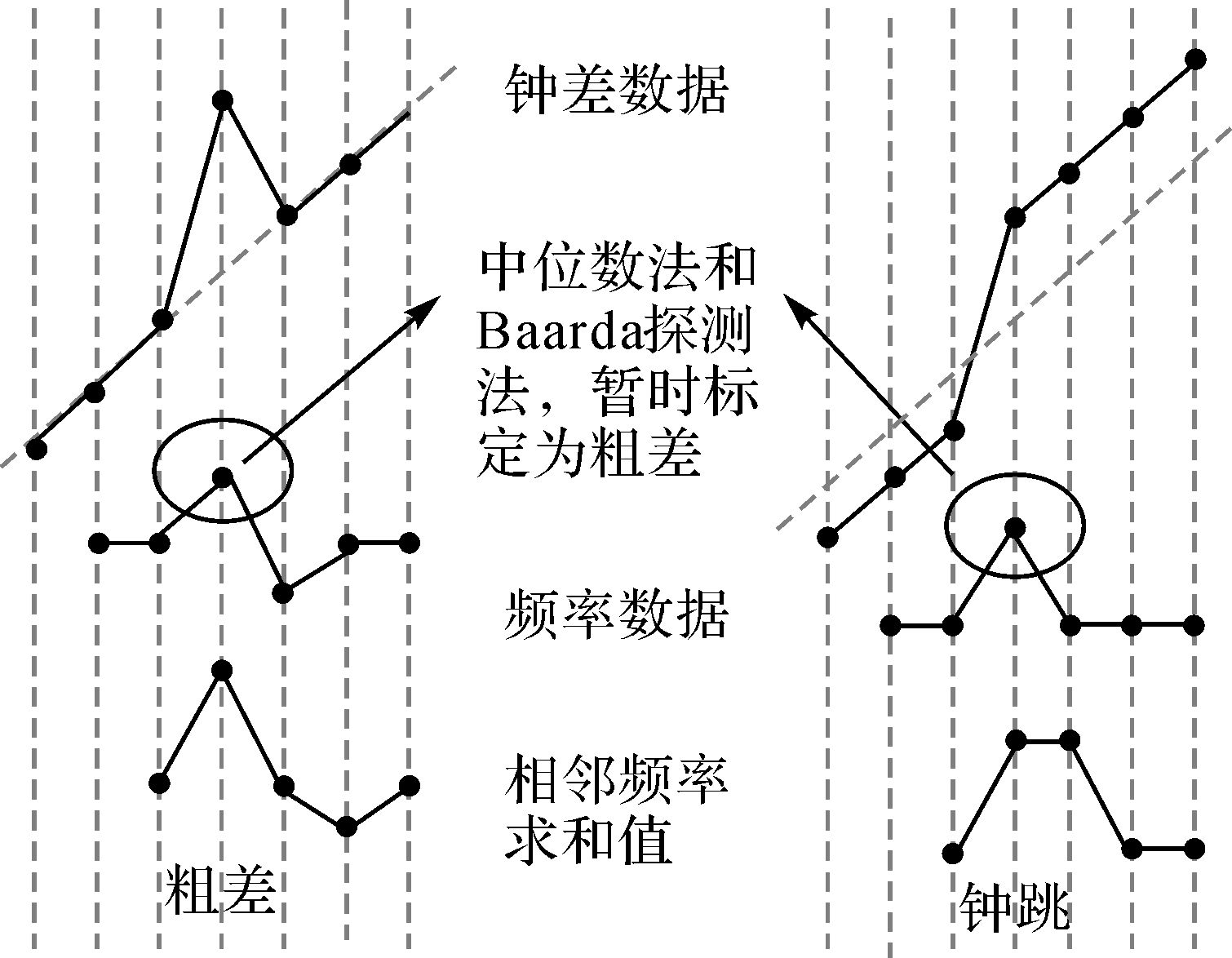
为了细致的辨别粗差和钟跳,本文采用如下方法处理:首先以天为单位,将钟差数据转化为频率;采用中位数法和Baarda数据探测法分析频率数据,探测粗差出现的历元,并标记这些历元,若出现粗差历元标记是连续的情况,很有可能是出现了钟差跳变。然后将被标记的历元附近的频率数据相邻两项求和,获得相应的频率求和项,如果在被标记的历元及其后一个历元出现两个峰值,则为相位跳变。具体过程如图 1所示。
|
| 图 1 粗差与钟跳区别示意 Fig. 1 The identification of clock error and clock jump |
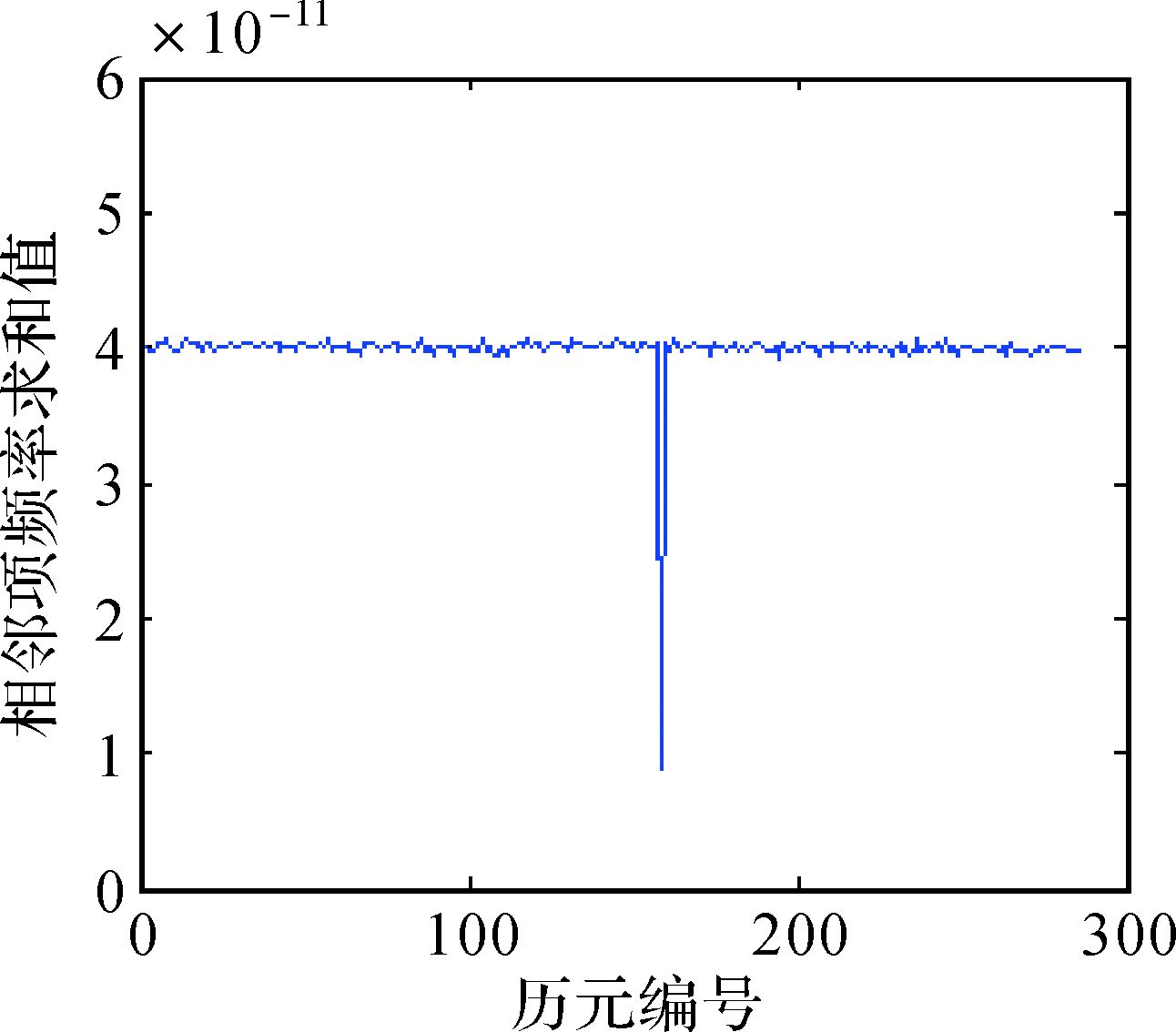
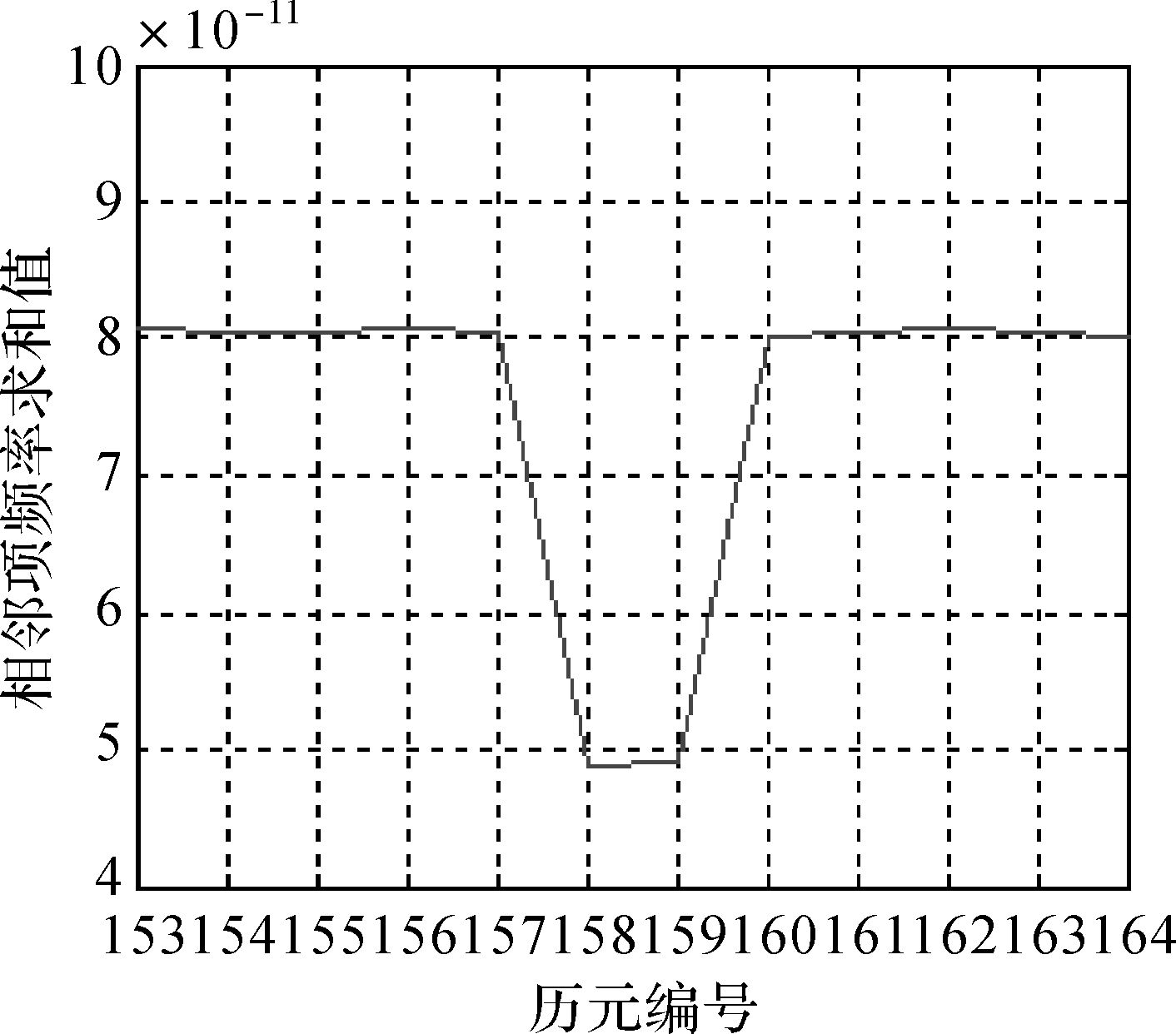
根据以上提出的钟跳探测方法,本文进行了如下试验;采用武汉大学IGS数据中心发布的2016年4月21日的钟差产品,对C01卫星按上述方法进行试验,采用中位数法的粗差探测以5δ作为限差。如图 2和图 3所示:根据粗差探测,可以确定粗差的历元编号;然后从相邻项的频率求和的结果中可以发现,在第158和159个历元处发生钟跳,即钟跳对应于频率数据的第159个历元,那么采用上述方法确定的钟跳出现在相位数据的第159和160个历元之间。因此在钟差拟合的过程中要对该天的数据分段处理,避免拟合精度较差,对卫星钟特性的频谱分析结果和钟差预报精度造成干扰。
|
| 图 2 钟跳识别 Fig. 2 The identification of clock jump |
|
| 图 3 钟跳识别局部图 Fig. 3 The local figure of clock jump |
2 质量分析和主周期确定 2.1 北斗卫星钟差数据质量分析
采用武汉大学IGS数据处理中心的事后钟差产品,对北斗导航系统卫星钟差数据质量进行分析统计。选用2016年1月1日至2016年11月1日(MJD 57388-57693) 总时长为306天,数据采样间隔为5 min的钟差产品进行分析。通过图 4可以发现北斗卫星钟差存在多次钟跳现象,大约每50天会出现一次大幅度的钟差跳变,因此在进行该时段的钟差预报和卫星钟性能评估时,要预先对钟差序列进行分段预处理,保证数据的质量。由图 5的统计结果表明(注:图 5中加粗的黑点部分为卫星钟差整天缺失的情况),北斗卫星导航系统的各类卫星钟差序列都存在较为严重的缺失,缺失率一般超过10%;其中GEO卫星的钟差缺失最为严重。同时在第29天至51天,第81至83天,第91至93天,以及第231至236天之间出现钟差数据完全缺失,势必会对该时段用户导航定位造成一定的影响。

|
| 图 4 C01卫星306天的钟差序列 Fig. 4 The satellite clock bias of C01 in 306 days |

|
| 图 5 北斗卫星钟差缺失统计 Fig. 5 The lost statistics of satellite clock bias |
2.2 周期项的获取
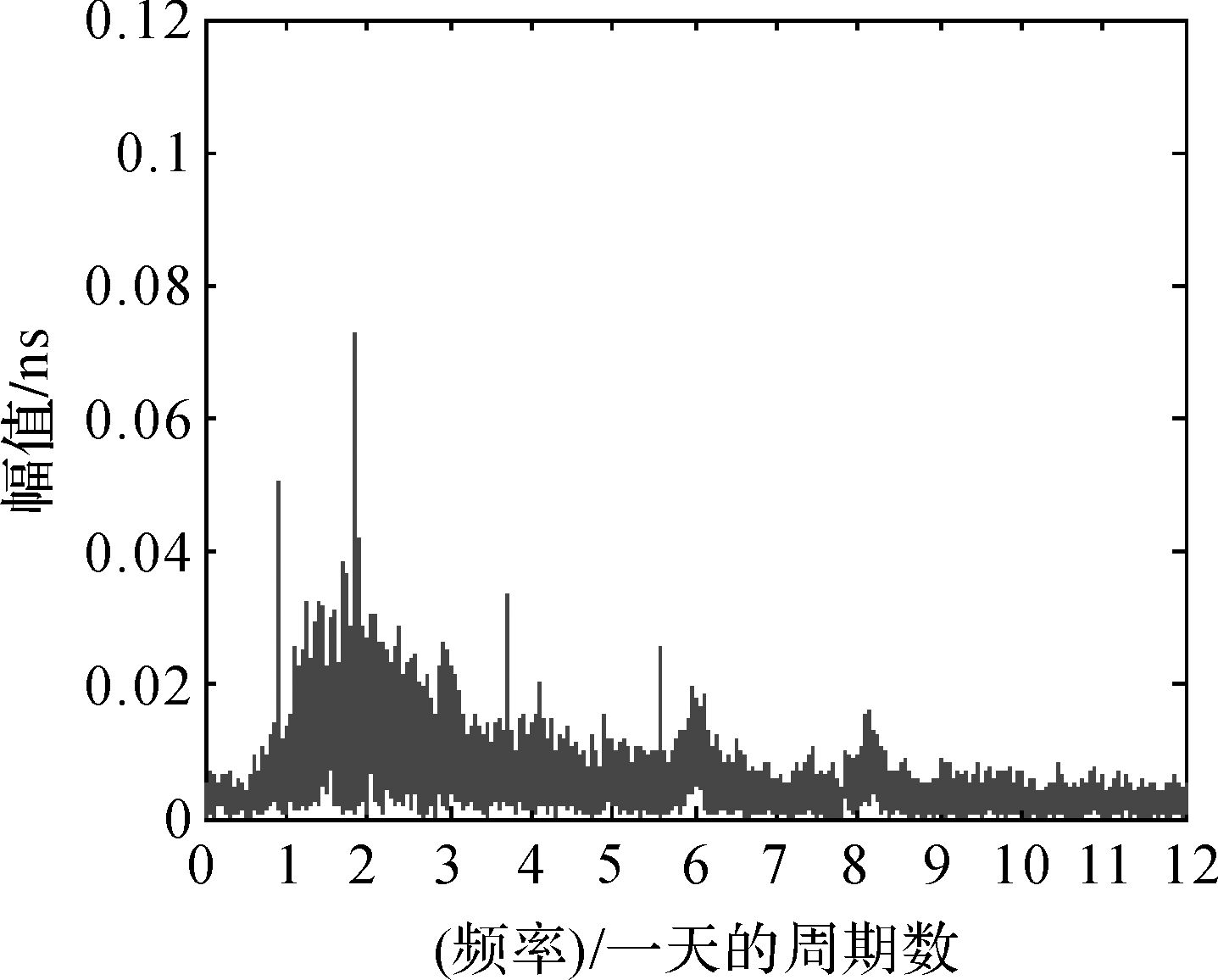
为了更完整地体现卫星钟的周期特性,分别选取钟差序列整天缺失相对较少的C01、C10、C12共3种类型的卫星,在去除趋势项的基础上采用快速傅里叶变换进行谱分析。注意在频谱值求解的过程中适当的调整残差个数(对多余项补零);使其与残差数据的长度对应的指数值最为接近[6-8]。采用预处理的钟差序列,然后对其去趋势项得到拟合残差序列;由于北斗钟差序列存在多天完全缺失的情况,所以在傅里叶变换之前,设置此处所对应的拟合残差值为零,然后将各天的拟合残差按时间序列拼接成一个完整的残差序列。最后对整合的残差序列进行傅里叶变换,获得卫星钟差的主要周期项。图 6—图 8为所对应的频谱分析结果。

|
| 图 6 C01卫星钟差频谱分析 Fig. 6 The Spectral analysis result of C01 |

|
| 图 7 C10卫星钟差频谱分析 Fig. 7 The Spectral analysis result of C01 |
|
| 图 8 C12卫星钟差频谱分析 Fig. 8 The Spectral analysis result of C01 |
采用各类缺失相对较少的卫星钟差序列,进行谱分析的结果显示,各类卫星钟呈现出不同的周期特性:GEO卫星的4个主周依次为12、24、8和6 h,IGSO卫星的主周期为24、12、8和6 h;而MEO卫星的3个主周期为12.911、6.444和24 h;符合北斗卫星钟差的周期特性[9-10]。其中IGSO和MEO的第一主周期近似等于其轨道周期,GEO卫星钟差的第1主周期为其轨道周期的一半,第2主周期近似等于其轨道周期[11-12];同时GEO和IGSO的卫星钟主周期对应的振幅,明显要高于MEO。这是因为MEO卫星钟相比于其他两类卫星钟具备相对较好的稳定性和较高的定位精度,从而定轨模型中未被考虑的轨道误差项较小,因此引起的周期项改正相对不太明显。
3 改进的钟差预报模型常规的二次多项式模型顾及卫星钟差的时频特性,模型中包含有相位、频率、频漂等因素。因此构建的模型为
 (1)
(1)
式中,a、b、c分别对应的是相位、频率、频漂;x(t)对应的是钟差序列;e对应的是残差。式(1) 的3个参数可以通过一定时长的钟差观测值,采用最小二乘法求得。然而对于实际的钟差预报而言,除了卫星钟差本身的趋势项变化规律外,还应当考虑到周期项的影响,除此之外,由于在精密定轨与时间同步解算卫星钟差的过程中,以天为单位的截取弧度,解算得到的轨道和钟差在各天的连接处,会出现一定程度的钟差跳变。因此为了更全面地分析钟差的特性,提高钟差预报的精度,要加入截断误差,即起始点偏差改正。具体方法是采用拟合数据的最后5个历元的钟差数据,预报下一时段的首历元钟差值,然后替换常规的二次多项式所预报的首历元钟差值,实现截断误差修正[13-14]。对应的修正模型可以表示为
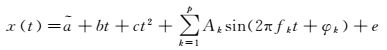 (2)
(2)
式中,a为相位修正项修正系数;f为主周期对应的频率;Ak、φk分别对应的周期项对应的振幅和相位;p为主周期个数;e为残差。该修正公式根据拟合数据的最后5个历元和预报的首历元之间极强的相关性,对常规的多项式模型中的相位项进行了修正,不改变与时间项相关的一次项和二次项,仅对拟合模型进行了平移;相当于对原模型进行了系统偏差修正,保留了整体预报模型的态势[13-15]。对于修正模型中存在的拟合残差项,要进行白噪声检验,通过拟合残差项的白噪声检验来调节主周期的个数(一般为2~3个主周期),确定合适的周期项进行钟差预报的周期性改正[16]。
4 算例分析 4.1 单天预报算例为了分析改进模型的钟差预报精度,采用武汉大学IGS中心发布的2016年8月31和9月1日事后的钟差产品(MJD 57631-57632) 进行建模和精度验证,分别进行了24 h、12 h和6 h的短期和超短期钟差预报,预报结果见表 1。
| 卫星类型 | 卫星号 | 拟合精度 | 预报精度/24 h | 预报精度/12 h | 预报精度/6 h | |||||||
| QP | Mod | QP | Mod | QP | Mod | QP | Mod | |||||
| GEO | C01 | 0.29 | 0.24 | 16.62 | 15.87 | 6.33 | 5.63 | 2.02 | 1.46 | |||
| C02 | 0.38 | 0.24 | 6.27 | 5.06 | 5.21 | 3.99 | 4.06 | 2.81 | ||||
| C03 | 0.39 | 0.33 | 4.17 | 3.01 | 3.14 | 1.94 | 2.7 | 1.53 | ||||
| C04 | 0.75 | 0.62 | 13.88 | 12.14 | 6.35 | 4.66 | 3.09 | 1.19 | ||||
| C05 | 0.57 | 0.31 | 12.17 | 10.94 | 6.69 | 5.41 | 4.15 | 2.82 | ||||
| IGSO | C06 | 1.32 | 1.17 | 77.78 | 73.38 | 37.04 | 32.53 | 18.96 | 14.28 | |||
| C07 | 0.6 | 0.49 | 14.1 | 13.27 | 5.5 | 4.76 | 1.73 | 1.26 | ||||
| C08 | 0.39 | 0.28 | 16.02 | 15.27 | 6.71 | 5.87 | 4.43 | 3.56 | ||||
| C09 | 0.18 | 0.17 | 8.73 | 8.49 | 4.74 | 4.49 | 2.59 | 2.33 | ||||
| C10 | 0.67 | 0.61 | 8.27 | 7.35 | 2.12 | 1.66 | 0.47 | 1.13 | ||||
| MEO | C11 | 0.3 | 0.28 | 0.69 | 0.8 | 0.63 | 1.09 | 0.83 | 0.48 | |||
| C12 | 0.24 | 0.2 | 1.6 | 1.35 | 1.69 | 1.43 | 1.67 | 1.41 | ||||
| C14 | 0.16 | 0.15 | 2.16 | 1.96 | 1.21 | 1.00 | 0.72 | 0.50 | ||||
| 注:QP代表二次多项式预报法;Mod代表修正模型预报法。 | ||||||||||||
从表 1的预报结果可知:采用顾及周期性改正结合起点偏差修正的谱分析法;对卫星钟差的拟合和预报精度都有一定程度的提升。GEO和IGSO由于其显著的周期特性,所以修正模型预报精度的提升程度要高于MEO卫星。同时卫星钟差的预报精度保持了常规二次多项式钟差预报的精度特点,即MEO卫星钟差预报的精度明显高于GEO和IGSO,符合星载原子钟自身的精度和性能特点;C06卫星由于在精密定轨与时间同步钟差解算的过程中,以天为单位选取轨道弧段,导致在各天之间的临界点出现较大钟差跳变,进而预报的精度较差。通过3个不同的时段的预报结果显示,随着预报时间的不断延长,预报精度显著降低;同时C11卫星的24 h和12 h的预报结果中,却出现了修正模型的精度反而低于常规的二次多项式的预报精度,这是由于MEO为卫星的周期特性不太显著,修正模型中加入的周期项过多,造成的过度拟合,降低了其预报的精度。
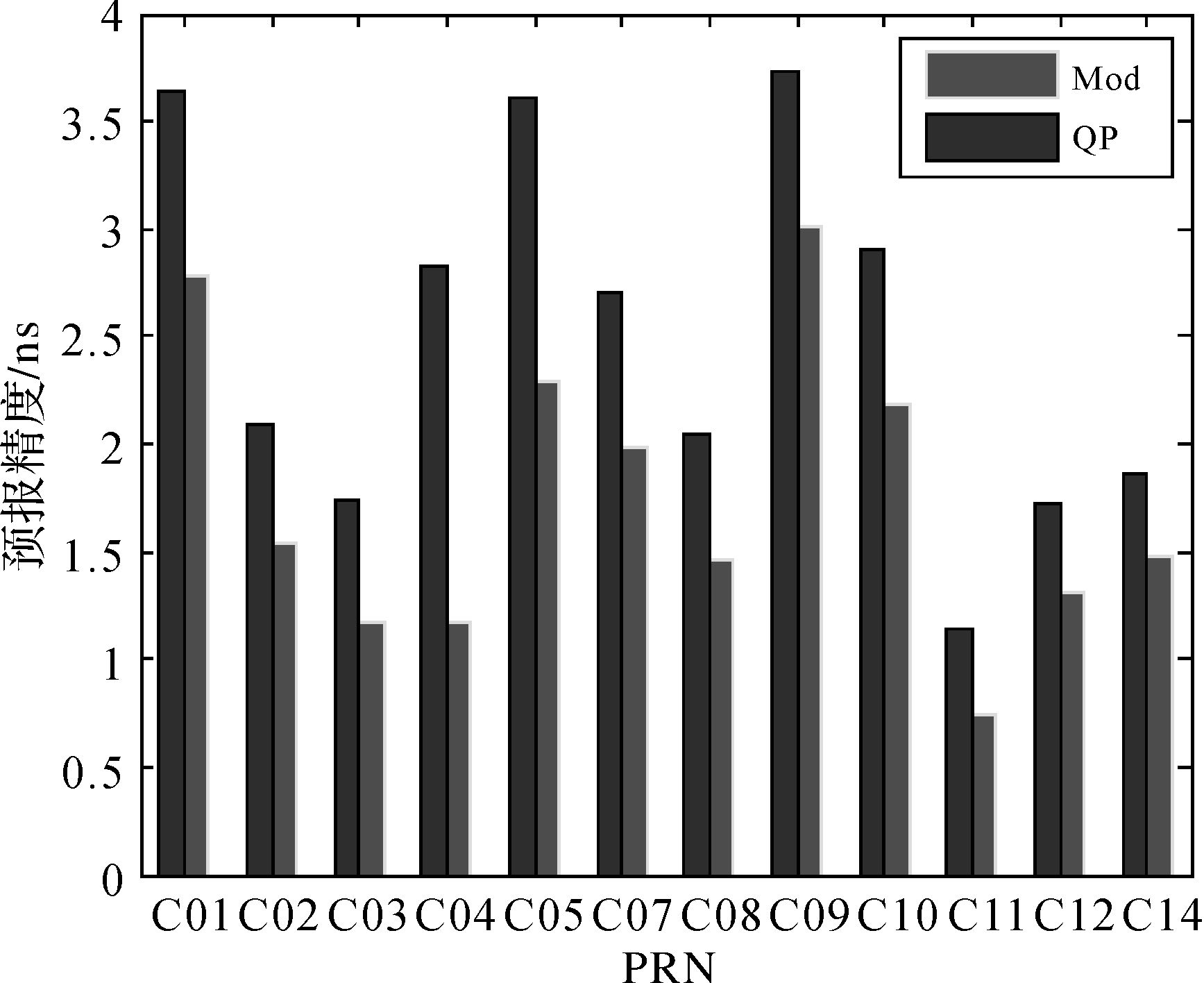
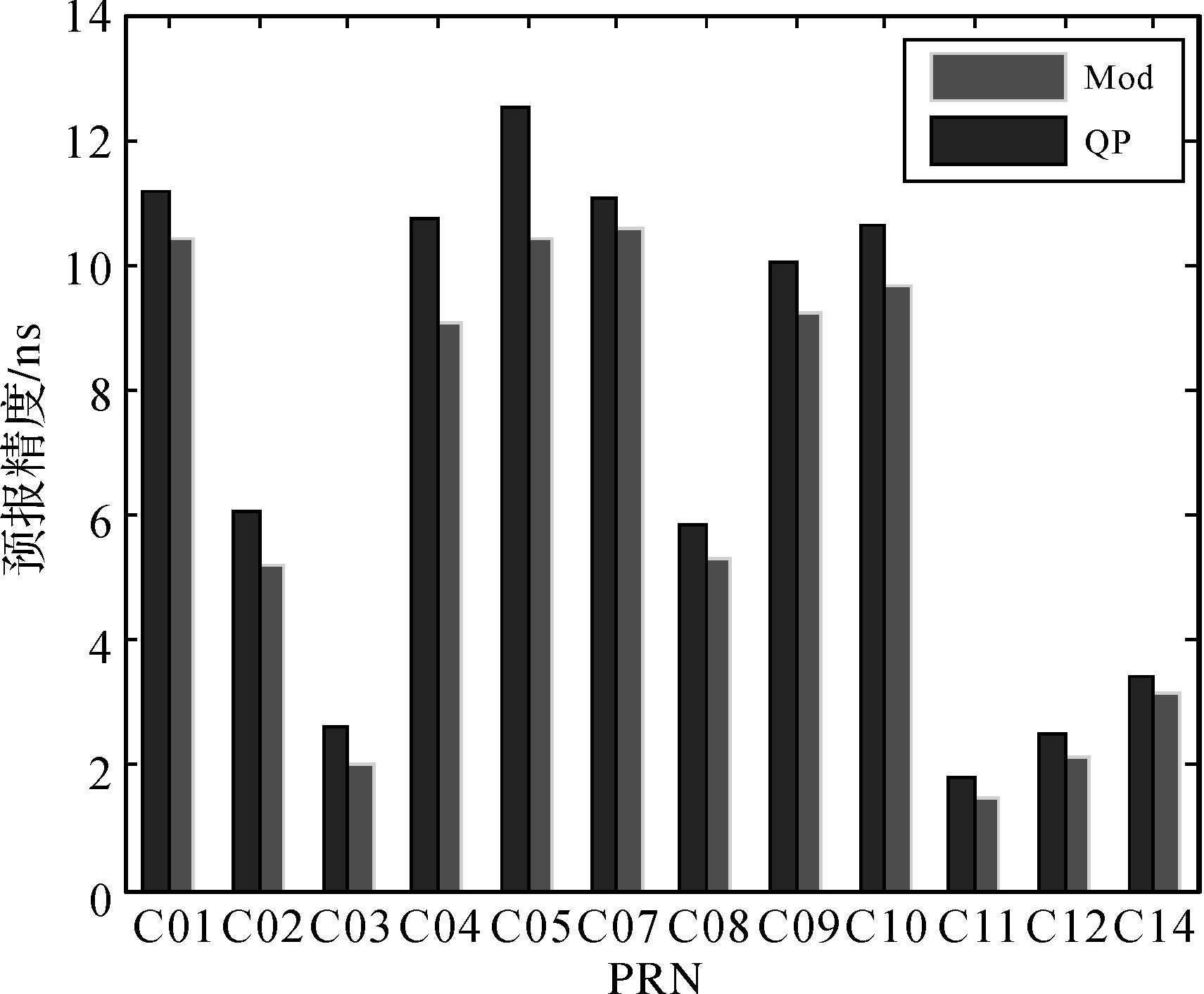
4.2 多天预报算例由于方案1中以单天的钟差产品,进行钟差预报和精度分析,数据相对较少,难以准确的体现模型的预报精度。所以本文选择2016年8月24日至2016年9月10日共18天的钟差产品,进行预报。其中钟差序列在2016年9月4日和9月5日存在调相过程,所以没有参与预报,其余16天的钟差产品进行的两周预报的精度结果如表 2所示,图 9、图 10和图 11分别为6 h、12 h及24 h的预报精度统计图:
| 卫星类型 | 卫星号 | 预报精度/24 h | 预报精度/12 h | 预报精度/6 h | |||||
| QP | Mod | QP | Mod | QP | Mod | ||||
| GEO | C01 | 11.19 | 10.43 | 5.95 | 5.14 | 3.64 | 2.78 | ||
| C02 | 6.05 | 5.17 | 3.58 | 2.76 | 2.09 | 1.54 | |||
| C03 | 2.60 | 2.00 | 1.91 | 1.06 | 1.74 | 1.18 | |||
| C04 | 10.77 | 9.09 | 5.24 | 3.70 | 2.82 | 1.17 | |||
| C05 | 12.50 | 10.40 | 7.12 | 5.19 | 3.61 | 2.30 | |||
| IGSO | C06 | 66.87 | 61.33 | 34.96 | 29.21 | 18.10 | 12.58 | ||
| C07 | 11.07 | 10.60 | 4.97 | 4.49 | 2.71 | 1.98 | |||
| C08 | 5.84 | 5.30 | 2.80 | 2.36 | 2.05 | 1.47 | |||
| C09 | 10.03 | 9.23 | 5.95 | 5.14 | 3.73 | 3.01 | |||
| C10 | 10.65 | 9.67 | 4.85 | 4.05 | 2.91 | 2.18 | |||
| MEO | C11 | 1.78 | 1.47 | 1.23 | 0.84 | 1.14 | 0.75 | ||
| C12 | 2.50 | 2.12 | 1.85 | 1.46 | 1.72 | 1.32 | |||
| C14 | 3.44 | 3.14 | 2.22 | 1.89 | 1.87 | 1.47 | |||
|
| 图 9 6 h的预报精度统计 Fig. 9 The prediction accuracy of 6 hours |

|
| 图 10 12 h的预报精度统计 Fig. 10 The prediction accuracy of 12 hours |
|
| 图 11 24 h的预报精度统计 Fig. 11 The prediction accuracy of 24 hours |
通过两周的预报精度分析可知,修正模型一定程度上对卫星钟差的预报精度有所提升,两周的预报结果,依然符合卫星钟差的实际特性;而且GEO和IGSO,这两种类型的卫星钟差的预报精度的提升程度高于MEO,这与两类钟差的显著周期特性有关;而且修正模型的预报精度较常规二次多项式模型对GEO、IGSO、MEO的精度提升约26%、21%和17%。随着预报时间的延长,预报误差有一定的累积。两组试验都出现C06卫星的拟合和预报精度较差,为了更直观地显示修正模型的预报精度,精度统计图中删除了C06卫星的结果,通过表 2的结果分析,该时间段的单天拟合数据段内C06卫星存在多处微小的钟跳,而且卫星钟差序列的起始偏差较大;因此建议对北斗卫星精密定轨模型进行相应的修正,提高IGSO的轨道和钟差的解算精度。
5 结论当前北斗导航系统处于全球组网的建设阶段,钟差数据存在大批量的缺失和阶段性的钟差跳变和粗差。本文针对这一现象,采用中位数法和Baarda数据探测法进行钟差数据的粗差探测,然后采用相邻项频率求和法,根据粗差和钟跳在频率求和值上的差异,分离粗差和钟跳,避免了钟差数据拟合过程中出现较大的误差;进而影响卫星钟差的周期特性和卫星钟差的预报精度。采用谱分析法分别对北斗卫星导航系统的星载原子钟进行分析,确定了其周期特性,其中IGSO和MEO的第1主周期和GEO的第2主周期,分别近似的等于其轨道周期。由于北斗卫星导航系统精密定轨与时间同步解算的钟差序列,存在各天之间的系统性偏差,因此在钟差预报的过程中对其进行起点偏差修正。根据两周的预报结果分析得出,北斗卫星24 h、12 h和6 h的平均预报精度分别为6.55 ns、3.17 ns和1.76 ns(剔除了预报精度较差的C06钟差预报的统计结果)。根据2016年前10个月共306天的钟差数据缺失统计发现,北斗卫星钟差数据会出现钟差数据缺失和个别卫星钟差数据质量较差的情况,建议iGMAS分析中心在后续的工作中,考虑适当调整监测站点的选取策略,并且对精密定轨模型进行改进,以达到对北斗卫星钟差产品的进一步完善。
致谢: 感谢武汉大学IGS数据中心提供的产品支持。
| [1] | 崔先强, 焦文海. 灰色系统模型在卫星钟差预报中的应用[J]. 武汉大学学报(信息科学版), 2005, 30(5): 447–450. CUI Xianqiang, JIAO Wenhai. Grey System Model for the Satellite Clock Error Predicting[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 447–450. |
| [2] | 郭海荣. 导航卫星原子钟时频特性分析理论与方法研究[D]. 郑州: 信息工程大学, 2006. GUO Hairong. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D]. Zhengzhou:Information Engineering University, 2006. |
| [3] | LOU Yidong, LIU Yang, SHI Chuang, et al. Precise Orbit Determination of BeiDou Constellation Based on BETS and MGEX Network[J]. Scientific Reports, 2014(4): 4692. |
| [4] | 李跃华, 蔺玉亭, 张达, 等. 钟差数据处理方法研究[C]//第二届中国卫星导航学术年会电子文集. 北京: 中国卫星导航学术年会组委会, 2011. LI Yuehua, LIN Yuting, ZHANG Da, et al. Method Research on Clock Deviation Process[C]//China Satellite Navigation Conference (CSNC). Beijing:China Satellite Navigation Academic Annual Conference Organizing Committee, 2011. |
| [5] | 吴静. 利用中位数的GPS卫星钟跳探测方法[J]. 测绘科学, 2015, 40(6): 36–41. WU Jing. Study on Detection of GPS Clock Jump Using Median Absolute Deviation[J]. Science of Surveying and Mapping, 2015, 40(6): 36–41. |
| [6] | LEE J Y, GREENGARD L. Short Note:the Type 3 Nonuniform FFT and Its Applications[J]. Journal of Computational Physics, 2005, 206(1): 1–5. DOI:10.1016/j.jcp.2004.12.004 |
| [7] | 黄观文, 张勤, 许国昌, 等. 基于频谱分析的IGS精密星历卫星钟差精度分析研究[J]. 武汉大学学报(信息科学版), 2008, 33(5): 496–499. HUANG Guanwen, ZHANG Qin, XU Guochang, et al. IGS Precise Satellite Clock Model Fitting and Its Precision by Using Spectral Analysis Method[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 496–499. |
| [8] | 程佩青. 数字信号处理教程[M]. 北京: 清华大学出版社, 2007. |
| [9] | CHEN Peiqing. Digital Signal Processing Course[M]. Beijing: Tsinghua University Press, 2007. |
| [10] | WANG Bin, LOU Yidong, LIU Jingnan, et al. Analysis of BDS Satellite Clocks in Orbit[J]. GPS Solutions, 2016, 20(4): 783–794. DOI:10.1007/s10291-015-0488-7 |
| [11] | LI Haojun, CHEN Yanling, WU Bin, et al. Modeling and Initial Assessment of the Inter-Frequency Clock Bias for COMPASS GEO Satellites[J]. Advances in Space Research, 2013, 51(12): 2277–2284. DOI:10.1016/j.asr.2013.02.012 |
| [12] | SHI Chuang, ZHAO Qile, LI Min, et al. Precise Orbit Determination of Beidou Satellites with Precise Positioning[J]. Science China Earth Sciences, 2012, 55(7): 1079–1086. DOI:10.1007/s11430-012-4446-8 |
| [13] | STEIGENBERGER P, HUGENTOBLER U, HAUSCHILD A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515–525. DOI:10.1007/s00190-013-0625-4 |
| [14] | HUANG Guanwen, ZHANG Qin, XU Guochang. Real-time Clock Offset Prediction with an Improved Model[J]. GPS Solutions, 2014, 18(1): 95–104. DOI:10.1007/s10291-013-0313-0 |
| [15] | 黄观文. GNSS星载原子钟质量评价及精密钟差算法研究[D]. 西安: 长安大学, 2012. HUANG Guanwen. Research on Algorithms of Precise Clock Offset and Quality Evaluation of GNSS Satellite Clock[D]. Xi'an:Chang'an University, 2012. |
| [16] | FU Wenju, ZHANG Qin, AO Meng, et al. A Real-time Prediction Algorithm of BDS Satellite Clock Offset Considering Phase Jumps[C]//SUN Jiadong, LIU Jingnan, FAN Shiwei, et al. China Satellite Navigation Conference (CSNC) 2015 Proceedings:Volume Ⅱ. Berlin Heidelberg:Springer, 2015:411-419. |
| [17] | 李清泉. 陀螺经纬仪时间观测数据函数模型的研究[J]. 武汉大学学报(信息科学版), 1990, 15(3): 11–20. LI Qingquan. Research of Function Model of Gyrocompass Transit Times[J]. Geomatics and Information Science of Wuhan University, 1990, 15(3): 11–20. |



