2. 中国卫星导航系统管理办公室测试评估研究中心, 北京 100094;
3. 武汉大学卫星导航定位技术研究中心, 武汉 430079;
4. 德国地学研究中心, 14473 波茨坦 德国
2. Test and Assessment Research Center, China Satellite Navigation Office, Beijing 100094, China;
3. Research Center of Positioning and Navigation Technology, Wuhan University, Wuhan 430079, China;
4. Helmholtz Centre Potsdam, German Research Centre for Geosciences(GFZ), Telegrafenberg, 14473 Potsdam, GermanyAbstract
近几年卫星导航系统行业应用发展迅速,随着航空市场、交通物流、海洋石油勘探、远洋运输、精密农业等行业的发展,对卫星导航定位性能提出了更高的需求。但目前卫星导航系统可以提供的标准定位精度不能满足米级及更高精度需求,迫切需要开展提升GNSS服务性能的技术研究。基于网络RTK技术的连续运行参考站系统(CORS)为目前提升GNSS性能较为成熟且可靠性较高的技术,已大规模应用于国土测绘及变形监测等领域[1]。但该技术依赖于密集的参考基准站,因此建设成本较高,且不适于大范围陆地或海洋应用。为解决此类问题,国外导航公司开始研制并建立星基差分增强定位系统,当前较为成熟的有OmniSTAR系统及StarFire系统[2-3],但该技术目前主要依赖国外。
我国自主研制的北斗卫星导航系统建设与发展迅速,目前可以提供与GPS相媲美的服务精度,能够满足广大用户在导航、定位、授时等方面的需求,具备了大规模商用的技术与产业基础[4]。近年来,Multi-GNSS精密定轨技术发展迅速,定轨精度不断提高[5-11],为基于提升GNSS空间信号精度的GNSS增强技术提供了必要条件。该技术通过提供较各卫星导航系统播发广播星历精度更高的星历产品,以增强并提升GNSS服务性能。
Multi-GNSS全球增强,依赖于实时增强信息—高精度的实时轨道及实时钟差。目前IGS系统已经提供精密卫星轨道和钟差产品,其超快速轨道时效性及精度已经满足实时要求,但其超快速钟差精度约3 ns[12],无法满足高精度需求。2002年开始,IGS开始实施实时计划,目前已提供0.3~0.8 ns的GPS/GLONASS实时钟差产品[13],但自主性无法保障。GNSS实时钟差估计首先需要高精度实时轨道,GNSS精密定轨方面国内外学者已开展了深入研究。文献[5]利用卡尔曼滤波初步实现了GPS实时轨道解算,GPS三维精度约3.5 cm;文献[6]提出了一种新的GLONASS模糊度固定方法,提高了GLONASS定轨过程中模糊度固定率,提升了GLONASS定轨精度;文献[7—10]在PANDA软件基础上深入研究了北斗卫星光压模型、偏航姿态模型等,显著提升了北斗各类卫星定轨精度,重复弧段卫星径向精度优于10 cm,法向优于20 cm;文献[11]针对IGS MGEX各分析中心提供的Galileo轨道进行了比较分析,使用SLR数据检校发现目前MGEX各分析中心提供的Galileo轨道存在5 cm的系统偏差,各家平均精密轨道精度约10 cm。GNSS实时钟差方面,文献[14—17]对传统的钟差解算模型进行了优化与改进,实现了GPS实时钟差高效解算,优化的模型可应用于GPS实时钟差1 s级更新;文献[18—19]开展了GPS/北斗融合实时钟差解算模型的研究,事后验证可获得0.15 ns钟差。
本文主要在文献[17—18]的研究基础上,深入研究了Multi-GNSS实时钟差融合解算算法,优化了一种Multi-GNSS实时钟差高频估计模型,基于PANDA软件开展了实时轨道数据处理,并深入分析了实时增强信息精度。在此基础上,利用目前所获取的Multi-GNSS实时数据流,搭建了GNSS实时增强系统原型,并开展了实时定位服务验证,就该原型系统所设计提供的厘米级服务及米级服务进行了精度分析。
1 精密钟差实时解算模型GNSS实时钟差解算基于实时精密定轨过程中生成的精密信息,通过固定卫星轨道、地球自转参数、测站坐标等,估计实时精密钟差。
1.1 非差模型在双频数据处理中一般采用无电离层组合观测值消除电离层,如果选取统一时间基准,则GPS/北斗/Galileo无电离层组合非差误差观测方程如下
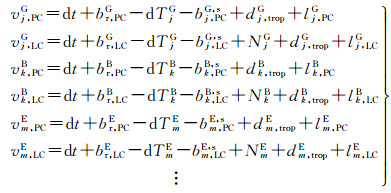 (1)
(1)
式中,G、B、E分别代表GPS、北斗及Galileo卫星;j、k、m分别代表同一历元第j颗GPS、第k颗北斗、第m颗Galileo卫星;PC、LC、N为无电离层组合伪距、载波相位及整周模糊度;v为残差信息;dt和dT为接收机和卫星钟差;dtrop是对流层延迟;l为星站几何距离与PC、LC观测值之差;br、bs分别代表观测值接收机端及卫星端信号延迟。
其中,伪距卫星端的信号延迟bPCs较稳定[20],可与卫星钟差进行合并,设
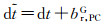
 (2)
(2)
设ISBB-G=br, PCB-br, PCG、ISBE-G=br, PCE-br, PCG,则式(2) 可转化为
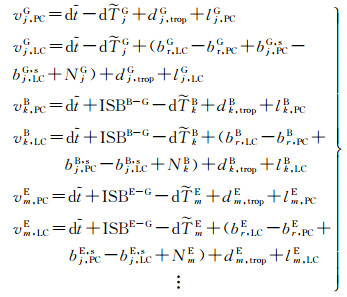 (3)
(3)
设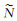
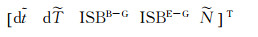
从非差模型待估参数来看,其中包含了大量模糊度参数,影响实时钟差解算速度。方程(3) 中GNSS载波观测值所包含的接收机端及卫星端信号延迟变化较为平稳[20],在无周跳的情况下可利用相邻历元作差消除模糊度参数,如式(4) 所示[18]
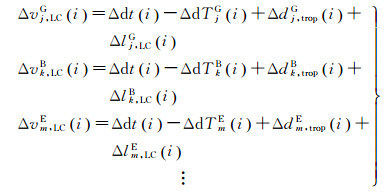 (4)
(4)
式中,Δ代表前后历元作差。综合考虑用户收敛速度、解算精度及实时增强信息计算效率,设计基于非差伪距及历元间单差载波构建多系统联合观测方程。通过历元间单差载波解算获得的钟差历元间相对变化,可由式(5) 恢复到绝对钟差值
 (5)
(5)
式中,ir0为接收机初始钟差历元;is0为卫星初始钟差历元。由式(3)—式(5),可形成如下方程
 (6)
(6)
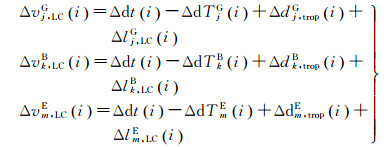 (7)
(7)
式中,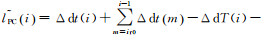
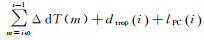
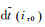
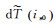
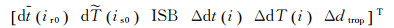
分析式(6)、式(7) 可得,该模型核心为利用伪距估计钟差初始值,利用载波变化估计钟差变化值,两者相互影响,收敛一段时间后可获得稳定的钟差值。在该模型中,消除了占待估参数最大比例的模糊度参数,可有效提升解算效率,且获得的钟差为绝对钟差,不会影响非差用户收敛速度。
2 实时增强信息处理策略与精度分析 2.1 数据处理策略实时轨道、实时钟差处理策略及参数模型如表 1所示。
| 参数 | 轨道估计模型 | 钟差估计模型 | ||
| 观 测 值 |
观测值 | 非差无电离层组合 | 非差无电离层伪距/历元间单差无电离层载波 | |
| 先验信息 | P1:1.0 m;L1:0.02周 | P1:1.0 m;L1:0.02周 | ||
| 截止高度角 | 7° | 7° | ||
| 观测值的权 | p=1, elev>30° p=2sin(elev), elev≤30° |
p=1, elev>30° p=2sin(elev), elev≤30° |
||
| 采样率 | 300 s | 实时5 s/事后验证30 s | ||
| 观测值弧段 | 2 d | — | ||
| 参 考 框 架 |
时间系统 | GPS时 | GPS时 | |
| 惯性参考框架 | ICRF J2000.0 | ICRF J2000.0 | ||
| 地固系参考框架 | ITRF2008 | ITRF2008 | ||
| 岁差章动 | IAU2000 | IAU2000 | ||
| EOP | IERS C04 | IERS C04 | ||
| 日月星历 | JPL DE405 | JPL DE405 | ||
| 轨 道 模 型 |
重力场 | EGM96 model(8×8) | — | |
| 海洋潮汐 | IERS conventions 2003 | IERS conventions 2003 | ||
| 地球固体潮 | IERS conventions 2003 | IERS conventions 2003 | ||
| 地球固体极潮 | IERS conventions 2003 | IERS conventions 2003 | ||
| 太阳光压模型 | CODE 5参数[21] | — | ||
| 天线相位缠绕 | 改正[22] | 改正 | ||
| 误 差 改 正 |
PCO/PCV | 卫星 | GPS, Galileo PCO:IGS08模型改正 北斗GEO PCO:IGS M-GEX提供 北斗IGSO/MEO PCO:ESA模型[23] GPS PCV:IGS08模型改正 北斗、Galileo PCV:未考虑 |
GPS, Galileo PCO:IGS08模型改正 北斗GEO PCO:IGS M-GEX提供 北斗IGSO/MEO PCO:ESA模型[23] GPS PCV:IGS08模型改正 北斗、Galileo PCV:未考虑 |
| 接收机 | GPS PCO:IGS08模型改正 北斗, Galileo PCO:同GPS GPS PCV:IGS08模型改正 北斗、Galileo PCV:同GPS |
GPS PCO:IGS08模型改正 北斗, Galileo PCO:同GPS GPS PCV:IGS08模型改正 北斗、Galileo PCV:同GPS |
||
| 相对论效应 | IERS conventions 2003 | IERS conventions 2003 | ||
| 参 数 估 计 |
平差方法 | 加权最小二乘 | 均方根信息滤波[24] | |
| 参考钟 | 星钟 | 星钟 | ||
| 卫星轨道 | 估计 | 固定 | ||
| 测站坐标 | 联合解算 | 固定 | ||
| 对流层 | Saastanmoine模型/GMF投影 分段两小时常数估计残差 |
Saastanmoine模型/GMF投影 随机游走估计残差 |
||
| 卫星钟差/接收机钟差 | 单历元估计+白噪声 | 单历元估计+白噪声 | ||
| 模糊度 | 双差固定 | 非差估计,历元间差分消除/新周跳估计 | ||
| 系统间偏差 | 常数估计 | 常数估计 | ||
实时轨道处理利用前48 h弧段观测文件进行精密定轨,预报获取实时轨道(预报6 h)。本文基于IGS核心站及M-GEX站(http://www.igs.org/network),设计使用80余Multi-GNSS跟踪站进行精密定轨,其中约40个可接收北斗数据,约60个可接收Galileo数据。设计使用60个站进行实时钟差验证,其中约40个可接收北斗数据,约50个可接收Galileo数据,站址分布见图 1。

|
| 图 1 实时轨道及钟差验证使用Multi-GNSS站址分布 Fig. 1 The distribution of multi-GNSS station in real-time orbit resolving and clock verification |
2.2 实时精密轨道
本文实时精密轨道基于PANDA软件[25-26],使用48 h观测数据进行精密定轨并预推6 h获取实时轨道。本文采用轨道重叠弧段进行精度比较[7-10],即利用前后相邻两天同一时刻解算弧段结果中后一天的前24 h观测部分,验证前一天轨道24 h重叠部分精度,并利用后一天的中间6 h观测部分验证前一天6 h实时轨道精度。
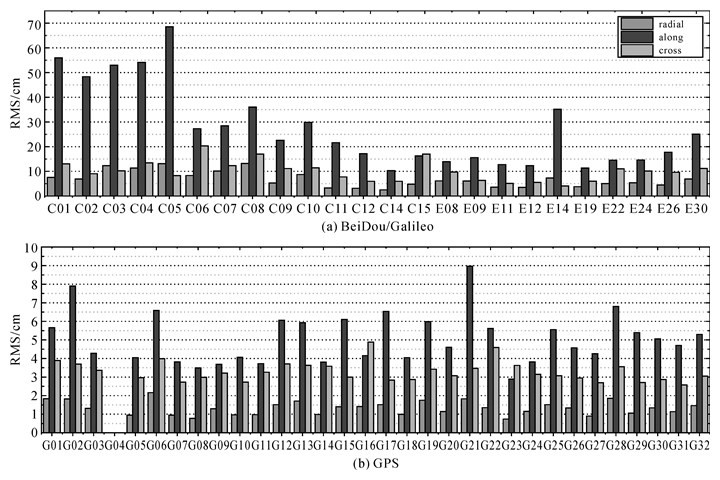
利用该方法,统计了2016-07-31—2016-08-30(DOY213—243) 连续一个月的实时轨道精度。图 2及图 3分别给出了各卫星精密轨道观测部分重叠弧段精度及实时部分重叠弧段精度,表 2给出了平均RMS精度统计。

|
| 图 2 精密轨道24 h观测部分重叠弧段精度 Fig. 2 Precision of POD 24 hours observation-part overlaps |
|
| 图 3 精密轨道6 h实时部分重叠弧段精度 Fig. 3 Precision of POD 6 hours real-time part overlaps |
| cm | |||||
| 卫星类型 | radial | along | cross | 3D | |
| 观 测 部 分 |
BDS-GEO | 6.82 | 51.27 | 11.93 | 53.1 |
| BDS-IGSO | 7.10 | 22.85 | 16.79 | 29.2 | |
| BDS-MEO | 2.41 | 9.99 | 5.93 | 11.9 | |
| Galileo | 3.38 | 10.86 | 7.88 | 13.8 | |
| GPS | 0.97 | 3.63 | 3.20 | 4.9 | |
| 预 报 部 分 |
BDS-GEO | 10.25 | 56.00 | 10.81 | 57.95 |
| BDS-IGSO | 8.41 | 26.74 | 14.87 | 31.73 | |
| BDS-MEO | 2.99 | 16.38 | 6.56 | 17.89 | |
| Galileo | 5.23 | 17.28 | 7.89 | 19.71 | |
| GPS | 1.33 | 5.08 | 3.30 | 6.20 | |
文献[27]中发现,综合影响用户定位解算为包含了轨道误差及卫星钟差的空间信号精度(SISRE),其中轨道径向误差较其他两方向误差较大影响了空间信号精度,亦即在站星观测方程中的比例最大,因此该部分重点关注各卫星径向误差。从统计结果来看,北斗GEO径向观测部分精度约7 cm,实时部分精度约10 cm;IGSO径向观测部分精度约7 cm,实时部分约8.5 cm;北斗MEO、Galileo及GPS径向观测部分1~3 cm,实时部分1~5 cm。
2.3 实时钟差性能分析利用上文中获取的实时轨道,选取上述试验观测段中8月4日至10日(DOY217—223) 连续7 d开展实时钟差解算试验。选择的约60个用于实时钟差试验的观测站分布如图 1。
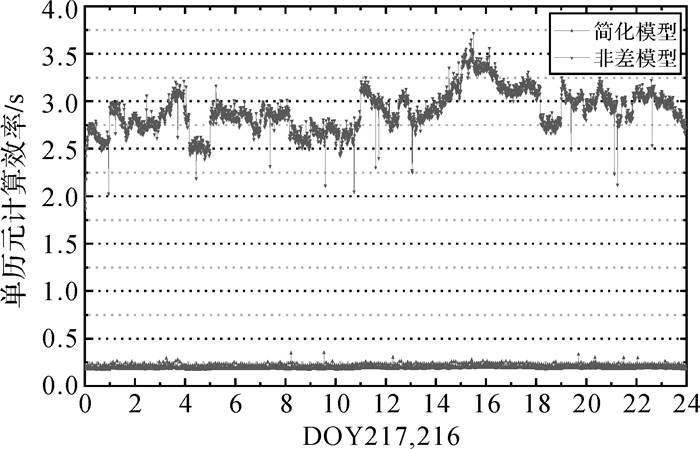
在同一服务器上,测试了8月4日(DOY 217) 的非差模型及简化模型单历元实时钟差解算效率,结果见图 4。从图 4中可以看出,正常情况下非差模型解算一个历元需要2.5~3.5 s,而简化模型仅需要0.2 s左右。随着参与解算站及卫星数量的增加,非差模型将不再满足于IGS建议的5 s级实时产品更新[15-16],因此实时钟差估计简化模型对于高频增强信息的提供具有很大优势。
|
| 图 4 简化模型及非差模型实时钟差估计效率对比 Fig. 4 The calculation efficiency comparison of real-time clock estimation of un-difference and simplified models |
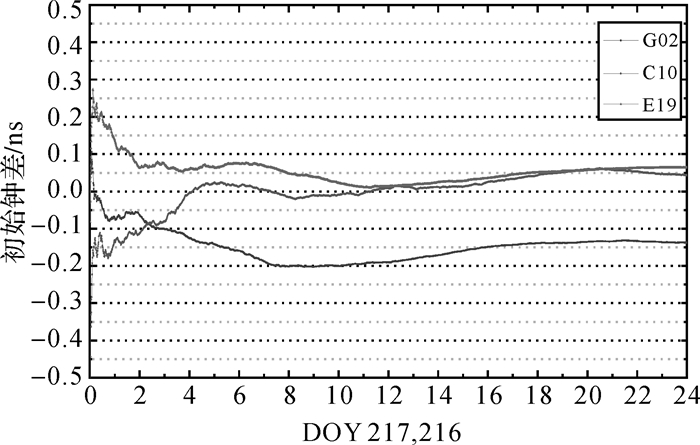
图 5给出了高频简化模型由伪距解算获得的初始钟差偏差随时间的变化。从图 5中可以看出,该模型中利用伪距估计钟差偏差约1 h后可收敛,收敛后钟差STD约0.02 ns。如若解算过程中某颗卫星失锁,重新捕获后则重新解算该颗卫星初始钟差。
|
| 图 5 简化模型计算获得的初始钟差偏差 Fig. 5 The time varying of initial clock bias in simplified model |
为验证实时钟差估计精度,选取德国地学研究中心提供的GBM最终钟差产品为参考。目前GFZ提供的GBM产品GPS轨道较IGS最终产品精度优于1 cm,钟差优于0.02 ns,SLR检校北斗轨道精度约10 cm[28]。本文利用二次差法对两模型获取的实时钟差进行精度分析[16-19]。
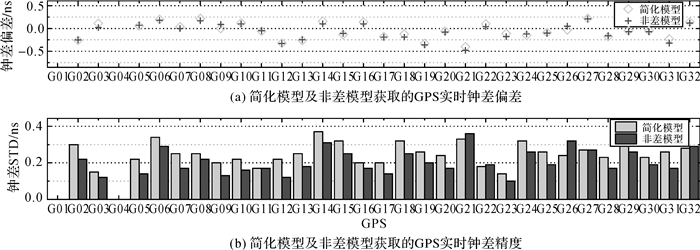
图 6给出了简化模型及非差模型估计的GPS实时钟差较GBM钟差的对比结果(选取G01为参考星)。发现简化模型估计的GPS卫星偏差较非差模型估计值基本吻合,两模型获得钟差偏差所有卫星均值分别为-0.05 ns和-0.07 ns,说明简化模型估计的钟差几乎不存在常偏,为绝对钟差。钟差精度统计结果显示利用上文获取的GPS实时轨道,简化模型可获取精度约0.22 ns的GPS实时钟差,非差模型可获取0.19 ns的实时钟差。
|
| 图 6 简化模型及非差模型获取的GPS实时钟差偏差及精度 Fig. 6 GPS real-time clock bias and precision of un-difference and simplified models |
图 7给出了简化模型及非差模型估计的北斗及Galileo实时钟差较GBM钟差的对比结果(分别选取C06、E08为参考星)。从结果中可以看出利用上文实时轨道,两模型估计的北斗GEO精度相当约0.50 ns;两模型获获取北斗IGSO/MEO卫星的实时钟差精度约0.24 ns;两模型获取的Galileo实时钟差精度相当,约0.32 ns。从结果来看,北斗GEO由于轨道精度影响较大,导致实时钟差精度较差。

|
| 图 7 简化模型及非差模型获取的北斗/Galileo实时钟差精度 Fig. 7 Precision comparison of BeiDou and Galileo real-time clock to GBM in un-difference and simplified models |
3 实时增强系统原型 3.1 原型构建
利用本文实时轨道处理策略及实时钟差算法,设计了Multi-GNSS全球实时增强系统,并完成了系统原型的构建。该系统主要流程包括获取全球GNSS实时跟踪站网观测数据、获取实时轨道增强信息、获取实时钟差增强信息及播发增强信息,如图 8所示。
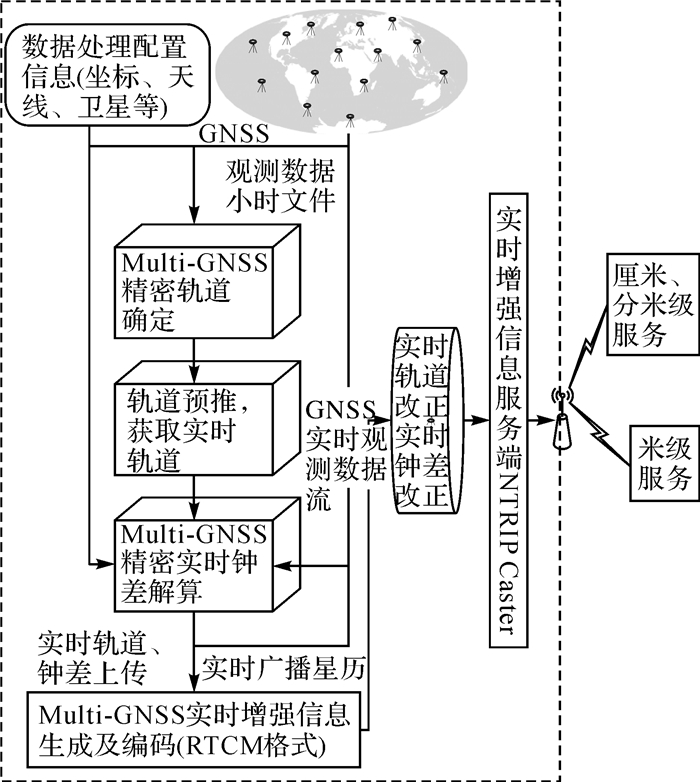
|
| 图 8 Multi-GNSS全球实时增强系统原型架构 Fig. 8 The prototype frame of multi-GNSS global real-time augmentation system |
该原型系统中,全球均匀布设Multi-GNSS观测站网,获取GNSS实时观测数据,并利用网络传输至数据处理中心;实时轨道处理平台每3小时利用前48 h弧段观测文件进行一次精密定轨,预报获取实时轨道(本文预报6 h),站址分布见图 1;实时钟差处理平台利用实时轨道、实时数据流,利用表 1中数据处理策略估计实时钟差。原型平台中解算实时钟差的测站主要来源于德国地学研究中心(GFZ)转发的德国大地测量局(BKG)提供的M-GEX实时数据流(http://mgex.igs-ip.net)[29],及在国内布设的实时观测站共约60个Multi-GNSS实时观测站,其中35个可观测北斗卫星,50余个可观测Galileo卫星,站址分布见图 9;增强信息播发平台将获取的实时增强信息及广播星历数据流,编码生成GPS、北斗及Galileo实时增强信息改正值,以Ntrip协议RTCM格式进行播发(https://igs.bkg.bund.de/ntrip/rtcmmessagetypes)[31]。
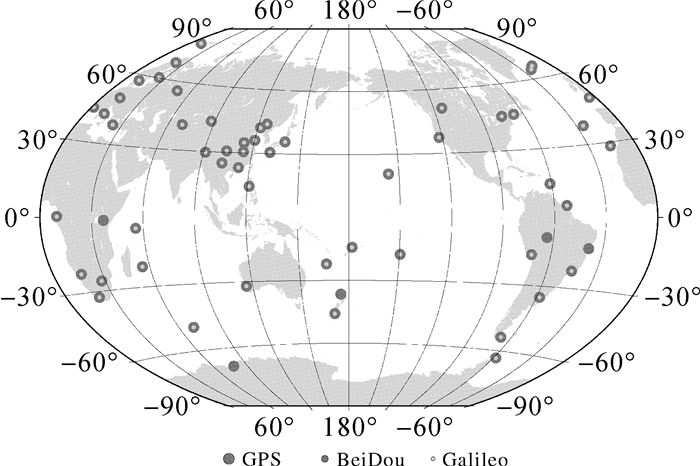
|
| 图 9 Multi-GNSS全球实时增强系统原型中实时GNSS站址分布 Fig. 9 The distribution of multi-GNSS real-time clock estimation stations |
需要指出的是,上文及该原型系统中实时轨道基于PANDA软件实现,增强信息播发基于BKG提供的BNC及NtripCaster软件实现[32]。目前Multi-GNSS全球实时增强系统原型平台已实时稳定运行并对外播发增强产品信息。
3.2 性能分析基于自主研发的实时精密定位软件,利用BKG播发的实时数据流,测试了搭建的GNSS全球实时增强原型系统性能,主要包括厘米级精密定位服务及米级服务验证。
图 10给出了CUT0站2016-10-31(DOY305) 连续13 h的GPS+BeiDou+Galileo实时PPP及单GPS实时PPP结果。从结果来看利用原型系统播发的实时增强信息,多系统实时PPP约15 min后收敛,单GPS约30 min收敛,多系统实时PPP可有效加速收敛,收敛后精度较单GPS PPP精度相当。
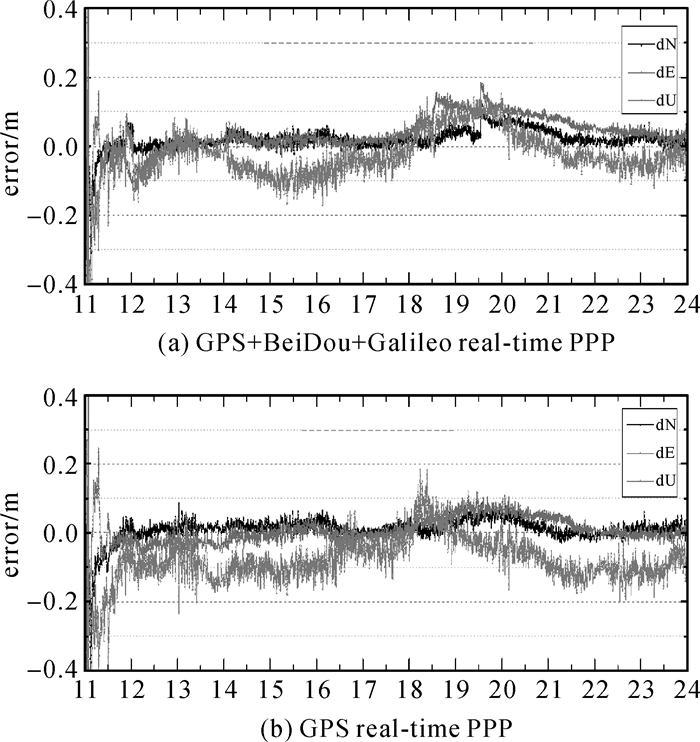
|
| 图 10 CUT0站基于增强信息的实时PPP对比(CUT0 2016-10-31 11:00—24:00)) Fig. 10 Comparison between multi-GNSS PPP and GPS PPP using augmentation messages in CUT0 |
图 11给出了GMSD站2016年10月25—26日利用伪距双频组合,使用实时增强信息进行GPS+BeiDou+Galileo实时定位的时序图。从结果来看,较使用广播星历的伪距定位,基于原型系统实时增强信息可明显提升定位的稳定性及精度,实现RMS水平约1 m、高程1.5~2.0 m的伪距定位服务。如若利用相位平滑伪距技术,则可获得更高精度的定位结果。
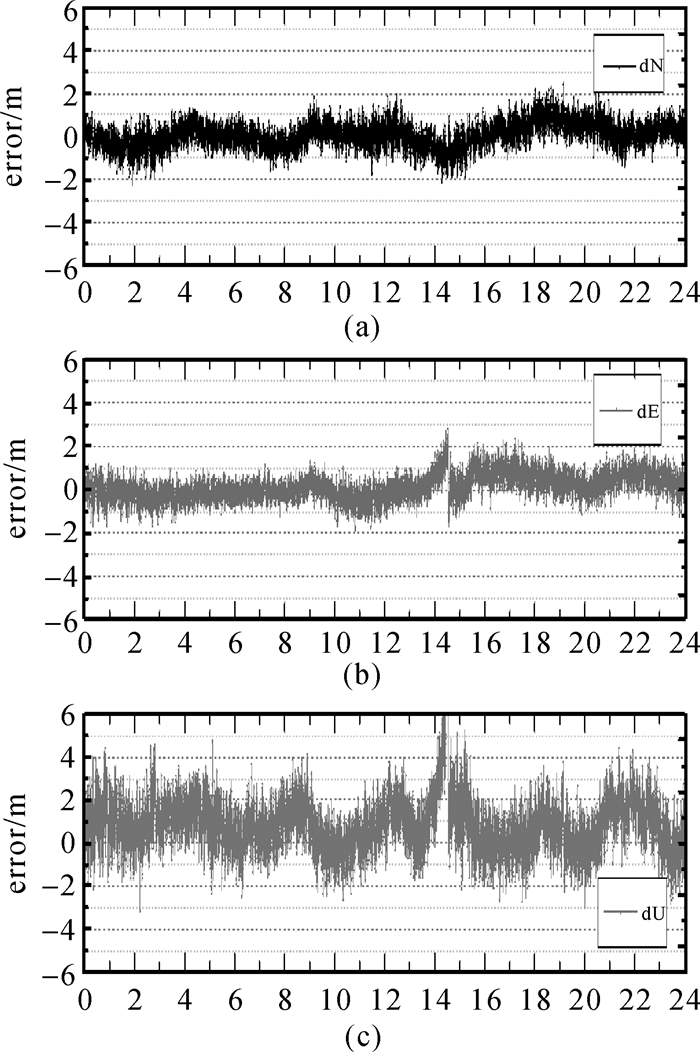
|
| 图 11 GMSD站基于增强信息的实时伪距定位时序图(GMSD 2016-10-25 10:00—2016-10-26 10:00) Fig. 11 Multi-GNSS pseudo-range positioning results based on augmentation messages in GMSD |
4 结论
GNSS增强技术通过提供较各卫星导航系统播发广播星历精度更高的星历产品,以增强并提升GNSS服务性能。本文主要深入研究了GNSS星基差分增强系统中实时钟差估计模型,在非差模型基础上优化模糊度参数,形成了适合高频钟差解算的钟差解算模型,并深入分析了实时轨道与实时钟差估计数据处理策略,在此基础上搭建了实时增强系统原型并对其精度及性能进行了分析,获得结果如下:
(1) 优化的实时钟差简化估计模型单历元解算效率较高,单历元解算时间仅为非差模型的1/10,可应用于实时钟差增强信息高频(如1 Hz)更新,解算获得的实时钟差不存在常偏为绝对钟差。
(2) GPS/北斗MEO/Galileo实时轨道径向重叠弧段精度1~5 cm,北斗GEO/IGSO卫星径向精度约10 cm。
(3) 基于实时轨道,通过高频简化模型可获得实时钟差精度GPS约0.22 ns,北斗GEO约0.5 ns、IGSO/MEO约0.24 ns,Galileo约0.32 ns。
(4) 利用实时数据流搭建了Multi-GNSS全球实时增强原型系统,并基于互联网实时播发增强信息,基于该原型系统可初步实现实时PPP厘米级服务,伪距定位米级服务。
本文优化的实时钟差估计模型可应用于高频GNSS增强服务,搭建的GNSS实时增强系统原型可在全球区域内提供实时、高精度和全天候的精密定位及导航服务,应用前景广阔。
致谢: 感谢德国地学研究中心提供的实时数据及数据处理硬件环境,以及邓志国博士提供的多系统高精度产品。
| [1] | 陈俊勇, 党亚民. 全球导航卫星系统的进展及建设CORS的思考[J]. 地理空间信息, 2009, 7(3): 1–4. CHEN Junyong, DANG Yamin. On the Progress in GNSS and the Construction of Its CORS System in China[J]. Geospatial Information, 2009, 7(3): 1–4. |
| [2] | OTT J E. The OMNISTAR Virtual Base Station System[C]//Proceedings of IEEE Position Location and Navigation Symposium. Atlanta, GA:IEEE, 1996:590-595. |
| [3] | DIXON K. StarFireTM:A Global SBAS for Sub-decimeter Precise Point Positioning[C]//Proceedings of the 19th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2006). Fort Worth, TX:ION, 2006:2286-2296. |
| [4] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [5] | LAURICHESSE D, CERRI L, BERTHIAS J P, et al. Real Time Precise GPS Constellation and Clocks Estimation by Means of a Kalman Filter[C]//Proceedings of the 26th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+2013). Nashville, TN:ION, 2013:1155-1163. |
| [6] | LIU Yang, GE Maorong, SHI Chuang, et al. Improving Integer Ambiguity Resolution for GLONASS Precise Orbit Determination[J]. Journal of Geodesy, 2016, 90(8): 715–726. DOI:10.1007/s00190-016-0904-y |
| [7] | GE Maorong, ZHANG Hongping, JIA Xiaolin, et al. What Is Achievable with Current COMPASS Constellation?[C]//Proceedings of the 25th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2012). Nashville, TN:ION, 2012:331-339. |
| [8] | ZHAO Qile, GUO Jing, LI Min, et al. Initial Results of Precise Orbit and Clock Determination for COMPASS Navigation Satellite System[J]. Journal of Geodesy, 2013, 87(5): 475–486. DOI:10.1007/s00190-013-0622-7 |
| [9] | GUO Jing, CHEN Guo, ZHAO Qile, et al. Comparison of Solar Radiation Pressure Models for BDS IGSO and MEO Satellites with Emphasis on Improving Orbit Quality[J]. GPS Solutions, 2016. DOI:10.1007/s10291-016-0540-2 |
| [10] | DAI Xiaolei, GE Maorong, LOU Yidong, et al. Estimating the Yaw-attitude of BDS IGSO and MEO Satellites[J]. Journal of Geodesy, 2015, 89(10): 1005–1018. DOI:10.1007/s00190-015-0829-x |
| [11] | STEIGENBERGER P, HUGENTOBLER U, LOYER S, et al. Galileo Orbit and Clock Quality of the IGS Multi-GNSS Experiment[J]. Advances in Space Research, 2015, 55(1): 269–281. DOI:10.1016/j.asr.2014.06.030 |
| [12] | International GNSS Service (IGS). Products[EB/OL].[2015-08-29].http://www.igs.org/products. |
| [13] | HADAS T, BOSY J. IGS RTS Precise Orbits and Clocks Verification and Quality Degradation over Time[J]. GPS Solutions, 2015, 19(1): 93–105. DOI:10.1007/s10291-014-0369-5 |
| [14] | BOCK H, DACH R, JÄGGI A, et al. High-rate GPS Clock Corrections from CODE:Support of 1 hz Applications[J]. Journal of Geodesy, 2009, 83(11): 1083–1094. DOI:10.1007/s00190-009-0326-1 |
| [15] | ZHANG Xiaohong, LI Xingxing, GUO Fei. Satellite Clock Estimation at 1 Hz for Realtime Kinematic PPP Applications[J]. GPS Solutions, 2011, 15(4): 315–324. DOI:10.1007/s10291-010-0191-7 |
| [16] | GE Maorong, CHEN Junping, DOUŠA J, et al. A Computationally Efficient Approach for Estimating High-rate Satellite Clock Corrections in Realtime[J]. GPS Solutions, 2012, 16(1): 9–17. DOI:10.1007/s10291-011-0206-z |
| [17] | CHEN Liang, GENG Changjiang, ZHOU Quan, et al. Estimation Strategy and Accuracy Analysis of GNSS Real-time Precise Satellite Clock Error[M]//SUN Jiadong, LIU Jingnan, FAN Shiwei, et al.China Satellite Navigation Conference (CSNC) 2015 Proceedings:Volume Ⅲ. Berlin Heidelberg:Springer, 2015:57-66. |
| [18] | 陈良, 耿长江, 周泉. 北斗/GPS实时精密卫星钟差融合解算模型及精度分析[J]. 测绘学报, 2016, 45(9): 1028–1034. CHEN Liang, GENG Changjiang, ZHOU Quan. Estimation Model and Accuracy Analysis of Beidou/GPS Real-time Precise Satellite Clock Error Integrated Resolving[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1028–1034. DOI:10.11947/j.AGCS.2016.20150296 |
| [19] | ZHANG Weixin, LOU Yidong, GU Shengfeng, et al. Joint Estimation of GPS/BDS Real-time Clocks and Initial Results[J]. GPS Solutions, 2016, 20(4): 665–676. DOI:10.1007/s10291-015-0476-y |
| [20] | DACH R, SCHAER S, HUGENTOBLER U, et al. Combined Multi-System GNSS Analysis for Time and Frequency Transfer[C]//Proceedings of the 20th European Frequency and Time Forum. Braunschweig, Germany:IEEE, 2006:530-537. |
| [21] | SPRINGER T A, BEUTLER G, ROTHACHER M. A New Solar Radiation Pressure Model for GPS Satellites[J]. GPS Solutions, 1999, 2(3): 50–62. DOI:10.1007/PL00012757 |
| [22] | WU J T, WU S C, HAJJ G A, et al. Effects of Antenna Orientation on GPS Carrier Phase[J]. Manuscripta Geodaetica, 1993(18): 91–98. |
| [23] | DILSSNER F, SPRINGER T, SCHÖNEMANN E, et al. Estimation of Satellite Antenna Phase Center Corrections for Beidou[C]//IGS Workshop. Pasadena, CA:IGS, 2014. |
| [24] | 赵齐乐, 刘经南, 葛茂荣, 等. 均方根信息滤波和平滑及其在低轨卫星星载GPS精密定轨中的应用[J]. 武汉大学学报(信息科学版), 2016, 31(1): 12–15. ZHAO Qile, LIU Jingnan, GE Maorong, et al. Applications of Square-Root Information Filtering and Smoothing on Orbit Determination of LEO Satellites with On-board GPS Data[J]. Geomatics and Information Science of Wuhan University, 2016, 31(1): 12–15. |
| [25] | LIU Jingnan, GE Maorong. PANDA Software and Its Preliminary Result of Positioning and Orbit Determination[J]. Wuhan University Journal of Natural Sciences, 2003, 8(2): 603–609. DOI:10.1007/BF02899825 |
| [26] | SHI C, ZHAO Q, GE M, et al. Introduction to PANDA Software and the Latest Development for High Precision GNSS Data Processing and Application[C]//IGS Analysis Center Workshop 2010. Newcastle upon Tyne, UK. |
| [27] | CHEN Liang, JIAO Wenhai, HUANG Xiaorui, et al. Study on Signal-in-space Errors Calculation Method and Statistical Characterization of Beidou Navigation Satellite System[M]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin Heidelberg:Springer, 2013:423-434. |
| [28] | DENG Z, FRITSCHE M, UHLEMANN M, et al. Reprocessing of GFZ Multi-GNSS product GBM[C]//IGS Workshop. Sydney Australia. |
| [29] | MONTENBRUCK O, STEIGENBERGER P, KHACHIKYAN R, et al. IGS-MGEX:Preparing the Ground for Multi-constellation GNSS Science[Z]. Inside GNSS, 2013, 9(1):42-49. |
| [30] | RTCM Standard 10403.2. Differential GNSS (Global Navigation Satellite Systems) Services-Version 3(February 1, 2013)[Z]. RTCM Paper 104-2013-SC104-STD, 2013. |
| [31] | STVRZE A, MERVART L, WEBER G, et al. The New Version 2.12 of BKG Ntrip Client (BNC)[C]//EGU General Assembly 2016. Vienna, Austria:[s.n.], 2016. |



