我国自行研制的北斗卫星导航系统正在国防建设与民用方面起着越来越大的作用[1]。于2020年,北斗将实现由35颗卫星构成的全球卫星导航系统,包括5颗静止轨道卫星、3颗倾斜同步轨道卫星(IGSO)和27颗中地球轨道卫星(MEO)[2]。北斗卫星系统这种含不同轨道类型的独特组网方式,为星间链路提供了极大的便利性。新一代的北斗卫星已可实现星间链路,并完成在轨验证工作,这为我国北斗系统实现全球监测以及自主定轨打下了基础。利用星间链路观测数据从理论上可以实现整个卫星导航系统的自主定轨,并已受到广泛的关注与研究[3-11]。然而,卫星运行过程中会受到多种复杂的摄动力的影响。如果不能对这些摄动力进行良好的改正,在没有地面或其他天体提供绝对约束,而仅有星间链路数据的条件下,导航系统会随着自主定轨时间的延长出现星座整体旋转[3, 5, 8-13]。卫星所受摄动力分为保守力和非保守力两部分:对于保守力,如地球非球形摄动、潮汐摄动、太阳月球和其他三体引力,现有的力学模型可以很精确地进行改正;而非保守力主要是太阳光压摄动,其不仅与太阳相对于轨道面的位置有关,还受卫星表面结构、表面材料老化和卫星姿态变化等因素影响,难以用模型精确改正。虽然学者已提出多种光压模型,如物理解析模型ROCK[14]和G2A[15],经验模型ECOM[16-17]、SPRINGER[18]和GSPM[19-20]模型,以及半解析模型Adjustable box-wing[21]模型等,但由于光压摄动的复杂性,目前还没有一种理想的模型能很好地对光压进行更正,因此光压成为影响导航卫星定轨精度的主要摄动力。
星载加速度计可以高精度地测量非保守力,主要用于重力学卫星(CHAMP、GRACE、GOCE)重力场反演及大气研究等任务。用于重力场反演时,先由精密定轨技术获得重力卫星的精密轨道,除地球重力场摄动外的卫星摄动力可由加速度计精确测定(非保守力)或利用模型算出(三体引力),则可以通过数值积分得到以引力位系数为待求参数的法方程,从而求解确定地球重力场模型[22-23];在大气密度研究中,通过模型分离星载加速度计所测的非保守力中的太阳光压、地球反照辐射等力后可以提取卫星所受的大气阻力,其可以用于计算大气热层密度[24-25]。一些研究表明,星载加速度计数据也可用于卫星的精密定轨[26-28]。采用SLR数据对CHAMP卫星进行精密定轨,分别使用加速度计(STAR)测量非保守力(太阳光压、大气阻力等)和用力学模型对非保守力进行改正,两种定轨结果相比,采用加速度计的定轨精度是模型改正精度的两倍[28]。利用GPS数据,分别使用先验的非保守力模型和加速度计数据(SuperSTAR)对GRACE卫星进行定轨,结果表明使用加速度计数据可以得到更好的轨道精度(各个方向优于2 cm),尤其是在卫星表面所受非保守力的变化频率较大的情况下,加速度计的优势更为明显[29]。使用星载加速度计还可以用来获得卫星定轨过程中经验加速度参数的约束条件,以提高卫星定轨精度[30]。目前,加速度计还没有在导航卫星定轨中得到应用。如果未来的北斗卫星都配备星上加速度计装置,使用高精度的加速度计来测量卫星所受非保守力,则可以避免使用复杂的光压模型。精确测量的非保守力,有助于提高卫星自主定轨精度,对于克服星座整体旋转,延长自主定轨时长提供了一种可能。
本研究主要通过模拟试验研究了使用星上加速度计对北斗卫星进行自主定轨的可行性。在时长为两个月的情况下,分析加速度计辅助自主定轨可以达到的精度,探讨导航卫星在没有地面提供数据支持条件下的生存能力。基于IGS发布的BD和GPS卫星精密轨道,采用经验光压模型ECOM来模拟卫星所受非保守力,积分得到模拟的卫星轨道,并生成星间链路数据。由星间链路数据,以及加速度计误差模型,对北斗卫星系统在使用加速度计数据条件下进行自主定轨与精度评定。另一方面,单纯使用星间链路数据和光压模型对卫星进行自主定轨和精度评定。比较两种方案下定轨结果,探讨加速度计能否提高自主定轨的性能。
1 基本模型与定轨算法本文研究主要对两种情形下自主定轨进行比较:① 使用加速度计测量非保守力辅助自主定轨; ② 采用光压模型改正进行自主定轨。本节介绍了该试验中所使用的加速度计误差模型和光压模型,并对自主定轨所使用的观测方程与约束条件进行了简要介绍。
1.1 加速度计与光压模型根据卫星任务需求,不同的星载加速度计具有不同的测量范围与分辨率[26]。3类重力卫星加速度计在SRF(satellite reference frame)敏感轴向的相关参数如表 1所示[31],如GRACE卫星,其星载加速度计SuperSTAR在两个敏感轴径向和切向的分辨率为1×10-10 m/s2/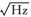
| 任务卫星 | CHAMP | GRACE | GOCE |
| 测量范围Y, Z/(m/s2) | ±10-4 | ±5×10-5 | ±6.5×10-6 |
| 分辨率Y, Z/ (m/s2/Hz1/2) | <10-8 | 10-10 | 2×10-12 |
星载加速度计数据由于受仪器误差的影响需要进行校准,通常采用比例-偏差模型作为加速度计校准的数学模型,其表达式如下
 (1)
(1)
加速度计的比例系数和偏差参数在精密定轨和重力场反演中通常需要进行准确估计。
GRACE卫星的技术说明中,通过对GRACE卫星星载加速度计长期估计的比例和偏差参数时间序列进行统计分析,给出了其先验的比例系数和两组由三次多项式表达的偏差参数[33]。该技术说明中推荐的偏差参数通常在数据处理中起到初始化的作用,其所推荐的比例参数在重力场反演中可直接使用而不再进行估计[22]。GRACE-A卫星先验加速度计偏差表达式如下
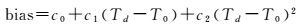 (2)
(2)
式中,T0=53 736。表 2给出了适用于时间2003-03-07后的表达式系数[33]。
| μm/s2 | |||
| 方向 | C0 | C1 | C2 |
| GRACE-A Xsrf | -1.209 5 | -4.128E-5 | 9.7E-9 |
| GRACE-A Ysrf | 29.337 0 | 6.515E-4 | -3.9E-7 |
| GRACE-A Zsrf | -0.560 6 | -2.352E-6 | 3.8E-9 |
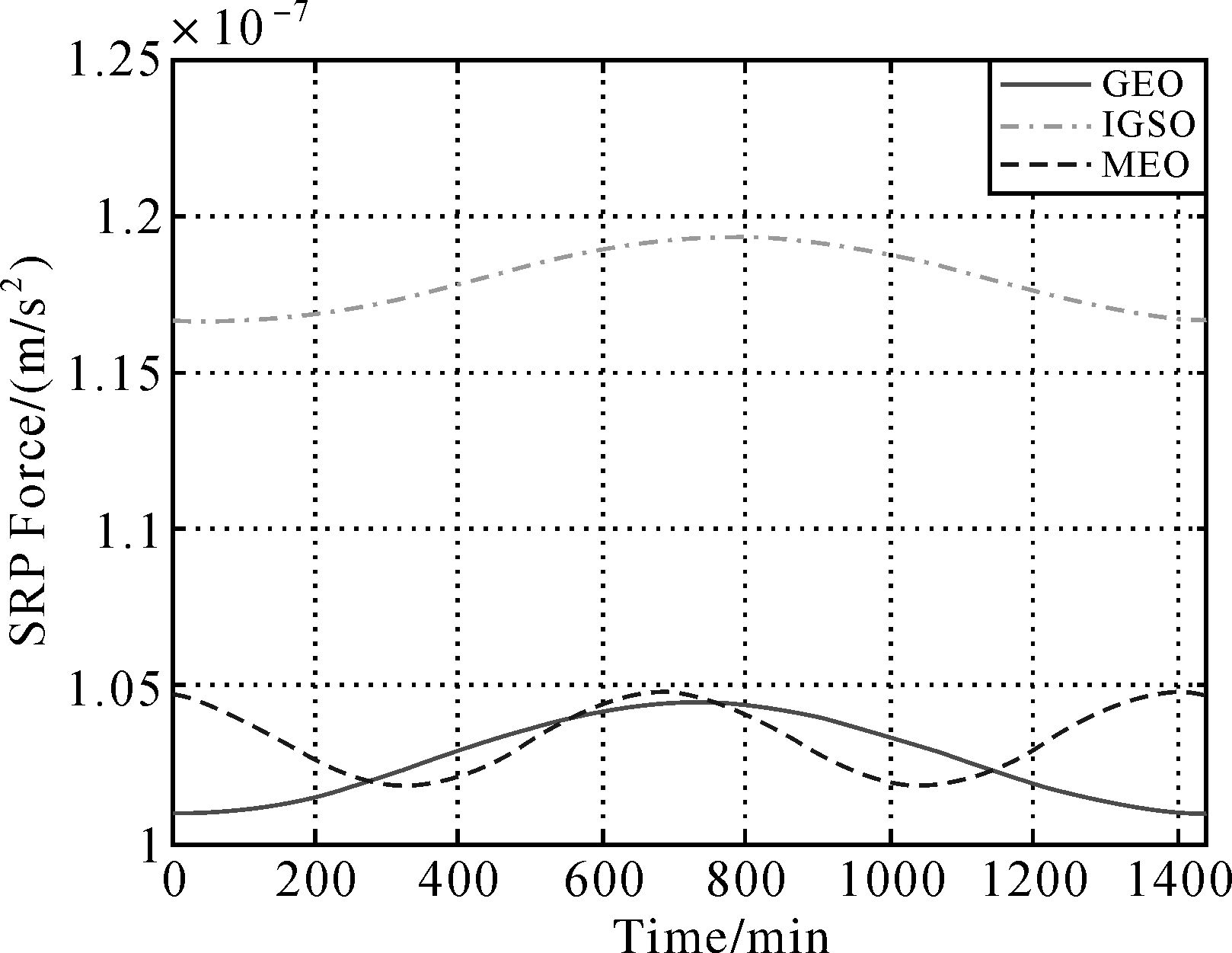
星载加速度计的设计应根据卫星的使用目的,主要从测量范围和测量精度两方面考虑。对于导航卫星而言,非保守力主要是太阳光压,BD的Prn01(GEO)、Prn06(IGSO)以及GPS的Prn01(MEO)卫星在2015-07-02所受太阳光压大小如图 1。可见3类导航卫星所受光压量级为10-7 m/s2,一般的重力卫星星载加速度计从测量范围上可以用来测量导航卫星所受的光压。若暂时不考虑卫星调轨所受的机动力,则测程为±2×10-7m/s2的加速度计已能较好满足导航卫星定轨需要。对用于北斗卫星自主定轨的星载加速度计的精度需求问题,本试验模拟了不同精度的加速度计进行卫星自主定轨。如上文所述,星载加速度计在使用中需要对其测量偏差进行校正。在本实验中,对于星载加速度计测量偏差的模拟主要基于常规的比例-偏差模型,如式(1) 所示。假设比例系数已通过长期的经验系数准确求出;对于偏差系数,借鉴GRACE-A卫星的偏差系数先验模型(表 2),模拟偏差量将其添加到卫星定轨的动力学模型中。
|
| 图 1 导航卫星太阳光压摄动 Fig. 1 The SRP forces of navigation satellites |
目前ECOM光压模型在多个数据处理中心使用,在本试验中主要采用ECOM模型来对IGS精密星历进行拟合,以提取卫星所受太阳光压来仿真生成连续的星历。ECOM模型表达式如下[16]
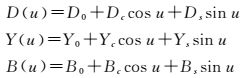 (3)
(3)
式中, u为卫星在其轨道面内相对于其升交点的角距;D(u)、Y(u)、B(u)分别为单位矢量eD、eY、eB的方向系数;eD为卫星—太阳方向单位矢量;eY为太阳能光板轴向单位矢量;eB、eD和eY构成右手坐标系。研究表明ECOM 5参数模型(Reduced ECOM)相对于完整的ECOM模型,在北斗IGSO、MEO定轨精度和计算效率上更有优势[34-35],其相对于完整的ECOM模型舍去了D、Y方向的周期项。该试验使用ECOM 5参数模型来对北斗卫星导航系统进行自主定轨。
1.2 自主定轨算法根据双频电离层、相对论效应、相位中心等改正后的卫星i与j之间双向伪距观测量,可建立如下观测方程
 (4)
(4)
式中,ρij和ρji为伪距观测值;Lij和Lji为星间几何距离;c为光速;δi1、δj1、δi2、δj2为卫星i、j在不同观测时刻的钟差;εij和εji为观测噪声。将卫星双向观测量进行相减可以得到自主定轨的时间同步观测方程,双向观测量相加并进行线性化,可以得到自主定轨的轨道确定观测方程。
1.2.1 时间同步观测方程 (5)
(5)
式中
 (6)
(6)
式中,tk1、tk2为卫星信号发射和接收的时刻;t0为定轨弧段的初始时刻;a0k、a1k为卫星时钟偏差和卫星钟差的一次多项式系数。
1.2.2 轨道确定观测方程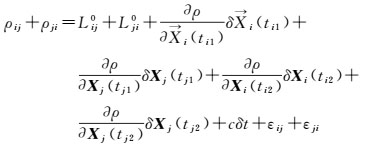 (7)
(7)
式中
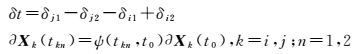 (8)
(8)
式中,ψ(tkn, t0)为状态转移矩阵;∂Xk为状态改正量。对卫星运动方程和变分方程进行数值积分,可分别得到卫星在任意时刻的状态和状态转移矩阵。
使用拓展卡尔曼滤波器进行集中式卫星自主定轨,分别由轨道确定观测方程和时间同步观测方程,同时估计所有卫星的轨道参数(位置、速度及动力学模型参数或加速度计偏差参数)和钟差参数,滤波步长为15 min。为了对星座整体旋转进行抑制,对于MEO和IGSO卫星,采用卡尔曼滤波计算轨道时各步预测的轨道倾角i和升交点赤经Ω作为滤波解算的约束条件;对于GEO卫星,由于轨道倾角为0,故采用第二类无奇点轨道根数h=sin icos Ω, k=sin isin Ω来建立约束条件方程[5]。
2 模拟试验由于北斗卫星系统目前还没有实现35颗星的全星座,所以本试验以GPS卫星取代BD的中轨卫星,研究对象为2015-07-02 00:00:00时起60 d内未进行轨道机动等操作具有连续精密星历的23颗GPS卫星,以及BD的5颗GEO卫星、5颗IGSO卫星。为了模拟更接近真实情况的非保守力,首先将研究时段内的IGS精密星历由动力学模型以天为单位进行拟合,估计出每颗卫星初始状态参数与光压参数(ECOM);然后由所估计的卫星参数, 通过数值积分,输出各个卫星在不同历元所受到的光压摄动(步长为5 min)。BD的GEO和IGSO卫星具有频繁的轨道机动,对于发生机动的卫星,采用前一天所估计的卫星参数,通过数值积分来模拟该天卫星所受的光压。利用所提取的光压摄动时间序列,结合其他卫星摄动力学模型,由数值积分生成试验所用33颗卫星参考星历。由模拟星历以及IGS发布的卫星钟差数据,采用时分多址(TDMA)的方式生成星间链路数据[3, 36],并添加相应的观测量误差(包括卫星钟差、相对论效应误差、卫星和接收机天线相位偏差、校正后信号发射与接收的硬件延迟误差以及测量随机噪声[37])。采用两种方案对卫星进行自主定轨试验,并对定轨结果进行对比。
方案1:仅使用星间链路数据进行自主定轨。结合Reduced ECOM光压模型,由时间同步观测方程和轨道确定观测方程,通过卡尔曼滤波分别估计卫星钟差和初始位置、速度与光压参数。
方案2:使用星间链路数据和星载加速度计数据进行自主定轨。星载加速度计可以准确测量非保守力(太阳光压),但本身会有观测误差和测量偏差。观测误差根据不同的加速度计精度指标(σ=1×10-10m/s2, σ=1×10-9m/s2, σ=5×10-9m/s2和σ=1×10-8m/s2),在定轨过程生成随机噪声;测量偏差由GRACE-A卫星加速度计的先验偏差模型进行模拟,偏差参数在自主定轨时需要进行估计。同样,由时间同步观测方程和轨道确定观测方程,通过卡尔曼滤波分别估计卫星钟差和初始位置、速度与加速度计偏差参数。
星间链路数据生成的参数设置如表 3所示。
| 参数项 | 参数配置 |
| 观测量采样步长/s | 300.0 |
| 卫星对间测量时间/s | 3.0 |
| GEO和IGSO卫星波束角 | 10.0°≤β≤45.0° |
| MEO卫星波束角 | 15.0°≤β≤60.0° |
| 观测量噪声/m | 0.33 |
| 发射信号固定偏差/m | 0.31 |
| 发射信号周期性偏差/m | 0.21 |
| 接收信号固定偏差/m | 0.51 |
| 接收信号周期性偏差/m | 0.27 |
按照1.2节所述算法对星座进行集中式自主定轨,最后将定轨结果与模拟的卫星星历进行对比,评价自主定轨精度。
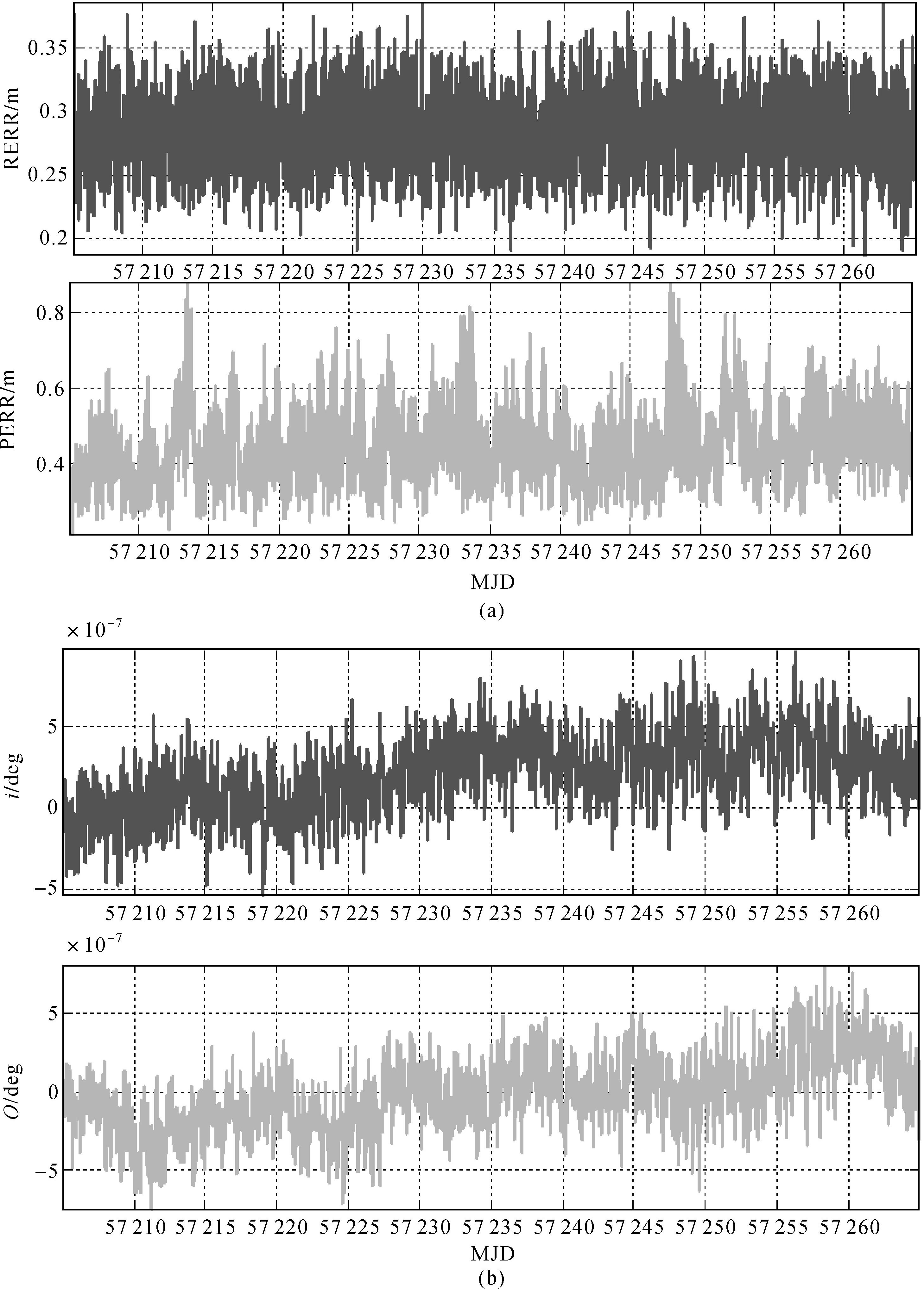
3 结果与分析 3.1 预测轨道精度在试验中采用了预测的轨道倾角i和升交点赤经Ω来抑制星座的整体旋转,因此预测的轨道精度影响着自主定轨结果。轨道初值和力学模型的准确性决定了轨道预测的精度。在该自主定轨试验中,预测轨道初值为上一步卡尔曼滤波计算结果;力学模型与自主定轨所使用模型一致,力模型参数或者加速度计校正参数也为上一步卡尔曼滤波计算结果。图 2与图 3分别给出了在使用光压模型和加速度计(精度为σ=1×10-9m/s2)进行自主定轨过程中预测轨道精度。图 2(a)、图 3(a)为所有卫星轨道在径向(RERR)和水平方向(PERR,即切向和法向)误差的RMS[36];图 2(b)、3(b)以一MEO卫星为例给出其轨道倾角i和升交点赤经Ω误差随时间的变化,横轴为时间轴MJD。由图可知,使用光压模型和使用加速度计进行自主定轨时预测轨道精度差别较大。使用光压模型定轨时,预测轨道在60 d内径向误差变化不大,约0.2~0.6 m,而水平方向误差随着时间逐渐增大至4 m,这与其位置参数轨道倾角i和升交点赤经Ω的变化趋势一致;使用加速度计定轨时,预测轨道误差随时间没有明显变化,径向误差在0.3 m左右波动,水平方向误差在分米级,轨道位置参数精度比使用光压模型预测精度高一个量级。可见,相比使用光压模型改正进行自主定轨,使用加速度计能提供更精确的预测轨道,基于此预测轨道对星座位置参数进行旋转约束,加速度计定轨能提供相对准确的约束条件。

|
| 图 2 使用光压模型定轨预测轨道精度 Fig. 2 Orbit prediction accuracy with SRP model |
|
| 图 3 使用加速度计定轨预测轨道精度 Fig. 3 Orbit prediction accuracy with accelerometer |
3.2 不同精度加速度计自主定轨
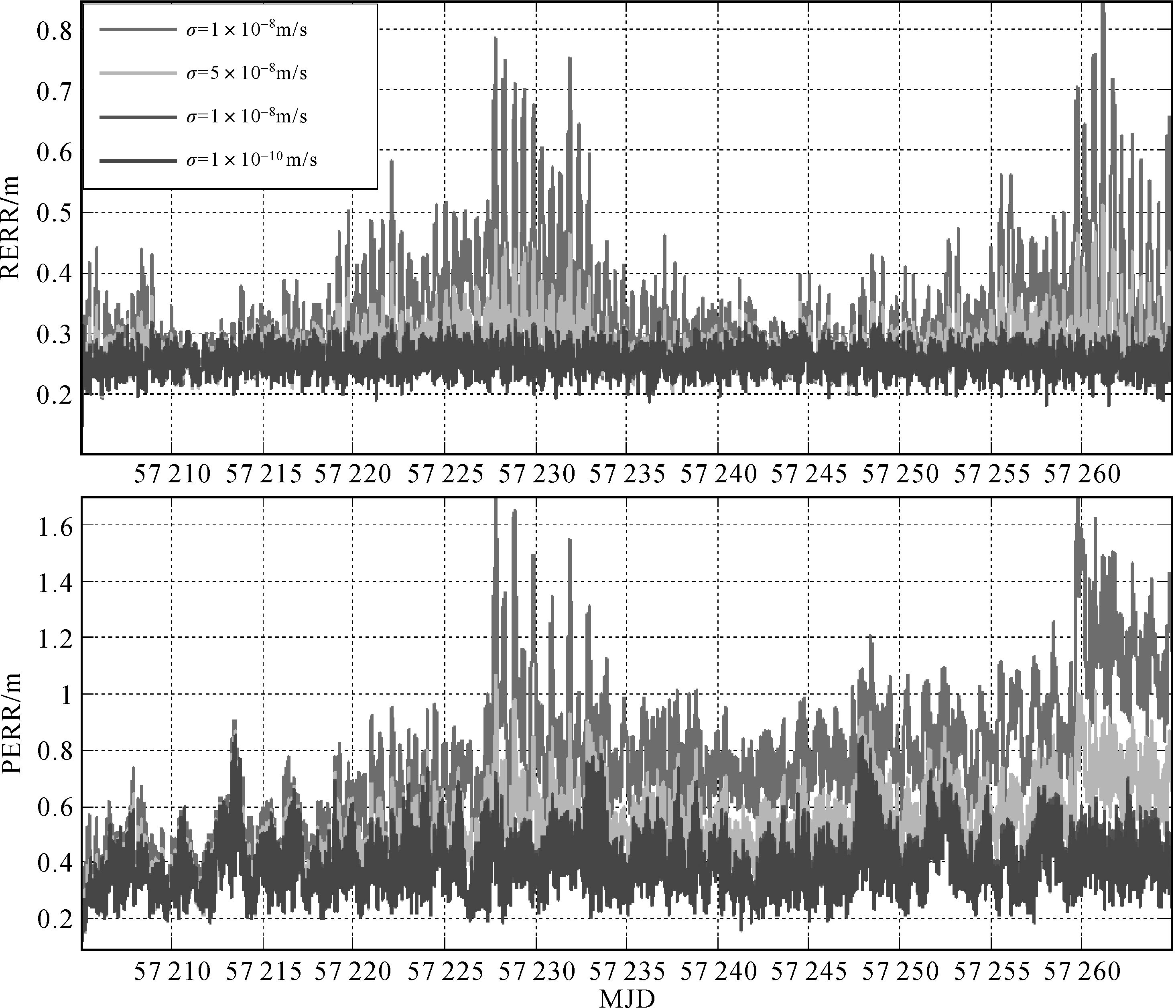
使用星上加速度计进行自主定轨,除了需要估计加速度计系统偏差参数,还要考虑其测量精度。使用不同精度(σ=1×10-10m/s2, σ=1×10-9m/s2, σ=5×10-9m/s2和σ=1×10-8m/s2)的加速度计进行卫星自主定轨,所有卫星轨道径向误差(RERR)和水平方向误差(PERR)的RMS统计结果如图 4所示,横轴为时间轴MJD。由图可知,在加速度计精度为1×10-8m/s2时,自主定轨60 d轨道径向误差达到0.8 m,水平方向误差最大为1.6 m;随着加速度计精度的改善,定轨精度也逐渐提高,而精度为1×10-9m/s2和1×10-10m/s2的加速度计在所定轨时段内定轨结果相当。因此,在当前模拟的星间观测数据精度条件下,精度为σ=1×10-9m/s2的加速度计较适用于导航卫星自主定轨。
|
| 图 4 不同精度加速度计定轨轨道精度 Fig. 4 Orbit determination accuracy with different accelerometers |
3.3 两种方案定轨结果精度评定
将生成星间链路数据所使用的仿真星历作为参考星历,对两种方案的自主定轨结果分别进行精度评定。
方案1:星间测距观测与光压模型定轨
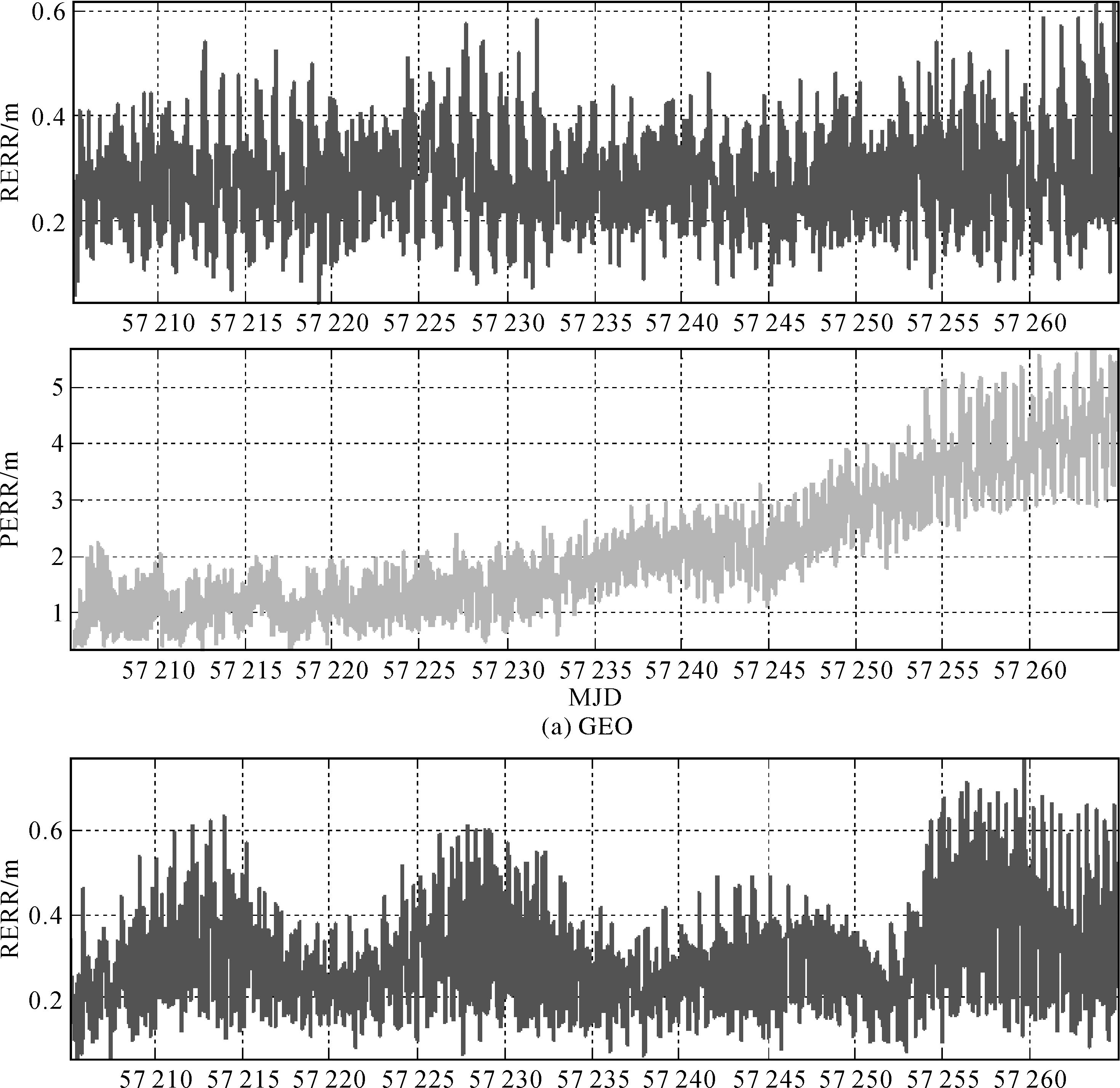
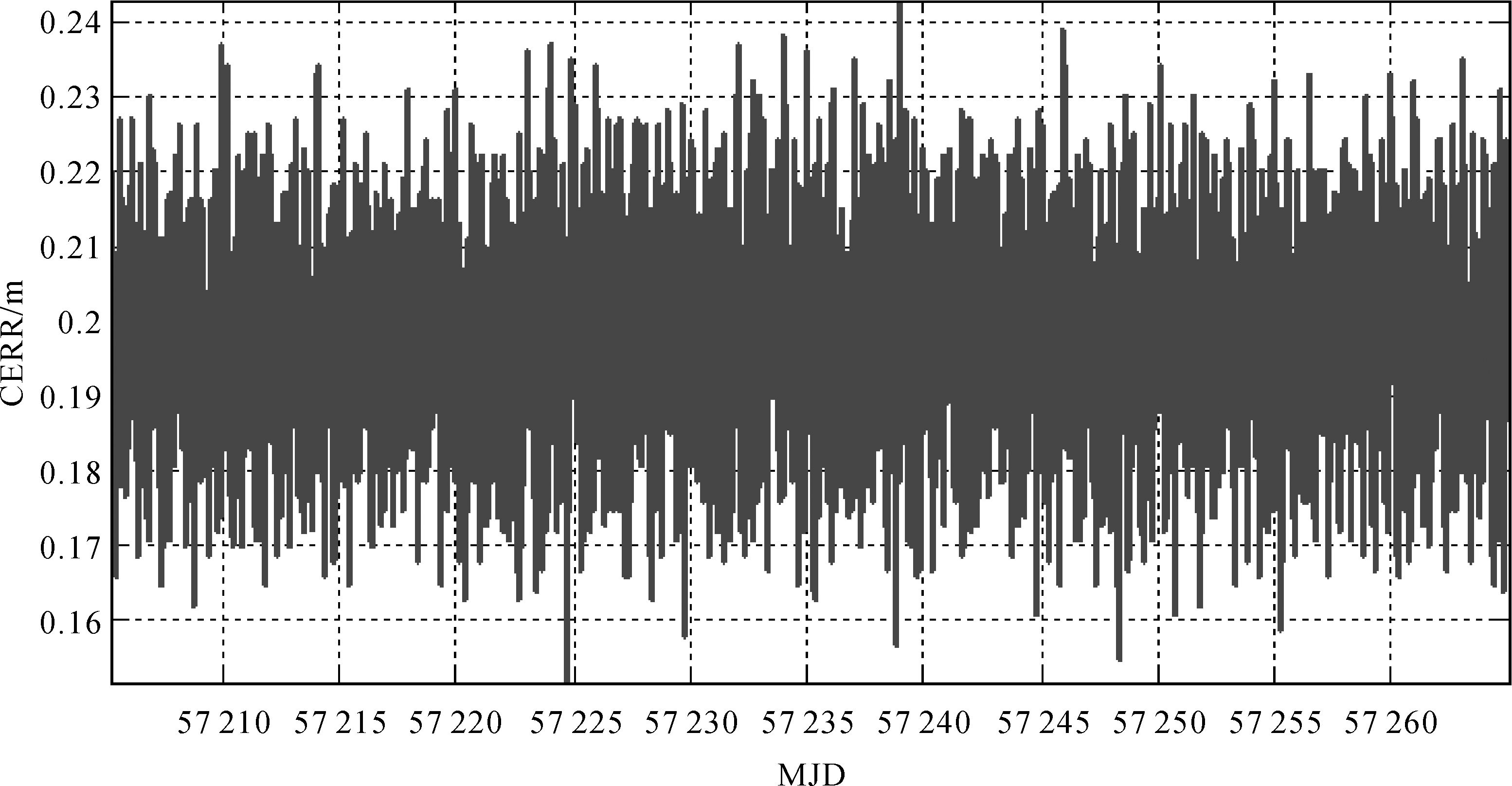
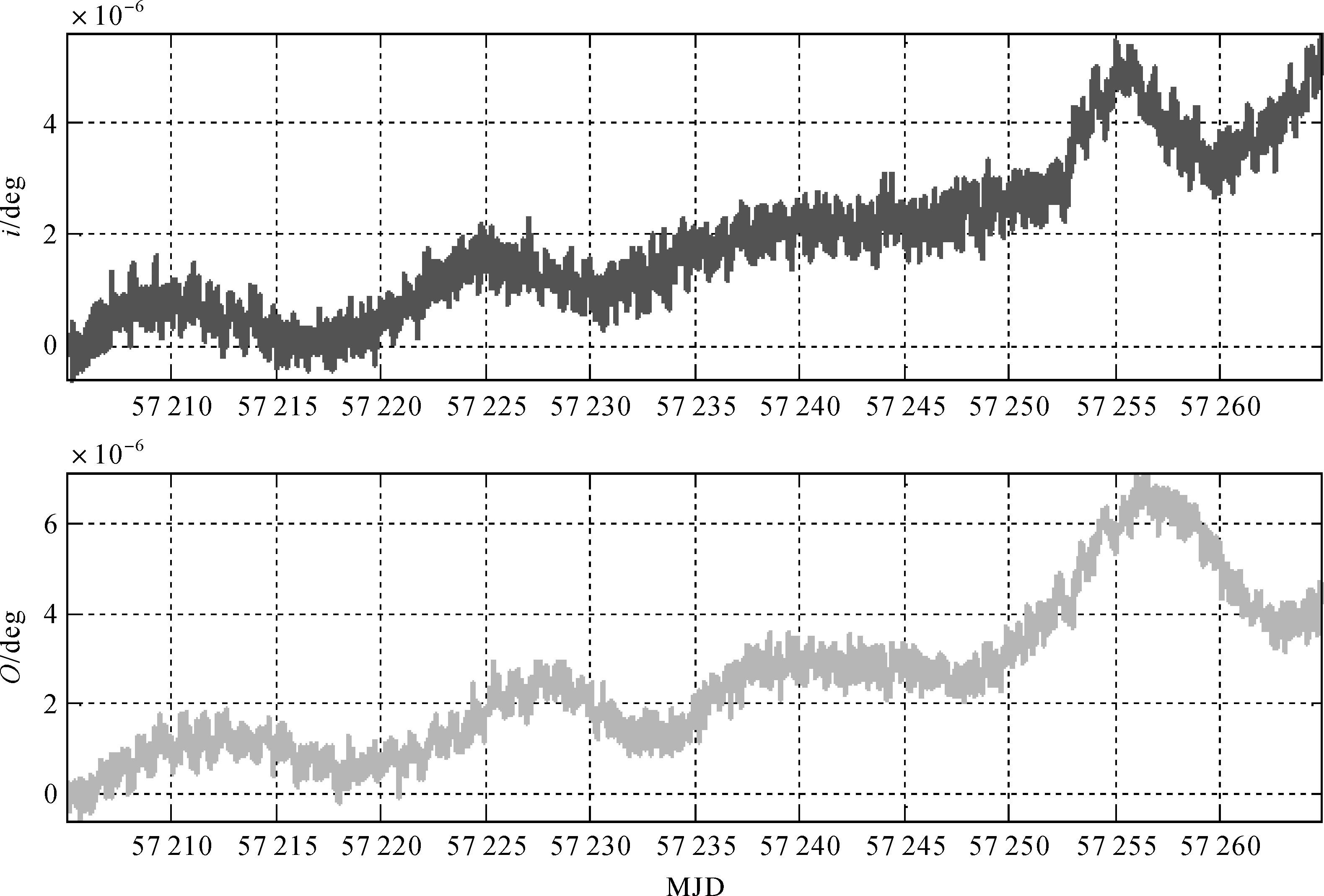
所有GEO、IGSO和MEO星座的径向误差RERR、水平方向误差PERR(法向与切向综合误差),以及全星座相对钟差投影至距离的误差CERR的RMS(计算公式[36])统计如图 5、图 6所示,横轴为时间轴MJD。由图 5可知,在使用光压模型进行光压摄动改正自主定轨60 d内,所有卫星径向最大误差约0.6 m;在水平方向,所有星座误差随着定轨时间的增长以相同的趋势逐渐增大,GEO和IGSO卫星最大误差达5.0~6.0 m,MEO卫星最大约3.0 m,这与星座的高度成一定的比例关系。由图 6知,卫星的相对钟差不受定轨时长的影响,保持在0.16~0.24 m。为了对定轨误差进一步分析,将一MEO卫星轨道形状参数(半长轴a和偏心率e)和位置参数(轨道倾角i和升交点赤经Ω)误差随时间的变化绘制如图 7和图 8所示。可以发现,卫星的形状参数误差随时间没有明显变化,而位置参数误差随着定轨时间的延长而发生偏移。统计所有卫星位置参数误差的变化,还可以发现同一轨道面上所有卫星轨道倾角i和升交点赤经Ω的变化趋势是一致的。由此可见,使用光压模型在一定程度上可以估计光压摄动,然而在只有距离观测量的情况下,残留误差会导致卫星轨道倾角i和升交点赤经Ω随着时间的延长而逐渐漂移,从而使星座产生整体旋转。另外,对比3.1节可以发现卫星定轨中的预测轨道与结果计算轨道误差非常接近,这是由于预测轨道是由上一步滤波结果只向前积分了一步,而预测轨道的位置参数又是定轨解算的约束条件。
|
| 图 5 使用光压模型定轨GEO、IGSO和MEO星座轨道误差 Fig. 5 GEO, IGSO and MEO satellites orbit determination accuracy with SRP model |
|
| 图 6 使用光压模型定轨全星座相对钟差 Fig. 6 The constellation relative clock error with SRP model |

|
| 图 7 使用光压模型定轨MEO轨道形状参数误差 Fig. 7 MEO satellites orbit determination shape parameters accuracy with SRP model |
|
| 图 8 使用光压模型定轨MEO轨道位置参数误差 Fig. 8 MEO satellites orbit determination position parameters accuracy with SRP model |
方案2:星间测距观测与星载加速度计定轨
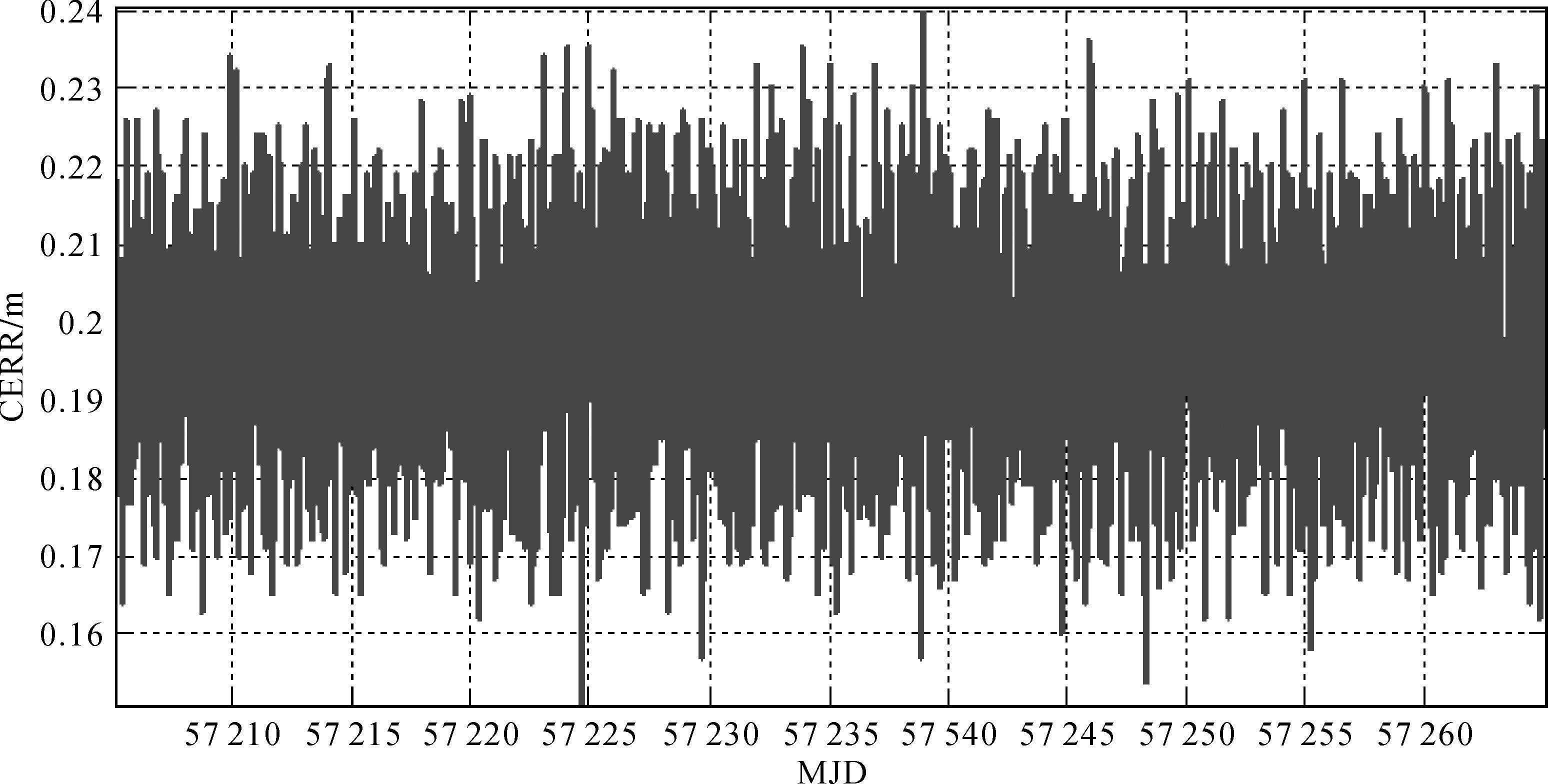
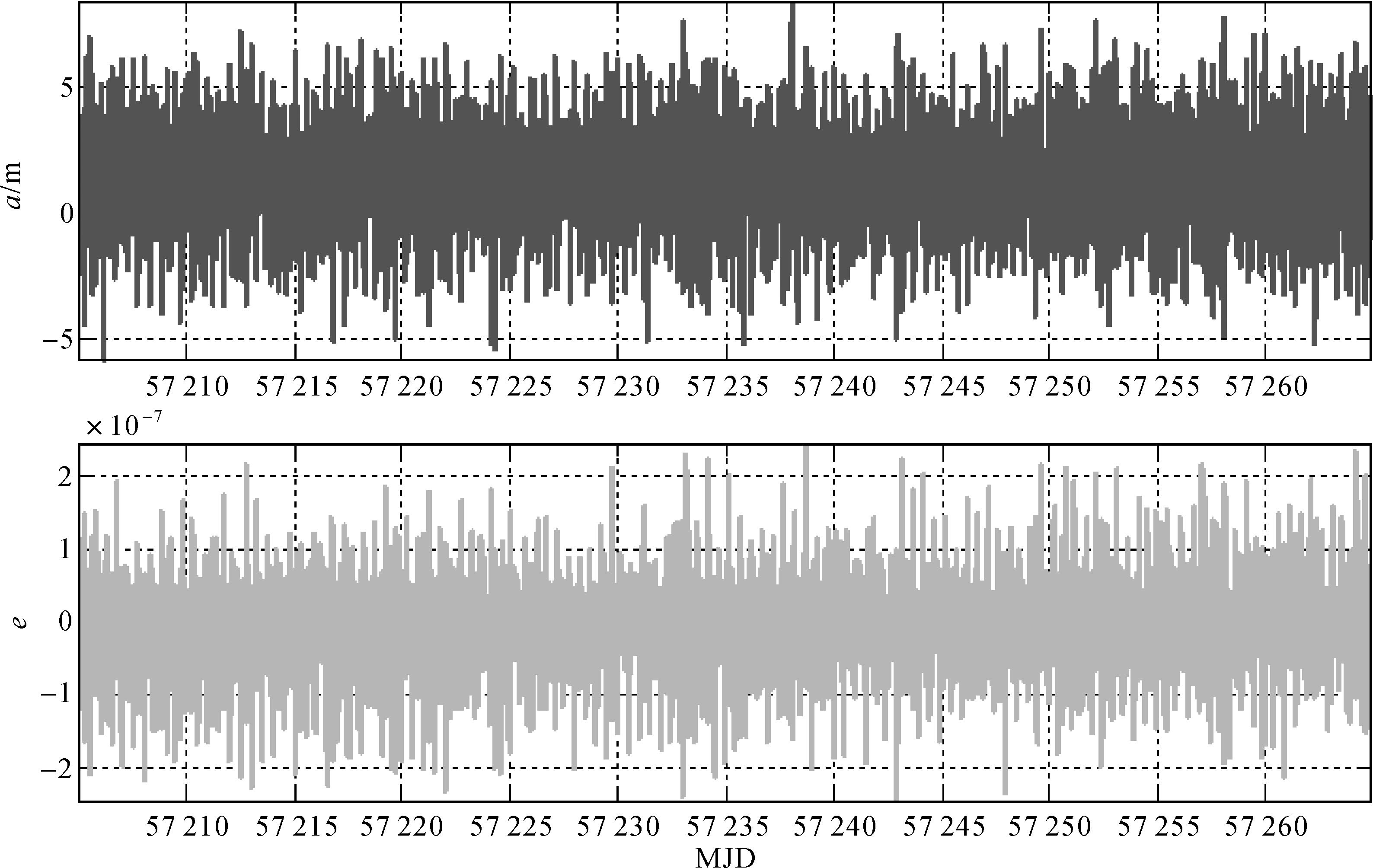
所有GEO、IGSO和MEO星座的径向误差RERR、水平方向误差PERR,以及全星座相对钟差投影至距离的误差CERR的RMS统计如图 9和图 10所示,横轴为时间轴MJD。由图可知,在使用星载加速度计(精度为1×10-9m/s2)测量非保守力自主定轨60 d内,受观测量系统偏差和观测噪声的影响,所有卫星径向精度约0.2~0.4 m,稍优于方案1,相对钟差精度与方案1近似;在水平方向,轨道误差随时间的累积比较缓慢,GEO、IGSO和MEO卫星最大误差分别约为2.0 m、0.6 m和0.3 m,IGSO和MEO卫星水平方向精度较方案1提高了一个量级。同样,图 11—图 12显示了一个MEO卫星轨道形状和位置参数误差的变化,与方案1近似轨道的形状参数误差基本不随时间变化,位置参数随着时间的延长发生缓慢漂移,变化量相对于使用光压模型低一个量级。

|
| 图 9 使用加速度计定轨GEO、IGSO和MEO星座轨道误差 Fig. 9 GEO, IGSO and MEO satellites orbit determination accuracy with accelerometers |
|
| 图 10 使用加速度计定轨全星座相对钟差 Fig. 10 The constellation relative clock error with accelerometers |
|
| 图 11 使用加速度计定轨MEO轨道形状参数误差 Fig. 11 MEO satellites orbit determination shape parameters accuracy with accelerometers |

|
| 图 12 使用加速度计定轨MEO轨道形状参数误差 Fig. 12 MEO satellites orbit determination shape parameters accuracy with accelerometers |
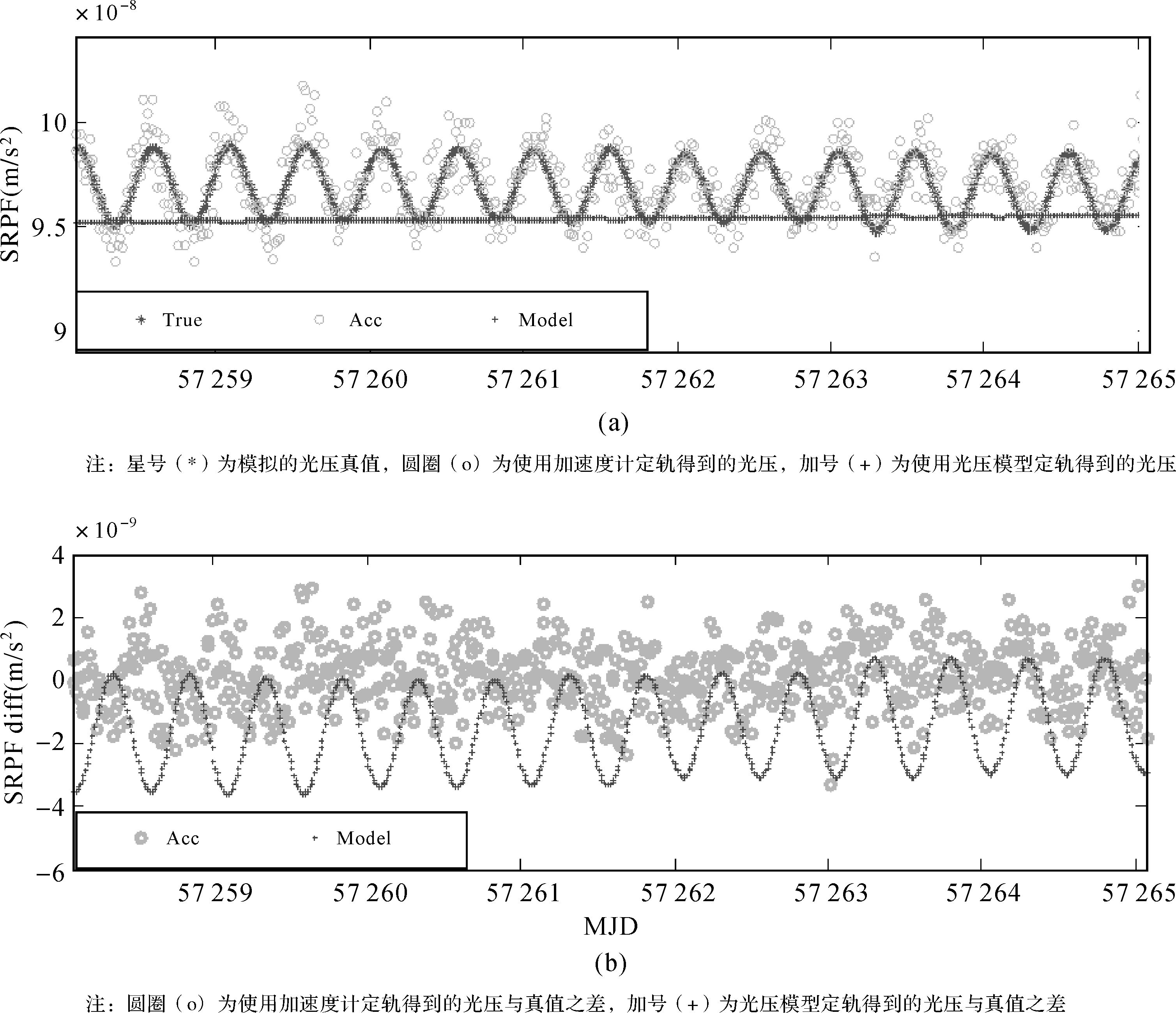
由以上结果可知,使用加速度计进行自主定轨较利用光压模型定轨能得到更高的轨道精度,延长卫星自主定轨运行时间。为了进一步分析使用加速度计定轨能得到较高精度的原因,图 13给出一个MEO卫星自主定轨最后一个星期内(第54~60 d)分别使用加速度计、光压模型得到的太阳光压和模拟的光压真值,以及两种方式求解的光压与真值之差。模拟的光压在相邻的两天之间不连续,是因为其是通过IGS精密星历以天为单位进行似合提取的。由图 13可以看到使用两种方式定轨都可以在一定程度上还原太阳光压。使用加速度计定轨求解的太阳光压误差主要是测量误差,即观测噪声(σ=1×10-9m/s2)和不能完全改正的测量偏差,所得到的光压会在真值上下波动(误差均值为-3.02×10-10m/s2);使用光压模型定轨得到的光压误差是估计误差,其呈现出明显的正弦周期性,且相对于零值具有系统性偏差(误差均值为-1.44×10-9m/s2)。由此可以推知,使用加速度计定轨时所求解的与其测量精度相关、围绕真值具有随机噪声的光压摄动力,虽然对轨道计算由一定影响,但由于是量级较小的随机误差,其对轨道误差随时间的积累影响较小;而使用光压模型定轨,能在一定的精度上估计卫星所受光压,但光压误差是均值不为零的周期性误差,这会使轨道误差随着定轨时间的延长而增大,在只有距离观测量的约束下出现星座整体旋转问题。
|
| 图 13 模拟光压与定轨解算光压 Fig. 13 Comparison of orbit determination derived SRP forces with the simulated true forces |
可见,使用合适的星载加速度计能够高精度地测量非保守力,为卫星动力学积分提供与实际情况更加吻合的力学模型,应用于导航卫星自主定轨中,减少了因为力学模型不准确而产生的轨道误差累积,可以有效地抑制星座整体旋转,提高卫星自主定轨精度。
4 结论与展望本文通过模拟试验,主要从定轨精度方面探讨了使用星载加速度计增强北斗卫星系统自主定轨性能的可行性。通过两种定轨方案对比,说明了采用加速度计辅助自主定轨的优势。
对于导航卫星而言,星载加速度计测量的非保守力主要是光压摄动,在常规的卫星定轨中光压通常需要建立模型与轨道状态参数同时估计。在本文研究中,方案1是使用常规的光压模型(Reduced ECOM)进行光压改正,在定轨过程中同时估计卫星位置、速度和光压参数;方案2是假定星载加速度计可以以一定的精度测量光压摄动,试验表明精度为1×10-9m/s2的加速度计可以满足分米级误差星间链路数据的导航卫星自主定轨,由于加速度计偏差的影响,在定轨过程中估计卫星的位置、速度以及加速度计偏差参数。
将模拟星间链路数据使用的星历作为参考星历对两种定轨方案进行精度评定。结果显示,使用光压模型进行自主定轨,在一定程度上可以对光压摄动进行改正,但残留误差会随着自主定轨时间的延长而累积,导致星座出现整体旋转。在观测数据噪声为0.33 m,信号发射与接收系统固定偏差和周期性偏差为0.21~0.51 m,自主定轨60 d内卫星径向误差受观测量误差的影响最大约0.6 m,但GEO和IGSO卫星水平方向误差因星座整体旋转达到5~6 m,MEO卫星约3 m。使用星载加速度计进行自主定轨,在相同的观测数据与定轨时长内,径向误差约0.2~0.4 m,水平方向GEO、IGSO和MEO卫星最大误差分别为2.0 m、0.6 m和0.3 m,IGSO和MEO卫星相对于使用光压模型改正定轨精度提高了一个量级。使用加速度计能够较好地还原卫星所受非保守力,而使用光压模型得到的光压与真值偏差具有周期与非零均值性。动力学模型的不准确会使积分解算的轨道出现误差,而自主定轨时星间链路的距离观测量不能对水平方向误差进行改正,从而使卫星星座出现整体旋转的问题。从本文的模型试验来看,合适加速度计能够提供准确的非保守力,能够有效地解决力学模型不准确导致的自主定轨星座随时间整体旋转的问题,提高定轨精度,延长定轨时长。鉴于本文是基于精密星历的模拟试验,也没有真实的卫星加速度计数据,在未来能够获得真实的星间链路数据或者星载加速度计数据的条件下,可进一步试验以验证本文所采用方案的有效性。
对北斗卫星进行自主定轨,还需要解决的一个问题就是GEO和IGSO星座的频繁机动。从定轨算法上,其可以通过自适应滤波等方法,在调轨期间减少对动力学模型的依赖,主要由观测值对卫星位置进行解算以实现星上连续定轨。而如果星载加速度计能在保证测量精度的前提下,测量范围达到一般轨道机动脉冲力的大小(10-5-10-4m/s2),则可以在卫星调轨期间仍然借助力学模型进行精密定轨。
| [1] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [2] | CSNO. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal (Version 2.0)[Z]. China Satellite Navigation Office, 2013. |
| [3] | 刘万科. 导航卫星自主定轨及星地联合定轨的方法研究和模拟计算[D]. 武汉: 武汉大学, 2008. LIU Wanke. Research and Simulation on Autonomous Orbit Determination and Combined Orbit Determination of Navigation Satellites[D]. Wuhan:Wuhan University, 2008. |
| [4] | 王威, 董绪荣, 柳丽, 等. 基于全球导航卫星系统的高轨卫星定轨理论研究及仿真实现[J]. 测绘学报, 2011, 40(S1): 6–10. WANG Wei, DONG Xurong, LIU Li, et al. Research and Simulation of Orbit Determination for Geostationary Satellite Based on GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 6–10. |
| [5] | 龚晓颖. 北斗系统集中式自主实时轨道确定与时间同步方法研究[D]. 武汉: 武汉大学, 2013: 86-120. GONG Xiaoying. Research on Centralized Autonomous Realtime Orbit Determination and Time Synchronization of BDS[D]. Wuhan:Wuhan University, 2013:86-120. |
| [6] | 陈艳玲, 胡小工, 周善石, 等. 基于星间测距的导航卫星自主定轨新算法[J]. 中国科学:物理学力学天文学, 2015, 45(7): 079511. CHEN Yanling, HU Xiaogong, ZHOU Shanshi, et al. A New Autonomous Orbit Determination Algorithm Based on Inter-satellite Ranging Measurements[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2015, 45(7): 079511. |
| [7] | HE Lina, ZHOU Hairui, ZHANG Gongyuan. Improving Extended Kalman Filter Algorithm in Satellite Autonomous Navigation[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2017, 231(4): 743–759. DOI:10.1177/0954410016641708 |
| [8] | CAI Zhiwu, HAN Chunhao, CHEN Jinping, et al. Constellation Rotation Error Analysis and Control in Long-term Autonomous Orbit Determination for Navigation Satellites[J]. Journal of Astronautics, 2008, 29(2): 522–528. |
| [9] | 李征航, 卢珍珠, 刘万科, 等. 导航卫星自主定轨中系统误差△Ω和△t的消除方法[J]. 武汉大学学报(信息科学版), 2007, 32(1): 27–30. LI Zhenghang, LU Zhenzhu, LIU Wanke, et al. Method for Eliminating Systematic Error △Ω and △t in Autonomous Orbit Determination of Navigation Satellites[J]. Geomatics and Information Science of Wuhan University, 2007, 32(1): 27–30. |
| [10] | 刘万科, 龚晓颖, 李征航, 等. 综合星间和地面测距数据的导航卫星联合定轨[J]. 武汉大学学报(信息科学版), 2010, 35(7): 811–815. LIU Wanke, GONG Xiaoying, LI Zhenghang, et al. Combined Orbit Determination of Navigation Satellites with Cross-Link Ranging Observations and Ground Tracking Observations[J]. Geomatics and Information Science of Wuhan University, 2010, 35(7): 811–815. |
| [11] | 杜玉军, 王甫红, 王泽民, 等. 导航卫星自主定轨星座旋转误差的地面校正算法[J]. 武汉大学学报(信息科学版), 2015, 40(4): 534–539. DU Yujun, WANG Fuhong, WANG Zemin, et al. A Correction Algorithm of Constellation Rotation Error in Autonomous Navigation Using Ground Stations[J]. Geomatics and Information Science of Wuhan University, 2015, 40(4): 534–539. |
| [12] | RAJAN J A, BRODIE P, RAWICZ H. Modernizing GPS Autonomous Navigation with Anchor Capability[C]//Proceedings of the 16th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS/GNSS 2003). Portland, OR:Oregon Convention Center, 2003:1534-1542. |
| [13] | RAJAN J A. Highlights of GPS Ⅱ-R Autonomous Navigation[C]//Proceedings of the 58th Annual Meeting of the Institute of Navigation and CIGTF 21st Guidance Test Symposium. Albuquerque, NM:Hyatt Regency Hotel, 2002:354-363. |
| [14] | FLIEGEL H F, GALLINI T E, SWIFT E R. Global Positioning System Radiation Force Model for Geodetic Applications[J]. Journal of Geophysical Research, 1992, 97(B1): 559–568. DOI:10.1029/91JB02564 |
| [15] | ZIEBART M, DARE P. Analytical Solar Radiation Pressure Modelling for GLONASS Using a Pixel Array[J]. Journal of Geodesy, 2001, 75(11): 587–599. DOI:10.1007/s001900000136 |
| [16] | BEUTLER G, BROCKMANN E, GURTNER W, et al. Extended Orbit Modeling Techniques at the CODE Processing Center of the International GPS Service for Geodynamics (IGS):Theory and Initial Result[J]. Manuscript Geodaetica, 1994, 19(6): 367–386. |
| [17] | ARNOLD D, MEINDL M, BEUTLER G, et al. CODE's New Solar Radiation Pressure Model for GNSS Orbit Determination[J]. Journal of Geodesy, 2015, 89(8): 775–791. DOI:10.1007/s00190-015-0814-4 |
| [18] | SPRINGER T A, BEUTLER G, ROTHACHER M. A New Solar Radiation Pressure Model for GPS Satellites[J]. GPS Solutions, 1999, 2(3): 50–62. DOI:10.1007/PL00012757 |
| [19] | BAR-SEVER Y E, RUSS K M. New and Improved Solar Radiation Models for GPS Satellites Based on Flight Data[R]. Air Force Materiel Command Space and Missile Systems Center/CZSF, Pasadena, CA:Jet Propulsion Laboratory, California Institute of Technology, 1997. |
| [20] | BAR-SEVER Y, KUANG D. New Empirically Derived Solar Radiation Pressure Model for Global Positioning System Satellites[R]. IPN Progress Report 42-159, [S.l.]:IPN, 2004. |
| [21] | RODRIGUEZ-SOLANO C J, HUGENTOBLER U, STEIGENBERGER P. Adjustable Box-Wing Model for Solar Radiation Pressure Impacting GPS Satellites[J]. Advances in Space Research, 2012, 49(7): 1113–1128. DOI:10.1016/j.asr.2012.01.016 |
| [22] | CHEN Qiujie, SHEN Yunzhong, CHEN Wu, et al. An Improved GRACE Monthly Gravity Field Solution by Modeling the Non-conservative Acceleration and Attitude Observation Errors[J]. Journal of Geodesy, 2016, 90(6): 503–523. DOI:10.1007/s00190-016-0889-6 |
| [23] | 陈秋杰, 沈云中, 张兴福, 等. 基于GRACE卫星数据的高精度全球静态重力场模型[J]. 测绘学报, 2016, 45(4): 396–403. CHEN Qiujie, SHEN Yunzhong, ZHANG Xingfu, et al. GRACE Data-based High Accuracy Global Static Earth's Gravity Field Mode[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 396–403. DOI:10.11947/j.AGCS.2016.20150422 |
| [24] | BRUINSMA S, TAMAGNAN D, BIANCALE R. Atmospheric Densities Derived from CHAMP/STAR Accelerometer Observations[J]. Planetary and Space Science, 2004, 52(4): 297–312. DOI:10.1016/j.pss.2003.11.004 |
| [25] | 李文文, 李敏, 施闯, 等. 基于GRACE星载加速度计数据的热层密度反演[J]. 地球物理学报, 2016, 59(9): 3159–3171. LI Wenwen, LI Min, SHI Chuang, et al. Thermosphere Mass Density Derivation Using On-board Accelerometer Observations from GRACE Satellites[J]. Chinese Journal of Geophysics, 2016, 59(9): 3159–3171. DOI:10.6038/cjg20160903 |
| [26] | TOUBOUL P, WILLEMENOT E, FOULON B, et al. Accelerometers for CHAMP, GRACE and GOCE Space Missions:Synergy and Evolution[J]. Bollettino di Geofisica Teorica ed Applicata, 1999, 40(3-4): 321–327. |
| [27] | PENG Dongju, WU Bin. Application of Accelerometer Data in Precise Orbit Determination of GRACE-A and-B[J]. Chinese Journal of Astronomy and Astrophysics, 2008, 8(5): 603–610. DOI:10.1088/1009-9271/8/5/11 |
| [28] | BRUINSMA S, LOYER S, LEMOINE J M, et al. The Impact of Accelerometry on Champ Orbit Determination[J]. Journal of Geodesy, 2003, 77(1-2): 86–93. DOI:10.1007/s00190-002-0304-3 |
| [29] | KANG Z, TAPLEY B, BETTADPUR S, et al. Precise Orbit Determination for GRACE Using Accelerometer Data[J]. Advances in Space Research, 2006, 38(9): 2131–2136. DOI:10.1016/j.asr.2006.02.021 |
| [30] | BOCK H, JÄGGI A, BEUTLER G, et al. GOCE:Precise Orbit Determination for the Entire Mission[J]. Journal of Geodesy, 2014, 88(11): 1047–1060. DOI:10.1007/s00190-014-0742-8 |
| [31] | TOUBOUL P, FOULON B, CHRISTOPHE B, et al. CHAMP, GRACE, GOCE Instruments and Beyond[M]//KENYON S, PACINO M, MARTI U. Geodesy for Planet Earth, International Association of Geodesy Symposia. Berlin Heidelberg:Springer, 2012:215-221. |
| [32] | FROMMKNECHT B. Integrated Sensor Analysis of the GRACE Mission[D]. Munich, Germany:Technical University Munich, 2007. |
| [33] | BETTADPUR S. Recommendation for A-Priori BIAS and Scale Parameters for Level-1B ACC Data (Version 2)[Z]. GRACE TN-02, 2009. |
| [34] | LOU Yidong, LIU Yang, SHI Chuang, et al. Precise Orbit Determination of BeiDou Constellation Based on BETS and MGEX Network[J]. Scientific Reports, 2014(4): 4692. |
| [35] | ZHAO Qile, GUO Jing, LI Min, et al. Initial Results of Precise Orbit and Clock Determination for Compass Navigation Satellite System[J]. Journal of Geodesy, 2013, 87(5): 475–486. DOI:10.1007/s00190-013-0622-7 |
| [36] | ANANDA M P, BERNSTEIN H, CUNNINGHAM K E, et al. Global Positioning System (GPS) Autonomous Navigation[C]//Proceedings of 1990 IEEE Position Location and Navigation Symposium-A Decade of Excellence in the Navigation Sciences. Las Vegas, NV:IEEE, 1990:497-508. |
| [37] | MARTOCCIA D, BERNSTEIN H, CHAN Y, et al. GPS Satellite Timing Performance Using the Autonomous Navigation[C]//Proceeding of the 11th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1998). Nashville, TN:[s.n.], 1998:1705-1712. |


