2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西安测绘研究所, 陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, ChinaAbstract
卫星精密定轨是利用卫星的测轨数据改进某一特定历元并不精确的卫星状态矢量直至精确的过程[1-2]。对于导航卫星,地面监测站接收的伪距、载波相位等下行数据是最基本的定轨观测量。为了获得高精度的卫星轨道,要求数量较多且全球分布的地面监测站来提升卫星跟踪弧段[3-5]。然而,北斗监测站建设受地缘因素影响较大,实现全球布站较为困难,要提高区域定轨精度,需通过其他测量手段获得更多的观测量,弥补区域地面站观测的局限。星间链路增强是目前较为先进的手段,即通过卫星间距离测量增加区域地面站难以跟踪的卫星弧段的观测量,提高定轨精度、提升系统可靠性和抗干扰性。GPS现代化的重要目标之一就是利用星间链路数据实现自主导航。星间链路技术也是北斗着力发展的关键技术,有望在北斗全球系统中全面使用,彻底改变监测站区域分布的局限性,达到与全球布站同样的定轨精度[6-12],目前相关技术已在全球卫星系统试验卫星中得到初步验证。此外,对地观测技术的迅速发展和星载GNSS定轨技术的成熟,越来越多的低轨卫星(如TOPEX、CHAMP、JASON,GRACE、GOCE等)通过星载GPS接收机实现了高精度定轨[13-15],一种利用低轨卫星星载数据增强GPS等导航卫星定轨的方法被提出来[16]。数量较多对位置精度要求较高的低轨卫星的星载接收机可获得高精度的伪距和载波观测数据,若将其视为运动的“监测站”,便可将星载数据与地面监测站数据结合,共同用于导航卫星精密轨道,提升观测弧段[17-18],2002年IGS成立了LEO工作组,开始组织各家分析中心探讨联合处理地面和LEO星载GNSS数据对GNSS精密轨道等产品的改进作用。基于以上考虑,本文以我国在建的北斗全球系统为研究背景,探讨利用低轨卫星星载数据和星间链路增强北斗卫星定轨的可行性和精度,分析低轨卫星数量、轨位分布对北斗卫星精密定轨的影响,比较低轨卫星和星间链路数据对于导航卫星精密定轨增强的效能。
1 联合定轨数学模型地面监测站数据、低轨卫星星载数据和星间链路数据联合定轨观测模型可以简单表示如下
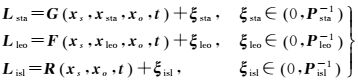 (1)
(1)
式中,Lsta、Lleo分别表示地面监测站接收机和星载接收机获得的北斗(BDS)观测数据;Lisl(isl:inter-satellite link)表示北斗卫星的星间测距数据;ξsta、ξleo、ξisl分别为相应的测量误差;Psta、Pleo、Pisl为对应的权矩阵;t为时间参数;xs为北斗卫星轨道有关参数;xleo为低轨卫星轨道有关参数;xsta为测站有关的参数,如站坐标、对流层延迟参数等;xo为观测量相关的参数,如载波相位模糊度、钟差参数、星间链路的设备时延等。
对上述观测方程进行线性化并改化为如下矩阵形式
 (2)
(2)
式中

式中,x(·)0表示参数初值;δ(·)表示参数的改正数,则对应的最小二乘解可以表示为
 (3)
(3)
式中,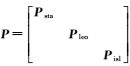
本文中联合定轨的主要任务是获得北斗卫星轨道参数,而解算中作为运动监测站的低轨卫星轨道参数仍为未知参数,需在定轨过程中一并解算,其受力更为复杂,尤其是太阳光压和大气阻力模型化较难[19]。因此,相比较传统依赖地面监测站的导航卫星精密定轨,利用低轨卫星星载数据进行北斗卫星轨道确定的关键是如何准确描述复杂的低轨卫星轨道。
2 观测数据仿真 2.1 导航星座和低轨卫星星座仿真本文数据仿真中涉及北斗和低轨卫星两类星座。北斗卫星共30颗,包括3颗GEO卫星(PRN1~PRN3)、3颗IGSO卫星(PRN4~PRN6) 和24颗MEO卫星(PRN7~PRN30)。其中,3颗GEO卫星分别定点于地固地理经度80°、110.5°和140°处,轨道高度为35 149 km;3颗IGSO轨道倾角55°,轨道高度为35 149 km,星下点与赤道交点经度118°;24颗MEO卫星构成Walker24/3/1星座(PRN7~30),轨道高度为21 527 km,倾角55°,偏心率为0.000 6。低轨卫星星座由太阳同步轨道卫星组成,构型为Walker24/6/1,卫星编号为PRN31~55,卫星轨道高度776.3 km、倾角98.498°、偏心率0.001 03。
2.2 观测链路与数据仿真地面站、低轨卫星和北斗卫星间可形成3类数据:① 星地数据为地面监测站接收的北斗卫星的下行L波段数据,仿真数据包括7个国内站(北京、三亚、喀什、成都、乌鲁木齐、绥阳和湛江)和3个国外iGMAS站[20](塔希提岛TAH1、巴西里约热内卢RDJN、德国布伦瑞克BRCH),仿真考虑的测量模型包括相对论、卫星天线相位中心、接收机天线相位中心、对流层等,其中,对流层为SAASTAMOINEN模型,伪距测量随机误差设定为0.3 m,相位测量随机误差设定为0.003 m;② 高低链路数据为低轨卫星星载接收机接收北斗卫星下行L波段数据,数据仿真考虑的误差模型及观测量随机误差与地面数据相同;③ 星间链路数据为北斗卫星相互之间通过Ka双向观测形成的伪距观测数据。星间链路数据采用单星12链路+高轨卫星单星(不含GEO卫星)6链路的固定观测拓扑结构,测量周期60 s,对向收发时延0.3 ns,采样间隔1.5 s,即每个测距时隙1.5 s,该时隙内仅一颗卫星发射测距信号,其他可视卫星接收测距信号[11]。根据北斗全球系统试验卫星定轨残差,星间观测量精度设置为0.1 m。
卫星动力学仿真模型中,太阳光压为T20先验模型,重力场模型北斗和低轨卫星分别采用10×10阶和140×140阶EIGEN-GL04C模型,日月位置使用JPL DE405行星星历,固体潮为TIDE2000。
3 数据试验 3.1 解算方案综合利用以上仿真的北斗对地面站数据、北斗与低轨卫星间的星载观测数据、北斗星间数据进行北斗卫星轨道确定。采用3 d弧段,解算参数包括:卫星轨道参数(含北斗和低轨卫星)、测站钟差、对流层参数(Davis模型),并在3 d弧段内解算12组对流层天顶延迟及梯度参数。导航卫星与低轨卫星动力学模型不同,特别是在大气阻力和光压模型解算上区别较大,具体见表 1。
| 力模型 | BDS | LEO |
| 地球引力场 | EIGEN-GL04C 10×10阶 | EIGEN-GL04C 140×140阶 |
| 潮汐引力位 | 固体潮、极潮、海潮 | 固体潮、极潮、海潮 |
| 第三体引力 | 日、月及行星(JPL DE405) | 日、月及行星(JPL DE405) |
| 后牛顿效应 | IERS2003 | IERS2003 |
| 大气阻力 | 不考虑 | 一个运行周期解算一组线性大气阻力参数 |
| 太阳光压 | 全弧段一组太阳辐射压系数(X、Z方向尺度因子及Y-bias) | 全弧段解算一组太阳辐射压系数(X、Y、Z方向公共尺度因子);一个运行周期单星解算一组T、N方向常数周期经验力,线性加速度经验力 |
3.2 结果分析
本文共设计了3类10组试验:第1类共6个试验,用于比较分析低轨卫星数量对北斗轨道确定精度的影响;第2类2个试验,用于比较分析特定数量下均匀分布的低轨卫星的轨位对北斗轨道确定精度的影响;第3类2个试验,用于比较分析星间链路和低轨卫星联合对导航卫星定轨精度的影响。
3.2.1 低轨卫星数量影响分析第1类试验中,方案Ⅰ、Ⅱ为传统地面监测站定轨,其中,方案Ⅱ在方案Ⅰ基础上增加了3个境外站;方案Ⅲ至Ⅵ是在方案Ⅰ基础上增加了Walker24/6/1低轨卫星星座或由该星座衍生出的子星座,各方案中低轨卫星数量由多到少,具体如下:
方案Ⅰ:国内7个监测站;
方案Ⅱ:方案Ⅰ增加3个境外站;
方案Ⅲ:方案Ⅰ增加24颗低轨卫星(Walker24/6/1);
方案Ⅳ:方案Ⅰ增加12颗低轨卫星(第1、3、5轨道面各选4颗卫星,即Walker12/3/1);
方案Ⅴ:方案Ⅰ增加6颗低轨卫星(第1、3、5轨道面各选2颗卫星,即Walker6/3/1);
方案Ⅵ:方案Ⅰ增加3颗低轨卫星(第1、3、5轨道面各选1颗卫星,即Walker3/3/1)。
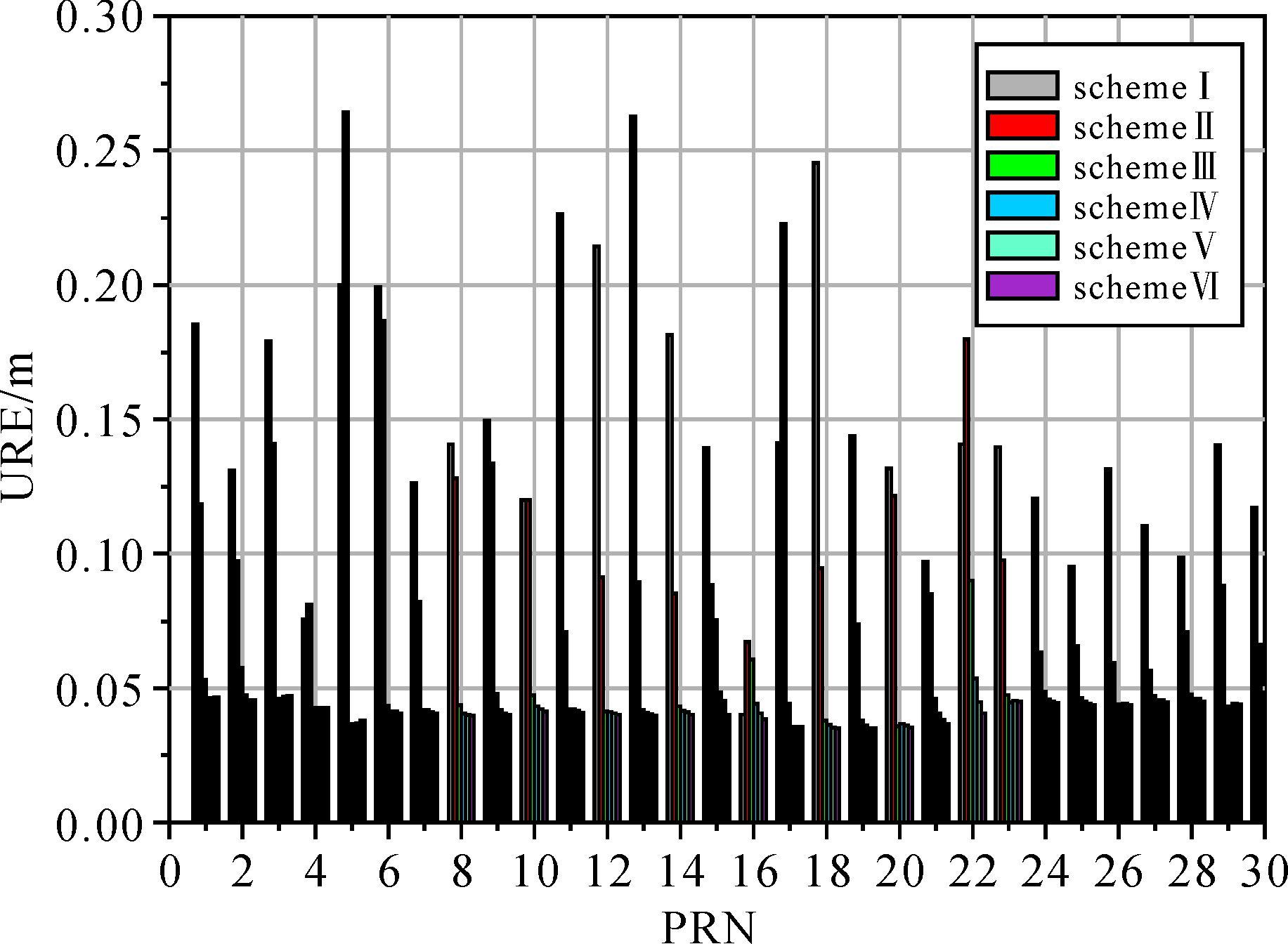
表 2和图 1分别给出了以上6种方案北斗卫星定轨精度统计结果和按卫星号统计的定轨URE。结果表明:① 仅依赖区域站或在此基础上增加少量境外站,北斗卫星轨道径向误差和URE均超过0.1 m;② 在方案Ⅰ基础上分别按照方案Ⅲ至Ⅵ增加一定数量的低轨卫星进行星地联合定轨,URE精度由0.155 m提升道0.041 m,提高约73%,达到厘米级精度;③ 从低轨卫星数量分析,低轨卫星由24颗减少道3颗,定轨精度降低幅度不大,加入3颗低轨卫星即可有效改进定轨精度,使URE优于5 cm;④ 方案Ⅲ至Ⅵ中解算的卫星钟差与方案Ⅰ结果相比较,改进量约25%;方案Ⅲ至Ⅵ相互间比较,不同数量均匀分布的低轨卫星对钟差改进差异不大,其原因可能由于少量低轨卫星情况下,区域地面站和低轨卫星难以通过导航卫星的衔接处于同一解算网中,实际钟差解算仍依赖区域地面监测站。
| 方案 | 方案特征 | R/m | T/m | N/m | POS/m | URE/m | CLK/ns |
| Ⅰ | 星地(区域7监测站) | 0.140 | 0.459 | 0.330 | 0.583 | 0.155 | 0.397 |
| Ⅱ | 星地(区域7+海外3监测站) | 0.106 | 0.338 | 0.269 | 0.445 | 0.117 | 0.347 |
| Ⅲ | 星地+24低轨(Walker24/6/1) | 0.009 | 0.256 | 0.207 | 0.329 | 0.041 | 0.309 |
| Ⅳ | 星地+12低轨(Walker12/3/1) | 0.011 | 0.258 | 0.208 | 0.332 | 0.042 | 0.298 |
| Ⅴ | 星地+6低轨(Walker6/3/1) | 0.014 | 0.256 | 0.206 | 0.329 | 0.042 | 0.294 |
| Ⅵ | 星地+3低轨(Walker3/3/1) | 0.028 | 0.253 | 0.203 | 0.326 | 0.048 | 0.296 |
|
| 图 1 方案Ⅰ-Ⅵ按卫星号统计的定轨URE Fig. 1 Statistics of the orbit determination URE according to satellite number in scheme Ⅰ-Ⅵ |
3.2.2 低轨卫星分布的影响分析
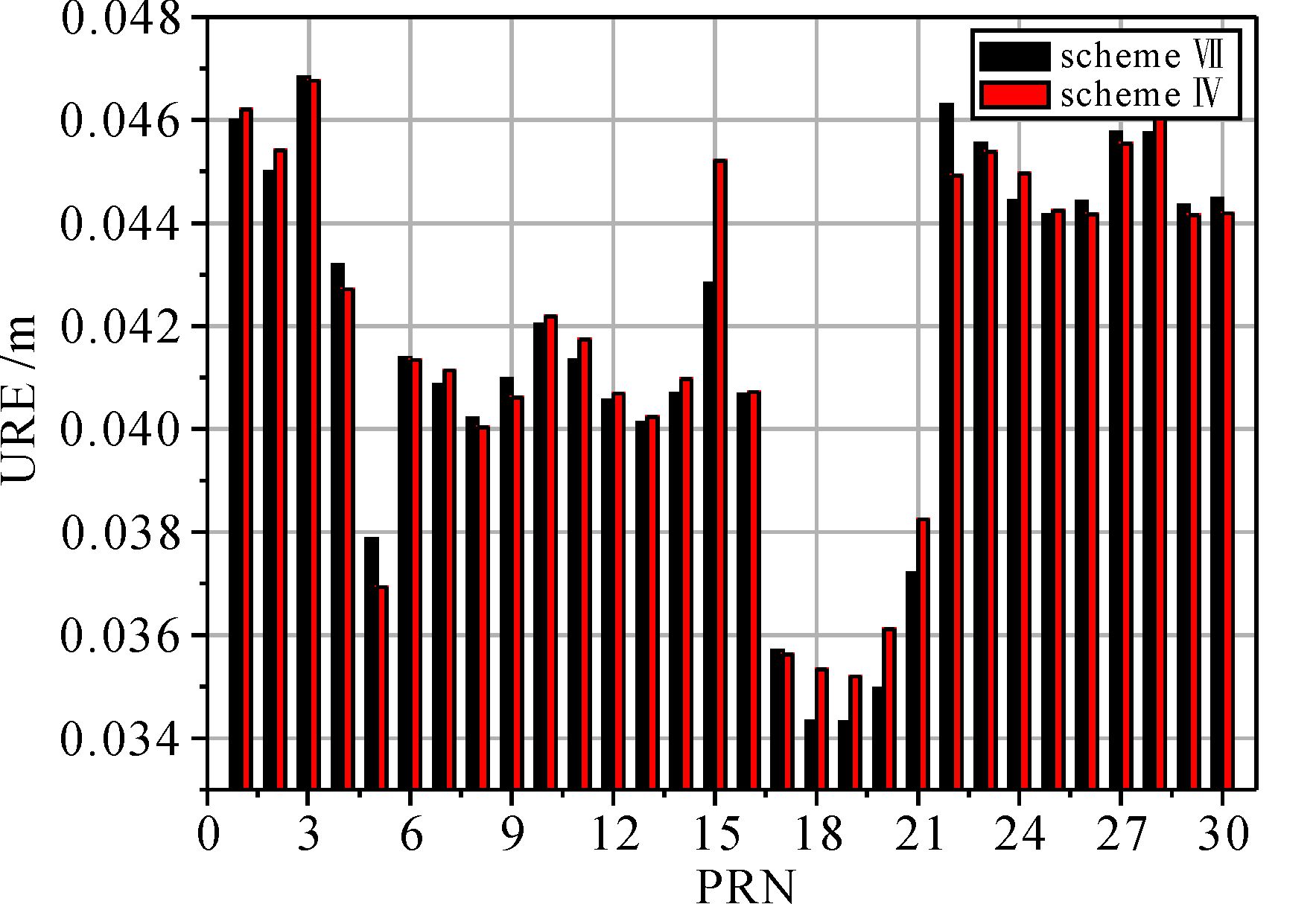
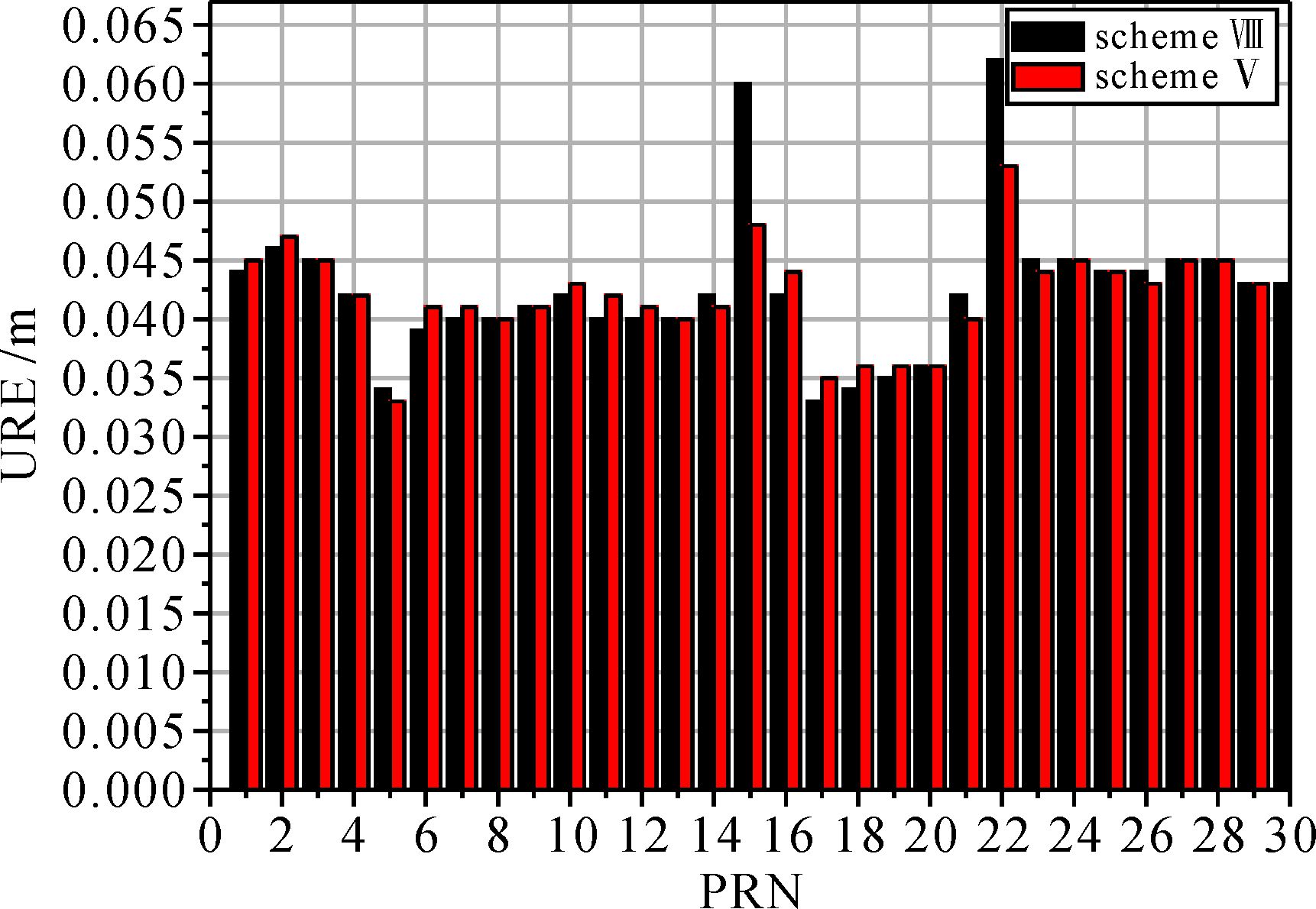
以上方案Ⅳ和方案Ⅴ中, 12颗低轨卫星为Walker24/6/1的子星座Walker12/3/1,6颗低轨卫星星座为Walker6/3/1。前者在第1、3、5轨道面上按90°等相位间隔选择12颗卫星,不同轨道面间相邻卫星相位相差30°;后者在第1、3、5每个轨道面上按180°等相位间隔选择6颗卫星,不同轨道面相邻卫星相位相差60°。为了分析低轨卫星分布对北斗定轨精度的影响,采用与方案Ⅳ和方案Ⅴ同样卫星数量但构型不同的两类低轨卫星星座,即Walker12/6/1和Walker6/6/1形成方案Ⅶ和方案Ⅷ进行定轨增强。按照与3.2.1中各方案相同的模型,得到方案Ⅶ、Ⅷ定轨结果如表 3所示,方案Ⅶ定轨URE为0.042 m,钟差精度0.291 ns,方案Ⅷ定轨URE为0.040 m,钟差精度0.294 ns。图 2和图 3分别给出了方案Ⅳ与方案Ⅶ、方案Ⅴ与方案Ⅷ的各自相互比较结果,可见两种方案得到的导航卫星轨道精度相当。由此得到结论,在低轨卫星数量一定情况下,不同分布的均匀低轨星座对于卫星定轨精度影响不大。
| 方案 | 方案特征 | R/m | T/m | N/m | POS/m | URE/m | CLK/ns |
| Ⅶ | 星地+12低轨(Walker12/6/1) | 0.012 | 0.232 | 0.199 | 0.319 | 0.042 | 0.291 |
| Ⅷ | 星地+6低轨(Walker6/6/1) | 0.017 | 0.231 | 0.189 | 0.299 | 0.040 | 0.294 |
|
| 图 2 方案Ⅶ与Ⅳ按卫星号统计的定轨URE Fig. 2 Orbit determination URE according to satellite number in scheme Ⅶ and Ⅳ |
|
| 图 3 Ⅷ与Ⅴ方案按卫星号统计的定轨URE Fig. 3 Orbit determination URE according to satellite number in scheme Ⅷ and Ⅴ |
3.2.3 低轨卫星与星间链路增强的比较
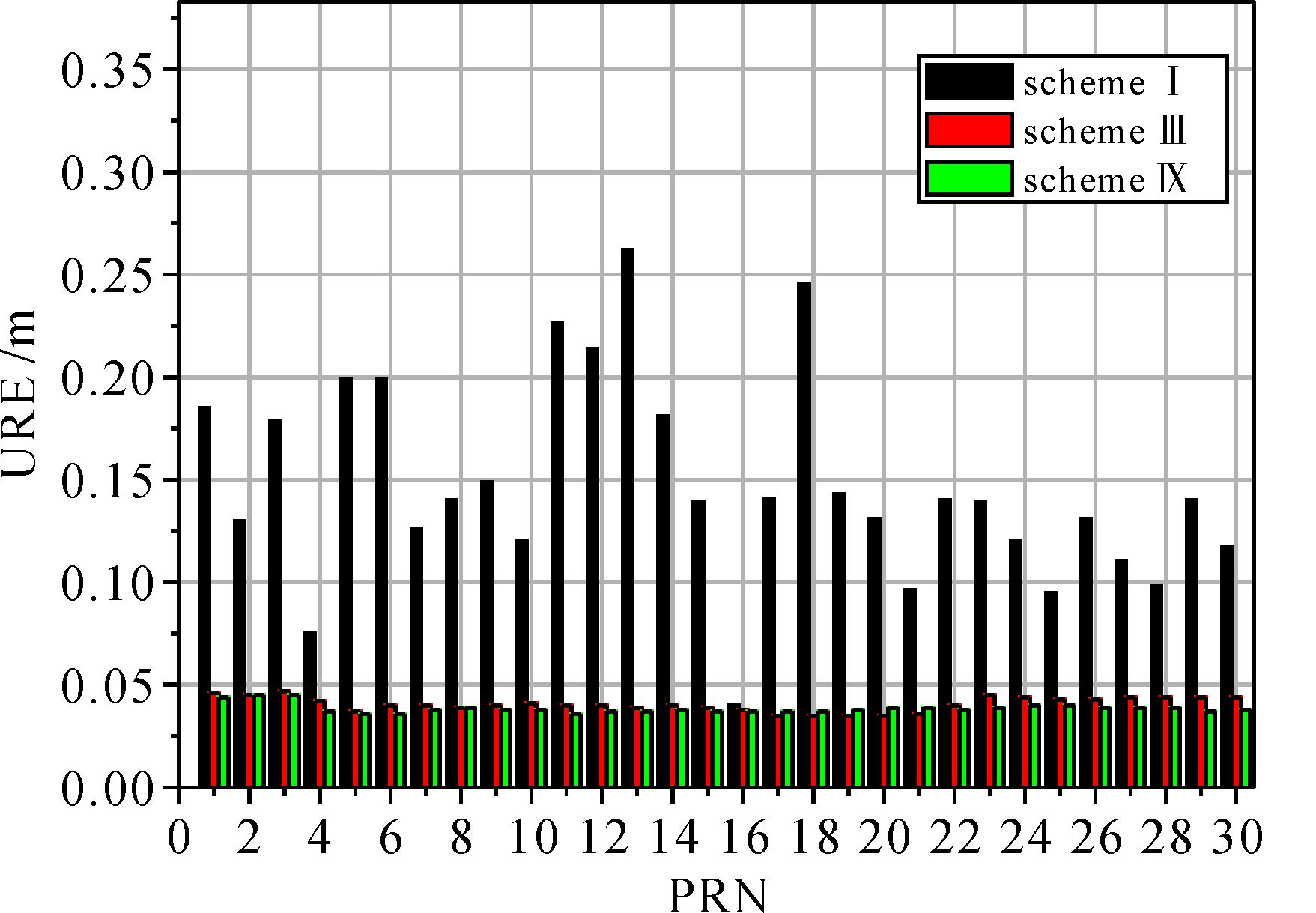
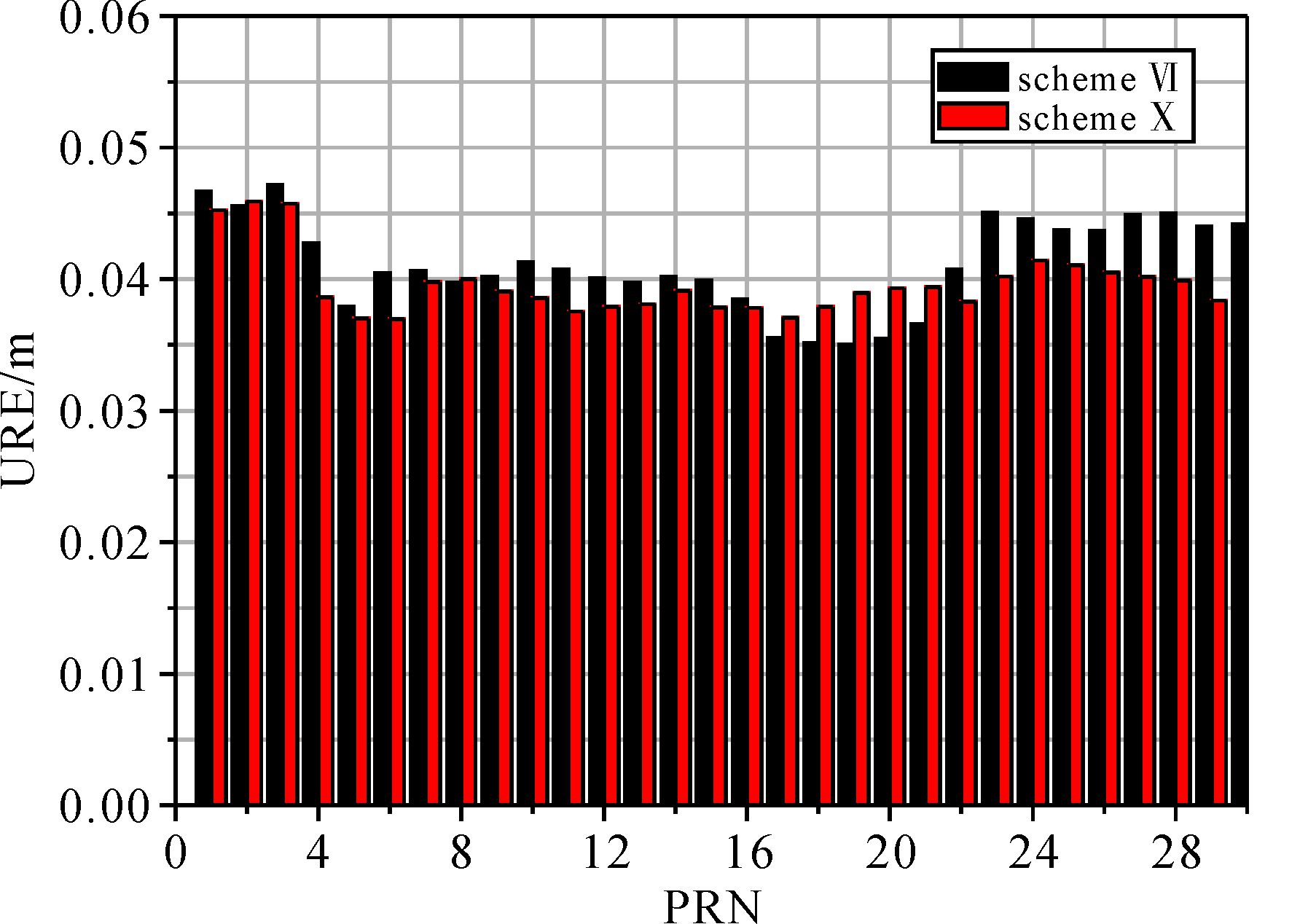
为比较低轨卫星和星间链路对于联合定轨精度的作用,在方案Ⅰ和方案Ⅵ基础上分别加入星间链路数据构成方案Ⅸ和方案Ⅹ,其定轨精度统计值如表 4所示。比较方案Ⅰ与方案Ⅲ、方案Ⅸ,即在地面基础上分别加入24颗低轨卫星数据和星间链路数据进行比较,结果如图 4所示,星间链路对于北斗轨道精度的提升作用略优于增加24颗低轨卫星。通过方案Ⅵ与方案Ⅹ比较分析地面数据和低轨卫星数据基础上增加星间链路数据对于北斗卫星轨道精度的改进情况,结果如表 4和图 5所示,北斗卫星定轨URE由0.048 m提升到0.039 m,而钟差精度则由0.296 ns略降为0.378 ns,分析原因:北斗星间双向测距存在的收发时延最终以系统残差形式影响钟差精度,数据仿真中的收发时延在定轨解算中部分被卫星钟差吸收,出现加入星间数据后卫星钟差略增大的情况,这也反映出在基于星地数据、低轨星载数据和星间链路数据联合定轨过程中,正确处理星间收发时延的重要性。
| 方案 | 方案特征 | R/m | T/m | N/m | POS/m | URE/m | CLK/ns |
| Ⅸ | 星地+星间 | 0.004 | 0.250 | 0.197 | 0.319 | 0.039 | 0.351 |
| Ⅹ | 星地+3低轨+星间 | 0.003 | 0.254 | 0.200 | 0.324 | 0.039 | 0.378 |
|
| 图 4 方案Ⅰ、Ⅲ及方案Ⅸ按卫星号统计的定轨URE Fig. 4 Orbit determination URE according to satellite number in scheme Ⅰ, Ⅲ and Ⅸ |
|
| 图 5 方案Ⅵ与方案Ⅹ按卫星号统计的定轨URE Fig. 5 Orbit determination URE according to satellite number in scheme Ⅵ and Ⅹ |
4 结论
联合地面监测站数据、星载数据和星间链路的导航卫星定轨,可有效提高区域监测站条件下导航卫星精密定轨精度,本文通过仿真试验与分析比较,得到主要结论如下:
(1) 在区域监测站基础上增加低轨卫星进行联合定轨,可显著提高导航卫星定轨精度。从低轨卫星数量来看,相比较区域地面站定轨精度,加入3颗低轨卫星可提升导航卫星定轨URE约73%,达到厘米量级,再增加更多低轨卫星对定轨精度提升作用有限。
(2) 增加低轨星载数据获得联合定轨方案,其钟差解算精度相比较区域地面站,精度提高约25%;相互间比较表明,低轨卫星数量对钟差不敏感。
(3) 通过对星座Walker12/3/1与Walker12/6/1、Walker6/3/1与Walker6/6/1的比较分析,低轨卫星数量一定情况下,均匀分布的不同构型的低轨卫星星座对增强导航卫星精度的影响较小。
(4) 北斗星间双向测距存在收发时延,最终以系统残差形式影响测距精度,数据仿真中设定收发时延在定轨解算中被卫星钟差吸收,导致卫星钟差解算精度略微变差,这也反映了在基于星地数据、低轨星载数据和星间链路数据联合定轨过程中,正确处理星间收发时延的重要性,也是今后研究的重点方向。
| [1] | SCHUTZ B E, TAPLEY B D, BORN G H. Statistical Orbit Determination[M]. Burlington: Elsevier Academic Press, 2004: 1-11. |
| [2] | 杜兰. GEO卫星精密定轨技术研究[D]. 郑州: 信息工程大学, 2006. DU Lan. A Study on the Precise Orbit Determination of Geostationary Satellite[D]. Zhengzhou:Information Engineering University, 2006. |
| [3] | LANGER J, FEESS W, HADDAD R, et al. Near-Term Integrity Improvements for the GPS Operational Control Segment[C]//Proceedings of Institute of Navigation GPS 2002 Conference. Portland:[s.n.], 2002:24-27. |
| [4] | STANTON B J, STROTHER R. Analysis of GPS Monitor Station Outages[C]//ION GNSS. Fort Worth, TX:[s.n.]. 2007:176-183. |
| [5] | 文援兰, 柳其许, 朱俊, 等. 测控站布局对区域卫星导航系统的影响[J]. 国防科技大学学报, 2007, 29(1): 1–6. WEN Yuanlan, LIU Qixu, ZHU Jun, et al. The Effect of TT & C Deployment on the Regional Satellite Navigation System[J]. Journal of National University of Defense Technology, 2007, 29(1): 1–6. |
| [6] | FERNÁNDEZ F A. Inter-Satellite Ranging and Inter-Satellite Communication Links for Enhancing GNSS Satellite Broadcast Navigation Data[J]. Advances in Space Research, 2011, 47(5): 786–801. DOI:10.1016/j.asr.2010.10.002 |
| [7] | ANANDA M P, BERNSTEIN H, CUNNINGHAM K E, et al. Global Positioning System (GPS) Autonomous Navigation[C]//Proceedings of IEEE Position Location and Navigation Symposium. Las Vegas, Nevada:IEEE, 1990:497-508. |
| [8] | 耿涛, 刘经南, 赵齐乐, 等. 星地监测网下的北斗导航卫星轨道确定[J]. 测绘学报, 2011, 40(S1): 46–51. GENG Tao, LIU Jingnan, ZHAO Qile, et al. Compass Precise Orbit Determination Based on Space-ground Monitoring Network[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 46–51. |
| [9] | 陈忠贵, 帅平, 曲广吉. 现代卫星导航系统技术特点与发展趋势分析[J]. 中国科学E辑:技术科学, 2009, 39(4): 686–695. CHEN Zhonggui, SHUAI Ping, QU Guangji. Analysis of the Current Satellite Navigation System Techniques[J]. Science in China (Series E), 2009, 39(4): 686–695. |
| [10] | 刘万科, 龚晓颖, 李征航, 等. 综合星间和地面测距数据的导航卫星联合定轨[J]. 武汉大学学报(信息科学版), 2010, 35(7): 811–815. LIU Wanke, GONG Xiaoying, LI Zhenghang, et al. Combined Orbit Determination of Navigation Satellites with Cross-Link Ranging Observations and Ground Tracking Observations[J]. Geomatics and Information Science of Wuhan University, 2010, 35(7): 811–815. |
| [11] | 宋小勇. COMPASS导航卫星定轨研究[D]. 西安: 长安大学, 2009. SONG Xiaoyong. Study on the Orbit Determination of COMPASS Navigation Satellites[D]. Xi'an:Chang'an University, 2009. |
| [12] | 林益明, 何善宝, 郑晋军, 等. 全球导航星座星间链路技术发展建议[J]. 航天器工程, 2010, 19(6): 1–7. LIN Yiming, HE Shanbao, ZHENG Jinjun, et al. Development Recommendation of Inter-Satellites Links in GNSS[J]. Spacecraft Engineering, 2010, 19(6): 1–7. |
| [13] | 李建成, 张守建, 邹贤才, 等. GRACE卫星非差运动学厘米级定轨[J]. 科学通报, 2009, 54(6): 2355–2362. LI Jiancheng, ZHANG Shoujian, ZOU Xiancai, et al. Precise Orbit Determination for GRACE with Zero-Difference Kinematic Method[J]. Chinese Science Bulletin, 2009, 54(6): 2355–2362. |
| [14] | BOCK H, JÄGGI A, ŠVEHLA D, et al. Precise Orbit Determination for the GOCE Satellite Using GPS[J]. Advances in Space Research, 2007, 39(10): 1638–1647. DOI:10.1016/j.asr.2007.02.053 |
| [15] | 赵齐乐. GPS导航星座及低轨卫星的精密定轨理论和软件研究[D]. 武汉: 武汉大学, 2004. ZHAO Qile. Research on Precision Orbit Determination Theory and Software of Both GPS Naviagation Constellation and LEO Satellites[D]. Wuhan:Wuhan University, 2004. |
| [16] | ZHU S, REIGBER C, KÖNIG R. Integrated Adjustment of CHAMP, GRACE, and GPS Data[J]. Journal of Geodesy, 2004, 78(1): 103–108. |
| [17] | 耿江辉, 施闯, 赵齐乐, 等. 联合地面和星载数据精密确定GPS卫星轨道[J]. 武汉大学学报(信息科学版), 2007, 32(10): 906–909. GENG Jianghui, SHI Chuang, ZHAO Qile, et al. GPS Precision Orbit Determination from Combined Ground and Space-borne Data[J]. Geomatics and Information Science of Wuhan University, 2007, 32(10): 906–909. |
| [18] | 冯来平, 阮仁桂, 吴显兵, 等. 联合低轨卫星和地面监测站数据确定导航卫星轨道[J]. 大地测量与地球动力学, 2016, 36(10): 864–869. FENG Laiping, RUAN Rengui, WU Xianbing, et al. Precise Orbit Determination of Navigation Satellite Using Joint Data from Regional Tracking Station and LEO[J]. Journal of Geodesy and Geodynamics, 2016, 36(10): 864–869. |
| [19] | 赵齐乐, 刘经南, 葛茂荣, 等. CHAMP卫星cm级精密定轨[J]. 武汉大学学报(信息科学版), 2006, 31(10): 879–882. ZHAO Qile, LIU Jingnan, GE Maorong, et al. Precision Orbit Determination of CHAMP Satellite with cm-Level Accuracy[J]. Geomatics and Information Science of Wuhan University, 2006, 31(10): 879–882. |
| [20] | 焦文海, 丁群, 李建文, 等. GNSS开放服务的监测评估[J]. 中国科学:物理学力学天文学, 2011, 41(5): 521–527. JIAO Wenhai, DING Qun, LI Jianwen, et al. Monitoring and Assessment of GNSS Open Services[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2011, 41(5): 521–527. |
| [21] | SPRINGER T A, BEUTLER G, ROTHACHER M. A New Solar Radiation Pressure Model for GPS Satellites[J]. Advances in Space Research, 1999, 23(4): 673–676. DOI:10.1016/S0273-1177(99)00158-1 |


