卫星导航系统广播星历包含了卫星轨道钟差等重要信息,且具有实时、易获取的特征[1],是保障实时定位、导航和授时(PNT)服务的基础和关键[2-3]。目前已有的卫星导航系统主要依赖少量的地面运控监测站对卫星轨道进行实时解算和预报,进而获取广播星历中的轨道产品,因此,预报轨道精度直接决定卫星导航系统的实时服务质量[4]。目前,受限于政治因素和国土面积的影响,我国的北斗二代卫星导航系统(BDS)存在地面运控监测站数量较少且为区域分布的缺陷,短期内难以实现全球建站[5-6]。BDS导航卫星星座主要由中圆轨道卫星(MEO)构成,区域地面监测站难以对全球运行的MEO形成连续多重覆盖观测,导致MEO轨道解算和预报精度偏低,影响卫星导航系统的实时服务性能。
针对MEO轨道精度提升问题,目前的研究主要依赖于更加合理分布的地面监测站[6],未来的导航系统设计和规划增加星间链路[7]。也有学者联合地面监测站和低轨卫星星载GNSS数据进行导航卫星轨道确定试验[8],但未涉及实时轨道预报问题。考虑到低轨卫星星载GNSS数据可以有效弥补地面区域监测站在空间覆盖和几何构型上的不足,且低轨卫星轨道解算精度已达到厘米级[9-12];基于此,本文设计了一种联合地面区域监测站和天基低轨卫星数据综合测定MEO卫星轨道的技术,即将星载GNSS接收机作为高动态的天基监测站,联合地面区域监测站数据对MEO轨道进行实时解算和预报,研究了天基和地面数据联合解算的策略和流程,并利用数值算例结果验证了本文方法的精度和有效性。
1 数学模型目前,卫星定轨的基本理论为二体问题,同时涉及保守力摄动、非保守力摄动和经验力摄动。
卫星的在轨运行是一个受摄运动过程[13],动力学信息涉及各种摄动,包括保守力摄动、非保守力摄动和经验力摄动。在轨卫星运动方程可描述如下[5, 13]
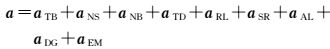 (1)
(1)
式中,aTB表示二体引力;aNS表示地球非球形部分引力;aNB表示除地球外的行星引力;aTD表示地球潮汐影响;aRL表示相对论效应影响;aSR表示太阳辐射压力;aAL表示地球红外辐射压力;aDG表示大气阻力;aEM表示其他经验作用力。
式(1) 可用卫星初始轨道参数描述[14]为
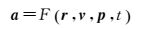 (2)
(2)
式中, r为位置矢量;v为速度矢量;p为动力学参数;t表示时间。
将运动方程表示为初值问题并根据估计理论可得到变分方程[15]。对运动方程和变分方程积分,可得到GNSS卫星和低轨卫星的状态转移矩阵φGNS(ti, t0)和φLEO(ti, t0),满足如下方程
 (3)
(3)
式中,XGNSi和XLEOi表示导航卫星和低轨卫星在i时刻的待估参数;XGNS0和XLEO0表示初始状态参数。可通过式(3) 将任意时刻的待估参数归算到初始时刻。
在导航卫星定轨过程中,地面监测站坐标固定,可以看成为已知量。低轨卫星可以看作为坐标待估的高动态运动的天基监测站。地面运控监测站和天基监测站接收到的导航信号的观测方程分别列出如下[16]
 (4)
(4)
式中,LGRO表示地面运控监测站对GNSS卫星信号的观测量;LLEO表示低轨卫星对GNSS卫星信号的观测量;FGRO表示地面运控监测站的观测函数;FLEO表示低轨卫星的观测函数;XGNS表示导航卫星的待估参数;XLEO表示低轨卫星的待估参数;XOTH表示其他待估参数;t表示时间参数;εGRO表示地面运控监测站的观测误差;εLEO表示天基监测站的观测误差。式(4) 经过线性化后,写成矩阵形式如下
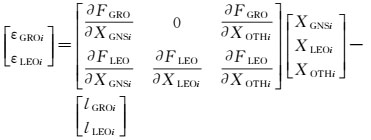 (5)
(5)
式中,lGROi=FGRO0-LGROi;lLEOi=FLEO0-LLEOi。
本文采用简化动力学定轨方法,合理平衡几何观测信息和动力学信息[13]。将式(3) 和式(5) 联合,可得到本文的简化动力学联合定轨观测模型。
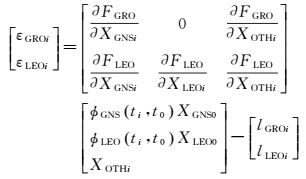 (6)
(6)
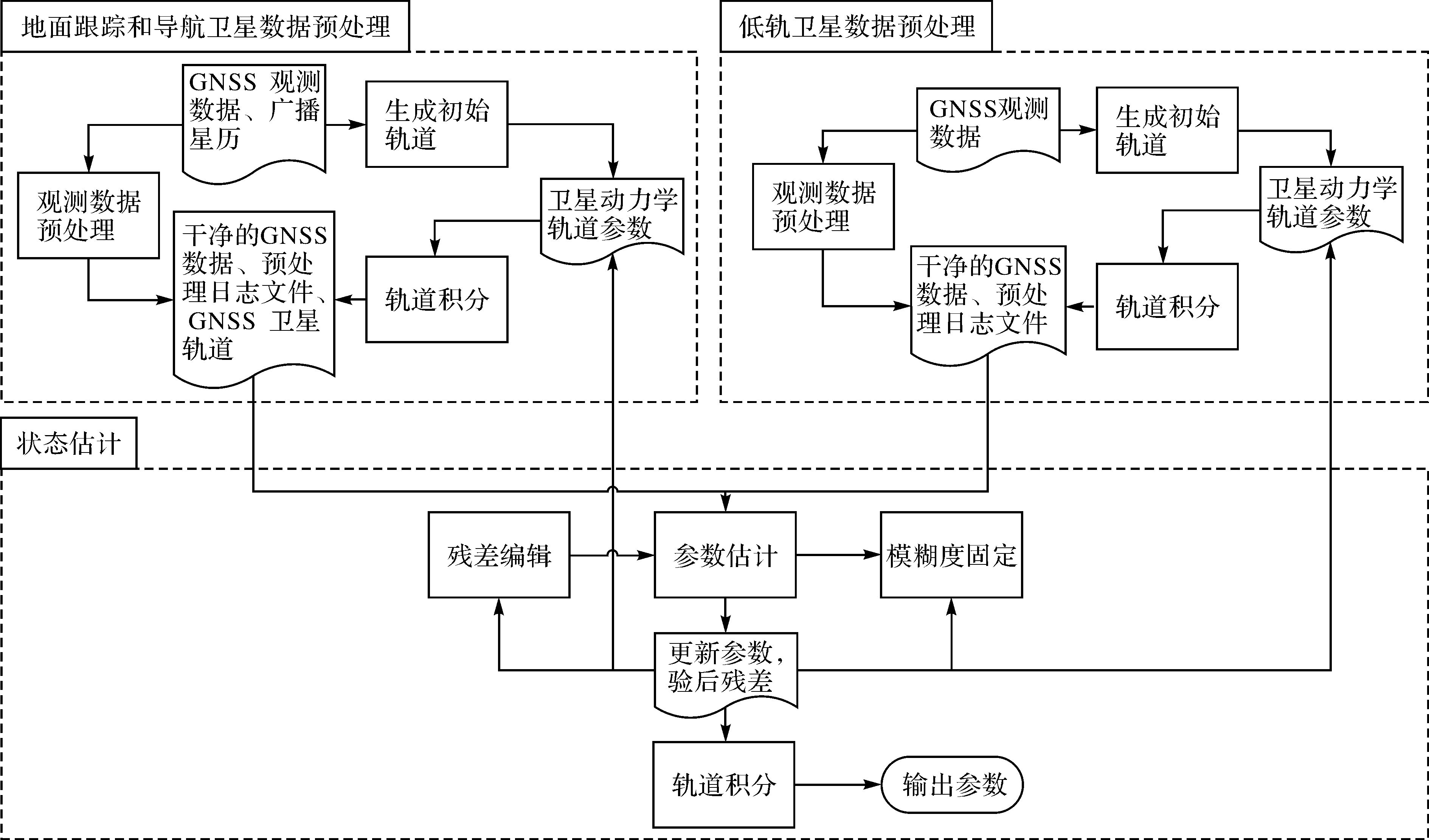
联合地面监测站、天基监测站数据解算和预报导航卫星轨道的基本流程为:分别对地面监测站和星载GNSS接收机的原始观测数据进行预处理,获取“干净”的GNSS数据和预处理日志文件;同时,通过低轨卫星的GNSS观测数据获取低轨卫星的初始轨道和动力学轨道参数;对导航卫星的广播星历进行预处理,生成导航卫星动力学参数和初始轨道。然后联合地面监测站和天基低轨卫星监测站数据迭代进行参数估计和残差编辑,同时解算导航卫星轨道、低轨卫星轨道以及其他必要参数;经过参数估计和残差编辑的迭代处理以及模糊度固定(如果可以正确固定)之后,即可获取实测轨道参数。在导航卫星实测轨道参数的基础上,进行轨道的外推,获取预报轨道参数。其基本流程如图 1所示。
|
| 图 1 联合天基监测站和地面监测数据确定导航卫星轨道流程图 Fig. 1 The process of combining space-based stations with ground monitoring data to determine satellite orbit |
3 算例及分析 3.1 数据源描述
目前在轨的CHAMP、GRACE和GOCE等低轨卫星上均搭载了星载GPS接收机;随着空间技术的不断发展,我国已经成功发射了多颗不同用途的低轨卫星,如海洋二号、天绘一号和风云三号卫星等,其上也搭载了星载GNSS接收机,可以接收到GPS或者GPS/BDS观测数据。考虑到星载GPS数据来源广泛且数据质量好,本文以GPS数据为例,来验证地面区域监测站联合天基低轨卫星数据确定MEO卫星轨道技术的可行性和精度。
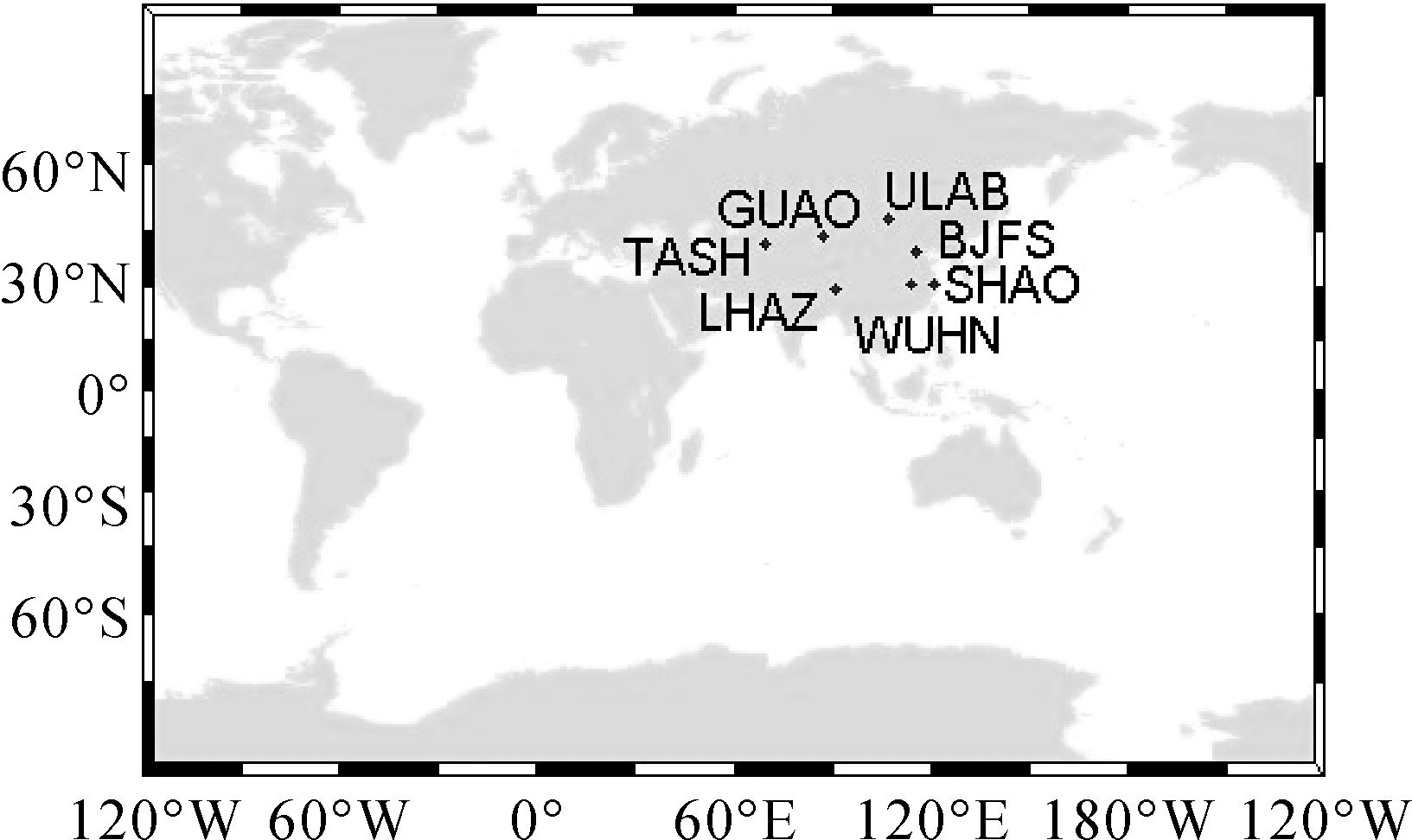
为了验证地面区域监测站的定轨效果,本文首先选取中国境内及边境附近的7个IGS监测站组成地面区域监测站网络,其测站分布如图 2所示;从IGS全球数据中心CDDIS下载2013年286—288连续3天的上述监测站观测数据,进行GPS卫星轨道解算和预报。
|
| 图 2 区域监测站网络测站分布 Fig. 2 The stations distribution of regional monitoring network |
GRACE卫星是美国国家航空航天局(NASA)跟德国航空中心(DLR)的合作项目,是观测地球重力场变化的卫星。GRACE包括两颗卫星:GRACE-A和GRACE-B,其轨道高度约为500 km,运行周期约为90 min。我国某低轨卫星高度略高于GRACE卫星,运行周期略大于90 min。本文选取了GRACE-A、GRACE-B和我国某低轨卫星的星载GPS观测数据。低轨卫星的状态参数描述如表 1所示。
| 力模型 | 描述 |
| 重力场模型 | EGM(120阶×120阶) |
| 三体引力 | JPL DE405行星星历 |
| 地球固体潮 | IERS Conventions 2003 |
| 海潮 | FES2004全球海潮模型 |
| 相对论效应 | IERS Conventions 2003 |
| 大气阻力 | CON/DTM94 |
| 太阳光压 | BOX-wing模型 |
| 惯性参考系 | J2000.0 |
| 岁差和章动模型 | IAU 2000A |
| 地球自转 | IERS EOP 08 C04(IAU 2000A) |
| 估计参数 | 描述 |
| 低轨卫星定轨弧段初始状态 | 三维惯性系位置和速度 |
| 大气阻力系数 | 6 h 1个 |
| 星载GNSS接收机钟差 | 1个历元1个 |
| 切向、法向、径向经验参数 | 1.5 h 1个 |
3.2 算例分析
为了验证天基低轨卫星数据对地面区域监测站网络定轨的增强效果,根据地面运控监测站和低轨卫星星载GPS数据的实际情况,本文设计了如下方案进行试验对比及分析。
方案1:采用中国境内及周边7个GPS地面监测站组成地面区域监测站网络,进行GPS卫星轨道解算与预报(地面区域监测站);
方案2:采用方案1中的地面区域监测站联合GRACE-A的星载GPS观测数据,进行GPS卫星轨道解算与预报(地面区域监测站+GRACE-A);
方案3:采用方案1中的地面区域监测站联合GRACE-B的星载GPS观测数据(地面区域监测站+GRACE-B);
方案4:采用方案1中的地面区域监测站联合我国某低轨卫星的星载GPS观测数据(地面区域监测站+LEOX);
方案5:采用方案1中的地面区域监测站联合GRACE-A和GRACE-B两颗低轨卫星的星载GPS观测数据(地面区域监测站+2LEO);
方案6:采用方案1中的地面区域监测站联合方案2—方案4中的3颗低轨卫星的星载GPS观测数据(地面区域监测站+3LEO)。
相关解算参数设置情况见表 2。
| 描述项目 | 地面监测站数据 | 星载GPS数据 |
| 弧长 | 3 d | 3 d |
| 采样率/s | 30 | 30 |
| 截止高度角 | 7° | 0° |
| 接收机钟差 | 选取某测站作为基准钟 | — |
| 电离层延迟 | 双频消电离层 | 双频消电离层 |
| 对流层延迟 | SAAS模型 | 无 |
| 模糊度 | 固定解/浮点解 | 浮点解 |
基于上述策略,本文首先分析了不同方案导航卫星的可见历元数;然后将解算的实测轨道同IGS公布的最终轨道比较,得到各方案卫星定轨实测精度;将外推的预报2~4 h的轨道同IGS公布的最终轨道比较,得到各方案卫星定轨预报精度;将解算的钟差同IGS公布的最终钟差比较,得到各方案卫星钟差解算精度。最后,对不同方案的卫星轨道钟差解算精度进行比较和分析。
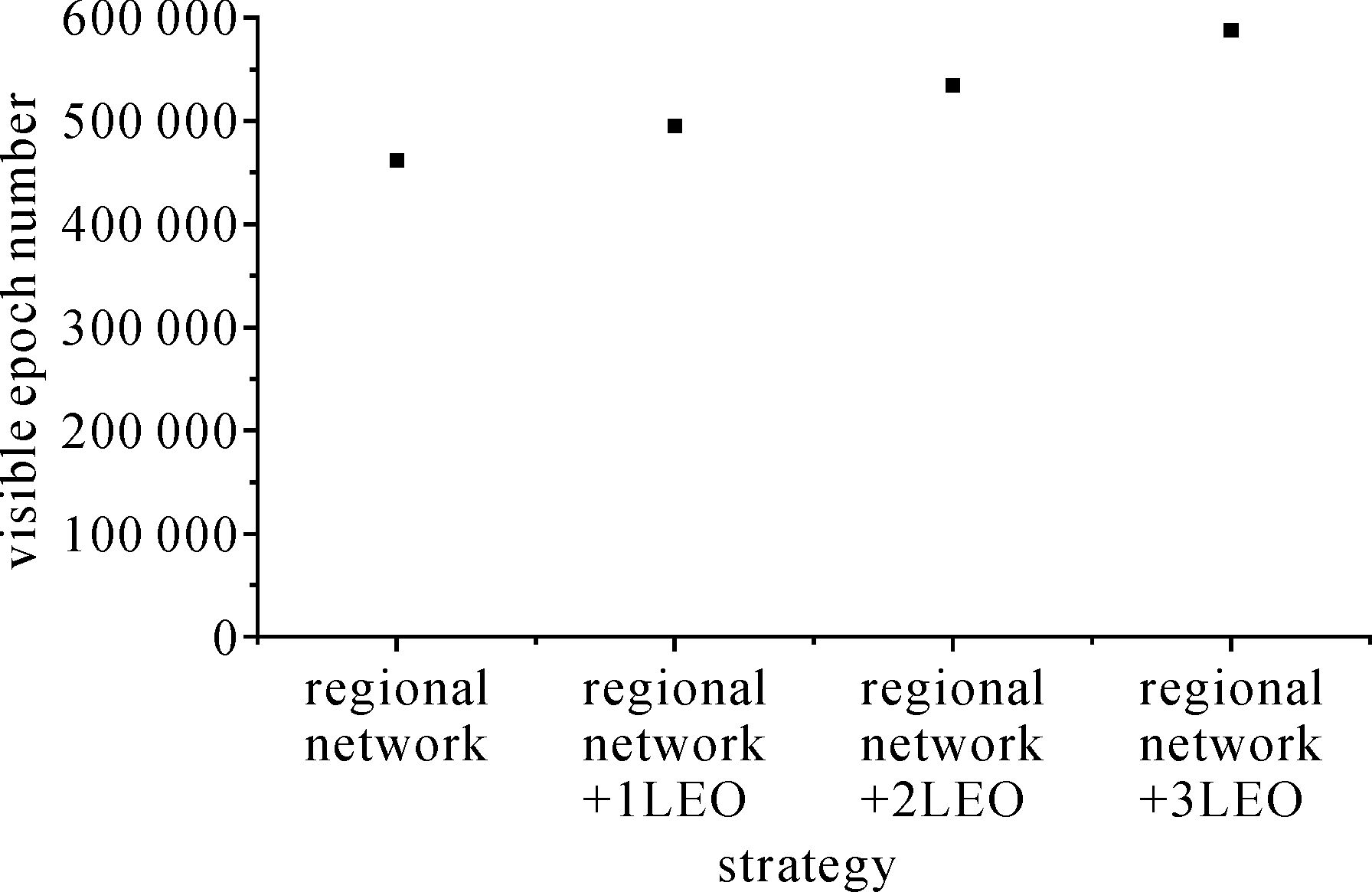
3.2.1 卫星可见历元数统计首先统计了地面区域监测站与加入不同数量低轨卫星数据后的卫星可见历元数,结果如图 3和表 3所示。
|
| 图 3 不同方案的可见历元数统计 Fig. 3 Statistical diagram of visible epochs of different schemes |
由图 3和表 3可见,每加入一颗低轨卫星数据,导航卫星定轨可用历元数增加约10%。表明低轨卫星数据的加入可有效增加导航卫星可用观测历元数。
| strategy | visible epoch number |
| regional network | 460 704 |
| regional network + 1LEO | 495 255 |
| regional network + 2LEO | 534 585 |
| regional network + 3LEO | 588 285 |
3.2.2 实测轨道精度统计及分析
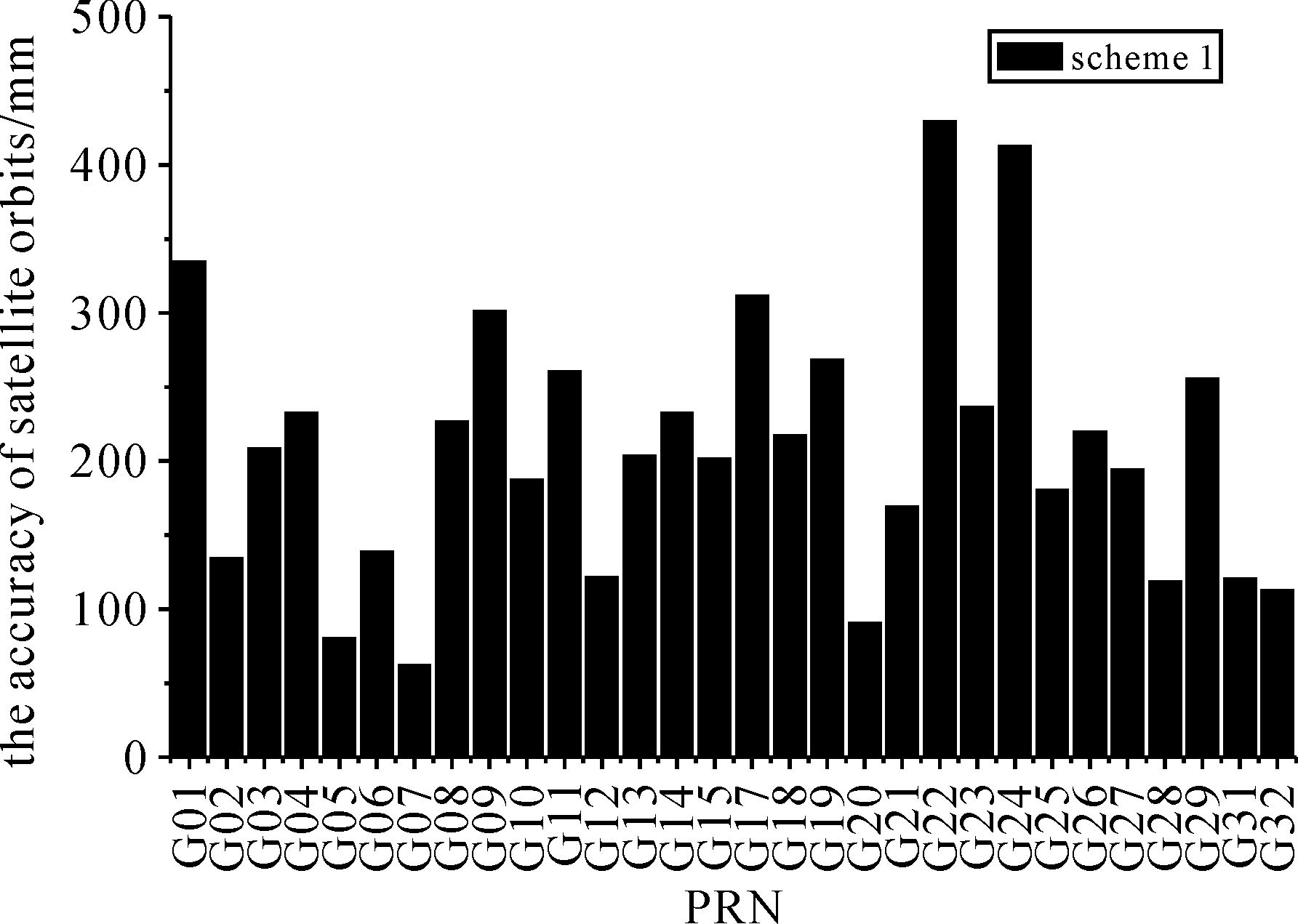
本文对不同方案的实测轨道精度进行统计计算,首先得到方案1的实测轨道精度结果见图 4。
|
| 图 4 方案1解算的GPS卫星轨道精度 Fig. 4 The precision of GPS satellite orbits of scheme 1 |
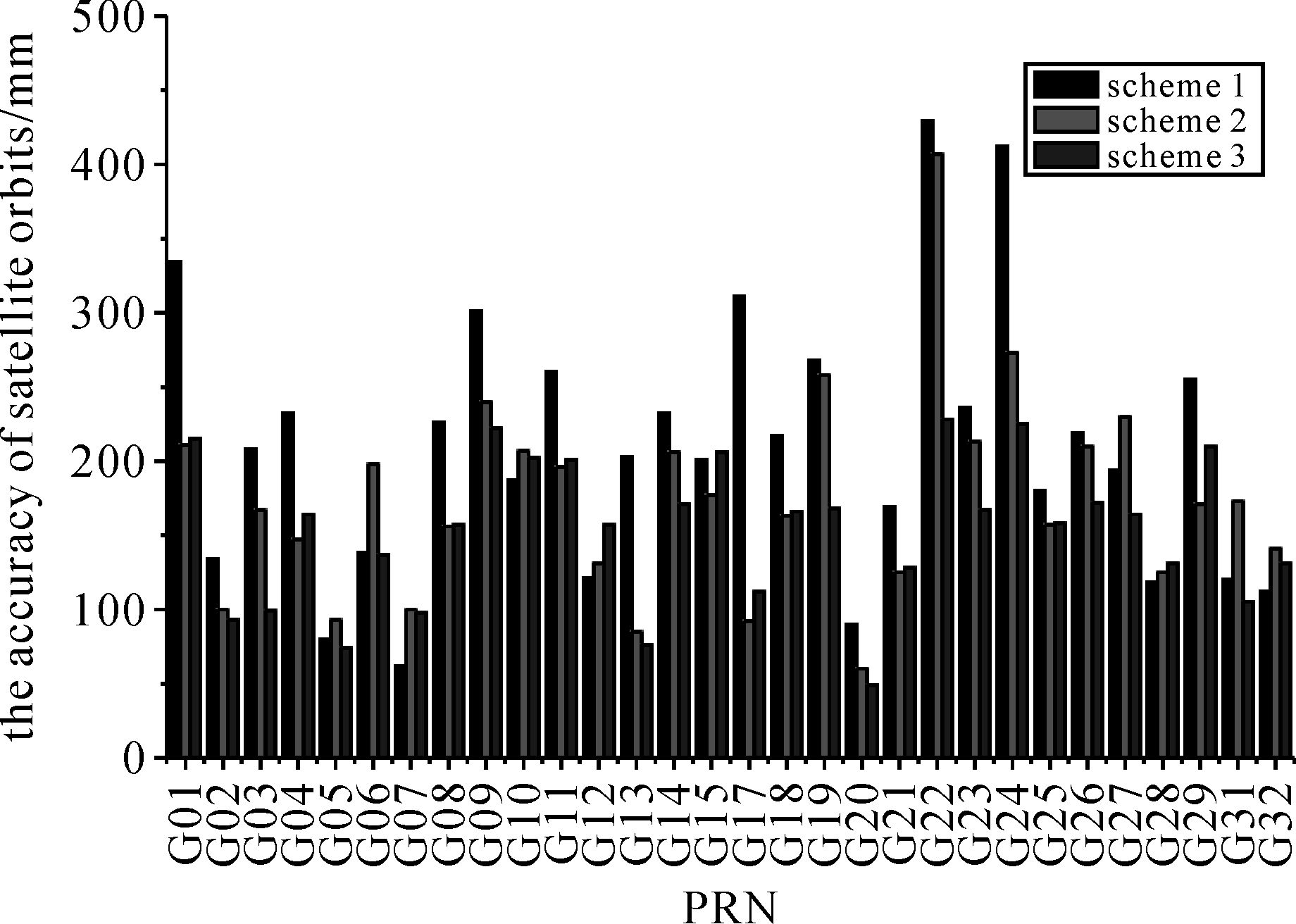
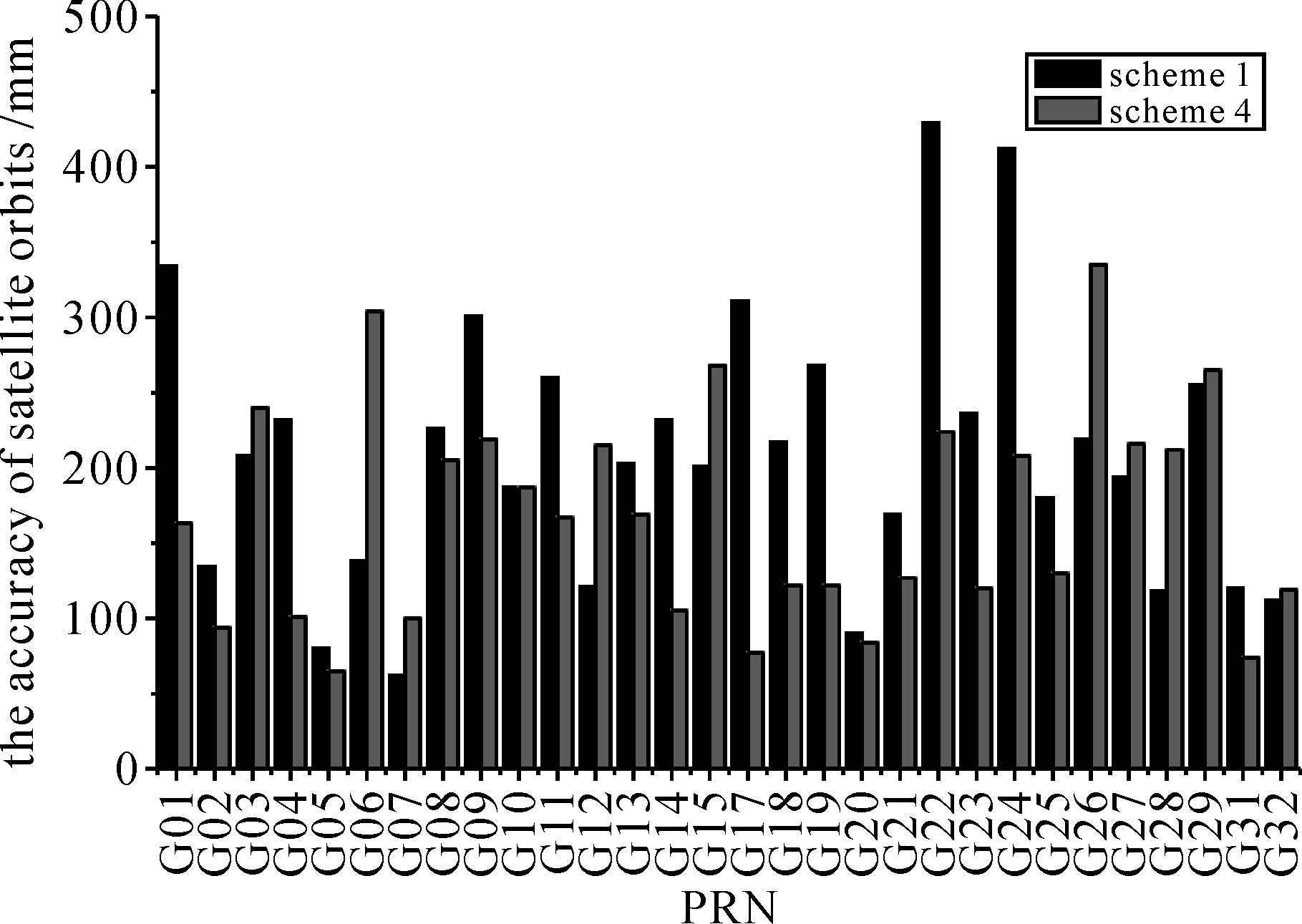
由图 4可以看出,地面区域监测网解算的MEO实测轨道精度偏低,平均为215 mm,远远低于基于全球均匀分布测站的定轨精度。由于目前低轨卫星的GPS定轨精度为厘米级,可以将低轨卫星看作低空的高动态天基监测站,同地面区域监测站网络联合定轨。基于此,本文在方案1的基础上分别增加了GRACE-A、GRACE-B和我国某低轨卫星的星载GPS监测数据组成地空联合监测网进行GPS定轨,即为方案2、方案3和方案4。方案2和方案3的GPS各卫星实测轨道精度同方案1比较如图 5所示,方案4的MEO各卫星实测轨道精度同方案1比较如图 6所示。各方案的平均实测轨道精度如表 4所示。
|
| 图 5 方案1、方案2和方案3的GPS定轨精度对比 Fig. 5 The comparison of GPS satellite orbits between scheme 1, 2 and 3 |
|
| 图 6 方案1和方案4的GPS定轨精度对比 Fig. 6 The comparison of GPS satellite orbits between scheme 1 and 4 |
| PRN | scheme 1 | scheme 2 | scheme 3 | scheme 4 |
| mean | 215 | 184 | 158 | 166 |
由图 5、图 6和表 4可见,方案2—4的MEO卫星定轨精度相对于方案1的提升分别为14.4%、26.5%和22.8%,平均提升约21%。分析原因为上述方案中的地面区域监测站网络对MEO卫星的观测弧长有限,高动态的天基监测站的加入,增加了MEO卫星的有效观测弧长。同时,考虑到低轨卫星天线的设计使得多路径效应影响很小,低轨卫星的高度导致其不受对流层影响,因此本文将天基低轨卫星观测数据的高度角设置为0°,有效改善了MEO卫星和测站的几何构型。
方案2和方案3的GRACE-A和GRACE-B卫星轨道高度为500 km,方案4的低轨卫星轨道高度约为900 km,不同高度的单颗低轨卫星对MEO定轨的增强效果相同,说明仅从低轨卫星高度考虑,其增强效果与高度关系不明显。
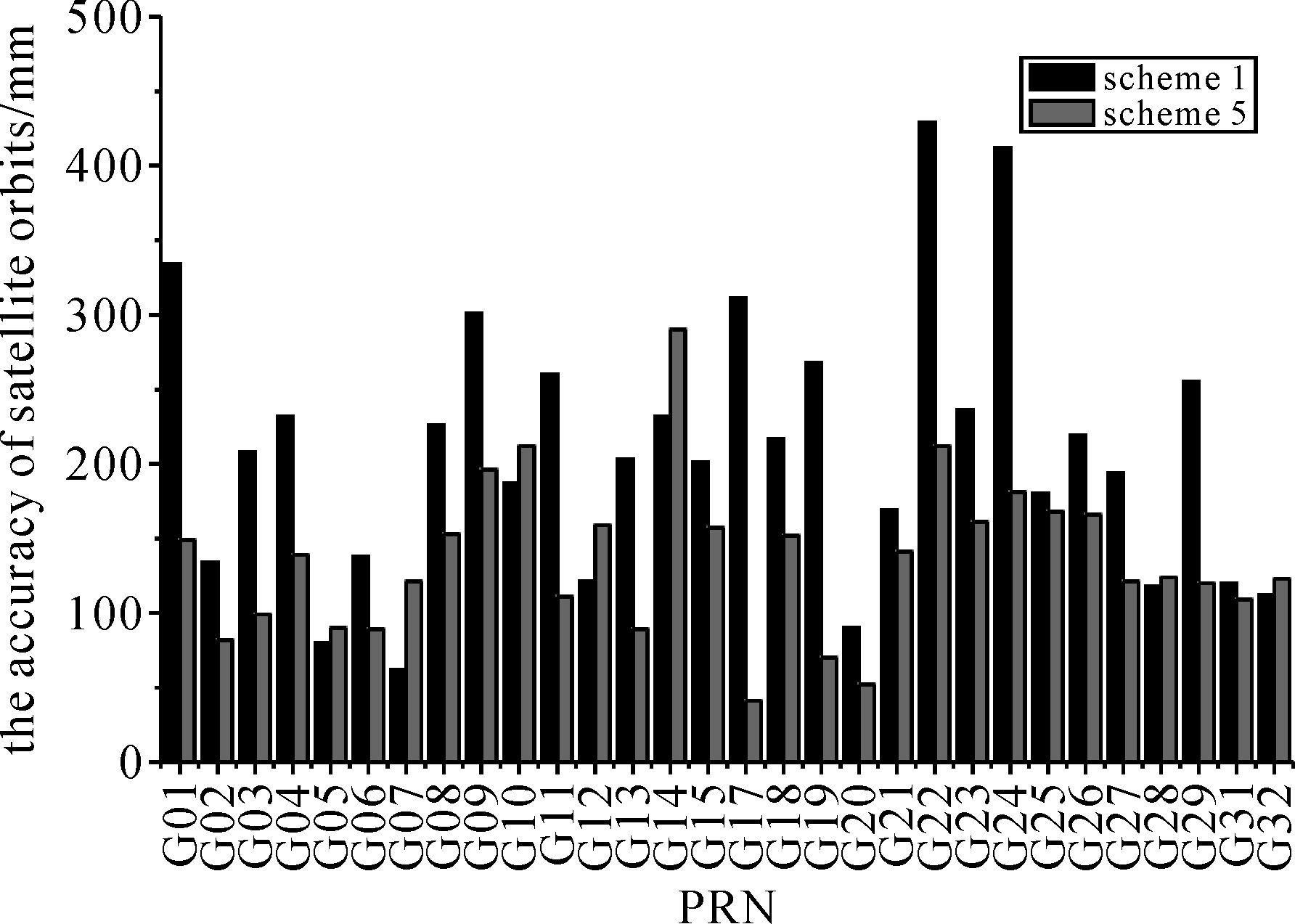
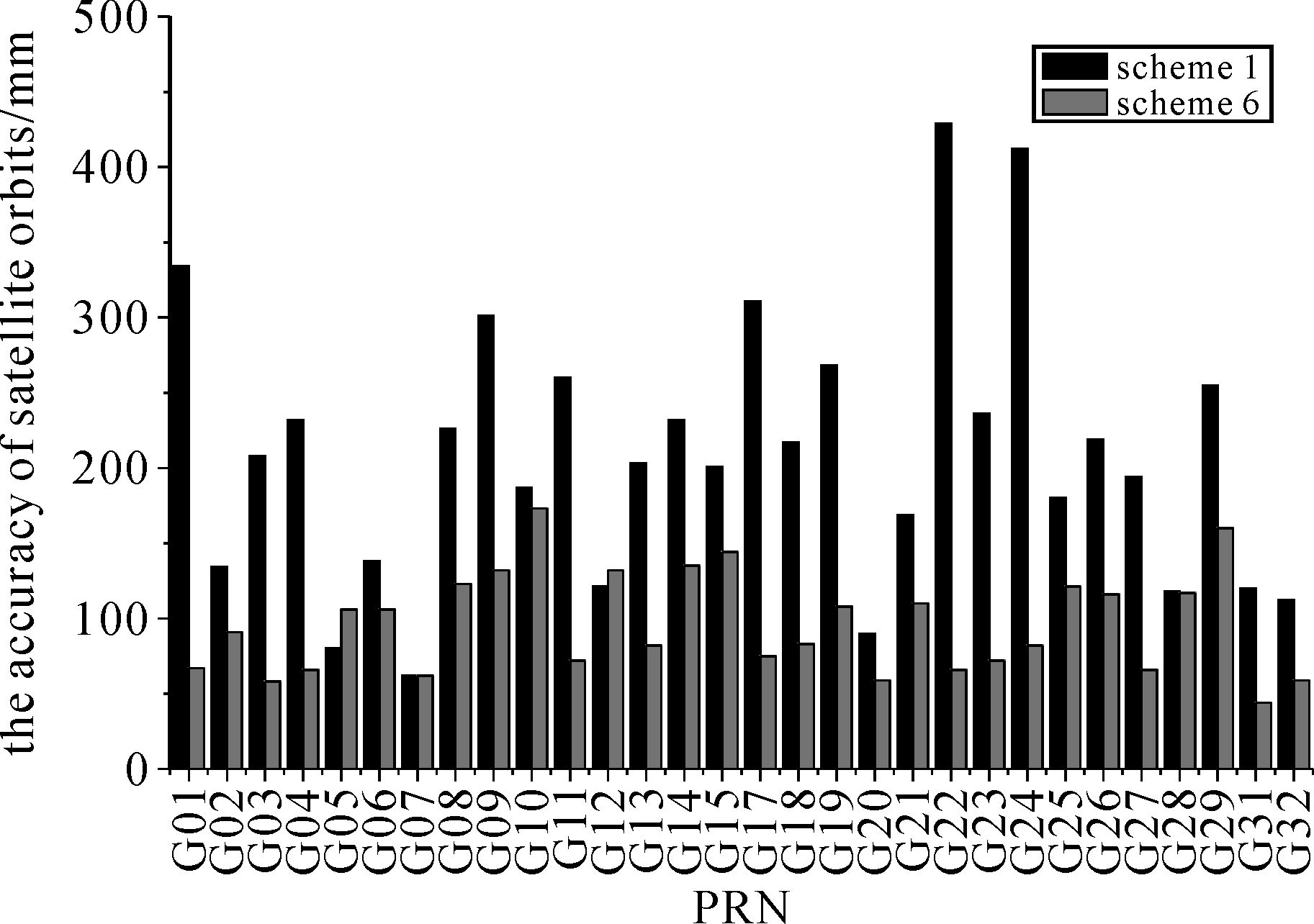
考虑到加入更多低轨卫星数据可以对MEO的有效观测弧长和几何构型有更大增强,本文设计了方案5将低轨卫星数量提升为2颗,方案6将天基监测站数量提升至3颗。方案5和方案6同方案1的定轨精度对比结果如图 7和图 8所示。
|
| 图 7 方案1和方案5的GPS定轨精度对比 Fig. 7 The comparison of GPS satellite orbits between scheme 1 and 5 |
|
| 图 8 方案1和方案6的GPS定轨精度对比 Fig. 8 The comparison of GPS satellite orbits between scheme 1 and 6 |
可知,方案5中地面区域运控监测站联合2颗低轨卫星同时解算,GPS卫星定轨精度有更加明显的提升,其平均轨道精度约为140 mm,相对于方案1,其定轨精度提升约34%。方案6中地面区域监测站联合三颗低轨卫星数据解算GPS卫星轨道,定轨精度优于100 mm,较方案1提升约55%。分析原因为更多的低轨卫星对有效轨道弧长和几何构型有更好的增强效果。
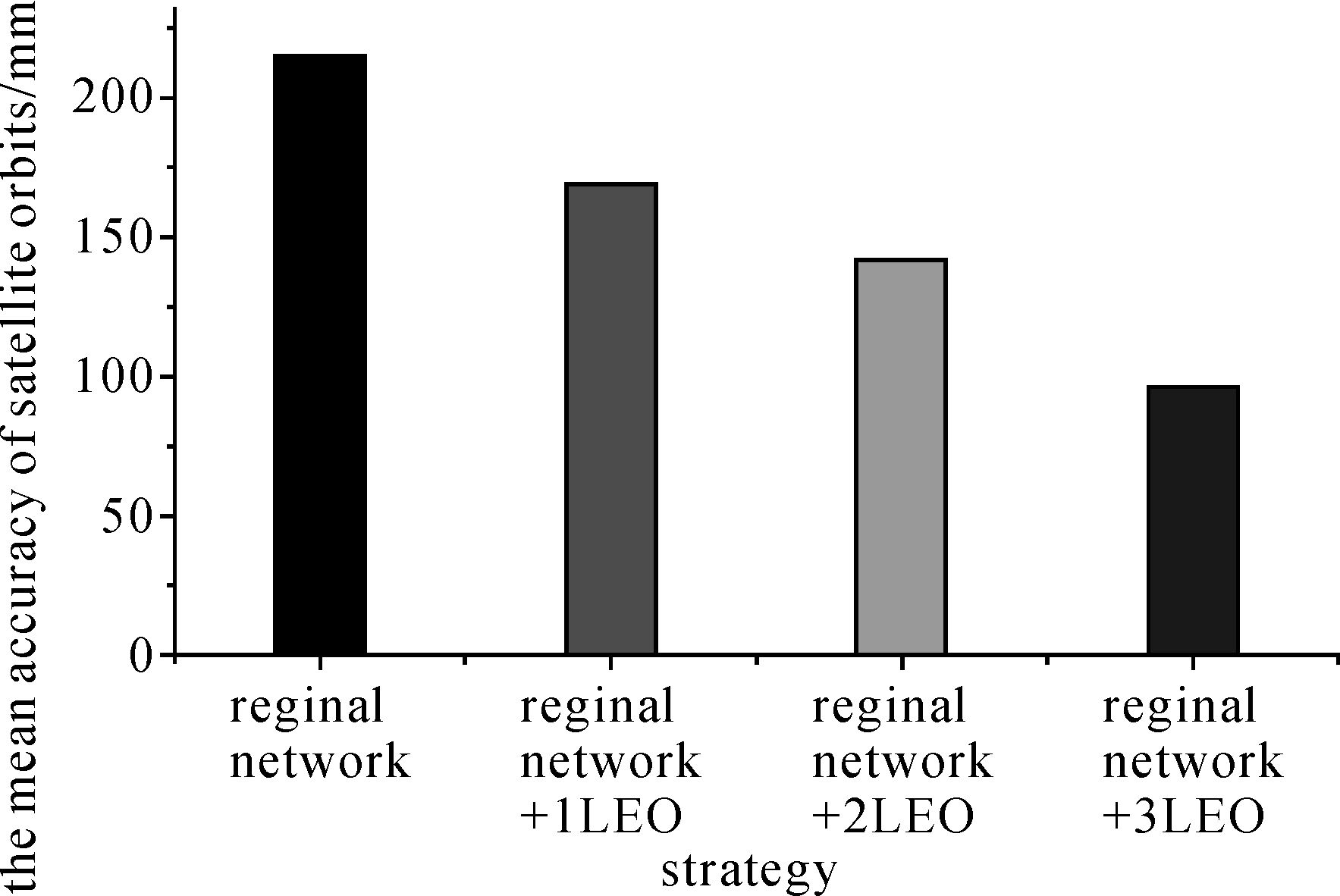
上述各方案MEO卫星轨道的精度提升情况如图 9所示。其中,区域网联合一颗低轨卫星的MEO轨道精度为方案2—4的结果的平均值。
|
| 图 9 不同方案的MEO轨道精度 Fig. 9 The measured orbit precision of MEO of different schemes |
通过上述对比可以看出,增加高精度的天基监测站,联合地面区域监测站进行MEO卫星定轨,可以显著提高MEO卫星实测轨道精度,3颗低轨卫星的加入可将定轨精度提升约50%。在低轨卫星数量少于3颗的情况下,增加的天基监测站数量越多,MEO定轨精度提升越高。分析原因为地面区域网对MEO连续跟踪的缺失弧段较多,不断增加的低轨卫星数据可有效补充其缺失弧段及改善其几何构型。随着低轨卫星数量不断增多,其增强效果将逐渐减弱,直到MEO卫星连续跟踪弧段完整。由于同一时段的在轨GNSS接收机数量有限,本文仅分析了最多3颗低轨卫星的增强效果。基于仿真数据对低轨卫星数量和分布进行系统分析,得到可靠的结论是值得进一步探讨的问题。
为进一步分析低轨卫星的加入对导航卫星轨道的增强效果,统计了不同方案的GPS卫星RNT 3个方向分量的精度,如图 10和表 5所示。

|
| 图 10 不同方案的RNT方向分量精度 Fig. 10 Accuracy of RNT direction component of different schemes |
| mm | |||
| strategy | radial orbital accuracy | tangential orbit accuracy | normal orbit accuracy |
| regional network | 257.581 | 219.484 | 100.484 |
| regional network+1LEO | 205.237 | 167.785 | 80.344 |
| regional network+2LEO | 174.484 | 137.968 | 67.935 |
| regional network+3LEO | 121.194 | 96.258 | 44.968 |
通过上述图表可以看出,不同数量的低轨卫星的加入对轨道径向精度提升率分别为20.3%、32.3%和52.9%;对法向精度提升率分别为23.6%、37.1%和56.1%;对切向精度提升率分别为20.0%、32.4%和55.2%。各方向的精度提升基本一致。
3.2.3 预报轨道精度统计及分析在MEO实测轨道的基础上,本文通过轨道外推,获得了不同方案的预报轨道,统计了预报2~4 h的轨道精度,不同方案结果对比如图 10所示。
由图 11可以看出,不同策略计算的预报2~4 h轨道精度分别为301 mm、238 mm、201 mm、132 mm;提升率分别为20.9%、33.2%和56.1%。由于计算的MEO卫星轨道是光滑的,外推的预报轨道精度提升效果与实测轨道一致。

|
| 图 11 不同方案的MEO预报2~4 h轨道精度 Fig. 11 The 2~4 hours prediction orbit precision of MEO of different schemes |
通过上述算例可以看出,地面区域监测网联合天基低轨卫星数据可以显著提升MEO预报轨道,从而提高MEO卫星广播星历轨道精度。
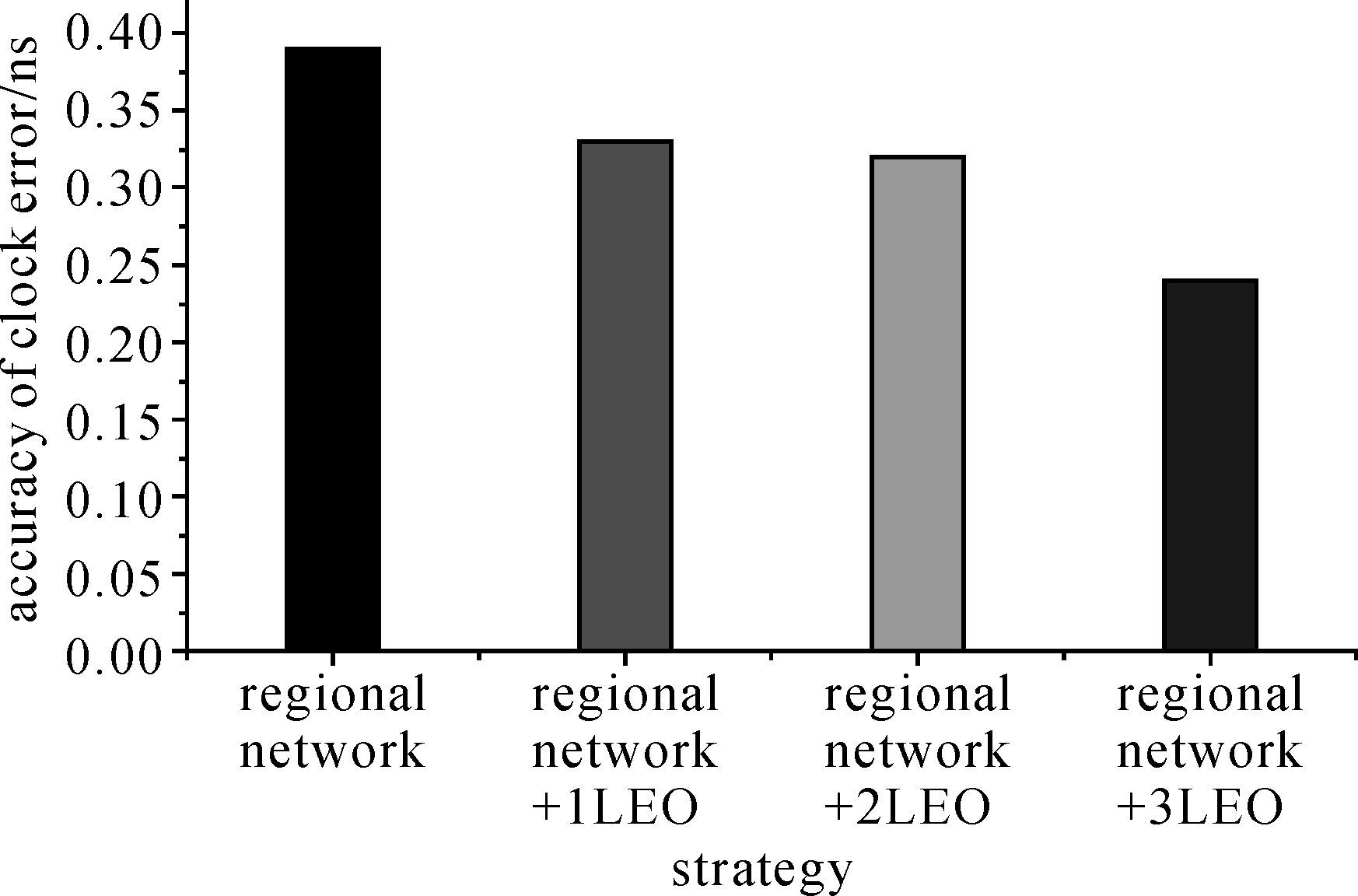
3.2.4 钟差精度统计及分析以事后的IGS精密钟差产品(.clk)作为真值,本文统计了不同方案的钟差精度见图 12和表 6。
|
| 图 12 不同方案的钟差精度 Fig. 12 Accuracy of clock error of different schemes |
| strategy | regional network | regional network+ 1LEO | regional network+ 2LEO | regional network+ 3LEO |
| accuracy of clock error/ns | 0.39 | 0.33 | 0.32 | 0.24 |
不同数量的低轨卫星的加入对卫星钟差的提升率分别为15.4%、17.9%和38.5%。加入1颗低轨卫星和2颗低轨卫星对GPS卫星钟差的影响基本不变,分析原因为加入的2颗低轨卫星为GRACE-A和GRACE-B,在同一轨道面上且相对距离较短,其观测数据具有较强相关性。
4 结论本文提出的区域监测站与低轨卫星数据联合测定MEO卫星轨道技术能够增加有效弧段长度,改善几何构型,大幅度提高MEO卫星轨道计算及预报精度。数值算例结果显示,在中国境内及周边7个地面区域监测站的基础上,依次增加1颗、2颗和3颗低轨卫星星载GPS数据,其实测轨道精度可分别提升约21.4%、33.9%和55.3%,且RNT 3个方向的轨道提升率基本一致;预报2~4 h轨道精度提升约20.9%、33.2%和56.1%;钟差精度提升约15.4%、17.9%和38.5%。建议我国BDS在区域测站分布阶段可采用联合低轨卫星数据方法提高北斗广播星历的MEO卫星轨道精度。
本文中未考虑实时定轨过程中,星载GNSS数据的通信和时效性问题,在后续研究中,可以考虑通过中继卫星等方法实现低轨卫星数据的实时通讯和传输。
致谢: 感谢iGMAS、MGEX、GFZ和IGS组织提供的数据及产品支持;感谢长安大学北斗分析与服务中心提供的技术支持。
| [1] | 陈明, 武军郦, 李志才. 北斗精密定轨及广播星历轨道精度评估[J]. 测绘工程, 2016, 25(11): 1–6. CHEN Ming, WU Junli, LI Zhicai. Precise Orbit Determination and Broadcast Ephemeris Accuracy Assessment and Analysis for BDS[J]. Engineering of Surveying and Mapping, 2016, 25(11): 1–6. |
| [2] | 杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 44(1): 72–81. YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary Assessment of the Navigation and Positioning Performance of BeiDou Regional Navigation Satellite System[J]. Science China Earth Sciences, 2014, 44(1): 72–81. |
| [3] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [4] | 朱永兴, 李斌, 于亮, 等. 基于精密星历的北斗卫星广播星历精度分析[J]. 全球定位系统, 2014, 39(1): 1–4. ZHU Yongxing, LI Bin, YU Liang, et al. Analysis of Beidou Satellite Broadcast Ephemeris Accuracy Based on Precise Ephemeris[J]. GNSS World of China, 2014, 39(1): 1–4. |
| [5] | WANG Le, ZHANG Qin, HUANG Guanwen, et al. BeiDou Satellite Navigation System (BDS) Real-Time Orbit Determination and Accuracy Analysis[C]//SUN Jiadong, LIU Jingnan, FAN Shiwei, et al. China Satellite Navigation Conference (CSNC) 2015 Proceedings:Volume Ⅱ. Berlin Heidelberg, Germany:Springer, 2015:523-532. |
| [6] | 张睿. BDS精密定轨关键技术研究[D]. 西安: 长安大学, 2016. ZHANG Rui. Research on Key Technologies of BDS Precise Orbit Determination[D]. Xi'an:Chang'an University, 2016. |
| [7] | 李龙龙, 耿国桐, 李作虎. 国外卫星导航系统星间链路发展研究[J]. 测绘科学技术学报, 2016, 33(2): 133–138. LI Longlong, GENG Guotong, LI Zuohu. Study of the Development of the Inter-Satellite Links in Foreign GNSS[J]. Journal of Geomatics Science and Technology, 2016, 33(2): 133–138. |
| [8] | ZHU S, REIGBER C, KÖNIG R. Integrated Adjustment of CHAMP, GRACE, and GPS Data[J]. Journal of Geodesy, 2004, 78(1): 103–108. |
| [9] | TAPLEY B D, RIES J C, DAVIS G W, et al. Precision Orbit Determination for TOPEX/POSEIDON[J]. Journal of Geophysical Research, 1994, 99(C12): 24383–24404. DOI:10.1029/94JC01645 |
| [10] | SCHUTZ B E, TAPLEY B D, ABUSALI P A M, et al. Dynamic Orbit Determination Using GPS Measurements from TOPEX/POSEIDON[J]. Geophysical Research Letters, 1994, 21(19): 2179–2182. DOI:10.1029/94GL01040 |
| [11] | 朱俊, 王家松, 陈建荣, 等. HY-2卫星DORIS厘米级精密定轨[J]. 宇航学报, 2013, 34(2): 163–169. ZHU Jun, WANG Jiasong, CHEN Jianrong, et al. Centimeter Precise Orbit Determination for HY-2 Via DORIS[J]. Journal of Astronautics, 2013, 34(2): 163–169. |
| [12] | 郭靖, 赵齐乐, 李敏, 等. 利用星载GPS观测数据确定海洋2A卫星cm级精密轨道[J]. 武汉大学学报(信息科学版), 2013, 38(1): 52–54. GUO Jing, ZHAO Qile, LI Min, et al. Centimeter Level Orbit Determination for HY2A Using GPS Data[J]. Geomatics and Information Science of Wuhan University, 2013, 38(1): 52–54. |
| [13] | 李济生. 人造卫星精密轨道确定[M]. 北京: 解放军出版社, 1995. LI Jisheng. Satellite Precision Orbit Determination[M]. Beijing: Chinese People's Liberation Army Publishing House, 1995. |
| [14] | 李敏. 多模GNSS融合精密定轨理论及其应用研究[D]. 武汉: 武汉大学, 2011. LI Min. Research on Multi-GNSS Precise Orbit Determination Theory and Application[D]. Wuhan:Wuhan University, 2011. |
| [15] | 赵齐乐. GPS导航星座及低轨卫星的精密定轨理论和软件研究[D]. 武汉: 武汉大学, 2004. ZHAO Qile. Research on Precision Orbit Determination Theory and Software of Both GPS Naviagation Constellation and LEO Satellites[D]. Wuhan:Wuhan University, 2004. |
| [16] | 匡翠林, 刘经南, 赵齐乐. 低轨卫星与GPS导航卫星联合定轨研究[J]. 大地测量与地球动力学, 2009, 29(2): 121–125. KUANG Cuilin, LIU Jingnan, ZHAO Qile. Precise Orbit Determination of Low Earth Orbit Satellite and GPS Satellite Based on Combined Orbit Determination Strategy[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 121–125. |



