2. 地球空间信息技术协同创新中心, 湖北 武汉 430079;
3. 武汉大学测绘学院导航定位技术研究中心, 湖北 武汉 430079
2. Collaborative Innovation Centre for Geospatial Technology, Wuhan 430079, China;
3. Research Center of Positioning and Navigation Technology, School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, ChinaAbstract
随着GPS和GLONASS系统的现代化以及Galileo和BeiDou卫星导航系统(BDS)的建设,GNSS正朝多频多系统的方向发展[1-2]。为了充分利用多系统信号资源,通常应尽可能使用上述四大系统可观测到的有效信号进行导航定位计算,以增强导航定位的性能。由于存在系统间偏差(ISB),在多系统组合精密相对定位中,通常是每个系统各自选择自己的参考星,在系统内组成双差观测值,然后联合各系统的双差观测值进行多系统相对定位解算,这种组合方式通常称为松组合模型。为了增加导航系统间的兼容性与互操作性,不同GNSS系统设计有重叠频率的信号[3]。此时,不同GNSS系统组成双差时可以只选择一颗参考卫星,这样不仅可形成系统内双差观测还可以形成系统间的双差观测,这种组合方式称之为紧组合模型[4-5]。在城市高楼、深山峡谷等信号遮挡比较严重,单个系统可观测的卫星数较少的环境下,松组合模型通常无法进行定位解算,而采用紧组合模型,可增加额外的观测方程,改善模型的强度,进而提高组合相对定位的可用性、可靠性以及精度。
然而,当使用紧组合相对定位模型时,必须考虑接收机间差分系统间偏差(DISB)对定位解算的影响[6-7]。文献[8—9]对GPS L1/L5-Galileo(Galileo in-orbit validation element,GIOVE)E1/E5a频点的接收机间DISB的大小与稳定性进行了分析。实测数据处理结果表明:相同类型接收机间的DISB接近于0,双差可以消除其影响;不同类型接收机间的DISB通常较大,但具有很好的稳定性,因此能够事先标定并进行改正。为了削弱残留的系统误差以及观测噪声的影响,文献[10]提出了对DISB参数分弧段(10 min)进行估计的方法,并对GPS L1-Galileo(in-orbit validation,IOV)E1频点的接收机间DISB的大小与稳定性进行了分析。数据处理结果表明,相较于单历元估计方法,分弧段估计时DISB参数具有更好的重复性。文献[11]进一步对不同类型接收机间的GPS L1/L2/L5-QZSS L1/L2/L5-Galileo(IOV)E1/E5a、BDS B2-Galileo(IOV)E5b频点的相位与伪距DISB进行了标定。针对由多台GNSS接收机所组成的短基线网,文献[12]提出了DISB的整网估计方法,并得到了与文献[11]相一致的结果。针对陆续发射的GPS Block IIF、Galileo(full-operational-capability,FOC)以及IRNSS(Indian regional navigation satellite system)新卫星,文献[13]首次对IRNSS L5-GPS L5-Galileo E5a-QZSS L5频点的接收机间DISB的大小与稳定性进行了分析,并得到了与文献[8—9]中一致的结论。相较于松组合模型,改正DISB后的紧组合模型不仅能够有效提高模糊度固定的成功率、降低模糊度固定的失败率、缩短模糊度的首次固定时间,同时还可以提高相对定位的可用性及精度[8-10, 13-15]。
目前,对GNSS紧组合相对定位模型的研究主要集中在GPS L1/L5-Galileo E1/E5a的重叠频率上,对BDS与其他系统的紧组合相对定位模型与性能研究较少。实际上,BDS的B2频点与Galileo的E5b频点的频率相同,因此可以在此重叠频率上实现BDS与Galileo的紧组合相对定位,有望提升BDS与Galileo在精密相对定位层面的互操作水平和可互换能力。
本文对BDS B2/Galileo E5b短基线紧组合相对定位的模型与算法进行研究,并对其性能进行分析。首先详细推导了BDS B2/Galileo E5b短基线紧组合相对定位的模型与算法,重点分析了BDS B2-Galileo E5b频点的接收机间DISB的长期稳定性;最后基于BDS B2/Galileo E5b单频单历元相对定位试验对系统间紧组合模型的效果进行了验证。
目前,BDS处于全球系统的建设阶段,正在逐步发射新一代导航卫星,这些卫星将发射新体制信号B1C与B2a,其与GPS L1/L5、Galileo E1/E5a频率重叠[16],也具有互操作与可互换的潜力。因此,本文对新一代BDS系统与其他GNSS系统在精密相对定位领域的互操作与可互换性能的研究也具有重要的参考价值。
1 BDS B2/GalileoE5b短基线相对定位模型多系统组合精密相对定位中,由于不同GNSS系统所采用的时间系统不同,需要将其统一到相同的时间系统下,此时可以对不同系统独立估计钟差或者引入系统间时间偏差参数[17]。另外,尽管不同GNSS系统的坐标系统也存在差异,但是这些差异在相对定位中可以忽略[18-19]。需要指出的是,当基线两端的接收机类型不相同时,BDS GEO (geostationary earth orbit)卫星与非GEO卫星之间可能存在伪距与相位ISTB(inter-satellite-type bias)的影响,在数据处理时需要进行考虑,可以事先标定并改正(伪距ISTB一般很小,也可以直接忽略其影响)[20-21]。在下面的公式推导中,本文默认已经在观测值上对可能存在的ISTB进行了处理,因此公式推导时将不再对ISTB进行考虑。
假设GNSS接收机k、l同步观测到BDS B2与Galileo E5b频点的载波相位与伪距观测值,则在BDS时(BDT)下,BDS卫星iB与接收机k的非差载波相位和伪距观测方程为
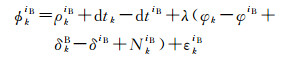 (1)
(1)
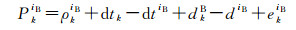 (2)
(2)
式中,φkiB表示以米为单位的载波相位观测值;ρkiB表示卫星iB与接收机k之间的几何距离;dtk表示接收机钟差;dtiB表示卫星钟差;λ表示B2(E5b)频率对应的波长;NkiB表示整周模糊度;φk表示接收机端的初始相位;δkB表示接收机端的相位硬件延迟;φiB表示卫星端的初始相位;δiB表示卫星端的相位硬件延迟;εkiB表示相位噪声;PkiB表示伪距观测值;dkB表示接收机端的伪距硬件延迟;diB表示卫星端的伪距硬件延迟;ekiB表示伪距噪声。需要指出的是,上标B表示该误差对所有的BDS卫星都相同。对于本文研究的短基线与零基线而言,大气延迟误差经过差分后可以消除或者忽略,为了简便没有在式(2) 中给出。
同样,Galileo的卫星jE与接收机k的非差载波相位和伪距观测方程为
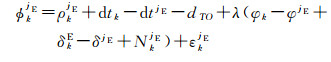 (3)
(3)
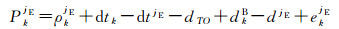 (4)
(4)
式中,上标E表示该误差对所有的Galileo卫星都相同;dTO表示Galileo时与BDS时的偏差(以m为单位)。
当在测站k、l间作差时,与卫星有关的误差如卫星钟差、卫星端的初始相位与硬件延迟误差以及系统间时间偏差dTO可以消除。此时,站间单差载波相位与伪距观测方程为
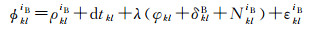 (5)
(5)
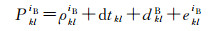 (6)
(6)
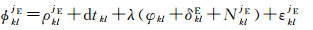 (7)
(7)
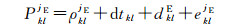 (8)
(8)
式中,φkliB、φkljE表示单差载波相位观测值;PkliB、PkljE表示单差伪距观测值;ρkliB、ρkljE分别表示卫星iB、jE与接收机k、l之间的单差几何距离;dtkl表示接收机k、l之间的单差钟差;NkliB、NkljE表示单差模糊度;φkl表示接收机端的单差初始相位;δklB、δklE分别表示接收机端对BDS、Galileo卫星的单差相位硬件延迟;dklB、dklE分别表示接收机端对BDS、Galileo卫星的单差伪距硬件延迟;εkliB、εkljE表示单差相位噪声;ekliB、ekljE表示单差伪距噪声。
1.1 松组合相对定位模型当在BDS与Galileo系统内各自组双差时,需要分别选择一颗BDS与Galileo卫星作为参考星。假设分别选择1B、1E作为BDS与Galileo的参考星,则BDS B2/GalileoE5b松组合模型为
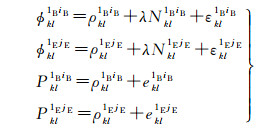 (9)
(9)
式中,iB=2B, 3B,…,mB;jE=2E, 3E,…,mE(mB、mE分别表示BDS与Galileo的可观测卫星数);φkl1BiB、φkl1EjE表示双差载波相位观测值;Pkl1BiB、Pkl1EjE表示双差伪距观测值;ρkl1BiB、ρkl1EjE表示双差几何距离;Nkl1BiB、Nkl1EjE表示双差模糊度;εkl1BiB、εkl1EjE表示双差载波相位噪声;ekl1BiB、ekl1EjE表示双差伪距噪声。
系统内双差可以进一步消除接收机相关的误差如单差接收机钟差、接收机端初始相位与硬件延迟误差,此时双差模糊度参数能够保持整数特性。松组合模型中,各个系统的双差观测方程相互函数独立,方程间仅通过位置参数建立关联。松组合模型实现起来比较简单,当前在多系统组合精密相对定位中被广泛采用。
1.2 估计DISB的紧组合相对定位模型当在BDS与Galileo系统间求双差时,则仅需选择一颗卫星作为参考星。当选择1B作为两个系统共同的参考星时,则BDS B2/GalileoE5b系统间双差观测方程为
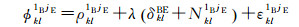 (10)
(10)
 (11)
(11)
式中,jE=1E, 2E,…,mE;δklBE=δklE-δklB、dklBE=dklE-dklB分别表示接收机间相位与伪距的差分系统间偏差(DISB)。DISB是由接收机对B2与E5b信号的硬件延迟不同引起的。式(10) 中,接收机间相位DISB参数δklBE与模糊度参数因为线性相关而无法分离,因此无法同时估计相位DISB参数与系统间双差整周模糊度参数Nkl1BjE。由于法方程存在秩亏,且秩亏数1,此时可以对参数进行重组
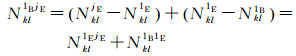 (12)
(12)
 (13)
(13)
即将jE相对于1B的模糊度转换为BDS/Galileo参考星之间的模糊度与Galileo系统内的模糊度之和,并将参考星间的模糊度参数Nkl1B1E和相位DISB参数合并在一起进行估计。此时,估计DISB的系统间紧组合相对定位模型为
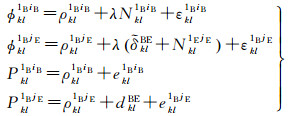 (14)
(14)
利用式(14) 进行参数估计时,虽然能够得到不受偏差影响的伪距DISB估值,但是相位DISB估值却会受到BDS参考星与Galileo参考星之间的双差模糊度的影响。需要说明的是,在进行标定时,直接对相位DISB估值取整即可,这不会对后续的应用产生影响[9-10]。
虽然系统间双差增加了观测方程的个数,但同时也增加了接收机间DISB参数。对于单历元而言,观测方程不会增加冗余,模型的强度不会增强,因而理论上不会提高模糊度固定效果与定位效果,但该模型建立了系统间双差模糊度之间的联系。
1.3 改正DISB的紧组合相对定位模型当接收机间DISB参数已经事先标定时,则可以直接在双差观测值上对其进行改正。改正DISB的紧组合相对定位模型为
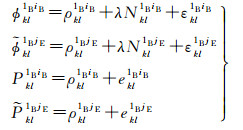 (15)
(15)
式中,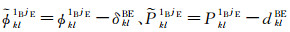
相较于松组合模型与估计DISB的紧组合模型,改正DISB的紧组合模型每个历元能够增加一个冗余观测数,进而能够提高模型的强度,因此理论上能够提高相对定位的结果。
在数据处理过程中,随机模型采用高度角相关模型[22]
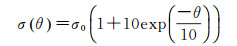 (16)
(16)
式中,σ(θ)表示非差观测值的标准差;θ表示卫星高度角;σ0表示天顶方向的非差伪距与相位观测值的标准差。在本文中,B2与E5b频点的天顶方向的伪距与相位观测值的标准差分别取0.3 m与3 mm[12]。
2 DISB稳定性分析 2.1 统计假设检验通过式(14) 获取每天的相位与伪距DISB估值序列后,可以使用假设检验的方法对相位与伪距DISB序列在每天内的稳定性进行评估。
假设一天内能够逐历元获取n个相位(或者伪距)DISB估值βklBE(1),βklBE(2),…,βklBE(n),则DISB的加权平均值及其精度可以通过式(17) 与式(18) 进行计算[23]
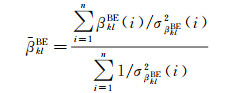 (17)
(17)
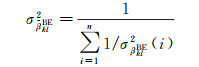 (18)
(18)
式中,σβklBE2(i)为βklBE(i)的验后方差。
在此基础上,可以使用检验量T对DISB在每天内的稳定性进行评估[23]
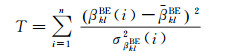 (19)
(19)
式中,βklBE(i)为正态分布的假设下,T为自由度为n-1的卡方检验。当显著性水平为α时,T的临界值为χα(t-1, 0)。如果T < χα2(t-1, 0),则表明DISB估值在一天内没有明显的变化。在本文中,显著性水平α的取值为5%。
2.2 试验数据本文使用澳大利亚科廷大学(Curtin University)的实测零基线/短基线GNSS数据(http://saegnss2.curtin.edu.au/ldc/)对BDS B2-Galileo E5b频点的接收机间DISB的长期稳定进行分析。使用的试验数据概况见表 1,时间段为2015年6月至2016年6月。在对DISB进行估计时使用单历元模式,并将基线向量固定为真值。截止高度角设置为10°,采样间隔为30 s。Galileo IOV与FOC卫星都将参与解算。需要指出的是,Galileo卫星E14与E18在发射时都进入了异常的轨道[24],导致没有可用的广播星历。因此在计算卫星位置与钟差时,Galileo使用精密星历,而BDS卫星则仍然使用广播星历。
| 测站 | GNSS接收类型 | 固件版本 | GNSS天线 | 备注 |
| CUT0 | Trimble NetR9 | 5.10 | TRM59800.00 SCIS | CUT0、CUT1、CUT2、CUT3为零基线:CUBB、SPA7均与CUT0组成短基线 |
| CUT1 | SEPT POLARX4 | 2.9.0 | TRM59800.00 SCIS | |
| CUT2 | Trimble NetR9 | 5.10 | TRM59800.00 SCIS | |
| CUT3 | JAVAD TRE_G3T DELTA | 3.6.3 | TRM59800.00 SCIS | |
| CUBB | JAVAD TRE_G3T DELTA | 3.6.3 | TRM59800.00 SCIS | |
| SPA7 | JAVAD TRE_G3T DELTA | 3.6.3 | TRM59800.00 SCIS |
2.3 不同情形下的DISB的特性分析 2.3.1 相同类型接收机(固件版本也相同) 2.3.1.1 Trimble NetR9
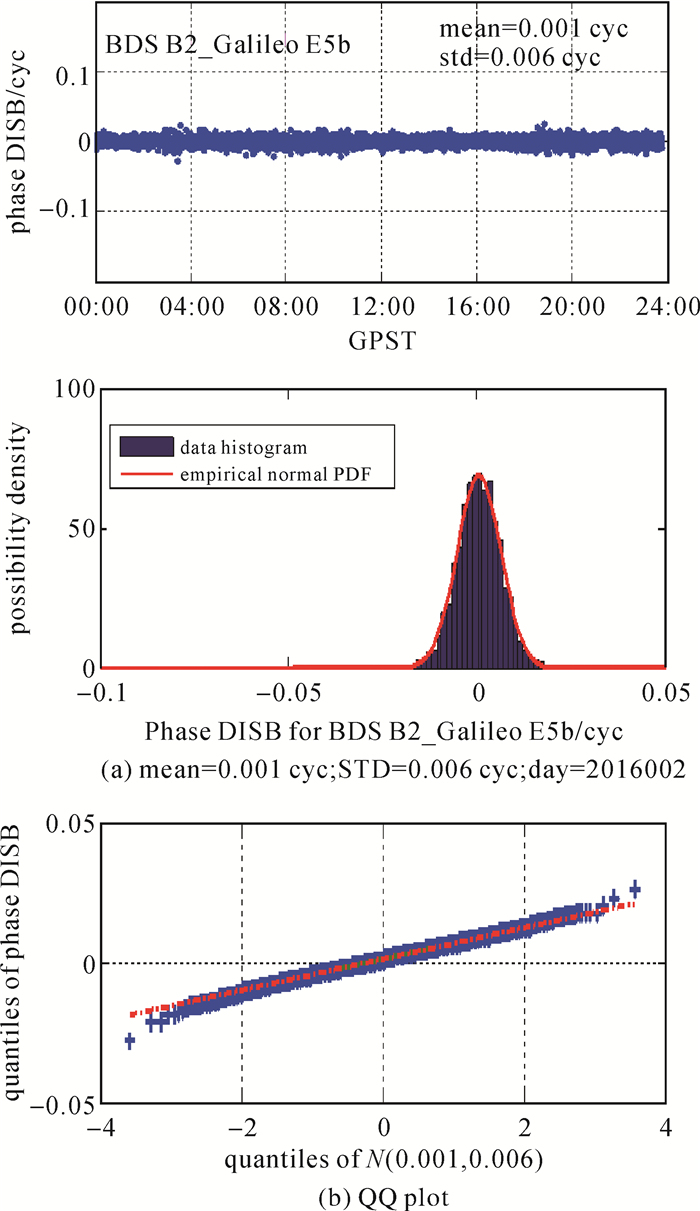
采用CUT2-CUT0零基线数据,观测时间段为2015年9月27日至2016年2月30日。图 1、图 2分别为2016年1月1日的相位与伪距的DISB序列、分布以及QQ图。由图可知,BDS B2-Galileo E5b频点的相位与伪距DISB都接近于0(0.001周与0.03 m),且十分稳定。DISB的分布与其理论分布符合得很好,同时QQ图上的点也近似地在一条直线附近,这都说明当天的DISB序列近似于服从正态分布。
|
| 图 1 相位DISB序列及分布 Fig. 1 Phase DISB series and distribution |

|
| 图 2 伪距DISB序列及分布 Fig. 2 Code DISB series and distribution |
图 3为观测时段内相位与伪距DISB的统计检验量与临界值(图中横轴代表的是从2015年1月1日开始算起的年积日,2016年则在此基础上继续累加,后面的图中也是如此)。由图可知,在观测时间段内,每天的DISB序列都满足T < χα2(t-1, 0),这表明DISB序列在每天内都是稳定的。需要指出的是,图 3中中断的地方表示数据缺失(后面的图中也是如此)。

|
| 图 3 相位与伪距DISB的统计检验量与临界值 Fig. 3 Test statistics and critical value for phase and code DISB |
观测时段内相位与伪距DISB序列如图 4所示。由图可知,在观测时间段内,DISB估值序列十分稳定,天与天之间的差异很小。也就是说,BDS B2-Galileo E5b频点的相位与伪距DISB具有很好的长期稳定性。

|
| 图 4 2015-09-27—2016-02-30相位与伪距DISB Fig. 4 Phase and code DISB 2015-09-27—2016-02-30 |
2.3.1.2 Javad TRE_G3T DELTA
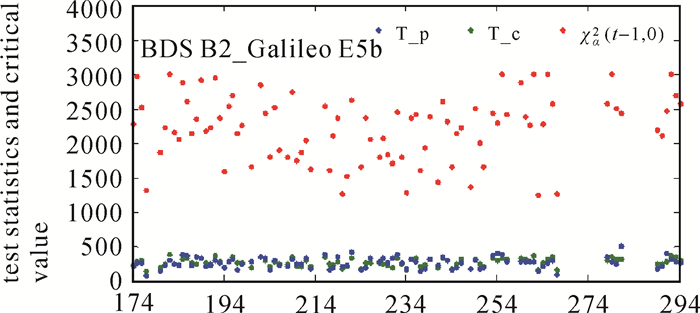
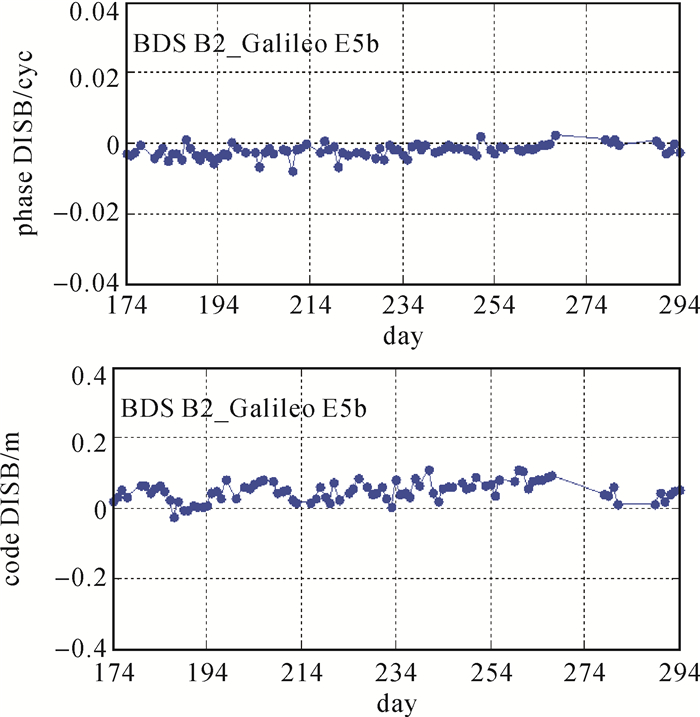
采用SPA7-CUBB短基线(基线长约为357.91 m)数据,观测时间段为2015-06-23—2015-10-21。图 5为观测时段内相位与伪距DISB的统计检验量与临界值。由图可知,每天的DISB序列都满足T < χα2(t-1, 0),DISB序列具有很好的天内稳定性。观测时段内DISB序列如图 6所示。由图可知,BDS B2-Galileo E5b相位与伪距DISB都接近于0,且在时间域上十分稳定。
|
| 图 5 相位与伪距DISB的统计检验量与临界值 Fig. 5 Test statistics and critical value for phase and code DISB |
|
| 图 6 2015-06-23—2015-10-21时段内相位与伪距DISB Fig. 6 Phase and code DISB 2015-06-23—2015-10-21 |
2.3.2 不同类型接收机 2.3.2.1 Septentrio POLARX4-Trimble NetR9
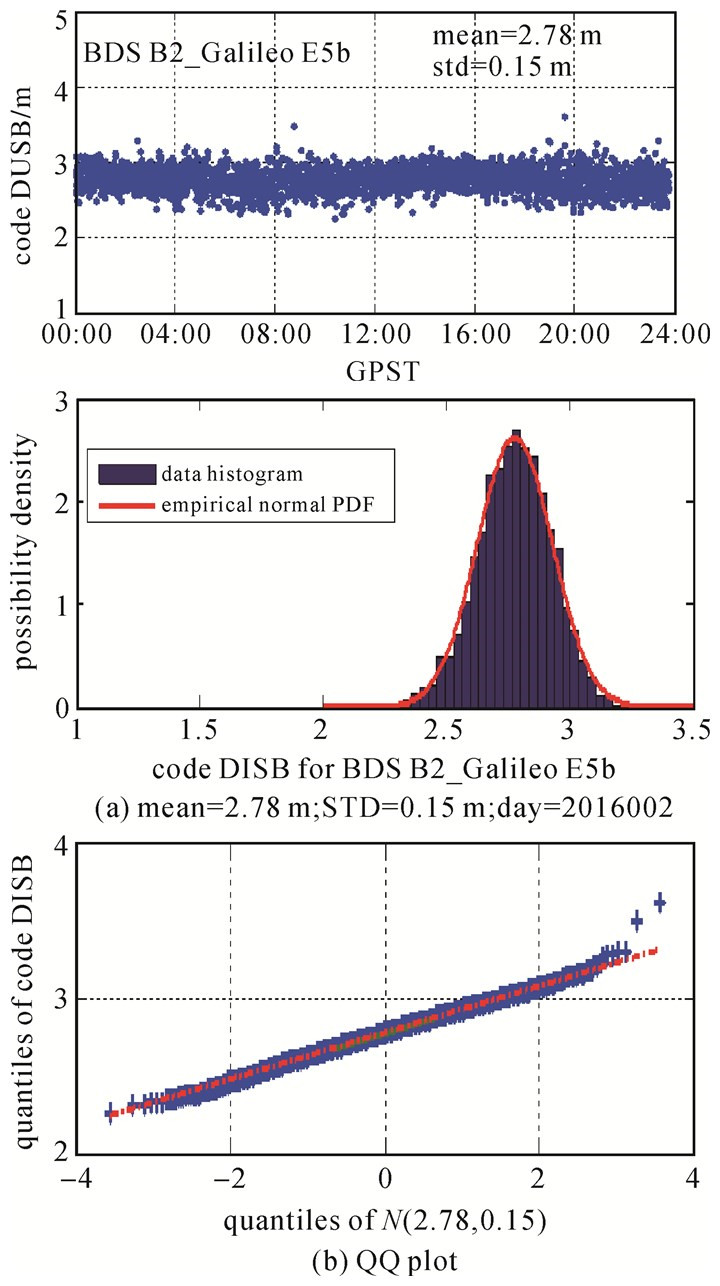
采用CUT1-CUT0零基线数据,数据时间段为2015-09-25—2016-05-30。图 7、图 8分别为2016年1月2日的相位与伪距的DISB序列、分布以及QQ图。由图可知,相位与伪距DISB分别为-0.244周、2.78 m。其大小虽然很显著,但是一天之内十分稳定。同时,DISB的分布与其理论分布也符合得很好,DISB序列近似于服从正态分布。

|
| 图 7 相位DISB序列及分布 Fig. 7 Phase DISB series and distribution |
|
| 图 8 伪距DISB序列及分布 Fig. 8 Code DISB series and distribution |
图 9为观测时段内相位与伪距DISB的统计检验量与临界值。图 10为观测时段内DISB序列。由图可知,BDS B2-Galileo E5b相位与伪距DISB具有很好的天内稳定性以及天与天间的长期稳定性。

|
| 图 9 相位与伪距DISB的统计检验量与临界值 Fig. 9 Test statistics and critical value for phase and code DISB |

|
| 图 10 2015-09-25—2016-05-30时段内相位与伪距DISB Fig. 10 Phase and code DISB 2015-09-25—2016-05-30 |
2.3.2.2 Javad TRE_G3T DELTA-Trimble NetR9
采用CUT3-CUT0零基线数据,数据时间段为2015-12-07—2016-05-30。图 11为观测时段内相位与伪距DISB的统计检验量与临界值。图 12为观测时段内DISB序列。由图可知,BDS B2-Galileo E5b频点的相位与伪距DISB较大,分别为-0.256周与2.68 m。尽管如此,相位与伪距DISB都具有很好的天内稳定性以及天与天间的长期稳定性。

|
| 图 11 相位与伪距DISB的统计检验量与临界值 Fig. 11 Test statistics and critical value for phase and code DISB |

|
| 图 12 2015-12-07—2016-05-30时段内相位与伪距DISB Fig. 12 Phase and code DISB 2015-12-07—2016-05-30 |
由前面的分析可知,基线两端的接收机类型(包括固件版本)相同时,BDS B2-Galileo E5b相位与伪距DISB接近于0;基线两端的接收机类型不同时,DISB则较大。DISB具有长期稳定性,因此可以事先标定并进行改正。
3 短基线紧组合相对定位模型性能评估本节将对BDS B2/Galileo E5b短基线紧组合(改正DISB)相对定位模型的性能进行评估。数据处理采用CUBB_CUT0短基线数据(采样间隔为30 s)。首先利用2015年10月8日的数据,依据式(14) 对DISB进行标定;然后采用2016年1月8日的数据,依据式(15),改正DISB后进行紧组合相对定位。数据处理时采用单历元模式,并通过统计实际成功率来对模糊度的固定效果进行评估[25]
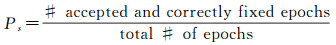 (19)
(19)
式中,在确定模糊度是否固定正确时,模糊度真值通过对整个观测时段的多频多系统观测值进行处理得到。模糊度固定采用LAMBDA方法,并采用FCRT(fixed critical-value ratio test)与FFRT(fixed failure rate ratio test)方法对模糊度进行确认[26-28]。采用FCRT对模糊度进行确认时,分别选取了1.5、2.0、2.5、3.0、3.5、4.0作为阈值(u);采用FFRT对模糊度进行确认时,失败率(Pf)取值为1%、0.1%。
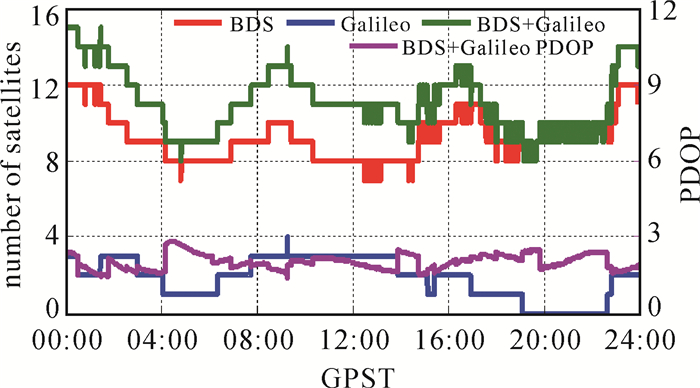
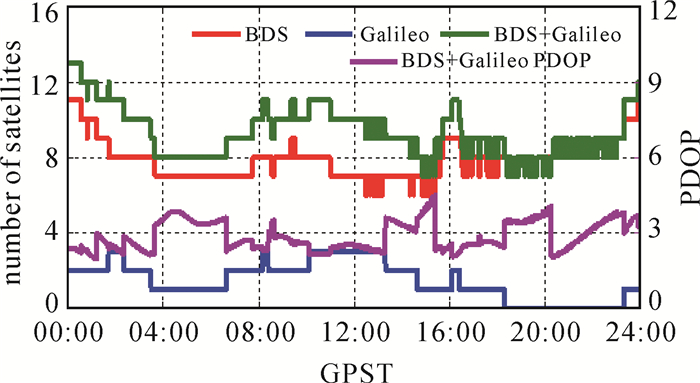
利用不同截止高度角对不同遮挡情况进行模拟。图 13与图 14分别为截止高度角为10°与20°时的可观测卫星数及PDOP。当截止高度角为10°时,观测时段内平均可观测的卫星数为11.3颗,平均PDOP为2.02;当截止高度角为20°时,观测时段内平均可观测的卫星数为9.3颗,平均PDOP为2.86。需要指出的是,GPST 20:00附近的时段内没有可观测的Galileo卫星,因此只能利用松组合模型进行定位解算。
|
| 图 13 截止高度角为10°时卫星数及PDOP Fig. 13 Number of satellites and PDOP with 10° elevation cut-off angle |
|
| 图 14 截止高度角为20°时卫星数及PDOP Fig. 14 Number of satellites and PDOP with 20° elevation cut-off angle |
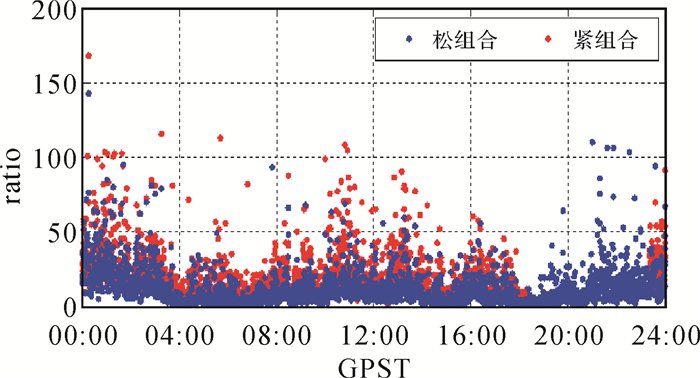
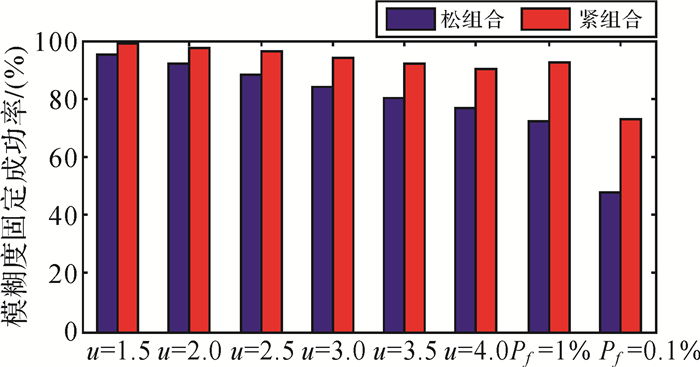
图 15与图 16分别为截止高度角为10°与20°时的模糊度固定Ratio值序列(图中紧组合模型特指改正DISB的紧组合模型,后面的图中也是如此)。由图可知,使用紧组合模型能够明显提高Ratio值。图 17与图 18分别为截止高度角为10°与20°时的模糊度固定实际成功率。由图可知,相对于松组合模型,紧组合模型能够显著提高模糊度固定效果。模糊度确认时阈值越大(模糊度检验越严格),模糊度固定率提高越明显。同时,相较于截止高度角为10°的情形,紧组合模型在截止高度角为20°时的效果更为显著。当截止高度角为10°时,采用不同模糊度确认策略,模糊度固定成功率分别可以提高约0.3%、0.9%、1.4%、2.1%、3.2%、4.2%、2.3%、13.4%;当截止高度角为20°时,模糊度固定成功率则可以提升约3%、5%、8%、10%、12%、14%、20%、25%。

|
| 图 15 截止高度角为10°时Ratio值 Fig. 15 Ratio with 10° elevation cut-off angle |
|
| 图 16 截止高度角为20°时Ratio值 Fig. 16 Ratio with 20° elevation cut-off angle |

|
| 图 17 截止高度角为10°时模糊度固定实际成功率 Fig. 17 The empirical ambiguity resolution success rate with 10° elevation cut-off angle |
|
| 图 18 截止高度角为20°时模糊度固定实际成功率 Fig. 18 The empirical ambiguity resolution success rate with 20° elevation cut-off angle |
截止高度角为20°、Ratio阈值取3时的模糊度正确固定解的坐标误差序列如图 19所示,统计结果如表 2所示。由图与表可知,紧组合模型能够获取略优于松组合模型的定位精度。

|
| 图 19 截止高度角为20°、u=3时正确固定解坐标误差序列 Fig. 19 Coordinate error series of correctly fixed solutions with 20° elevation cut-off angle and u=3 |
| cm | ||||
| E | N | U | ||
| 松组合 | 平均值 | 0.10 | -0.01 | 0.15 |
| 标准差 | 0.25 | 0.32 | 0.97 | |
| 紧组合 | 平均值 | 0.02 | -0.01 | 0.09 |
| 标准差 | 0.24 | 0.29 | 0.86 | |
4 结论
本文详细推导了BDS B2/Galileo E5b短基线紧组合相对定位的模型与算法,并重点分析了BDS B2-Galileo E5b频点的接收机间DISB的长期稳定性。数据处理结果表明:基线两端的接收机类型(包括固件版本)相同时,BDS B2-Galileo E5b相位与伪距DISB接近于0;基线两端的接收机类型不同时,DISB较大,但是具有很好的长期稳定性。最后基于BDS B2/Galileo E5b单频单历元相对定位实验对系统间紧组合模型的效果进行了验证。短基线数据处理结果表明,相对于传统的松组合模型,使用改正DISB的紧组合模型能够显著提高模糊度固定的成功率。尤其是在遮挡比较严重、单系统可观测到的卫星数较少的情形下,模糊度固定成功率可以提高10%~25%。
致谢: 感谢科廷大学(Curtin University)提供GNSS数据以及MGEX提供广播星历与精密星历产品。
| [1] | 任晓东, 张柯柯, 李星星, 等. BeiDou、Galileo、GLONASS、GPS多系统融合精密单点[J]. 测绘学报, 2015, 44(12): 1307–1313. REN Xiaodong, ZHANG Keke, LI Xingxing, et al. Precise Point Positioning with Multi-constellation Satellite Systems:BeiDou、Galileo、GLONASS、GPS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1307–1313. DOI:10.11947/j.AGCS.2015.20140568 |
| [2] | 姚宜斌, 胡明贤, 许超钤. 基于DREAMNET的GPS/BDS/GLONASS多系统网络RTK定位性能分析[J]. 测绘学报, 2016, 45(9): 1009–1018. YAO Yibin, HU Mingxian, XU Chaoqian. Positioning Accuracy Analysis of GPS/BDS/GLONASS Network RTK Based on DREAMNET[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1009–1018. DOI:10.11947/j.AGCS.2016.20160133 |
| [3] | 杨元喜, 陆明泉, 韩春好. GNSS互操作若干问题[J]. 测绘学报, 2016, 45(3): 253–259. YANG Yuanxi, LU Mingquan, HAN Chunhao. Some Notes on Interoperability of GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 253–259. DOI:10.11947/j.AGCS.2016.20150653 |
| [4] | JULIEN O, ALVES P, CANNON M E, et al. A Tightly Coupled GPS/GALILEO Combination for Improved Ambiguity Resolution[C]//Proceedings of the European Navigation Conference (ENC-GNSS'03). Graz:[s.n.], 2003:1-14. |
| [5] | JULIEN O, CANNON M E, ALVES P, et al. Triple Frequency Ambiguity Resolution Using GPS/Galileo[J]. European Journal of Navigation, , 2(2): 51–57. |
| [6] | HEGARTY C, POWERS E, FONVILLE B. Accounting for Timing Biases between GPS, Modernized GPS, and Galileo Signals[C]//Proceedings of the 36th Annual Precise Time and Time Systems and Applications Meeting. Washington DC:Naval Observatory, 2005:307-317. |
| [7] | MONTENBRUCK O, HAUSCHILD A, HESSELS U. Characterization of GPS/GIOVE Sensor Stations in the CONGO Network[J]. GPS Solutions, 2011, 15(3): 193–205. DOI:10.1007/s10291-010-0182-8 |
| [8] | ODIJK D, TEUNISSEN P J G. Characterization of Between-receiver GPS-Galileo Inter-system Biases and Their Effect on Mixed Ambiguity Resolution[J]. GPS Solutions, 2013, 17(4): 521–533. DOI:10.1007/s10291-012-0298-0 |
| [9] | ODIJK D, TEUNISSEN P J G, HUISMAN L. First Results of Mixed GPS+GIOVE Single-frequency RTK in Australia[J]. Journal of Spatial Science, 2012, 57(1): 3–18. DOI:10.1080/14498596.2012.679247 |
| [10] | PAZIEWSKI J, WIELGOSZ P. Accounting for Galileo-GPS Inter-system Biases in Precise Satellite Positioning[J]. Journal of Geodesy, 2015, 89(1): 81–93. DOI:10.1007/s00190-014-0763-3 |
| [11] | ODIJK D, TEUNISSEN P J G. Estimation of Differential Inter-system Biases between the Overlapping Frequencies of GPS, Galileo, BeiDou and QZSS[C]//Proceedings of the 4th International Colloquium Scientific and Fundamental Aspects of the Galileo Programme. Prague:Czech Republic, 2013:4-6. |
| [12] | YUAN Yunbin, ZHANG Baocheng. Retrieval of Inter-system Biases (ISBs) Using a Network of Multi-GNSS Receivers[J]. Journal of Global Positioning Systems, 2014, 13(1): 22–29. |
| [13] | ODIJK D, NADARAJAH N, ZAMINPARDAZ S, et al. GPS, Galileo, QZSS and IRNSS Differential ISBs:Estimation and Application[J]. GPS Solutions, 2016. DOI:10.1007/s10291-016-0536-y |
| [14] | ODOLINSKI R, TEUNISSEN P J G, ODIJK D. Combined BDS, Galileo, QZSS and GPS Single-frequency RTK[J]. GPS Solutions, 2015, 19(1): 151–163. DOI:10.1007/s10291-014-0376-6 |
| [15] | ODOLINSKI R, TEUNISSEN P J G, ODIJK D. Combined GPS+BDS+Galileo+QZSS for Long Baseline RTK Positioning[C]//Proceedings of the 27th International Technical Meeting of the ION Satellite Division, ION GNSS+2014. Tampa, Florida:Institute of Navigation, 2014. |
| [16] | XIAO Wei, LIU Wenxiang, SUN Guangfu. Modernization Milestone:BeiDou M2-S Initial Signal Analysis[J]. GPS Solutions, 2016, 20(1): 125–133. DOI:10.1007/s10291-015-0496-7 |
| [17] | WANG J, KNIGHT N L, LU X. Impact of the GNSS Time Offsets on Positioning Reliability[J]. Journal of Global Positioning Systems, 2011, 10(2): 165–172. DOI:10.5081/jgps |
| [18] | DENG Chenlong, TANG Weiming, LIU Jingnan, et al. Reliable Single-epoch Ambiguity Resolution for Short Baselines Using Combined GPS/BeiDou System[J]. GPS Solutions, 2014, 18(3): 375–386. DOI:10.1007/s10291-013-0337-5 |
| [19] | GENDT G, ALTAMIMI Z, DACH R, et al. GGSP:Realisation and Maintenance of the Galileo Terrestrial Reference Frame[J]. Advances in Space Research, 2011, 47(2): 174–185. DOI:10.1016/j.asr.2010.02.001 |
| [20] | NADARAJAH N, TEUNISSEN P J G, SLEEWAEGEN J M, et al. The Mixed-receiver BeiDou Inter-satellite-Type Bias and Its Impact on RTK Positioning[J]. GPS Solutions, 2015, 19(3): 357–368. DOI:10.1007/s10291-014-0392-6 |
| [21] | NADARAJAH N, TEUNISSEN P J G, RAZIQ N. BeiDou Inter-satellite-type Bias Evaluation and Calibration for Mixed Receiver Attitude Determination[J]. Sensors, 2013, 13(7): 9435–9463. DOI:10.3390/s130709435 |
| [22] | EUELER H J, Goad C C. On Optimal Filtering of GPS Dual Frequency Observations without Using Orbit Information[J]. Bulletin Géodésique, 1991, 65(2): 130–143. DOI:10.1007/BF00806368 |
| [23] | ZHANG Baocheng, TEUNISSEN P J G. Zero-baseline Analysis of GPS/BeiDou/Galileo Between-receiver Differential Code Biases (BR-DCBs):Time-wise Retrieval and Preliminary Characterization[J]. Navigation, 2016, 63(2): 181–191. DOI:10.1002/navi.132 |
| [24] | HELLEMANS A. A Simple Plumbing Problem Sent Galileo Satellites into Wrong Orbits[EB/OL]. (2014-10-13). http://spectrum.ieee.org/tech-talk/aerospace/satellites/a-simple-plumbing-problem-sent-galileo-satellites-into-wrong-orbits. |
| [25] | ODOLINSKI R, ODIJK D, TEUNISSEN P J G. Combined GPS and BeiDou Instantaneous RTK Positioning[J]. Navigation, 2014, 61(2): 135–148. DOI:10.1002/navi.61 |
| [26] | VERHAGEN S, TEUNISSEN P J G. The Ratio Test for Future GNSS Ambiguity Resolution[J]. GPS Solutions, 2013, 17(4): 535–548. DOI:10.1007/s10291-012-0299-z |
| [27] | TEUNISSEN P J G. Success Probability of Integer GPS Ambiguity Rounding and Bootstrapping[J]. Journal of Geodesy, 1998, 72(10): 606–612. DOI:10.1007/s001900050199 |
| [28] | TEUNISSEN P J G, VERHAGEN S. The GNSS Ambiguity Ratio-test Revisited:A Better Way of Using It[J]. Survey Review, 2009, 41(312): 138–151. DOI:10.1179/003962609X390058 |



