2. 95989部队, 北京 100076
2. Troops 95989, Beijing 100076, China
空间填充曲线 (space filling curve,SFC) 是连续整数或关键字值与多维空间中的单元之间可逆的一一映射关系。空间填充曲线建立了高维空间中的单元与一维空间中的单元之间的对应,起到了降维的作用。同时,空间填充曲线的聚簇性特征[1],即曲线上相邻的单元在高维空间中也是相邻的,使其成为设计空间索引算法的重要工具。
常用的空间填充曲线包括Hilbert曲线、Z序曲线 (也称N序曲线、Morton曲线)、行序曲线、行优先曲线、Gray曲线、双Gray曲线、Carton对角曲线、螺旋曲线、U形曲线等。按照映射方法的特点,一般将空间填充曲线分为递归方法和非递归方法两类,前者包括Hilbert曲线、Z序曲线、Gray曲线、双Gray曲线、U形曲线等,后者包括行序曲线、行优先曲线、Carton对角曲线、螺旋曲线等。大量理论分析与应用验证表明[2],Hilbert曲线聚簇性最优而映射过程最为复杂,Z序曲线邻近性最差而映射过程最为简单。
Hilbert曲线编码的经典方法是由文献[1]针对二维空间构造提出的。该算法是基于Morton码的二进制位操作法,算法复杂度为O(n2)。文献[3]根据Hilbert曲线的空间层次分解特征,通过栅格空间层次分解与构造域状态转移向量,设计了二维空间中Hilbert码的递归生成算法,算法复杂度为O(max (n))。文献[4]设计了基于状态转移矩阵的Hilbert码快速生成算法,将Hilbert状态转移矩阵转换为C++中的数组运算, 减少了Hilbert码计算过程中的嵌套循环及迭代处理,将算法复杂度降为O(n)。上述编码方法都只是在二维空间中进行讨论的。文献[5]研究了n维Hilbert曲线的生成问题,提出基于静态演化规则、自底向上的生成算法,算法复杂度为O(nlogn)。文献[6]设计了任意维空间中具有线性复杂度的Hilbert码算法。
在全球离散网格研究中,网格单元编码算法是一个重要的基础问题。文献[7]提出了基于Hilbert曲线的全球离散网格影像金字塔索引算法,文献[8]基于Z曲线设计了球体退化八叉树网格的编码算法,文献[9]提出基于Hilbert曲线的扩展八叉树剖分网格编码算法,文献[10]将Hilbert曲线扩展应用到地月一体圈层立体网格的编码算法中。利用空间填充曲线的降维和聚簇性,设计高效的网格单元编码算法,是利用全球离散网格组织管理全球范围、多源、多分辨率数据的一个重要研究方向[11]。
对于三维立体网格,使用Hilbert曲线进行网格单元编码的一个前提条件是3个维度上的网格剖分层级相同,即每个维度上的网格单元数量相等。但实际应用中的数据在各空间维度上往往不是均匀分布的,就会出现大量网格单元空置,引起大量的索引冗余,影响空间数据检索查询效率。因此,应考察实际数据在不同维度上粒度分布差异对Hilbert索引计算的影响,分析索引冗余的原因,研究建立“紧致”的Hilbert索引。
下面先分析在立体网格上建立Hilbert索引的过程,指出导致索引冗余的原因,然后提出适应不同维度分布差异的紧致Hilbert曲线索引算法,并对算法效率进行分析和验证。
1 Hilbert曲线索引算法 1.1 Hilbert曲线Hilbert曲线因其良好的空间局部性得到比较深入的研究,出现了各种曲线构造和编码算法,其中最经典是文献[12]提出的算法[12],文献[13]对其进行实现[13],文献[14]提出了改进该算法[14],使其得到广泛应用。下面对Butz算法[15]进行简要分析,特别是考察其几何构造特点。
空间填充曲线具有自相似性,一般根据其递归特点加以构造。Hilbert曲线的构造过程也是如此。以二维Hilbert曲线为例,令曲线始于左下角,止于左上角。1阶Hilbert曲线定义在2×2网格上,k阶Hilbert曲线定义在2k×2k网格上,在2k+1×2k+1网格上构造k+1阶Hilbert曲线的步骤为:
(1) 取k阶Hilbert曲线的一个副本,逆时针旋转90°放置于左下方2k×2k网格中;
(2) 取k阶Hilbert曲线的一个副本,顺时针旋转90°放置于左上方2k×2k网格中;
(3) 取k阶Hilbert曲线的一个副本,放置于右侧的两个2k×2k网格中;
(4) 将4个2k×2k网格中的k阶Hilbert曲线依次连接起来。
构造n维网格Hilbert曲线时,其1阶曲线上存在2n个点,为每个点分配一个n-bit标识码,形式为b=[βn-1βn-2…β0][2],其中βi∈B(B={0, 1}) 表示该点在维度i上的位置 (0为低位,1为高位)。实际上,b是一个非负整数,取值范围是0~2n-1,即与曲线上的点为一一对应关系。这与Gray码[15]的结构是一致的。下面采用Gray码描述Hilbert曲线构造。
1.2 基于Gray码的Hilbert曲线构造方法 1.2.1 Gray码对于任一非负整数x,其二进制码表示为x=(xkxk-1…x2x1x1x0)2。规定Gray变换为:gk=xk,gi=xi⊕xi+1,其中,i=1, 2, …, k-1,⊕代表模2加法,则得到一个二进制码表示的整数gx=(gkgk-1…g1g0)2,称gx为x的Gray码。
Gray码对数字进行排序后,在给定底数时相邻数字的排序码仅在1个bit上不同。根据Gray码构造规则,给出关于Gray码的一些性质[9]。
(1) Gray码编码:Gray码序列的生成函数为
 (1)
(1)
式中,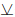
(2) Gray码逆变换:对于非负整数i,令m=log2(i+1),则i的二进制表示需要m bit,存在
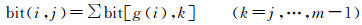 (2)
(2)
式中,bit (a, k) 表示非负整数a的第k个比特的值。
(3) Gray码维度变化:序列g(i) 由g(i)=tsb (i) 给出,其中tsb是i的二进制表达中trailing set的比特数。
(4) Gray码对称性:给定n∈N和0≤i < 2n,存在
 (3)
(3)
(5) g(i) 的对称性:序列g(i) 是对称的,使得对于0≤i < 2n-2,存在g(i)=g(2n-2-i)。
1.2.2 入口点Gray码的顺序可以视为Rn空间中单位超立方体上顶点的次序。在2维空间中递归构造Hilbert曲线时,需要放大到曲线上每一个点 (子超立方体),然后利用经过变换、旋转的初始曲线将其代替,必须通过2n个子超立方体确定Hilbert曲线的方向。这些子Hilbert曲线的朝向必须使曲线从当前子超立方体的出口到下一个子超立方体的入口之间连续。此外,父级超立方体的入口和出口必须与第1个子超立方体的入口、最后一个子超立方体的出口相一致。
采用与父级超立方体顶点标记相同的顺序,令e(i)、f(i) 分别表示按Gray码次序排序的第i个子超立方体中的入口和出口顶点。因为第i个和第i+1个子超立方体沿第g(i) 个坐标轴是相邻的,则必有f(i) 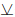
与父级超立方体中的入口和出后点一样,子超立方体的入口点和出口点必相邻。也就是说,e(i) 和f(i) 仅在某一bit上有差别,故必存在d(i)∈Zn,使得e(i)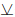
 (4)
(4)
此外,e(0) 与父级超立方体的入口点相同,而f(2n-1) 与父级超立方体的出口点相同。
1.2.3 旋转和反射在Gray码标准方法[15]中,给定起始点为gc (0)=0,终止点为gc (2n-1)=2n-1,其中暗含有:起点e=0,内部方向d=n-1,出口e=2n-1。所以,可以考虑定义一种几何变换,使由e和d定义的Hilbert曲线上按Gray码次序的子超立方体映射到标准的Gray码。
定义右比特位旋转操作符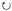
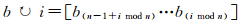 (5)
(5)
式中,b=[bn-1…b0][2]。
形式上,式 (5) 函数将b中的n bits旋转到i的右侧。类似的可以对应定义左比特位旋转操作符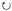
给定e和d,定义如下T变换
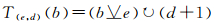 (6)
(6)
上述变换是两个双向映射操作符的组合体,这个映射变化是其自身的双射。下面在入口点和出口点上分析这个映射变换。
(1) 变换入口点和出口点:利用T(e, d)将e和f对应的变换到Bn(对应n比特的正整数集合) 上Gray码序列的第一个和最后一个,即
 (7)
(7)
(2) T(e, d)逆变换:T(e, d)的逆变换是其自身的T(e, d)变换,如下式给出
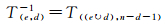 (8)
(8)
由上述过程,可以从e开始沿方向d开始构造Hilbert曲线。
定义
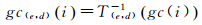 (9)
(9)
据前文所述,gc(e, d)生成的序列是一个Gray码序列,而且该Gray码序列开始和终止于预定点,通过映射T(e, d)将其变换回标准的Gray码。因此,形成了通过超立方体上预定义的任意入口点和方向,连续地构造Hilbert曲线的工具。
下面给出一个组合变换,在后续讨论中会用到。
考虑如下的组合变换
 (10)
(10)
它符合
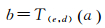 (11)
(11)
式中,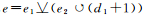
需要说明的是,T变换是对单位超立方体顶点的二进制标记方法的几何诠释。位旋转操作符可以作为Rn中的旋转操作符,而异或操作符可以视为镜像操作,即当bit (e, i)=1时,反转坐标轴i。所以,T变换可以作为Rn空间上的旋转、反射操作符。
1.3 基于Gray码的Hilbert索引算法考虑一个由n维向量构成的空间,向量中每个组分都是m-bit整数,给定Hilbert曲线穿行于该网格空间,需要确定给定点p=[p0, …, pn-1]的Hilbert索引h。
对于给定点p,析出一个n-bit整数
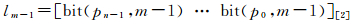 (12)
(12)
l的每一bit表示点p是否落入相对某一给定坐标轴的下方或上方的点集中。由此,lm-1可以指示出点p位于哪一个子超立方体内,也即通过点p所属超立方体的顶点可获得Hilbert曲线的顶点。
根据旋转和反射,在给定e和d后,可以确定包含点p的子超立方体的Hilbert索引,过程分为两步:
(1) 对空间做旋转和反射,有lm-1=T(e, d)(lm-1);
(2) 确定关联的子超立方体的Hilbert索引,有wm-1=gc(1(lm-1)。
下面计算e(wm-1) 和d(wm-1),从而确定点p所属超立方体中的入口点和方向。e(wm-1) 和d(wm-1) 的值是相对于变换空间的,因此将这个变换与已有变换组合起来,有e=e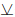
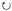
 (13)
(13)
上述过程可以表述为下面的算法:

下面为HilbertIndex的逆向变换算法:

通过对经典的Hilbert曲线构造过程的分析,提出基于Gray码描述Hilbert曲线排序方法,在此基础上给出了Hilbert索引的计算方法。
2 紧致Hilbert曲线索引对于n维数据集,其中的数据点p(Bm0×…×Bmn-1=P,其中mi代表数据点在维度i上的密度。在建立Hilbert索引时,索引长度M′=m×n bit,其中m=maxi{mi}。但是,每一个数据点实际上只需要M=∑imibit的存储空间。显然,M′>M,这表明存在索引空间浪费。针对Hilbert曲线索引在多维数据集上的冗余性,文献[9]进行了详细分析。
构建“紧致”的Hilbert索引,就是希望使索引长度M′=M,同时保持对所有数据点的Hilbert排序。最简单直接的方法是令Hilbert曲线穿过网格空间中实际存在的所有数据点,计算每个点的标记码,并基于标记码进行排序,然后将排序结果作为索引使用。但是,这需要在所有数据点上建立唯一标识码,这样的标识码在数量上与数据点数量一样庞大,显然失去了使用价值。
2.1 Gray码排序算法对于每一个Gray码gc (i),对应的有一个n-bit整数。令μ表示一个掩模,π表示一个模式,则有π∧μ=0(∧表示位操作符中的与)。下面的讨论将对gc (i) 加以限定:在bit (μ, j)=0时,有bit (gc (i), j)=bit (π, j)。实际上,这等价于限定gc (i) 的值满足gc (i)∧!μ=π(!表示位操作符中的与)。
令I表示满足这一条件的整数集合,I={i|gc (i)∧!μ=π}。用‖μ‖表示I中无约束比特位的数量,显然有|I|=2‖μ‖≤2n(|·|表示集合的势)。由此可以确定一个‖μ‖-bit的数用来表示Gray码的排序,对于∀i≠j,当且仅当Gray码排序函数gcr (i) < gcr (j) 时,有i < j。由此可见,对于I中的所有实体,gcr (i) 恒等于i的排序码。但是,需要建立直接计算排序码的方法,而不是通过枚举整个I集合的方式实现。
表 1中给出了一个计算示例,其中n=6,‖μ‖=3,μ=[010110][2],π=[001000][2]。为了说明掩模和模式的作用,在表中用下划线标示出了无约束位。
| gc (i) | 8 | 10 | 12 | 14 | 20 | 26 | 28 | 30 |
| i | 15 | 12 | 8 | 11 | 16 | 19 | 23 | 20 |
| gcr (i) | 3 | 2 | 0 | 1 | 4 | 5 | 7 | 6 |
| [gc (i)][2] | 001000 | 001010 | 001100 | 001110 | 011000 | 011010 | 011100 | 011110 |
| [i][2] | 001111 | 001100 | 001000 | 001011 | 010000 | 010011 | 010111 | 010100 |
| [gcr(i)][2] | 011 | 010 | 000 | 001 | 100 | 101 | 111 | 110 |
从表 1中可以发现,gcr (i) 的值可以将i中的无约束位连接起来得到。下面给出这一性质的形式化描述。
令U={u0 < … < u‖u‖-1}表示掩模μ中无约束位标识的集合,对于所有0≤k≤‖μ‖,存在bit (u, uk)=1,同时令π表示μ下的模式。对于a≠b∈I,用i表示a与b之间的最重要的不匹配位,即i=max{k|bit (a, k)(bit (b, k)},i∈U。
对于Gray码的排序,当i≠j∈I,定义
 (14)
(14)
则有:当且仅当i≠j,存在i < j,也即Gray码的排序是通过gcr (i)=i给定的。
下面给出Gray码排序算法。
算法3:Gray码排序算法——GrayCodeRank (n, μ, π, i)

上述算法根据给定的n、μ、π、i计算gcr (i)。确定gcr (i) 后,自然需要反算i和gc (i)。由于i∈I,对于k∉U,存在bit (gc (i), k)=bit (π, k)。当k∈U,有bit (i, k)=bit (gc (i), j),其中k=μj。若给定任一k,则可知bit (i, k) 或bit (gc (i), k)。按照bit (gc (i), k)=bit (i, k)+bit (i, k+1) 的形式填满空位。如果按照重要性从高到低处理各个位,则可以通过k步操作得到bit (i, k+1),从而处理完未知的位。这一过程可以描述为Gray码排序反算算法,如下所示。
算法4:Gray码排序反算算法——GrayCodeRankInverse (n, μ, π, r)

下面以Gray码排序方法为基础,设计提出紧致Hilbert曲线索引计算方法。
2.2 紧致Hilbert曲线索引计算方法计算Hilbert索引时,需要在各个维度上确定点位于哪个半平面。在算法的每一次迭代i中得到一个整数l,满足
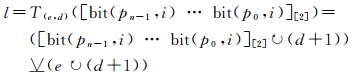 (15)
(15)
考虑实际应用中的数据各个维度上的分布不同,在第j个维度可以用mj-bit表示,而不是统一用m-bit表示各个维度。当i≥mj,无论点p的位置如何,均有bit (pj, i)=0。
在每次迭代i中,定义
μ=[αn-1…α0][2]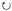
 (16)
(16)
 (17)
(17)
显然,l∧!μ=π,于是利用GrayCodeRankInverse计算gc-1(l),得到一个‖μ‖-bit排序 (与gc-1(l) 相对排序一致)。在每次迭代i中,可以追加‖μ‖-bit值gcr (gc-1(l)),以替代原本的向h追加n-bit值gc-1(l)。在0≤i < mj迭代中,每个维度j将对μ贡献一个1-bit,每迭代一次就在索引h中增加一个单独的bit。这样每个维度j将在h中增加mj-bit。所以,最终索引h长度为M=∑jmj。如此构造就保证了Hilbert曲线编码与数据本身的分布特征保持一致。
上述处理过程对应着掩模提取算法和紧致Hilbert曲线索引算法,具体描述如下。
算法6:掩模提取算法——ExtractMask (n, m0, …, mn-1, i)

掩模提取算法 (ExtractMask) 是为了表示紧致Hilbert曲线索引算法在给定的迭代i时所处理的坐标轴。
算法7:紧致Hilbert曲线索引算法——CompactHilbertIndex (n, m0, …, mn-1, p)

利用上述紧致Hilbert曲线索引的方法,可以实现针对空间数据分布特征的存储效率更高的索引,从而有效提高数据访问和查询的效率。
3 试验分析利用一组实际数据检验紧致Hilbert曲线索引的构造和排序性能。利用模拟数据,通过调整生成参数,分析紧致Hilbert曲线索引的性能随维度增加而出现的变化,建立模拟数据用于测试。利用C++对本文提出的标准Hilbert索引和紧致Hilbert曲线索引加以实现,并与Moore对Butz算法的实现[14]作比较。
3.1 适用范围Moore的Hilbert索引实现存在一个约束,即nm≤64,其中,n表示维数,m表示每个维度上的网格数为2m,即网格总数为2nm。当维数为3,则Moore的Hilbert索引每个维度上的网格数为不超过221,最多支持263个网格单元。与Moore的Hilbert索引实现[14]相比,紧致Hilbert曲线索引对维数和每个维度上的网格数据没有限制。
3.2 存储消耗试验中使用的实际数据为一组数据点,每个数据点的有4个维度,数据点总量约为770万,根据每个维度上数据点组分值的分布,计算得到该组数据点各维度的势分别为834 406、139、24、6,对应的标识码长度为20、8、5、4 bits。分别利用标准Hilbert索引和紧致Hilbert曲线索引加以组织,得到标准Hilbert索引长度为4×max (20, 8, 5, 4)=80,而紧致Hilbert曲线索引长度为∑{20, 8, 5, 4}=37,相比标准Hilbert索引节省存储空间,仅为前者的46.25%。
3.3 索引构造耗时理论上,紧致Hilbert曲线索引比常规Hilbert索引的耗时稍多,二者时间消耗之比随编码长度保持稳定。考虑到掩模提取算法 (ExtractMask) 和Gray码排序算法 (GrayCodeRank) 的时间复杂度均为O(n),gc-1(t) 计算方法的时间复杂度也为O(n)(经过优化可以达到O(logn)),所以常规Hilbert索引算法 (HilbertIndex) 和紧致Hilbert曲线索引算法 (CompactHilbertIndex) 的复杂度均为O(mn),相比之下,紧致Hilbert曲线索引的计算消耗稍大一些,二者之比为常数。
比较本文所提出的标准Hilbert索引、紧致Hilbert曲线索引与Moore所实现Hilbert索引的构造耗时情况,以随机生成的数据集合进行测试,其中数据点总数N、每个维度上的规则网格指数m、维数n和实际标识码总长度M是可调整的。
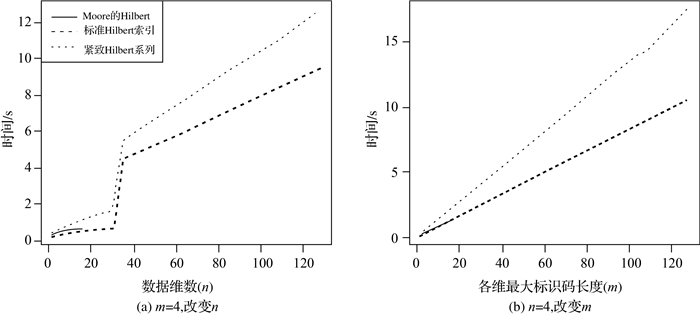
在测试中,设定N=1 000 000,m=4,M=nm/2。结果显示 (图 1):标准Hilbert索引和紧致Hilbert曲线索引构造耗时曲线在n=32处出现拐点;紧致Hilbert曲线索引的构造时间高于标准Hilbert索引,随着维数增加,紧致Hilbert曲线索引构造耗时超过标准Hilbert索引的40%;本文设计的标准Hilbert索引相比Moore实现的Hilbert索引耗时更短,而且本文设计的标准Hilbert索引和紧致Hilbert曲线索引不存在Moore所实现Hilbert索引的nm≤64限制。
|
| 图 1 索引构造耗时比较 Fig. 1 The time consuming of index construction |
3.4 排序性能
排序是SFC的典型应用。基于Hilbert曲线进行排序的基本方法是计算每个网格单元的Hilbert索引,然后按索引值排序。但是,这些索引的数量往往远大于实际数据点的数量,造成存储空间的浪费。实际应用中,通常采用现场排序的策略。Moore采取的方法是建立动态索引比较机制,同时计算两个待比较数据点的索引,并且计算精度以能够确定二者的相对大小为准。这一机制的优势在于几乎不需要显式的存储Hilbert索引,缺点是几乎所有的点都被计算了两遍。
在紧致Hilbert曲线索引中,索引数量与实际数据点数量相同。利用紧致Hilbert曲线索引进行排序,首先用紧致Hilbert曲线索引代替实际数据点,消耗为O(Nmn);然后对这些索引进行排序,消耗为O(N(logN+mn))。由于mn < log2N,紧致Hilbert曲线索引的排序消耗趋近于Fill提出的动态Hilbert排序[16]O(N log2N),但总体更优。
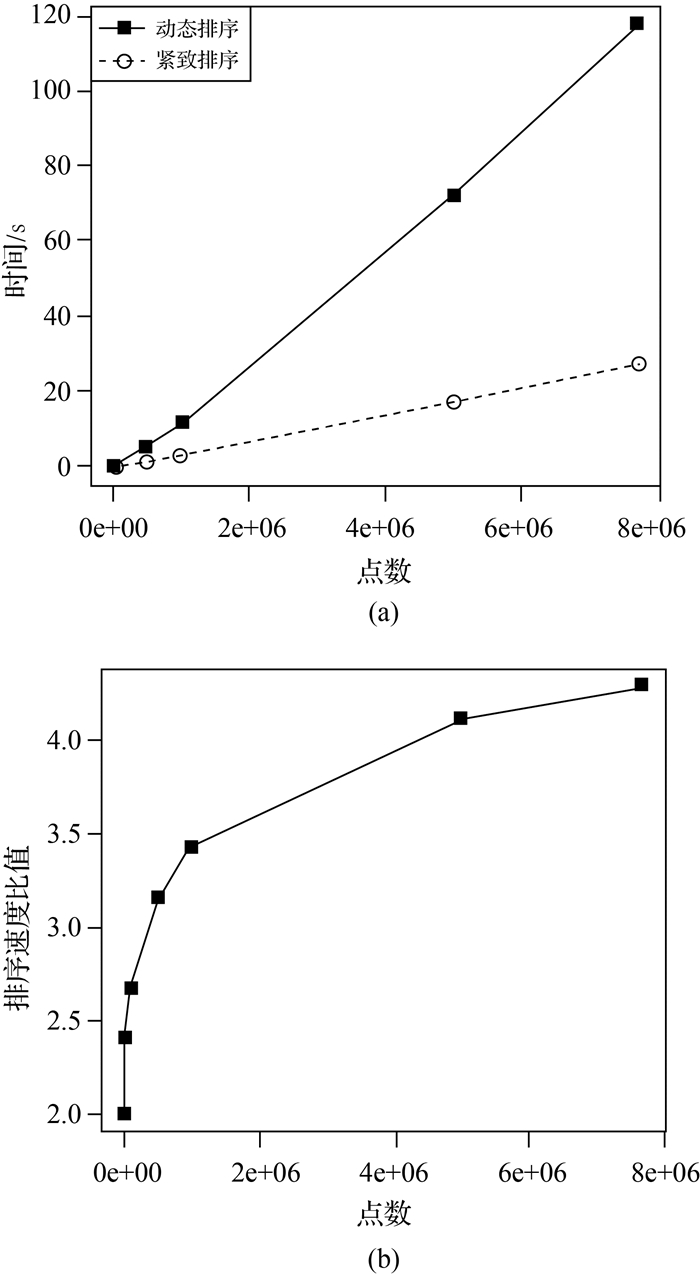
利用实际数据进行紧致Hilbert排序与动态Hilbert排序的比较试验。图 2是在实际数据上进行测试的结果。测试结果与理论分析一致,紧致Hilbert排序优于动态Hilbert排序,随着数据量增加,紧致Hilbert曲线索引在排序性能上的优势越来越明显,二者排序速度比值趋向于4.3。
|
| 图 2 紧致Hilbert曲线索引和常规Hilbert索引的排序性能比较 Fig. 2 The sorting performance compare between compact Hilbert index and standard Hilbert index |
4 结束语
Hilbert曲线是设计全球立体网格多维数据索引的重要工具。但当数据集在不同维度上的分布密度存在较大差异时,常规Hilbert曲线索引会出现大量的冗余。对此,本文利用Gray码推导分析了Hilbert曲线索引的构造特点,进而设计实现了紧致Hilbert曲线索引算法,在保持Hilbert曲线良好聚簇性的同时,避免了数据维度分布差异带来的索引冗余问题。试验结果表明,相比常规Hilbert索引,紧致Hilbert曲线索引计算复杂度相当,在实例数据测试中编码耗时减少约40%,索引存储空间减少约46%,排序加速比趋向于4.3。
| [1] | FALOUTSOS C, ROSEMAN S. Fractals for Secondary Key Retrieval[C]//Proceeding of the 8th ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems. Philadelphia:ACM, 1989:247-252. |
| [2] | CHEN H L, CHANG Y I. All-Nearest-Neighbors Finding Based on the Hilbert Curve[J]. Expert Systems with Applications, 2011, 38(6): 7462–7475. DOI:10.1016/j.eswa.2010.12.077 |
| [3] | 陆锋, 周成虎. 一种基于空间层次分解的Hilbert码生成算法[J]. 中国图象图形学报, 2001, 6A(5): 465–469. LU Feng, ZHOU Chenghu. An Algorithm for Hilbert Ordering Code Based on Spatial Hierarchical Decomposition[J]. Journal of Image and Graphics, 2001, 6A(5): 465–469. |
| [4] | 李绍俊, 钟耳顺, 王少华, 等. 基于状态转移矩阵的Hilbert码快速生成算法[J]. 地球信息科学, 2014, 16(6): 846–851. LI Shaojun, ZHONG Ershun, WANG Shaohua, et al. An Algorithm for Hilbert Ordering Code Based on State-Transition Matrix[J]. Journal of Geo-Information Science, 2014, 16(6): 846–851. |
| [5] | 李晨阳, 段雄文, 冯玉才. N维Hilbert曲线生成算法[J]. 中国图象图形学报, 2006, 11(8): 1068–1075. LI Chenyang, DUAN Xiongwen, FENG Yucai. Algorithm for Generating N-Dimensional Hilbert Curve[J]. Journal of Image and Graphics, 2006, 11(8): 1068–1075. |
| [6] | 刘辉, 冷伟, 崔涛. 高维Hilbert曲线的编码与解码算法设计[J]. 数值计算与计算机应用, 2015, 36(1): 42–58. LIU Hui, LENG Wei, CUI Tao. Development of Encoding and Decoding Algorithms for High Dimensional Hilbert Curve[J]. Journal on Numerical Methods and Computer Applications, 2015, 36(1): 42–58. |
| [7] | 程承旗, 张恩东, 万元嵬, 等. 遥感影像剖分金字塔研究[J]. 地理与地理信息科学, 2010, 26(1): 19–23. CHENG Chengqi, ZHANG Endong, WAN Yuanwei, et al. Research on Remote Sensing Image Subdivision Pyramid[J]. Geography and Geo-Information Science, 2010, 26(1): 19–23. |
| [8] | 余接情, 吴立新. 适应性球体退化八叉树格网及其编码[J]. 地理与地理信息科学, 2012, 28(1): 14–18. YU Jieqing, WU Lixin. Adaptable Spheroid Degenerated-Octree Grid and Its Coding Method[J]. Geography and Geo-Information Science, 2012, 28(1): 14–18. |
| [9] | 曹雪峰. 地球圈层空间网格理论与算法研究[D]. 郑州: 解放军信息工程大学, 2012. CAO Xuefeng. Research on Earth Sphere Shell Space Grid Theory and Algorithms[D]. Zhengzhou:The PLA Information Engineering University, 2012. |
| [10] | 张宗佩. 地月圈层立体网格理论与应用研究[D]. 郑州: 解放军信息工程大学, 2015. ZHANG Zongpei. Research on Earth-Lunar Sphere Shell Space Grid Theory and Application[D]. Zhengzhou:The PLA Information Engineering University, 2015. |
| [11] | 万刚, 曹雪峰, 李科, 等. 地理空间信息网格理论与技术[M]. 北京: 测绘出版社, 2016. WAN Gang, CAO Xuefeng, LI Ke, et al. Geospatial Information Grid Theory and Technology[M]. Beijing: Surveying and Mapping Press, 2016. |
| [12] | BUTZ A R. Alternative Algorithm for Hilbert's Space-Filling Curve[J]. IEEE Transactions on Computers, 1971, 20(4): 424–426. |
| [13] | THOMAS S W. Utah Raster Toolkit[EB/OL].[2016-02-03]. http://web.mit.edu/afs/athena/contrib/urt/src/urt3.1/urt-3.1b.tar.gz. |
| [14] | MOORE D. Fast Hilbert Curve Generation, Sorting, and Range Queries[EB/OL].[2016-05-01]. http://www.tiac.net/~sw/2008/10/Hilbert/moore/index.html. |
| [15] | GRAY F. Pulse Code Communication:US, 2632058[P]. 1953-03-17. |
| [16] | FILL J A, JANSON S. The Number of Bit Comparisons Used By Quicksort:An Average-Case Analysis[C]//Proceedings of the 15th Annual ACM-SIAM Symposium on Discrete Algorithms. New York:AVM, 2004:300-307. |


