2. 北京师范大学地表过程与资源生态国家重点实验室, 北京 100875;
3. 北京大学工学院, 北京 100871;
4. 北京苍穹数码测绘有限公司, 北京 100081
2. State Key Laboratory of Earth Surface Process and Resource Ecology, Beijing Normal University, Beijing 100875, China;
3. College of Engineering, Peking University, Beijing 100871, China;
4. KQ GEO Technologies CO., LTD., Beijing 100081, China
空间位置一直是地理学研究中的核心问题,随着地理信息科学的发展, 地理学围绕着人类社会活动等问题,不断与其他学科相互交叉渗透。从地理学的角度来看,人类社会中每个个体的活动均如同分子运动, 看似杂乱无序, 实则存在潜在的模式, 发现这种模式并揭示其影响因素, 需要采集海量的个体活动数据[1]。基于海量个体活动性时空数据, 可以计算个体移动宏观统计特征, 进而考虑时空异质性, 对人类移动模式作出解释,最终在个体行为和宏观社会经济现象之间建立联系, 并服务于相关应用[2]。近年来, 随着手机等移动互联网设备的广泛使用, 基于移动互联网的社会研究成为当前地理学研究的热点[3-4]。利用该方法采集个体时空数据具有以下两个优势:①数据空间定位精度高、信息真实,且覆盖范围广个体位置和移动信息真实。②数据具有较强的时效性,采集、处理成本较低,适合大规模、长时间采集。
地理学的分形研究手段在2004—2005年被亚历山大定量化[5-6],并被精确的数学语言严格描述。根据亚历山大的定义,能够利用分形的研究思路抓住地理实体的整体性以及递归性来描述其分化程度。本文选取带有地理位置信息的Flickr数据代表人类社会活动的空间分布。地理对象的空间分化程度可以通过HT-指数来表征:HT-指数越高,对应整体上分化程度更高。
本文选取2004到2014年5月份之间在中国境内上传至Flickr的包含位置信息的数据作为研究对象,构造了5种类型的空间网格,以HT-指数为标准对数据进行定量的规则化分形研究,分析了基于空间网格的人类活动空间多尺度特征,利用了香农的信息熵理论对其进行验证[7-8]。
1 理论方法 1.1 Alexander分形理论Alexander提出的分形理论的核心思想与传统的地理学分形理论有所不同,其“分形”主要是指一种小物体占多数而大物体占少数的可递归的分布模式。例如在城市地理中,城市规模 (人口、占地面积等) 大的城市的个数较少,而城市规模小的城市个数很多[5];在自然地理中,高海拔地区在陆地的占地面积较小,而大部分陆地的海拔都不高。而且这种分布是可递归的,也即在占多数的小物体的内部依然存在小物体占多数而大物体占少数的情况。这种递归的层次性越高代表发育越成熟,分化程度越高,状态越稳定。
1.2 HT-指数HT-指数是一种分形的计算方法[13],描述了地理实体的分化程度和递归的层次性。HT-指数不但衡量了地理特征的内在层次,它也提出了一种新的测量地理特征空间异质性的方法[9]。
HT-指数的计算方法是:①将一组数据Dk={Xi按照从大到小的顺序进行排列;②取这组数据的均值X,并将Dk分为两部分,其中大于X的部分称为“头部”DkH,小于X的部分称为“尾部”DkT;③如果尾部的长度相比于X总长度的比例小于阈值α(本研究参照Jiang等人在2015年的研究成果[9],此处选为0.4),即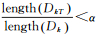
HT-指数越高,代表分形的层次越多,完整性越强。HT-指数已经在城市扩张[9-10]、人类社会活动[11]、地理空间分布分析[12]、空间可视化[13]等多个领域得到了广泛的应用。
2 数据准备 2.1 Flickr数据Flickr是雅虎公司旗下一家提供免费及付费数字照片存储、分享方案的在线服务。它同时也是一个网络共享的社区工具,吸引了大量的在线用户参与,大量共享数字媒体对象被上传到Flickr上。这些照片和视频提供了极为丰富的信息,涵盖拍摄时的娱乐、旅游、个人记录,以及诸多其他方面的信息。整体来看,Flickr数据不单是快照所捕捉的画面,也是关于潮流趋势、现象或事件证据、社交环境以及社会动态的信息的体现。这使得Flickr的社交生态系统形成了一个充满活力的环境,让众多研究者能够大规模寻找许多研究问题的解决方案[14]。
本文使用的Flickr数据集来源于YFCC100M数据集[14]。我们选用的数据集包含2004到2014年5月份之间在中国境内上传至Flickr并包含位置信息的数据。数据集的文件格式为ShapeFiles, 共有2 171 162张图片。
2.2 空间网格空间信息剖分组织的基本思路是基于地球空间剖分理论,为全球空间信息建立多级索引,根据地球空间剖分框架中离散剖分面片的结构体系,设计地球空间剖分数据模型,设计大到整个地球,小到厘米精度的全球空间信息索引体系,实现海量空间数据的快速检索和更新[15-17]。
本文采用的空间网格来自GeoSOT全球剖分网格系统。因为在GeoSOT剖分系统中,采用的是基于多层次面片的多尺度空间表达方法,同一地区的不同层次面片是向下包含和细分的,不同层次的面片编码反映了这种纵向联系,表现出了良好的多尺度特性。这种基于多层次面片的表达和多尺度特性符合HT-指数对地理特征空间异质性计算的方法。
GeoSOT网格是一套以空间信息剖分组织理论为基础的全球空间信息组织方式。GeoSOT索引基于经纬度坐标空间定义,原点为本初子午线与赤道的交点。GeoSOT采用全四分递归剖分。为使网格范围保持整度、整分和整秒,GeoSOT将地球经纬度坐标空间作了3次扩展:将360°×180°空间扩展到512°×512°,将每度的60′空间扩展到64′,将每分的60″空间扩展到64″。GeoSOT的0级网格为经纬度坐标空间512°×512°,对应信息体区域是全球。接下来,下一级剖分面片由上一级剖分面片递归四叉划分得到,直到32级为止,32级网格范围为1/2048″×1/2048″[18]。
在本文中,笔者采用的GeoSOT网格中的第7级、第9级、第13级、第14级以及1/4°×1/4°的网格作为我们分析的空间网格。各GeoSOT层级的网格的特性如表 1所示。
| 层级 | 赤道附近大致尺度 | 网格范围 |
| 7 | 512公里网格 | 4°×4° |
| 9 | 128公里网格 | 1°×1° |
| 13 | 8公里网格 | 4′×4′ |
| 14 | 4公里网格 | 2′×2′ |
3 试验设计
选定5类网格,其网格范围分别为4°×4°、1°×1°、1/4°×1/4°、4′×4′、2′×2′,并均以 (0, 0) 点为原点。选定中国行政区划图与5类网格相交,获得与其有交集的网格集,图 2为与中国地图相交的1°网格集。统计该网格集中每个网格内部所包含的Flickr点的数量,生成5个向量,依次定义为Dk(k=1, 2, 3, 4, 5),并计算其HT-指数。除此之外,笔者还计算了5类结果中所对应的信息熵[7-8],其对应的计算公式为H(p1, p2, …, pn)=Σk=1n-pklog2pk,其中H(p1, p2, …, pn) 为信息熵值,pk为不同区间的值所占的比例,并满足Σk=1npk=1,n代表划分的区间数量,在本研究中设为10。信息熵衡量了一个系统的复杂度信息熵大的系统的信息量大,结构复杂。
4 结果分析 4.1 Rank-Count结果在获得5个不同层级的网格后,笔者将各个层级的网格的内部点数从大到小排列,并获取了在各个层级上的排序后的每个网格的顺序 (Rank) 和内部点数 (Count),并将五组曲线按照“对数-对数”的方式在图 1绘制出来。并将每组曲线的log (Count) 值相对于log (Rank) 值进行了一次线性回归,求得的一次项系数k值同样在图 1标出。k系数接近-2,与文献[19]用自然城市法对全球城市的求得的回归计算结果是一致的。
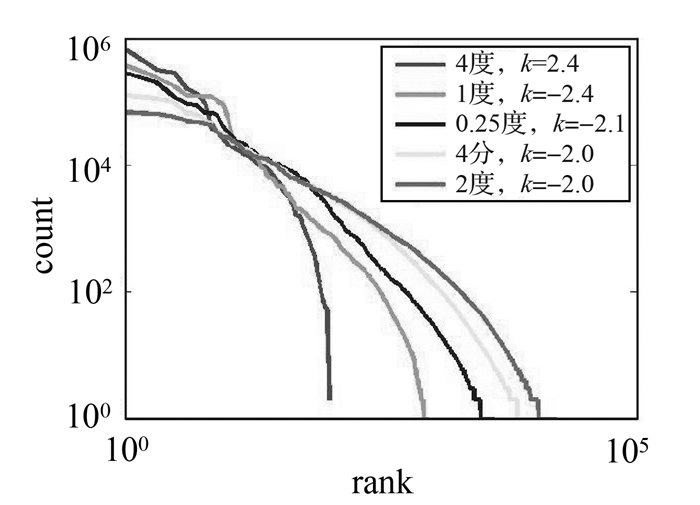
|
| 图 1 Rank-count结果 Fig. 1 Rank-count results |
4.2 HT-指数结果
针对不同层级的网格的结果,笔者计算出了其各自的HT-指数,结果如表 2所示。
| 网格范围 | 网格数量 | 总点数 | 平均点数 | 最大点数 | 非0比例 (%) | HT-指数 | 信息熵 |
| 4°×4° | 100 | 2 075 425 | 20 754.3 | 666 463 | 99.0 | 4 | 0.442 543 |
| 1°×1° | 1140 | 1 975 890 | 1 733.2 | 372 113 | 80.8 | 5 | 0.092 905 |
| 1/4°×1/4° | 16 201 | 1 943 872 | 120.0 | 280 814 | 25.2 | 5 | 0.009 763 |
| 4′×4′ | 219 988 | 2 021 203 | 9.2 | 124 345 | 4.5 | 8 | 0.001 757 |
| 2′×2′ | 873 575 | 2 143 281 | 2.5 | 66 847 | 1.9 | 8 | 0.000 809 |
网格数量表示网格集所包含的所有网格的个数,随着网格范围的减小,网格所描述的空间尺度随之降低,网格数量不断增加。同时,随着网格范围的减小,每个网格所包含的平均Flickr点数在降低,网格内的最大点数的值同样在降低,包含的Flickr点数为非0的网格所占比例也在降低。除HT-指数之外,笔者还计算出了其信息熵,用于比较。HT-指数随着网格范围的减小而不断上升,信息熵在不断下降。
5 总结带有空间位置信息的Flickr数据代表了某一地区的社交环境以及社会动态的信息,某一地区的Flickr数据量越大,则代表活跃程度越高。本文以5类规则划分的空间网格为参照,根据Alexander的分形理论,从不同的尺度对中国境内的Flickr进行分布的分析。主要可以得出以下几点结论。
(1) 随着网格的范围由大变小,其每个网格所对应的空间尺度在逐渐降低,对于地理空间刻画的粒度更为精细。其平均点数、网格内最大点数、非0比例都呈下降趋势。
(2) 不同范围的网格展现了不同尺度的空间分布特征。在高尺度时,其表现的较为粗略,认为各个网格内部认为是均一的,各个不同网格之间的差异较大,异质性强,但由于分析不够深入,所以分化程度并不够,HT-指数也较低。而低尺度时,每个网格所对应的空间范围很小,刻画更为精细,不同网格之间差异不大,分化程度较强,而每个网格本身表现的信息有限。因此,尺度的特征一定程度上与人文地理特征是有正相关性的。能够用网格作为控制尺度的工具来从不同尺度来认知人类社会活动的分布关系。
(3) 信息熵的结果证明了HT-指数的正确性。因为随着尺度的降低,整个系统被划分得更为细致,网格与网格之间的区分程度被稀释了,而信息熵也就随之降低。
| [1] | 刘瑜, 肖昱, 高松, 等. 基于位置感知设备的人类移动研究综述[J]. 地理与地理信息科学, 2011, 27(4): 8–13, 31. LIU Yu, XIAO Yu, GAO Song, et al. Human Movement Research Review Based on Location Aware Devices[J]. Geography and Geo-Information Science, 2011, 27(4): 8–13, 31. |
| [2] | BAYIR M A, DEMIRBAS M, EAGLE N. Mobility Profiler:A Framework for Discovering Mobility Profiles of Cell Phone Users[J]. Pervasive and Mobile Computing, 2010, 6(4): 435–454. DOI:10.1016/j.pmcj.2010.01.003 |
| [3] | BLONDEL V D, DECUYPER A, KRINGS G. A Survey of Results on Mobile Phone Datasets Analysis[J]. EPJ Data Science, 2015, 4: 10. DOI:10.1140/epjds/s13688-015-0046-0 |
| [4] | PHITHAKKITNUKOON S, SMOREDA Z, OLIVIER P. Socio-Geography of Human Mobility:A Study Using Longitudinal Mobile Phone Data[J]. PLoS One, 2012, 7(6): e39253. DOI:10.1371/journal.pone.0039253 |
| [5] | ALEXANDER C. The Nature of Order:An Essay on the Art of Building and the Nature of the Universe, Book 3-A Vision of A Living World[M]. Berkeley, CA: Routledge, 2005. |
| [6] | ANDERSON G, GE Ying. Do Economic Reforms Accelerate Urban Growth? The Case of China[J]. Urban Studies, 2004, 41(11): 2197–2210. DOI:10.1080/0042098042000268410 |
| [7] | RÉNYI A. On Measures of Entropy and Information[C]//Proceedings of the 4th Berkeley Symphony Mathematical Statistics and Probability. Berkeley, CA:[s.n.], 1961. |
| [8] | SHANNON C E, WEAVER W. The Mathematical Theory of Communication[M]. Urbana: University of Illinois Press, 1971. |
| [9] | JIANG Bin. A City Is a Complex Network[C]//MEHAFFY M W. Christopher Alexander A City is Not a Tree:50th Anniversary Edition. Portland, OR:Sustasis Press, 2015. |
| [10] | JIANG Bin, YIN Junjun. Ht-Index for Quantifying the Fractal or Scaling Structure of Geographic Features[J]. Annals of the Association of American Geographers, 2014, 104(3): 530–540. DOI:10.1080/00045608.2013.834239 |
| [11] | JIANG Bin. Street Hierarchies:A Minority of Streets Account for A Majority of Traffic Flow[J]. International Journal of Geographical Information Science, 2009, 23(8): 1033–1048. DOI:10.1080/13658810802004648 |
| [12] | JIANG Bin, LIU Xintao. Scaling of Geographic Space from the Perspective of City and Field Blocks and Using Volunteered Geographic Information[J]. International Journal of Geographical Information Science, 2012, 26(2): 215–229. DOI:10.1080/13658816.2011.575074 |
| [13] | JIANG Bin. Wholeness as A Hierarchical Graph to Capture the Nature of Space[J]. International Journal of Geographical Information Science, 2015, 29(9): 1632–1648. DOI:10.1080/13658816.2015.1038542 |
| [14] | JIANG Bin. Head/Tail Breaks for Visualization of City Structure and Dynamics[J]. Cities, 2015, 43: 69–77. DOI:10.1016/j.cities.2014.11.013 |
| [15] | THOMEE B, SHAMMA D A, FRIEDLAND G, et al. YFCC100M:the New Data in Multimedia Research[J]. Communications of the ACM, 2016, 59(2): 64–73. DOI:10.1145/2886013 |
| [16] | 程承旗. 空间信息剖分组织导论[M]. 北京: 科学出版社, 2012. CHENG Chengqi. An Introduction to Spatial Information Subdivision Organization[M]. Beijing: Science Press, 2012. |
| [17] | 李德仁, 朱欣焰, 龚健雅. 从数字地图到空间信息网格——空间信息多级网格理论思考[J]. 武汉大学学报 (信息科学版), 2003, 28(6): 642–650. LI Deren, ZHU Xinyan, GONG Jianya. From Digital Map to Spatial Information Multi-Grid-A Thought of Spatial Information Multi-Grid Theory[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 642–650. |
| [18] | 宋树华, 程承旗, 关丽, 等. 全球空间数据剖分模型分析[J]. 地理与地理信息科学, 2008, 24(4): 11–15. SONG Shuhua, CHENG Chengqi, GUAN Li, et al. Analysis on Global Geodata Partitioning Models[J]. Geography and Geo-Information Science, 2008, 24(4): 11–15. |
| [19] | 金安, 程承旗. 基于全球剖分网格的空间数据编码方法[J]. 测绘科学技术学报, 2013, 30(3): 284–287. JIN An, CHENG Chengqi. Spatial Data Coding Method Based on Global Subdivision Grid[J]. Journal of Geomatics Science and Technology, 2013, 30(3): 284–287. |
| [20] | JIANG Bin, YIN Junjun, LIU Qingling. Zipf's Law for All the Natural Cities Around the World[J]. International Journal of Geographical Information Science, 2015, 29(3): 498–522. DOI:10.1080/13658816.2014.988715 |



