2. 国防科学技术大学信息系统工程重点实验室, 湖南 长沙 410073;
3. 北京大学遥感与地理信息系统研究所, 北京 100871
2. Science and Technology on Information Systems Engineering Laboratory, National University of Defense Technology, Changsha 410073, China;
3. Institute of Remote Sensing and GIS, Peking University, Beijing 100871, China
随着大数据时代的到来,信息的保有量和增长率变得越来越大,对海量数据的组织管理和分析也显得越来越重要。分析这些信息,无论是经济、社会还是人文,还是地理、天文或其他科学,其中大部分数据都是与时空密切关联的,即在某一时刻或某一时间段内采集得到或计算产生的某一区域的数据信息。大数据时代更加催生了海量带时空信息的数据,例如视频数据、交通数据、社交数据等。目前,针对时空数据的研究,多数研究集中在空间数据方面,而时间信息往往只是采用简单的方式进行辅助处理,例如:时间戳[1-2]、字符串[3]、时间计数[4]等方式,这些方式分散在文件系统[5-11]、数据库系统[12-13]和各类编程语言[14-17]中。而真实情况却是,大数据中存在的时间信息多种多样,数据尺度与精度也各不相同,有的采用时刻计数,有的采用准确时间段,有的采用模糊时间范围[18],这些时间信息并没有充分得到利用,而且在很多场合,传统的时间信息处理方式在应用上存在一些不足,特别表现在下面两个方面[19]。
(1) 多尺度时间信息难以统一组织。目前,一种时间标识方式一般对应一种时间尺度,这种情况在数据库系统中尤其明显。比如,将字段设置为Date数据类型,即表明这种时间编码方式只能存储“一天”时间尺度的数据,这样,对于时间尺度为1年的“赤壁之战”事件就只能存储成“208-01-01”这一错误的时间;时间尺度为1天的“五四运动”事件可以准确存储为“1919-05-04”;时间尺度为1秒的“汶川地震”事件就只能舍弃精度,存储为“2008-05-12”。可以发现,在传统的时间标识中,多尺度时间被强制地、有损地转换为单尺度时间进行存储。另一种方式,如果直接采用字符串的方式记录多尺度时间,亦存在字符串存储空间大、长度不一致、格式难统一、计算不方便等一系列问题。
(2) 多尺度时间计算效率有待提升。目前存储和组织多尺度时间数据,一般采用字符串方法,如“2013年5月14日下午3点半”记录为“2013-05-14T15:30”。字符串方法能简洁直观地记录多尺度时间,但其在计算方面的劣势明显。例如:在字符串“2013-12-31”进行加1天的操作,需要先将其解码,提取年为2013,月为12,日为31;然后按照历法规则加1天,计算结果为年为2014,月为1,日为1;再将计算结果编码为字符串“2014-01-01”。字符串解码的过程中,需要对字符按存储格式进行分割;编码的过程中,需要对字符进行规则连接。不像传统处理单尺度时间的数据类型都是整数,编码解码过程快。因此,在进行时间计算时,字符串解码与编码过程复杂,耗时多,极大地降低计算效率。
1 多尺度时间段整数编码方法首先给出几个基本概念。
(1) 单尺度时间段编码 (single time segment coding,STSC) 指的是使用一种固定的尺度 (例如:μs) 来表示所有的时间段的一种编码形式。
(2) 多尺度时间段编码 (multi-scale time segment coding,MTSC) 指使用多种不同的尺度 (例如:年、月、日、时、分、秒、…) 来表示各种时间段的一种编码形式。
在本文中,利用整数的方式对单 (多) 尺度时间段进行编码,也称为单尺度时间段的整数编码 (single time segment integer coding,STSIC) 和多尺度时间段的整数编码 (multi-scale time segment integer coding,MTSIC)。
本文方案的设计依据目前世界上广泛使用的时间系统和历法系统,针对计算机处理的特点,选择整数的方式进行时间段进行编码,兼顾时间段的连续性和时间尺度的多样性,一方面考虑编码组织与存储的可行性,另一方面考虑编码应用的高效性。选择时间段整数编码的设计基础如下。
(1) 历法系统:采用格里历,即公历[20]。
(2) 时间系统:采用协调世界时 (UTC) 系统,最小粒度到微秒,并考虑公元前时间的记录。
在时间段编码的设计中,不存储时区信息,基于两方面的考虑:一是时区信息并没有增加更多的日期或时间信息,它只是表达的是地方时与零时区之间时间差异;二是编码中添加时区信息,会增加不必要的编码复杂度和使用复杂度。不记录时区信息,只需要把日期和时间信息进行编码并保存,在具体使用的时候根据当前设置的时区进行计算即可。
下面给出时间段的输入,公元A年B月C日D:E:F.GH,其中:A代表年 (yr)(可以用负数表示公元前),B代表月 (mon),C代表日 (d),D代表小时 (h),E代表分钟 (min),F代表秒钟 (s),G代表毫秒 (ms),H代表微秒 (μs),该时间段的尺度是μs。当然如果输入只给到G、F、E、…、A截至,那么对应的时间段的尺度就分别是μs、ms、s、…、yr。输出是MTSIC,即使用一种整数的编码形式来表达多种不同尺度 (例如:年、月、日、时、分、秒、…) 的时间段。生成MTSIC的基本思路是首先将输入时间段信息转换成一个STSIC;然后根据时间段的尺度信息,将STSIC转成一个MTSIC形式。
1.1 单尺度时间段编码的生成将一个输入形式的时间段转成单尺度时间段的整数编码Tc。用一个m bit的整数 (在现有64 bit的计算机上,m=64,其他位数的系统上可以相应调整) 来编码时间,各种尺度的时间段按照最小尺度 (例如:μs) 进行单尺度整数编码,其中:
(1) 年计数的整数A转换成 (m-46) bit二进制数,正负采用其补码设计,第1位是符号位,表示公元前后,范围公元前2m-47年—公元2m-47-1年;
(2) 月计数的整数B转换成4 bit二进制数,表示0~15,其中0、13、14、15在月份中无效,不会在编码中体现;
(3) 日计数的整数C转换成5 bit二进制数,表示0~31,其中0在日计数中无效,不会在编码中体现;
(4) 时计数的整数D转换成5 bit二进制数,表示0~31,其中24~31在时计数中无效,不会在编码中体现;
(5) 分计数的整数E转换成6 bit二进制数,表示0~63,其中60~63在分计数中无效,不会在编码中体现;
(6) 秒计数的整数F转换成6 bit二进制数,表示0~63,其中60~63在秒计数中无效,不会在编码中体现;
(7) 毫秒计数的整数G转换成10 bit二进制数,表示0~1023,其中1000~1023在毫秒计数中无效,不会在编码中体现;
(8) 微秒计数的整数H转换成10 bit二进制数,表示0~1023,其中1000~1023在微秒计数中无效,不会在编码中体现。
Tc使用A((m-46) bit)、B(4 bit)、C(5 bit)、D(5 bit)、E(6 bit)、F(6 bit)、G(10 bit)、H(10 bit) 的不同大小的整数在位域上直接进行内存的连接,形成m bit的整数编码时间,该单尺度时间段编码的范围:公元前2m-47年—公元2m-47-1年,使用整数-2m-1~2m-1-1来表示。
下面以m=64为例,适应现有64 bit的计算机,Tc表示的1 μs尺度下形成的整型数编码,采用64 bit整数从-263~263-1表示公元前131 072年—公元131 071年,如图 1所示。

|
| 图 1 μs尺度下的整数编码 Fig. 1 Integer coding in 1 μs scale |
需要说明的是,上面设计的单尺度时间段编码 (时间尺度1 μs) 并不是一个连续的整数,这指的是公元前2m-47年—公元2m-47-1年中任意1 μs尺度的时间段,都存在一个m bit的整数与其对应;但是不是所有的m bit整数都能找到一个公元前2m-47年—公元2m-47-1年中的1 μs尺度的时间段与其对应,这导致单尺度时间段整数编码在按照数值大小排序的时候并不是连续的。之所以这样设计的原因是,年、月、日、时、分、秒、毫秒、微秒等时间尺度,并不是1 μs尺度的2n倍,但是为了在后面多尺度编码中包含这些常见的时间尺度,并且在传统时间分量和单尺度时间段编码之间相互转换的过程中仅仅只是一个内存的拷贝。
1.2 多尺度时间段编码的生成多尺度时间段编码是为了在一个整数编码中即表示时间位置又表示时间尺度,它由单尺度时间编码转换得到。单尺度编码Tc (m bit整数) 转成多尺度编码MTc (m bit整数),其中需要输入多尺度编码的尺度N。
例如:2016年3月1日就要输入“日”对应的尺度,描述的是1日全天时间段;2016年3月1日0时0分就要输入“分”对应的尺度,描述的是0分0秒~0分50秒整个时间段;如果不区分时间尺度,那么这两个时间段所对应的都是2016年3月1日0时0分0秒0毫秒0微妙,也就是单尺度时间段的表达。
本节设计的多尺度时间段整数编码,充分考虑时间的尺度特性,其设计初衷考虑了对年、月、日、时、分、秒、毫秒、微秒等常见时间尺度的包含关系。在算法实现中,利用计算机二进制整数的特点,设计了一种二叉树的层次结构,其特殊的地方是在二叉树的层次中使用特定的若干层级将年 (yr)、月 (mon)、日 (d)、时 (h)、分 (min)、秒 (s)、毫秒 (ms)、微秒 (μs) 这些常见时间尺度完全包含。
由于单尺度编码本身已经基本占满了全部m bit的整数,虽然仍有部分整数为空,但是剩下的整数个数是不够将不同尺度的所有时间段都不重复地存储下来的。因此本文采用的方法是取出m bit整数中的1 bit,用于专门存储多尺度的时间段整数编码,这样能表达1 μs单尺度时间段的范围就变成公元前2m-48年—公元2m-48-1年,使用整数-2m-2—2m-2-1,余下的空间还可以存储2m-1个整数,可以用于存储其他尺度的时间段。
根据这样的设计,多尺度整数编码 (m bit) 共能支持m-1个尺度层级,其中尺度最小的是第m-1级,最大是第1级,相邻尺度的时间段大小差异是2倍。在第m-1级上,支持2m-1个整数,在第m-2级上,支持2m-2个整数,…,在第1级上,支持2个整数。根据等比数列求和的特性,从第m-2级到第1级,共有2m-1-2个整数,小于从单尺度整数到多尺度整数转换中余下的空间2m-1个整数,因此这种转换方法可以留下足够的整数个数用于记录全部m-1个尺度层级的时间段,在理论上是可行的。表 1中以64 bit整数为例,给出了63个时间尺度层次的划分情况。
| 层级 | 时间尺度/a | 层级 | 时间尺度 | 层级 | 时间尺度 | 层级 | 时间尺度 |
| 1 | 65 536 | 17 | (12 mon)1 a | 33 | 16 min | 49 | 16 ms |
| 2 | 32 768 | 18 | 8 mon | 34 | 8 min | 50 | 8 ms |
| 3 | 16 384 | 19 | 4 mon | 35 | 4 min | 51 | 4 ms |
| 4 | 8192 | 20 | 2 mon | 36 | 2 min | 52 | 2 ms |
| 5 | 4096 | 21 | (28/29/30/31 d)1 mon | 37 | (60 s)1 min | 53 | (1000 μs)1 ms |
| 6 | 2048 | 22 | 16 d | 38 | 32 s | 54 | 512 μs |
| 7 | 1024 | 23 | 8 d | 39 | 16 s | 55 | 256 μs |
| 8 | 512 | 24 | 4 d | 40 | 8 s | 56 | 128 μs |
| 9 | 256 | 25 | 2 d | 41 | 4 s | 57 | 64 μs |
| 10 | 128 | 26 | (24 h)1 d | 42 | 2 s | 58 | 32 μs |
| 11 | 64 | 27 | 16 h | 43 | (1000 ms)1 s | 59 | 16 μs |
| 12 | 32 | 28 | 8 h | 44 | 512 ms | 60 | 8 μs |
| 13 | 16 | 29 | 4 h | 45 | 256 ms | 61 | 4 μs |
| 14 | 8 | 30 | 2 h | 46 | 128 ms | 62 | 2 μs |
| 15 | 4 | 31 | (60 min)1 h | 47 | 64 ms | 63 | 1 μs |
| 16 | 2 | 32 | 32 min | 48 | 32 ms |
表 1中使用64 bit的整数表达了63种时间尺度,包括:1 μs、2 μs、…、1 ms、2 ms、…、1 s、2 s、…、1 min、2 min、…、1 h、2 h、…、1 d、2 d、…、1 mon、2 mon、…、1 yr、2 yr、…、65 536 yr,不同尺度间的进制是2。
为了使m bit整数能够同时支持多尺度时间段编码,取出m bit整数中的1 bit,用来专门存储多尺度的时间段整数编码,多尺度时间段整数编码的设计需要考虑下面两个方面的内容:
(1) 不同尺度时间段整数编码后的排序应该和时间段在时序上前后关系保持一致;
(2) 不同尺度时间段整数编码后应该能体现时间段的包含层级关系。例如:2015年对应的整数编码应该能够通过运算快速得到包含2015年内任意时间段编码的整数区间,并且是连续的。
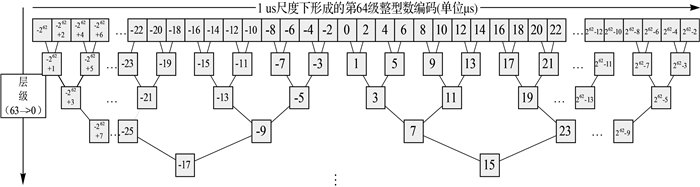
多尺度时间段整数编码的本质为剖分:在限定的时间域上 (公元前2m-48年—公元2m-48-1年),通过7次时间进制扩展 (将1年扩展为16个月、将1个月扩展为32 d、将1 d扩展为32 h、1 h扩展为64 min、1 min扩展为64 s、1 s扩展为1024 ms、1 ms扩展为1024 μs),实现年、月、日、时、分、秒的二叉树剖分,形成一个大至2m-47年时间尺度 (0级)、小至1 μs级时间尺度 (63级),共64层的时间段组成的二叉树结构,从而构成一个多尺度、统一化的离散时间编码体系,如图 2所示。
|
| 图 2 多尺度下的时间段整数编码。以64 bit整数为例,横向从公元前65 536年至公元65 535年,纵向从1 μs时间尺度 (63级) 到131 072年时间尺度 (0级) Fig. 2 Integer coding for multi-scale time segment. Take 64 bit for instance, from B.C.65 536 to A.D.65 535 in row, from the timescale 1 μs (level 63) to 131 072 years (level 0) |
多尺度时间剖分编码由64级构成,采用格里历历法标准和UTC时间标准。在最高1 μs的精度下,64 bit多尺度时间剖分编码能存储的时间范围从公元前65 536年至公元65 535年。下面给出单尺度编码Tc (m bit整数) 转成多尺度编码MTc (m bit整数) 的方法,输入多尺度编码的层级N(N的数值可以由表 1查询得到) 和单尺度编码Tc。
为了保持整数编码的特点和效率,整个算法过程中只涉及整数的位运算和整数的加减运算,具体的实现方法如下。
(1) 计算m-1级多尺度整数编码:Tc=Tc≪1;
(2) 寻找第N层级的编码中,排序最靠近整数0的时间段编码:DetaT=1≪(m-N-1);
(3) 计算第N层的时间段编码
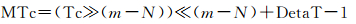
多尺度时间段整数编码的时间编码的范围:公元前2m-48年~公元2m-48-1年。
能够表达m-1种不同的时间尺度,对应不同层级的时间段编码。其中包括了常用的时间单位年、月、日、时、分、秒、毫秒、微秒,全部支持的时间段尺度如表 1和表 2所示。
| 时间段 | 编码层级 | 多尺度整数编码 |
| 2016年5月14日15时30分23秒870毫秒124微妙 | 63 | 283774738205716728 |
| 2016年5月14日15时30分23秒870毫秒 | 53 | 283774738205717503 |
| 2016年5月14日15时30分23秒 | 43 | 283774738204983295 |
| 2016年5月14日15时30分 | 37 | 283774738222809087 |
| 2016年5月14日15时 | 31 | 283774738424135679 |
| 2016年5月14日 | 26 | 283774742719102975 |
| 2016年5月 | 21 | 283775155035963391 |
| 2016年 | 17 | 283797145268518911 |
| 说明:时间编码尺度可以不仅限于上表中的年 (17级)、月 (21级)、日 (26级)、时 (31级)、分 (37级)、秒 (43级)、毫秒 (53级)、微秒 (63级)8个尺度,可以根据应用和算法需要使用更多的尺度,在64 bit计算机中可以使用63种不同层级 (尺度) 的时间段整数编码。 | ||
经过上述的转换后,多尺度时间段变成了m bit的一维整型数编码,该编码可以作为信息的时间属性在计算机或数据库中进行存储,按照该整数属性建立B树、B+树索引或其他一维索引,由于该整数中本身包含了时间顺序和尺度顺序,因此只需要简单地使用该编码的一维排序,就可以形成多尺度时间段信息的存储与索引方式。
2 多尺度时间段整数编码的计算多尺度时间段整数编码计算指的是利用整数的简单计算规则 (加减运算、位运算等) 来实现多尺度时间的关系运算,包括相互转换、包含、被包含、时态计算等。本节结合MTSIC的特点,重点研究其中的一些基础运算,在这些基础运算之上,还可以发展出更多复杂的时间关系运算方法。
2.1 多尺度时间段编码的层级计算多尺度时间段编码是一个整数,只能表示一个一维的量,使用时并不能从数值上直接看出时间段的尺度和层级,这给时间段编码的层级关系使用带来了很大困难,本节的内容主要用于解决该问题。
对于存储的多尺度时间段整数编码MTc,计算其所对应的层级N,可以采用下面的算法:
(1) 如果MTc是偶数,即MTc & 1=0,层次N=m-1。
(2) 如果MTc是奇数,通过异或运算计算整数Mid=(MTc-1)^(MTc+1),其目的是计算MTc-1和MTc+1前面高位有多少位是相同的,找这两个多尺度整数编码最近的相同父时间段编码。
(3) 通过整数Mid左边有多少位是0,来计算多尺度时间段整数编码MTc的层级N。
对于Mid的位数m不是2的整数次幂的情况,通过Mid的右移操作≫,来判断0位的数目。
反之,Mid的位数m是2的整数次幂时 (m=2n),可以采用分支方法计算,效率更高更稳定。初始化N=0,循环变量i从n到1,其中每一步包括:
对于数Mid,通过掩码 (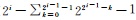
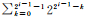
以m=64为例,分支方法明确如下,初始化N=0:
(1) 对于数Mid,通过掩码0xFFFFFFFF 00000000取高位,然后右移≫32位得到Mid0,判断此时的Mid0是否为0。如果Mid0不为0,Mid=Mid0,且N保持不变;否则,通过掩码计算Mid=Mid & 0x00000000FFFFFFFF,N=32。
(2) 对于数Mid,通过掩码0xFFFF0000取高位,然后右移≫16位得到Mid0,判断此时的Mid0是否为0。如果Mid0不为0,Mid=Mid0,且N保持不变;否则,通过掩码计算Mid=Mid & 0x0000FFFF,N=N+16。
(3) 对于数Mid,通过掩码0xFF00取高位,然后右移≫8位得到Mid0,判断此时的Mid0是否为0。如果Mid0不为0,Mid=Mid0,且N保持不变;否则,通过掩码计算Mid=Mid & 0x00FF,N=N+8。
(4) 对于数Mid,通过掩码0xF0取高位,然后右移≫4位得到Mid0,判断此时的Mid0是否为0。如果Mid0不为0,Mid=Mid0,且N保持不变;否则,通过掩码计算Mid=Mid & 0x0F,N=N+4。
(5) 对于数Mid,通过掩码0xC取高位,然后右移≫2位得到Mid0,判断此时的Mid0是否为0。如果Mid0不为0,Mid=Mid0,且N保持不变;否则,通过掩码计算Mid=Mid & 0x3,N=N+2。
(6) 对于数Mid,通过掩码0x2取高位,然后右移≫1位得到Mid0,判断此时的Mid0是否为0。如果Mid0不为0,Mid=Mid0,且N保持不变;否则,通过掩码计算Mid=Mid & 0x1,N=N+1。
例如:
多尺度时间段整数编码MTc=(283774738222809087)10,计算对应的层级N
步骤1:MTc & 1=1,MTc是奇数,计算
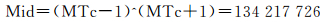
步骤2:通过分支方法确定整数Mid (64 bit) 左边有多少位是0,计算多尺度时间段整数编码MTc的层级N。
(134217726)10=(111111111111111111111111110)2 Mid0=((111111111111111111111111110)2 & 0xFFFFFFFF00000000)≫32=0,计算Mid=Mid & 0x00000000FFFFFFFF=(1111111111111 11111111111110)2,N=32;
Mid0=((111111111111111111111111110)2 & 0xFFFF0000)≫16=(11111111111)2,Mid=Mid0,N=32;
Mid0=((11111111111)2 & 0xFF00)≫8=(111)2,Mid=Mid0,N=32;
Mid0=((111)2 & 0xF0)≫4=0,计算Mid=Mid & 0x0F=(111)2,N=36;
Mid0=((111)2 & 0xC)≫2=1,Mid=Mid0,N=36;
Mid0=(1 & 0x2)≫1=0,计算Mid=Mid & 0x1=1,N=37。
得到N=37。
2.2 多尺度时间段编码的层次关系计算多尺度时间段编码的层次关系计算包括:包含关系计算和被包含关系计算两种。
(1) 多尺度时间段整数编码的子时间区间包含查询:给定多尺度时间段整数编码MTc(整数),对应的层级为N,计算其包含的所有第N′层的时间码NT,N′≥N。
多尺度时间整数编码在整数排序上,满足时间包含关系。层级为N的时间,包含最小尺度 (1~(m-1) 级) 的范围[A, B],即A≤NT≤B。其中,A=MTc-1≪(m-N-1)+1,B=MTc+1≪(m-N-1)-1。
例如:
以m=64为例,多尺度时间段整数编码MTc=(283774738222809087)10,其对应层次N=37,计算其包含的所有第N′层的时间码NT,N′≥37:

(2) 多尺度时间段整数编码MTc的被包含运算指的是当前时间段的父时间段编码FTc的查询运算,假设其中MTc的层级为N,计算向上N′层 (N′=1, 2, 3, …) 的父时间段编码FTc,采用下面方式:
计算第N-N′层次的时间段编码中最接近0的参考时间段编码:OTn=1≪(63-N+N′);
计算第N-N′级的父时间段编码:
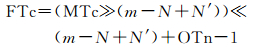
例如:
以m=64为例,多尺度时间段整数编码MTc=(283774738222809087)10,其对应层次N=37,计算向上16层级的父时间段编码:
计算第N-N′=21层次的时间段编码中最接近0的参考时间段编码:
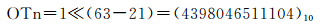
计算第21级的父时间段编码:
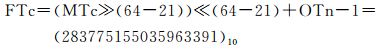
多尺度时间段整数编码MTc转换成单尺度时间段整数编码Tc,计算其对应的层级N,则:
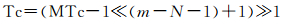
将Tc对应的m bit整数按照A((m-46) bit)、B(4 bit)、C(5 bit)、D(5 bit)、E(6 bit)、F(6 bit)、G(10 bit)、H(10 bit) 位域宽度直接取出,形成MTc对应的传统时间表达方式:公元A年B月C日D:E:F.GH。
例如:
以m=64为例,多尺度时间段整数编码MTc=(283775155035963391)10,其中层级N=21,其对应的单尺度时间段编码:
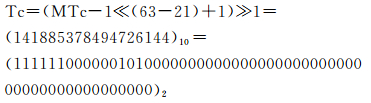
按照A(18 bit)、B(4 bit)、C(5 bit)、D(5 bit)、E(6 bit)、F(6 bit)、G(10 bit)、H(10 bit) 位域宽度直接取出:
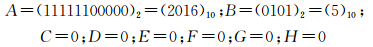
得到传统时间表达方式:公元2016年5月。
2.4 多尺度时间段编码时态关系计算计算多尺度时间段整数编码MTc1和MTc2之间的时态关系,判断是否相交、相接或相离。
利用3.2节中的方法计算MTc1编码所有子时间码包含区间[A1,B1],MTc2编码所有子时间码包含区间[A2,B2];
如果B1 < A2,MTc1和MTc2相离且MTc1在MTc2之前;如果B2 < A1,MTc1和MTc2相离且MTc2在MTc1之前;
如果A1 < A2且B2 < B1,MTc1包含MTc2;如果A2 < A1且B1 < B2,MTc1被MTc2包含;
如果A1 < A2且A2 < B1且B1 < B2,MTc1和MTc2相交且MTc1在MTc2之前;如果A2 < A1且A1 < B2且B2 < B1,MTc1和MTc2相交且MTc2在MTc1之前。
例如:
以m=64为例,两个多尺度时间段整数编码分别为:MTc1=(283775155035963391)10,MTc2=(283774738222809087)10,计算两个时间段的时态关系:
① (283775155035963391)10的字时间码区间[(283770756989452288)10,(283779553082474494)10];(283774738222809087)10的字时间码区间[(283774738155700224)10,(283774738289917950)10];
②满足 (283770756989452288)10 < (283774738155700224)10且 (283774738289917950)10 < (283779553082474494)10,则MTc1包含MTc2。
3 试验与分析将多尺度时间段整数编码MTSIC与现有各类时间编码段表达方式进行对比,对比对象主要有:字符串、多列时间分量、起始时间的方法,表 3是几种时间段编码在表达方式上的对比。本文设计了3个方面的试验,以证明MTSIC的有效性:
| 存储方法 | 方法描述 | 存储举例 |
| 字符串 | 采用一个字符串数据类型字段存储时间。 | "-2015-06" "2015-06-12T10" "2015-06-12T10:23" "2015-06-12T10:23:45.135246" |
| 多列时间分量 | 采用多列整数字段分别存储年、月、日、时、分、秒、毫秒、微秒信息。 | -2015,06,NULL,NULL,NULL,NULL,NULL,NULL 2015,06,12,10,NULL,NULL,NULL,NULL 2015,06,12,10,23,NULL,NULL,NULL 2015,06,12,10,23,45,135,246 |
| 起止时间 | 采用两列日期/时间类型字段分别存储开始时间和终止时间。 | -2015-06-01T00:00:00.000000~-2015-06-30T23:59:59.999999 2015-06-12T00:00:00.000000~2015-06-12T23:59:59.999999 2015-06-12T10:00:00.000000~2015-06-12T10:23:59.999999 2015-06-12T10:23:45.135246~2015-06-12T10:23:45.135246 |
| 多尺度时间段整数编码MTSIC | 采用一列整数字段存储多尺度时间段整数编码。 | "-2015-06"的多尺度整数编码为:-283634417547608065 "2015-06-12T10"的多尺度整数编码为:283642204323315711" 2015-06-12T10:23"的多尺度整数编码为:283642203182465023" 2015-06-12T10:23:45.135246"的多尺度整数编码为:283642203210004972 |
试验1:从单尺度时间段整数编码STSIC到多尺度时间段整数编码MTSIC的转换效率的测试。
试验2:相比于利用字符串对多尺度时间段进行编码和解码,MTSIC对时间段进行编码和解码的效率。
试验3:多尺度时间段整数编码MTSIC在多尺度时间检索上的对比。
多尺度时间可选尺度限定为常用时间单位,即1年、1个月、1日、1小时、1分钟、1秒、1毫秒、1微秒。
开发试验环境:Windows 7,Intel (R) Core (TM) i7-2720QM CPU @2.20 GHz, 64 bit,4 GB,Visual Studio 2013,C++,Oracle 11 g。
3.1 从单尺度时间段整数编码STSIC到多尺度时间段整数编码MTSIC的转换效率的测试针对单尺度时间剖分编码、多尺度时间剖分编码 (随机选择63层、43层、26层、17层) 进行编码生成试验。设计试验流程如下:
(1) 生成n个微秒级随机时间。
(2) 对上述n个随机时间进行单尺度时间段编码。
(3) 将上述n个单尺度编码转换为第63层多尺度时间剖分编码,统计总耗时。
(4) 将上述n个单尺度编码转换为第43层多尺度时间剖分编码,统计总耗时。
(5) 将上述n个单尺度编码转换为第26层多尺度时间剖分编码,统计总耗时。
(6) 将上述n个单尺度编码转换为第17层多尺度时间段整数编码,统计总耗时。
将n分别取5 000 000、10 000 000、50 000 000,分别进行10次试验,取平均值,最终统计信息如表 4所示。由于Visual Studio 2013的release模式下对程序进行了优化处理,使得耗时几乎为0,无法测得正确值。由于并不做对比,因此此处在win32 debug非调试模式下进行测试,测试效率随计算规模n的变化情况。
| 操作 | 5 000 000 | 10 000 000 | 50 000 000 |
| 转换为第63层MTSIC | 193.749 | 387.298 | 1958.02 |
| 转换为第43层MTSIC | 193.495 | 383.517 | 1942.90 |
| 转换为第26层MTSIC | 192.726 | 383.542 | 1948.26 |
| 转换为第17层MTSIC | 194.992 | 388.157 | 1942.66 |
由试验结果可知:多尺度时间段整数编码每一层级的转换效率是一样的,从单尺度时间段编码转换到多尺度时间段整数编码的过程,与转换的层级无关,只与转换编码个数相关,其时间复杂度为O(n)。
3.2 MTSIC对时间段进行编码和解码的测试针对字符串方法与MTSIC对多尺度时间段进行编码和解码的效率进行比较,设计试验流程如下:
(1) 生成n个随机时间 (时间尺度也随机,可能为1年、1个月、1日、1小时、1分钟、1秒、1毫秒、1微秒)
(2) 将上述n个随机时间生成字符串编码 (形如“2015-09”、“2015-09-01T10:00:00.0001000”) 统计总生成耗时。
(3) 将上述生成的字符串编码还原为时间,即提取出每个时间分量,统计总耗时。
(4) 将上述n个随机时间生成无损层级的MTSIC (如“2015-09”正好生成第21层级的编码),统计总生成耗时。
(5) 将上述生成的时间剖分编码还原为时间,即提取出每个时间分量,统计总耗时。
将n分别取10 000 000、50 000 000、100 000 000,分别进行10次试验,取平均值,统计信息如表 5所示。
| 操作 | 10 000 000 | 50 000 000 | 100 000 000 | |
| MTSIC | 编码 | 0 | 0 | 0 |
| 解码 | 84.616 6 | 421.643 5 | 846.897 7 | |
| 总时间 | 84.616 6 | 421.643 5 | 846.897 7 | |
| 字符串 | 编码 | 303.607 | 1 498.782 | 3 020.386 |
| 解码 | 8 903.443 | 44 211.851 | 8 9892.432 | |
| 总时间 | 9 207.050 | 45 710.633 | 9 2912.818 | |
由试验结果可知:编码阶段,MTSIC方法的效率几乎耗时为0,字符串编码方法大约是在30 000 ms的效率情况;解码阶段,MTSIC方法的效率约是字符串方法的105倍;编码与解码整个阶段,MTSIC方法的效率约是字符串方法的108倍,其中大部分耗时在解码的过程中。
分析原因如下:在字符串方法对时间进行编码时,需要将时间分量按照指定的格式转换为字符串,不仅涉及整型转字符串的过程,还涉及字符串拼接过程;而MTSIC对时间段进行编码时,只需要进行4次移位操作和1次加法操作。在字符串方法进行解码时,需要对字符串进行分割;而MTSIC只需要简单的计算操作得到单尺度时间剖分编码,再通过访问位域成员的方式,获取时间分量。
3.3 MTSIC的检索对比试验中采用B+树数据结构 (目前大部分的商业数据库采用的1维索引都是B+树[21]),对生成的MTSIC和字符串编码进行索引,然后进行查询效率对比。之所以这么设计,主要有两个方面的原因:
(1) 只和字符串进行对比,是因为在表 3中的4种时间段编码方式中,多列时间分量和起止时间法都无法采用1维的方式进行多尺度时间段的编码,导致这两种方法的查询效率较字符串而言都低[19],因此本论文只采用字符串进行对比。
(2) 采用B+树的方法进行代码试验,而不直接采用数据库,这是因为现有的Oracle、MySQL等数据库在处理64 bit整数类型的时候,使用的是字符串的实现方法[22],这样采用MTSIC和字符串差异就不是特别明显,因此,鉴于在数据库平台下MTSIC的对比试验,高度依赖于数据库平台内部对不同数据类型和索引的实现方式,因此,采用平台无关的方式,比较MTSIC和字符串方法进行多尺度时间段检索的性能差异。
MTSIC检索试验流程设计如下:
采用随机的方法,生成1970年至2015年间随机的多尺度时间 (时间尺度可能为1年、1个月、1日、1小时、1分钟、1秒、1毫秒、1微秒),输出为规则格式的文本,再将文本中数据批量转换。
插入建树。将所有的多尺度时间剖分编码采用逐个插入的方式,生成B+树,统计建树时间。将所有字符串编码采用逐个插入的方式,生成B+树,统计建树时间。
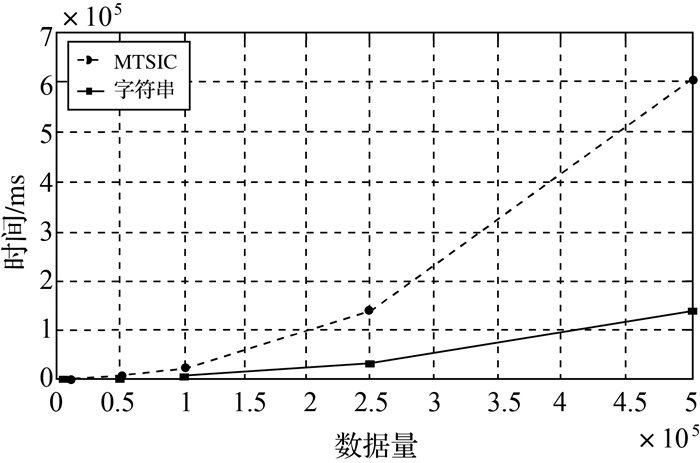
相交查询。基于建立的B+树,利用顺序检索方法进行相交查询。假设时间查询区间为2014-11-15—2015-02-15,构建SQL相交查询语句。依次对5 000、10 000、50 000、100 000、250 000、500 000个数量级的随机多尺度时间进行测试。统计插入建树耗时如表 6和图 3所示。在同等数据量的情况下,基于字符串编码建立B+树明显慢于基于MTSIC建立B+树,平均耗时为4.6倍。
| 5000 | 10 000 | 50 000 | 100 000 | 250 000 | 500 000 | |
| MTSIC | 14.91 | 51.92 | 1 66.28 | 4 920.11 | 31 820.20 | 135 627.00 |
| 字符串 | 73.82 | 239.65 | 5 712.28 | 22 859.00 | 142 105.00 | 604 565.00 |
|
| 图 3 B+树-插入建树时间 Fig. 3 Time of inserting and constructing the B+Tree |
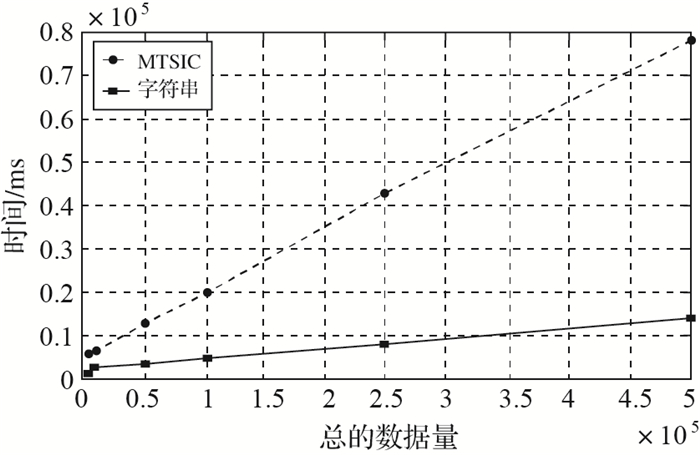
在建立的多尺度时间剖分编码B+树和字符串B+树上,分别进行相交查询,查询区间为“2014-11-15—2015-02-15”。每次查询执行10遍,取10次查询的平均值作为最终统计结果。得到的结果集数量如表 7所示,查询时间统计情况,如表 8和图 3所示。在同等数据量的情况下,相交查询耗时情况:字符串方法平均耗时为多尺度时间剖分编码方法的4倍。
| 5000 | 10 000 | 50 000 | 100 000 | 250 000 | 500 000 | |
| 结果数量 | 57 | 110 | 518 | 1036 | 2566 | 5275 |
| 5000 | 10 000 | 50 000 | 100 000 | 250 000 | 500 000 | |
| MTSIC | 0.014 9 | 0.028 1 | 0.036 7 | 0.050 3 | 0.083 4 | 0.144 3 |
| 字符串 | 0.058 9 | 0.065 2 | 0.125 8 | 0.198 3 | 0.430 4 | 0.780 3 |
|
| 图 4 B+树-相交查询时间 Fig. 4 Intersectant inquiry of B+Tree |
由上述试验结果,可知MTSIC方法在建立索引与使用索引进行查询时,效率均高于字符串方法。综上所述:
(1) 在编码和解码计算方面,MTSIC比字符串时间段有明显优势。编码阶段,MTSIC的耗时基本为0;解码阶段,MTSIC的效率约是字符串方法的105倍;编码与解码整个阶段,MTSIC方法的效率约是字符串方法的108倍。
(2) 由于数据库采用字符串来存储整数,因此脱离数据库单纯比较MTSIC和字符串时间段编码方法的检索效率显得很重要。在建立B+树及时间查询方面,MTSIC相对于字符串时间段编码有很明显的优势。在同等数据量的情况下,建立B+树索引过程中,基于字符串时间段编码明显慢于MTSIC,平均耗时为多尺度时间段整数编码的4.6倍。在同等数据量的情况下,相交查询检索耗时情况:字符串时间段编码方法平均耗时为MTSIC方法的4倍。
本文研究了一种新型的多尺度时间段的剖分方法与整数编码计算,其目标是解决未来大数据中,特别是时空大数据中的复杂海量的时间数据类型。从论文的试验来看,新型的MTSIC及其相关方法在时间关系计算的很多方面都具有特殊的优势,可以作为大数据环境中时间信息标识、记录、计算和统计一种有效工具,当然基于MTSIC的时间关系计算还有很多其他的内容需要挖掘,限于篇幅,另文详述。
另外,需要特别提出的是本文提出的多尺度时间段整数编码的设计思路,同样可以使用在2D、3D甚至N-D的格网化编码设计中,可以衍生出许多的编码类型,并可以支持同类的时空计算,相关衍生与应用另文详述。
| [1] | FAIRBANKS K D. An Analysis of Ext4 for Digital Forensics[J]. Digital Investigation, 2012, 9(S): 118–S130. |
| [2] | Ext4 Wiki. Ext4 Disk Layout[EB/OL]. (2016-02-16)[2016-03-01]. https://ext4.wiki.kernel.org/index.php/Ext4_Disk_Layout. |
| [3] | GILMORE W J. MySQL Storage Engines and Datatypes[M]//Beginning PHP and MySQL:From Novice to Professional.[s.l.]:Apress, 2008:693-729. |
| [4] | Joda-Time. Joda-Time[EB/OL]. (2016-01-28)[2016-02-20]. http://www.joda.org/joda-time/userguide.html |
| [5] | 戴士剑, 陈永红. 数据恢复技术[M]. 北京: 电子工业出版社, 2003. DAI Shijian, CHEN Yonghong. Data Recovery Technology[M]. Beijing: Electronic Industry Press, 2003. |
| [6] | 邓剑, 杨晓非, 廖俊卿. FAT文件系统原理及实现[J]. 计算机与数字工程, 2005, 33(9): 105–108. DENG Jian, YANG Xiaofei, LIAO Junqin. Analysis and Realization of FAT Management System[J]. Computer and Digital Engineering, 2005, 33(9): 105–108. |
| [7] | 滕冲, 方靖然, 张国臣. Windows系统中文件时间属性的变化及影响因素[J]. 刑事技术, 2009(5): 3–5. TENG Chong, FANG Jingran, ZHANG Guochen. Change and Influencing Factors of File Time Attribute in Windows System[J]. Forensic Science and Technology, 2009(5): 3–5. |
| [8] | 罗文华. NTFS文件系统下利用MFT记录修改时间分析文件 (夹) 操作行为[J]. 中国刑警学院学报, 2012(4): 24–26. LUO Wenhua. An Operational Behavior About Using MFT to Record and Modificate Time Analysis File in NTFS File System[J]. Journal of China Criminal Police University, 2012(4): 24–26. |
| [9] | 徐国天. 基于EXT3文件系统数据恢复方法的研究[J]. 信息网络安全, 2012(3): 63–65. XU Guotian. The Research of File Recovery Method on EXT3 File System[J]. Netinfo Security, 2012(3): 63–65. |
| [10] | 倪宝童, 马海军. Linux标准教程[M]. 北京: 清华大学出版社, 2013. NI Baotong, MA Haijun. Standard Linux[M]. Beijing: Tsinghua University Press, 2013. |
| [11] | MSDN Library. File Times[EB/OL].[2016-02-02]. https://msdn.microsoft.com/en-us/library/windows/desktop/ms724290(v=vs.85).aspx. |
| [12] | 裘旭光, 刘晶. 数据库系统原理与应用教程[M]. 北京: 清华大学出版社, 2003. QIU Xuguang, LIU Jing. Theory and Application of Database System[M]. Beijing: Tsinghua University Press, 2003. |
| [13] | ISO. ISO/IEC 9075 Information Technology-Database Languages-SQL[S]. 2011. |
| [14] | PLAUGER P J. The Standard C Library[M]. Englewood Cliffs, N.J.: Prentice Hall, 1992. |
| [15] | HINNANT H E, BROWN W E, GARLAND J, et al. A Foundation to Sleep On-Clocks, Points in Time, and Time Durations[EB/OL]. (2008-05-18)[2016-02-12]. http://www.open-std.org/jtc1/sc22/wg21/docs/papers/2008/n2615.html. |
| [16] | ISO. ISO/IEC 14882:2011 Information Technology-Programming Languages-C++[S]. 2011. |
| [17] | MSDN Library. 32-Bit Windows Time/Date Formats[EB/OL].[2016-02-17]. https://msdn.microsoft.com/en-us/library/9kkf9tah.aspx |
| [18] | 维基百科. 各地日期和时间表示法[EB/OL]. [2014-12-01]. http://huaban.com/pins/148404692/. Wikipedia. Date and Time Representation by Country[EB/OL].[2014-12-01]. http://huaban.com/pins/148404692/. |
| [19] | 王林. 时间剖分编码模型研究[D]. 北京: 北京大学, 2016. WANG Lin. Study of Time Subcivision Coding Model[D]. Beijing:Perking University, 2016. |
| [20] | 萧耐园. 周期律在公历纪日中的快速显示及其应用[J]. 南京大学学报 (自然科学版), 1995, 31(4): 539–547. XIAO Naiyuan. A Rapid Reval of Periodicities on Measure of the Civil Calendars' Dates and Its Aplications[J]. Journal of Nanjing University (Natural Sciences), 1995, 31(4): 539–547. |
| [21] | TOMAZIC S, PAVLOVIC V, MILOVANOVIC J, et al. Fast File Existence Checking in Archiving Systems[J]. ACM Transactions on Storage (TOS), 2011, 7(1): 2. |
| [22] | GREENER S G, RAVADA S. Applying and Extending Oracle Spatial[M]. Birmingham: Packt Publishing, 2013. |


