2012年,Goodchild、Huadong Guo等十多名美、中、外著名专家就数字地球国际会议讨论结果,联合著文“Next-generation Digital Earth”[1],高度赞扬了使用多种分层平铺结构的全球离散格网系统DGGS (discrete global grids system)[2-3]。其采用预先计算的“瓷砖”结构,以优化本地计算且提高使用中细节管理水平,为“科学使用的虚拟地球最吸引人的特点之一”[1],明确提出:“我们期待支持空间定位和详细的三维结构导航,它对地球上任何地方具有厘米级的精度”[1]。2015年,Ali Mahdavi-Amiri, Troy Alderson and Faramarz Samavati在Computers & Graphics撰文“A Survey of Digital Earth”[4],同样高度赞扬了DGGSs,并提出地理信息系统专家面临的主要挑战之一是数据集成。他认为另一个挑战在于处理的非欧球形性质地球,并认为“许多基础和实际的研究问题和挑战仍然没有解决。”[4] DGGSs剖分确实令人印象深刻,但是,其对数字地球和地球剖分的描述,仍与WGS-84椭球精化及大数据、物联网发展有一定距离。
1.1 20多年来,中外著名专家提出众多DGGSs剖分方案[5-33]三维DGGSs地球剖分网格理论上是包容所有分辨率 (层次) 的地球数据网格集合,是幂集,至今所有汇集到的地学“位”数据及其时空变异可以说都是它的子集。它的空间结构、度量,决定了地理信息最基本的规则。在GPS和北斗等系统中,空、时数据都可以规范地表达和分析,并能用确定的精度进行多尺度各种操作。多年来众多剖分研究,一般按剖分方式的不同将格网归纳为3种类型:经纬度格网、自适应格网和正多面体格网。各有不少优点和长处,但仍存在一些需要深入和统一的问题。
1.1.1 经纬度格网剖分这是应用最早的科学查询和空间剖分方法之一[6, 8-10, 11-14, 16-19, 23-25, 29]。其中可分为椭球 (面、体) 上和球 (面、体) 上的剖分两种。它们各自又可分为:等间隔格网,变间隔格网两类。主流地图的分带分幅和众多算法和软件是以经纬度等间隔格网剖分地球面为基础,而近年来剖分方案大都采取了变间隔经纬网剖分方法,也形成一定趋势[11-14, 16-18, 19, 23-25, 29]。
1.1.2 球面自适应格网球面自适应格网是以球面上实体要素为基础,按照实体的某种特征 (主要是Voronoi多边形或TIN结构) 剖分球面单元的方法[31-32]。
1.1.3 球面正多面体格网20世纪80年代末,国内外许多学者开始研究球面正多面体格网模型。基本方法是把理想多面体 (正四面体、正六面体、正八面体、正十二面体、正二十面体) 的边投影到球面上作为大圆弧段,形成球面三角形 (或四边形、五边形、六边形) 的边并覆盖整个球面,作为全球剖分的基础,然后对球面多边形进行递归剖分,形成具有众多研究方法、方案的剖分途径[2, 7, 4-5, 20-22, 26-28, 33],其度量 (Metric) 采用了球的大圆弧段。其中,球面三角形、菱形和六边形是目前最流行的球面剖分单元细胞 (Cell)。这里面较为基础、最有影响、应用最为普遍的是三角形剖分方案—O-QTM[33]。该误差理论分析尚较薄弱,宏观计量似欠严密,也缺少剖分中度量显式定义和“参考点”计算必须要素 (此参考点在Goodchild剖分标准中占4/14之多),因此,剖分和度量操作较为复杂困难。
1.1.4 若干初步简析综上所述,初步列表并简析如下表 1:
| 剖分方式 | 主要优点 | 主要不足 |
| 等间隔经纬格网变间隔经纬格网 | 运用最广:模拟历史条件下久经经验和应用 | 需严格区分尺度,运用正球或椭球及各类同或不同间隔 |
| 球面自适应格网 | 比规则格网有更大灵活性,可予补充 | 难予递归剖分,剖分对象必用正球体面,高准确度困难 |
| 球面正多面体格网 | 格网有很大灵活性,对球剖分较好 | 剖分及度量不易,剖分对象必用正球体 (面),高准确度困难 |
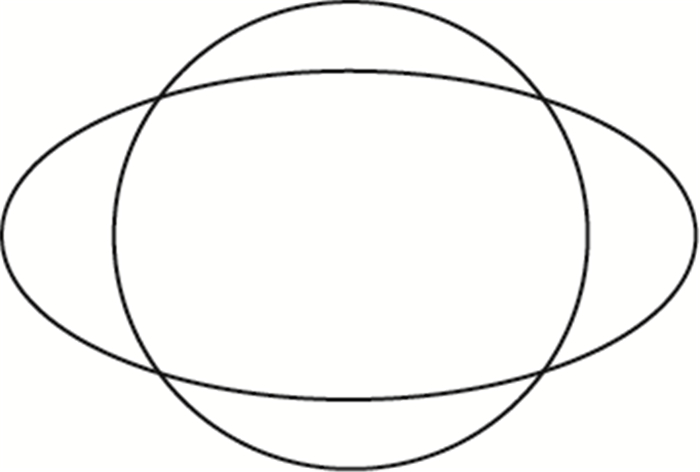
正球面与 (WGS-84) 椭球面度量的准确度差别。当今此差别已非常显著,有下列算例:在WGS-84椭球参数下,假设有一球心设置在的旋转椭球体质心的球,两者赤道面与旋转轴重合,如图 1所示,那么无论球半径怎样设计,球与椭球的北 (南) 极及赤道最东 (西) 点 (设为“东 (西) 极”) 两对点中,偏差将不会小于长短轴差的一半约10 692.342 9 m,以长、短轴平均长度作球半径的正球来代替WGS-84椭球进行计算,其粗略估计,(北、东极) 最大点位偏差将不会低于10 692.342 9 m;而椭球的北极至赤道最东点 (“东极”) 间椭球上最短程路径长为1/4椭圆长10 001 965.729 5 m,而 (球与椭球交点约在B=45.072 2°处),同两点间球形上计算最短程路径长为10 001 981.539 2 m。表明球计算比椭球上最少会大15.809 9 m。因此,使用球模型的位置及基础度量的准确度将无法满足文献[1]所提出三维的厘米级精度。
|
| 图 1 同心同轴的球与椭球匹配 Fig. 1 The matching of concentric coaxial sphere and ellipsoid |
至于整个球面正多面体格网途径,鉴于其目前只能通过球面三角建立地理球面 (ϕ,λ) 和球面极坐标 (α,z) 的变换途径相严密联系[34],在球面这种“各向同性、各点同性”特殊曲面上实施,若搬到椭球面、体上实施,也即整体大地椭球面 (B, L) 和整体球面极坐标 (α,z) 的严密变换和度量,有关方法 (甚至途径) 也尚未见到有关文献。这样,厘米级空间准确度的前景或许不易满足。
1.2 自1994年“Goodchd标准”以来,剖分标准的研究不多,有些不同意见1994年,Goodchild发表了地球剖分网格的14个格网准则,其后经过许多学者的不断补充和修改,Kimerling等把它归纳为研究全球格网模型所应遵守的一般标准[5],此标准起了重要的历史作用,推动了DGG等剖分的蓬勃发展,提出了层次结构、剖分格网 (cell)、格网剖分点、参考点等基础的重要概念。
但较长时间中,这标准达14项之多,显得较粗,主、次、深、浅疏理不够,剖析不深,其中“剖分格网具有相同的面积”的要求是不够实际的。另外,14个标准中并无准确度的要求,也令人思索。
其后,有关准则的研究并不多见,文献[19]在实践和分析众多剖分实例后,正确指出任何一个DGG系统在数学上不可能同时满足上述条件,一个比较优秀的模型应该是根据具体的应用在各项标准间寻求一个合理的平衡。
当今,剖分研究已历时较长,相关的成果较为丰富,但仍是各种剖分难于趋同,可以说,除开问题本身外,剖分标准研究尚不充分。
2 地球剖分中的定位及度量地球剖分网格或全球位置定位框架系一种科学简明的空间参考系统,它是使用特定规则的层次划分对地球的地理空间表面或三维地理空间进行层次剖分而形成的二维或三维网格 (多边形或多面体) 集合,具有全球完整覆盖、无缝无叠、拓扑同胚特点;具有统一规范的递归剖分层次系统、编码运算等特性,全兼容各分辨率;具有位置准确性及其度量准确性。它是地球信息空间的离散化、具体化、系统化的表现,是空间实体点、线、面、体、场存在、组织、表达的具体数字形式。剖分格网集是地球剖分最终的目标,是地理信息科学和数字地球中重要的基础性问题。
2.1 “Discrete Global Grid Systems (DGGSs)”的本源是连续的地球度量空间[35-38]地球剖分的客观对象是本主题的由来与本源,这是一个地理信息的度量空间,具有其独特的拓扑和度量特性[35-38]。这个度量空间主要就是精化了的地球椭球体、大地坐标系{B, L, H}和大地线尺度三者。
研究和确定地球形状、大小是大地测量学科基本科学任务,理论和实践已获证实和不断精化,并已成为地球科学的最重要基础。
研究和测定地球形状、大小和地球重力场,以及测定地面点几何位置的学科,这是地球科学中大地测量学科的科学任务。20世纪下半叶,以电磁波测距、卫星定位系统、甚长基线干涉测量、卫星测距 (SLR) 等为代表的系列新测量技术,给大地测量带来了革命性的变革,特别是80年代后, GPS全面使用、GLONASS、北斗系统相继使用,使长距离绝对定位精度达毫米级、亚毫米级[39],换句话说,该短期内已使定位精度提高了4~5个数量级。已经建立了高准确的地球空间的连续模型,且为科学和社会发展予以充分证实,并正在不断精化之中。其简单明确的表述即是WGS-84:World Geodetic System 1984,其椭球采用国际大地测量和地球物理联合会推荐值,是目前最适合GPS和北斗等的坐标系统。其大地坐标系 (B, L, H) 是和WGS-84质心坐标系完全等价的,它以椭球面当基准,与地理学是以地面作为“中心”曲面特点相吻合,此大地线尺度 (Metric) 即是该地球椭球下的最短程线度量函数。这就地球、或地理空间或地球信息度量空间连续的科学模型。今天,大数据模式以及物联网的迅猛发展,任何时刻都使全球人、物、事、设备的全球空间的定位,室内、外定位,在高精度条件下,已能并趋统一。科学发展的能力、社会发展的需要已有机地在地球剖分问题上高度耦合,而文献[1]中提出的“三维结构”和“厘米级精度”成了“剖分”重要关键。
对于地球剖分,离散 (Discrete) 本意是如何将已用连续数量关系建立起来的地球空间的科学模型离散化,变成各种分辨率下的单元集{Cell}, 便于计算机加以处理。因而这种离散化效果检验标准应该也只能是数据本源:地球空间连续的科学模型,这是地球空间剖分、全球位置统一探测和服务科学问题的具体客观对象。因此,文献[1]提出厘米级精度的三维结构是自然的、必须的。
地球三维 (或二维) 剖分本身并不包括地图投影。地球的三维 (或二维) 剖分本身即是把地球空间的科学模型 (椭球体WGS-84、及其下的大地坐标系和大地线尺度) 离散化的方法和技术,而地图投影则是把三维椭球面或球面,展开至平面实施可视化 (及度量) 的学科,两者有紧密的联系,但各有其不同的主要内容和主题。由于三维椭球面或球面是不可展曲面,加上地图投影把之展为平面,既可平面可视化,又便于人工平面度量,但不可避免地增加了固有的变形。此变形,并非剖分所必需,计入“剖分”不恰当。并且变形较大的“平面度量”对于数字状态下的“剖分”及其度量并无多大意义。而仅就可视化而言,地图投影的设计前提和范畴可以非常宽松,因此对地球剖分中地图投影的标准化、规范化具有重要意义。
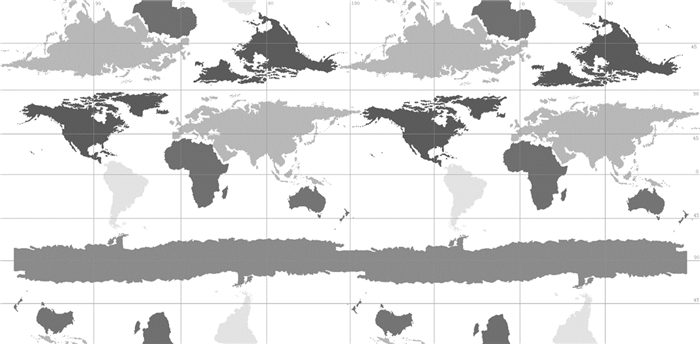
为此,文献[40]可视化界面借用椭球圆柱等距投影,利用开了口的椭球面,边缘延伸半个球面 (或更大),以在全球主区 (经度:0°—360°;纬度:90°S—90°N),仿造“椭球面”拓扑环境主区与椭球面1:1对应且双向连续,没有边缘,都有半个球面的连续区 (其余辅区,采用主区相应子区全等映射,按延伸方向,拼接而成);而计算方面,度量 (metric) 则采用椭球上的大地线尺度 (机器) 计算。这样,在可视的互动环境下,创建了全球一次性全可视、全部度量数据无变形的优异可视环境,图 2。它优于所有地图投影,也优于通常所见的不到1/2对象的外心透视投影 (追求透视效果者例外)。有益于全球剖分及全球二维 (B, L) 信息可视。
它的特点是:全球的一次全览性,视图主区具有与椭球面/球面相同的拓扑性质,符合人们总需要一个平板型的地球,能够一次性地看到整个表面[1];具有全球经向平行对称性,纬向赤道的对称性;便于全球各分辨率信息规范地 (平行式) 分解、合成与融合,使人便于不同辨率下的分析、对比、判别。
为地图可视的版幅、印刷等而提出的分幅、合幅等要求,在数字状态下已不复存在。显然,数字状态下地球剖分,各窗口、各层次cell的汇集、有序组合将方便、快捷、灵活得多,本质是窗口和连续可视要求,没必要机械仿照地图可视的分幅、合幅等要求。
2.2 地球度量空间的意义实体的定位是实体在所选坐标系内的度量,所有空间的度量、地理实体的大小和形状的度量是空间分析重要基础, 是空间最基础的数量特征,既是剖分实施及检验所必须,而度量的基准是尺度。
尺度的数学定义[41]:假定D是一个集,J是一个把D×D变进R1维实数域的变换,如果对于所有的x∈D、y∈D,z∈D满足:①J(x, y)≥0等号当且仅当x=y时成立;②J(x, y)=J(y, x);③J(x, y)+J(y, z)≥J(x, z)。
那么称J为D的一个尺度,J(x, y) 是在这个尺度下x与y的距离,D是以J为尺度的尺度空间 (距离空间)。如果条件①中,没有当且仅当x=y时等号成立的限制,②、③不变,则称J为D的一个拟尺度。
上述尺度空间也称度量空间。根据上述定义, 不同的定义尺度 (metric) 具有不同的度量空间, 反之, 也同样成立。
一实体对其他实体的作用和相互作用都是通过空间进行的, 距离是空间中实体最普遍基本关系,是量化了的关系在实数域上的表现,尺度决定了整个空间及其中所有实体的空间结构和基本特性。
地球信息度量空间三要素[36, 38, 42]。地球大小和形状是地球科学重要空间基准,往往是影响定位、度量准确度最基础因素,地球空间及其下实体本征度量空间就是地球信息度量空间。空间参考体系——定形、定位、定向地球椭球体WGS-84协议椭球就是目前时期最好的选择。地球空间的坐标系统大地测量学中对地球主要采用了两种完全等价的并且相互间转换方便的坐标系统,即地心坐标系统 (X、Y、Z) 和大地坐标系统 (B、L、H),对于活动以地球面为基本中心曲面的地理空间而言,采用大地坐标系统比地心坐标系统更为方便和稳定。空间尺度—椭球面上大地线尺度。尺度 (Metric) 是量化的标准,它决定于空间和对象的性质、范围及精度要求。空间分析是与空间几何量相关的分析,采用不同尺度将有不同结果,地球椭球体的本征尺度就是大地线尺度。
至今, 并没有国际标准支撑球模型及其发展, 理论和实践表明,它和地球椭球体有较大偏差,它是在各类应用中, 椭球模型的临时替代物;而若采用各种地图投影的平面,由于它不可避免具有大的变形,因而当今已不宜用它作度量,往往用作可视化和大概的估量。
前述算例,从实践证实了地球度量空间的理论阐述是不能违背的,现代地球剖分不能再以正球面或投影平面为基础,必须采用以WGS-84为标志的椭球系统。
2.3 现代数字地球“三维结构及厘米级准确度”的革命性要求[1],将引起度量和空间分析格局的重大变化,也影响剖分工作使GIS的地理空间真正统一于地球科学的地球空间是GIS正确发展的迫切需要。地球信息度量空间的理论问题全面影响并左右GIS的理论和技术。由习惯的欧氏空间平面投影度量或地理球面 (ϕ,λ) 度量,实现到地球椭球体这样一个度量空间的进展, 必将造成GIS整个理论和技术体系的重大变化。要求各区域乃至全球“三维结构及厘米级准确度”是过去从没有达到的革命性要求。相应于此,下面几点已逐渐明朗:
(1) 传统的平面介质地图所用的地图投影在数字地球或GIS中已失去原有的可信度量作用,而仅保持可视化作用 (包括可视化下的图形交互作用)。
(2) 计算机上数字地球或GIS可以采用数字计算技术使地球椭球体面 (体) 上的度量达到足够高的准确度,出现度量既无角度变形又无面积变形似乎理想境界,这是地图投影梦寐难求的。
(3) 传统的地理球面 (ϕ,λ) 坐标系统及其各种地图投影,主要是准确度问题,一般都不作为地形图使用,只能作为中、小比例尺地图所使用。那么地理球面 (ϕ,λ) 坐标系统及其球面度量能否取代地球椭球体度量空间 (比如WGS-84)?前述算例表明:这个代替是有条件的,而厘米级的精度要求下,基本是不可能的,并且只有椭球的三维剖分才能达到高精度的理论要求。
(4) 现有DGG剖分,绝大多数是针对二维球面或椭球面的,针对三维球体或椭球的剖分尚少[29],而椭球型三维剖分则更少。很明显,地理空间比二维球面或椭球面宽广得多,且上天入地,正动态扩展,剖分应面向椭球型三维。
(5) 剖分的cell及cell集合的运算及其相对应的点、线、面及其组合集合的运算的整个计算体系是否完整,灵活,准确,全面适合于该空间的定位、度量及空间分析。其中,剖分后的网格cell怎么度量与计算将是不可忽视的核心问题。
剖分后所形成的三维 (或二维) 网格cell是三维 (或二维) 闭区间点集,它不应也不能由多对区间端点 (即剖分点) 实施后续计算,一般采用“网格参考点 (grid reference point)”取代网格实施[2, 5],这时,一是“网格参考点”选取原则;二是这种取代后,后续的系列计算意义、定义及其规则;三是对于后述各种重要计算的严密误差预估计,是所有剖分方法必不可少的。
这些问题良好的解决,能在技术上妥善解决以下5个全球范围问题:全球连续可视化;多维、多源、多分辨率信息数据全球统一、互容、系统的定位框架;长度、面积、方向和体积等全球的精密度量;空间分析的正确性;信息系统工程的优化结构, 即具有易扩充、组合、分解的动态性、统一的规范性、计算的优化性。
3 地球剖分的椭球三维途径 3.1 当前地球空间剖分网格缺少三维剖分及高精度描述当代科技的发展,促进了现代大地测量学迅猛发展,人们对地球度量空间的时、空认识出现了质的飞跃。相应之下,地球剖分并未全面适应这种发展,绝大部分剖分方法和方案囿于球面或二维,而囿于球面的剖分,就跟局限于球面的地图投影一样,无论如何仍跳不出精度低,不能适用于大、中、小比例尺地形图,更不能胜任对地球 (椭球) 信息度量空间的剖分,以及精密定位、度量和分析。文献[1]指出的我们期待支持空间定位和详细的三维结构导航,它对地球上任何地方具有厘米级的精度,重要且尖锐。目前,尽管已有了相当多具有优秀方案,但不能回避关键之处,具有厘米级精度的三维地球剖分是明显缺乏的,同时剖分的标准论述中长期缺少准确度标准,并且缺少与之紧密相关的误差分析及评价研究。
应当指出,得到Goodchild赞扬的GGS剖分学者在2008年著文,经多年的剖分研究后,高度重视和研究了“metric”问题[5]。而文献[19]则是长期研究剖分的基础上,着重提出了GGS的准确度和误差,并慎重提出了DGG剖分面临的诸多问题源于对DGG的定位,也说明了剖分所面临的深层矛盾。
度量是度量空间集合中元素最基本、普遍的关系,是最基本、普遍关系的量化表述,便于特征考察、研究及结构分类。剖分实施离不开度量,剖分的实现离不开度量的检验,而剖分的准确度是度量准确度总体表现。
3.2 地球剖分的准确度、逻辑一致性和完整性的理论阐述十分必需相应于地球空间本源,地球剖分的数据质量本身应由空间数据质量理论予以全面描述和确证。这主要就是相对于一定分辨率规格剖分数据的准确度:位置和度量关系的准确度;逻辑一致性:拓扑一致性、度量关系一致性;完整性:它首先指特征或实体完整性、或空间剖分的完整性,必须兼容所有分辨率:历史的、现有的,并涵盖今后几十年地理信息发展,其次指编码特征与所有相关属性间的匹配程度[40],应是完全匹配而无遗漏。
3.3 地球椭球的三维剖分 3.3.1 运用 (B, L, H) 曲面族剖分地球椭球体结构数百年来,大地测量学理论和技术结晶已经提供了这种剖分的康庄大道,3组正交的 (B, L, H) 曲面族实施地球椭球体结构的剖分[39],只有它能够提供理想的高精度。
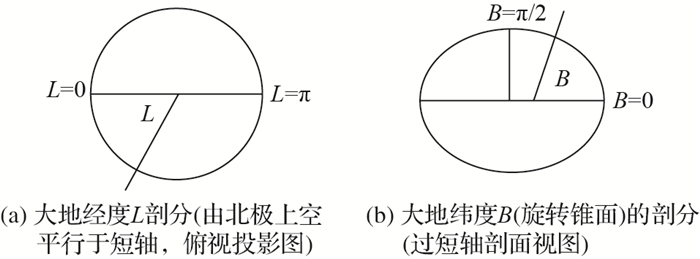
采用B、L、H正交的参数曲面能够严密、统一、有限、递归地、无缝无叠地、高精度地剖分地球椭球体结构的三维地理空间。并且理论和实践已经有所证实,采用B、L、H正交的参数曲面能够统一、高精度地探测、检索全球位置,严密、统一、高精度地度量全球各层剖分“细胞”间的基本关系,并正确实施全地理空间的空间分析。这里H就是大地高,其值域是高度距离,设定 (WGS-84的椭球面为H=0, Hmax≥H≥Hmin的情况下),而π/2≥B≥0, 2π≥L≥0,就是大地经、纬度,它们的值域是弧度, 如图 3、4所示。
|
| 图 3 剖分示意图 Fig. 3 Sketch of triangulation |

|
| 图 4 大地高H剖分的简图 Fig. 4 Sketch of geodetic height H triangulation |
测度和度量理论认为:
一个拓扑空间M被称为紧致的,如果对M的任何开覆盖,总存在有限的子覆盖,因为地球度量空间是一个有界闭集,凡是有界闭集都是紧致的,因此,地球度量空间中一定存在有限多个邻域,完全掩盖了地球度量空间;数字地球所指的地球椭球形状的大地理空间是紧致的,其各种有限三维单纯剖分的图形是紧致的;且地球度量空间是没有孤立点的空间闭集,是完备集,由此决定了剖分的有限的科学序列,即可如此递归地剖分下去 (即是有限的子覆盖),直至达到人们所需的任意三维分辨率大小,并且凡是如此可以有限单纯剖分的各阶段图形也必是紧致的[43]。
采用上述地球信息度量空间的科学概念,将可以实现正确且精密的地球空间度量,也可以统一、有限、递归地、无缝无叠地剖分下去,实现地理 (椭球) 空间的剖分完整性。实现这种剖分理论上严密性阐述,十分关键。
在 (B, L, H) 各自传统区间剖分,实际剖分技术应是简单、方便、通用的 (递归可操作的),与经验常识全衔接,易与传统优秀方法融合,避免冲突和漏洞。由图 3和图 4可见,在极点附近,并无L或B的剖分困难,与其他位置均处同样状态,H的剖分更是如此。
3.3.2 地图代数对定位和度量的准确度DGG网格本质上是二维或三维地球度量空间上指定分辨率相应颗粒集合的幂集,其相应一指定分辨率的颗粒集合类同于二维或三维栅格阵列。其每一个栅格都是个有界闭集,因此我们采用地图代数中的相应定义[42, 44]。
定义网格 (或栅格) 的位置由它的中心 (即前述参考点) 代为计算:B中、L中、H中分别为网格 (或栅格) 各坐标上、下界的中点,这时,该分辨率网格的位置误差将不大于1/2颗粒直径 (二维正方形栅格则为0.5×21/2),相应的,两网格 (或栅格) 间距离的误差将不大于1个颗粒直径 (二维正方形栅格则为21/2)。显然定位和度量的误差是确定的,随分辨率的颗粒度大小而变化,并随颗粒度变小而趋于0。在网格计算中,两点间的计算由点所在网格间的计算来实施,而网格间的计算由所在网格中心的计算来得到,这就是网格计算与点计算的差别和内在联系。它总是可计算的,且有确定的误差,只有误差可接受,网格及其计算才值得进行,否则应提高分辨率,缩小颗粒度,再实施网格计算。
在上述定义下,可定义网格g和网格集S的距离度量, 并进而定义网格集S1与S2间的距离度量
D(g, S)=min (g, gi)∧gi ∈S;
D(S1, S2)=min (s1i, s2j)
∧s1i∈S1∧s2j∈S2
地图代数在正常定义了点间度量的基础上[41],运用集合论,在上述准确度的误差范围内,用数字计算作工具,简单而又牢靠地依托于度量几何理论和技术基础之上,实现了该度量空间域模型的严实度量 (网格g和网格集S、网格集S1与S2、图形集间)[45-46]。具体讲,也即实现各分辨率下Cell间的度量,这个度量的准确度,就是剖分的准确度。
对于在传统的矢量实数运算体系中的这种度量、运算,除非人们十分熟悉的欧几里德式的空间,其几何学规则已知,对于地球及非欧度量空间,不可数集合计算是有不少障碍的;而相对于可数集合 (栅格集、格网集、离散集) 上的度量、运算,只要计算条件允许,都可以简单、牢靠地完成,不仅在欧氏空间,而且在定义了 (点对点) 度量函数的空间都方便,当然其中包括地球信息度量空间和障碍空间,展示了这种可数集合上代数计算的重大意义。
地图代数正是奔着度量和实数空间到整数空间变换两个基点去的,以尺度的正确性和量度的准确性以及效率 (时、空复杂性) 为基础,以空间数据组织的简单、通用、规范性和‘0’初始化为基础,简明展现了空间计算的魅力[40, 44]。
3.3.3 初步证实了椭球实体三维剖分途径地图代数研究以点集变换与运算的代数观念来全面而本质地阐述图形符号可视化及空间分析的理论与方法。地图代数体系将地球椭球视为整体研究对象,超越了传统的欧几里得空间的局限性,为区域 (以至全球) 地理空间信息定位和研究提供统一而规范的基础。[45]
多年来,地图代数在二维部分,运用了矩形网格,较多地实施了地球度量空间的研究,并利用这研究的结果,实施了多尺度定位、剖分、度量及分析,与众多研究一样,持续证实了地球椭球的B、L剖分是一条行之有效的途径:它剖分完备,定位、度量和分析理论和实际上高准确,而加上H参数的三维剖分发展,将是一个有优良前景的途径。
此 (B, L, H) 剖分途径其唯一的缺点是极点附近的计算易出现不稳定性。实际上,这往往是由于前述投影与剖分没有科学划分,产生不必要纠缠,而导致在地图投影图上剖分发生的问题。理论和实际上均表明,也不可能存在剖分方便,变形无激烈变化之处的全球图形连续的地图投影。
可以通过前述剖分与投影分离,图形计算与变形计算相分离来解决。在真实椭球上度量格网各种几何指标,计算结果没有长度和角度变形,也就没有极点附近ΔB或ΔL引起的长度或角度变形率激烈变化。
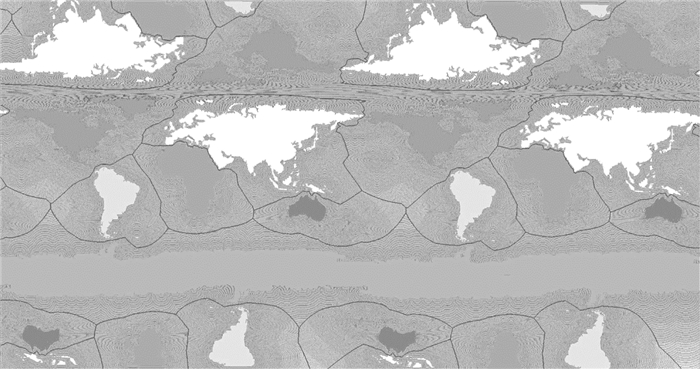
文献[40]中全球大洲的Voronoi图 (图 5) 表明,极点附近的度量计算决定于大地线尺度计算公式的质量和实际设计,只要公式能在极点附近用,其度量理论和实践上都没问题。图 5中全球各处度量变换实例表明:其多分辨率相应的各颗粒实际计算 (计算本质是平行的) 也没有问题,而且理论和实践上,可用地图投影变换灵活地变成人们想要的各种视图,可更贴合人们视感和合理需求,准确度始终无虑[47-48]。至于极点附近细胞大小悬殊,是真实,但不是扭曲,尤其在较高分辨率的数字状态下,数据操作的效率和准确性是传统地图类模拟操作方式不可比拟的。
4 结语
由于数字地球和GPS、北斗系统、大数据、物联网的迅速发展,人、事、物全球及室内外、信息的定时 (timing)、定位 (Localizatio)、探测 (detection)、测度 (measurement)、度量 (metric)、分析 (analysis)、管理 (Administration) 和计算 (calculation) 已整体进入高精度、三维的新时期。作为空间数据模型及最广泛的空间数据体,地球剖分和位置框架研究意义重大,研究内容丰富,影响深远。采用球实体及相应二维剖分,尽管有很多优点,但相对于全球三维定位、定时、度量和分析的现代发展要求,面向WGS-84椭球实施三组正交的 (B, L, H) 曲面族剖分是目前能够获得高准确度的正确途径,还是应予主要注意力于椭球实体及三维剖分途径;大力强化相对薄弱的剖分质量理论基础的研究,尤其是剖分的完整性理论、准确度及度量理论以及逻辑一致性理论等研究,发展并完善地球格网化分标准。
地球剖分和位置框架三维高精度确立,将把地球科学从困扰了人们数百年的神秘“两张皮”基准 (椭球面 (数学的)、大地水准面 (物理的)) 下解放出来,通过[39]
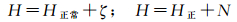
严密统一为科学的“一张皮”,这将具有重大的科学意义及巨大的现实意义。
| [1] | GOODCHILD M F, GUO Huadong, ANNONI A, et al. Next-Generation Digital Earth[J]. Proceedings of the National Academy of Sciences of the United States of America, 2012, 109(28): 11088–11094. DOI:10.1073/pnas.1202383109 |
| [2] | SAHR K, WHITE D, KIMERLING A J. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121–134. DOI:10.1559/152304003100011090 |
| [3] | BAR-ZEEV A. How Google Earth[really] works[EB/OL]. (2007-07-03)[2011-07-16]. . |
| [4] | MAHDAVI-AMIRI A, ALDERSON T, SAMAVATI F. A Survey of Digital Earth[J]. Computers & Graphics, 2015, 53: 95–117. |
| [5] | GREGORY M J, KIMERLING A J, WHITE D, et al. A Comparison of Intercell Metrics on Discrete Global Grid Systems[J]. Computers, Environment and Urban Systems, 2008, 32(3): 188–203. DOI:10.1016/j.compenvurbsys.2007.11.003 |
| [6] | KOLLER D, LINDSTROM P, RIBARSKY W, et al. Virtual GIS:A Real-Time 3D Geographic Information System[C]//Proceedings of 1995 IEEE Conference on Visualization. Atlanta, GA:IEEE, 1995:94-100, 443. |
| [7] | DUTTON G H. A Hierarchical Coordinate System for Geoprocessing and Cartography[M]. Berlin Heidelberg: Springer, 1999. |
| [8] | HITCHNER L E. A Virtual Planetary Exploration:Very Large Virtual Environment[C]//ACM SIGGRAPH'92 Tutorial on Implementing Immersive Virtual Environments. Moffett Field, CA:NASA Ames Research Center, 1992. |
| [9] | FALBY J S, ZYDA M J, PRATT D R, et al. NPSNET:Hierarchical Data Structures for Real-Time Three-Dimensional Visual Simulation[J]. Computers & Graphics, 1993, 17(1): 65–69. |
| [10] | REDDY M, LECLERC Y, IVERSON L, et al. Terra Vision Ⅱ:Visualizing Massive Terrain Databases in VRML[J]. IEEE Computer Graphics and Applications, 1999, 19(2): 30–38. DOI:10.1109/38.749120 |
| [11] | 李德仁, 肖志峰, 朱欣焰, 等. 空间信息多级网格的划分方法及编码研究[J]. 测绘学报, 2006, 35(1): 52–56, 70. LI Deren, XIAO Zhifeng, ZHU Xinyan, et al. Research on Grid Division and Encoding of Spatial Information Multi-Grids[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1): 52–56, 70. DOI:10.3321/j.issn:1001-1595.2006.01.011 |
| [12] | 李德仁, 朱欣焰, 龚健雅. 从数字地图到空间信息网格-空间信息多级网格理论思考[J]. 武汉大学学报 (信息科学版), 2003, 28(6): 642–650. LI Deren, ZHU Xinyan, GONG Jianya. From Digital Map to Spatial Information Multi-grid-A Thought of Spatial Information Multi-grid Theory[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 642–650. |
| [13] | 李德仁, 邵振峰, 朱欣焰. 论空间信息多级格网及其典型应用[J]. 武汉大学学报 (信息科学版), 2004, 29(11): 945–950. LI Deren, SHAO Zhenfeng, ZHU Xinyan. Spatial Information Multi-grid and Its Typical Application[J]. Geomatics and Information Science of Wuhan University, 2004, 29(11): 945–950. |
| [14] | 邵振峰, 李德仁. 基于网格计算环境下的空间信息多级格网研究[J]. 地理信息世界, 2005, 3(2): 31–35. SHAO Zhenfeng, LI Deren. Study on Spatial Information Multi-grid under Grid Computing Environment[J]. Geomatics World, 2005, 3(2): 31–35. |
| [15] | NIMA.Digital Terrain Elevation Data[DB/OL].[2005-12-13]. http://www.globalsecurity.org/intell/systems/dted.htm. |
| [16] | BJORKE J T, GRYTTEN J K, GER M, et a1. A global grid model based on "Constant Area" quadrilaterals[C]//VIRANTAUS K, TVEITE H. Proceedings of the 9th Scandinavian Research Conference on Geographical Information Science, ScanGIS'2003. Espoo, Finland:Helsinki University of Technology, 2003, 3:239-250. |
| [17] | BJØRKE J T, NILSEN S. Examination of A Constant-Area Quadrilateral Grid in Representation of Global Digital Elevation Models[J]. International Journal of Geographical Information Science, 2004, 18(7): 653–664. DOI:10.1080/13658810410001705334 |
| [18] | SEONG J C. Implementation of an Equal-Area Gridding Method for Global-Scale Image Archiving[J]. Photogrammetric Engineering & Remote Sensing, 2005, 71(5): 623–627. |
| [19] | 赵学胜, 王磊, 王洪彬, 等. 全球离散格网的建模方法及基本问题[J]. 地理与地理信息科学, 2012, 28(1): 29–34. ZHAO Xuesheng, WANG Lei, WANG Hongbin, et al. Modeling Methods and Basic Problems of Discrete Global Grids[J]. Geography and Geo-Information Science, 2012, 28(1): 29–34. |
| [20] | 崔马军, 赵学胜. 球面退化四叉树格网的剖分及变形分析[J]. 地理与地理信息科学, 2007, 23(6): 23–25. CUI Majun, ZHAO Xuesheng. Tessellation and Distortion Analysis Based on Spherical DQG[J]. Geography and Geo-Information Science, 2007, 23(6): 23–25. |
| [21] | 赵学胜, 陈军, 王金庄. 基于O-QTM的球面VORONOI图的生成算法[J]. 测绘学报, 2002, 31(2): 157–163. ZHAO Xuesheng, CHEN Jun, WANG Jinzhuang. QTM-based Algorithm for the Generating of Voronoi Diagram for Spherical Objects[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 157–163. DOI:10.3321/j.issn:1001-1595.2002.02.013 |
| [22] | 赵学胜, 孙文彬, 陈军. 基于QTM的全球离散格网变形分布及收敛分析[J]. 中国矿业大学学报, 2005, 34(4): 438–442. ZHAO Xuesheng, SUN Wenbin, CHEN Jun. Distortion Distribution and Convergent Analysis of the Global Discrete Grid Based on QTM[J]. Journal of China University of Mining & Technology, 2005, 34(4): 438–442. |
| [23] | 程承旗, 关丽. 基于地图分幅拓展的全球剖分模型及其地址编码研究[J]. 测绘学报, 2010, 39(3): 295–302. CHENG Chengqi, GUAN Li. The Global Subdivision Grid Based on Extended Mapping Division and Its Address Coding[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(3): 295–302. |
| [24] | 李世忠, 宋树华, 程承旗, 等. 基于GeoSOT网格的"天绘一号"卫星影像数据组织[J]. 遥感学报, 2012, 16(S1): 102–107. LI Shizhong, SONG Shuhua, CHENG Chengqi, et al. Mapping Satellite-1 Remote Sensing Data Organization Based on GeoSOT[J]. Journal of Remote Sensing, 2012, 16(S1): 102–107. |
| [25] | 宋树华, 程承旗, 关丽, 等. 全球空间数据剖分模型分析[J]. 地理与地理信息科学, 2008, 24(4): 11–15. SONG Shuhua, CHENG Chengqi, GUAN Li, et al. Analysis on Global Geodata Partitioning Models[J]. Geography and Geo-Information Science, 2008, 24(4): 11–15. |
| [26] | 贲进, 童晓冲, 周成虎, 等. 正八面体的六边形离散格网系统生成算法[J]. 地球信息科学学报, 2015, 17(7): 789–797. BEN Jin, TONG Xiaochong, ZHOU Chenghu, et al. Construction Algorithm of Octahedron Based Hexagon Grid Systems[J]. Journal of Geo-Information Science, 2015, 17(7): 789–797. |
| [27] | 童晓冲, 贲进, 秦志远, 等. 基于全球离散网格框架的局部网格划分[J]. 测绘学报, 2009, 38(6): 506–513. TONG Xiaochong, BEN Jin, QIN Zhiyuan, et al. The Subdivision of Partial Grid Based on Discrete Global Grid Systems[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(6): 506–513. DOI:10.3321/j.issn:1001-1595.2009.06.007 |
| [28] | 袁文, 庄大方, 袁武, 等. 离散三角网格系统距离量测方法[J]. 测绘学报, 2011, 40(1): 59–65. YUAN Wen, ZHUANG Dafang, YUAN Wu, et al. Distance Function for the Triangular Grids[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 59–65. |
| [29] | 吴立新, 余接情. 基于球体退化八叉树的全球三维网格与变形特征[J]. 地理与地理信息科学, 2009, 25(1): 1–4. WU Lixin, YU Jieqing. Global 3D-Grid Based on Sphere Degenerated Octree and Its Distortion Features[J]. Geography and Geo-Information Science, 2009, 25(1): 1–4. |
| [30] | 江锦成, 郭甲腾, 吴立新, 等. 三维地学实体多粒度栅格剖分与布尔运算的并行算法[J]. 科技导报, 2011, 29(35): 18–23. JIANG Jincheng, GUO Jiateng, WU Lixin, et al. Multi-Granularity Rasterization and Boolean Operation Parallel Algorithm for 3D Spatial Entities[J]. Science & Technology Review, 2011, 29(35): 18–23. |
| [31] | LUKATELA H. Hipparchus Geopositioning Model:An Overview[C]//Proceedings of Eighth International Symposium on Computer-Automated Cartography. Baltimore, Maryland:[s.n.], 1987. |
| [32] | KOLAR J. Representation of the geographic terrain surface using global indexing[C]//Proceeding of 12th International Conference on Geoinformatics. Sweden:[s.n.], 2004. |
| [33] | 陈军. Voronoi动态空间数据模型[M].北京:测绘出版社, 2002:8, 1-62, 87-130. CHEN Jun.Voronoi Dynamic Spatial Data Model[M].Beijing:Surveying and Mapping Press, 2002:8, 1-62, 87-130. |
| [34] | 胡毓巨, 龚剑文. 地图投影[M]. 武汉: 武汉测绘科技大学出版社, 1997: 19-47. HU Liuju, GONG Jianwen. Map Projection[M]. Wuhan: Wuhan Surveying and Mapping Science and Technology University Press, 1997: 19-47. |
| [35] | 胡鹏, 吴艳兰, 杨传勇, 等. 大型GIS与数字地球的空间数学基础研究[J]. 武汉大学学报 (信息科学版), 2001, 26(4): 296–302. HU Peng, WU Yanlan, YANG Chuanyong, et al. Research on System Space Mathematical Base of Large-scale GIS and the Digital Earth[J]. Geomatics and Information Science of Wuhan University, 2001, 26(4): 296–302. |
| [36] | 胡鹏, 胡毓钜, 杨传勇, 等. 我国地球空间数据框架的设计思想、技术路线及若干理论问题讨论[J]. 武汉大学学报 (信息科学版), 2002, 27(3): 283–288. HU Peng, HU Yuju, YANG Chuanyong, et al. Design Thinking, Technical Route and Some Theoretical Issues on the Geospatial Digital Framework[J]. Geomatics and Information Science of Wuhan University, 2002, 27(3): 283–288. |
| [37] | 胡鹏, 杨传勇, 胡海, 等. GIS的基本理论问题——地图代数的空间观[J]. 武汉大学学报 (信息科学版), 2002, 27(6): 616–621. HU Peng, YANG Chuanyong, HU Hai, et al. Basic Theoretical Problem of GIS-Space View of Map Algebr[J]. Geomatics and Information Science of Wuhan University, 2002, 27(6): 616–621. |
| [38] | 胡鹏, 刘沛兰, 胡海, 等. 地球信息的度量空间和Global GIS[J]. 武汉大学学报 (信息科学版), 2005, 30(4): 317–321. HU Peng, LIU Peilan, HU Hai, et al. Metric Space of Earth Information and Global GIS[J]. Geomatics and Information Science of Wuhan University, 2005, 30(4): 317–321. |
| [39] | 胡鹏, 游涟, 杨传勇, 等. 地图代数[M]. 武汉: 武汉大学出版社, 2002: 1-126. HU Peng, You Lian, YANG Chuanyong, et al. Map Algebra[M]. Wuhan: Wuhan University Press, 2002: 1-126. |
| [40] | 孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 2版. 武汉: 武汉大学出版社, 2010: 4-61, 64-167. KONG Xiangyuan, GUO Jiming, LIU Zongquan. Fundamentals of Geodetic Surveying[M]. 2nd ed. Wuhan:Wuhan University Press, 2008:4-61, 64-167. |
| [41] | 胡鹏, 李圣权, 胡海. 地球信息理论和零初始化问题[M]. 北京: 测绘出版社, 2006: 1. HU Peng, LI Shengquan, HU Hai. Geographic Information Theory and Zero Initialization Problem[M]. Beijing: Surveying and Mapping Press, 2006: 1. |
| [42] | 《数学手册》编写组. 数学手册[M]. 北京: 高等教育出版社, 1979: 1112-1114, 1121-1123. 《Handbook of Mathematics》Write Groups. Handbook of Mathematics[M]. Beijing:People Education Press, 1979:1112-1114, 1121-1123. |
| [43] | 江泽坚, 吴智泉. 实变函数论[M]. 北京: 人民教育出版社, 1961: 1-107. JIANG Zejian, WU Zhiquan. Real Function Theory[M]. Beijing: People Education Press, 1961: 1-107. |
| [44] | 胡鹏, 游连, 胡海.地图代数概论[M].北京:测绘出版社, 2008:12-30, 217-223. HU Pen, YOU Lian, HU Hai.Introduction to Map Algebra[M]. Beijing:Surveying and Mapping Press, 2008:12-30, 217-223. |
| [45] | 中国测绘学会. 中国测绘学科发展蓝皮书[M]. 北京: 测绘出版社, 2003. Chinese Society of Geodesy, Photogrammetry and Cartography. Blue Book of China's Surveying and Mapping Discipline Development[M]. Beijing: Surveying and Mapping Press, 2003. |
| [46] | 胡海, 吴艳兰. 椭球面上混合基线图形的缓冲区和等比例线问题[J]. 测绘工程, 2011, 20(3): 1–4, 8. HU Hai, WU Yanlan. Problems of Graphics Buffers and the Proportion Line of Ellipsoid Mixed Baseline (or Normal Curve)[J]. Engineering of Surveying and Mapping, 2011, 20(3): 1–4, 8. DOI:10.3969/j.issn.1006-7949.2011.03.001 |
| [47] | HU HAI, LIU XIAOHANG, HU PENG. Voronoi Diagram Generation on the Ellipsoidal Earth[J]. Computers & Geosciences, 2014, 73: 81–87. |
| [48] | HU H, YOU L, YANG H, et al. A Global Modeling Method based on Geographical Distance Fields[C]. AAG Annual Meeting, 2016. |