2. 61541部队, 北京 100094;
3. 中国石油新疆油田公司数据公司, 克拉玛依 834000;
4. 中国天绘卫星中心, 北京 102102;
5. 中国运载火箭技术研究院研究发展中心, 北京 100076;
6. 海参某局, 北京 100841;
7. 国家信息中心, 北京 100045
2. Troops 61541, Beijing 100094, China;
3. Data Company of Xinjiang Oilfield Branch of Petrochina, Karamay 834000, China;
4. TH Center of China, Beijing 102102, China;
5. China Academy of Launch Vehicle Technology Research and Development Center, Beijing 100076, China;
6. Naval Staff, Beijing 100841, China;
7. State Information Center, Beijing 100045, China
当前的空间数据组织方面,尤其是地图数据,在统一组织方面已经形成一套完整的体系,如我国1992年颁布的《国家基本比例尺地形图分幅和编号GB/T130 89—92》标准等。针对遥感影像数据的组织与管理方面,在某类或者某系列卫星的影像数据统一组织上也有很完备的体系[1],但缺少适合所有遥感卫星影像数据的统一组织上的网格框架,由此给基于遥感影像数据共享、检索、全球无缝表达、分发、编目、计算以及数据更新等应用带来诸多问题。本文从遥感影像数据特点出发,归纳了统一组织框架的设计原则和设计难点,分析了几种剖分格网作为遥感影像统一组织框架的优势和缺陷,为遥感影像统一组织提供参考。
1 遥感影像统一组织框架设计原则与难点遥感数据作为空间数据的一种,通常与传统的地图数据结合使用。因此,全球遥感影像的统一组织框架需考虑国家标准地图分幅体系与卫星数据分景体系之间兼容问题。
遥感卫星影像数据是关于地球表层或者地球表面附近区域信息的快照,具有与地球形状相似的性质。因此,全球遥感影像统一组织框架既要满足全球尺度无缝覆盖的要求,又要满足局部平面表达、精准量算的要求。如何在两者之间达到平衡,成为组织框架设计的难点之一。
我国现阶段对全球的空间数据采用经纬度进行组织,而对局部区域或者平面空间数据采用高斯坐标系下的地图分幅框架进行组织。鉴于我国空间数据组织现状,依据全球离散网格模型标准[2],国内外研究比较多的地球剖分模型,如基于三角形或菱形的剖分模型[3-11]、基于正六边形剖分模型[12-16]、以及基于Voronoi图的剖分模型[17-20],并不能很好地适合我国空间数据组织与管理。因此,在设计全球遥感影像数据统一组织框架时,在符合“Goodchild标准”[2]的前提下还需遵循如下原则:
(1) 可与地图分幅体系兼容。框架中各级不同大小的网格单元,又称剖分单元,能很方便地兼容或者成为地图分幅的有机部分,便于用于传统空间数据整合。
(2) 划分单元的形状尽量为矩形或正方形。框架中的网格单元形状最好为矩形或正方形,使其既可与影像中的像元点阵很好地对应,又便于影像的表达。
(3) 具有完整的编码体系。框架有一个完整的编码体系,使得大到地球、小到厘米级网格都有编码,且层与层之间的编码有很好的嵌套关系,以便于计算。
(4) 每个单元格具有明确的地理位置。框架中每个网格都有固定的空间范围,即每个网格中心、四个角点都有明确的坐标位置,可方便地与影像中坐标对应;每个网格编码在地球上具有准确的地理含义。
(5) 便于多源数据融合。在采用统一组织框架网格来切割影像时,可根据不同的分辨率,便于多源数据融合。
2 几种剖分格网分析鉴于国内外学者对柏拉图立体、正多边形、Voronoi图等剖分模型进行了深入研究,并根据统一组织框架设计原则,本文只对等距、等纬差、正六面体、GeoSOT等几种剖分格网用于遥感影像统一组织的方案进行分析,具体如下。
2.1 等距格网等距剖分网格即基于CGCS2000大地坐标系统的地球椭球体,沿经线方向采用等距、沿纬线方向采用与纬圈相等的正方形建立全球等距格网框架。因此,等距剖分格网又分如下两种情况。
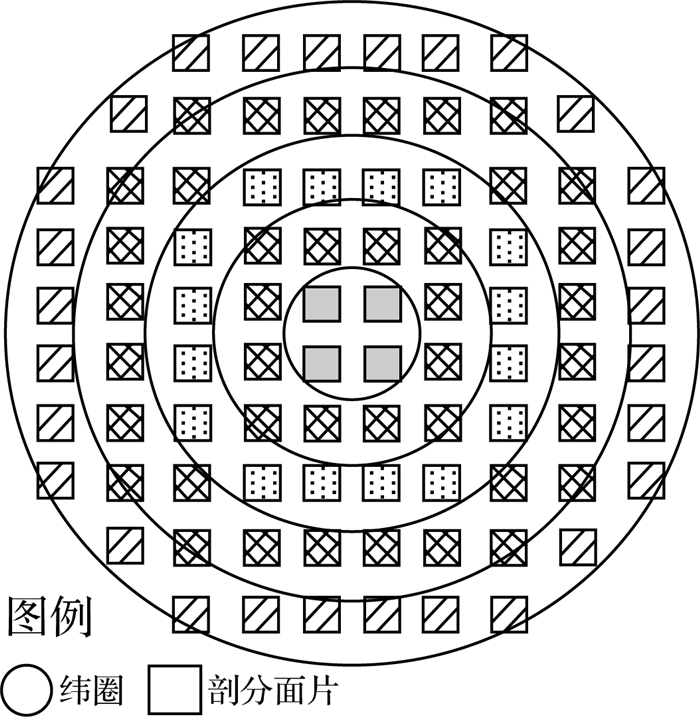
2.1.1 基于基点的等距剖分格网框架基于基点的等距剖分格网是指剖分单元以地球表面某点作为起始点形成全球无缝覆盖的等距剖分格网。比较典型的基点是地球两极点、本初子午线与赤道的交点、任意其他经线与赤道的交点。为了便于描述与计算,本文将其基点设为北极点,并假设正方形剖分单元的边长为d。基于北极的等距剖分格网示意图如图 1,图中剖分单元的边长与两个纬圈之间的距离相等,并采用不同的填充对不同距离的剖分面片进行区别。
|
| 图 1 基于北极的等距剖分格网示意图 Fig. 1 The equidistant subdivision grid based on the arctic pole |
基于CGCS2000椭球体[21-22],若假设以正方形边长d为从北极点到某纬度之间沿大圆经线的弧长,则通过式 (1) 可算出该纬线圈所处的纬度,并由式 (2) 计算出纬圈的半径,由此得计算纬圈的周长。
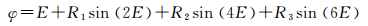 (1)
(1)
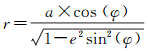 (2)
(2)
式中,a为长半轴;e为第一偏心率;ϕ为纬度,E=(l0-d)/A0,l0为北极到赤道的距离;A0、R1、R2、R3见文献[23]中具体定义。
当d=25 km时,等距剖分格网分析统计如表 1所示。
| 距北极弧长/m | 纬度/(°) | 纬圈半径/m | 纬圈周长/m | 面片数 | 面片周长/m | 纬圈、面片周长之差/m |
| 25 000 | 89.776 | 25 000.399 | 157 082.137 | 4 | 200 000 | 42 917.863 |
| 50 000 | 89.552 | 49 999.291 | 314 154.81 | 16 | 400 000 | 85 845.19 |
| 75 000 | 89.329 | 74 998.522 | 471 229.611 | 36 | 600 000 | 128 770.389 |
| 100 000 | 89.105 | 99 995.468 | 628290.057 | 60 | 600 000 | 28 290.057 |
| 125 000 | 88.881 | 124 991.975 | 785 347.738 | 88 | 600 000 | 185 347.738 |
| 150 000 | 88.657 | 149 986.535 | 942 393.191 | 132 | 800 000 | 142 393.191 |
| 175 000 | 88.433 | 174 977.643 | 1 099 416.957 | 172 | 800 000 | 299 416.957 |
| 200 000 | 88.209 | 199 967.144 | 1 256 430.621 | 224 | 1 000 000 | 256 430.621 |
| 225 000 | 87.986 | 224 953.531 | 1 413 424.724 | 284 | 1 000 000 | 413 424.724 |
| 250 000 | 87.762 | 249 936.416 | 1 570 396.82 | 344 | 1 200 000 | 370 396.82 |
| | | | | | | |
由表 1可知,在第一圈剖分面片的周长与对应纬圈周长之差已经达到了42 917.863 m,并随着正方形单元从北极向赤道逼近,它们之间的差值越大。当d取不同的值时,也有类似的规律。因此,基于基点的等距剖分格网不能很好满足框架设计原则。
2.1.2 基于经线的等距剖分格网框架基于经线的等距剖分格网与基于基点的等距格网相似,只是在剖分面片的展开方式上,基于经线的等距剖分格网以某一经线作为“起跑线”,每一等距纬圈的剖分面片覆盖地球并由此展开 (如图 2),剖分单元的边长与两个纬圈之间的距离相等,并采用不同的填充对不同纬圈的剖分面片进行区别。

|
| 图 2 基于本初子午线的等距剖分格网示意图 Fig. 2 The equidistant subdivision grid based on the prime meridian |
采用式 (1) 可计算出不同纬圈的纬度,并由式 (2) 计算出各纬圈的半径。在此基础上,计算出各个纬圈内正方形面片的个数,即可计算在此高纬部分的各个正方形单元的重叠度,计算结果见表 2。
| 距北极点的弧长/m | 纬度/(°) | 纬圈半径/m | 纬圈周长/m | 上下纬圈周长之差/m | 面片数 | 高纬重叠百分比/(%) |
| 25 000 | 89.776 | 25 000.399 | 157 082.137 | 157 082.137 | 6.28 | 100 |
| 50 000 | 89.552 | 49 999.291 | 314 154.810 | 157 072.674 | 12.57 | 50.00 |
| 75 000 | 89.329 | 74 998.522 | 471 229.611 | 157 074.800 | 18.85 | 33.33 |
| 100 000 | 89.105 | 99 995.468 | 628 290.057 | 157 060.446 | 25.13 | 25.00 |
| 125 000 | 88.881 | 124 991.975 | 785 347.738 | 157 057.681 | 31.41 | 20.00 |
| | | | | | | |
| 9 950 000 | 0.470 | 6 377 923.880 | 40 073 677.611 | 1 598.321 | 1 602.95 | 0.004 0 |
| 9 975 000 | 0.244 | 6 378 079.613 | 40 074 656.110 | 978.498 | 1 602.99 | 0.002 4 |
| 10 000 000 | 0.018 | 6 378 136.695 | 40 075 014.769 | 358.660 | 1 603.00 | 0.000 9 |
在每个纬圈内,正方形面片均不能完整地覆盖整个纬度带,且在高纬区域,越靠近极地,正方形单元之间的重叠度越大。因此,这种剖分方式也不能使得正方形无缝无叠地覆盖整个地球。
2.2 等纬差格网在传统的测绘数据管理上,多是采用等经差、等纬差方式对空间数据进行组织和管理,例如我国标准地形图分幅管理机制即采用这种方式。且当经差或者纬差小到一定程度时,其所代表地球表面的地理空间范围可以近似视为平面,如在赤道附近经度相差10′×10′的区域,其范围约为一个18.5 km×18.5 km。
若遥感影像统一组织框架采用纬差为φ′、以及纬差φ′对应的地表距离为正方形的边长为剖分单元进行等纬差剖分,其中,φ′=1、2、3、…、30。
基于式 (2) 的纬圈半径,可算出每一纬度所对应的纬圈周长、相邻两纬圈之间的距离,以及两者的比值,即为纬差φ′对应的正方形网格个数。为了计算方便,取φ′=10,其计算结果如表 3所示。
| 纬度 | 纬圈 | 上下纬圈周长之差/m | 上下纬圈的距离/m | 面片数 | |
| 半径/m | 周长/m | ||||
| 10′ | 6 378 110.196 | 40 074 848.27 | 505.241 | 18 429.046 | 2 174.548 |
| 20′ | 6 378 029.784 | 40 074 343.03 | 842.064 | 18 429.05 | 2 174.52 |
| 30′ | 6 377 895.766 | 40 073 500.97 | 1 178.880 | 18 429.056 | 2 174.474 |
| | | | | | |
| 87°10′ | 316 334.686 | 1 987 589.451 | 116 828.202 | 18 615.176 | 106.773 |
| 87°20′ | 297 740.900 1 | 1 870 761.249 | 116 844.228 | 18 615.23 | 100.496 |
| 87°30′ | 279 144.563 6 | 1 753 917.021 | 116 859.614 | 18 615.281 | 94.219 |
| 87°40′ | 260 545.778 4 | 1 637 057.407 | 116 873.623 | 18 615.329 | 87.941 |
| 87°50′ | 241 944.763 7 | 1 520 183.784 | 116 886.622 | 18 615.373 | 81.663 |
| 88° | 223 341.68 | 1 403 297.162 | 116 898.983 | 18 615.414 | 75.384 |
根据表 3结果分析,按此种剖分方案,某一地图图幅内剖分面片的分布如图 3。出现这种现象的原因是,由于从赤道到两极等纬差之间的地表距离并不相等,导致不同纬度带的正方形单元大小不相等,也不能完全部覆盖该纬度带对应的整个图幅。

|
| 图 3 等纬差标准剖分框架示意图 Fig. 3 The equal difference of longitude and latitude subdivision grid |
2.3 正六面体格网 2.3.1 基于正六面体的剖分框架
针对剖分单元为矩形或正方形的原则,在柏拉图立体中,正六面体内接地球,有可能使得地球表面剖分为由多个四边形组成,如图 4。

|
| 图 4 基于正六面体的剖分框架示意图 Fig. 4 The subdivision grid based on cube |
基于图 4中正六面体的剖分框架具体剖分步骤如下:
(1) 设地球球面内接的正六面体棱长为d,赤道面与六面体的一面平行。六面体对角线等于球面直径,即
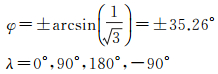
即8点为 (35.264 390°,0°)、(-35.264 390°,0°)、(35.264 390°,90°)、(-35.264 390°,90°)、(35.264 390°,180°)、(-35.264 390°,180°)、(35.264 390°,-90°)、(-35.264 390°,-90°),其相应的直角坐标容易计算,此处略。
(2) 从步骤 (1) 任选一面进行讨论,不妨选如下四边形:(35.264 390°,0°)、(35.264 390°,90°)、(-35.264 390°,90°)、(-35.264 390°,0°)。由此可知0级剖分对应的边长为赤道周长的四分之一,即约10 008 014.6 m。
(3) 将上一步得到的四边形,逐个进行 (近似)4等分:分别取各边中点,并用测地线 (大圆弧) 连接对边的中点 (如图 4(c))。
(4) 对同一分辨率的每个四边形,重复步骤 (3)。
(5) 当分辨率逐级提高 (四边形边长逐级减半) 时,对上一级的四边形逐个重复步骤 (3)、(4)。
由此即可得到由不同层级、不同尺度的剖分面片无缝覆盖地球表面的剖分体系。
2.3.2 变形分析下面对基于正六面体剖分框架中的剖分面片的面积变形、边长变形和角度变形进行分析。
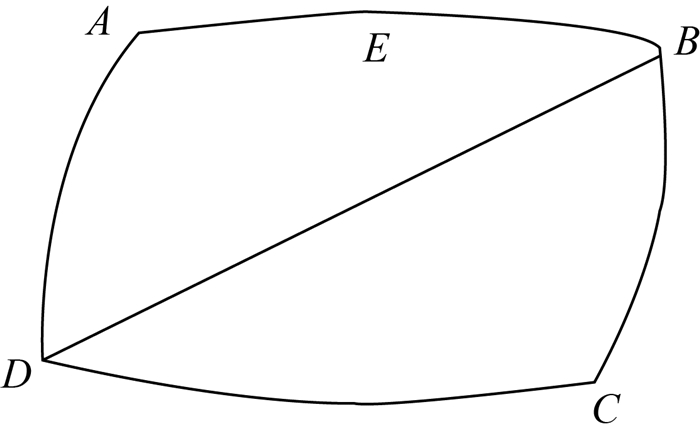
2.3.2.1 剖分面片的面积变形分析该剖分体系中的剖分面片在地球表面为一个椭球面四边形 (如图 5)。设任意一个椭球面四边形ABCD,其面积的计算方法:
|
| 图 5 球面四边形ABCD示意图 Fig. 5 The ellipsoidal quadrilateral ABCD |
先用余弦公式求出四边形的4个球面角,然后代入式 (3) 即可得到面积:
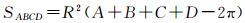 (3)
(3)
式中,A、B、C、D分别为椭球四边形ABCD顶点所对应的内侧球面角。球面角的计算方法:
设AD、AB分别为过A点沿着曲线AD、AB的切线,相应的切面法向量分别为nAD、nAB,则球面角∠DAB(即角A) 满足
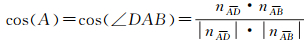 (4)
(4)
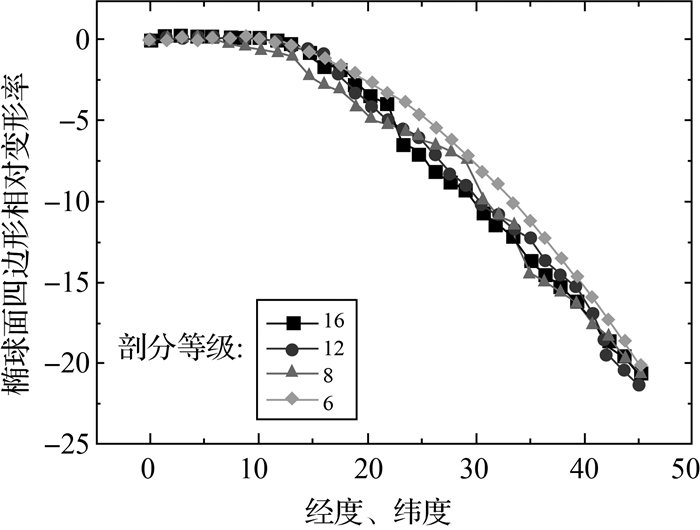
通过式 (3) 和式 (4),即可分析出不同剖分层级上剖分面片的面积变形情况,如图 6和表 4所示。
|
| 图 6 部分等级剖分面片面积变形分布图 Fig. 6 The distribution curve about deformation area of some subdivision cell |
| 参数 | 剖分等级 (将初始面的中线逐级二等分) | |||||||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| 标准边长/m | 2 502 003.6 | 1 251 001.8 | 625 500.9 | 312 750.4 | 156 375.2 | 78 187.6 | 39 093.8 | 19 546.9 | 9 773.4 | 4 886.7 | 2 443.3 | 1 221.7 | 610.8 | 305.4 | 152.7 | 76.3 |
| 正变形极值/(%) | 0.240 612 | 0.240 678 | 0.553 685 | 0.669 133 | 0.665 818 | 0.643 806 | 0.637 877 | 0.631 11 | 0.628 115 | 0.626 558 | 0.625 765 | 0.625 049 | 0.624 652 | 0.624 439 | 0.624 323 | 0.624 323 |
| 负变形极值/(%) | -2.351 87 | -7.874 66 | -13.677 1 | -17.325 6 | -19.334 4 | -20.384 4 | -20.920 8 | -20.452 5 | -21.328 | -21.302 8 | -21.290 2 | -20.935 1 | -21.222 4 | -21.366 7 | -21.439 | -21.438 7 |
由图 6可知,以初始剖分 (0级) 中心线为参照 (下同),沿水平方向,剖分面片的面积变形随着经度的增加而增加;沿竖直方向,随着纬度的增加而增加。可归纳为:距离初始剖分中心线越远,剖分面片的面积变形越大。
2.3.2.2 剖分面片边长变形分形剖分面片的边长,等于过该球面曲线两端点大圆的劣弧之长,用球面距离公式即可得到。图 7和表 5是部分等级剖分面片的边长变形分析结果。

|
| 图 7 部分等级剖分面片边长变形分布图 Fig. 7 The distribution curve about deformation side of some subdivision cell |
| 参数 | 剖分等级 (将初始面的中线逐级二等分) | |||||||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| 标准边长/m | 2 502 003.6 | 1 251 001.8 | 625 500.9 | 312 750.4 | 156 375.2 | 78 187.6 | 39 093.8 | 19 546.9 | 9 773.4 | 4 886.7 | 2 443.3 | 1 221.7 | 610.8 | 305.4 | 152.7 | 76.3 |
| 正变形极值/% | 0.109 046 | 0.109 016 | 0.514 298 | 0.109 046 | 0.514 296 | 0.516 595 | 0.517 335 | 0.517 335 | 0.517 335 | 0.517 335 | 0.517 335 | 0.517 053 | 0.516 862 | 0.516 758 | 0.516 705 | 0.516 666 |
| 负变形极值/% | -5.68 488 | -11.129 7 | -15.942 1 | -18.648 9 | -20.075 2 | -20.806 3 | -21.176 3 | -21.549 3 | -21.455 8 | -21.409 1 | -21.385 7 | -21.025 6 | -21.31 | -21.452 8 | -21.524 4 | -21.523 7 |
2.3.2.3 剖分面片角度变形分形
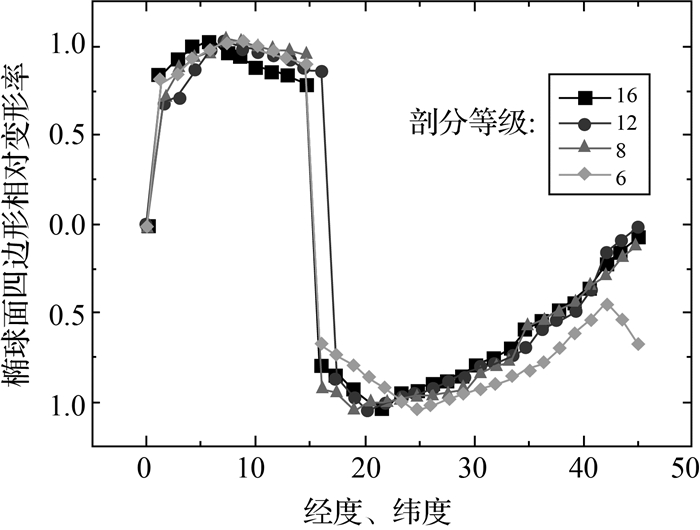
剖分面片内侧夹角,即为该四边形顶点所对应的球面角,计算方法见式 (4)。图 8和表 6是部分等级剖分面片的角度变形分析结果。
|
| 图 8 部分等级剖分面片角度变形分布图 (与90°对比) Fig. 8 The distribution curve about deformation angle of some subdivision cell (compare with 90°) |
| 参数 | 剖分等级 (将初始面的中线逐级二等分) | |||||||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| 标准边长/m | 2 502 003.6 | 1 251 001.8 | 625 500.9 | 312 750.4 | 156 375.2 | 78 187.6 | 39 093.8 | 19 546.9 | 9 773.4 | 4 886.7 | 2 443.3 | 1 221.7 | 610.8 | 305.4 | 152.7 | 76.3 |
| 正变形极值/% | 6.456 212 | 4.942 149 | 4.781 048 | 1.557 311 | 1.217 592 | 1.035 448 | 1.028 926 | 1.025 667 | 1.027 296 | 1.028 111 | 1.028 518 | 1.024 874 | 1.030 636 | 1.033 522 | 1.034 966 | 1.034 936 |
| 负变形极值/% | -2.423 564 | -2.422 564 | -2.040 443 | -1.222 417 | -1.035 448 | -1.035 448 | -1.035 448 | -1.028 926 | -1.028 926 | -1.028 926 | -1.028 926 | -1.024 394 | -1.030 396 | -1.033 402 | -1.034 906 | -1.034 906 |
根据上述分析可知,采用正六面体剖分地球的方式,虽然有可能到一定尺度后的剖分面片为正方形、且不同层级之间的剖分面片具有较好的递归关系,但存在如下问题:
(1) 虽然正六面体的6个面为正方形,但根据其等分递归生成的剖分面片并不都是正方形,只是特定的层级上的剖分面片接近正方形;
(2) 剖分面片与传统测绘中的经纬度并没有很明确的关系,尤其是两极剖分面片,如图 4(a)中的⑤、⑥对应的区域。因为在0级剖分面片⑤和⑥区域,在细分到1级剖分面片时,虽然可以与地球±45°和±135°经线重合,然而在继续按四等分剖分时,不再可能与经线、纬线重合。因此会增加与传统测绘数据之间转换的难度。
(3) 由于正六面体的8个顶点所在地球表面的纬度比较特殊,南北纬35.264 390°,则在与地图分幅的对应关系上,必然会割裂该区域的地图图幅。
因此,基于正六面体的格网剖分框架并不能很好地满足遥感数据统一组织框架设计原则。
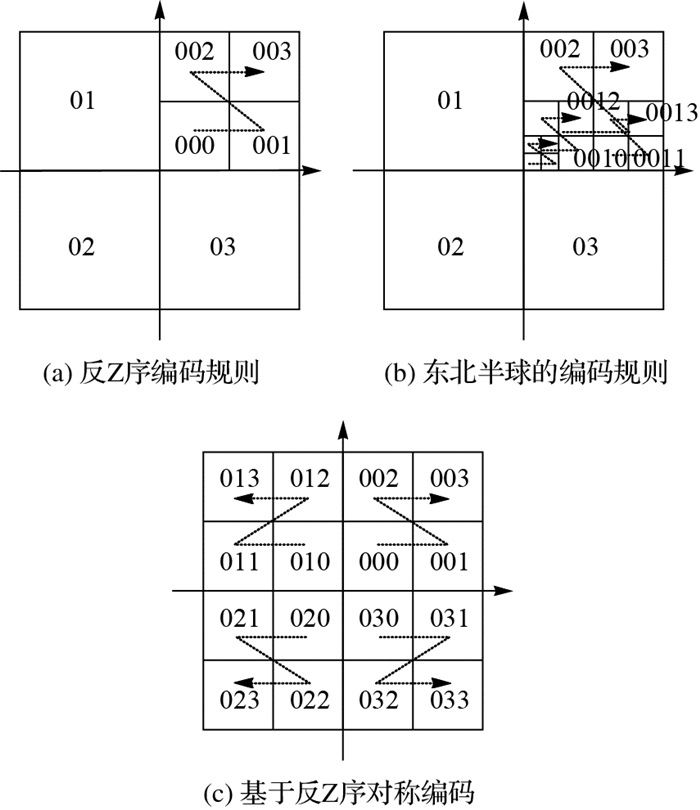
2.4 GeoSOT格网为了解决跨部门间、部门内各业务阶段遥感影像数据组织基准不统一的问题,以北京大学程承旗教授为首的研究团队提出了GeoSOT剖分网格[24-26]。GeoSOT网格首先将地球表面空间扩展为512°×512°,面片中心与赤道和本初子午线的交点重合。在此基础上递归四叉剖分至1°剖分网格。然后将1°网格扩展为64′,再对其递归四叉剖分至1′剖分网格。最后将1′剖分网格扩展至64″,再递归四叉剖分至 (1/2048)″(如图 9)。在此基础上利用64 bit的反Z序对称编码对每个剖分面片进行唯一标识[24](如图 10)。
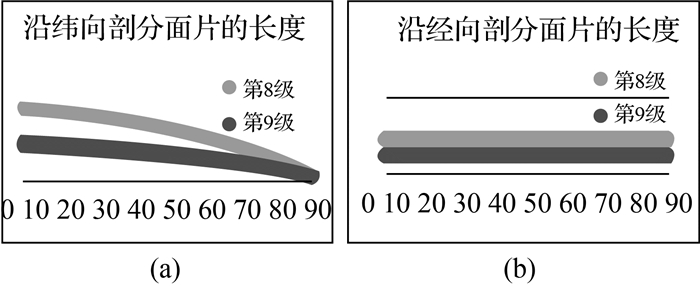
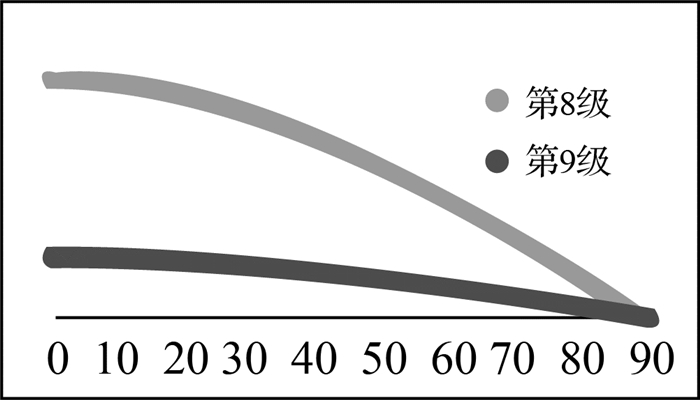
通过GeoSOT划分框架可知,GeoSOT网格面片不仅可实现全球覆盖而且可对每个剖分面片进行唯一标识。但由于GeoSOT网格是基于等经纬度进行划分,GeoSOT网格剖分面片没有角度变形,其边长长度沿经线方向没有变形 (图 11(b))、沿纬向方向随着纬度增加逐渐变小 (图 11(a)),剖分面片的面积也是随着纬度的增加逐渐变小 (图 12)。其中,剖分面片面积计算公式与式 (3) 相同。
|
| 图 11 GeoSOT网格剖分面片长度变形分布图 Fig. 11 The distribution curve about side of GeoSOT subdivision cells |
|
| 图 12 GeoSOT网格剖分面片面积变形分布图 Fig. 12 The distribution curve about area of GeoSOT subdivision cells |
且经过研究证明,GeoSOT网格与Google Earth、Worldwind、Bing Maps和天地图等格比较,GeoSOT网格与测绘数据地图图幅具有很好的同构性[24],更适合对传统空间数据和遥感数据进行组织管理。
综上,GeoSOT网格符合全球遥感数据统一组织框架设计的各项原则,可用于遥感影像的统一组织。
3 结论通过对等距、等纬差、正六面体等几种剖分格网方案分析,采用矩形或正方形理论上不能无缝覆盖地球表面或者其剖分面片编码与传统测绘数据之间进行快速地转换,而GeoSOT剖分网格能够很好地与我国测绘数据地图图幅框架同构,可作为全球遥感影像统一组织框架。
| [1] | 宋树华. 遥感数据标准分景框架及其应用模型研究[D]. 北京: 北京大学, 2011. SONG Shuhua. Research on A Universal Scene Model of Remote Sensing Data and Its Applications[D]. Beijing:Peking University 2011. |
| [2] | 赵学胜, 王磊, 王洪彬, 等. 全球离散格网的建模方法及基本问题[J]. 地理与地理信息科学, 2012, 28(1): 29–34. ZHAO Xuesheng, WANG Lei, WANG Hongbin, et al. Modeling Methods and Basic Problems of Discrete Global Grids[J]. Geography and Geo-Information Science, 2012, 28(1): 29–34. |
| [3] | BUCKMINSTER-FULLER R, APPLEWHITE E J. Synergetics[M]. New York: MacMillan, 1975: 876. |
| [4] | LUGO J A, CLARKE K C. Implementation of Triangulated Quadtree Sequencing for A Global Relief Data Structure[C]//Proceedings of Auto Carto 12, ACSM/ASPRS. Charlotte, NC:[s.n.], 1995:147-156. |
| [5] | OTOO E J, ZHU Hongwen. Indexing on Spherical Surfaces Using Semi-Quadcodes[C]//Proceedings of the 3rd International Symposium on Advances in Spatial Databases. Berlin Heidelberg:Springer, 1993:510-529. |
| [6] | SAHR K, WHITE D, KIMERLING A J. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121–134. DOI:10.1559/152304003100011090 |
| [7] | FEKETE G, TREINISH L A. Sphere Quadtrees:A New Data Structure to Support the Visualization of Spherically Distributed Data[C]//Proceedings of the SPIE 1259, Extracting Meaning from Complex Data:Processing, Display, Interaction. Santa Clara:SPIE, 1990, 1259:242. |
| [8] | DUTTON G. Encoding and Handling Geospatial Data with Hierarchical Triangular Meshes[C]//Proceeding of the 7th International Symposium on Spatial data Handling. Delft:[s.n.], 1997:505-518. |
| [9] | HEIKES R, RANDALL D A. Numerical Integration of the Shallow-Water Equations on A Twisted Icosahedral Grid. Part Ⅰ:Basic Design and Results of Tests[J]. Monthly Weather Review, 1995, 123(6): 1826–1880. |
| [10] | HEIKES R, RANDALL D A. Numerical Integration of the Shallow-Water Equations on A Twisted Icosahedral Grid. Part Ⅱ. A Detailed Description of the Grid and An Analysis of Numerical Accuracy[J]. Monthly Weather Review, 1995, 123(6): 1881–1887. DOI:10.1175/1520-0493(1995)123<1881:NIOTSW>2.0.CO;2 |
| [11] | WHITE D. Global Grids from Recursive Diamond Subdivisions of the Surface of An Octahedron or Icosahedron[J]. Environmental Monitoring and Assessment, 2000, 64(1): 93–103. DOI:10.1023/A:1006407023786 |
| [12] | CONWAY J H, SLOANE N J A. Sphere Packings, Lattices and Groups[M]. New York: Springer-Verlag, 1988: 679. |
| [13] | FRISCH U, HASSLACHER B, POMEAU Y. Lattice-Gas Automata for the Navier-Stokes equation[J]. Physical Review Letters, 1986, 56(14): 1505–1508. DOI:10.1103/PhysRevLett.56.1505 |
| [14] | ROTHMAN D H, ZALESKI S. Lattice-Gas Cellular Automata:Simple Models of Complex Hydrodynamics[M]. Cambridge: Cambridge University Press, 1997: 297. |
| [15] | WILLIAMSON D L. Integration of the Barotropic Vorticity Equation on A Spherical Geodesic Grid[J]. Tellus, 1968, 20(4): 642–653. DOI:10.3402/tellusa.v20i4.10044 |
| [16] | ZHANG Yongsheng, BEN Jin, TONG Xiaochong, et al. Geospatial Information Processing Method Based on Spherical Hexagon Grid System[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2006, 23(2): 110–114. |
| [17] | YANG Weiping, GOLD C. Managing Spatial Objects with the VMO-Tree[C]//Proceeding of the 7th International Symposium on Spatial Data Handling. Netherlands:[s.n.], 1996:15-31. |
| [18] | GOLD C, MOSTAFAVI M A. Towards the Global GIS[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2000, 55(3): 150–163. DOI:10.1016/S0924-2716(00)00016-2 |
| [19] | 赵学胜. 基于QTM的球面Voronoi数据模型[M]. 北京: 测绘出版社, 2004. ZHAO Xuesheng. Spherical Voronoi Data Model Based on QTM[M]. Beijing: Surveying and Mapping Press, 2004. |
| [20] | 赵学胜, 陈军, 王金庄. 基于O-QTM的球面Voronoi图的生成算法[J]. 测绘学报, 2002, 31(2): 157–163. ZHAO Xuesheng, CHEN Jun, WANG Jinzhuang. QTM-based Algorithm for the Generating of Voronoi Diagram for Spherical Objects[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 157–163. DOI:10.3321/j.issn:1001-1595.2002.02.013 |
| [21] | 魏子卿. 2000中国大地坐标系[J]. 大地测量与地球动力学, 2008, 28(6): 1–5. WEI Ziqing. China Geodetic Coordinate System 2000[J]. Journal of Geodesy and Geodynamics, 2008, 28(6): 1–5. |
| [22] | 魏子卿. 2000中国大地坐标系及其与WGS84的比较[J]. 大地测量与地球动力学, 2008, 28(5): 1–5. WEI Ziqing. China Geodetic Coordinate System 2000 and Its Comparison with WGS84[J]. Journal of Geodesy and Geodynamics, 2008, 28(5): 1–5. |
| [23] | 杨国清, 李晓. 子午线长度正反算公式及相应系数值[J]. 测绘通报, 2010(6): 36–37, 40. YANG Guoqing, LI Xiao. Formulas and Relevant Coefficients for Computing the Lenth of Meridian[J]. Bulletin of Surveying and Mapping, 2010(6): 36–37, 40. |
| [24] | 宋树华, 程承旗, 濮国梁, 等. 全球遥感数据剖分组织的GeoSOT网格应用[J]. 测绘学报, 2014, 43(8): 869–876. SONG Shuhua, CHENG Chengqi, PU Guoliang, et al. Global Remote Sensing Data Subdivision Organization Based on GeoSOT[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 869–876. |
| [25] | 李世忠, 宋树华, 程承旗, 等. 基于GeoSOT网格的"天绘一号"卫星影像数据组织[J]. 遥感学报, 2012, 16(S): 102–107. LI Shizhong, SONG Shuhua, CHENG Chengqi, et al. Mapping Satellite-1 remote sensing data organization based on GeoSOT[J]. Journal of Remote Sensing, 2012, 16(S): 102–107. |
| [26] | FANG Dong, CHENG Chengqi, GUO Shide. Design and research on GeoIP[C]//Proceedings of the 14th International Conference on Computer Supported Cooperative Work in Design. Shanghai:IEEE, 2010, 13-17. |