非线性是地球系统过程的重要特征[1]。地球内部热平衡、地震传播、火山喷发、海水运动等均为非线性的复杂过程。元胞自动机具有结构简单、易并行等特点,通过时空离散及简单的局部作用即可模拟出系列复杂的全局行为,被誉为宏观与微观的连接纽带[2],常作为非线性科学研究的一种工具,已广泛应用于大气、流体力学、地球物理等领域。大气领域中,文献[3]综合各种影响因素,利用随机性元胞自动机分别对区域的大气碳循环、大气深对流过程进行了模拟。文献[4]利用概率型元胞自动机对美国Mt.St.Helens火山的火山灰传输过程进行了模拟研究,其结果与现场数据具有很好的一致性。文献[5]利用三维元胞自动机对区域大气污染物的扩散问题进行了模拟研究。文献[6]利用二维元胞自动机对地表的热量传输进行了模拟,该方法的精度可与传统反演方法相媲美。固体地球及流体力学领域中,文献[7]利用二维元胞自动机对希腊Xanthi地区的地震活动进行了模拟。文献[8]利用二维元胞自动机对地震弹性动力波进行了模拟,所得到的压力、剪切力及表面波等结果与有限差分的模拟结果非常相似。文献[9]利用元胞自动机对2004年欧洲埃特纳火山岩浆流动进行了模拟。在地理领域中,元胞自动机被广泛地应用于城市发展与土地模拟与预测[10-11]、交通流模拟[12]等方面,有关研究不胜枚举。
现有文献主要从元胞自动机的领域应用开展研究,较少从元胞自动机的空间演化形式开展深层思考。众所周知,空间特征是地球系统过程的最重要特征。地球系统过程的产生、发展、消亡均离不开地球系统空间。不同于欧氏空间,地球系统空间属于球体流形空间,存在一些天然的约束 (如重力)。这些天然约束使得地球系统空间上的现象及过程有着某种特殊的空间演化趋势。然而,现有地学领域的元胞自动机仍然基于欧氏空间,忽略了地球系统空间的天然约束,使得元胞自动机模拟计算时未考虑元胞状态的传递方向与真实运动的趋势方向的一致性问题,带来了一定程度的结果扭曲。为此,本文立足地球系统的天然约束拟提出一种面向地球系统过程的元胞自动机;同时,以满足该约束的全球三维格网—SDOG-ESSG[13]为元胞空间设计地球系统元胞自动机的框架,然后以地壳的热传导为例开展初步的模拟试验,并在一定区域尺度下与数值模拟软件进行比较,以验证地球系统元胞自动机的可行性。
1 地球系统元胞自动机 1.1 地球系统元胞自动机的定义地球系统是一个在重力约束下的作用空间。在重力约束下,地球上各物质按其密度差异井然有序地沿垂直分布与分层,大到地球系统的圈层 (内核、外核、下地幔、上地幔、地壳、大气圈、电离层),小到圈层的各组成部分均满足这一规律,如,对流层分为行星边界层和自由大气层[14],海水分为表层、次表层、深层[15]。同样,在重力约束下,层与层之间的物质和能量运动或交换被限制在沿垂直方向 (重力方向) 进行,如地幔柱的对流,大气垂直运动等;而层内的物质和能量运动或交换则被限制在沿垂直方向和水平方向 (即球面方向) 同时进行,如海水的水平运动和垂直对流、板块的水平运动和抬升、大气的水平输送和垂直对流等。此外,受太阳辐射的影响,地球气候、水文、生物和土壤等自然要素大致地按纬度变化方向逐渐更替的分布;受地球自转的作用,重力加速度、向心力、线速度沿着纬度的变化而发生变化,且地球上运动的物体不可避免地会受到科氏力 (地转偏向力) 的影响,而这种科氏力使得地球上的现象表现为严重的经纬偏向趋势,如在北半球沿经线方向流动的河水,对右岸的冲刷大于左岸,而北向南运动的季风始终向西方向偏移[15]。即在重力、太阳辐射、地球自转等影响下,地球上的物质和能量呈现沿/背重力方向及沿经纬方向运动及交换的约束与趋势,这种约束与趋势对于地球上的各种现象及过程是隐含的、内在的、不可避免的。为此,在元胞自动机模拟时需顾及这种隐含的内在趋势。
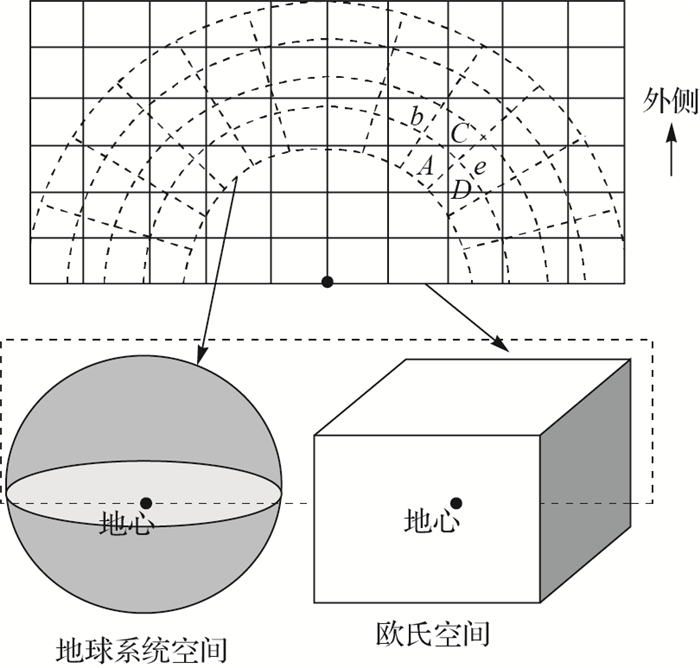
元胞自动机的核心是通过离散化手段将模拟对象离散化为独立的元胞个体,并借助一定的演化规则实现元胞与元胞之间的状态传递。现有元胞自动机均假设元胞与元胞间的状态传递被约束在欧氏空间的3个轴方向。由上可知,在重力等因素约束下的地球系统空间并非属于欧氏空间,而属于球体流形空间,如图 1所示。图 1的虚线部分为地球系统空间格网的纵剖面,实线部分为欧氏空间格网的纵剖面。可以看出,格网A在地球系统空间下的外侧格网是C,东侧 (或右侧) 格网是D,而在欧氏空间下则分别变为b和e。空间约束的不同导致了不同的传递关系,而状态传递是元胞自动机进行演化的核心。为此,以欧氏空间为约束的元胞自动机方法无法有效地模拟沿/背重力方向及沿经纬方向的运动趋势,将导致扭曲的结果。由此,笔者提出了地球系统元胞自动机的概念,它是一种在地球重力等天然约束下,沿物质与能量的运动趋势方向进行状态传递的一种元胞自动机。
|
| 图 1 地球系统空间与欧氏空间 Fig. 1 Earth system space and Euclidean space |
1.2 基于SDOG-ESSG的地球系统元胞自动机框架
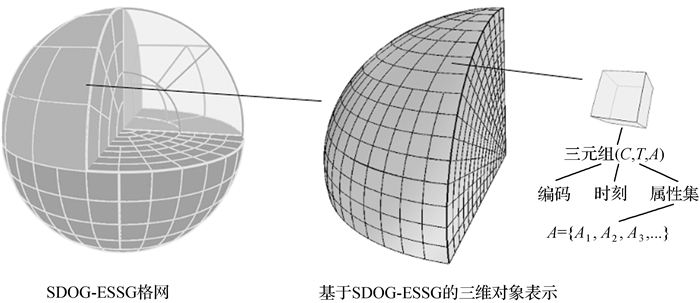
SDOG-ESSG[13]是构建在球体退化八叉树格网 (spheroid degenerated octree grid, SDOG) 之上且满足地球重力等天然约束的一种地球系统空间格网 (图 2(a)),具有圈层式结构、地理一致性、层次化剖分、适应性分辨率等特点,已用于全球岩石圈三维建模与可视化[16-17]及全球大气温度场可视[18]等方面,可用于地球系统元胞自动机的元胞空间构建。SDOG-ESSG的每个格网可视为地球系统元胞自动机的每个元胞,格网的属性可视为元胞的状态,而邻近的格网可视为元胞的邻居。借助三元组 (C,T,A) 表达模型[16](图 2(b)) 可实现任一元胞任一演化时刻的元胞状态的表达。三元组表达模型中,C用来表示元胞的标识码或线性坐标; T用来表示元胞演化的时间信息; A用来表示元胞对应的状态属性。文献[13, 16]的SDOG-ESSG三维建模方法可用于初始元胞状态的构建。在构建初始元胞空间之后,还需准确获取邻居元胞状态才能进行下一时刻中心元胞的状态计算。
|
| 图 2 SDOG-ESSG及元胞状态表达 Fig. 2 SDOG-ESSG and representation on cell's state |
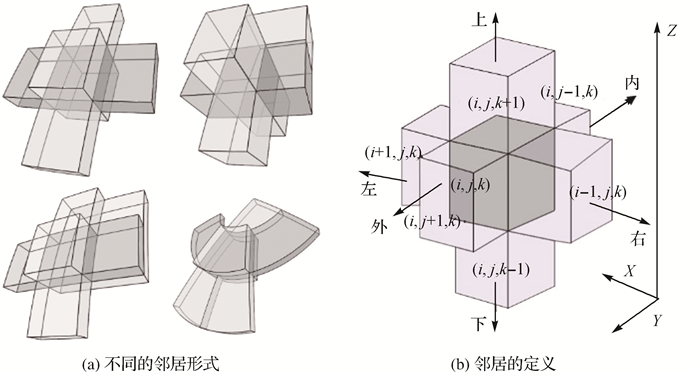
传统元胞自动机邻居模型主要有Von Neumann型、Moore型、扩展的Moore型和Margolus型等。受球体空间的制约,球体空间格网不能像欧氏空间格网一样具有严格的规整性及严密的一致邻近性。SDOG-ESSG是一种球体空间三维格网,受其特定剖分方式的影响存在着不定的数量邻近格网,不能直接套用上述邻居模型,需进行适当的改进。本文以Von Neumann型邻居模型为基础,为中心元胞定义了6~10个不等数量的面邻近格网作为邻居元胞,邻居的数量取决于当前元胞所处的位置[19]。对于北半球而言,中心元胞的东、西、北邻近及内邻近均只有1个邻居,而南邻近及外邻近由于退化的原因则分别可能存在2个或4个情况邻居,但对于绝大多数中心元胞而言,其邻近数量为6个 (如图 3(a)左上角子图)。对于某一个方向上存在多个邻居情况 (如图 3(a)右上角的北邻近方向),模拟计算时我们可取两者的平均状态作为两个元胞的共同状态。
|
| 图 3 基于SDOG-ESSG的地球系统元胞自动机邻居模型 Fig. 3 Neighbor model of earth system cellular automata based on SDOG-ESSG |
由三元组表达特点可知,邻居元胞状态的获取需先获得邻居元胞的标识码,然后再根据该标识码获取相应的元胞状态。文献[19]给出了由中心格网码计算面邻近格网码的算法。根据该算法,可快速获取任一中心元胞所有邻居元胞的标志码。
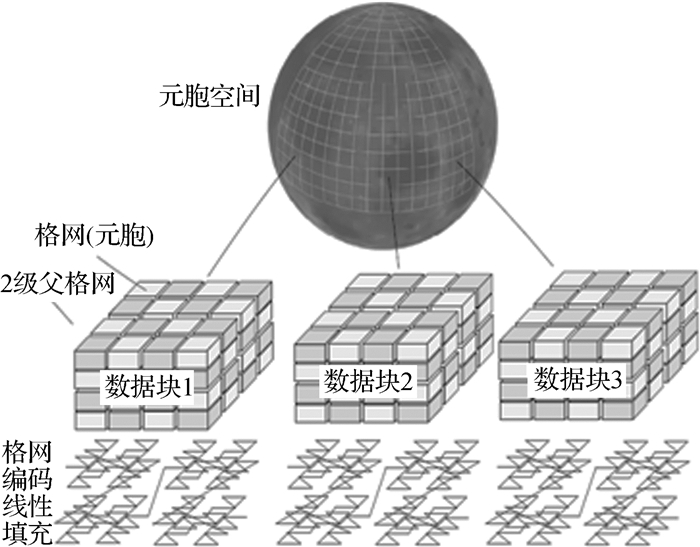
三元组模型本质上为一种关系模型,可通过查找算法获取指定元胞标志码的状态值。然而,基于SDOG-ESSG的地球系统元胞自动机为三维元胞自动机,其元胞数量比二维元胞自动机多一个数量级,通常难以直接全部载入内存,需借助一定的外存策略。由SDOG-ESSG的层次剖分特性可知,邻近格网以较大概率落在中心格网的n级父格网中 (图 4)。为减少内存负担及提高数据的存取效率,可采取分块存储、按需调度的策略,即先将元胞空间按一定层次的SDOG-ESSG格网进行分块,然后根据中心元胞的位置调入相应的数据块至内存。对于每一数据块,通常按照元胞标志码的升序/降序进行排列 (文献[13, 16]的建模方法可保证所构建的初始元胞按标志码升序进行排列)。对于任意给定中心元胞,首先将该元胞所在的块调入内存,然后根据上文方法计算邻居元胞的标志码,最后根据该标志码从内存中的数据块读取相应元胞的状态值。由于元胞标志码唯一且按一定顺序进行排列,故可在数据块中通过随机访问的方式快速读取指定元胞的状态值。用于分块的格网称为索引格网。索引格网的层次一般为元胞所在格网的n级父格网的层次。为保证数据块被调度的次数最少,中心元胞的遍历应按照SDOG-ESSG格网线性编码顺序进行遍历。
|
| 图 4 分块存储策略 Fig. 4 Strategy of storage by block |
一旦中心元胞及邻居元胞的状态已知,则下一时刻中心元胞状态可根据演化规则进行计算。不同的应用对应不同的演化规则。演化规则通常应遵循地球系统过程的物理规律。下文将根据热力学规律设计地壳热传导元胞自动机的演化规则。
2 地壳热传导元胞自动机演化规则的设计及模拟试验 2.1 地壳热传导元胞自动机演化规则的设计热量传输有热传导、热辐射和热对流3种方式。热传导通常发生在有温差的固体中;热对流通常发生在有流变物质且有大量物质发生位移的地方;热辐射一般发生在温度较高的区域,不需要借助任何介质,直接以电磁波的形式向外直接发射传热。地球内部分为地壳、上下地幔、内外地核等几个圈层。地壳绝大部分由固体岩石构成,温度不是很高,地壳的热状况几乎为晶格传导所支配,其热量运输以热传导为主[20]。为此,本文将地壳内部的热量传输简化为只有热传导这一种热量传输过程。
傅里叶定律为热传导的基本定律。由傅里叶定律及能量守恒定律可推导出三维非稳态的热传导微分方程[21]
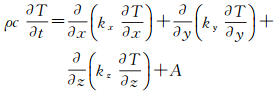 (1)
(1)
式中,T为温度 (℃);t为时间 (s);kx、ky、kz分别为x、y、z方向上的地壳物质的热导率 (W·m-1·K-1);ρ为地壳物质的密度 (kg·m-3);c为地壳物质的比热容 (J·kg-1K-1);A为地壳物质的生热率 (W·m-3)。
通过二阶中心差分法对式 (1) 进行时空离散化
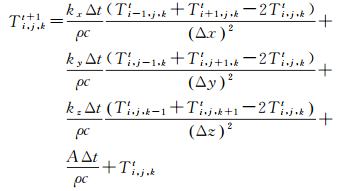 (2)
(2)
式中,Ti, j, kt+1为中心元胞t+1时刻的温度;Δx、Δy、Δz表示元胞的大小; Δt为单位时间 (s),i、j、k为3个轴方向序号 (图 3(b)); A、k、ρ、c的含义同式 (1)。
式 (2) 为地壳非边界元胞的热传导的规则,即下一时刻中心元胞的温度值取决于当前时刻中心元胞、邻居元胞间的温度差及元胞的密度、比热容、热传导率、生热率等物理量。
地壳的下边界为地幔,而地幔的温度一般认为是1300°。故可在地壳下边界增加一层元胞,并将该层元胞温度设为1300°恒温。地壳的上边界为大气层,地壳与大气层时刻存在着热量交换。地表热流 (q) 反映单位时间单位面积内由地表所流出的热量,数值上等于地表温度梯度与岩石热导率之积[20]。故对于上边界元胞,其下一时刻中心元胞的温度值可借助q来计算
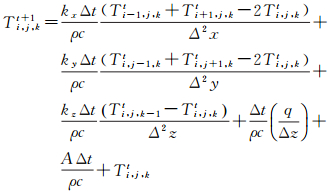 (3)
(3)
式 (3) 反映了地壳上边界元胞的温度演化规则。
2.2 地壳热传导元胞自动机模拟试验由2.1可知,地壳热传导模拟试验需要地壳物质的密度、热导率、比热容、生热率、初始温度场、地表热流等数据。表 1给出了模拟所需的数据来源。
| 数据 | 数据来源 |
| 地壳的构成 | Crust1.0模型: http://igppweb.ucsd.edu/~gabi/crust1.html |
| 地表温度 | 美国国家环境预报中心:http://www.esrl.noaa.gov |
| 地表热流 | TC1模型:http://www.lithosphere.info./downloads.html |
| 密度、比热容、热导率、生热率 | Wang[22]、Artemieva[23] |
| 注:地表温度用于反演初始地壳温度场,具体方法见文献[24]。地壳不同物质的密度、比热容、热导率、生热率较难获得,本文试验采用了平均值。 | |
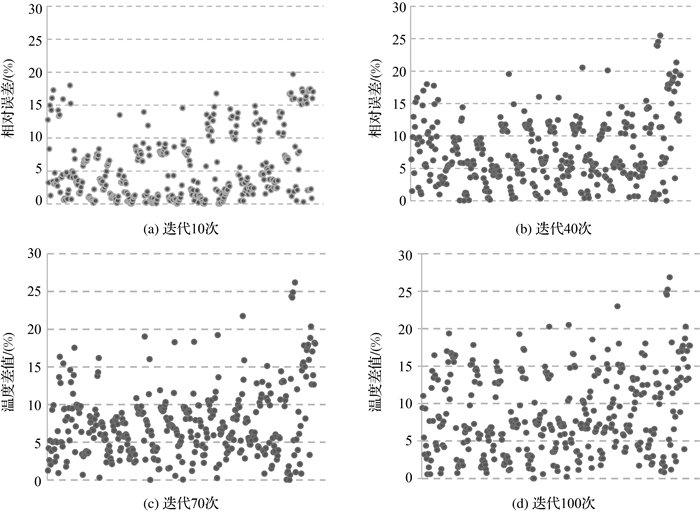
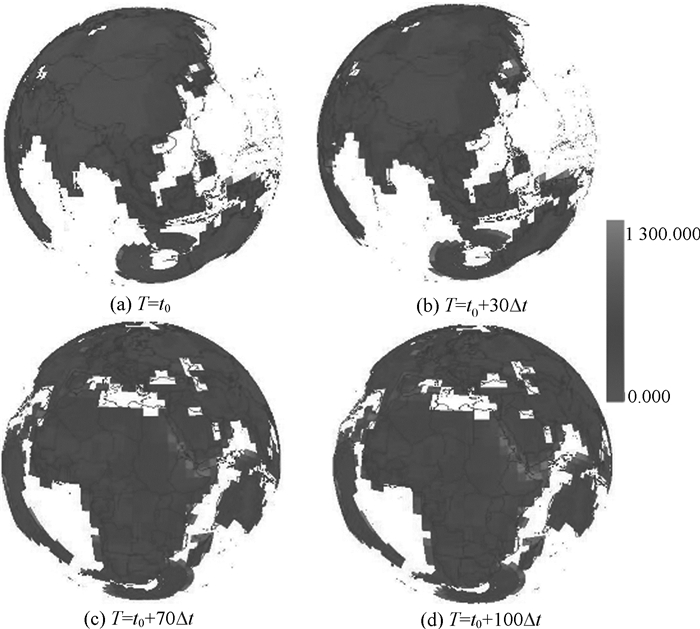
一方面,大尺度的真实试验确实难以开展;另一方面,地球内部物理参量 (如热导率、密度、生热率) 可获取的数据粒度较粗,尚不足以进行真实试验验证。为此,为验证本方法的可行性,本文以Comsol Multiphysics数值模拟软件的地壳热传导模拟结果为参考真值进行比对。由于数值模拟软件以欧氏空间为基础,不合适作为全球尺度的数值模拟。为此,本文选取了56.953 1°E—104.766°E、28.828 1°N—42.890 6°N这一局部区域为试验范围,并将元胞自动机的元胞与数值模拟软件的格网单元设置为一致大小 (157 km×157 km×6.25 km),并设置时间间隔为十万年 (3.153 6×1012 s)。图 5给出了相对于数值模拟方法本方法在不同迭代次数下地壳某一深度处模拟温度的相对误差散点图。图中可以看出,所有相对误差都控制在27%以内,且相对误差在0%~20%区间的元胞数量占了90%以上。可见,本文方法具有一定程度的可行性。此外,图 6给出了全球范围不同迭代次数的元胞自动机的温度模拟结果。可以看出,随着迭代的推进,温度呈逐渐增大趋势,在下边界持续加热的状态下,从径向方向的下边界传导过来的热量,不断地传递给地壳中间的元胞,使其温度值逐渐升高。
|
| 图 5 地壳6.25 km深处模拟温度的相对误差散点图 Fig. 5 Scatter of relative error on the simulated temperature at the depth of 6.25 km |
|
| 图 6 地壳12.5 km深处地球系统元胞自动机温度模拟结果 Fig. 6 Result of simulated temperature at the depth of 12.5 km by earth system cellular automata |
3 结论
在地球重力等约束下,地球系统过程的物质与能量有着沿/背重力方向及经纬方向的趋势。传统元胞自动机在地球系统过程模拟时存在元胞状态传递方向的扭曲。为此,本文提出了面向地球系统过程模拟的地球系统元胞自动机,并以SDOG-ESSG为元胞空间提出并设计了地球系统元胞自动机的框架,包括元胞的表达与构建、元胞邻居模型等方面内容。为验证地球系统元胞自动机的可行性,本文以地壳热传导为例,结合热力学规律设计了元胞的演化规则,并开展了初步模拟试验及与现有通用方法 (数值模拟) 的比较试验。试验表明:相对于数值模拟,基于地球系统元胞自动机经多次迭代后精度可达到27%。虽然这一精度不足以说明本方法的正确性及可靠性,但鉴于目前的研究属于初探,应用模型仍有较多的改善空间,因此,基于地球系统元胞自动机的模拟方法仍具有一定的可行性,可作为地球系统过程模拟的一种新思路。
| [1] | 陈述彭. 地球系统科学[M]. 合肥: 中国科技大学出版社, 1998. CHEN Shupeng. Earth System Science[M]. Hefei: Press of University of Science and Technology of China, 1998. |
| [2] | HOEKSTRA A G, KROC J, SLOOT P M A. Simulating Complex Systems by Cellular Automata[M]. Berlin Heidelberg: Springer-Verlag, 2010. |
| [3] | BENGTSSON L, STEINHEIMER M, BECHTOLD P, et al. A Stochastic Parametrization for Deep Convection Using Cellular Automata[J]. Quarterly Journal of the Royal Meteorological Society, 2013, 139(675): 1533–1543. DOI:10.1002/qj.v139.675 |
| [4] | TSUNEMATSU K, FALCONE J L, BONADONNA C, et al. Applying a Cellular Automata Method for the Study of Transport and Deposition of Volcanic Particles[M]//UMEO H, MORISHITA S, NISHINARI K, et al. Cellular Automata. Berlin Heidelberg:Springer, 2008:393-400. |
| [5] | MARÍN M, RAUCH V, ROJAS-MOLINA A, et al. Cellular Automata Simulation of Dispersion of Pollutants[J]. Computational Materials Science, 2000, 18(2): 132–140. DOI:10.1016/S0927-0256(00)00097-5 |
| [6] | PERIDIER V J. Estimating Transient Surface Heating Using A Cellular Automaton Energy-transport Model[J]. Complex Systems, 2005, 16(2): 139–153. |
| [7] | GEORGOUDAS I G, SIRAKOULIS G C, SCORDILIS E M, et al. A Cellular Automaton Simulation Tool for Modelling Seismicity in the Region of Xanthi[J]. Environmental Modelling & Software, 2007, 22(10): 1455–1464. |
| [8] | LEAMY M J. Application of Cellular Automata Modeling to Seismic Elastodynamics[J]. International Journal of Solids and Structures, 2008, 45(17): 4835–4849. DOI:10.1016/j.ijsolstr.2008.04.021 |
| [9] | DEL NEGRO C, FORTUNA L, HERAULT A, et al. Simulations of the 2004 Lava Flow at Etna Volcano Using the Magflow Cellular Automata Model[J]. Bulletin of Volcanology, 2008, 70(7): 805–812. DOI:10.1007/s00445-007-0168-8 |
| [10] | LIU Xiaoping, LI Xia, LIU Lin, et al. A Bottom-Up Approach to Discover Transition Rules of Cellular Automata Using Ant Intelligence[J]. International Journal of Geographical Information Science, 2008, 22(11-12): 1247–1269. DOI:10.1080/13658810701757510 |
| [11] | ABURAS M M, HO Y M, RAMLI M F, et al. The Simulation and Prediction of Spatio-Temporal Urban Growth Trends Using Cellular Automata Models:A Review[J]. International Journal of Applied Earth Observation and Geoinformation, 2016, 52: 380–389. DOI:10.1016/j.jag.2016.07.007 |
| [12] | LI Qilang, WONG S C, MI Jie. A Cellular Automata Traffic Flow Model Considering the Heterogeneity of Acceleration and Delay Probability[J]. Physica A:Statistical Mechanics and its Applications, 2016, 456: 128–134. DOI:10.1016/j.physa.2016.03.026 |
| [13] | 余接情. 基于SDOG的地球系统空间格网及其三维建模应用[D]. 北京: 北京师范大学, 2012. YU Jieqing. SDOG-Based Earth System Spatial Grid and Its Application on 3D Modeling[D]. Beijing:Beijing Normal University, 2012. |
| [14] | 何金海, 郭品文, 银燕, 等. 大气科学概论[M]. 北京: 气象出版社, 2012. HE Jinhai, GUO Pinwen, YIN Yan, et al. Introduction to Atmospheric Science[M]. Beijing: China Meteorological Press, 2012. |
| [15] | 伍光和, 蔡运龙. 综合自然地理学[M]. 2版. 北京: 高等教育出版社, 2004. WU Guanghe, CAI Yunlong. Comprehensive Physical Geography[M]. 2nd ed. Beijing: Higher Education Press, 2004. |
| [16] | 余接情, 吴立新, 訾国杰, 等. 基于SDOG的岩石圈多尺度三维建模与可视化方法[J]. 中国科学:地球科学, 2012, 55(6): 1012–1020. YU Jieqing, WU Lixin, ZI Guojie, et al. SDOG-Based Multi-Scale 3D Modeling and Visualization on Global Lithosphere[J]. Science China Earth Sciences, 2012, 55(6): 1012–1020. DOI:10.1007/s11430-012-4387-2 |
| [17] | YU Jieqing, WU Lixin, LI Zhifeng, et al. An SDOG-Based Intrinsic Method for Three-Dimensional Modelling of Large-Scale Spatial Objects[J]. Annals of GIS, 2012, 18(4): 267–278. DOI:10.1080/19475683.2012.727865 |
| [18] | 李志锋, 吴立新, 薄海光, 等. 基于VisIt的全球科学数据并行可视化——以大气温度场为例[J]. 地理与地理信息科学, 2012, 28(1): 24–28. LI Zhifeng, WU Lixin, BO Haiguang, et al. VisIt-Based Parallel Visualization of Global Scientific Data:Atmosphere Temperature Field Being A Case[J]. Geography and Geo-Information Science, 2012, 28(1): 24–28. |
| [19] | 余接情, 吴立新, 贾永基, 等. SDOG-ESSG的几何分布规律及面邻近计算[J]. 中国矿业大学学报, 2015, 44(2): 359–366. YU Jieqing, WU Lixin, JIA Yongji, et al. The Face-Neighbor Calculation and Geometric Distribution Rules of SDOG-ESSG[J]. Journal of China University of Mining & Technology, 2015, 44(2): 359–366. |
| [20] | 滕吉文. 固体地球物理学概论[M]. 北京: 地震出版社, 2003. TENG Jiwen. Introduction to Solid Geophysics[M]. Beijing: Seismological Press, 2003. |
| [21] | 胡汉平, 程文龙. 热物理学概论[M]. 2版. 合肥: 中国科学技术大学出版社, 2009. HU Hanping, CHENG Wenlong. Introduction to Thermophysics[M]. 2nd ed. Hefei: Press of University of Science and Technology of China, 2009. |
| [22] | WANG Yang. Heat Flow Pattern and Lateral Variations of Lithosphere Strength in China Mainland:Constraints on Active Deformation[J]. Physics of the Earth and Planetary Interiors, 2001, 126(3-4): 121–146. DOI:10.1016/S0031-9201(01)00251-5 |
| [23] | ARTEMIEVA I M, MOONEY W D. Thermal Thickness and Evolution of Precambrian Lithosphere:A Global Study[J]. Journal of Geophysical Research:Atmospheres, 2001, 106(B8): 16387–16414. DOI:10.1029/2000JB900439 |
| [24] | 史謌. 地球物理学基础[M]. 北京: 北京大学出版社, 2002. SHI Ge. Basic of Geophysics[M]. Beijing: Peking University Press, 2002. |


