2. 中国矿业大学 (北京) 地球科学与测绘工程学院, 北京 100083;
3. 扬州环境资源职业技术学院, 江苏 扬州 225127
2. College of Geoscience and Surveying Engineering, China University of Mining and Technology (Beijing), Beijing 100083, China;
3. Yangzhou Vocational College of Environment and Resources, Yangzhou 225127, China
随着数字地球以及智慧地球的发展,对全球范围海量数据组织管理的效率、检索速度、表达准确性都提出了越来越高的要求。地球椭球面属于非欧氏空间,而现有基于地图投影的方法,是将球面投影到平面的模拟方法,在涉及全球大尺度空间时,在长度、面积等基础几何量的量算上,会引起明显的偏差[1],也易出现数据重叠、断裂及空间关系的不一致性等问题[2-3],而这种度量下的空间分析也因此缺乏足够的可信度[4]。另外,传统以地图投影为基础的数据结构和表达,在本质上是单一尺度的,在对多尺度的数据进行集成和管理时有一定局限性[5]。全球离散格网 (discrete global grid, DGG) 模型是一种基于球面的、通过无限细分的方式来拟合逼近地球真实表面形态的优良模型,其层次性和全球连续性特征,不仅克服了度量空间上的各向异性问题,而且网格多分辨率的特性还很好地实现不同精度下、同一空间位置的合理表达和分析问题[6-7]。全球离散格网在为数字地球提供地理参考、检索、地理空间数据集的分散需求等方面具有无可比拟的优势。自20世纪80年代以来,人们对全球离散网格系统进行了大量的研究[8-30],按剖分方法不同可以将传统的全球离散格网系统分成3种类型:基于经纬线的球面剖分格网、基于自适应格网的球面剖分格网和基于球内接正多面体的球面剖分格网[31]。其中,球面退化四叉树经纬线格网 (degenerate quadtree latitude/longitude grid,DQLLG) 就是基于球面内接正八面体剖分方法和经纬线剖分方法融合衍生出来的一种新的全球离散格网系统,文献[32]分析了该格网的特点及单元变形情况:球面DQLLG形状简单、大小近似相等,并具有层次嵌套性,便于空间数据的多层次多分辨率表达。然而这种剖分是在正球面上进行的,不是对更接近于地球的椭球面的剖分,没有顾及到地球的真实形状,这样在表达全球尺度数据时,数据质量特别是位置、尺度等的准确性会有一些偏差。WGS-84椭球体是目前全球使用最广泛的地球参考椭球体,为此,作者将正球面DQLLG改进并发展到椭球面上,实现对WGS-84椭球面的层次剖分,分析了格网的特点,并对剖分后不同层次格网单元的面积、边长进行了计算,还就格网单元的面积、边长的变化情况与基于正球面的剖分进行了对比,旨在为后续基于椭球面DQLLG的几何变形分布规律、收敛性和精度分析以及构建全球地理信息系统的适用性和商业实用性研究提供基础。
1 WGS-84椭球面DQLLG剖分 1.1 剖分原理 1.1.1 剖分基础利用WGS-84椭球面上的0°、90°、180°和270°子午线和赤道将椭球表面分割成8个区域,从0°子午线开始自西向东、先北半球再南半球把这8个区域分别编码为0~7,如图 1所示。这8个区域是8个全等的椭球面等腰三角形,均匀而规则地覆盖在椭球面上,这8个全等的椭球面等腰三角形就是整个椭球面的一个初始剖分,也是基于WGS-84椭球面的DQLLG剖分基础,每一个这样的三角形就称为一个初始剖分三角形。由于他们的性质都是相同的,本文仅研究其中一个初始剖分三角形的剖分,然后推广到其他7个三角形,进而推广到全球。为表述方便清楚,对这些椭球面等腰三角形的边作如下约定:赤道为底边,子午线为腰。

|
| 图 1 椭球面的初始剖分和编码 Fig. 1 Original triangulars and codes |
1.1.2 多层次递归剖分方法
对WGS-84椭球面初始剖分后,就可以应用退化四叉树平分经纬度方法对WGS-84椭球面进行多层次递归剖分了。对于任意一个初始剖分三角形,首先将其3个顶点的经纬度进行两两平分,得到3个新点p1、p2、p3(p1、p2、p3 3个点都位于椭球面上,p1、p2分别在两腰上,p3在底边上),用平行圈弧段连接p1、p2两点;再取平行圈弧段p1、p2的中点p4,用子午线弧段连接p3、p4两点;这样该初始剖分三角形就被分割为3部分:一个位于顶部的新的椭球面等腰子三角形和两个位于底部的椭球面等腰梯形,实现对地球椭球面的一次细分,即第1层次剖分 (如图 2(a)所示)。然后对第1层次剖分产生的椭球面等腰子三角形,按照第1层次剖分方法进行细分;对任意一个椭球面等腰梯形,先将该椭球面等腰梯形4个顶点的经纬度进行两两平分,得到4个新点,再将两对边上的新点用子午线弧段或平行圈弧段连接,就把该椭球面梯形分成了4个新的更小的椭球面等腰梯形;这时就把原初始剖分三角形分割成了11部分:1个椭球面等腰三角形和10个椭球面等腰梯形,实现对地球椭球面的进一步细分,即完成对初始剖分三角形的第2层次剖分 (如图 2(b)所示)。第3层次、第4层次等按照上述方法依次递归剖分,直到满足所需精度的第n层 (n=1, 2, …)。多层次递归剖分过程中椭球面梯形都是按完全四叉树进行细分,椭球面三角形都是按退化四叉树进行细分,每个八分体可用一个退化四叉树表达,整个剖分过程的树形结构如图 2(d)表示。
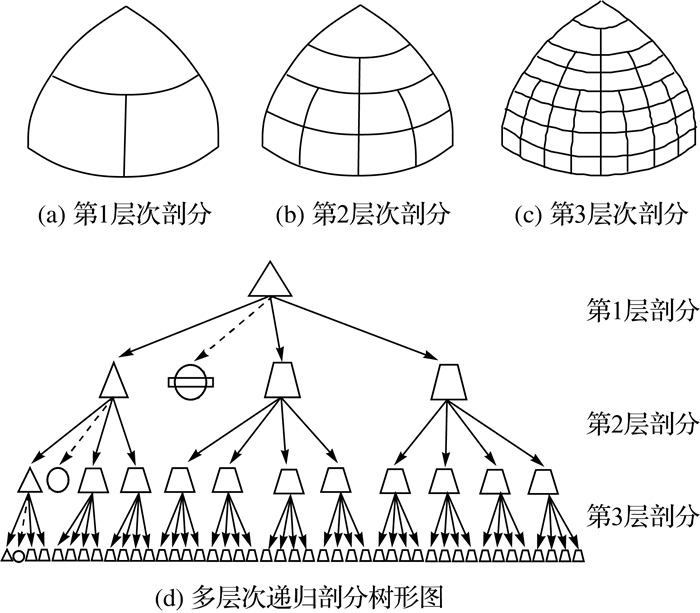
|
| 图 2 基于DQLLG的椭球面初始剖分三角形不同层次剖分 Fig. 2 Hierarchical subdivisions of an original ellipsoidal facet triangular at different level based on DQLLG |
1.1.3 剖分特点
通过对上述剖分过程分析可以得出椭球面DQLLG具有以下特点:
(1) 有效解决了传统经纬度格网两极数据冗余的问题。由赤道到两极,格网经度差逐渐增大,格网数逐渐减少,到极点处只有4个格网。同一剖分层次,DQLLG单元数量比传统经纬度格网单元数量明显减少。剖分层次为n时,每一个初始剖分三角形内,DQLLG单元数量为 (2×22n+1)/3,传统经纬度剖分单元数量为22n,两者的比值约为2/3。
(2) 多层次嵌套性。经纬度平分保证了相邻层次格网节点具有简单明确的层次、位置对应关系,椭球面DQLLG剖分每一层次格网都是上一层次格网的细分,相邻四个格网单元 (仅两极是3个) 的组合就是上一层次格网单元,相邻剖分层次格网单元的经纬度间隔相差一倍,且下一层次格网单元保留其上一层次格网单元的边界线,不同层次格网单元是简单的等价或包含关系,并且可以无限细分,在全球范围内是连续的、无缝的、稳定的和近似均匀的椭球面格网层次结构,层次索引、多分辨率的数据组织及压缩存储等操作比较方便。
(3) 方向一致性。基于DQLLG的WGS-84椭球面剖分方法实质是经纬度平均分割法,是把传统的球面四叉树剖分法如QTM (quaternary triangular mesh) 得到的中心那个子三角形退化成一条子午线弧段,形成两个椭球面等腰梯形后得到的 (如图 3所示)。两极的8个椭球面等腰三角形的顶点都在极点;所有椭球面等腰梯形都朝极点收敛,克服了QTM形成的三角形格网方向不确定性的缺陷[33]。
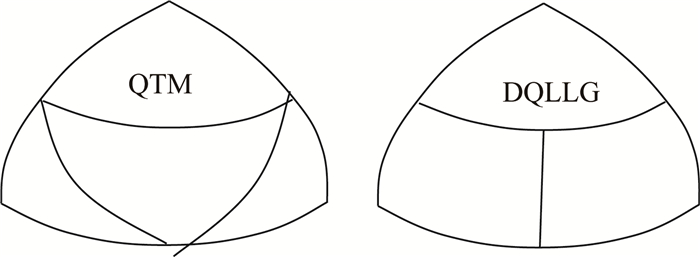
|
| 图 3 QTM与DQLLG三角形细分过程比较 Fig. 3 Triangle subdivision process comparison between QTM and DQLLG |
(4) 平移重合且轴对称。任意一个格网单元或多个相邻格网单元的组合,沿平行圈左右平移任意整数倍单元格距离或单元格组合距离,都会与其他单元格或单元格组合重合;沿子午线上下移动,都会有相应的单元格或组合与其依经纬度间隔重合;以任何格网单元的腰所在的子午线为轴,轴两侧的格网都是关于该轴对称的,并且南北半球的格网以赤道为轴对称。
(5) 格网结构简单、几何形状相同。除两极8个剖分单元为全等的椭球面三角形外,其余格网全部是椭球面等腰梯形,几何形状都相同,且所有梯形单元以经纬度差全等或相差整数倍的经度差,邻近搜索和查询方便。
(6) 四边形经纬度格网更适合一般常用数据的表达。椭球面DQLLG本质是经纬度格网,经纬度格网已被人们广泛采用,它非常符合人们的习惯,已经根植在笔者关于地球的思维中,具有永远不可替代的地位[34],许多有关全球范围的空间数据格式也是以经纬度格网表达的。另外,不管是各种电子显示设备、纸张、地图还是栅格影像数据,绝大多数的地理信息表达、传播媒介都是四边形的,与三角形、六边形等相比,椭球面DQLLG的四边形格网更适合于这些地理的数据制图和显示设备的表达。
1.2 格网单元经纬度计算椭球面DQLLG格网单元沿纬度逐行的和沿经度逐列分布的规律性是非常明显的,因此可以定义格网的行列坐标系,通过行列号来标识格网任一格网单元的位置,进而确定其经纬度坐标。
1.2.1 格网行列定义规则对任意初始剖分椭球面三角形,以极点为原点O;以西侧子午圈作为行号轴r,以极点到赤道方向为行号轴正方向;以平行圈作为列号轴c,以自西向东方向为列号轴正方向;以一个格网单元为单位长度,用 (r, c) 表示格网单元的行列坐标, 其中r、c分别表示行号和列号,建立椭球面DQLLG格网行列号坐标轴系统,如图 4所示。原点处的行列号均为0。
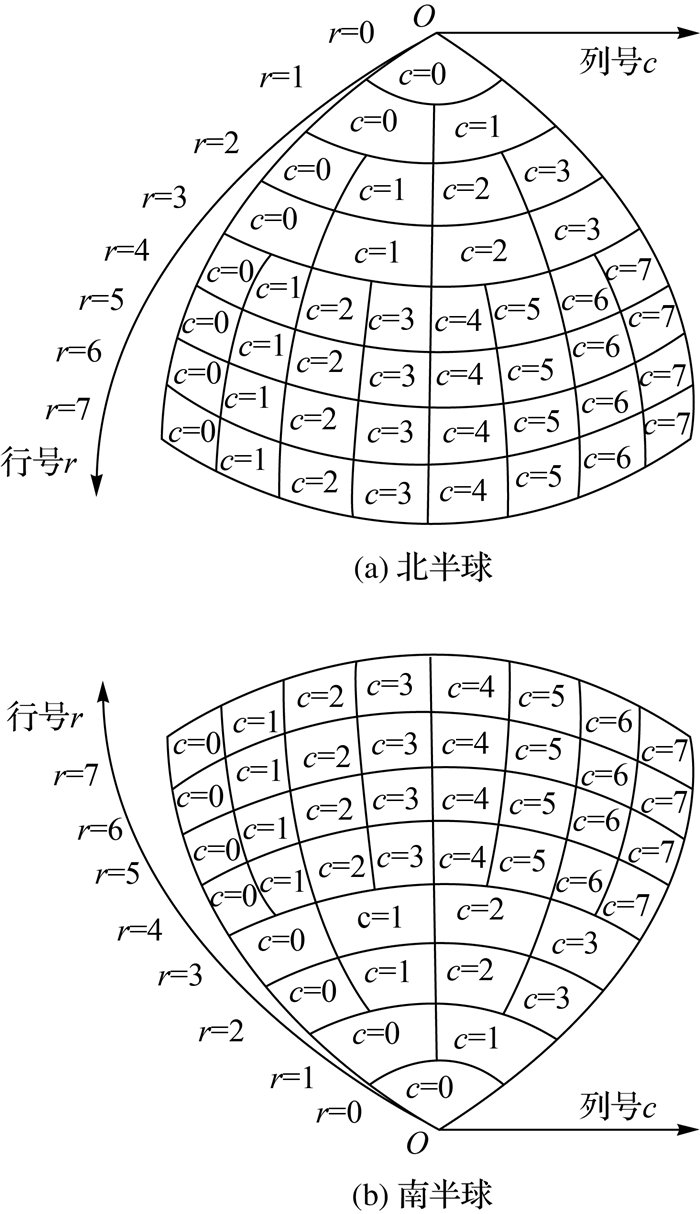
|
| 图 4 格网行列号定义 Fig. 4 Row and column coordinate system |
1.2.2 格网单元经纬度
由剖分过程可知,所有格网单元的纬度差都是相等的,经度差是不完全等。格网单元的纬度差用ΔB表示,经度差用ΔL表示,格网剖分层次为n。在任意初始剖分椭球面三角形内,格网每一行的纬度差
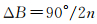 (1)
(1)
两极8个椭球面三角形格网单元中心经度分别为45°、135°、225°、315°;若在北半球,其纬度为90°-ΔB、在南半球则为-90°+ΔB。
除此以外的所有椭球面梯形单元,其经度差ΔL与其所在行的行号r有关,与剖分层次无关。从行列号定义规则可以容易得出第r行格网单元经度差ΔL
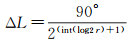 (2)
(2)
则在编码为0的初始剖分三角形内,行列坐标为 (r, c) 的格网单元的左上角点 (这里约定:由极点到赤道的方向为向上,由赤道到极点的方向为向下,行号轴正方向为上,列号轴正方向为右) 的经、纬度
经度:
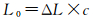 (3)
(3)
纬度:
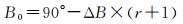 (4)
(4)
根据梯形格网单元所在的初始剖分椭球面三角形的不同,行列坐标为 (r, c) 的格网单元的左上角点在椭球面的实际经度、纬度如表 1所示。梯形格网单元其他三个角点的经、纬度与该左上角点的经纬度相同或相差一个经纬差,格网中心经纬度与该左上角点的经纬度相差半个经纬差。
| 初始剖分三角形编码 | 实际经度L | 实际纬度B |
| 0 | L0 | B0 |
| 1 | 90°+L0 | B0 |
| 2 | 180+L0 | B0 |
| 3 | 270+L0 | B0 |
| 4 | L0 | -B0 |
| 5 | 90°+L0 | -B0 |
| 6 | 180+L0 | -B0 |
| 7 | 270+L0 | -B0 |
总之,对于任意一个椭球面梯形格网单元,只要知道其所在初始剖分三角形内的行列号 (r, c) 及格网的剖分层次n,就可以得到该格网单元的中心点及4个角点的经纬度坐标;同样,知道某点的经纬度坐标,也可以得到其所在的格网单元。
2 WGS-84椭球面DQLLG格网单元几何计算及分析本文所用WGS-84椭球体的数学公式及相关参数如下
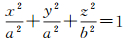 (5)
(5)
式中,长半轴a=6 378 137.000 m,为赤道半径,短半轴b为极轴半径,扁率f=1/298.257 223 563;第一偏心率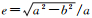
因为所有各网单元都是按经纬线划分,所以求格网边长就是求子午圈弧段和平行圈弧段的长度,格网面积就是求两条子午圈线和两条平行圈线在椭球面上所围成部分的面积。
由于椭球面的弧长和多边形面积计算没有固定的公式,本文均采用微分原理进行求解。
(1) 计算子午线弧长。如图 3(a)所示,子午线上有微分弧ΔSL,M是该微分弧曲率半径,则
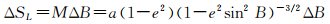 (6)
(6)
(2) 计算平行圈弧长。对于旋转椭球体而言,平行圈实际上就是一个圆,所以求平行圈弧长也就是一段圆弧长。如图 3(b)所示,平行圈上有微分弧ΔSB,对应的圆心角为ΔL(也是微分弧ΔSB的经度差),N是卯酉圈曲率半径,则
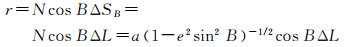 (7)
(7)
(3) 格网单元面积计算。所有格网本质上都是由两条子午圈线和两条平行圈线所围成的椭球面梯形,两极八个椭球面三角形,可以看作一条纬线弧长缩短到几乎为零。如图 3(c)所示,ΔA是椭球面微分梯形,两条平行圈微分弧平均值为ΔSB,则
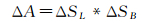 (8)
(8)
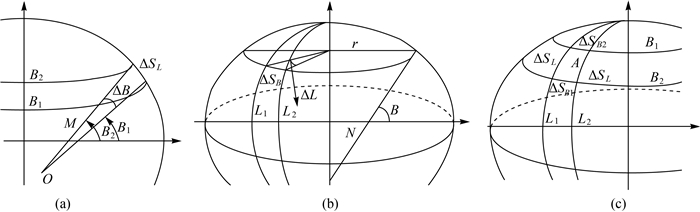
|
| 图 5 经纬线弧段的长度及经纬线围成椭球面四边形面积微分示意图 Fig. 5 Differential schematic of longitude and latitude lines arc length and ellipsoidal quadrangle area |
应用文献[35]关于椭球面子午线弧长、平行圈弧长、椭球面梯形的面积计算方法过程,计算不同剖分层次椭球面DQLLG格网单元边长、面积,计算结果如表 2所示。
| 剖分层次 | 单元个数 | Lmax/m | Lmin/m | Lmax/Lmin | Amax/m2 | Amin/m2 | Amax/Amin |
| 4 | 43 | 1 960 885.825 | 887 026.895 | 2.211 | 1.989E+12 | 1.209E+12 | 1.646 |
| 5 | 683 | 493 246.741 | 221 756.724 | 2.224 | 1.418E+11 | 7.096E+10 | 1.998 |
| 6 | 2731 | 246 699.172 | 110 878.362 | 2.225 | 3.657E+10 | 1.754E+10 | 2.086 |
| 7 | 10 923 | 123 359.063 | 55 439.181 | 2.225 | 9.324E+09 | 4.358E+09 | 2.140 |
| 8 | 43 691 | 61 680.716 | 27 719.590 | 2.225 | 2.368E+09 | 1.086E+09 | 2.180 |
| 9 | 174 763 | 30 840.506 | 13 859.795 | 2.225 | 5.967E+08 | 2.712E+08 | 2.201 |
| 10 | 699 051 | 15 420.272 | 6 929.898 | 2.225 | 1.499E+08 | 6.774E+07 | 2.214 |
| 11 | 2 796 203 | 7 710.138 | 3 464.949 | 2.225 | 3.763E+07 | 1.693E+07 | 2.223 |
| 12 | 11 184 811 | 3 855.069 | 1 732.474 | 2.225 | 9.426E+06 | 4.231E+06 | 2.228 |
| 13 | 4.473e+07 | 1 927.535 | 866.237 | 2.225 | 2.360E+06 | 1.058E+06 | 2.231 |
| 14 | 1.789e+08 | 963.767 | 433.119 | 2.225 | 590 489.356 | 264 416.288 | 2.233 |
| 15 | 7.158e+08 | 481.884 | 216.559 | 2.225 | 147 694.428 | 66 102.509 | 2.234 |
| 16 | 2.863e+09 | 240.942 | 108.280 | 2.225 | 36 935.618 | 16 525.432 | 2.235 |
| 17 | 1.145e+10 | 120.471 | 54.140 | 2.225 | 9 236.160 | 4 131.334 | 2.236 |
| 18 | 4.581e+10 | 60.235 | 27.070 | 2.225 | 2 309.322 | 1 032.830 | 2.236 |
| 19 | 1.833e+11 | 30.118 | 13.535 | 2.225 | 577.377 | 258.207 | 2.236 |
| 20 | 7.330e+11 | 15.059 | 6.767 | 2.225 | 144.353 | 64.552 | 2.236 |
| 21 | 2.932e+12 | 7.529 | 3.384 | 2.225 | 36.089 | 16.138 | 2.236 |
| 22 | 1.173e+13 | 3.765 | 1.692 | 2.225 | 9.023 | 4.034 | 2.236 |
| 23 | 4.691e+13 | 1.882 | 0.846 | 2.225 | 2.256 | 1.009 | 2.236 |
| 24 | 1.876e+14 | 0.941 | 0.423 | 2.225 | 0.564 | 0.252 | 2.236 |
可以发现,基于WGS-84椭球面DQLLG剖分格网随着剖分层次的逐渐增加,格网边长、面积都趋于稳定,格网最大最小边长之比和最大最小面积之比都由最初的逐渐增大到最后趋于稳定;最大最小边长之比Lmax/Lmin在剖分层次6层之后,已经可以很稳健地收敛到2.225;最大最小面积之比Amax/Amin,在剖分层次17层之后,逐渐收敛到2.236;两者都不超过2.24,这保证了DQLLG格网粒度的相对均匀性。
通过与球面DQLLG剖分比较,发现基于WGS-84椭球面DQLLG剖分格网单元最大与最小面积的比值Amax/Amin、最大与最小边长的比值Lmax/Lmin都略有变化,但都相差很小,变化趋势都相同 (如图 6所示)。
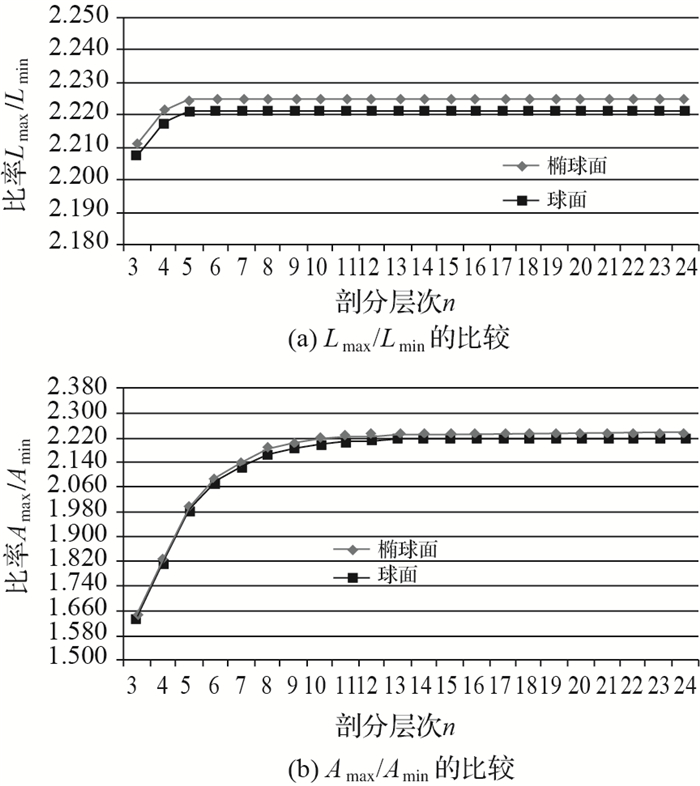
|
| 图 6 椭球面和正球面DQLLG剖分单元Lmax/Lmin及Amax/Amin的比较 Fig. 6 Comparison DQLLG cell's Lmax/Lmin and Amax/Amin between ellipsoidal and spherical |
3 结论
椭球面DQLLG不但顾及了地球的真实形状,还有效解决了传统经纬度格网两极数据冗余、奇异的问题,克服了三角形、菱形、六边形等其他球面格网方向不确定性的缺陷;格网边长、面积计算及分析也表明其格网粒度近似均匀,与正球面DQLLG相比虽然边长和面积的最大与最小值的比略有变化,但变化不大,保持了较好的规则性;椭球面DQLLG格网线与经纬线重合,能与经纬度坐标系统直接转换,进而可以通过一定的操作和计算与其他投影坐标系统、地心直角坐标系统以及椭球面三角形、菱形、六边形等其他全球格网系统进行转换;还可以通过连接四边形的中心与角点、对角点等方式,将椭球面四边形直接转换成椭球面三角形,这种最简单的多边形;经纬度格网的本质是四边形格网,很适合于一般地图、遥感影像数据制图和数据显示设备的表达等;格网可以无重叠覆盖整个地球,既保留了拓扑关系,也实现了全球范围的统一定位;格网可以无限次递归细分,也为实现层次索引、多分辨率数据组织及数据压缩存储等操作提供了方便;更重要的一点,全球格网单元沿赤道呈轴对称,且随纬度不同呈条带性,同一纬度条带的格网都是相同的,这也与地球南北半球气候、动物、植物及其他客观地理现象的条带性、对称性一致。上述这些特点表明,应用DQLLG处理全球问题有其特有优势。基于WGS-84椭球面DQLLG的几何变形分布规律、精度分析、全球海量数据有效组织管理表达以及在解决全球范围实际问题中的应用,将成为今后重要的研究方向。
| [1] | 周成虎, 欧阳, 马廷. 地理格网模型研究进展[J]. 地理科学进展, 2009, 28(5): 657–662. ZHOU Chenghu, OU Yang, MA Ting. Progresses of Geographical Grid Systems Researches[J]. Progress in Geography, 2009, 28(5): 657–662. |
| [2] | GOLD C, MOSTAFAVI M A. Towards the Global GIS[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2000, 55(3): 150–163. DOI:10.1016/S0924-2716(00)00016-2 |
| [3] | DUTTON G. Universal Geospatial Data Exchange Via Global Hierarchical Coordinate[C]//Proceedings of 2000 International Conference on Discrete Global Grids. Santa Barbara, CA:[s.n.], 2000. |
| [4] | 胡鹏, 吴艳兰, 杨传勇, 等. 大型GIS与数字地球的空间数学基础研究[J]. 武汉大学学报 (信息科学版), 2001, 26(4): 296–302. HU Peng, WU Yanlan, YANG Chuanyong, et al. Research on System Space Mathematical Base of Large-scale GIS and the Digital Earth[J]. Geomatics and Information Science of Wuhan University, 2001, 26(4): 296–302. |
| [5] | 赵学胜. 基于QTM的球面Voronoi数据模型研究[M]. 北京: 测绘出版社, 2004. ZHAO Xuesheng. Spherical Voronoi Data Model based on QTM[M]. Beijing: Surveying and Mapping Press, 2004. |
| [6] | DUTTON G H. A Hierarchical Coordinate System for Geoprocessing and Cartography[M]. Berlin Heidelberg: Springer-Verlag, 1999. |
| [7] | LUKATELA H. Ellipsoidal Area Computations of Large Terrestrial Objects[C]//Proceedings of the 1st International Conference on Discrete Grids'2000. Santa Barbara:[s.n.], 2000. |
| [8] | SAHR K, WHITE D, KIMERLING A J. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121–134. DOI:10.1559/152304003100011090 |
| [9] | BARTHOLDI Ⅲ J J, GOLDSMAN P. Continuous Indexing of Hierarchical Subdivisions of the Globe[J]. International Journal of Geographical Information Science, 2001, 15(6): 489–522. DOI:10.1080/13658810110043603 |
| [10] | BJØRKE J T, GRYTTEN J K, HÆGER M, et al. A Global Grid Model Based on "Constant Area" Quadrilaterals[C]//ScanGIS'2003-The 9th Scandinavian Research Conference on Geographical Information Science. Espoo, Finland:GIS, 2003, 3:238-250. |
| [11] | DUTTON G. Polyhedral Hierarchical Tessellations:The Shape of GIS to Come[J]. International Journal of Geographical Information Science, 1991, 1(3): 49–55. |
| [12] | GOODCHILD M E. Criteria for Evaluation of Global Grid Models for Environmental Monitoring and Analysis[R]. Handout from NCGIA Initiative 15. See Spatial Analysis on the Sphere:A Review, by Rob Raskin.NCGIA Technical Report, 1994:94-7. |
| [13] | KIMERLING J A, SAHR K, WHITE D, et al. Comparing Geometrical Properties of Global Grids[J]. Cartography and Geographic Information Science, 1999, 26(4): 271–288. DOI:10.1559/152304099782294186 |
| [14] | GOODCHILD M F, YANG Shiren. A Hierarchical Spatial Data Structure for Global Geographic Information Systems[J]. CVGIP:Graphical Models and Image Processing, 1992, 54(1): 31–44. DOI:10.1016/1049-9652(92)90032-S |
| [15] | 贲进, 童晓冲, 张衡, 等. 一种通用球面等积离散网格生成算法[J]. 测绘学院学报, 2005, 22(4): 252–255, 258. BEN Jin, TONG Xiaochong, ZHANG Heng, et al. A Universal Generation Algorithm of Spherical Equal-Area Discrete Grid[J]. Journal of Institute of Surveying and Mapping, 2005, 22(4): 252–255, 258. |
| [16] | 贲进, 童晓冲, 周成虎, 等. 正八面体的六边形离散格网系统生成算法[J]. 地球信息科学学报, 2015, 17(7): 789–797. BEN Jin, TONG Xiaochong, ZHOU Chenghu, et al. Construction Algorithm of Octahedron Based Hexagon Grid Systems[J]. Journal of Geo-Information Science, 2015, 17(7): 789–797. |
| [17] | 贲进, 童晓冲, 张永生, 等. 球面等积网格系统生成算法与软件模型研究[J]. 测绘学报, 2007, 36(2): 187–191. BEN Jin, TONG Xiaochong, ZHANG Yongsheng, et al. Research on Generating Algorithm and Software Model of Discrete Global Grid Systems[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 187–191. DOI:10.3321/j.issn:1001-1595.2007.02.013 |
| [18] | 贲进, 童晓冲, 元朝鹏. 孔径为4的全球六边形格网系统索引方法[J]. 测绘学报, 2011, 40(6): 785–789, 795. BEN Jin, TONG Xiaochong, YUAN Zhaopeng. Indexing Schema of the Aperture 4 Hexagonal Discrete Global Grid System[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 785–789, 795. |
| [19] | 童晓冲, 贲进, 秦志远, 等. 基于全球离散网格框架的局部网格划分[J]. 测绘学报, 2009, 38(6): 506–513. TONG Xiaochong, BEN Jin, QIN Zhiyuan, et al. The Subdivision of Partial Grid Based on Discrete Global Grid Systems[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(6): 506–513. DOI:10.3321/j.issn:1001-1595.2009.06.007 |
| [20] | 童晓冲, 贲进, 汪滢. 利用数值投影变换构建全球六边形离散格网[J]. 测绘学报, 2013, 42(2): 268–276. TONG Xiaochong, BEN Jin, WANG Ying. The Construction of Hexagonal Discrete Global Grid by Numerical Projection Transformation[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 268–276. |
| [21] | 童晓冲, 贲进, 张永生. 基于二十面体剖分格网的球面实体表达与Voronoi图生成[J]. 武汉大学学报 (信息科学版), 2006, 31(11): 966–970. TONG Xiaochong, BEN Jin, ZHANG Yongsheng. Expression of Spherical Entities and Generation of Voronoi Diagram Based on Truncated Icosahedron DGG[J]. Geomatics and Information Science of Wuhan University, 2006, 31(11): 966–970. |
| [22] | 童晓冲, 贲进, 张永生. 全球多分辨率六边形网格剖分及地址编码规则[J]. 测绘学报, 2007, 36(4): 428–435. TONG Xiaochong, BEN Jin, ZHANG Yongsheng. The Subdivision of Global Multi-resolution Hexagonal Grid and the Rules of Address Coding[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 428–435. DOI:10.3321/j.issn:1001-1595.2007.04.012 |
| [23] | TONG Xiaochong. The Principles and Methods of Discrete Global Grid Systems for Geospatial Information Subdivision Organization[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 536. |
| [24] | 童晓冲. 空间信息剖分组织的全球离散格网理论与方法[J]. 测绘学报, 2011, 40(4): 536. TONG Xiaochong. The Principles and Methods of Discrete Global Grid Systems for Geospatial Information Subdivision Organization[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 536. |
| [25] | 赵学胜, 白建军, 王志鹏. 基于QTM的全球地形自适应可视化模型[J]. 测绘学报, 2007, 36(3): 316–320. ZHAO Xuesheng, BAI Jianjun, WANG Zhipeng. An Adaptive Visualized Model of the Global Terrain Based on QTM[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 316–320. DOI:10.3321/j.issn:1001-1595.2007.03.013 |
| [26] | 赵学胜, 白建军. 基于菱形块的全球离散格网层次建模[J]. 中国矿业大学学报, 2007, 36(3): 397–401. ZHAO Xuesheng, BAI Jianjun. Hierarchical Model of Global Discrete Grids Based on Diamonds[J]. Journal of China University of Mining & Technology, 2007, 36(3): 397–401. |
| [27] | 赵学胜, 陈军. 基于球面四元三角网剖分的层次空间关系推理[J]. 测绘学报, 2001, 30(4): 355–360. ZHAO Xuesheng, CHEN Jun. Hierarchical Spatial Relation Reasoning Based on Spherical O-QTM Partition[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 355–360. DOI:10.3321/j.issn:1001-1595.2001.04.015 |
| [28] | 赵学胜, 崔马军, 李昂, 等. 球面退化四叉树格网单元的邻近搜索算法[J]. 武汉大学学报 (信息科学版), 2009, 34(4): 479–482. ZHAO Xuesheng, CUI Majun, LI Ang, et al. An Adjacent Searching Algorithm of Degenerate Quadtree Grid on Spherical Facet[J]. Geomatics and Information Science of Wuhan University, 2009, 34(4): 479–482. |
| [29] | 赵学胜, 苑争一, 赵龙飞, 等. 一种改进的近似等面积QTM剖分模型[J]. 测绘学报, 2016, 45(1): 112–118. ZHAO Xuesheng, YUAN Zhengyi, ZHAO Longfei, et al. An Improved QTM Subdivision Model with Approximate Equal-Area[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 112–118. DOI:10.11947/j.AGCS.2016.20140598 |
| [30] | 胡佰林, 赵学胜. 基于投影的球面退化四叉树格网路径搜索算法及其效率测试[J]. 河南理工大学学报 (自然科学版), 2013, 32(3): 293–297. HU Bailin, ZHAO Xuesheng. An Algorithm of Searching Degenerate Quadtree Grid Cells Along a Path[J]. Journal of Henan Polytechnic University (Natural Science), 2013, 32(3): 293–297. |
| [31] | 赵学胜, 王磊, 王洪彬, 等. 全球离散格网的建模方法及基本问题[J]. 地理与地理信息科学, 2012, 28(1): 29–34. ZHAO Xuesheng, WANG Lei, WANG Hongbin, et al. Modeling Methods and Basic Problems of Discrete Global Grids[J]. Geography and Geo-Information Science, 2012, 28(1): 29–34. |
| [32] | 崔马军, 赵学胜. 球面退化四叉树格网的剖分及变形分析[J]. 地理与地理信息科学, 2007, 23(6): 23–25. CUI Majun, ZHAO Xuesheng. Tessellation and Distortion Analysis Based on Spherical DQG[J]. Geography and Geo-Information Science, 2007, 23(6): 23–25. |
| [33] | 赵学胜, 侯妙乐, 白建军. 全球离散格网的空间数字建模[M]. 北京: 测绘出版社, 2007. ZHAO Xuesheng, HOU Miaole, BAI Jianjun. Spatial Digital Modeling of the Global Discrete Grids[M]. Beijing: Surveying and Mapping Press, 2007. |
| [34] | KIESTER A R, SAHR K. Introduction to discrete global grids[J]. Computers, Environment and Urban Systems, 2008, 32(3): 173. DOI:10.1016/j.compenvurbsys.2008.04.001 |
| [35] | 孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 2版. 武汉: 武汉大学出版社, 2010. KONG Xiangyuan, GUO Jiming, LIU Zongquan. Foundation of Geodesy[M]. 2nd ed. Wuhan: Wuhan University Press, 2010. |


