2. 江苏省地理信息资源开发与利用协同创新中心, 江苏 南京 210023;
3. 江苏省地理环境演化国家重点试验室培育建设点, 江苏 南京 210023
2. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China;
3. State Key Laboratory Cultivation Base of Geographical Environment Evolution (Jiangsu Province), Nanjing 210023, China
为了有效管理全球多尺度海量空间数据,多位学者研究了基于正多面体剖分地球的方法,将地球表面剖分成面积、形状近似相等,具有多分辨率层次结构的格网单元[1],称为正多面体全球离散格网系统 (discrete global grid system,DGGS)。常见的正多面体全球离散格网系统包括基于正六面体的四边形格网[2-5]、基于正八面体的三角形格网[6-10]、基于正八面体的菱形格网[11-12]与基于正八面体的六边形格网[13]和基于正二十面体的三角形格网[14-17]、基于正二十面体的菱形格网[18-19]与基于正二十面体的六边形格网[20-22]。正多面体全球离散格网基于正多面体与球面的映射关系进行球面递归剖分[23],在全球范围内是无缝的、稳定的和近似均匀的,在空间数据表达[24-26]、地球系统模式计算[27-28]方面得到了深入研究,已成为当前全球离散格网研究热点之一。
总的来说,基于几种正多面体剖分球面各有千秋。正六面体的每个面均是正方形,可以生成类似于经纬格网的交错格网,因而被应用于地球系统模式计算中[4]。正八面体的6个顶点可以定位在两个极点和4个等分的赤道点上,任意的经纬度坐标能较容易地定位到其中一个面上[29],鉴于该特性可以较容易地实现空间数据的表达,如经典的QTM模型[6]。一般而言,多面体的面越小,在和球面转换过程中的变形就越小[30]。相比较而言,二十面体是几种正多面体中面最小,最接近球面的正多面体,在此基础上剖分的全球离散格网变形相对较小,具有更均匀的几何性质,有利于全球空间数据集成与地球系统模式计算,因此逐步引起相关学者的关注[19, 23, 28]。
相关研究者基于正二十面体三角形格网、六边形格网的剖分方法分别设计了其相应的格网编码方案。Fekete利用正二十面体三角形格网建立了SQT编码,并在此基础上研究了球面空间上的邻近分析和可视化[14]。袁文采用L型空间填充曲线设计了正二十面体三角形格网的面片编码模型,并给出了面片节点的生成、访问及寻址算法[17]。Sahr受到GBT结构的启发,在球面上借助与广义平衡三进制类似的编码运算,提出了正二十面体六边形格网编码和快速索引算法[22]。童晓冲基于全球六边形格网提出了具备层次性的金字塔结构编码方案,采用递归方法设计并实现了编码与地理坐标的转换算法[31]。正二十面体菱形格网虽然有成熟的剖分方案[18-19],但鲜有对其编码模型的研究。全球离散格网通常使用格网编码代替地理坐标进行各种空间操作,因此编码模型是格网系统至关重要的组成部分。格网编码既隐含了对应单元的位置信息,又表达了比例尺和精度[30]。鉴于此,本文拟研究基于正二十面体菱形离散格网的编码模型。
基于正二十面体的球面菱形离散格网,有别于结构简单的正八面体,其初始菱形块的边线并不贴合经纬线,且几何性质、拓扑性质上都更为复杂,这对构建正二十面体球面菱形离散格网的层次编码模型和建立其与地理坐标间的映射关系转换带来了新的挑战。但值得注意的是,球面菱形离散格网采用四叉树剖分,在基础菱形内,其几何结构与平面栅格类似,适于现有的空间填充曲线的应用。目前应用最广泛的空间填充曲线包括Z曲线、Gray曲线及Hilbert曲线,不同的空间填充曲线具有不同的空间聚集能力,因而使得索引效率存在差异[32]。其中,Hilbert曲线被证明能够最好保持空间点的局部邻接性[33],即保证在多维空间上邻近的对象映射到一维线性空间上也是邻近的,已被广泛应用于空间数据库的几何索引中[34]。
因此,本文基于Hilbert曲线构建了正二十面体球面菱形离散格网的编码模型,在此基础上研究了格网单元编码与地理坐标的相互转化算法,并设计了相关试验,对转换精度与效率进行了分析。
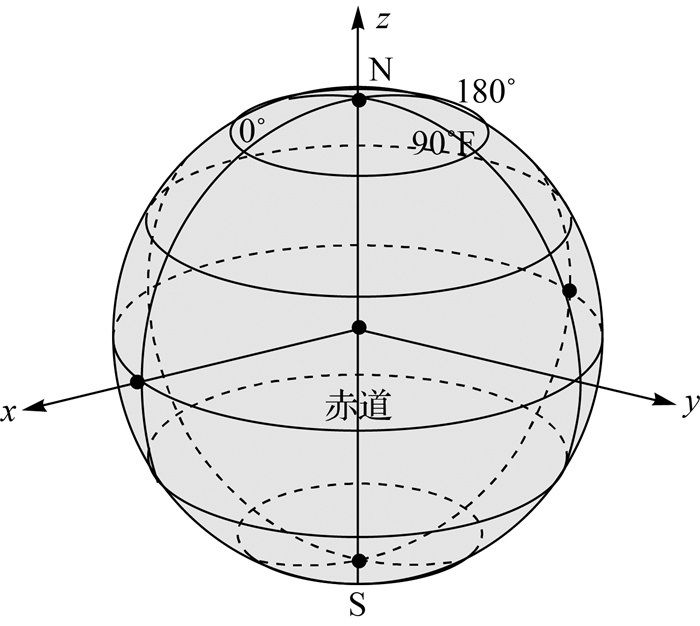
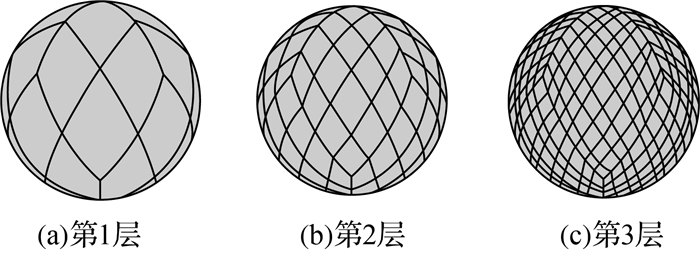
1 正二十面体球面菱形离散格网剖分方法本文所采用的剖分方法[19]以球体的内接正二十面体作为球面格网划分的基础,在两个极点各放置一个顶点,其中一条通过北极的边线投影和0°经线重合 (图 1)。经纬度坐标下南北极两处存在极点奇异性,因而需将球面上的几何位置转为以球心为原点的三维直角坐标系 (图 2) 形式表达[19]。合并相邻的南北向三角形形成10个球面菱形,在三维直角坐标系下对球面菱形进行细化,采用大圆弧平分法确定4条边的中点,点连线的球面投影即把球面菱形分为4个小球面菱形,依次类推,完成对整个球面近似均匀的剖分 (图 3)。基于此方法所得到的格网整体分布均匀,格网单元面积、角度形变小、排列紧致[19]。
|
| 图 2 经纬度与空间直角坐标系的对应关系 Fig. 2 Relationship between Lon/Lat and it's coordination system |
|
| 图 3 基于正二十面体的球面层次剖分 Fig. 3 Spherical hierarchical subdivision based on icosahedron |
2 正二十面体球面菱形离散格网编码模型
本文所提出的编码模型包括区位码和Hilbert码两部分组成,可以采用如下CODE的形式表示
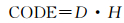 (1)
(1)
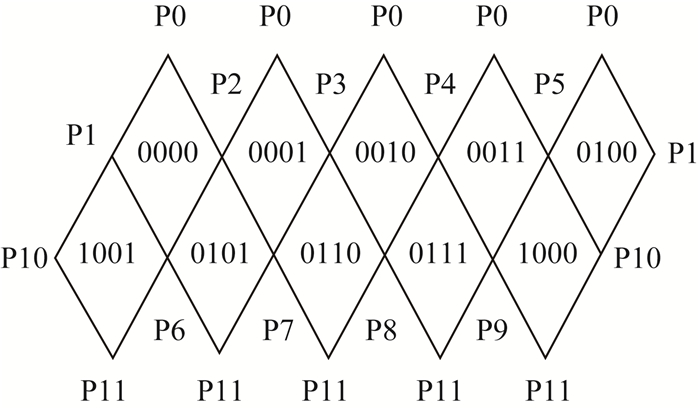
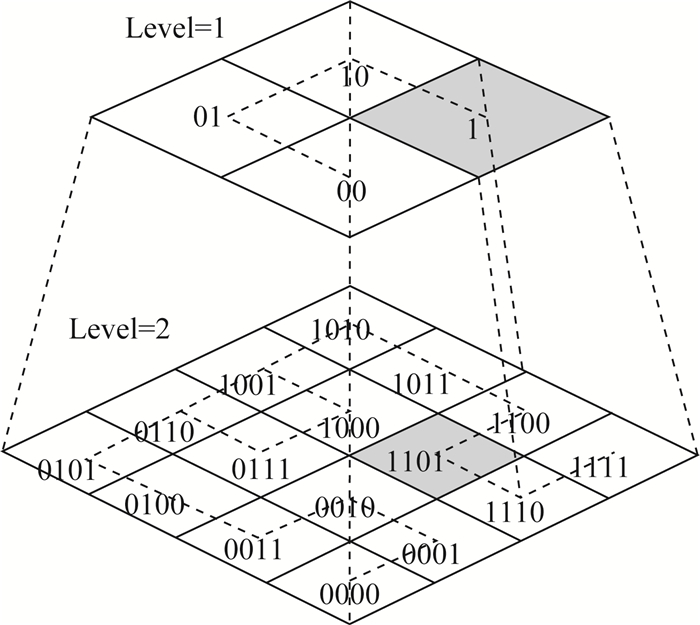
式中,D表示区位码,用于索引正二十面体球面菱形格网的十个初始菱形块,采用二进制码表示,在计算机上占2个字节 (16位)。H为Hilbert码,以每个初始菱形块左顶点对应的格网单元为起始点建立Hilbert填充曲线,对某个基菱形上的格网单元进行索引,同样以二进制表示,每层于末尾增加2位 (bit),因而隐含了格网的剖分层级、父子单元的Hilbert码。本文规定以正二十面体0号基菱形为例,由Hilbert码便能定位格网单元在基菱形内的位置,如图 5中第2层的菱形块对应的格网编码为00001101。
|
| 图 4 正二十面体球面菱形离散格网区位编码 Fig. 4 Domain's code of DDGG based on icosahedron |
|
| 图 5 球面菱形离散格网0号基菱形内Hilbert编码 Fig. 5 Hilbert code of DDGG's 0 initial diamond |
3 格网编码与地理坐标的相互转换
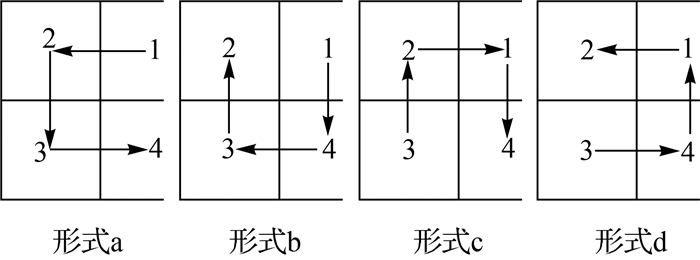
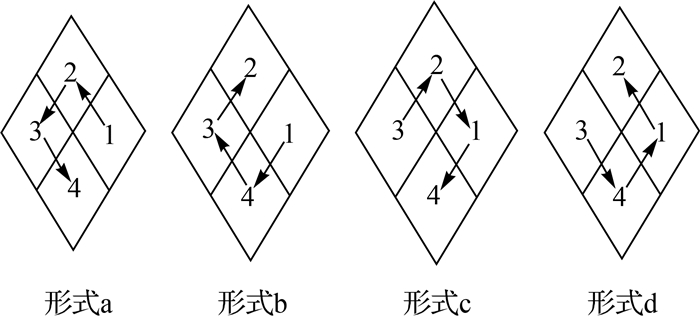
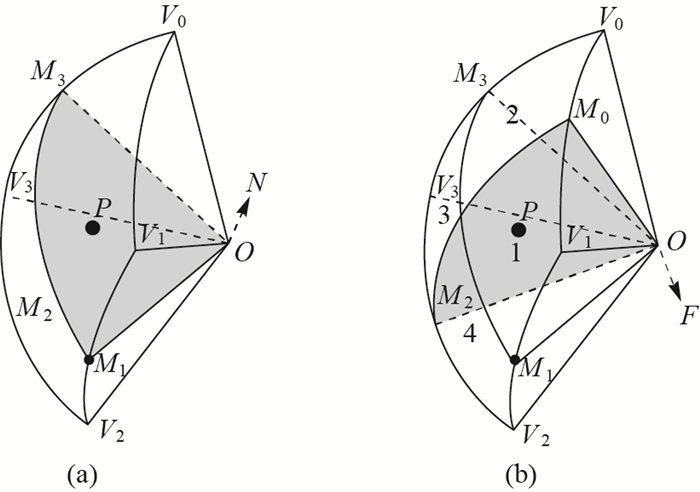
陆锋根据Hilbert曲线的递归构造过程,提出了一种基于空间层次分解的Hilbert空间排列码生成算法,使用可迭代规则对空间进行逐步细化[35]。其中,Hilbert曲线分为4种子象限形态,这决定了存在4种形式的状态转移向量,即{1,2,3,4},{1,4,3,2},{3,2,1,4}和{3,4,1,2}(图 6)。球面菱形离散格网在初始菱形块内可以看作是倾斜的平面栅格,通过旋转平面栅格上的状态可以得到球面菱形块上Hilbert曲线的4种状态转移向量 (图 7)。在空间层次分解时,结合象限的Hilbert码和状态转移向量可以推导出子象限的Hilbert码和状态转移向量,其中状态转移向量表明子象限中曲线的旋转与反射。
|
| 图 6 Hilbert空间曲线的状态转移向量 Fig. 6 State transition vector of the Hilbert curve |
|
| 图 7 球面菱形块上Hilbert曲线的状态转移向量 Fig. 7 State transition vector of the Hilbert curve on spherical diamond |
本文借鉴Hilbert曲线的空间层次分解方法,设计了地理坐标与格网编码相互转换的算法。
地理坐标到格网编码的转换实质是任意球面点在格网上确定其所属格网单元的过程。本文首先根据待求点所在的地图比例尺查找确定其所在的目标层次L,在判断待求点是否在指定剖分层次的基础上,通过平面方程判别法逐层求取待定点在下一剖分层次中所属的子菱形Hilbert码,最终得到地理坐标所属的球面菱形格网单元的编码。具体的步骤如下 (图 8)。
|
| 图 8 地理坐标到单元编码转换的流程 Fig. 8 Process of converting geographical coordinate to code |
(1) 采用文献[19]中的经纬度与空间之间坐标的转换方法,将待定点P的地理坐标转换至空间直角坐标系 (图 2),初始化状态转移向量V,Hilbert码H,剖分计数l:H=0,l=0;
(2) 判断地理坐标的落点区域,即正二十面体菱形格网的初始菱形块d,得到对应的二进制区位码:D=d,并以该初始菱形块为当前基菱形;
(3) 若当前菱形的剖分层次l为目标层次L,则当前菱形块即为地理坐标在指定剖分层次上对应的格网单元,将二进制区位码D与Hilbert码H组合成编码CODE并输出,算法结束;否则,进入下一步;
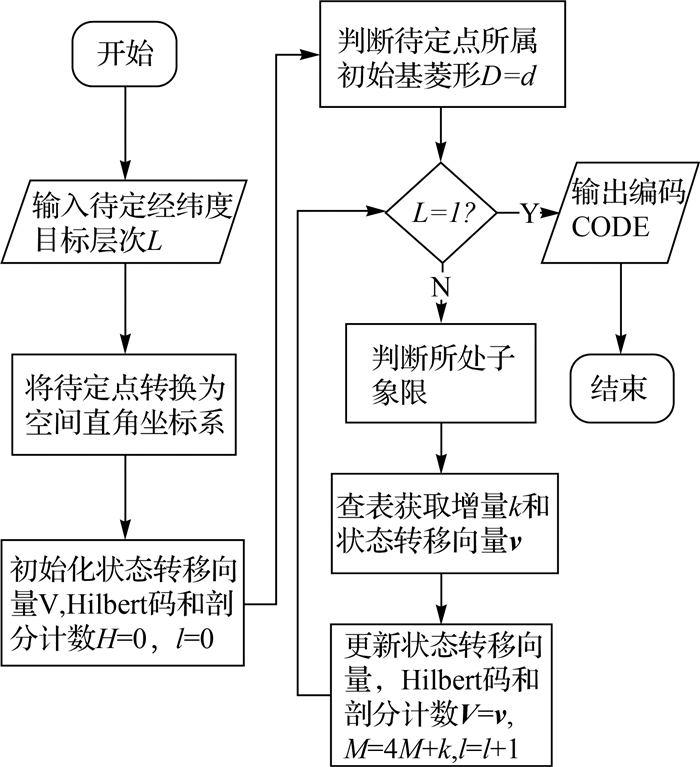
(4) 以当前菱形边界V1V2的中点M1、V0V3的中点M3以及球心O构成平面OM1M3,求其三维空间中的平面方程。由于平面OM1M3经过球心O,则可得平面OM1M3的法向量
(5) 采用的同样的方法,再对另外一个方向上菱形边界V0V1的中点M0、V2V3的中点M2和球心O构成平面OM0M2进行位置判断 (图 9),得出P点在菱形块内所处的象限,由象限号和状态转移向量V通过表 1获得该象限Hilbert码的二进制增量k和新状态转移量v,重新设定状态转移向量V=v,将增量k添加在Hilbert码尾部,更新Hilbert码和剖分计数:H=Hk,l=l+1,返回步骤 (3)。
|
| 图 9 待定点和平面位置关系判断 Fig. 9 Judgement on spatial relationship between point and plane |
| 状态向量 | a | b | c | d | |||||||||||||||
| 象限 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |||
| 状态转移向量 | b | a | a | c | a | d | b | b | c | c | d | a | d | b | c | d | |||
| Hilbert码增量 | 00 | 01 | 10 | 11 | 00 | 11 | 10 | 01 | 10 | 01 | 00 | 11 | 10 | 11 | 00 | 01 | |||
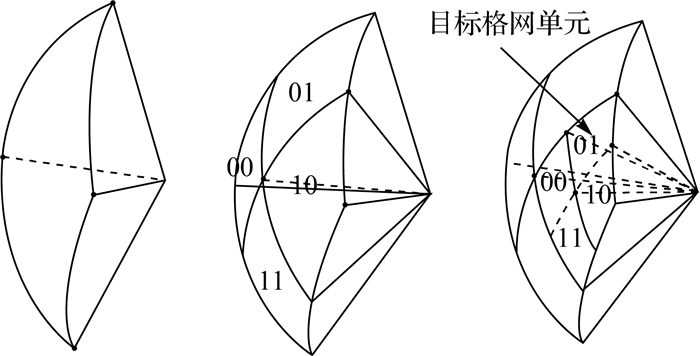
从格网编码到地理坐标的转换实际上是一个格网单元的编码到格网单元中心点的球面经纬坐标的转换。本文中格网单元的中心点即为菱形单元短轴的中点。转换的基本思想是根据编码进行单元的逐层递归逼近,直至定位到编码所对应的菱形单元,再求出中点即可 (图 10)。具体过程如下:
|
| 图 10 目标格网单元确定过程 Fig. 10 Process of conforming targeted grid's cell |
(1) 根据正二十面体与球面的对应关系获取格网编码中区位码D对应的初始菱形顶点坐标V0、V1、V2、V3;
(2) 设定初始状态转移向量V,初始化格网剖分计数:l=0,目标层次L为Hilbert码M位数的二分之一;
(3) 若当前菱形的层次l为目标层次L,输出菱形单元中点的经纬度坐标,算法结束;否则,进入下一步;
(4) 取Hilbert码中的第2l+1、2l+2位二进制码组成Hilbert增量k,由增量k和状态转移向量V根据表 2确定单元在当前菱形块下所属的象限号,依据状态转移向量V与得到的象限号通过表 1获得该象限内的新状态转移向量v,重新设定状态转移向量:V=v;
| 状态向量 | a | b | c | d | |||||||||||||||
| Hilbert码增量 | 00 | 01 | 10 | 11 | 00 | 01 | 10 | 11 | 00 | 01 | 10 | 11 | 00 | 01 | 10 | 11 | |||
| 象限 | 1 | 2 | 3 | 4 | 1 | 4 | 3 | 2 | 3 | 2 | 1 | 4 | 3 | 4 | 1 | 2 | |||
(5) 获取当前象限对应菱形块的四个顶点,更新顶点坐标V0、V1、V2、V3和剖分计数l:l=l+1。返回步骤 (3)。
4 试验与分析有多种评价标准可以用来衡量地理坐标与格网编码间相互转换的精度,最常见的是绝对精度[31]。绝对精度指的是将地理坐标形式的点或球面编码转换为对应的格网编码或地理坐标后,再将其转换回输入形式得到输出结果,对比输入和输出的坐标点球面距离或者编码值,如果二者在一个格网剖分单元内,则转换算法符合格网绝对精度的要求。
为了分析本文提出的编码转换算法效率与精度,选择不同数量的 (2000、1万、10万、100万) 随机坐标点在不同层次下 (12、14、16、19、21层,对应比例尺分别为1:400万、1:100万、1:25万、1:5万、1:1万) 进行编码与地理坐标的相互转换试验,与White提出的Morton码编码方案[18]进行比较,并以绝对精度[31]为编码转换精度评判标准。主要硬件配置环境为:CPU为Intel (R) Core (TM) i7-4770 3.10 GHz,8 GB内存,1 TB硬盘,采用VC++ 2013作为基础开发平台。试验结果如下 (表 3)。
| 层次 | 点数 | 地理坐标转格网编码 | 格网编码转地理坐标 | |||||
| Hilbert/s | Morton/s | 绝对精度/m | Hilbert/s | Morton/s | 绝对精度 | |||
| 12 | 2000 | 0.004 | 0.004 | 1443.17 | 0.001 | 0.001 | 1个格网单元 | |
| 1万 | 0.034 | 0.039 | 0.013 | 0.021 | ||||
| 10万 | 0.359 | 0.358 | 0.208 | 0.213 | ||||
| 100万 | 3.636 | 3.692 | 2.058 | 2.002 | ||||
| 14 | 2000 | 0.005 | 0.005 | 246.49 | 0.001 | 0.001 | 1个格网单元 | |
| 1万 | 0.043 | 0.045 | 0.012 | 0.025 | ||||
| 10万 | 0.417 | 0.423 | 0.19 | 0.217 | ||||
| 100万 | 4.045 | 4.081 | 2.170 | 2.161 | ||||
| 16 | 2000 | 0.006 | 0.006 | 52.67 | 0.001 | 0.001 | 1个格网单元 | |
| 1万 | 0.057 | 0.052 | 0.019 | 0.023 | ||||
| 10万 | 0.459 | 0.463 | 0.21 | 0.298 | ||||
| 100万 | 4.525 | 4.601 | 2.505 | 2.510 | ||||
| 19 | 2000 | 0.006 | 0.006 | 9.65 | 0.002 | 0.002 | 1个格网单元 | |
| 1万 | 0.051 | 0.049 | 0.026 | 0.029 | ||||
| 10万 | 0.528 | 0.523 | 0.287 | 0.311 | ||||
| 100万 | 5.246 | 5.301 | 3.026 | 3.060 | ||||
| 21 | 2000 | 0.007 | 0.006 | 0.30 | 0.002 | 0.002 | 1个格网单元 | |
| 1万 | 0.069 | 0.059 | 0.029 | 0.031 | ||||
| 10万 | 0.712 | 0.581 | 0.314 | 0.328 | ||||
| 100万 | 5.677 | 5.735 | 3.296 | 3.256 | ||||
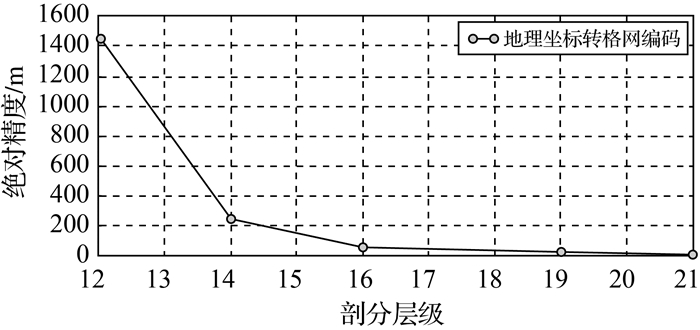
从图 11可以发现,地理坐标转格网编码后的绝对精度误差随着剖分层级的增加而迅速减小,综合对应剖分层级 (12、14、16、19、21层) 下菱形单元的边长表 4来看,转换的绝对精度始终控制在一个格网单元内。从表 3可知,格网编码转地理坐标后格网编码值保持不变,前后所表示的格网单元始终为同一个单元。综上分析,本文提出的坐标编码转换算法以递归逼近方法为基础,相当于进行了一次格网单元局部的递归剖分,因而可以保证转换算法满足绝对精度的要求。
|
| 图 11 不同剖分层级下的地理坐标转格网编码的转换精度 Fig. 11 Conversion efficiency of geographical coordinates into codes on different subdivision level |
| 剖分层次 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 菱形边长/m | 5000 | 2000 | 1000 | 610 | 305 | 153 | 76 |
| 对应比例尺 | 1:1000万 | 1:500万 | 无 | 1:100万 | 1:50万 | 1:25万 | 1:10万 |
| 剖分层次 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 菱形边长/m | 38 | 18 | 10 | 5 | 2 | 1 | 0.6 |
| 对应比例尺 | 1:5万 | 无 | 1:1万 | 1:5000 | 1:2500 | 1:1000 | 1:500 |
将本文所提出的编码方案与White在Z曲线基础上提出的编码方案[18]进行地理坐标与格网编码转换的对比试验。从图 12可以发现,随着剖分层级的增加,基于两种编码模型的地理坐标与网格编码的转换效率均逐步下降,转换耗时呈现线性增长,而两者之间的效率表现几近一致。由于格网的剖分中心、菱形块的棱边中点与球心构成两个扇面,子菱形归属只需要与这两个扇面进行2次位置判断 (图 9),因而均能够在顾及转换精度的前提下实现坐标向编码的快速转换。
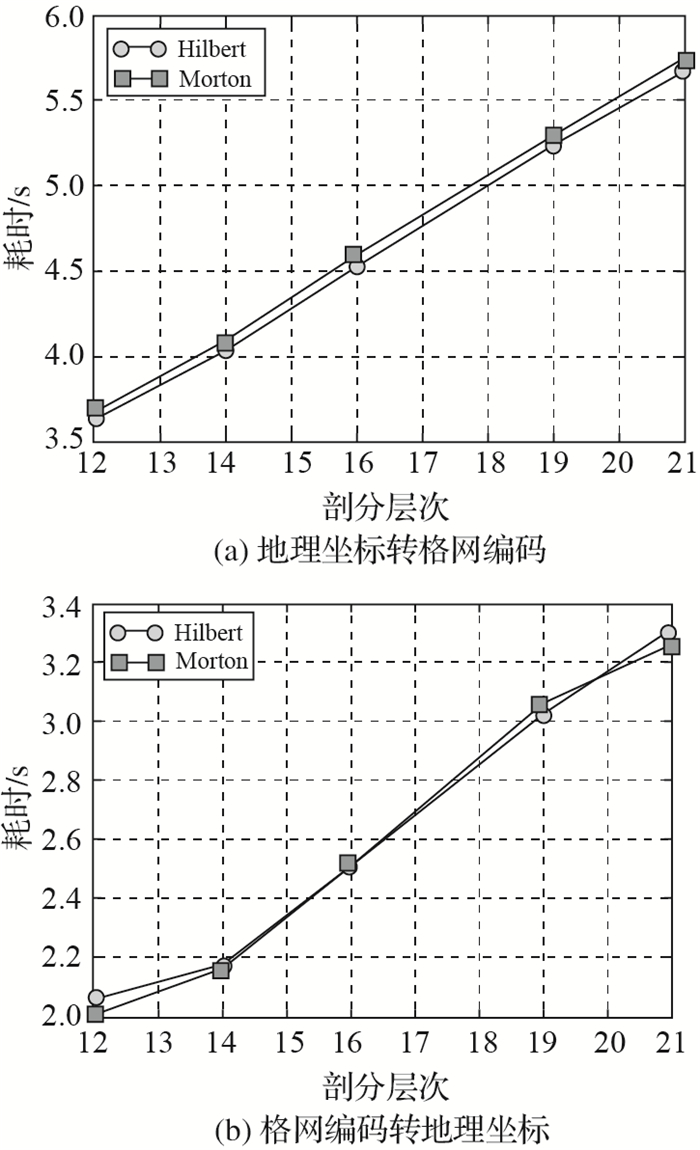
|
| 图 12 100万随机点在不同层级下的地理坐标与格网编码的相互转换 Fig. 12 Conversion between 1 million geographical coordinates and codes on different subdivision level |
值得注意的是,相比White在Z曲线基础上提出的编码方案,本文所提出的基于Hilbert曲线的编码模型对于空间数据的局部邻接性保持更好,因此在后续的空间数据索引、拓扑分析等方面具有明显的优势。
5 结论本文在正二十面体球面菱形离散格网剖分方法的基础上,考虑到在球面上难以直接构建全球连续的菱形格网编码,利用基础菱形内部与二维栅格的相似性,采用分区编码与二进位的Hilbert曲线结合的方案,构建了一种具有层次结构的正二十面体球面菱形离散格网编码模型。基于此,本文借鉴平面栅格上基于空间层次分解的Hilbert码的生成算法,采用迭代细化的规则方法构造球面Hilbert曲线的同时实现了经纬度向格网编码的转换,并进一步实现了对球面菱形离散格网编码的反向解码。研究表明,由于球面菱形离散格网在结构上与平面规则格网具有相似性,因此基于Hilbert曲线的编码模型能够在地理坐标与格网编码转换方面兼具效率与精度,可以支撑全球海量空间数据建模、集成管理以及各类空间分析。
| [1] | GOODCHILD M F. Discrete Global Grids:Retrospect and Prospect[J]. Geography and Geo-Information Science, 2012, 28(1): 1–6. |
| [2] | SADOURNY R. Conservative Finite-Difference Approximations of the Primitive Equations on Quasi-Uniform Spherical Grids[J]. Monthly Weather Review, 1972, 100(2): 136–144. DOI:10.1175/1520-0493(1972)100<0136:CFAOTP>2.3.CO;2 |
| [3] | RANČIĆ M, PURSER R J, MESINGER F. A Global Shallow-Water Model Using an Expanded Spherical Cube:Gnomonic Versus Conformal Coordinates[J]. Quarterly Journal of the Royal Meteorological Society, 1996, 122(532): 959–982. DOI:10.1002/(ISSN)1477-870X |
| [4] | MCGREGOR J L. Semi-Lagrangian Advection on Conformal-Cubic Grids[J]. Monthly Weather Review, 1996, 124(6): 1311–1322. DOI:10.1175/1520-0493(1996)124<1311:SLAOCC>2.0.CO;2 |
| [5] | RONCHI C, IACONO R, PAOLUCCI P S. The "Cubed Sphere":A New Method for the Solution of Partial Differential Equations in Spherical Geometry[J]. Journal of Computational Physics, 1996, 124(1): 93–114. DOI:10.1006/jcph.1996.0047 |
| [6] | DUTTON G. Encoding and Handling Geospatial Data with Hierarchical Triangular Meshes[C]//Proceedings of the 7th International Symposium on Spatial Data Handling. Netherlands:Taylor & Francis, 1996:1397-1398. |
| [7] | 孙文彬, 赵学胜. 基于QTM格网的空间数据无缝层次建模[J]. 中国矿业大学学报, 2008, 37(5): 675–679. SUN Wenbin, ZHAO Xuesheng. A Hierachical Seamless Model of Spatial Data Based on QTM[J]. Journal of China University of Mining & Technology, 2008, 37(5): 675–679. |
| [8] | 崔马军, 高彦丽, 赵学胜. 球面DQG地址码与经纬度坐标的快速转换算法[J]. 地理与地理信息科学, 2009, 25(3): 42–44. CUI Majun, GAO Yanli, ZHAO Xuesheng. A Fast Translating Algorithm between DQG Code and Longitude/Latitude Coordinates[J]. Geography and Geo-Information Science, 2009, 25(3): 42–44. |
| [9] | 赵学胜, 陈军. QTM地址码与经纬度坐标的快速转换算法[J]. 测绘学报, 2003, 32(3): 272–277. ZHAO Xuesheng, CHEN Jun. Fast Translating Algorithm between QTM Code and Longitude/Latitude Coordination[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(3): 272–277. DOI:10.3321/j.issn:1001-1595.2003.03.017 |
| [10] | 侯妙乐, 姜晓轶, 赵学胜, 等. 基于QTM的海平面上升分析与模拟[J]. 地理与地理信息科学, 2012, 28(1): 35–38. HOU Miaole, JIANG Xiaoyi, ZHAO Xuesheng, et al. Analysis and Simulation of Sea Level Rise Based on QTM[J]. Geography and Geo-Information Science, 2012, 28(1): 35–38. |
| [11] | 白建军, 赵学胜, 陈军. 基于线性四叉树的全球离散格网索引[J]. 武汉大学学报 (信息科学版), 2005, 30(9): 805–808. BAI Jianjun, ZHAO Xuesheng, CHEN Jun. Indexing of Discrete Global Grids Using Linear Quadtree[J]. Geomatics and Information Science of Wuhan University, 2005, 30(9): 805–808. |
| [12] | 刘光鑫. 基于菱形离散格网的中国海潮波系统数据集成方法[D]. 赣州: 江西理工大学, 2013. LIU Guangxin. Data's Integration of China Sea Tide System Based on Diamond Discrete Global Grid[D]. Ganzhou:Jiangxi University of Science and Technology, 2013. |
| [13] | 白建军. 基于正八面体的四孔六边形球面格网编码及索引[J]. 遥感学报, 2011, 15(6): 1131–1146. BAI Jianjun. Location Coding and Indexing Aperture 4 Hexagonal Discrete Global Grid Based on Octahedron[J]. Journal of Remote Sensing, 2011, 15(6): 1131–1146. |
| [14] | FEKETE G, TREINISH L A. Sphere Quadtrees:A New Data Structure to Support the Visualization of Spherically Distributed Data[C]//Proceedings of the SPIE 1259, Extracting Meaning from Complex Data:Processing, Display, Interaction. Santa Clara:SPIE, 1990, 1259:242. |
| [15] | TOMITA H, TSUGAWA M, SATOH M, et al. Shallow Water Model on A Modified Icosahedral Geodesic Grid by Using Spring Dynamics[J]. Journal of Computational Physics, 2001, 174(2): 579–613. DOI:10.1006/jcph.2001.6897 |
| [16] | SATOH M, MATSUNO T, TOMITA H, et al. Nonhydrostatic Icosahedral Atmospheric Model (NICAM) for Global Cloud Resolving Simulations[J]. Journal of Computational Physics, 2008, 227(7): 3486–3514. DOI:10.1016/j.jcp.2007.02.006 |
| [17] | 袁文, 程承旗, 马蔼乃, 等. 球面三角区域四叉树L空间填充曲线[J]. 中国科学E辑工程科学材料科学, 2004, 34(5): 584–600. YUAN Wen, CHENG Chengqi, MA Ainai, et al. L Curve for Spherical Triangle Region Quadtrees[J]. Science in China Series E Engineering & Materials Science, 2004, 34(5): 584–600. |
| [18] | WHITE D. Global Grids from Recursive Diamond Subdivisions of the Surface of an Octahedron or Icosahedron[J]. Environmental Monitoring and Assessment, 2000, 64(1): 93–103. DOI:10.1023/A:1006407023786 |
| [19] | 周良辰, 盛业华, 林冰仙, 等. 球面菱形离散格网正二十面体剖分法[J]. 测绘学报, 2014, 43(12): 1293–1299. ZHOU Liangchen, SHENG Yehua, LIN Bingxian, et al. Diamond Discrete Grid Subdivision Method for Spherical Surface with Icosahedron[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1293–1299. DOI:10.13485/j.cnki.11-2089.2014.0192 |
| [20] | 贲进. 地球空间信息离散网格数据模型的理论与算法研究[D]. 郑州: 解放军信息工程大学, 2005. BEN Jin. A Study of the Theory and Algorithms of Discrete Global Grid Data Model for Geospatial Information Management[D]. Zhengzhou:The PLA Information Engineering University, 2005. |
| [21] | 张永生, 贲进, 童晓冲, 等. 基于球面六边形网格系统的空间信息处理方法[J]. 测绘科学技术学报, 2006, 23(2): 110–114. ZHANG Yongsheng, BEN Jin, TONG Xiaochong, et al. Geospatial Information Processing Method Based on Spherical Hexagon Grid System[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2006, 23(2): 110–114. |
| [22] | SAHR K. Location Coding on Icosahedral Aperture 3 Hexagon Discrete Global Grids[J]. Computers, Environment and Urban Systems, 2008, 32(3): 174–187. DOI:10.1016/j.compenvurbsys.2007.11.005 |
| [23] | 赵学胜, 王磊, 王洪彬, 等. 全球离散格网的建模方法及基本问题[J]. 地理与地理信息科学, 2012, 28(1): 29–34. ZHAO Xuesheng, WANG Lei, WANG Hongbin, et al. Modeling Methods and Basic Problems of Discrete Global Grids[J]. Geography and Geo-Information Science, 2012, 28(1): 29–34. |
| [24] | 周成虎, 欧阳, 马廷. 地理格网模型研究进展[J]. 地理科学进展, 2009, 28(5): 657–662. ZHOU Chenghu, OU Yang, Ma Ting. Progresses of Geographical Grid Systems Researches[J]. Progress in Geography, 2009, 28(5): 657–662. |
| [25] | 宋树华, 程承旗, 关丽, 等. 全球空间数据剖分模型分析[J]. 地理与地理信息科学, 2008, 24(4): 11–15. SONG Shuhua, CHENG Chengqi, GUAN Li, et al. Analysis on Global Geodata Partitioning Models[J]. Geography and Geo-Information Science, 2008, 24(4): 11–15. |
| [26] | 赵学胜, 白建军, 王志鹏. 基于QTM的全球地形自适应可视化模型[J]. 测绘学报, 2007, 36(3): 316–320. ZHAO Xuesheng, BAI Jianjun, WANG Zhipeng. An Adaptive Visualized Model of the Global Terrain Based on QTM[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 316–320. DOI:10.3321/j.issn:1001-1595.2007.03.013 |
| [27] | STANIFORTH A, THUBURN J. Horizontal Grids for Global Weather and Climate Prediction Models:A Review[J]. Quarterly Journal of the Royal Meteorological Society, 2012, 138(662): 1–26. DOI:10.1002/qj.v138.662 |
| [28] | RANDALL D A, RINGLER T D, HEIKES R P, et al. Climate Modeling with Spherical Geodesic Grids[J]. Computing in Science & Engineering, 2002, 4(5): 32–41. |
| [29] | 张胜茂. 基于正八面体球面离散格网模型的全球遥感影像浏览系统研究[D]. 上海: 华东师范大学, 2009. ZHANG Shengmao. Research of Global Remote Sensing Image Browser System Based on Octahedron Discrete Global Grids Model[D]. Shanghai:East China Normal University, 2009. |
| [30] | 童晓冲. 全球多分辨率网格系统数字空间构建及索引机制研究[D]. 郑州: 解放军信息工程大学, 2006. TONG Xiaochong. The Construct of Digital Space of Global Mul-resolution Grid System and the Study of Index Mechanism[D]. Zhengzhou:The PLA Information Engineering University, 2006. |
| [31] | 童晓冲, 张永生, 贲进. 经纬度坐标与QTM编码的三向互化算法及其精度评价标准[J]. 武汉大学学报 (信息科学版), 2006, 31(1): 27–30. TONG Xiaochong, ZHANG Yongsheng, BEN Jin. Three Orientation Translating Algorithm of Long./Lat. Coordination and QTM Code Along with Its Criterion Judge of Precision[J]. Geomatics and Information Science of Wuhan University, 2006, 31(1): 27–30. |
| [32] | FALOUTSOS C, ROSEMAN S. Fractals for Secondary Key Retrieval[C]//Proceedings of the 8th ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems. New York, NY, USA:ACM, 1989:247-252. |
| [33] | MOON B, JAGADISH H V, FALOUTSOS C, et al. Analysis of the Clustering Properties of the Hilbert Space-Filling Curve[J]. IEEE Transactions on Knowledge and Data Engineering, 2001, 13(1): 124–141. DOI:10.1109/69.908985 |
| [34] | KAMEL I, FALOUTSOS C. Hilbert R-Tree:An Improved R-Tree Using Fractals[C]//Proceedings of the 20th International Conference on Very Large Data Bases. San Francisco, CA, USA:Morgan Kaufmann Publishers Inc., 1994:500-509. |
| [35] | 陆锋, 周成虎. 一种基于空间层次分解的Hilbert码生成算法[J]. 中国图象图形学报, 2001, 6(5): 465–469. LU Feng, ZHOU Chenghu. An Algorithm for Hilbert Ordering Code Based on Spatial Hierarchical Decomposition[J]. Journal of Image and Graphics, 2001, 6(5): 465–469. |