2. 国家信息中心, 北京 100045;
3. 后勤科学研究所, 北京 100071
2. National Information Center, Beijing 100045, China;
3. Logistics Science Research Institute, Beijing 100072, China
地形量化技术是采用一定的数学模型和数据结构,对地形、地物特征进行提取、标定和格式化,形成符合一定规范的地形数据集,为模拟对抗、虚拟漫游等应用系统提供地形信息的查询、调用和更新等服务[1]。在军事应用方面,该技术主要为特定军事问题的定量分析提供地形方面的基础数据。
常用的地形量化方法主要有标高法和分类法两种,两者之中又以分类法的应用更为广泛。地形的分类法描述,一般是先对地形分类,再对描述参数定级,最后划分作战地域。现有计算机作战仿真系统中,通常需要把地理环境数据按一定分辨率处理成按网格存储的数据,然后在此基础上展开各种行动的推演模拟、辅助决策、效能评估等。这些参与计算的网格首先需要能够在平面上形成连续且无重叠拼接的图形,如方形网格和六角网格[2]。以兵棋系统为代表的作战训练模拟系统就是采用六角格作为地形量化信息的承载网格。这种以六边形网格为信息承载的地形量方法在网格紧凑性、一致临近关系、等方向性方面具有较好的优势[3]。但是随着作战要素的不断增加,战场信息的日益丰富,传统的以六角格在数据组织,地形量化聚合以及网格多层次性方面存在一些欠缺。与之相比,方形网格不仅可以以网格为单元负载地形量化信息,还可以作为数据组织框架;同时地形量化方法简便、具有良好的多分辨率特性。
本文在2n一维整型数组地理坐标的全球剖分网格 (geographical coordinate global subdivision grid with one-dimension-integer on Two to nth power,GeoSOT) 框架下,以网格作为地形量化和数据记录的单元,在建立空间数据与网格单元之间映射关系的基础上,实现基于四边形网格的地形量化模型,为地形分析提供了量化数据支撑。
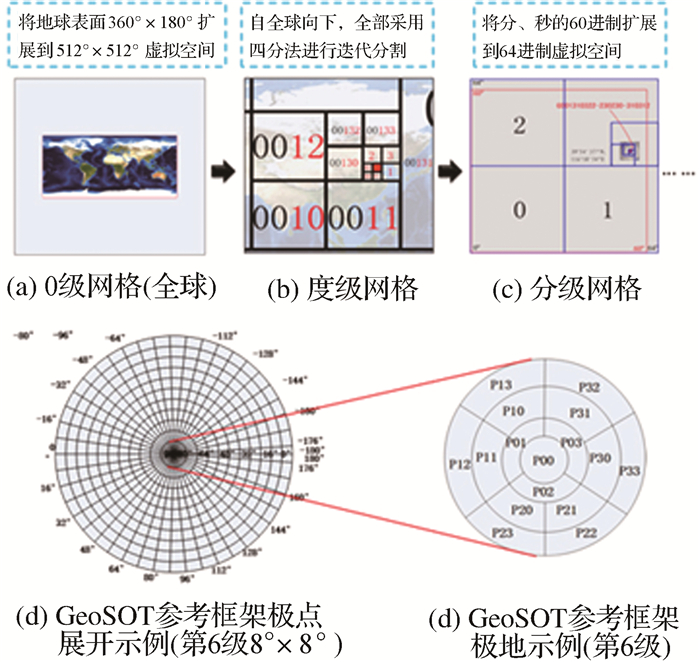
1 GeoSOT原理及优势分析 1.1 GeoSOT网格与编码通过3次地球扩展 (将地球表面真实空间扩展为512°×512°、将1°扩展为64′、将1′扩展为64″) 实现整度、整分的四叉树划分,网格间隔依次为{29°、28°、27°、26°、25°、24°、23°、22°、21°、20°、25′、24′、23′、22′、21′、20′、25″、24″、23″、22″、21″、20″、2-1″、2-2″、2-3″、2-4″、2-5″、2-6″、2-7″、2-8″、2-9″、2-10″、2-11″},从而形成一个上至全球 (0级)、下至厘米级边长 (32级) 的多尺度网格体系。[4]
|
| 图 1 GeoSOT地球剖分参考框架示意图 Fig. 1 GeoSOT discrete grid model reference frame |
在GeoSOT网格划分的基础上,按照“Z”序为每个网格赋予层次性编码,编码形式主要有四进制一维数组 (图 2)、二进制一维数组 (四进制编码的二进制形式) 和二进制二维数组 (二进制一维数组的交叉分组)3种,均由度级、分级、秒及秒小数三部分组成。例如,四进制一维形式的编码12,其二进制一维形式的编码为0110,二进制二维形式的编码为 (01,10)。

|
| 图 2 GeoSOT网格编码示意图 Fig. 2 GeoSOT grid identification code |
1.2 优势性分析
之所以采用GeoSOT地球剖分网格作为地形量化的承载单元,是因为其具有以下5个方面的优势[4-6]。
(1) 全球无缝无叠:GeoSOT是基于经纬度体系的全球剖分,球面任一位置或区域至少归属于一个网格,且同一层级的任意两个网格之间不相交,可满足全球任意范围内的地形量化需求。
(2) 网格粒度丰富:GeoSOT包含32级规则网格,网格粒度最小可至1.5 cm (赤道附近),且理论上可继续细分,完全能够满足地形量化网格的精度需求。
(3) 多尺度嵌套与关联:GeoSOT经由四叉树递归剖分形成,相邻层级的网格之间具有严丝合缝的嵌套关系,小尺度的4个网格即可聚合成更大尺度的1个网格,可满足地形量化数据在不同层级间的向下分解及向上聚合需求。
(4) 网格编码设计科学合理:GeoSOT网格编码具有全球唯一、向下递归以及二进制一维的特性,可以通过网格编码建立不同地形量化分量之间的关联关系。
(5) 编码代数体系科学高效:GeoSOT提供了一套基于网格编码的代数运算方法,摆脱复杂的经纬度浮点运算,将网格编码作为输入与输出,不仅为基于网格的空间计算与分析奠定了理论基础,也为地形量化后的分析提供了方法和手段。
2 地形量化的数据源用于进行地形量化的原始数据主要包括数字高程模型 (digital eelevation model)、数字表面模型 (digital surface model) 和各种地物矢量数据、兵要数据、遥感影像等[7]。规则格网的DEM、DSM数据是地形数据的主要来源,诸如坡度、坡向、坡度变化率等相关地形因子都可在高程信息的基础上派生出来。地物矢量数据是构建地形量化模型中地物影响因素最为主要的数据源,尤其居民地、道路水系、植被等地物影响因素不可或缺,具体表现为点、线、面3种不同形式。兵要数据是按照兵要实体划分,具有丰富的属性和多媒体数据,由于兵要信息数据是以矢量数据形式采集和存储的,其地形量化方法与地物矢量数据类似。影像数据在地形量化方面的应用主要表现为通过人工或自动方式识别影像中发生变化的地物信息,如居民地、道路等,然后将提取后的变化信息以点、线、面的形式进行存储。
通过上述分析,可以看出地形量化的主要对象为以点、线、面为代表的矢量数据和规则格网数据。因此,本文地形量化模型也以矢量数据和规则格网数据为主要研究对象。
3 基于GeoSOT的地形量化模型 3.1 矢量数据的地形量化矢量数据的地形量化方法,是在GeoSOT地球剖分网格的基础上,将参与量化的矢量数据选择合适的网格层级进行网格离散化,然后通过网格编码建立地形量化分量之间的关联关系。以兵棋为代表的六角网格量化方法,通常将量化后的数据设置为六角格的属性或六角格边的属性。本文中均以网格单元作为数据承载的对象,量化后的数据均以网格单元属性进行记录和存储。每个格元除了存储数据的原始属性信息外,还存储该地形因子在不同应用模式下的影响系数[9]。
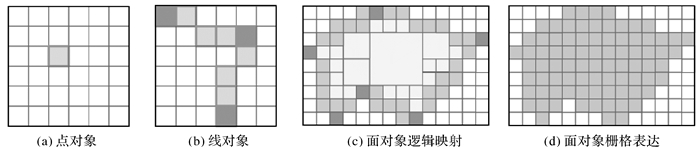
3.1.1 点对象现实世界中并不存在真正的点,而是在一定的数据精度条件下,实体的长度和面积足够小,则将其抽象为点。例如,矢量数据中的居民地、机场,在大区域应用研究中,将其视为点对象,在较小范围区域研究应用中,又可视为面对象。以点对象的量化为例,选择合适层级,根据点对象经纬度坐标数据,映射到GeoSOT网格单元,并计算剖分空间中所对应的网格编码。如3(a) 所示,在剖分空间中,该点状对象Point映射为精度层级Level下的一个网格Code,即
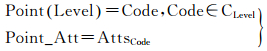 (1)
(1)
式中,Point_Att表示Point的属性,AttsCode表示该网格Code的关联属性集合。对于一个点状剖分实体,属性继承其映射网格的关联属性。
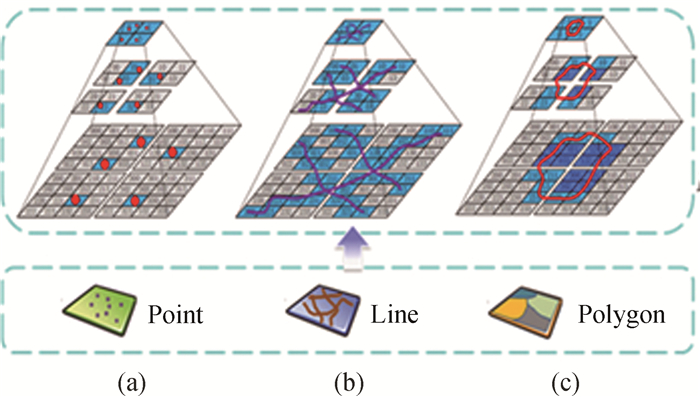
3.1.2 线对象矢量数据量化中的线对象以道路和水系为代表,其中道路主要影响车辆的机动性能,道路网结构与密度影响机动速度,道路的等级越高,通行能力越强,机动速度越快;水系要素主要表现为对人员的阻割、障碍作用。在线对象的量化过程中,线实体表达为一串由相邻的同级剖分网格连接的、呈线状延伸的网格集合。每个网格单元还被赋予了该对象包括通行能力、阻割系数等不同应用场下的影响系数信息。如图 3(b)所示,线状实体Line映射为精度层级Level下的单一尺度网格集合Codes,即
 (2)
(2)
|
| 图 3 矢量数据地形量化示意图 Fig. 3 Vector data terrain quontization method |
式中,Line_Att表示Line的属性,AttsCodei表示Codei的关联属性集合。对于一个线状剖分实体,属性继承其映射网格集合的所有关联属性。
在进行线对象的地形量化时,可以采用Level+n(n≥1) 层级进行网格离散化处理,更为精细的网格表达可以在一定程度上规避缺失网格边属性缺失的问题。
3.1.3 面对象面对象的量化主要以居民地、植被以及面状水系为代表,对作战行动的突出影响反映在障阻与隐蔽方面。面状对象是将一组点对象按照一定的顺序依次连接而得到的封闭且连通的二维实体,该实体的剖分逻辑映射网格分为边界和内部网格两个部分。如图 3(c)所示,在剖分空间,面状实体Area映射为精度层级Level下单尺度边界网格集合BCodes和多尺度内部网格集合ICodes,即
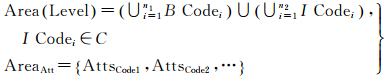 (3)
(3)
式中,Area_Att表示Area的属性,AttsCodei表示Codei的关联属性集合。对于一个面状剖分实体,属性继承其映射网格集合的所有关联属性。
另外,当面状实体的剖分逻辑映射网格均转化为精度层级Level下的单一尺度网格,即式 (3) 中的I Codei∈C替换为I Codei∈CLevel时,得到面状实体的剖分栅格表达形式,如图 3(d)所示,式 (4) 同时记录了面实体的轮廓与内部信息,与传统栅格记录方式一致
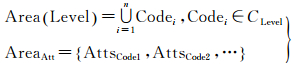 (4)
(4)
在图 3中,面对像的两种地形量化的表达形式,是同层级网格下的网格聚合,即在制定网格层级Level下,具有相同属性且相邻联通的网格单元可以将其向上聚合为上一层级甚至更高层级的网格单元,属性信息不变。
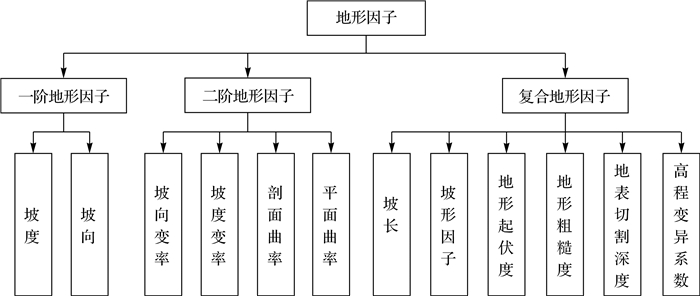
3.2 规则格网数据的地形量化以DEM、DSM为代表的规则格网数据是地貌量化数据的主要来源。其量化方法主要是在其高层信息的基础上,通过进一步计算得到各个不同指标的地貌因子,图 4详细列出了地貌因子的分类。然而,地形表面千变万化,形态各异,要通过地形因子反映这些地形特征,首先应对地形表面进行数学化表达,简单的数学曲面一般很难反映地形的变化特征,理论上任何复杂的曲面都可以用高次多项式以任意精度去逼近[8-9],但在实际应用中多项式系数也不是越高越好,应根据实际数据精度和算法适应性确定多项式次数,一般不会高于三次。如果对拟合曲面多项式求一阶导数并进行组合,可以得到如坡度、坡向、变差系数、变异系数等的地形因子;如果对多项式求二阶导数并进行组合则可以得到坡度变化率、坡向变化率、曲率等地形因子,通过对一阶、二阶地形因子进行复合计算,还可以得到一系列复合地形因子。具体的计算方法此处不再赘述,需要强调的是,每个GeoSOT网格单元都存储记录该格元所对应的地形因子分量信息。
|
| 图 4 点、线、面实体剖分表达效果示意图 Fig. 4 Point, line and polygon feature expression method |
|
| 图 5 地貌因子分类体系 Fig. 5 Geomor phologic factors classification system |
3.3 地形量化数据的组织与存储
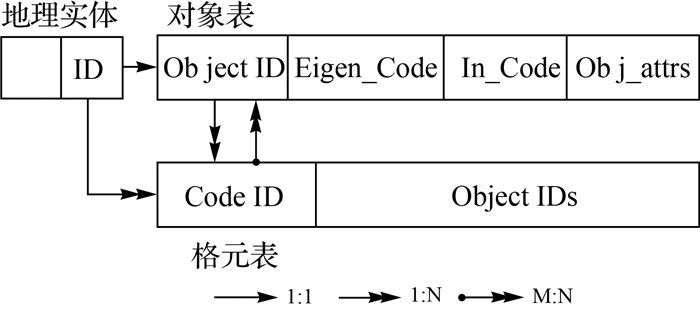
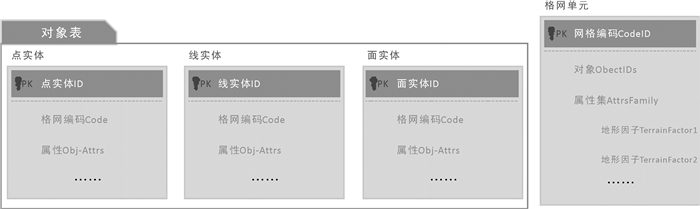
地形量化后的数据以GeoSOT网格单元作为承载对象,因此数据的组织与存储具有网格和对象两种组织方式。格元表中,以GeoSOT编码作为数据表的主键,记录标识码ID,用于唯一地标识剖分空间的网格,同时记录网格内的各类关联信息,包括实体对象、属性信息、地形因子的影响系数等,便于面向区域的空间操作,为地形量化后的分析计算提供支撑。对象表中,每个对象记录都具有标识ID码,用于唯一地标识确定一个空间对象,同时记录对象相关属性信息,满足现有系统对基于对象的传统数据操作。对象表和格元表通过格元表中Objects字段进行关联,支持格元-对象的协同关联操作。[10]
对象表仅对地物因子而言,以地理实体的一体化网格编码Code来记录实体整体的空间区位信息,以Obj-Attrs字段集合记录对象的非空间属性,具体的字段设置由应用需求和场景决定。格元表以多尺度的网格编码CodeID为主键,并设置ObjectIDs记录与网格相交的实体对象集,AttrsFamily属性集记录地形量化信息以及各类地形因子的影响系数等。从规格网格数据如DEM、DSM数据中计算得出的地形量化数据主要存储在该表中。格元表也可称为剖分关联表。各表的物理存储结构如图 6所示。
|
| 图 6 剖分数据表结构示意图 Fig. 6 Subdivision data table structure |
3.4 地形量化数据的聚合
所谓地形量化数据的聚合,是指由较低网格层级的地形量化数据通过网格之间的聚合方式,形成更高网格层级的量化数据。前文在面数据网格量化的过程中,简要介绍了具有相同属性、相同空间范围的格元数据,可在面要素内部进行同级网格之间的聚合。那么此处的网格聚合是网格剖分的逆向, 是对低层级量化数据在GeoSOT剖分网格的基础上,以2n向上聚合更高层级的网格。聚合后的网格量化数据由低层级网格数据按权重求取均值得到
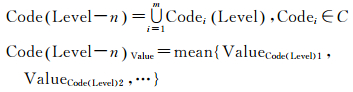 (5)
(5)
采用本文提出的地形量化模型,在车辆越野通行能力分析中对模型的可行性以及网格向上聚合能力进行应用验证。验证方法为:分别采用GeoSOT第17层级 (16″) 网格、19层级 (4″) 网格分别对地形、地貌、土壤、植被、水文等对车辆速度产生影响的地形数据进行基于网格的量化,将量化后的数据按照地形因子的不同进行分层处理,对给定层的每个网格单元分配车辆减速系数Ci(Ci∈[0%,100%]) 并作为格元表中的一个属性项进行存储,然后计算越野机动合成建模图层中每个网格单元的车辆移动速度衰减值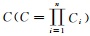
由于本文试验用DSM数据所在区域的地图矢量数据中植被、管线数据缺失,在实验过程中未找到合适的矢量数据替代,无法完整展现各地形影响因素的综合影响效果,故选用其他地区1:25万矢量数据和DEM数据来说明基网格的越野机动通行能力分析的实际应用效果。
4.2 试验方法(1) 确定地貌、植被、土质、水系、居民地、道路、障碍物、其他影响因素8个地形因子分量进行地形量化分析;
(2) 选择GeoSOT第17层级16″、19层级4″网格,分别对DEM和矢量数据采用本文提供的方法将计算后的地形因子分量数据依次作为数据项存储在各自层级的剖分格元表中;
(3) 计算每个网格单元对应的复合减速系数,以正常车速60 km/h计算对应地域内的数据计算通行速度,图 7中颜色越深,通行能力越差。
|
| 图 7 物理存储表结构 Fig. 7 Physical storage table structure |
(4) 应用网格向上聚合方法,从19级层级网格向上计算17层级网格对应的地形量化数据,生成实验效果图,对比二者之间的一致性。

|
| 图 8 越野通行能力分析 Fig. 8 Cross-country capacity analysis |
4.3 结果分析
通过本文提供的量化模型,实现了矢量数据中居民地、植被、水系、交通等图层中线、面对象的网格剖分,并进行了网格单元的赋值处理,完成了矢量数据的地形量化。此外,利用DEM数据计算了该区域内地形的坡面参数 (坡度、坡向),并对应矢量数据网格单元进行了量化数据赋值处理,完成了DEM数据的地形量化。试验效果与实际地形通行能力基本相符,验证了基于网格的地形量化方法的可行性。利用通过19层网格向17层网格的聚合计算,计算结果基本一致。验证了地形量化中由低级网格向高级网格聚合的可行性。
5 结论与展望本文在GeoSOT的基础上建立了基于四边形网格的地形量化模型,采用GeoSOT二进制一维编码,实现了多层地形量化数据的关联、检索,为地形量化数据的组织与管理提供了方法。与六角格的地形量化模型相比,该模型量化方法简单,且网格层次丰富,可以选取任意合适网格层级进行地形量化计算。此外,该方法具有更好的向上聚合能力,可以不必通过重新计算,便可通过网格聚合方法得到更高层级的地形量化数据。然而本文的试验仅验证了数据模型的可行性,在地形量化效率和地形量化结果准确性方面的评价标准还不严格,需要进一步研究完善。
此外,本文仅采用网格化的方法讨论了矢量和规则格网数据的地形量化模型,对于基于编码的空间运算和分析的应用并不深入,下一步的工作是在地形量化的基础上运用GeoSOT特有的编码代数体系进行地形量化之上的地形分析研究。
| [1] | 郭齐胜, 郅志刚, 杨瑞平, 等. 装备效能评估概论[M]. 北京: 国防工业出版社, 2005. GUO Qisheng, ZHI Zhigang, YANG Ruiping, et al. Introduction to Weapons Equipment Systems Effectiveness Evaluation Methods[M]. Beijing: National Defence Industry Press, 2005. |
| [2] | 刘雅, 乔晓, 鱼江海. 兵棋地图地形量化方法及其实现[J]. 指挥信息系统与技, 2013, 4(3): 71–75. LIU Ya, QIAO Xiao, YU Jianghai. Methods and Implementation for Terrain Quantization of Wargame Map[J]. Command Information System and Technology, 2013, 4(3): 71–75. |
| [3] | 周成军, 张锦明, 范嘉宾, 等. 训练模拟系统中地形量化模型的探讨[J]. 测绘科学技术学报, 2010, 27(2): 149–152. ZHOU Chengjun, ZHANG Jinming, FAN Jiabin, et al. Research Terrain Measured Model Applied in the Training Simulation System[J]. Journal of Geomatics Science and Technology, 2010, 27(2): 149–152. |
| [4] | 程承旗, 任伏虎, 濮国梁, 等. 空间信息剖分组织导论[M]. 北京: 科学出版社, 2012. CHENG Chengqi, REN Fuhu, PU Guoliang, et al. An Introduce to Spatial Information Subdivision Organization[M]. Beijing: Science Press, 2012. |
| [5] | 程承旗, 关丽. 基于地图分幅拓展的全球剖分模型及其地址编码研究[J]. 测绘学报, 2010, 39(3): 295–302. CHENG Chengqi, GUAN Li. The Global Subdivision Grid Based on Extended Mapping Division and Its Address Coding[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(3): 295–302. |
| [6] | 吕雪锋, 廖永丰, 程承旗, 等. 基于GeoSOT区位标识的多源遥感数据组织研究[J]. 北京大学学报 (自然科学版), 2014, 50(2): 331–340. LÜ Xuefeng, LIAO Yongfeng, CHENG Chengqi, et al. Multi-Source Remote Sensing Data Organization Based on GeoSOT Location Identification[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2014, 50(2): 331–340. |
| [7] | 赵鹏. 基于栅格中间层的地形分析方法研究[D]. 郑州: 解放军信息工程大学, 2013. ZHAO Peng. Research on The Terrain Analysis Method Based on The Raster Layer[D]. Zhengzhou:PLA Information Engineering University, 2013. |
| [8] | 陈东. GIS剖分数据模型研究[D]. 北京: 北京大学, 2016. CHEN Dong. Subdivision Data Model of GIS[D]. Beijing:Peking University, 2016. |
| [9] | 吕雪锋. 基于GeoSOT剖分编码的空间信息区位标识研究[D]. 北京: 北京大学, 2012. LÜ Xuefeng. Spatial Information Location Identification Based on GeoSOT Grid Coding[D]. Beijing:Peking University, 2012. |
| [10] | ZHOU Qiming, LEES B, TANG Guoan. Advances in Digital Terrain Analysis[M]. Berlin Heidelberg: Springer-Verlag, 2008. |
| [11] | WILSON J P, GALLANT J C. Terrain Analysis:Principles and Application[M]. New York: John Wiley & Sons, 2000. |
| [12] | HENGL T, REUTER H I. Geomorphometry Concepts, Software, Applications[M]. Amsterdam, Boston: Elsevier, 2009. |
| [13] | CARTWRIGHT W, GARTNER G, MENG Liqiu, et al. Lecture Notes in Geoinformation and Cartography[M]//ZHOU Qiming, LEES B, TANG Guoan. Advances in Digital Terrain Analysis. Berlin Heidelberg:Springer-Verlag, 2008. |



