进入21世纪,地理空间信息网格 (geospatial information grid) 技术得到迅速发展,其多样化的表现形式使得人们产生困惑。它仅仅是一种剖分算法,还是数据组织模型?或者只是传统技术的另一种“时髦”的称谓,地图投影、栅格数据、DEM数据、影像金字塔等属于地理空间信息网格吗?它的价值在哪里,未来会怎样?本文对地理空间信息网格基本概念、发展历史和未来发展趋势给出描述。
1 地理空间信息网格是地理空间网格在信息化条件下的技术形态对地理空间信息网格的认识必须统一到地理空间网格 (geospatial grid) 的基本概念上来。地理空间网格是人类在认识地形环境过程中逐渐形成的一种基本理论和方法,即通过一定规则组织起来的、连续的、多分辨率的网格单元,逐步逼近最真实的地球,把空间的不确定性因素控制在相应的尺度范围之内。
1.1 地理空间网格的基本特征通过多年来的讨论[1-5],地理空间网格的基本特征可明确为:
(1) 基准性。建立严格的空间、时间数学控制模型,在参考椭球、大地坐标系等方面确保一致。
(2) 连续性。将地球空间整体或局部剖分为若干网格单元,连续地描述空间事件和空间对象,保证空间上不重叠。
(3) 唯一性。每一个网格单元表达唯一确定的空间位置,编码不能出现二义性。
(4) 多尺度性。实现对地球空间的层次化剖分与编码,建立不同层级的网格单元之间的嵌套隶属关系,能够组织多分辨率空间数据,支持多尺度空间现象和过程的描述与分析。
(5) 近似性。表现为一系列同层接近、邻层相同、逐层一致的几何近似性结构特点。
(6) 适应性。既为跨领域研究提供统一的基础结构,又要适应不同领域对地理空间信息的个性化需求。
(7) 关联性。地理关联,是将地理空间数据转化到网格的框架中,使网格单元成为地理空间数据组织管理与分析应用的基本单元;剖分关联,是指剖分算法遵循严格的数学组织规则,网格单元之间存在着密切的空间关联关系,同时各种网格剖分算法之间可以相互转换。
1.2 地理空间信息网格的广义和狭义认识地理空间信息网格则是地理空间网格在信息化时代的体现,有广义和狭义两种描述方式。广义上的地理空间信息网格是指以计算机、测绘、遥感、导航等科学为基础,构建的天地一体的空间信息获取、存储、分发、计算、服务体系,包括计算网格、数据网格、服务网格3部分[6]。其中,地理空间计算网格是指将网络上分布的、与地理空间信息领域相关的、各种同构与异构的计算机、工作站、机群等设备的计算能力聚合起来,形成相对用户透明、虚拟的高性能计算环境;地理空间数据网格是指与信息化技术环境相适应,将地理空间数据进行网格化剖分和组织,使其支持海量存储、管理与调度,支持多维空间信息的融合、分析;地理空间服务网格是在计算网格和数据网格的基础上,支持各种同构/异构的地理空间服务资源的动态加入/退出、自治管理、分发等。
狭义上的地理空间信息网格是指地理空间数据网格,即按照严格的空间剖分规则,构建一系列紧密关联的空间单元集合,支持地理空间数据的网格同化、网格存储,多维环境信息网格融合和网格分析等[5]。
2 地理空间网格发展历史在人类认知客观世界的过程中,曾产生过一系列的科学方法论和技术。地理空间网格就是这样一种人类空间认知的重要思想和理论、方法。地理空间网格的发展大致可分为古代地理空间网格、近代地理空间网格、现代地理空间网格三种阶段,具体表现为多种形式。
2.1 古代地理空间网格古代中国是典型的陆地型国家。对地球的认知是“天圆地方”的思想,在中国古代地图作品中充分体出这种最初的原始平面空间划分思想,最典型的是我国古代夏商周时期的“井田制”。公元200多年,“计里划方”思想出现在西晋地图学家裴秀提出“制图六体”理论中,成为中国古代和近代地图编制、进行精度控制与量算的基本方法。典型产品有:唐代贾耽绘制的《海内华夷图》、北宋沈括绘制的《天下州县图》、宋代刻于岐山石碑上的《禹迹图》、元代朱思本绘制的《舆地图》、明代罗洪先绘制的《广舆图》等等。
古代希腊是典型的海洋型国家。对地球是球形的认识,来自于古希腊人观察从远方驶来的帆船时,先看到船帆再看到船身的现象。约公元前500年,哲学家毕达格拉斯最早提出地球球形学说。公元前334年,地理学家尼尔库斯在亚历山大东征中第一次在地图上划出了一条纬线。公元前300年,天文学家埃拉托斯在编制以地中海为中心的世界地图上绘制了7条经线和6条纬线。公元前134年天文学家依巴谷绘制星图的同时,设计了喜帕恰斯经纬线体系。公元127年克罗狄斯·托勒密绘制出著名的“托勒密地图”,在地图上绘制了经纬线网。
可以看出,古代人类出于对所处生活地域和地球的认识,一直在寻找一种能够解释自然现象,可以用数学来表达的工具。用点、线、面来表示空间对象是人类空间抽象思维上的一个显著进步,最为典型的是古希腊学者已经从数学和天文学出发,尝试用抽象概念的形式解释事物的本质。无论是东方的“井田制”、“计里画方”,还是西方初期的“经纬度”,表现形式仍是相对具体和直观的,是通过一种简单的网格划分来实现控制地图的比例和绘制精度,是一种“规则化”的“概略控制”的思想。这种古代的地理空间“朴素”网格思想与当时人类的认知能力是一致的。人类开始急切地认识自己周围的世界。
2.2 近代地理空间网格经过漫长的中世纪徘徊,14世纪文艺复兴之后,人类历史进入了地理大发现时代。随着国家意识的强化和空间拓展的需要,地图在国家之间的外交谈判、军事斗争中发挥着越来越重要的作用,人类迫切需要建立更加精密的地理空间表达体系。
1406年,托勒密的《地理学指南》开始广为流传,人们学会了通过不同的投影网格选取面来观测世界,利用经纬度制表法来进行空间数据精确化和标准化表达。1569年,荷兰地图学家墨卡托首次采用正轴等角圆柱投影编制航海图,开辟了人类利用地图投影科学认知地球的新纪元。
1615年,荷兰数学家斯涅耳发明了大地三角测量方法,几何大地测量学成为建立国家大地网和工程测量控制网的基本方法之一。1669—1733年,法国卡西尼家族在测量子午弧的过程中,构建出与天文测定的基本网相联结的法国一级三角点的三角网络,第一次精确地测算出法国的全国面积与形状,接着又构建了二级与三级的三角点网络,以此作为大比例尺地图的基础性架构。此后,欧洲很多国家都开展了大规模的全国性三角测量工作。
为了保证测量坐标系的准确性,天文学家从大量观测地球形状的工作中提出了参考椭球体重要理论,并以此构建独立的大地坐标系。参考椭球理论的出现提供了一个重要的空间基准和严格的数学模型。这个阶段主要的参考椭球体有1800年法国的德兰勃椭球,1830年法国的埃弗瑞斯椭球,1841年德国的贝塞尔椭球,1866年英国的克拉克椭球等。1910年的美国海福特椭球成为国际上第一个推荐值。1941年前苏联提出克拉索夫斯基参考椭球模型。
为了满足世界各国的不同需要,各国规定使用了不同的地图投影方法作为地图的数学基础,主要有1752年法国的彭纳投影、1772年德国的兰勃特投影、1912年德国的高斯-克吕格投影等。
1891年,德国地理学家彭克提出世界各国共同编制百万分之一比例尺世界地图的建议。1913年在巴黎世界地图会议上通过了《国际百万分之一世界地图编制细则》,成为之后世界多国地形图生产的基本标准。此时,人类已经具备构建全球统一的地理空间框架的理论和实践能力。
整个17至19世纪,人类认识客观世界的方法取得了巨大的发展。试验和数学是占统治地位的科学方法,人们通过归纳和演绎,从细节上把握思维对象和客观世界。唯物辩证法产生,给出了一种从总体上把握客观世界,并指导实践科学的思维方法。这个阶段,人类虽然站在地球表面,但通过大范围的地理观测实践,已经掌握了认知所处星球的有效科学工具,这就是解析几何理论、微积分理论、大地测量理论和地图投影理论。无论是椭球理论模型的“经纬网”,还是实地布设的“三角控制网”,以及地图投影后的“坐标网”,都在追求一种严格“数学规则”下的可控制量测的目标,共同构成这种近代的地理空间“量测”网格思想。
2.3 现代地理空间网格以第一次世界大战为分界线,现代人类社会在短短的100年内取得了巨大的科技成就。这个阶段,地理空间网格思想及技术有了显著的进步,其内涵和外沿产生巨大的变化,称之为“地理空间信息网格”。
2.3.1 全球化的人类活动,需要以全球为对象的新坐标框架第一次世界大战前后,为了提高炮兵的射击精度,各国根据军事需要纷纷使用等角投影。1917年法国改彭纳等面积投影为兰勃特等角投影,德国也将卡西尼投影改算为高斯-克吕格投影,并使用了军用坐标网。1928年前苏联建立按经差6°分带的高斯-克吕格投影,开创了大范围统一全国地形图投影的先例。
第二次世界大战以后,美国为了配合其“全球战略”的需要,于1948年提出“通用横轴墨卡托投影”(universal transverse mercator projection,UTM) 和“通用极球面投影”(universal polar stereographic projection,UPS)。为适应全球作战和指挥业务的方便,美军制定了军用坐标参考系 (military geographic reference system,MGRS) 标准。在全球8°×6°分区的基础上,MGRS按照100 km边长绘制“方格”坐标网,通过逐步细化可以达到米级网格,支持全球唯一编码。MGRS用网格编码法替代图幅分幅编号法,在统一标定位置、指示区域上具有很好的效果,历经多次作战检验。2001年9·11事件以后,MGRS成为美国国家网格 (united states national grid,USNG) 标准。
20世纪50年代末,卫星和远程弹道武器出现后,为了精确推算轨道与跟踪观测,必须建立新型地心坐标系。世界上第一个统一的地心坐标系是1984年WGS-84世界大地坐标系。2008年中国全面启用2000国家大地坐标系。
坐标网、比例尺、大地控制网 (平面控制网和高程控制网) 统称为地图的数学基础,是地图上确定地理要素分布位置和几何精度的基本依据。这种“全球连续覆盖”、“唯一”、“尺度+控制”的理念,正是传统地理空间网格的核心思想。
2.3.2 航测、制图技术的现代化,需要相一致的空间数据模型1903年飞机问世,1910年德国研制成功了用于航空摄影测量的立体测图仪,人类跨入从空中进行地形图测绘的新阶段。1957年,前苏联发射了第一颗人造地球卫星,开创了人类从新的高度进行全球性观测的新纪元。航空航天对地观测所获取的都是行扫描的遥感影像数据,以像素作为空间对应的基本单元,是一种多分辨率的“像素”网格,具备了“海量”特征,影像金字塔等技术成为影像“像素”网格管理和应用的重要工具。
1946年世界上第一台数字式电子计算机诞生,20世纪50年代后计算机技术开始应用于地图制图领域。栅格数字地图是将地球表面划分为大小、均匀、紧密相邻的网格阵列,按行与列排列、具有不同灰度或颜色的阵列数据。为了更好地存储、管理地理空间数据,人们开始使用空间数据库技术。空间数据的整体管理仍遵循传统纸质地图的分幅组织方法。
1999年,Google Earth在全球空间信息的网络存储与管理方面取得了巨大突破,多尺度、多源、海量地理空间数据的网络快速浏览成为现实。它打破传统纸质地图的分幅组织管理方法,完全以分块、分层的思想组织管理空间数据。为了应对网络环境下地理空间数据的获取、存储、检索等应用需要,“网格剖分”的概念开始提出。
2.3.3 信息化知识服务的需求,需要最佳的认知工具和应用平台1956年美国Miller教授提出数字高程模型 (digital elevation model,DEM) 概念。DEM有规则网格 (Grid) 和不规则三角网 (TIN) 两种表现形式,通过细节分层 (level of details,LOD) 技术实现多级表示。规则网格数字高程模型 (Grid DEM) 具有地理空间网格的典型特征,如“严格空间基准”、“规则化”、“近似性”、“多分辨率”、“连续性”等,不规则三角网虽然描述空间特征更加优秀,但却不符合“规则化”和“近似性”的特征。DEM最大的进步是使地理空间网格具备了“分析”的特征,利用网格单元之间的空间关联性,结合属性数据可以进行空间分析,支持多种复杂空间问题的求解。从1967年世界上第一个地理信息系统 (Canada geographic information system,CGIS) 在加拿大诞生起,地理信息系统技术得到飞速发展。其中数字高程模型都是重要的空间分析源数据。
20世纪90年代,人们提出虚拟地理环境 (virtual geographic environment,VGE) 概念。1998年美国副总统戈尔描述的“数字地球”就是一个以地球坐标为依据的、具有多分辨率的、多维海量数据和多维显示的虚拟地球系统。其核心就是基于地理空间信息网格的多维空间数据组织模型,使得VGE集成政治、经济、军事、地理、大气、地球物理等多门学科的知识和机理,成为多学科应用的平台。长期以来,地学领域中研究地壳构造、地质、地震、海洋、大气、地球物理的学者一直从自身专业角度出发,已设计了多种类型的全球或局部三维网格模型。与上述研究有所区别的是,VGE更要求基于统一的地理空间框架,进行严格的地球空间多级网格剖分,构建基于网格的空间数据组织模型,支持多维信息的融合、可视与分析。真正意义上的“地理空间信息网格”概念开始出现,地理空间信息网格成为VGE的核心数学基础之一。
1992年文献[7]提出了一种全球地理信息层次数据结构。1998年文献[8]提出离散全球网格系统 (discrete global grid systems,DGGS) 思想。2000年文献[9]提出全球四元三角形网格思想。文献[10-16]提出了多种类型的地球球面网格剖分方案。虽然各有不同的应用范畴,其实质均是基于地理空间信息网格的多维空间数据组织模型。
从数学模型上来看,地理空间信息网格可以分为4类:①地理空间信息平面网格,包括地图投影经纬线网格、图像像素网格、数字地形模型网格,都是在二维平面上描述地理空间实体及现象;②地理空间信息球面网格,直接在地球参考球体 (椭球体) 面上进行系列网格剖分,构建空间数据组织模型;③地理空间信息立体网格,将地球球面扩展为地球立体空间,支持三维、动态空间对象表达;④地理空间信息时空网格,在地球空间立体网格基础上增加时间编码,支持复杂时间变化事件的组织管理。从平面网格、球面网格,扩展为立体网格和时空网格,是一脉相承的。
2.3.4 计算网格等新技术发展,推动计算科学与空间科学的结合随着互联网等信息化技术的发展,出现一系列与网格相关的概念。例如,Net主要指网络、网状物、通信网、计算机网、神经网等含义;Network特指计算机网络;Grid主要是指格子、地图坐标方格、输电网等含义。虽然它们的共同之处都是由相互交叉的若干条边构成,相互支撑、相互关联;但Grid更强调严格的数学模型,空间的规则性和形状的近似性。
21世纪起始,美国计算机学家Ian Foster在《The Grid: Blue print for a New Computing Infrastructure》[17]一书中指出:“网格是建筑在互联网上的一组新兴技术,它将高速互联网、高性能计算机、大型数据库、传感器、远程设备融为一体,为用户提供更多的资源、功能和交互性”。这里的Grid是计算网格 (computing grid) 的概念,主要指网络环境中计算资源、软件、数据的整合和利用。而地理空间信息网格是指地理空间信息资源的整合、组织管理和共享应用的基础。两者虽然都具有“信息化”、“整合资源”、“广域分布”、“基础平台”等共同特征,但是不同领域的不同概念。如何建立两种网格的科学、实用的联系?信息网格 (information grid)、知识网格 (knowledge grid) 等一系列新概念已经提出。
1999年,美军国防信息系统局提出全球信息网格 (global information grid,GIG) 计划,目标是构建一个全球互联、对端对终端、高度集成的一体化作战信息系统,通过全维、立体、多频谱、多节点的网格化的信息,在恰当的时间、恰当的地点,以恰当的方式向恰当的人员,安全、及时、准确地提供所需的作战信息资源。GIG中的Grid是一个以网络为中心的作战指挥平台,并不是美军传统的MGRS中的Grid概念。这个阶段,Grid名词的不同使用引发了很多概念上的争议和混淆,2014年美国国防信息系统局已将GIG改名为国防信息网络 (Department of Defense Information Network,DoDIN)。
3 地理空间信息网格的科学思考面对当今社会中科技的迅猛发展,地理空间信息网格作为一种人类认知空间环境的理论和方法,已经焕发出新的活力。
3.1 地理空间信息网格研究对象是信息化的地球系统 3.1.1 地球系统是一个复杂巨系统基于地理空间信息网格技术可以构建地球模拟系统。地理空间信息网格的建立要严格遵循地球时空基准,满足多类型空间实体和空间现象的需求,诸如人类的空间迁移行为、商品物流的轨迹、电磁环境的构设、网络环境的表达等。1997年日本建立“地球模拟器”、2001年欧盟建立“地球系统建模欧洲网”、2005年澳大利亚建立“地球系统模拟器”等都是基于地理空间信息网格模型管理时空数据。
3.1.2 研究对象扩展到地球空间系统地理空间信息网格研究对象已经超越了传统地表空间、近地轨道空间,扩展到地月空间、月球空间、太阳系空间等。把地球和地球外层空间当作一个整体或系统来研究,需要统一表达整体太阳系与地月系、地球坐标系的各类型天球坐标系,遵循地球自转、公转的时间规律,要考虑相对论中时间的变化、时间漩涡的影响。
3.1.3 把握信息化应用模式必须把握信息化条件下地理空间信息网格应用的基本特征。
(1) 应用领域全球化。地理空间信息网格的研究必须建立全球化的基本观点,研究范围涉及整个地球系统、地球空间系统甚至外层空间系统,研究领域涉及陆、海、空、天、电、网等多维环境。
(2) 地理空间信息高度离散化。建设越来越高密度、高精度的大地控制网;获取越来越多类型、多分辨率的航空航天观测遥感影像;建立越来越多尺度、矢量栅格一体的地理信息数据库。
(3) 应用平台网络化。分布式网络环境下的地理信息公共服务应用已经成为地理空间信息化的基本特征,其核心同样是地理空间信息网格技术,支持网格数据存储、网络数据传输、灵活的客户端应用。
(4) 服务智能化。依托高效的空间网格数据组织模型,能够支撑多维空间信息的融合,开展各类型智能化空间分析研究。
3.2 模型理论是地理空间信息网格的基础理论 3.2.1 地理空间信息网格是信息化条件下的地图投影模型传统地图投影是地球球面到欧氏空间二维平面的转换,地理空间信息网格可以看作是信息化条件下的地图投影。
地理空间信息球面网格,是用若干层网格单元表面逼近地球参考面,每一层的网格单元分辨率不同,每一层的投影变换函数都是不同的 (中纬度和高纬度不同),其数学表达式为
 (1)
(1)
式中,X、Y是网格单元内投影平面直角坐标;B、L是地球表面经纬度地理坐标;F1、F2是变换函数;m、n是网格单元行列编码。
地理空间信息立体网格,是将球面网格方案延伸到立体空间,用一系列空间的网格体单元逼近地球空间系统。在每一个网格体单元内采用不同层次概念,每一层次的网格单元分辨率不同,每一层次的投影变换函数都是不同的。数学表达式为
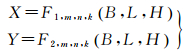 (2)
(2)
式中,X、Y、Z是投影单元体内直角坐标;B、L、H是地球空间经纬度、高度地理坐标;F1、F2、F3是变换函数;m、n、k是行列高编码。
由于地理空间信息网格模型均有着严格的数学模型,因此多种网格模型之间支持相互转换。以地理空间信息球面网格为例,投影转换实质就是建立两个曲面场之间的点对应关系,包括反解和正解两种方法。地理空间信息网格相互转换的基础条件有三个:描述对象是同一的,不能跨越维度,例如均以地球球面为研究对象或者均以地球立体空间为研究对象;坐标基础是统一的,都是地心坐标系和地球参考系;剖分标准是一致的,均遵循地理空间信息网格的基本特征。
3.2.2 地理空间信息网格是信息化条件下的数据组织模型地理空间信息网格可以作为支持地理空间数据的组织调度的索引。地理空间逻辑数据模型可以分为基于对象模型、基于域/场模型、基于网络模型三种。地理空间信息网格在管理域/场数据上具有先天的优势,可以直接将栅格数据按照地理空间信息网格剖分原则进行分割,以网格单元和分层的方式进行组织管理和运算,适合局部区域、重点目标空间数据的快速更新和应用。地理空间信息网格在管理对象数据和网络数据上可以发挥空间索引的作用,对点状、线状、面状目标所压盖的空间单元进行记录,形成逻辑和物理地址索引文件,支持快速调度。
地理空间信息网格可以作为支持陆海空天多维空间数据融合集成的框架。基于地理空间信息网格可以构建陆海空天统一的多维空间数据组织模型,支撑地表、地下、水下、大气、近地轨道、地月等多维空间数据的融合、可视化及应用。例如,支持地下环境准确定位,地下物理过程模拟;支持在海洋水圈空间中准确定位,统一组织管理水下环境数据,海洋环境可视化、海洋三维空间精细化分析等;支持大尺度的全球气象环境和小尺度的局部气象环境统一描述,从水平和垂直两方面进行精细化的表达和分析;支持地表空间、大气空间到近地轨道空间一体化数据组织,支持航天测控准确描述和预测,空间气象环境的精确建模和分析;支持空间多坐标系之间变换,星际导航、轨道设计,高精度行星表面定位、行星测量、行星制图等。
3.2.3 网格是新一代的空间分析模型空间数据高度离散化支撑空间分析的细化。地理空间信息网格支持多尺度的网格单元表达,分辨率可以达米、厘米甚至更高,网格单元内存储的数据颗粒度更高,可以支撑更加丰富的专题信息分析和网格计算,网格分析的结果也更加精确。
基于网格的空间代数运算支撑新型空间关系分析法则。网格代数是在网格编码原理基础上建立加法、减法、成分代数运算法则,满足结合律、交换律、封闭性等代数运算性质。通过网格代数运算,可以将空间实体之间的关系运算转变为网格空间单元之间的关系运算,大大简化空间关系运算流程,提高运算效率。基于网格模型的新一代地理信息系统GRID GIS呼之欲出。
多维空间信息融合推动空间分析模型的精化。基于地理空间信息网格技术可以构建支持多维空间信息统一存储、统一表达和统一分析的数据组织模型,优化空间分析结果。例如:构建城市经济数据网格、交通数据网格、医疗数据网格、通信数据网格、商业数据网格、环保数据网格等,支持城市精确管理;基于地理空间信息网格,可以构建新一代指挥信息系统,支持多维战场环境的深度融合和战场时空冲突分析,实现基于网格的代码指挥。
时空网格将促进时空分析跨越式发展。基于地理空间网格技术可以构建时空一体化的时空大数据组织模型,创新时空分析模型。例如:基于空间立体网格建立空间碎片网格化数据管理机制,提高空间碎片防撞预警与安全分析效率;利用网格时空编码描述作战计划并进行时空推理与分析,推理作战计划各要素与时空约束条件之间的矛盾、作战计划之间及其内部行动之间的时空矛盾,以保证作战计划拟制的科学性。
3.3 构建现代地理空间信息网格体系 3.3.1 统一地理空间信息网格标准,支撑国家空间数据基础设施建设(1) 可作为地理空间信息交换标准。基于地理空间信息网格建立统一的地理空间数据区位标识体系,为建立统一的跨部门空间数据交换提供了理论和技术支撑。
(2) 可作为统一的对地观测网格数据组织标准。在多种对地观测系统的数据预处理、数据承载、数据分发及数据处理与应用诸环节建立统一的网格组织技术体制。
(3) 可作为统一的地面人文数据采集标准。将网格单元与物联网设备相联系,按照统一的网格数据标准采集空间和非空间数据,支持地理大数据更新。
(4) 可作为导航定位编码标准。将地理空间信息网格与传统地图参考坐标系相结合,标识空间对象在地球表面上的区位位置,还可以方便地标识其在立体空间中的区位位置,实现空间对象空、天、地、地 (水) 下统一的位置标识。
3.3.2 构建空间传感器和大数据的网格服务体系,支持智慧地球系统需要(1) 构建统一智能化空间感知体系。构建包括对地观测网格和地面人文数据网格在内的网格体系,将所有传感器空间感知数据融合进入地理空间信息网格体系中,进行数据甄别、支撑数据分析、快速数据检索、服务数据应用。
(2) 构建统一的空间位置标识体系。为空间信息位置服务提供一种新型的信息定位与关联方法,将社交网络中文本、视频进行语义转换进行网格化存储;将不同对象之间的N维关联降为一维关联;展开对不同对象之间地理空间关联程度的度量与计算;支持空间大数据分析。
(3) 构建新型空间信息组织模型。支持地表、天空、地下、水下、太空任何目标的相应的网格单元 (或网格单元集合) 的真三维表达,实现空间信息在地理空间信息网格中的统一管理。空间范围可以从地心至地球外层空间,将三维实体坐标、属性信息 (如湿度、温度、浓度等) 化为实体单元,每一尺度的体元可以连续、无缝、唯一地充满着整个地球立体空间。
(4) 构建多维海量信息可视化平台。设计适应我国国情的、自主可控的地理空间网格算法和编码标准,融合现有各部门空间数据格式,发展一种更高效的全球三维地理信息平台,支持各业务部门空间信息的综合表达与管理。
3.3.3 构建基于网格的机器人空间认知系统,支持智能化平台的空间行为传统的基于对象和基于网络的空间环境描述模型于智能化机器人平台并不是最佳的,机器人导航需要极高分辨率的三维地图。地理空间信息网格可以在机器人空间感知上提出有效的解决方案,支持基于网格导航、基于网格寻路、基于网格避障等。基于网格的机器人空间认知系统涉及高分辨率空间数据采集、海量空间数据管理与存储、网络数据分发、视频三维空间重建、自主路径规划等一系列关键技术,是地理空间信息网格技术的新的典型应用,将具有广阔的发展前景。
4 结论本文主要对地理空间信息网格进行理论特征分析与发展趋势探索,从地理空间网格历史演进脉络入手,认为地理空间网格是一种人类空间认知的重要思想和理论、方法,地理空间信息网格是信息化条件下的地理空间网格。需要进一步指出的是,地理空间信息网格以信息化的地球系统为研究对象,以模型理论为基础理论,未来将发展出现代地理空间网格的标准体系和服务体系,不仅服务于人,还将服务于智能化平台,具有广阔的发展前景。
| [1] | GOODCHILD M F. Criteria for Evaluation of Global Grid Models for Environmental Monitoring and Analysis[R]. NCGIA Technical Report 94, 1994. |
| [2] | KIMERLING J A, SAHR K, WHITE D, et al. Comparing Geometrical Properties of Global Grids[J]. Cartography and Geographic Information Science, 1999, 26(4): 271–288. DOI:10.1559/152304099782294186 |
| [3] | 赵学胜, 王磊, 王洪彬, 等. 全球离散格网的建模方法及基本问题[J]. 地理与地理信息科学, 2012, 28(1): 29–34. ZHAO Xuesheng, WANG Lei, WANG Hongbin, et al. Modeling Methods and Basic Problems of Discrete Global Grids[J]. Geography and Geo-Information Science, 2012, 28(1): 29–34. |
| [4] | 吴立新, 余接情. 地球系统空间格网及其应用模式[J]. 地理与地理信息科学, 2012, 28(1): 7–13. WU Lixin, YU Jieqing. Earth System Spatial Grid and Its ApplicationModes[J]. Geography and Geo-Information Science, 2012, 28(1): 7–13. |
| [5] | 万刚, 曹雪峰, 李科, 等. 地理空间信息网格理论与技术[M]. 北京: 测绘出版社, 2016. WAN Gang, CAO Xuefeng, LI Ke, et al. Geospatial Information Grid Theory and Technology[M]. Beijing: Surveying and Mapping Press, 2016. |
| [6] | 高俊. 网格与测绘[J]. 军事测绘, 2005(1): 5–9. GAO Jun. Grid and Surveying and Mapping[J]. Military Surveying and Mapping, 2005(1): 5–9. |
| [7] | GOODCHILD M F, YANG Shiren. A Hierarchical Spatial Data Structure for Global Geographic Information Systems[J]. CVGIP:Graphical Models and Image Processing, 1992, 54(1): 31–44. DOI:10.1016/1049-9652(92)90032-S |
| [8] | SAHR K, WHITE D, KIMERLING A J. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121–134. DOI:10.1559/152304003100011090 |
| [9] | DUTTON G H. A Hierarchical Coordinate System for Geoprocessing and Cartography[M]. Springer Berlin: Springer-Verlag, 1999. |
| [10] | 陈述彭, 陈秋晓, 周成虎. 网格地图与网格计算[J]. 测绘科学, 2002, 27(4): 1–6. CHEN Shupeng, CHEN Qiuxiao, ZHOU Chenghu. Grid Mapping and Grid Computing[J]. Science of Surveying and Mapping, 2002, 27(4): 1–6. |
| [11] | 李德仁, 肖志峰, 朱欣焰, 等. 空间信息多级网格的划分方法及编码研究[J]. 测绘学报, 2006, 35(1): 52–56, 70. LI Deren, XIAO Zhifeng, ZHU Xinyan, et al. Research on Grid Division and Encoding of Spatial Information Multi-Grids[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1): 52–56, 70. DOI:10.3321/j.issn:1001-1595.2006.01.011 |
| [12] | MA Ting, ZHOU Chenghu, XIE Yichun, et al. A discrete square global grid system based on the parallels plane projection[J]. International Journal of Geographical Information Science, 2009, 23(10): 1297–1313. DOI:10.1080/13658810802344150 |
| [13] | 吴立新, 余接情. 基于球体退化八叉树的全球三维网格与变形特征[J]. 地理与地理信息科学, 2009, 25(1): 1–4. WU Lixin, YU Jieqing. Global 3D-Grid Based on Sphere Degenerated Octree and Its Distortion Features[J]. Geography and Geo-Information Science, 2009, 25(1): 1–4. |
| [14] | 程承旗, 任伏虎, 濮国梁, 等. 空间信息剖分组织导论[M]. 北京: 科学出版社, 2012. CHENG Chengqi, REN Fuhu, PU Guoliang, et al. An Introduce to Spatial Information Subdivision Organization[M]. Beijing: Science Press, 2012. |
| [15] | 赵学胜, 侯妙乐, 白建军. 全球离散格网的空间数字建模[M]. 北京: 测绘出版社, 2007. ZHAO Xuesheng, HOU Miaole, BAI Jianjun. Spatial Digital Modeling of the Global Discrete Grid[M]. Beijing: Surveying and Mapping Press, 2007. |
| [16] | 童晓冲, 贲进. 空间信息剖分组织的全球离散格网理论与方法[M]. 北京: 测绘出版社, 2016. TONG Xiaochong, BEN Jin. The Principles and Methods of Discrete Global Grid Systems for Geospatial Information Subdivision Organization[M]. Beijing: Surveying and Mapping Press, 2016. |
| [17] | FOSTERI, KESSELMAN C. The Grid:Blueprint for A New Computing Infrastructure[M]. San Francisco, CA: Morgan Kaufman Publishers, 1998. |


