2. 北京师范大学减灾与应急管理研究院, 北京 100875
2. Academe of Disaster Reduction and Emergency Management, Beijing Normal University, Beijing, 100875, China
近年来,利用GIS技术进行洪水淹没研究特别是城市内涝研究成为了研究热点,国内外许多学者在这方面做过相关工作,并取得了一定的成果[1]。文献[2]基于GIS模拟了暴雨径流情况下的城市洪水淹没过程。文献[3]利用GIS系统模拟河流在区域上的淹没情况,并对损失进行评估。文献[4]利用GIS对河流水深及周边地形进行建模,用于分析淹没范围。文献[5-6]利用基于GIS的地貌模型来模拟城市雨水径流可能的淹没演进路径。文献[7]基于ArcGIS平台进行二维洪水模拟,并以此建立了综合的洪水管理框架。文献[8]提出了基于GIS复杂地形洪水淹没区有源淹没和无源淹没两种情况下,采用种子蔓延算法的淹没区范围计算方法,并选择区域进行了试验。文献[9]以数字高程模型 (DEM) 为基础,将地形的连通性与三角单元或者任意多边形格网模型技术相结合的方法求解洪水淹没区范围。
这些方法在洪水淹没模拟上能够取得一定的效果,但是普遍只关注洪水最终的淹没范围,而对于洪水的演进过程,沿时间轴的属性变化并考虑较少;另外,目前大多数的研究仍然是基于地形的洪水推演方法,对于城市区域的建筑物等特殊阻拦体,研究较少;部分学者采用地形和建筑物混合的几何数据模型来研究城市内涝推演的情况[10],虽然也取得了较好的效果,但是数据模型复杂等因素带来计算复杂与效率偏低。
本文采用离散格网剖分的方式,建立了一种基于规则多尺度离散格网的城市几何模型,通过三维的地形测量数据和二维的建筑物矢量数据的融合,形成了规则的地表模型,该模型同时考虑了城市地形和建筑等特殊阻拦体。在此基础上,利用体积+时间序列方法,实现了城市内涝洪水的模拟实时推演。
1 城市格网模型的建立在多尺度格网模型的研究中,三角形、四边形 (包括矩形、菱形、平行四边形等)、六边形是常见的格网单元形态[11],本文采用多尺度六边形离散格网作为城市格网模型的构建基础单元,主要是因为六边形格网具备各向同性等几何特性[11],更加适合空间的几何分析与处理,较四边形和三角形格网具有更高的处理精度[12]。本文在处理城市地形和城市建筑等不同对象时,采用同样的离散化数据建立城市格网模型,使得在洪水推演过程中可以采用相同的策略。在实际的城市应用中,大部分城区可以提供的数据主要是城市的建筑物二维矢量地图和城市地形的DEM数据,而较少能提供三维的城市模型数据,因此即使想使用三维的建筑物模型作为基础数据,也是相对比较困难的,本文针对城市地形的DEM数据和城市建筑物二维矢量边界数据,分别研究其格网化方法。
1.1 城市DEM数据的六边形格网采样在确定研究区域后,本文采用的模型拟使用局部城市格网模型,以保证城市格网的高精度与数据管理的可靠性,并根据初始化设定的精度获取格网,格网交点的DEM会根据插值算法自动生成,这样保证DEM的高程数据原始精度完全不损失,生成的六边形格网就是要进行洪水淹没分析的格网模型。在实际应用中,需要根据特定防洪区域的微地形修正DEM数据,以保证地形数据的准确,根据实测微地形 (如堤防、水利工程等) 数据修正DEM (DSM) 的栅格高程值。下面具体讨论六边形格网城市模型的采样方法:
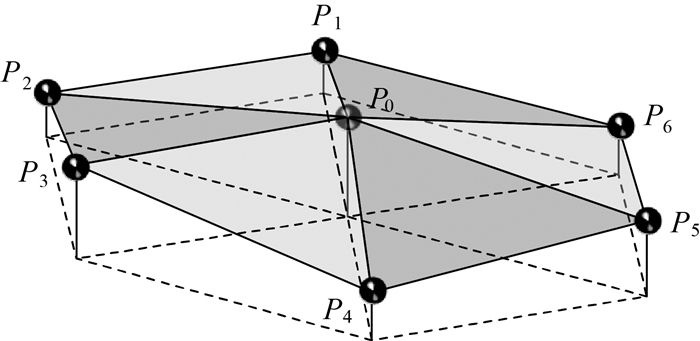
六边形格网可以看成是一个六棱柱。观察六边形格网的特点,它由中心1个节点与周围6个节点组成,传统的采样方式形成的六棱柱格网中,7个节点处的高度一致,如果对7个节点分别进行内插,这样得到7个值,将这7个高度值连接在一起,形成了一个新的六棱柱,只是该六棱柱的顶部不一定是一个平面 (图 1)。
|
| 图 1 六边形格网的棱柱表示 Fig. 1 Prism representation of hexagonal grid |
这样的采样方式,将过去由一点确定的格网单元变成由多点确定的格网单元,相邻单元的过渡将更加平滑。这种格网定义方式,将DEM的显示与数据值的获取分开:
(1) 在DEM显示中,一个六边形格网由7个高度值组成,共同组成格网立方体,格网值出现在节点处,给6个三角面的每一个顶点赋予高程,其中六边形单元被明显放大。
(2) 在格网值获取的过程中,按照传统思路,一个格网只能获得一个高程信息,而图 1的格网六棱柱包含7个高程信息,最直接的方式就是寻找一个与该六棱柱同底的柱体,使两个柱体的体积相等,则新柱体的高度就是获取格网的高程值。
|
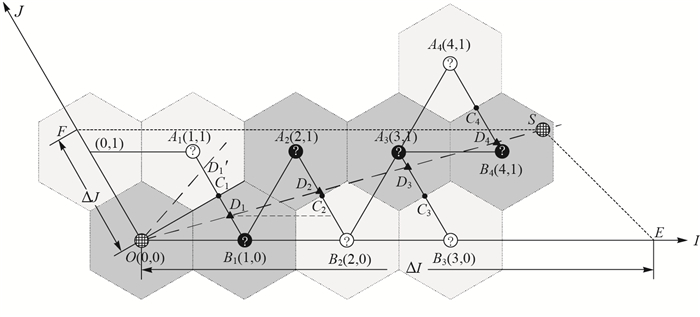
| 图 2 1/6圆域内的六边形格网上的矢量线生产算法 Fig. 2 Vector line production algorithm on the hexagonal grid within circular domain of 1/6 |
在重采样方法上,由于用户提供的地面测量值并不一定是均匀分布的测量点,因此采用基于TIN的双线性内插方法。它的基本过程包括两步:三角构网过程与双线性内插过程。
常用的构网方法有角度判断法、泰森 (Thicssion) 多边形与狄洛尼 (Delaunay) 三角网。后者由任一三角形开始构建的三角网是唯一的,在本方案中,选择该方法。该方法能够保证在构网过程中,每一个控制点都参加构网,不会出现交叉、裂缝等不正常现象,三角网中的双线性内插方法见文献[13]。
1.2 城市建筑物矢量边界的格网化在进行洪水演进的过程中,需要考虑到建筑物的遮挡与拦截作用,因此需要获得地表的DSM模型,即包括建筑物表面信息的地表数据。但是,在大多数情况下,这个数据的获取比较困难,因此本文采用矢量边界数据的格网化来进行地表DSM的构建。建筑物的边界数据可以是采集的封闭矢量线或者面信息,通过这样的信息可以将格网上对应网格立起来,形成高于地表的格网表面。下面是矢量数据格网化的基本方法,分成线数据和面数据的格网化:
线数据的格网化:设线实体任意两个相邻节点单元分别为
建立以G0为原点O的单元120°斜坐标系,见图 2。首先考虑六边形格网在1/6个圆域内的情况,从原点O出发,引向S点 (G1) 的直线OS,其中S的单元斜坐标为ΔI, ΔJ,即在OI轴上OE=ΔI,OJ轴上OF=ΔJ。直线OS从上下 (J方向上) 两个六边形单元中穿过,令上面的单元中心为Ai,上面的单元中心为Bi,AiBi∩两单元的共同边界=Ci,OS∩AiBi=Di,其中i=1, 2, …, ΔI。给出六边形格网下单元激活原则:如果OS从CiBi段通过,激活单元Bi;如果从AiCi段通过,激活单元Ai。下文给出矢量边界六边形格网化的算法步骤:
Step1:按照边的顺序输入多边形的所有边节点In, Jn, n∈[0, N-1], n∈Z,确定多边形包容盒的范围Imin=min{In}, Imax=max{In},Jmin=min{Jn},Jmax=max{Jn},初始化变量数组的所有元素:BImax-Imin+1, Jmax-Jmin+1=0;初始化循环变量n=0。
Step2:(1) 标定节点。if n≤N-1:初始化F=false,转到Step3;else:i=0,转到Step5。
Step3:k=1, whileJn=Jn-k:{k=k+1, F=true},if Jn>Jn-k:LogicL=false;else:LogicL=true;k=1, whileJn=Jn+k:{k=k+1, F=true},if Jn>Jn+k:LogicR=false;else:LogicR=true。
Step4:if LogicL=LogicR:BIn+Imin-1, Jn+Jmin-1=2,n=n+1;else:if F:{BIn+Imin-1, Jn+Jmin-1=2,BIn+Imin-1, Jn+1+Jmin-1=1,n=n+2};else:{BIn+Imin-1, Jn+Jmin-1=1,n=n+1}。
Step5:(2) 勾画轮廓线。if n≤N-1:调用前面矢量边界六边形格网化的算法 (算法Step 4, 5, 6中,内层if和else以后都加上:if j=ΔY:break;else:Bi+Xmin-1, y+Ymin-1=Bi+Xmin-1, j+Ymin-1+1。将“激活单元i, j”去掉);else:n=0,转到Step6;
Step6:(3) 格网行填充。if n < ΔJ:初始化变量Logic=false,j=0,while j < ΔI:{if Logic:激活单元 (j, i);if Bj+Imin-1, i+Jmin-1≠0:{Bj+Imin-1, i+Jmin-1=Bj+Imin-1, i+Jmin-1-1,Logic=!Logic,j=j-1};j=j+1};else:程序结束。
这里给出的任意两个六边形单元间的直线生成算法是离散格网上线实体表达生成算法的基础,任意一条线实体都可以用多条折线段首尾相连得到,即对于格网上的线实体G0, G1, G2, …Gi, …GN,都可以用上面算法计算任意两单元间的直线填充单元。
面数据是建立在线数据基础上的,由一系列封闭边界线组成的几何多边图形。在采用离散格网对面实体进行表达的过程中需要同时表达边界与区域内部,与传统矢量数据仅用一系列顶点组成的简单边界线比较起来,这样的表示方法不但具有前者的高精度,又具有便于空间关系推理计算的优越性。
一般情况的多边形填充算法应用于矩形的光栅显示设备,最简单的方法是检查光栅中的每一个单元是否处于多边形内,由于大部分单元不在多边形内,因此这种方法效率很低,计算多边形的包容盒可以减少计算量。在填充算法的选择上,本文采用了边标志算法作为基础,主要原因是边标志算法只访问每个单元一次,对输入/输出的要求较边填充或栅格填充等算法要低得多[14]。用软件实现时,有序边表和边标志算法有相同的执行效率,然而,边标志算法更适用于硬件或固件实现,这时它的执行效率比有序表算法快一到两个数量级[14]。平面六边形格网与传统光栅扫描器的区别体现在:①坐标定义不一样;②单元间拓扑关系不一致导致封闭实体内外定义不同[15]。本文在分析现有矩形格网上的多边形区域边标志填充算法的基础上,针对该算法在处理任意多边形和水平边界时存在的问题[16]进行修改,并将其扩展到六边形离散格网上,具体的算法如下:
Step1:按照边的顺序输入多边形的所有边节点In, Jn, n∈[0, N-1], n∈Z,确定多边形包容盒的范围Imin=min{In}, Imax=max{In},Jmin=min{Jn},Jmax=max{Jn},初始化变量数组的所有元素:BImax-Imin+1, Jmax-Jmin+1=0;初始化循环变量n=0。
Step2:(1) 标定节点。if n≤N-1:初始化F=false,转到Step3;else:i=0,转到Step5。
Step3:k=1, whileJn=Jn-k:{k=k+1, F=true},if Jn>Jn-k:LogicL=false;else:LogicL=true;k=1, whileJn=Jn+k:{k=k+1, F=true},if Jn>Jn+k:LogicR=false;else:LogicR=true。
Step4:if LogicL=LogicR:BIn+Imin-1, Jn+Jmin-1=2,n=n+1;else:if F:BIn+Imin-1, Jn+Jmin-1=2,BIn+Imin-1, Jn+1+Jmin-1=1,n=n+2;else:{BIn+Imin-1, Jn+Jmin-1=1,n=n+1}。
Step5:(2) 勾画轮廓线。if n≤N-1:调用前面矢量边界六边形格网化的算法 (算法Step 4, 5, 6中,内层if和else以后都加上:if j=ΔY:break;else:Bi+Xmin-1, y+Ymin-1=Bi+Xmin-1, j+Ymin-1+1。将“激活单元i, j”去掉);else:n=0,转到Step6;
Step6:(3) 格网行填充。if n < ΔJ:初始化变量Logic=false,j=0,while j < ΔI:if Logic:激活单元j, i;if Bj+Imin-1, i+Jmin-1≠0:{Bj+Imin-1, i+Jmin-1=Bj+Imin-1, i+Jmin-1-1,Logic=!Logic,j=j-1};j=j+1};else:程序结束。
得到城市建筑物边界矢量的格网填充数据后,为了保证矢量格网能和地形格网一样,为城市内涝推演提供支撑,需要增加高程信息。考虑到大部分城市内涝过程中,建筑物相对高大,洪水难以完全没顶,可以考虑给建筑物添加一个相对大的高程H,在立体空间上形成能够拦水的围栏,形成围栏的城市建筑物矢量格网,可以与地形格网一样,直接参与洪水推演。
2 基于城市格网模型的推演首先,针对某一个特定城区的内涝淹没分析,为减少数据量和便于分析,根据洪水风险,预先圈定一个最大的可能淹没范围。根据需要的精度值,在圈定的可能范围内建立格网,利用插值法读取每个格网所在位置的高程数据,并以单个格网作为淹没范围计算的基本单位。
其次,城市内涝淹没范围的模拟是一个复杂的时空模拟问题,要想完全解决这个问题非常困难。虽然可以用数学模型来模拟洪水演进,但由于洪水演进过程十分复杂,至今还不能用数学物理方程严格地描述其中每一个过程。因此,现有洪水演进模型在许多环节上仍主要借助于概念性元素模拟或经验函数关系描述,而且模型中存在一些假设和简化。本项目采用了“体积法”[17]数值模拟方法来计算淹没的范围。
最后,基于城市区域高精度的格网模型求取给定水位条件下的淹没区,需考虑“流通”淹没的情形,即洪水只淹没它能流到的地方。相当于突发城市内涝洪水向邻域泛滥,比较适合探寻连通区域的处理方法就是连通性判断递归算法。该算法是一种基于空间特征的扩散探测算法,其核心思想是将给定起始格网点赋予特定的属性,在某一平面区域上沿六边形格网的6个方向游动扩散,求取满足给定条件、符合数据采集分析精度、且具有连通关联分布的点的集合。利用递归算法计算淹没区,就是按给定水位条件,求取满足精度、连通性要求的点的集合,该集合给出的连续平面就是所要求的淹没区范围。满足水位条件但与起始点不具备连通关联性的其他连续平面,将不能进入集合区内。淹没区计算的准确性在很大程度上依赖高程数据的分辨率。每一个象元都代表着地面上一个区域,且每一个象元都拥有自己的高程值和精度。
目前不少学者采用体积法进行洪水推演,但是大多采用的是正向推演过程[10, 17],由过程到状态,即已知洪水出水口位置,通过地表格网进行洪水推演,按照等距时间,按照空间关联进行关联计算,将满足所有条件的连通关联淹没点,存入缓存区,并不断地进行累加,从而使淹没区域不断扩大。该方法存在的问题是,运算量巨大,并且在多个出水口的状态下,需要采用并行的方法,并且需要频繁地将淹没区进行合并,实现难度很大,效率很低。本文针对上面存在的方式,提出了一种逆向的水流推演方法,由状态到过程,即以洪水的水淹深度为基础,通过与出水口的连通性,考虑水淹的过程,具体的问题假设和方法如下:
2.1 问题假设(1) 已知有N个城市出水口,分布在城市格网的的不同位置,用集合O={Oi}表示,其中Oi代表第i个出水口所处的格网。整个城市格网用集合C来表示,考虑到问题的简化,城市格网的层级考虑是单尺度的。
(2) 城市内涝洪水的最高水位为Hmax,最低水位为Hmin,水位高低的每次的步进为ΔHj(上涨或下降),Vi表示第i个入水口的出水速度,假设出水水量充足。
2.2 算法步骤Step1:预处理,计算洪水如果正好淹到出水口Oi,Oi可以连通到的整个区域的所有网格集合。调用子流程,计算与每一个Oi可以直接联通的区域网格集合Mi。
Step2:逆向处理,从Hmax→Hmin进行循环,每次洪水下降ΔHj,逐次计算淹没范围。
Step3:洪水水位从Hj+1降到Hj,Hj+1的时刻为tj+1,当洪水高程为Hj时,此时时刻为tj,通过高程直接计算tj时刻整个城市格网集合C中,位于水平面之下的格网集合CD以及正好处于水平面处的格网集合CP,其中CP⊂CD;并将Oi中低于水位Hj出水口集合记为A,高于水位Hj出水口的集合记为B,对两类集合分别计算洪水联通。
Step4:对于A类出水口,由于其低于当前水平面,根据每一个A类出水口的联通区域Mi,计算由所有A类出水口可以淹没的范围Area1=∪{Mi∩CD}。
Step5:对于B类出水口,由于其高于当前水平面,因此需要计算与B联通的刚好被洪水淹没的格网点集合,对于B中任意一个出水口,计算Mi∩CP,并在其中选择任意一个格网单元Bwi,针对B类每一个出水口中对应的Bwi,利用子流程,计算与Mwi可以直接联通的区域网格集合Mwi,计算由所有B类出水口可以淹没的范围Area2=∪Mwi∩CD。
Step6:计算Areaj=Area1∪Area2,即为洪水高程为Hj时,所有被淹的格网区域。
Step7:计算Δ=Areaj+1-Areaj,除以∑Vi,得到水位从Hj+1降到Hj的时间差Δtj,则tj=tj+1-Δtj。
Step8:当洪水水位降至Hmin时,停止循环。将循环过程中不同水位Hj得到的淹没区域Areaj和时间tj倒序排列,即可得到t0, t1, …, tmax不同时刻的洪水高度H0, H1, …, Hmax以及淹没范围Area0, Area1, …, Areamax。
2.3 子流程,完成同等高度水位的区域联通计算Step1:对于整个城市格网区域,输入水位高程H,计算所有在该水位以下的格网集合CD,形成0-1矩阵 (六边形格网,排列成斜120°坐标系),其中1代表水位以下,0表示水位以上。
Step2:对于出水口O,判断0-1矩阵中1的格网与O之间的联通性,采用邻接矩阵存储格网之间的联通性,对于六边形格网,根据周围格网0-1值建立邻接矩阵 (1为联通,0为不联通),采用广度深度遍历的最小生成树方法,以O为连接点获得整个区域的联通情况,返回该联通集合M。
上文算法采用多次集合操作的方式完成区域洪水淹没范围计算问题,其核心是生成联通区域和集合求交操作,算法比较简洁,较传统的正向方法,实现逻辑和效率都有较大改善。本文算法是基于单尺度格网实现的推演方法,如果采用多尺度的方法,效率应该会有更大的提高。
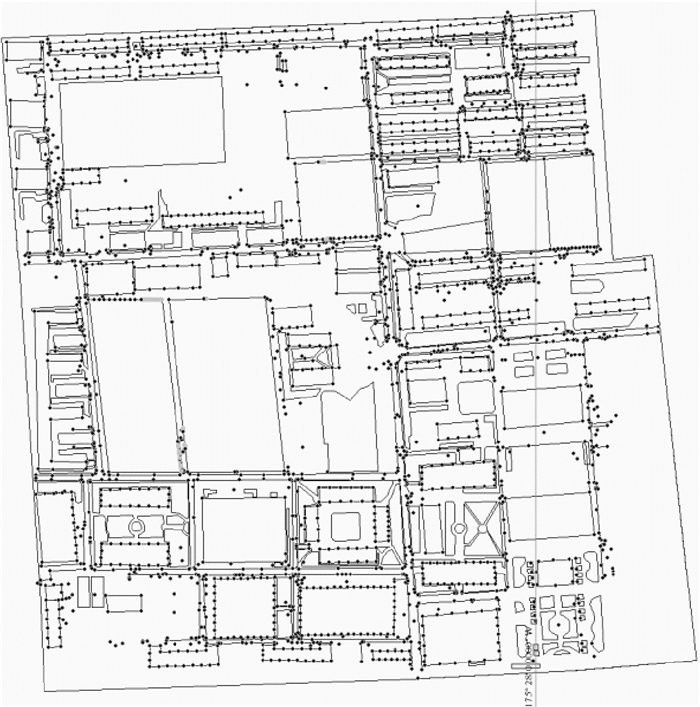
3 试验与分析论文的试验数据采用2012年北京师范大学校园内的基础测绘数据和矢量采集数据[10],见图 3。试验采用的六边形格网是文献[18]提出的全球离散格网系统 (discrete global grid systems,DGGS)。
|
| 图 3 北京师范大学典型试验区 (其中·为测量点) Fig. 3 Representative experiment zone of Beijing Normal University (Among·express measuring point) |
图 4是该区域利用测量点内插的地形数据的六边形格网采样结果,该图对应DGGS的层次是19层,格网平均半径11.268 2 m[18]。

|
| 图 4 地形数据的六边形格网采样建模结果 Fig. 4 The result of modeling based on hexagonal grid of topographical data |
针对格网上矢量建筑物的边界信息,进行格网化填充试验,只需矢量化数据即可生成带建筑物边缘信息的DSM数据。至于建筑物的高度信息,可以从矢量边界中提取,简化的方法也可以直接赋予一个必定高于水位线的值,反正在洪水内涝模拟中,建筑物不可能被完全没顶,所以不会影响到模拟的效果与真实性。试验在不同分辨率层次上,同一个矢量数据进行填充,生成格网化DSM的情况,六边形格网层级从18层—22层,格网半径从22.536 5 m~1.92 m,图 5是其中第18层、20层和22层的效果。

|
| 图 5 不同分辨率层次的DGGS上,矢量数据叠加地形生成的格网化地表模型 Fig. 5 The surface model of grid by overlying vector data and topographic data on the DGGS of different resolution |
在洪水淹没试验中,考虑到北师大本身地形高程的差异,取模拟试验数据中Hmax=49.0 m,Hmin=50.5 m,其中ΔH=0.1 m,格网选择第20层DGGS进行模拟,格网单元半径5.634 1 m,该区域共8428个网格,区域范围左上角经纬度 (116.354 591 508 8°, 39.964 030 578 5°),右下角经纬度 (116.364 494 960 2°, 39.956 556 948 4°)。随机生成5个涌水点,5个涌水点的速度保持一致,皆为17.423 09 m3/min。在上文的洪水推演算法中,得到不同洪水高度时的洪水淹没范围的效果,图 6是其中一组的模拟推演效果,出水口位置见图 6(a)。图 7是北京师范大学内60 min内内涝洪水演进效果的三维可视化效果。表 1显示的是洪水模拟过程中 (49.0 m~50.5 m),每次水位上升的时间耗时和被洪水淹没的网格数,由于地表变化是不规律的,导致上涨相同水位,耗时是不同的,并且其规律只与地表模型本身的形态相关。

|
| 图 6 六边形格网内涝水淹演进数据生成 Fig. 6 Data generation of waterlogging flood routing within hexagonal grid |

|
| 图 7 北京师范大学校园内30 min内内涝洪水演进效果 Fig. 7 The result of waterlogging flood routing within 30 minutes in the Beijing Normal University |
| 序号 | 水位高度/m | 洪水演进时间/min | 被淹网格数 |
| 1 | 49.0 | 0 | 4621 |
| 2 | 49.1 | 7.573 485 375 894 12 | 4629 |
| 3 | 49.2 | 12.306 913 735 827 9 | 4634 |
| 4 | 49.3 | 24.613 827 471 655 9 | 4647 |
| 5 | 49.4 | 35.974 055 535 497 1 | 4659 |
| 6 | 49.5 | 46.387 597 927 351 5 | 4670 |
| 7 | 49.6 | 49.227 654 943 311 8 | 4673 |
| 8 | 49.7 | 51.121 026 287 285 3 | 4675 |
| 9 | 49.8 | 53.014 397 631 258 8 | 4677 |
| 10 | 49.9 | 59.641 197 335 166 2 | 4684 |
| 11 | 50.0 | 63.427 940 023 113 2 | 4688 |
| 12 | 50.1 | 65.321 311 367 086 8 | 4690 |
| 13 | 50.2 | 67.214 682 711 060 3 | 4692 |
| 14 | 50.3 | 69.108 054 055 033 8 | 4694 |
| 15 | 50.4 | 71.001 425 399 007 3 | 4696 |
| 16 | 50.5 | 71.948 111 070 994 1 | 4697 |
4 结语
本文研究了一种基于六边形格网的城市内涝洪水演进方法,讨论了城市格网模型的构建方法,以及基于格网地表一的洪水推演模拟方法,并通过实际数据完成了典型区域的洪水时刻演进试验,得到了洪水范围的覆盖情况。
需要说明的是,本文提出的基于六边形格网的城市内涝演进方法只是从基本原理和方法上对城市内涝的洪水运动进行了初步模拟,只考虑了洪水从特定的出水口涌出的情况,而真实情况的城市内涝包括诸多下水口、自然渗透以及高空降雨等多种情况,因此设计的规则将更加复杂,在基于格网的洪水演进的大框架下,该方法可以进行如下改进。
(1) 对于水平面之上的,可以不予考虑; 而对于水平面以下的,可以采用和低于水平面出水口相同的方法进行处理,只是在计算增量的时候采用减法计算。
(2) 对于自然渗透和高空降雨可以认为是局部网格的一种平均的增加或者减少的操作,只需要在水位的增加较少过程中加上或减去一个均匀变换的定值即可。
致谢: 感谢民政部国家减灾中心的吕雪锋博士以及中国再保险集团李志锋博士的大力支持与帮助。
| [1] | 左文涛. 基于Google Earth的风暴潮洪水演进动态可视化研究[D]. 天津: 天津大学, 2012. ZUO Wentao. Study on Google Earth-based Visualization of Storm Surge Flood Routing[D].Tianjin:Tianjin University, 2012. |
| [2] | CHEN Jian, HILL A A, URBANO L D. A GIS-based Model for Urban Flood Inundation[J]. Journal of Hydrology, 2009, 373(1-2): 184–192. DOI:10.1016/j.jhydrol.2009.04.021 |
| [3] | RAMLAL B, BABAN S M J. Developing a GIS Based Integrated Approach to Flood Management in Trinidad, West Indies[J]. Journal of Environmental Management, 2008, 88(4): 1131–1140. DOI:10.1016/j.jenvman.2007.06.010 |
| [4] | MERWADE V, COOK A, COONROD J. GIS Techniques For Creating River Terrain Models for Hydrodynamic Modeling and Flood Inundation Mapping[J]. Environmental Modelling & Software, 2008, 23(10-11): 1300–1311. |
| [5] | LIU Y B, GEBREMESKEL S, SMEDT F D, et al. A Diffusive Transport Approach for Flow Routing in GIS-based Flood Modeling[J]. Journal of Hydrology, 2003, 283(1-4): 91–106. DOI:10.1016/S0022-1694(03)00242-7 |
| [6] | LHOMME J, BOUVIER C, PERRIN J L. Applying A GIS-based Geomorphological Routing Model in Urban Catchments[J]. Journal of Hydrology, 2004, 299(3-4): 203–216. DOI:10.1016/S0022-1694(04)00367-1 |
| [7] | QI Honghai, ALTINAKAR M S. A GIS-Based Decision Support System for Integrated Flood Management Under Uncertainty With Two Dimensional Numerical Simulations[J]. Environmental Modelling & Software, 2011, 26(6): 817–821. |
| [8] | 刘仁义, 刘南. 基于GIS的复杂地形洪水淹没区计算方法[J]. 地理学报, 2001, 56(1): 1–6. LIU Renyi, LIU Nan. A GIS Based Model for Calculating of Flood Area[J]. Acta Geographica Sinica, 2001, 56(1): 1–6. |
| [9] | 丁志雄, 李纪人, 李琳. 基于GIS格网模型的洪水淹没分析方法[J]. 水利学报, 2004(6): 56–60, 67. DING Zhixiong, LI Jiren, LI Lin. Method for Flood Submergence Analysis Based on GIS Grid Model[J]. Shuili Xuebao, 2004(6): 56–60, 67. |
| [10] | 李志锋. 基于CD-TIN的城市内涝淹没模拟与隐患推演研究[D]. 北京: 北京师范大学, 2014. LI Zhifeng. Urban Storm Flood Inundation Simulation and Analysis Models for Incipient Faults using CD-TIN[D]. Beijing:Beijing Normal University, 2014. |
| [11] | SAHR K, WHITE D, KIMERLING A J. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121–134. DOI:10.1559/152304003100011090 |
| [12] | MIDDLETON L, SIVASWAMY J. Hexagonal Image Processing[M]. London: Springer, 2005. |
| [13] | 朱长青, 史文中. 空间分析建模与原理[M]. 北京: 科学出版社, 2006. ZHU Changqing, SHI Wenzhong. Spatial Analysis and Modeling[M]. Beijing: Science Press, 2006. |
| [14] | ROGERS D F. 计算机图形学的算法基础[M]. 石教英, 彭群生, 译. 2版. 北京: 机械工业出版社, 2002: 46-57. ROGERS D F. Procedural Elements for Computer Graphics[M]. SHI Jiaoying, PENG Qunsheng, Trans. 2nd ed. Beijing:China Machine Press, 2002:46-57. |
| [15] | 章毓晋. 图像工程[M]. 2版. 北京: 清华大学出版社, 2007. ZHANG Yujin. Image Engineering[M]. 2nd ed. Beijing: Tsinghua University Press, 2007. |
| [16] | 张志刚, 刘小冬, 张志强, 等. 改进的多边形扫描转换方法[J]. 计算机工程与应用, 2009, 45(4): 193–195. ZHANG Zhigang, LIU Xiaodong, ZHANG Zhiqiang, et al. Improved Method for Polygon Scan Conversion[J]. Computer Engineering and Applications, 2009, 45(4): 193–195. |
| [17] | 刘小生, 黄玉生. "体积法"洪水淹没范围模拟计算[J]. 测绘通报, 2004(12): 47–49. LIU Xiaosheng, HUANG Yusheng. Analog Calculation of Submerged Area with Bulk Method[J]. Bulletin of Surveying and Mapping, 2004(12): 47–49. DOI:10.3969/j.issn.0494-0911.2004.12.015 |
| [18] | 童晓冲, 贲进. 空间信息剖分组织的全球离散格网理论与方法[M]. 北京: 测绘出版社, 2016. TONG Xiaochong, BEN Jin. The Principles and Methods of Discrete Global Grid Systems for Geospatial Information Subdivision Organization[M]. Beijing: Surveying and Mapping Press, 2016. |



