2. 61243部队, 甘肃 兰州 730020
2. 61243 Troops, Lanzhou 730020, China
大数据时代下,人们获取地理空间信息的方式越加丰富与快捷,空间数据急剧增长,人们对空间认知的需求逐渐增多,传统的空间数据组织与表达方法具有一定的局限性,如:传统的方法仅适用于局部范围,缺乏一种全球范围内统一的空间数据组织与表达,各个区域之间所采用的坐标系不统一、不能相互兼容、可拼接性差等问题;传统的方法已远远不能满足信息大众化时代下人们对空间信息服务提出的需求,其空间数据组织与表达模式的滞后,导致“数据丰富,信息、知识贫乏”的现象[1-2]。因此,如何充分利用多源、海量、多尺度的空间数据进行智能化表达、显示和传输并提供灵活高效的网络化地理信息服务是当前亟待思考和解决的问题。
地球剖分网格系统是将地球表面划分为一系列形状相似、大小规则、相互嵌套的多层次面片集合,通过对剖分面片进行有序编码,为空间信息的标识、存储和索引、计算、表达及服务等提供基础,具有海量空间数据的无缝拼接、多尺度全球覆盖表达、层次关联以及组织与表达统一的特点[3-5]。地球剖分网格系统建立了稳定的球面区域划分规范与区域位置标识体系,对地理位置进行标识与组织,实现了对地理空间的有效模拟,避免了传统空间数据模型平面尺度的局限性,为空间大数据的多尺度表达与应用提供一种新的思路与方法。
本文提出一种剖分网格下顾及用户兴趣的矢量地图多尺度表达方法,其核心思路是:利用网络挖掘出的POI数据建立空间兴趣场模型,得到整个研究区域的用户兴趣度分布;对空间数据进行预处理,划分用户兴趣等级,并依据用户兴趣度大小对空间数据进行按次序分级组织;利用GeoSOT剖分理论将地理空间剖分为不同层次的面片,建立尺度与面片对应关系,在不同尺度下,依据各个面片用户兴趣度不同,表达出详细程度不同的空间要素,实现依据用户兴趣度的空间要素的多尺度表达。
1 空间兴趣场模型 1.1 空间兴趣场概念地理位置描述了地理空间中地理实体的空间和时间关系,地理位置具有唯一性、确定性、地理性和空间性的特性[6]。地理位置能够反映地理实体之间一种多维的空间关系,是在不同尺度上占据着特定空间,具有不同的相对地位和地理特点,对其政治、经济、文化有着深远的影响。因此,对地理位置的研究在地理学研究领域有着重大意义和应用价值。
近年来,新兴技术层出不穷,人们可获取的信息量呈爆炸式增长,其中80%的信息与空间位置有关[7],位置数据是大数据中重要的组成部分,描述了地理实体的属性特征、时空分布和时间特征,是地理空间的基本要素,反映了人们对地理空间的认知水平和逼近程度,是提供地理信息服务的重要支撑,为空间环境认知、智慧城市建设、用户社会个性化信息服务以及城市地理国情关联分析等提供基础数据及关键性的解决技术方法。
大众用户对地理实体的兴趣表现为对其关注度较高,经常查询访问感兴趣的地理位置,或利用与其相关的空间媒体数据如地理标签、文字、图片等对该地理位置进行描述。这些地理实体连续分布在地球表面,因此,用户的兴趣也是连续分布于整个地理空间中。本文提出一种空间兴趣场的概念,描述用户对地理实体的兴趣度空间分布特征。
空间兴趣场是基于位置数据及用户兴趣信息共同构成的覆盖整个地理空间的一种场模型。将地理空间中各个地理实体抽象为节点,兴趣场信号的强弱描述用户对各个节点的地理实体的感兴趣度。该模型是将用户兴趣在地理空间中进行定位,进行空间化表示,利用位置信息描述地理空间中各个实体之间的相互关系,能够客观反映出用户在地理空间中的兴趣特征、空间分布及兴趣变化趋势规律。
1.2 基于POI的空间兴趣场构建兴趣点 (points of interest, POI) 是众源地理数据的一项重要内容[8],也是地理空间信息中的一个重要组成部分, 常常大量存储在数字地图中,并广泛应用于地理信息服务。
POI是地图服务中一种重要的矢量化表达形式,与面向大众的基于位置服务密切相关,描述了人们日常生活中最常见地理实体的空间信息和属性信息,如实体的名称、类别、地理坐标等。POI最主要的特征是具有与位置相关的信息,通过这个位置信息可以提供与该位置相关的面向大众用户的应用、产品或服务。POI可以引起用户的关注,在地图服务中承载着地理目标的查询、属性查看、路径规划及辅助定位等功能,用户利用这些功能找到感兴趣的目标的地理位置及其相关的属性信息。POI不仅能够记录人类的真实活动情况,而且能够反映出人们对于地理位置的感兴趣度。通过对位置数据中POI数据进行深入挖掘与分析,能够得到反映社会现象、广大用户兴趣的地理空间分布规律和特征知识。
本文的试验数据是利用网页爬虫在百度地图上爬取了35 362个郑州市区POI数据,涵盖了办公、餐饮酒楼、地名地址、房产小区、公司企业、购物、机构团体、基础设施、交通设施、教育教学、酒店宾馆、旅游景点等17个类别,再利用格拉布斯准则法 (Grubbs)[9]对POI点的热度进行了异常值剔除,最终筛选得到1000个POI点。POI数据包含类型编码、名称、经度、纬度、Hot (热度值)、邮政编码和地址等字段,具体数据格式如表 1所示。
| 类型编码 | 名称 | 经度/(°) | 纬度/(°) | Hot | 邮政编码 | 地址 |
| 101036 | 凤祥酒店 | 113.697 395 | 34.775 424 | 11 | 410105 | 河南省郑州市经一路与黄河路交叉路口向北50米 |
| 163000 | 郑州西流湖度假村 | 113.577 82 | 34.781 36 | 352 | 410102 | 河南省郑州市中原区 |
| 281200 | 火炬大厦 | 113.565 099 | 34.811 12 | 54 | 410102 | 河南省郑州市中原区市高新区国槐街8号 |
POI数据是以离散的点状要素的形式存在于地图中,具有准确的空间位置属性,可通过大量离散POI数据的空间插值来反演获得整个研究区域的热度信息,建立空间兴趣场模型。
本文采用Kriging插值方法对POI数据进行空间插值,将POI点的热度值作为观测值,其坐标数据作为区域变化量,对郑州区域的热度值进行估计。根据插值后获得的郑州市的热度信息,得到整个郑州区域的空间兴趣场 (图 1),模型效果图中,以高低程度表示用户兴趣度大小,以特殊高亮的形式和颜色变化显示用户兴趣分布及变化情况。

|
| 图 1 郑州市部分地区感兴趣场模型效果图 Fig. 1 Interest field model of Zhengzhou |
2 GeoSOT剖分网格理论
地球剖分模型是近年来提出的一种全新空间数据模型,它是利用球形剖分的方式将地球表面划分为近似等面积和等形状的多级多层次面片,并进行规则编码,进而建立起全球统一的多分辨率层次化的空间数据组织和索引模型[10-12]。2 n一维整型数组的全球经纬度剖分格网 (geographic coordinate subdivision grid with one-dimension-integral coding on 2n-tree,GeoSOT) 剖分网格是由文献[13]提出的一种等经纬度的四叉树剖分网格模型。这种剖分网格是基于地理坐标系统划分的网格系统,在全球范围内是无缝的、稳定的并近似均匀的,可实现层次之间的有机关联。其剖分面片具有可标识性、层次性、聚合性和关联性等特点,为矢量数地图多尺度表达提供基础。
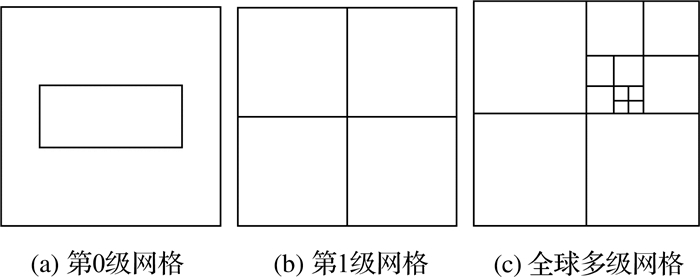
2.1 GeoSOT剖分模型GeoSOT剖分模型在对地球表面经纬度空间范围经过3次扩展 (即180°×360°扩展为512°×512°,1°×1°(60′×60′) 网格单元扩展为64′×64′,1′×1′(60″×60″) 网格单元扩展到64″×64″) 基础上进行严格的递归四叉剖分,如图 2所示,形成了覆盖整个地球的GeoSOT剖分格网。该网格通过空间扩展使网格具有整数特征,形成了“度”级、“分”级、“秒”级的层次网格。通过递归四叉剖分,GeoSOT剖分网格上下层级之间面积之比大致为4:1,是均匀变化的。
|
| 图 2 GeoSOT剖分网格 Fig. 2 GeoSOT subdivision grids |
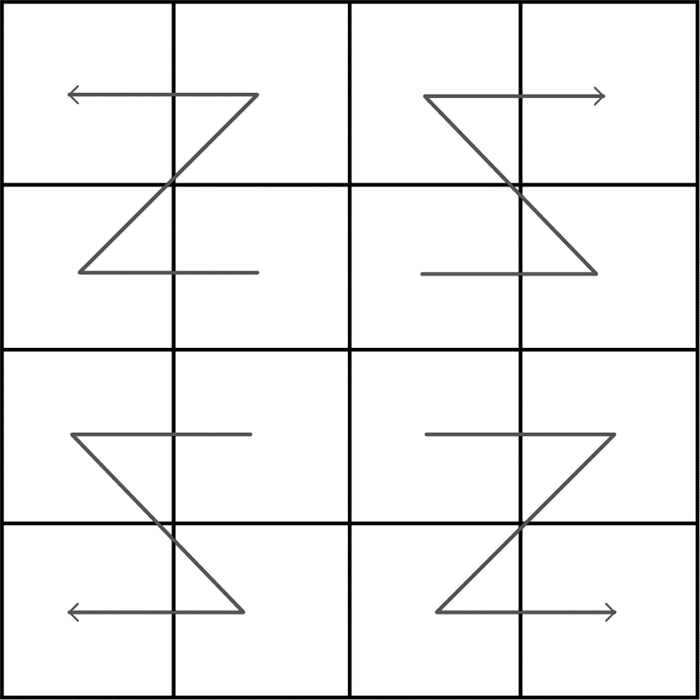
针对GeoSOT剖分网格方法,采用0、1、2、3的四进制数进行Z序编码,如图 3所示。每个剖分面片具有唯一的编码,每个子面片的编码可在其父码末尾加上一位。地址码越短,表达的空间区域范围越大,尺度越大;地址码越短,表达的空间区域范围越小,尺度越小。这样编码不仅反映了表达的尺度信息,同时体现了层次性特征。
|
| 图 3 GeoSOT剖分网格编码示意图 Fig. 3 Diagram of GeoSOT subdivision grids coding |
2.2 GeoSOT剖分网格尺度划分
利用GeoSOT剖分理论,实现矢量地图的多尺度表达,主要利用了地球剖分的空间层次性,通过对地球表面空间的递归性剖分,使各级剖分层次在结构上形成了从上而下的嵌套与从属关联关系。剖分面片的空间层次性隐含了空间尺度特征,剖分面片的层次、大小与空间尺度存在着一定的联系[14]。
剖分网格尺度划分主要是建立GeoSOT剖分网格与地图比例尺之间的联系。以我国国家基本比例尺地形图为基础,建立GeoSOT剖分网格与高斯剖分网格之间的对应关系,依次分为1:100万、1:50万、1:25万、1:10万、1:5万、1:2.5万、1:1万、1:5000、1:2000比例尺对应的9个层次级别,得到GeoSOT剖分网格与地图比例尺对应表 (表 2)。
| 层级 | 剖分网格层级 | 剖分网格单元大小 | 对应比例尺 |
| 1 | 第7级 | 4°网格 | 1:100万 |
| 2 | 第8级 | 2°网格 | 1:50万 |
| 3 | 第9级 | 1°网格 | 1:25万 |
| 4 | 第14级 | 2′网格 | 1:10万 |
| 5 | 第14级 | 2′网格 | 1:5万 |
| 6 | 第15级 | 1′网格 | 1:2.5万 |
| 7 | 第20级 | 2″网格 | 1:1万 |
| 8 | 第21级 | 1″网格 | 1:5000 |
| 9 | 第21级 | 1″网格 | 1:2000 |
3 GeoSOT剖分网格下顾及用户兴趣的空间数据多尺度表达策略
本文为实现按用户兴趣有效地分层次对矢量地图进行多尺度表达,提出了一种GeoSOT剖分网格下顾及用户兴趣的矢量地图多尺度表达策略,使空间数据在GeoSOT剖分网格框架下,能够根据按用户兴趣多层次进行表达,以方便数据的动态操作和多尺度的管理。
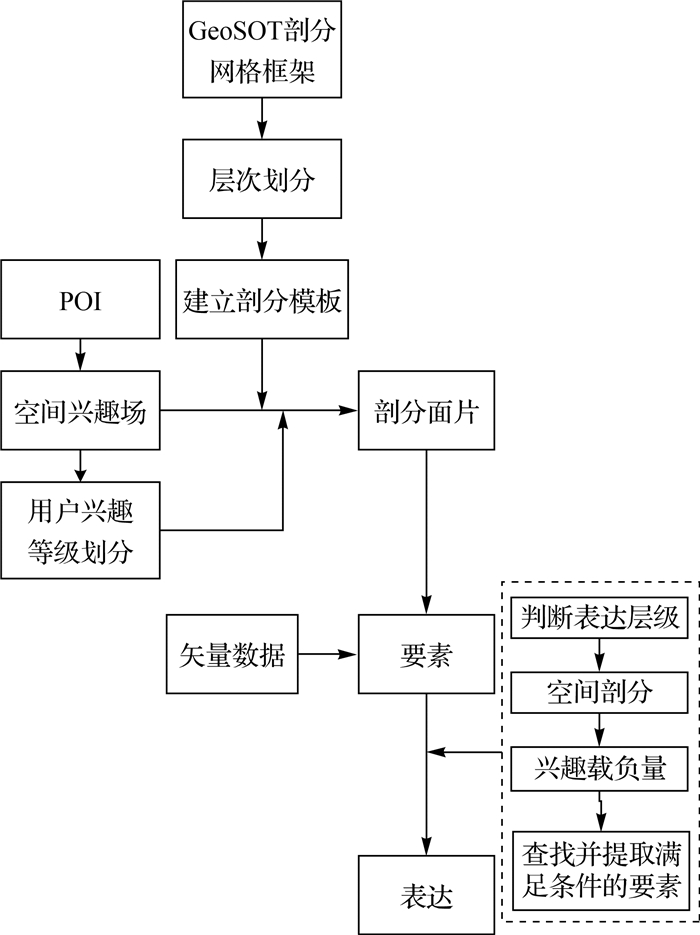
基本流程如图 5所示,主要分为空间数据预处理、空间剖分及面片兴趣度的确定、空间数据组织及索引、兴趣场约束下多尺度表达等部分。
|
| 图 4 剖分网格下顾及兴趣场多尺度表达基本流程 Fig. 4 The basic procedure of multi-scale representation considering user interest on subdivision gird |

|
| 图 5 基于GeoSOT剖分网格的空间数据组织 Fig. 5 Spatial Data Organization Based on GeoSOT subdivision grids |
3.1 空间数据预处理
在地图表达过程中,随尺度的变化,空间数据的表现形态也在不断变化。因此,在多尺度表达中,需要对空间数据进行一种多尺度、层次化的描述,即记录空间数据随尺度变化的各个空间状态,使得较为重要的空间要素优先存储和显示,能够实现一种知识级的多尺度表达。空间数据的多层次结构化组织是依据空间要素的重要性对空间数据进行有序化管理,将海量、杂乱无章的空间信息组织为有序集合,实现空间数据的高效存储、索引、表达、应用、服务等。
在实际的地理信息中,地理要素由于种类繁多,每个地理要素的地理位置、所处层次的重要性和作用不同,一般将其进行分类分级,并在地图显示时,不同等级的要素显示层级级别范围 (即要素在地图表达时显示的生命周期)。因此,要对空间数据进行分类分级处理,基本思路为:
(1) 根据空间数据的基本数据类型,分为点、线、面三类进行处理。
(2) 根据GB/T13923—2006标准《基础地理信息要素分类与代码》对空间要素进行分类,确定每个类别下的各个要素显示的比例尺范围及相应的剖分层级范围,如表 3所示。
| ID | 要素名称 | 类型 | 类别 | 比例尺范围 | 层级范围 |
| 10482 | 河南财经政法大学 | 点 | 大学 | 1:5000~1:10万 | 4~8 |
| 18146 | 郑州市植物园 | 点 | 植物园 | 1:500~1:1万 | 7~9 |
| 25347 | 科学大道 | 线 | 主干道 | 1:500~1:100万 | 1~9 |
| 18354 | 机场高速 | 线 | 高速公路 | 1:500~1:100万 | 1~9 |
3.2 空间剖分及面片兴趣度的确定
根据GeoSOT剖分网格框架对研究区域进行层次划分,建立剖分模板,得到各层级的剖分面片。再依据所构建的空间兴趣场,确定各个剖分面片的兴趣度。
根据数据本身有断点的这一特点,对空间兴趣场中用户兴趣进行分级,使分级后的组内差异最小, 组间差异最大,利用自然间断点分级法 (Jenks)[15],将用户兴趣分为10个等级。
由于人们对空间各个区域感兴趣程度不同,需要根据空间兴趣场,通过面片所在区域的位置,以该区域内的平均用户兴趣等级作为该区域的所表达的用户兴趣度。
3.3 空间数据组织及索引根据剖分模板,对空间数据进行空间划分并建立层次索引。
在GeoSOT剖分网格下,将地理空间划分成以剖分网格为单元的面片区域。以剖分面片为基本表达的单元,采用四叉树结构对剖分面片进行分层组织,再将空间数据按所在面片进行分块划分成不同的集合,各个面片中的要素按次序分级分层次组织,即空间要素集合中按用户兴趣度由大到小的顺序进行线性排序,并按序记录相应的标识ID、显示的剖分层级及兴趣度等信息。因此,空间数据能够在横向上按兴趣度进行有序组织,在纵向上按尺度建立索引。
因此,各个层次级别与相应层次的空间要素建立关联。通过剖分层次与尺度的对应关系,能够把相应用户需求尺度的空间要素提取并表达出来。呈现的组织结构如图 5所示。在不同尺度下,根据面片所表达的用户兴趣程度不同,各个面片区域中表达的空间要素呈现不同的详细程度,使兴趣度高的面片区域表达内容较为详细,即用户兴趣度较高的要素能够优先表达。基于GeoSOT剖分网格的空间数据组织结构,能够满足用户兴趣高效地对海量空间数据进行索引与表达。
3.4 兴趣场约束下多尺度表达地图应用时,由于用户对地图上不同区域的兴趣度不同,本文提出兴趣载负量的概念。兴趣载负量是衡量某一区域内用户兴趣的大小,即区域面积内用户兴趣的总和。设在某区域平均兴趣度为I,该区域兴趣载负量Z可利用式 (1) 计算
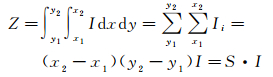 (1)
(1)
即可表示为
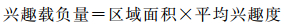 (2)
(2)
由于对地图认知和兴趣的限制,人们在应用地图时,对地图兴趣度往往是集中于某个或某些区域,不可能对地图全部的细节都感兴趣,也不现实。因此,可认为地图的兴趣载负量也是有一定限度的,并且兴趣度高区域的兴趣载负量与兴趣度低区域的兴趣载负量处于一种平衡的状态。
本文方法是希望在某一层级表达时,剖分后的各个表达的面片的兴趣载负量之间是平衡的,使整个地图兴趣处于饱和状态。当地图为k级表达时,首先确定该比例尺下剖分后所在的层级,然后进行空间划分,如图 6(a)所示。当地图为k+1级表达,将k级面片进行递归四叉剖分,如图 6(b)所示。将兴趣场引入到剖分空间中,将其按GeoSOT的k+1级格网进行划分,构建兴趣模板,再根据式 (1),将k+1级网格与所对应的兴趣模板相乘,计算得到各个剖分面片的兴趣载负量。比较各个剖分面片的兴趣载负量,若四个相邻面片S11、S12、S13、S14的兴趣载负量之和与另一面片S30的兴趣载负量相等,即
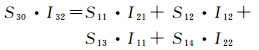 (2)
(2)

|
| 图 6 兴趣场约束下多尺度表达 Fig. 6 Multi-scale representation based on interest field model |
则将面片S11、S12、S13、S14进行聚合,利用其上一层级面片 (即父面片)S1进行表达,并查找与提取各个面片所包含的要素集合中在k层表达的要素,如图 6(c)所示,实现了一种剖分网格下顾及兴趣场多尺度表达。
当由小尺度到大尺度变换时,即地图为由k级变为k+1级表达时,对原剖分网格中各个面片进行四叉划分,得到子剖分面片,计算各个子剖分面片的兴趣度及兴趣载负量,同上一步,若相邻4个子面片与某一面片兴趣载负量相等,即用k级面片表达。由于不同层次面片之间具有继承与被继承的关系,高层次面片包含了低层次面片的信息。依次比较4个子面片兴趣度与父面片兴趣度,当子面片兴趣度大于等于父面片兴趣度,保留在k级中该子面片表达的要素;当子面片兴趣度小于父面片兴趣度时,保留在k级中该子面片表达的要素,并再表达出显示范围在[k, k+1]尺度之间的要素。该步骤将兴趣度高的要素保留,兴趣度较低的要素逐渐进行表达。
当由大尺度到小尺度变换时,即地图为由k级变为k-1级表达时,由于剖分面片具有空间聚合性,即低层次的较小相邻剖分面片可以聚合生成高层次的较大面片。因此,按剖分规则,对原剖分网格中相邻的4个面片进行聚合,形成高层次的父面片,而对在k级尺度中已利用k-1级表达的面片保持不变,确定各个面片的兴趣度。依次比较原4个子面片兴趣度与父面片兴趣度,当原子面片大于等于父面片兴趣度时,保留在k级中该子面片表达的要素;当原子面片兴趣度小于父面片兴趣度时,在k级中该子面片表达的要素中删除显示范围在[k-1, k]尺度之间的要素。该步骤能够将兴趣度高的要素进行优先表达。
4 试验与分析为实现剖分网格下顾及用户兴趣的矢量地图多尺度表达,验证本文提出研究思路的有效性,本文对剖分网格下传统多尺度表达方法与顾及用户兴趣多尺度表达方法进行比较,以郑州市点状要素多尺度表达为例,进行了仿真试验。试验数据是采集的1000个郑州市POI数据及全国1:25万基础矢量数据中郑州市区内点状数据。
为衡量利用本方法对点状数据表达显示效果,采用地图面积载负量作为量化评判指标。地图载负量是衡量地图中能够表达地物信息多少的数量标志[16]。地图的面积载负量是指地图上所有符号和注记所占面积与图幅总面积之比。有如下公式
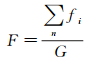 (2)
(2)
式中,G为总图幅面积;fi为符号和注记所占面积。通过计算,得到各个尺度下地图面积载负量。
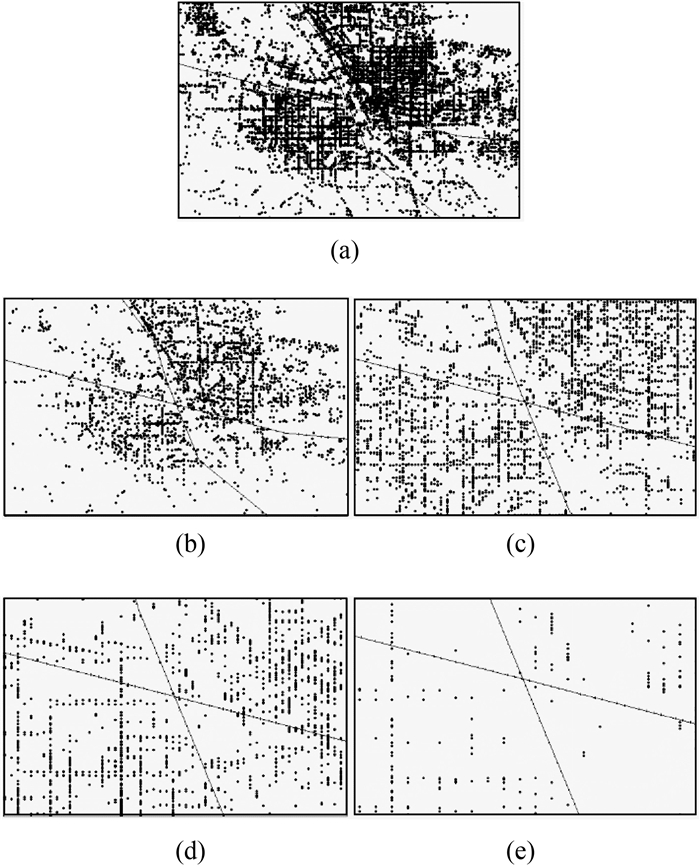
试验结果如图 7所示,图 7(a)为1:10万比例尺下的原始数据,利用本文的方法对点状要素进行多尺度表达,图 7(b)—(e)分别是在1:10万 (第4级)、1:5万 (第5级)、1:2.5万 (第6级)、1:1万 (第7级) 比例尺下的表达效果,由此可以看出,在表达时,相对重要的点状要素首先显示,随比例尺的增加,尺度的减小,其他点状要素逐渐显示出来,呈现出了由概略到详细、由重要到次要的效果。
|
| 图 7 顾及用户兴趣的点状要素多尺度表达 Fig. 7 Multi-scale representation method of point data considering user interest |
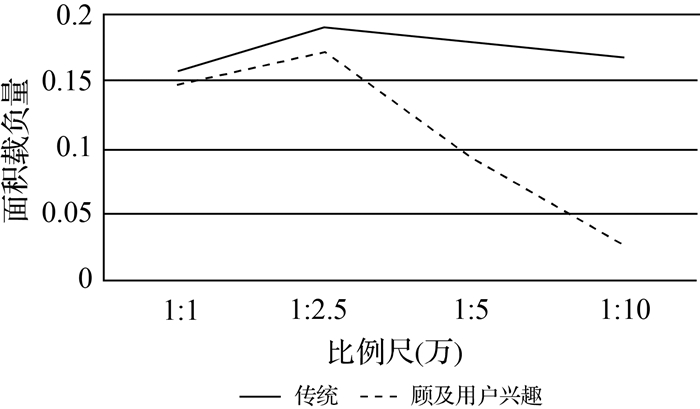
图 8为剖分网格下不同尺度传统多尺度表达方法与本文提出的顾及用户兴趣多尺度表达方法的比较,由图 8可知,传统方法在不同比例尺下的地图面积载负量呈现整体较为平稳的趋势;顾及用户兴趣的方法在小比例尺下,顾及用户兴趣的方法面积载负量较小,远远小于传统方法,随比例尺逐渐增大面积载负量逐渐递增。
|
| 图 8 剖分网格下不同比例尺的传统多尺度表达方法与本文方法比较 Fig. 8 The comparison with traditional representation method and the suggested method in different scale on subdivision gird |
在1:10万比例尺下,选取兴趣级别分别为3、5、7的3个剖分面片,并计算每个面片区域在不同比例尺下的载负量。由表 4可知,利用本文方法得到的矢量地图在比例尺介于1:1万与1:5万时其面积载负量逐渐增加,当比例尺小于1:5万时,载负量逐渐减小;不同兴趣度区域的载负量总体变化大致相同;不同兴趣度区域的载负量存在明显差异,在同一比例尺下,兴趣度高区域的载负量比兴趣度低区域载负量高,而且在较小比例尺下,兴趣度高区域具有较高载负量值,说明兴趣度高的数据能够优先显示。
| 比例尺/(万) | 1:10 | 1:5 | 1:2.5 | 1:1 |
| 全图 | 0.029 | 0.093 | 0.172 | 0.158 |
| 3级兴趣面片 | 0.009 | 0.041 | 0.089 | 0.099 |
| 5级兴趣面片 | 0.047 | 0.125 | 0.201 | 0.195 |
| 7级兴趣面片 | 0.267 | 0.282 | 0.305 | 0.311 |
5 结论
本文提出一种剖分网格下顾及用户兴趣的矢量地图多尺度表达方法,首先利用研究区域的大量POI数据构建覆盖整个地理空间的兴趣场模型,描述用户对地理信息的兴趣强度空间分布及其变化趋势,再对空间要素进行分类分级,确定其表达的尺度范围,最后利用地球剖分理论对空间范围进行不同层次的区域划分,根据各个区域用户兴趣程度,进行空间数据不同详细程度的表达与显示,实现一种基于用户兴趣的空间数据多尺度表达。试验表明该方法根据海量网络数据挖掘用户感兴趣地理信息,并在多尺度表达过程中,地图上人们关注的重要信息能够较为优先表达与显示,次要信息随尺度的减小进而表达与显示出来,满足用户兴趣需求的同时,具有较好的多尺度表达效果,有着实际的研究意义与应用价值。在尺度变换过程中,还要考虑到空间要素跨面片、不同尺度间要素变换的连续性等问题,需要进一步研究。
| [1] | 诸云强, 孙九林, 廖顺宝, 等. 地球系统科学数据共享研究与实践[J]. 地球信息科学学报, 2010, 12(1): 1–8. ZHU Yunqiang, SUN Jiulin, LIAO Shunbao, et al. Earth System Scientific Data Sharing Research and Practice[J]. Journal of Geo-information Science, 2010, 12(1): 1–8. DOI:10.3724/SP.J.1047.2010.00001 |
| [2] | GOODCHILD M F, FU P, PAUL R. Sharing Geographic Information:An Assessment of the Geospatial One-Stop[J]. Annals of the Association of American Geographers, 2007, 97(2): 250–266. DOI:10.1111/j.1467-8306.2007.00534.x |
| [3] | 关丽, 吕雪锋. 多级地理空间网格框架及其关键技术初探[J]. 地理与地理信息科学, 2011, 27(3): 1–6. GUAN Li, LYU Xuefeng. Multi-scale Geospatial Grid Framework and Its Key Technologies[J]. Geography and Geo-Information Science, 2011, 27(3): 1–6. |
| [4] | SAHR K, WHITE D. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121–134. DOI:10.1559/152304003100011090 |
| [5] | GOODCHILD M. Discrete Global Grids for Digital Earth[C]//International Conference on Discrete Global Grids. Santa Barbara:[s. n.], 2000. |
| [6] | 赵建军. 地理位置的深度解析及其应用价值[J]. 山东师范大学学报 (自然科学版), 2010, 25(4): 87–91. ZHAO Jianjun. Deep Analysis of Geographical Position and Its Practical Value[J]. Journal of Shandong Normal University (Natural Science), 2010, 25(4): 87–91. |
| [7] | 朱欣焰, 周成虎, 呙维, 等. 全息位置地图概念内涵及其关键技术初探[J]. 武汉大学学报 (信息科学版), 2015, 40(3): 285–295. ZHU Xinyan, ZHOU Chenghu, GUO Wei, et al. Preliminary Study on Conception and Key Technologies of the Location-based Pan-information Map[J]. Geomatics and Information Science of Wuhan University, 2015, 40(3): 285–295. |
| [8] | 杨敏, 艾廷华, 卢威, 等.自发地理信息兴趣点数据在线综合与多尺度可视化方法[J].测绘学报, 2015, 44(2):228-234. YANG Min, AI Tinghua, LU Wei, CHENG Xiaoqiang, ZHOU Qi. A Real-time Generalization and Multi-scale Visualization Method for POI Data in Volunteered Geographic Information[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2):228-234. http://xb.sinomaps.com/CN/abstract/abstract6492.shtml |
| [9] | 韩江洪, 王景华, 徐娟, 等. 具有误差处理功能的动平衡标定方法研究[J]. 仪器仪表学报, 2013, 34(7): 1454–1461. HAN Jianghong, WANG Jinghua, XU Juan, et al. Research on New Dynamic Balance Calibration Method with Measurement Error Processing Function[J]. Chinese Journal of Scientific Instrument, 2013, 34(7): 1454–1461. |
| [10] | 李德仁, 肖志峰, 朱欣焰. 论空间信息多级网格的划分方法及编码研究[J]. 测绘学报, 2006, 35(1): 52–56. LI Deren, XIAO Zhifeng, ZHU Xinyan. Research on Grid Division and Encoding of Spatial Information Multi-grids[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1): 52–56. |
| [11] | 赵学胜. 全球离散格网的空间数字建模[M]. 北京: 测绘出版社, 2007. ZHAO Xuesheng. Spatial Digital Modeling of Discrete Global Grid[M]. Beijing: Mapping Publishing Company, 2007. |
| [12] | 童晓冲. 空间信息剖分组织的全球离散格网理论与方法[D]. 郑州: 信息工程大学, 2010. TONG Xiaochong. The Principles and Methods of Discrete Global Grid Systems for Geospatial Information Subdivision Organization[D]. Zhengzhou:Information Engineering University, 2010. |
| [13] | 宋树华, 程承旗, 濮国梁, 等. 全球遥感数据剖分组织的GeoSOT网格应用[J]. 测绘学报, 2014(8): 869–876. SONG Shuhua, CHENG Chengqi, PU Guoliang, et al. Global Remote Sensing Data Subdivision Organization Grid[J]. Acta Geodaetica et Cartographica Sinica, 2014(8): 869–876. |
| [14] | 程承旗, 任伏虎, 濮国梁, 等. 空间信息剖分组织导论[M]. 科学出版社, 2012. CHENG Chengqi, REN Fuhu, PU Guoliang, et al. Introduction to Spatial Information Section[M].The Science Publishing Company, 2012 |
| [15] | JENKS, GEORGE F. The data model concept in statistical mapping[C]//International Yearbook of Cartography.[s.l.]:IEEE, 1967:186-190. |
| [16] | 张昊, 江南, 曹亚妮. 网络电子地图多尺度显示的分析与研究[J]. 测绘通报, 2014(1): 90–93. ZHANG Hao, JIANG Nan, CAO Yani. The Analysis and Study of Multi-scale Display for Network Electronic Map[J]. Bulletin of Surveying and Mapping, 2014(1): 90–93. |


