2. 地球空间信息技术协同创新中心, 湖北 武汉 430079
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China
随着GPS、无线通信和移动设备的结合与发展,时空轨迹数据获取技术突飞猛进,相关行业已经累积了海量的时空轨迹数据。如何分析挖掘这些时空轨迹数据,从中提取信息与知识,已逐渐受到国内外学者的重视,成为空间信息领域的一大研究热点。轨迹Stop/Move模型是近年来提出的一种较为新颖的轨迹分析方法[1-2],该方法首先将轨迹点序列划分为Stop/Move序列,并赋予相关语义,在此基础上可以开展语义更为明确的分析挖掘研究[3-4]。Stop,即停留,指在移动对象的轨迹中静止或在一定范围内缓慢移动的部分,是轨迹中具有重要语义特征的点序列。一方面,停留提取是支持面向轨迹数据的知识发现与行为识别的重要手段,如从候鸟轨迹中发现迁徙过程中的停歇地,从渔船轨迹中分析出海过程中的捕鱼行为;另一方面,从轨迹停留出发,研究大量轨迹在停留-移动序列上的相似性,可以进一步发掘移动对象的时空移动模式[5-6],从而为城市交通、居民出行提供决策支持。以出租车轨迹数据为例,在停留提取的基础上,分析出租车司机的午餐行为在空间和时间上的分布,可以辅助政府设计合理的出租车就餐点,从而提高出租车的服务效率,并方便居民出行;又如微软的GeoLife项目[7],通过收集游客轨迹数据,并分析挖掘其中关于停留-移动的频繁模式,在旅游线路推荐和朋友圈发现等方面进行了一些有益尝试。为此,国内外学者提出了多种停留提取方法,大致可以分为集成地理背景信息的方法[8-9]、基于轨迹导出特征的方法[10-11]、密度聚类法[12-14]以及逐级合并方法[15]。
集成地理背景信息的方法是指在轨迹停留提取过程中,从地理背景信息出发,通过检测移动对象相对于不同地理实体(POI、ROI)的时空关系来识别轨迹停留。具体来说,这类方法通过计算轨迹在地理实体内部或其邻域范围内的累积连续停留时间,来判断轨迹在该处是否存在停留。该类方法适用于在已有地理背景数据环境下查询或挖掘轨迹与地理实体间联系的应用,但无法从地理背景信息缺失的区域提取出停留[9]。
基于轨迹导出特征的方法通过在轨迹中诸如速度、加速度、点密度、转向角、信号缺失等一个或多个特征上设置规则,已从轨迹数据中提取出停留。如文献[10]通过设置累积转向角阈值来发现渔船轨迹中方向频繁变化的捕鱼点;文献[11]综合利用信号在缺失时间、转向角多上的多个规则来挖掘居民出行中的活动地点。由于轨迹停留识别的最佳特征选取往往取决于特定的数据或应用,使得该类方法的通用性受到一定程度的制约。
密度聚类法通过在传统的空间密度聚类方法中引入时间维信息,从轨迹中提取时空两方面同时聚集的停留。如基于DBSCAN算法的改进算法CB-SMoT[12]、TrajDBSCAN[13],该类方法针对轨迹的时空特征,重新定义了如邻居、核心点、密度可达、密度相连等DBSCAN算法中的基本概念;又如文献[14]对OPTICS中的可达距离在轨迹数据上进行重新定义,设计了适用于轨迹的停留提取算法T-OPTICS。该类方法面向轨迹数据,对传统密度聚类算法进行了相应扩展,但在处理带长距离漂移的轨迹数据时,其停留识别的效果不佳,易将单个停留误识别为多个停留[14-15]。
为了克服漂移噪声对停留识别的影响,文献[15]针对居民出行轨迹提出了逐级合并的停留识别方法,该方法首先使用简单的速度判别准则,将轨迹初步分为停留/移动类型子轨迹,并根据有意义的停留与移动在持续时间、跨越距离上的限制,动态更新子轨迹的停留/移动标签,并通过逐级合并相同类型相邻的子轨迹来优化识别结果。该方法虽然在一定程度上克服了噪声对停留识别的影响,但是其简单合并策略易于导致不同停留的误合并。
通过对现有停留提取研究的总结,笔者发现:①现有研究往往侧重于停留的定义或停留识别准则的选取,对表征停留本身的时空聚集程度及其可视化方法却较少研究;②现有研究较少考虑含大量漂移噪声的室内停留的优化处理问题,对轨迹停留的复杂多样性考虑不足。为此,本文基于核密度思想提出停留指数,并据此设计停留指数图,直观表达轨迹点的时空聚集程度变化,在此基础上,本文开发停留提取算法,并采用自采轨迹和GeoLife轨迹[16]开展试验,结果表明该算法在停留提取方面具有较高的正确率,能够识别复杂多样的轨迹停留。
1 轨迹及其停留轨迹是在给定时间段内,被考察目标在地理空间中有目的的移动[2],可抽象表达为从时间到空间的函数: 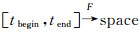
定义1(轨迹):traj=(tid, < p0, p1, …, pN>),其中,pi=(xi, yi, ti), 0≤i≤N,且∀i < j,有ti < tj。
tid是轨迹的唯一标识,pi=(xi, yi, ti)是构成轨迹的1个时空点,其中:xi和yi是二维欧氏空间中的坐标值(通常为经纬度),ti是时间全序轴上的时刻值,xi、yi和ti均来自于实数域。p0和pN是两个特殊时空点,即始点和终点。
轨迹在其生命周期内并不是一直移动,可能出于某一目的在某一地点停留一段时间(如就餐和加油等)。在该段时间内,轨迹的空间位置保持不变或在较小范围内变化;此后,轨迹继续在空间中移动,并到达下一地点停留,或者抵达终点。停留,即Stop,是轨迹点序列中的一个连续子序列:
定义2(停留):stop=(tid, sid, < ps, ps+1, …, pe>),其中,0 < s < e < N,并满足下述两个条件:①原地静止或在小范围空间内移动;②持续足够长的时间。
由定义2可知,停留不是由绝对速度定义而来,而是在时空两维中,由空间范围和时间长度两者共同界定的概念。由于受到多种因素影响,轨迹停留呈现出复杂多样的特征:从发生地点来看,可以是室内,也可以是室外;从外在表现来看,停留可以是绝对静止、小范围内移动,或者两者的结合;而从数据承载上来看,停留可以是单个轨迹点,多个或者大量连续的轨迹点。
2 停留指数及其可视化核密度分析法[18-19]作为一种基于密度的空间点模式分析技术,是研究空间点聚集性的有效方法。该方法通过对核密度的计算,得到核密度在空间上的分布,并据此提取具有重要语义的聚集模式,如交通事件、犯罪热点等[20-21]。通常来说,移动对象接近停留点时速度逐步降低,停留期间,速度为零或者很低,而离开停留点后,速度将逐步提高,因而,从数据承载方面来看,停留表现为大量轨迹点在局部小范围内的聚集,据此,本文从核密度思想出发,提出停留指数,以反映轨迹在其生命周期内时空聚集程度的变化,在此基础上以可视化方式直观揭示轨迹的“潜在”停留,并进一步发展出轨迹停留的自动提取算法。
2.1 停留指数核密度法通过累计目标点邻域内其他点对中心点的空间权重,估算目标点处的密度,见式(1)
 (1)
(1)
式中,n是落在目标点s距离为h的邻域内的点数;函数K是核函数,其值随着s与点Ci的距离的增大而递减。K函数的性质体现了空间影响随距离衰减的地理学第一定律[22-23],是核密度思想的核心。
由于记录方式或信号质量等原因,轨迹数据的采样频率并非是恒等不变的。因而,在将核密度法应用于轨迹点停留指数的计算时,除了考虑邻域内的点数和空间距离之外,应进一步将点在邻域内的逗留时间纳入进来,以反映轨迹在目标点领域内(即空间维信息)的逗留时间(即时间维信息)。据此,轨迹点的停留指数定义如下
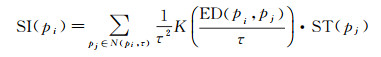 (2)
(2)
式中,N(pi, τ)表示目标点Pi距离为τ的邻域,落在其中的点被称作邻域点(包括目标点自身);ED(pi, pj)是邻域点Pj到目标点Pi的欧氏距离;ST(Pj)是点Pj在N(pi, τ)内的逗留时间。不难看出,目标点pi的停留指数SI(pi)的计算需要累计每一个邻域点的时空贡献。从停留指数的本质来看,可将邻域点时空贡献理解为带空间权重(即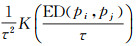
一种简单直观的计算ST(Pj)的方法是取Pj到Pj+1的时间采样间隔,即ST(Pj)=interval(Pj, Pj+1)=Pj+1·tj+1-Pj·tj。由于轨迹是现实世界中对象的连续移动在计算机世界中的离散化表达,上述方法将人为隔断跨越邻域的相邻轨迹点之间的时空联系,势必造成边缘点时空贡献的误计算。
设想图 1(a)所示的情形,pj到pj+1的子轨迹跨越了N(pi, τ)边界,而在实际情况中,pj和pj+1可能间隔很久(如经过长距离隧道所造成的信号丢失),故以时间采样间隔来计算邻域点的时空贡献将导致点pi停留指数的计算结果虚高。考虑到轨迹移动的连续性,在计算点pj的逗留时间时,仅需考虑子轨迹pj→pj+1落在N(pi, τ)内的部分(在图 1中由实线表示)所对应的时间,故停留时间的计算公式如下

|
| 图 1 逗留时间计算与空间权重校正 Fig. 1 Calculation of stop time (ST) and its spatial weight correction |
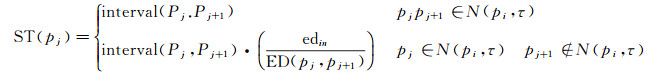 (3)
(3)
式中,edin为子轨迹pj→pj+1在邻域内的长度。此处,笔者假设轨迹对象在两个采样点之间匀速运动。
需要指出的是,当pj不在邻域内,而pj+1在邻域内,即pj∉N(pi, τ), pj+1∈N(pi, τ)时,或者更进一步,当pj和pj+1均不在邻域内,而子轨迹pj→pj+1与邻域相交,即pj, pj+1∉N(pi, τ), pj→pj+1∩N(pi, τ)≠Ø时,需要考虑pj,并将其时空贡献纳入到目标点pi停留指数的计算中。为此,拟引入一个伪邻域点,将其设为子轨迹pj→pj+1与N(pi, τ)边界在时间轴上的第一个交点,记为p′j(即图 1中的白点)。由此可知,停留指数的计算不仅需要考虑真邻域点,而且需要考虑伪邻域点,且在两种情形下均可用式(3)来计算逗留时间。
2.1.2 空间权重校正在更复杂的轨迹移动中,轨迹可能多次进出邻域,而每次进出时引入的邻域点对目标点的时空贡献显然是不相同的。图 1(b)示意了一条轨迹连续两次进出N(pi, τ)的过程,按照时间顺序是:enter1→leave1→enter2→leave2,形成两段落在N(pi, τ)内的子轨迹,即stay1和stay2。不同于stay1,stay2在邻域内不存在到目标点pi的直接通路,故在计算邻域点时空贡献时,应对stay1与stay2加以区分。不难得出,stay2上的邻域点,设为pj,对目标点pi的时空贡献不仅取决于pj到pi的欧氏距离,还应考虑轨迹在pi与pj之间的移动距离。据此,笔者对邻域点pj时空贡献的空间权重进行校正,引入如下所示的校正因子
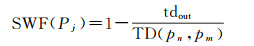 (4)
(4)
式中,n=min(i, j);m=max(i, j);TD(pn, pm)为轨迹从pn到pm的移动距离;tdout为其中不在邻域内的长度,称作脱离距离。当轨迹从pn移动到pm时未曾脱离邻域,即脱离距离为0,那么SWP(Pj)=1,这意味着无需对pj时空贡献进行校正。
校正因子依据邻域点的脱离距离对其时空贡献进行矫正:对于噪声导致的暂时脱离邻域的情形,由于脱离距离较短,其对时空贡献的影响可忽略不计;而对于离开-返回形成的脱离邻域的情形,由于脱离距离通常较长,其时空贡献将被调至较低水平。
综上所述,选取高斯核函数作为K函数,并移除常系数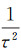
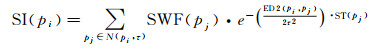 (5)
(5)
需要说明的是,此处去掉常系数是为了更好地反映时空贡献蕴含的语义,即保证目标点pi本身在对于pi停留指数的时空贡献中:空间权重为1,逗留时间则依赖于点pi+1的空间分布情况,具体由式(3)决定。
由定义(2)可知,停留是移动对象在一定时长内保持静止或在小范围内移动的状态,相应于该定义,停留指数在小范围内(领域半径)计算移动对象累积的逗留时间。式(5)之所以采用高斯函数,其原因在于为不同邻域点的逗留时间赋予不同的空间衰减权,从而反映出轨迹点的不同时空聚集程度,即邻域点的空间分布越集中于目标点附近,目标点的停留指数则越高,这也符合人们对于停留的直观认识。不同于CB-SMoT等在扩展DBSCAN算法时先空间,后时间的做法,停留指数在累积每一个邻域点的贡献时,同时考虑其时空特征(即空间距离和逗留时间),不仅可以表征大量轨迹点聚集所形成的停留,而且能够反映轨迹点较少(甚至仅有一个轨迹点)但持续时间较长的停留。后者一般对应于移动对象在停留期间GPS设备降低采样频率、不采样、甚至关机的情形,而CB-SMoT等方法在处理由此形成的停留时往往无能为力。
由式(5)可知,停留指数仅由移动对象在邻域内的逗留时间决定,与速度并不发生直接的关系。设想如下情形:飞机在机场上空盘旋时,虽然速度很高,但始终徘徊于机场附近,故由机场这一邻域决定的停留指数仍然较大。但在一般情况下,停留指数与速度存在一种间接的反比关系,比如移动对象通过邻域的速度越大,所花费的时间越少,因而其停留指数越小,反之亦然。
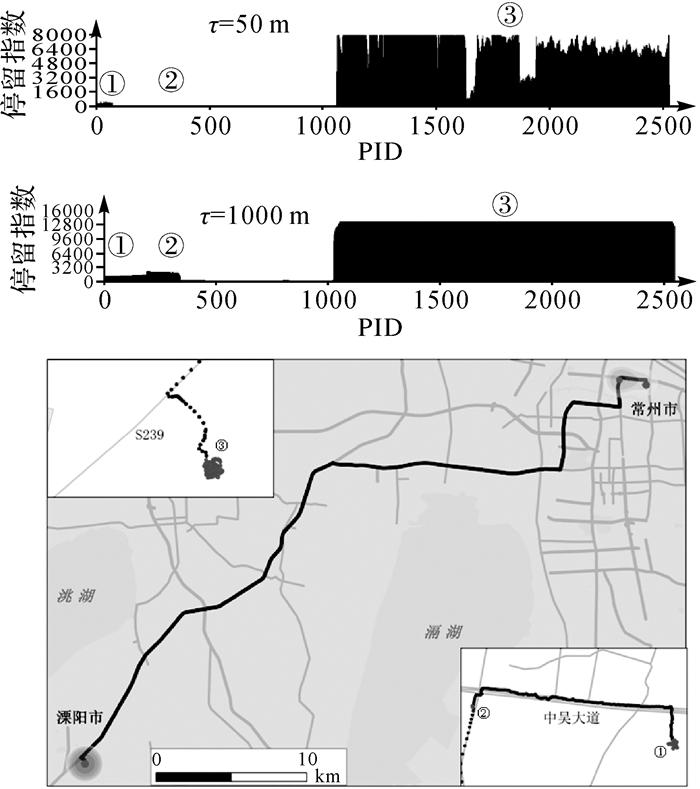
2.2 停留指数图以轨迹点为横轴,停留指数为纵轴,即可绘出轨迹的停留指数图。图 2是一条从常州自驾到溧阳的轨迹的停留指数图,从上到下分别是τ=50 m和τ=1000 m的停留指数图,以及相应于τ=1000 m的热力图。为了显示方便,图 2所示的停留指数图在纵轴进行了最大值截断。借助于图形化表达的停留指数图,用户不必解译晦涩难懂的轨迹数据,即可获知轨迹在其生命周期中的移动-停留情况。以图 2为例,不难得出此次自驾之旅有3次明显的停留行为,且停留③持续了较长时间。此外,同停留①相比,参与停留②的轨迹点虽少,但其停留指数较高。
|
| 图 2 轨迹停留指数图样例 Fig. 2 Example of a trajectory and its stop index plot |
需要指出的是,停留是与空间尺度相关的概念,以长距离自驾为例,大尺度上可将在城镇的一次落脚休整看作一个大停留,而缩放到小尺度之后,则可将这次落脚细分为多个小停留,如就餐、购物和住店等。不难得出,停留指数通过邻域半径τ建立起同空间尺度的关系,因而在不同大小的邻域半径下,可以观察到不同尺度下的停留情况。继续以图 2为例,当τ增大到1000 m时,在τ=50 m时观察到的前2小个停留被连接成1个大停留,即在大尺度下可将在常州市的2次停留看作1个停留。
3 基于停留指数的停留提取从轨迹停留指数的可视化结果不难看出,实际停留对应的子轨迹具有较高的停留指数值,这启发笔者试着从停留指数发现并提取停留,为此,拟从轨迹中搜索高停留指数的轨迹点序列形成的子轨迹,即潜在停留段。
定义3(潜在停留段):给定轨迹Traj和邻域半径τ,潜在停留段S=pi→pi+1→…pj是traj中的子轨迹,j≥i,且满足:
(1) ∀k, i≥k≥j,SI(pk)≥ΔSI。
(2) 若存在点pi-1或点pj+1,则SI(Pi-1)<ΔSI, SI(pj+1)<ΔSI。其中,ΔSI是判别潜在停留段的阈值。
潜在停留段可以由大量高停留指数的轨迹点组成,如图 2中的③,也可以由几个、甚至一个高停留指数的轨迹点组成,如图 2中的②。潜在停留段判别阈值ΔSI是提取潜在停留段的关键,若设置得太小,则会提取出较多的伪停留,而若设置得太大,则会忽略掉一些较短的停留。为此,本文给出在邻域半径τ下,潜在停留段判别阈值的推荐值的计算公式
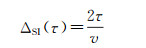 (6)
(6)
式中,v是静止判别阈值,为轨迹对象以速度v作匀速直线运动通过邻域所需的最长时间。在式(6)中,静止判别阈值v的选取需要考虑移动对象的速度,一般来说,移动对象的速度越快,v应设置得越大,但与此同时,τ也应相应增大,以匹配移动对象的速度能力。考虑到人的正常步行速度在5 km/h左右[24],本文将静止判别阈值设定为v=0.6 m/s,实际上,这也是大部分相关研究所使用的静止判别标准[15]。
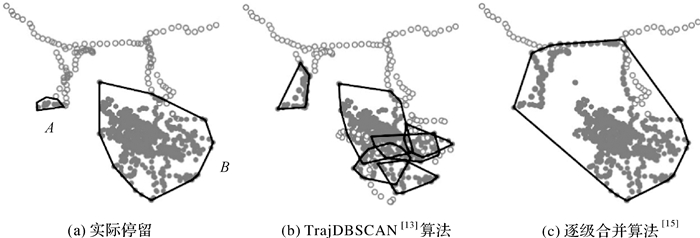
在GPS信号良好时,一个潜在停留段即对应一个实际停留。但是,由于室内遮挡或高楼反射等原因,GPS的定位精度变差,产生漂移噪声,一个完整的停留将对应多个潜在停留段。如果处理不当,很可能将该完整停留误识别成多个停留,这也是现有停留识别方法都难以有效解决的问题[12-14]。文献[14]提出的逐级合并停留识别方法虽然在克服噪声方面效果较好,但简单的合并规则也导致了误合并的发生[15]。图 3展示了一条有2次实际停留行为的轨迹,以及TrajDBSCAN算法和文献[14]算法在各自文章的推荐参数下对停留的识别结果,其中,TrajDBSCAN法将B处的停留识别成了5个停留,而逐级合并算法则将2个停留合并成1个停留。
|
| 图 3 不同算法的停留识别结果对比 Fig. 3 Comparison of stop results extracted by different algorithms |
在研究和总结现有方法对于停留识别的基础上,本文针对源于停留指数的潜在停留段,提出了一种基于时空邻近关系的逐级合并方法,据此发展出基于停留指数的停留识别算法。首先给出停留段概念,它或者对应潜在停留段,或者由潜在停留段合并而来,然后定义停留段的时空相邻关系,如下:
定义4(时空相邻停留段):对于轨迹traj的两个停留段Sa与Sb,设Sa发生在Sb之前,若Sa与Sb满足下面两个条件之一,那么Sa与Sb时空相邻。
(1) 若Sa与Sb是两个连续的停留段,即中间不存在其他停留段,且Itv(Sa, Sb)≤MinMov。
(2) 若Sa与Sb的凸包重叠,且Itv(Sa, Sb)≤ω·MinMov,ω>1。
其中,Itv(Sa, Sb)表示停留段Sa与Sb之间的时间间隔;MinMov表示一个有意义的移动应持续的最短时间。
当Sa与Sb时空相邻时,可以将Sa与Sb,以及Sa与Sb之间的轨迹点,合并成一个新停留段。在定义4的2个条件中:条件1用于合并因短时脱离形成的两个连续停留段,而条件2用于合并被噪声数据隔开的停留段。此外,条件2的两个输入停留段并不要求是连续的,从而放宽了时间间隔方面的要求,本文统一取ω=2。
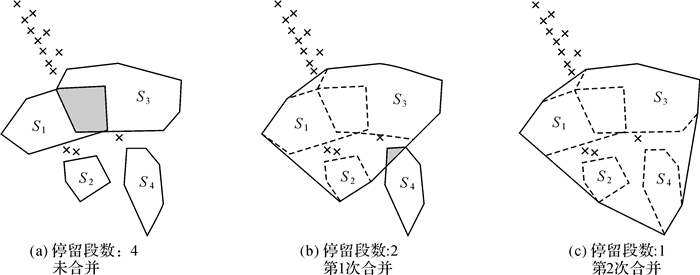
停留的提取可以从定位潜在停留段开始,通过逐级合并时空相邻的停留段,最终得到完整的停留。在逐级合并中,时空相邻小停留段被合并成大停留段,大停留段则继承小停留段的时间范围,并将小停留段共同的凸包作为自身的凸包,以参与下一级合并。因此,停留段的逐级合并,实质上是停留段时空范围的扩张过程。图 4示意了4个潜在停留段的合并过程,按照时间顺序分别为:S1→S2→S3→S4。
|
| 图 4 潜在停留段合并 Fig. 4 Merge of potential stops |
在第1级合并中,由于S1和S3凸包重叠,使得S1、S2、S3被成功合并,其结果凸包与S4的凸包重叠,从而触发第2级合并,最终使得4个潜在停留段被合并成1个停留段。需要指出的是,在合并停留段时,小停留段之间的轨迹点(即停留指数值较低的非停留段部分)并不参与大停留段凸包合并,这是因为非停留段部分可能包含噪声数据,若将其加入合并,势必将导致大停留段的空间范围的假性扩张,从而有可能触发误合并。
综上所述,不难得出基于停留指数的轨迹停留提取算法,其伪代码如下:
算法:基于停留指数的轨迹停留提取算法
输入:traj, τ, MinMov
输出:停留段集合SC
1. for轨迹中的每一个点
2.根据τ计算Traj中轨迹点的停留指数
3. end for
4.据定义(3)提取所有潜在停留段,标记为未访问,并加入到SC
5. while在SC中存在未被访问的停留段
6.从SC中取出一个尚未被访问的停留段S,并标记为已访问
7. if在SC中存在与S时空相邻的停留段//据定义(4)
8.将S与其时空相邻的所有停留段合并成大停留段S‘
9.将S与其时空相邻的所有停留段的共同凸包设为S‘的凸包
10.将与S时空相邻的所有停留段标记为已访问
11.将S‘加入到SC,并标记为未访问
12. end if
13. end while
14.输出停留段集合SC
4 轨迹停留提取试验为了验证基于停留指数的轨迹停留提取方法的有效性,本节分别选用自采和GeoLife两组居民出行的轨迹,对日常出行中感兴趣的停留开展提取试验。试验轨迹涵盖了步行、公共交通、驾车等多种出行方式,其中自采轨迹为由Garmin eTrex 20设备采集的8条轨迹数据,该设备内置GLONASS和GPS双星系统,室外定位精度约为15 m,轨迹点采样间隔被固定为3 s;GeoLife轨迹是微软亚洲研究院发布的免费轨迹数据源,由于其数据采集设备规格参差不齐,笔者从中选取了15条出行信息丰富,停留数量较多、且带有噪声的轨迹,其采样间隔为5 s。
4.1 参数设置停留提取算法的运行共依赖于2个参数,即邻域半径τ和移动最短持续时间MinMov,需要指出的是,停留是一个与空间尺度相关的概念(见2.2节),因而,提取算法的参数也应与用户所关注的空间尺度相适应。考虑到GPS设备的定位误差一般在15 m左右,在城市范围内研究停留提取问题时,可依据轨迹数据的噪声情况,将参数τ设置为30~90 m之间的值,不宜过大,也不宜过小。过大时,潜在停留段的边界将会向两端膨胀,从而可能引发相邻停留的错误合并;过小时,潜在停留段的边界会收缩,甚至消失,从而可能导致停留未被提取。参数MinMov的设置同样与轨迹数据的噪声情况有关:当GPS信号质量较差时,单个停留易被分割成多潜在停留段,应适当增大MinMov值,以增强潜在停留段的合并能力,反之则需减小MinMov值。
考虑到试验数据均为居民在城市范围内的出行数据,本文选择τ=50 m,作为停留提取的尺度参数,以保证识别结果在边界范围上的合理性。同时,试验数据存在较多室内停留,致使GPS信号质量较差,数据噪声较大,本文采用MinMov=300 s作为停留合并的阈值,以确保停留识别的完整性。此外,根据定义(2),停留应持续一定的时间,其值设置实际上是一个应用相关的问题。本文将其设置为180 s,即表示仅对持续时间超过此值的停留感兴趣,意在剔除那些因为短时减速慢行形成的,但语义蕴含较弱的停留。
4.2 结果分析针对自采轨迹和GeoLife轨迹的试验结果分别见表 1和表 2所示,其中,真实停留数是通过人工检验得到的实际停留的数目,发现停留数是通过算法输出的停留数,正确识别停留数为输出的停留中真实停留的数目,合并停留数为通过合并手段得到的停留数,未识别停留数为真实停留中未被识别的停留数。以第13条GeoLife轨迹为例,其停留指数图见图 5所示,相应的停留提取结果表 2第14行:人工检出6个停留,算法输出6个停留,其中有3个为合并而来,而在这6个输出停留中,5个是真实停留,意味着有1个真实停留未被检出,且多检出1个伪停留。
| 轨迹ID | 真实停留数 | 发现停留数 | 正确识别停留数 | 合并停留数 | 未识别停留数 |
| 1 | 5 | 4 | 4 | 1 | 1 |
| 2 | 1 | 4 | 1 | 0 | 0 |
| 3 | 2 | 2 | 2 | 1 | 0 |
| 4 | 5 | 5 | 5 | 1 | 0 |
| 5 | 2 | 3 | 2 | 0 | 0 |
| 6 | 3 | 5 | 3 | 2 | 0 |
| 7 | 5 | 5 | 5 | 1 | 0 |
| 8 | 5 | 4 | 4 | 0 | 1 |
| 共计 | 28 | 32 | 26 | 6 | 2 |
| 轨迹ID | 真实停留数 | 发现停留数 | 正确识别停留数 | 合并停留数 | 未识别停留数 |
| 1 | 15 | 18 | 14 | 10 | 1 |
| 2 | 12 | 15 | 12 | 7 | 0 |
| 3 | 14 | 18 | 13 | 4 | 1 |
| 4 | 13 | 16 | 13 | 6 | 0 |
| 5 | 15 | 16 | 14 | 3 | 1 |
| 6 | 10 | 13 | 9 | 4 | 1 |
| 7 | 15 | 15 | 15 | 5 | 0 |
| 8 | 8 | 8 | 7 | 5 | 1 |
| 9 | 6 | 7 | 6 | 3 | 0 |
| 10 | 4 | 5 | 4 | 3 | 0 |
| 11 | 8 | 8 | 8 | 1 | 0 |
| 12 | 12 | 13 | 11 | 9 | 1 |
| 13 | 6 | 6 | 5 | 3 | 1 |
| 14 | 13 | 15 | 12 | 4 | 1 |
| 15 | 1 | 1 | 1 | 1 | 0 |
| 共计 | 152 | 174 | 143 | 68 | 8 |
从表 1和表 2可以得出,尽管试验轨迹带有不少含漂移噪声的室内停留,本文方法对于真实停留的正确检测率仍然超过了90%。以图 5所示的第13条GeoLife轨迹为例,⑤为带漂移噪声的长时室内停留,借助于时空相邻停留段的逐级合并,算法成功提取出该停留,且其完整性与实际基本相符。自采数据总共仅有6处输出停留是通过合并得到的,原因在于自采数据的定位精度和采样频率较高,一些室内停留甚至无需通过合并即可被完整的提取出来;而对于GeoLife数据来说,大量的漂移噪声将实际停留分割成多个高停留指数的潜在停留段,有将近4成的输出停留是通过合并得来的。

|
| 图 5 GeoLife样例轨迹的停留指数图 Fig. 5 Example of GeoLife trajectory and its stop index plot |
从表 1和表 2也可以看出,本文方法主要存在两方面的问题:一是误识别,即输出伪停留;二是未识别,即有真实停留未被检出。从本质上来看,这两个问题的原因是相同的,即由于飘移噪声的影响,属于一个实际停留的多个停留段的时间间隔过大或者凸包不重叠,导致实际停留未能被正确合并出来,使得这些停留段或者被误识别为多个小停留(即发生误识别,如图 5中位于Ⅰ区的⑥,经过合并后仍然被分割成两个凸包不重叠的子停留),或者因短于180 s而被去除(即导致未识别,如图 5中位于Ⅱ区的①)。
5 总结与展望本文在分析与总结现有的轨迹停留识别方法的基础之上,提出了基于核密度思想、顾及时空邻近性,表征轨迹点时空聚集程度的数值指标:停留指数,并进一步发展出停留指数图。停留指数取决于轨迹在邻域内的逗留时间,符合人们对于停留的直观认识;停留指数图通过邻域半径建立起同空间尺度的关系,以可视化的方式表达不同尺度下的轨迹停留情况。源于停留指数,本文首先定义潜在停留段,提出了逐级合并的轨迹停留识别算法。该算法充分分析了潜在停留段之间的时空邻近关系,能够识别复杂多样的轨迹停留:GPS信号良好的停留可直接由潜在停留段得来,而GPS信号微弱的停留则可通过合并多个潜在停留段而来。基于自采轨迹和GeoLife轨迹的试验表明,本文方法可以直观展示轨迹在其生命周期内时空聚集程度的变化,且能更进一步、有效提取包括单点/多点和室内/室外在内的多类型、含噪声的轨迹停留。
本文算法的不足是在处理带有严重漂移噪声的长时室内停留时,仍有可能发生误识别和未识别的情形,后续研究将结合地理空间上下文信息,包括路网匹配信息和地理逆编码信息,以进一步合并由噪声隔开的停留段。
| [1] | SPACCAPIETRA S, PARENT C, DAMIANI M L, et al. A Conceptual View on Trajectories[J]. Data and Knowledge Engineering , 2008, 65 (1) : 126 –146. DOI:10.1016/j.datak.2007.10.008 |
| [2] | YAN Zhixian, CHAKRABORTY D, PARENT C, et al. Semantic Trajectories: Mobility Data Computation and Annotation[J]. ACM Transactions on Intelligent Systems and Technology , 2013, 4 (3) : 49 . |
| [3] | PARENT C, SPACCAPIETRA S, RENSO C, et al. Semantic Trajectories Modeling and Analysis[J]. ACM Computing Surveys , 2013, 45 (4) : 42 . |
| [4] | 向隆刚, 吴涛, 龚健雅. 面向地理空间信息的轨迹模型及时空模式查询[J]. 测绘学报 , 2014, 43 (9) : 982–988. XIANG Longgang, WU Tao, GONG Jianya. A Geo-spatial Information Oriented Trajectory Model and Spatio-temporal Pattern Querying[J]. Acta Geodaetica et Cartographica Sinica , 2014, 43 (9) : 982 –988. DOI:10.13485/j.cnki.11-2089.2014.0121 |
| [5] | 齐凌艳, 陈荣国, 温馨. 基于语义轨迹停留点的位置服务匹配与应用研究[J]. 地球信息科学学报 , 2014, 16 (5) : 720–726. QI Lingyan, CHEN Rongguo, WEN Xin. Research on the LBS Matching Based on Stay Point of the Semantic Trajectory[J]. Journal of Geo-Information Science , 2014, 16 (5) : 720 –726. |
| [6] | VIEIRA M, BAKALOV P, TSOTRAS V J. Querying Trajectories Using Flexible Patterns[C]//Proceedings of the 13th International Conference on Extending Database Technology. New York: ACM, 2010: 406-417. |
| [7] | GIANNOTTI F, NANNI M, PEDRESCHI D, et al. Trajectory Pattern Mining[C]//Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2007: 330-339. |
| [8] | ZHENG Yu, ZHANG Lizhu, XIE Xing, et al. Mining Interesting Locations and Travel Sequences from GPS Trajectories[C]//Proceedings of the 18th International Conference on World Wide Web. New York: ACM, 2009: 791-800. |
| [9] | ALVARES L, BOGORNY V, KUIJPERS B, et al. A Model for Enriching Trajectories with Semantic Geographical Information[C]//Proceedings of the 15th Annual ACM International Symposium on Advances in Geographic Information Systems. New York: ACM, 2007. |
| [10] | ROCHA J M R, TIMES V C, OLIVEIRA G, et al. DB-SMoT: A Direction-based Spatio-temporal Clustering Method[C]//Proceedings of the 5th IEEE International Conference Intelligent Systems. London: IEEE, 2010: 114-119. |
| [11] | STOPHER P, JIANG Q, FITZGERALD C. Processing GPS Data from Travel Surveys[C]//Proceedings of the 2nd International Colloquium on the Behavioral Foundations of Integrated Land-use and Transportation Models: Frameworks, Models and Applications. Toronto: [s.n.], 2005. |
| [12] | TIETBOHL A, BOGORNY V, KUIJPERS B, et al. A Clustering-based Approach for Discovering Interesting Places in Trajectories[C]//Proceedings of the 2008 ACM Symposium on Applied Computing. New York: ACM, 2008: 863-868. |
| [13] | TRAN L H, NGUYEN Q V H, NGOC H, et al. Robust and Hierarchical Stop Discovery in Sparse and Diverse Trajectories[EB/OL]. (2012-06-15)[2015-09-24]. http://cn.bing.com/academic/profile?id=1894965895&v=paper_preview&mkt=zh-cn |
| [14] | ZIMMERMANN M, KIRSTE T, SPILIOPOULOU M. Finding Stops in Error-Prone Trajectories of Moving Objects with Time-based Clustering[M]//TAVANGARIAN D, KIRSTE T, TIMMERMANN D, et al. Intelligent Interactive Assistance and Mobile Multimedia Computing. Berlin: Springer, 2009, 53: 275-286. |
| [15] | 张治华.基于GPS轨迹的出行信息提取研究[D].上海:华东师范大学, 2010. ZHANG Zhihua. Deriving Trip Information from GPS Trajectories[D]. Shanghai: East China Normal University, 2010. |
| [16] | Microsoft Research. GeoLife GPS Trajectories[EB/OL]. [2015-06-10]. http://research.microsoft.com/en-us/downloads/b16d359d-d164-469e-9fd4-daa38f2b2e13. |
| [17] | 向隆刚, 龚健雅, 吴涛, 等. 一种面向Stop/Move抽象的轨迹时空关系[J]. 武汉大学学报(信息科学版) , 2014, 39 (8) : 956–962. XIANG Longgang, GONG Jianya, WU Tao, et al. Spatio-temporal Trajectory Relationships Based on Stop/Move Abstraction[J]. Geomatics and Information Science of Wuhan University , 2014, 39 (8) : 956 –962. |
| [18] | PARZEN E. On Estimation of a Probability Density Function and Mode[J]. The Annals of Mathematical Statistics , 1962, 33 (8) : 1065 –1076. |
| [19] | 王远飞, 何洪林. 空间数据分析方法[M]. 北京: 科学出版社, 2007 : 57 -93. WANG Yuanfei, HE Honglin. Spatial Data Analysis Methods[M]. Beijing: Science Press, 2007 : 57 -93. |
| [20] | 禹文豪, 艾廷华. 核密度估计法支持下的网络空间POI点可视化与分析[J]. 测绘学报 , 2015, 44 (1) : 82–90. YU Wenhao, AI Tinghua. The Visualization and Analysis of POI Features under Network Space Supported by Kernel Density Estimation[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (1) : 82 –90. DOI:10.11947/j.AGCS.2015.20130538 |
| [21] | SCHABENBERGER O, GOTWAY C A. Statistical Methods for Spatial Data Analysis[M]. Boca Raton: Chapman & Hall /CRC, 2005 . |
| [22] | MILLER H J. Tobler's First Law and Spatial Analysis[J]. Annals of the Association of American Geographers , 2004, 94 (2) : 284 –289. DOI:10.1111/j.1467-8306.2004.09402005.x |
| [23] | 李小文, 曹春香, 常超一. 地理学第一定律与时空邻近度的提出[J]. 自然杂志 , 2007, 29 (2) : 69–71. LI Xiaowen, CAO Chunxiang, CHANG Chaoyi. The First Law of Geography and Spatial-temporal Proximity[J]. Chinese Journal of Nature , 2007, 29 (2) : 69 –71. |
| [24] | CHANDRA S, BHARTI A K. Speed Distribution Curves for Pedestrians during Walking and Crossing[J]. Procedia-social and Behavioral Sciences , 2013 (104) : 660 –667. |



