示意性地图(schematic map)始于19世纪初,是对网络线性要素进行简化,舍去与地图主题无关的地图要素,对地图中的线性要素进行概略性表达的地图。伦敦地铁图是示意性地图的代表,它将地铁线绘制成水平、垂直、对角线方向,并保留相对的拓扑信息,提供给用户简洁清晰的地图信息[1]。之后,示意性地图被广泛地应用于各个领域,如道路交通网[2]、公交线路网、电力网[3]、河流网[4]等。
示意性地图应用领域的不同,所关注的信息也会不同,因而在绘制道路网示意性地图时与绘制地铁图将有所区别。对此,国内外学者对示意地图进行了相关的研究。文献[5-7]研究自动化生成示意性地铁图的方法,算法简单方便,但未考虑原始线形,示意结果图与原始图有较大差别,并不适合道路网的自动示意化。文献[8-9]在考虑原始线形的基础上,基于道路网的路段进行示意化过程,以独立网络弧段作为基本单元。尽管示意图接近原始道路网,但图形容易产生锯齿效应,简化程度不够。文献[10]提出基于动态分段,以路径为单位,顾忌路径等级、长度等指标进行道路网示意化。然而对于某些道路网数据,并不存在路径等级等属性数据,无法进行动态分段;且在实际路网中,有些路径过长,有些路径过短,则造成结果的变形。文献[11]以闭合多边形(网眼)为基本单位,利用网眼的独立性与邻接性,提出了基于拓扑关系直接定位点线的多边形生长算法。然而该算法仅考虑了节点之间的部分方位信息以及保证了拓扑不变形,而没有参考图形的长度信息,使得示意化后的结果图在形状上有明显的变形。文献[12]提出基于路划(stroke)的自动化示意化方法,主要通过属性一致性或几何连通性组织网络弧段从而构造stroke,以stroke为基本单元进行排序、形状简化、拓扑验证,最终生成示意图,算法考虑了线的原始形状,但过于繁琐复杂,多次迭代,时间耗费大。
本文对以上算法进行分析和对比,提出基于stroke构造、移位一体化的道路网示意化方法,并提出利用相似分形维数来定量评估示意化结果。算法在考虑原始线形的基础上,使示意化过程更为简单,时间效率更高,示意化过程中拓扑冲突减少,同时具有较高的清晰度和认知度。
1 基于道路网stroke的示意化 1.1 道路网stroke模型道路网数据作为一种基础地理数据,一般以节点-弧段的拓扑结构存储于GIS中。然而这种以节点和弧段构成的道路网络,不符合人们头脑中现实路径的认知整体性。文献[12]提出根据感知分组“良好连续性”原则,将数条相对连续的路段连接成一个整体构建成一个“stroke”,考虑道路的自然形态单元,具有很好的连通性。构建stroke的方法分为基于几何特征和基于语义特性两种。前者考虑道路网在只有几何特征的基础上,根据几何连通性组织构造stroke;后者利用属性信息的一致性来构造stroke。而通常的做法是以几何连通性为主,辅以名称、类别等语义信息来进行判断构造。由于实际道路网数据往往缺失语义信息或者语义信息不全,本文采用基于几何特征的双向探测方法来构建stroke,具体算法如下。
(1) 读取道路网结构,得到节点集合P{p1, p2, …,pn}以及弧段集合E{e1, e2, …,em}。
(2) 顺序读取弧段集中的一弧段,作为起始弧段,判断是否归属于某一stroke:若属于,则继续判断下一弧段;若不属于,则建立新stroke,执行(3)。
(3) 利用起始弧段的首、尾节点进行双向空间搜索,找出与其相邻的弧段。判断相邻弧段是否都归属于某一stroke,若是,则回到(2);若不是,则继续判断新弧段与起始弧段间的夹角是否大于某一阈值:若大于等于某一阈值,则与该弧段相连构成stroke;若小于某一阈值,则结束。该相邻新弧段作为起始弧段,重复执行(3)。
(4) 重复(2)-(3),直至所有弧段集都遍历完,所有stroke构建完成。
1.2 基于stroke的示意化方法分析道路网stroke模型近年来被学者应用于路网示意化[12]、路网综合[13-14]中,顾及了路网语义、几何及拓扑的特征,保持了路网的完整性和连通性。对于道路网基于stroke的示意化方法,文献[12]给出了具体算法思路,如下:
(1) 通过属性一致性或者几何连通性构造stroke。
(2) stroke按照一定规则进行排序。
(3) 根据方向偏离或者方向变化来重新划分子stroke。
(4) 对子stroke进行示意化。
(5) 最后检查拓扑一致性,移位纠正。
然而,该算法过程复杂,多次迭代,耗时长,且在示意化过程中易出现以下问题:
(1) 一般stroke构造结合几何和语义特征进行一致性判断,完成stroke构造后,根据若干指标(重要度、连通度、中心度等)计算其重要性的权值,并以此排序[15]。然而,在实际应用中,道路网数据并不尽如人意,往往存在语义信息不全甚至没有的问题。因而根据语义信息构造stroke存在许多实际问题。
(2) 在对stroke根据一定指标进行排序后,按照重要性由大至小来进行示意化,直至完成所有stroke的示意化。但是在这种重要性排序的前提下,难以维持拓扑一致性,可能导致示意图局部集中,而忽略区域分布特征的问题,拓扑冲突问题明显。如图 1(a),在路a、b已示意化的前提下,对路c进行示意化时,使得a、b与c的相交点发生变化,从而引起拓扑冲突问题。

|
| 图 1 拓扑问题 Fig. 1 Topological problem |
为解决以上问题,本文仅考虑道路网的几何特征和拓扑关系来构造stroke,提出stroke构造、移位一体化的算法,使得示意化过程简单,时间效率高,减少了拓扑冲突问题,保证拓扑一致性及路网的均衡分布。
2 基于stroke构造、移位一体化的示意化方法本节将针对1.2节中所出现的问题进行讨论。首先,针对上文所述语义信息问题,本文不考虑语义特征,主要采用基于几何特征的双向探测方法来构建stroke,算法见1.1节。其次,对于stroke排序后示意化而引起的拓扑不一致以及局部集中问题,本文提出基于stroke构造、移位一体化的示意化方法,在对道路网进行stroke划分构造的同时,直接对其进行渐进式的移位示意化以及拓扑检查。如图 1(b),按1-7顺序逐次构造stroke并同时进行投影移位,避免图 1(a)中的拓扑冲突。
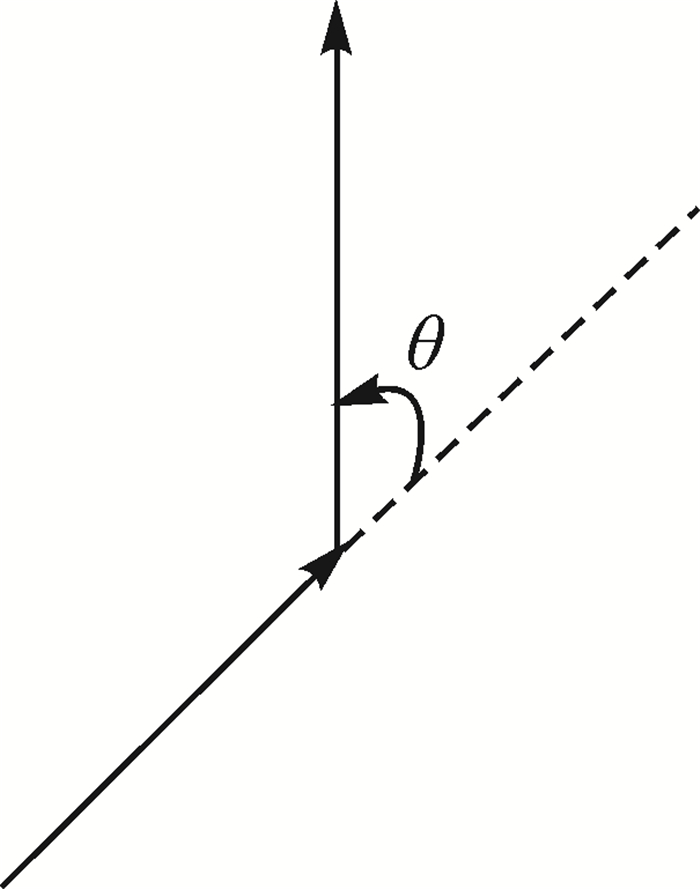
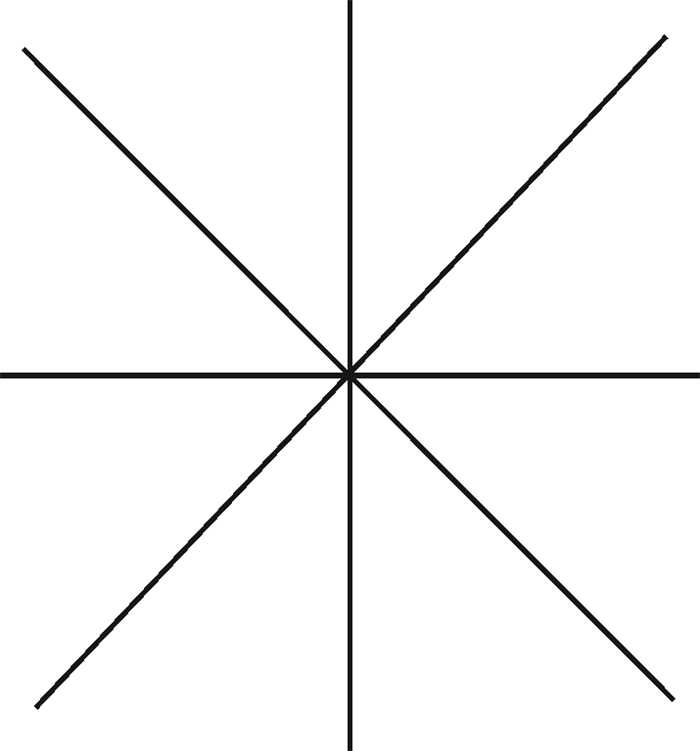
2.1 stroke构造根据“良好连续性”的原则[16],本文以方向变化一致的视为同一stroke,即相邻两条线段的偏斜角(图 2)是否超过某一阈值,若超过则分段;不超过,则视为同一stroke。本文主要采用8方位示意化方法(图 3),即将stroke投影映射到水平、垂直、对角线方位上。通过计算其方位角α与{0°,45°,90°,135°,180°,225°,270°,315°}中任意角度αi比较,求最小值
|
| 图 2 偏斜角 Fig. 2 Deflection angle |
|
| 图 3 8方位示意化 Fig. 3 8-direction schematic |
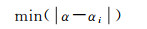 (1)
(1)
满足最小值时的αi即为该stroke的方向。由式(1)可知,当两线段的偏斜角大于22.5°时,归为不同方向。因而本文将22.5°视为stroke自动划分阈值。
在示意化算法实现过程中,笔者发现若遇到道路交叉点这一特殊要素时,往往情况复杂,易引起道路拓扑变化,进而影响交叉点相连的数条线段。因而,本文对于交叉点,将其视为stroke构造划分的重要依据。
2.2 stroke移位投影、拓扑检查构造完成的stroke需进行移位处理。由式(1)求得的新方位角αi,根据式(2)采用投影的方式对其进行方位判断后实现移位
 (2)
(2)
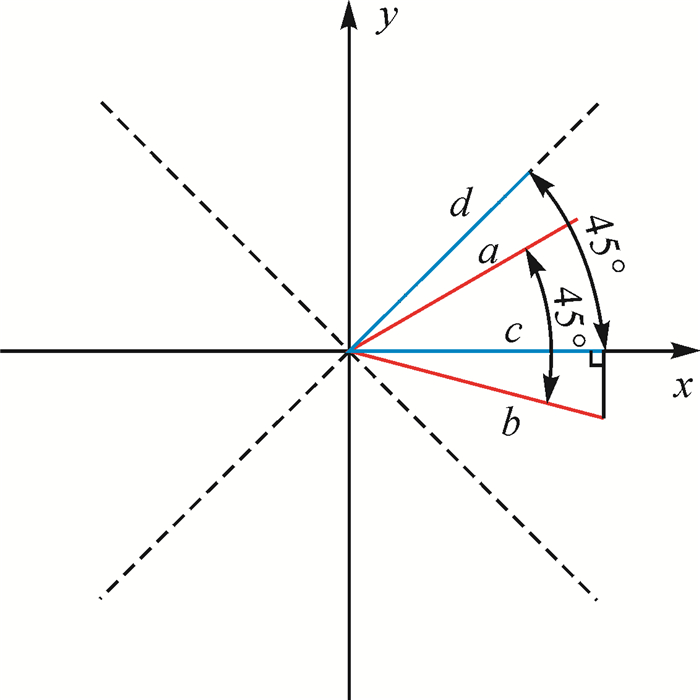
以下以45°投影为例进行说明。如图 4,线段a的新方位角为45°,对其进行投影移位:首先,将a正方向旋转45°至线段b;然后将线段b投影到水平位置,x不变,y为起始点y值,成为线段c;最后将线段c反旋转45°至线段d。线段d即为线段a的新移位位置。
|
| 图 4 45°投影位移图 Fig. 4 45° projection and displacement map |
是否将某一stroke位移至新的位置,还需通过拓扑检查,判断新位置是否与原图发生拓扑冲突,若发生拓扑冲突,需计算新的位置。本文涉及的拓扑检查主要见参考文献[17],其详细介绍了拓扑关系一致性检查和新点位的计算。
2.3 stroke构造、移位一体化算法本文提出的基于stroke构造、移位一体化的道路网示意化方法,是在对道路网进行2.1节划分构造的同时,直接渐进式地对stroke进行2.2节的移位投影和拓扑检查,以保证算法的时间效率和拓扑一致性,同时减少因拓扑冲突引起的移位过程。具体算法如下:
(1) 从地图的左下角的第1条开始标记,得到所有未处理线段segment集合S={S1, S2, …, Sm},共m段,起始弧段SQ=S1。
(2) 判断集合S是否为空,若为空,循环结束;若不为空,则判断SQ是否为空,若为空,遍历集合S,任取Si作为SQ。初始化stroke={SQ},SQ移除集合S,且SQ=null。
(3) 判断与当前stroke相邻线段Sl是否属于集合S,若属于,则继续(4),若不属于则跳至(6)。
(4) 判断当前stroke与Sl的中间点是否为交叉点,若是,SQ=Sl,构造完成跳至(6);若不是,继续(5)。
(5)判断stroke与Sl的偏斜角是否超过阈值,若超过阈值,构造完成,SQ=Sl,跳至(6);若不超过阈值,构造stroke={SQ, Sl},Sl移除集合S,继续(3)。
(6)对当前stroke投影移位。
(7)对当前stroke拓扑检查:若拓扑一致,跳至(2)重新开始构造stroke;若拓扑冲突,重新计算新位置后重复执行(7)。
上述方法,在集合S处理完成的同时,所有stroke示意化的过程也已完成,保证了示意结果道路目标的均匀性,缓解了以往等级划分stroke而导致的局部集中问题。同时,整个过程时间效率上明显优于以往的方法,且拓扑也较易保持,有效地完成了道路网的示意化过程,也保证了道路网的连通性,示意结果的空间认知也有效地得到保证。
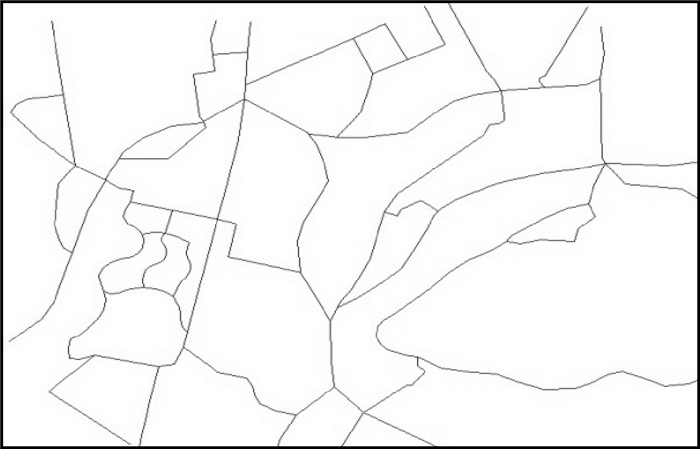
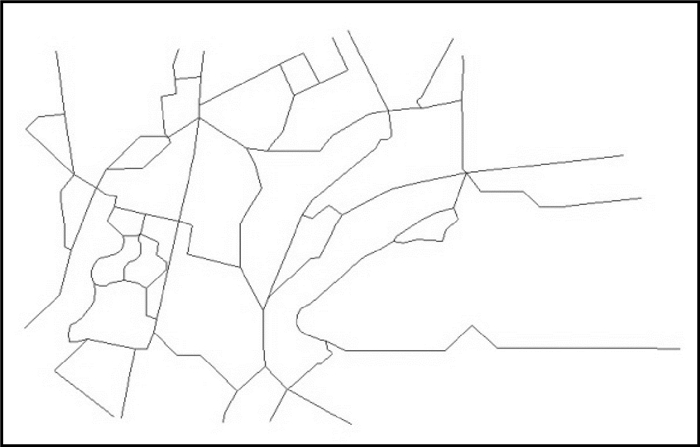
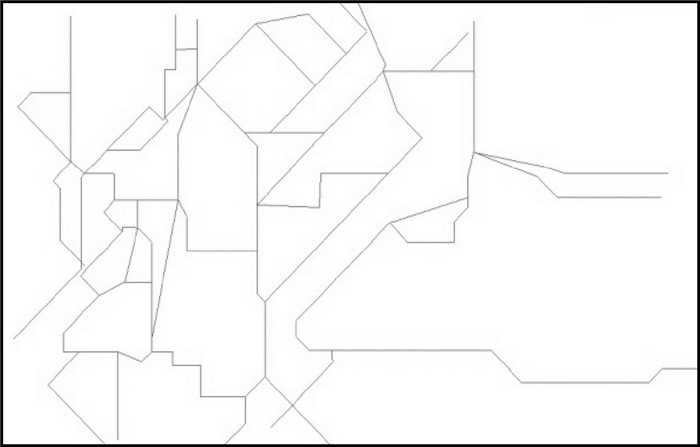
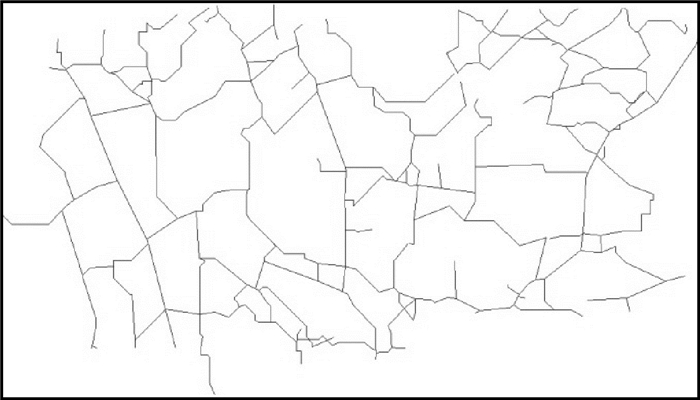
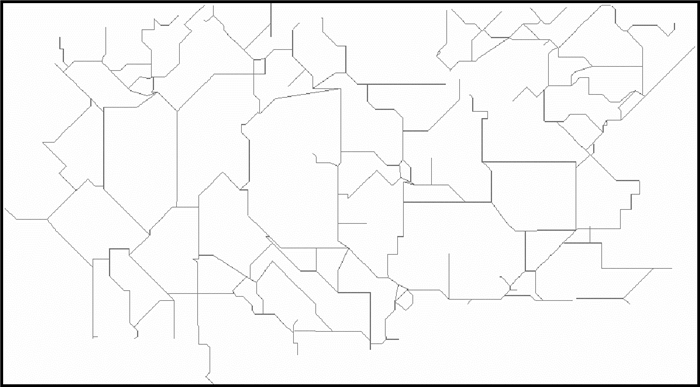
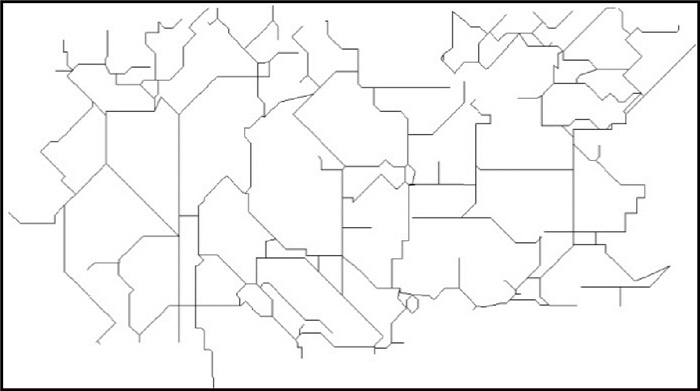
3 试验及分析 3.1 试验数据与结果为验证本文中所提出的示意化方法的高效性,试验采用两组真实道路网数据。数据1为某校园真实矢量道路网数据,见图 5;数据2为英国英格兰东部Waveney地区的部分道路网数据,见图 9。本文利用这两组数据,实现以独立网络弧段为基本单元的示意化试验(试验1)以及文献[12]的stroke排序方法的试验(试验2),对比stroke构造、移位一体化试验(试验3)来生成示意化结果。图 6-图 8为数据1的3组试验结果,图 10-图 12为数据2的3组试验结果。
|
| 图 5 原始图(数据1) Fig. 5 Original map (data 1) |
|
| 图 6 试验1图(数据1) Fig. 6 Experiment 1 map (data 1) |

|
| 图 7 试验2图(数据1) Fig. 7 Experiment 2 map (data 1) |
|
| 图 8 试验3图(数据1) Fig. 8 Experiment 3 map (data 1) |

|
| 图 9 原始图(数据2) Fig. 9 Original map (data 2) |
|
| 图 10 试验1图(数据2) Fig. 10 Experiment 1 map (data 2) |
|
| 图 11 试验2图(数据2) Fig. 11 Experiment 2 map (data 2) |
|
| 图 12 试验3图(数据2) Fig. 12 Experiment 3 map (data 2) |
3.2 定性分析
试验结果从简化度、空间认知度和时间效率3方面来进行定性评估。首先,分别对比图 5-图 8以及图 9-图 12,不难发现3个试验都从不同程度上对原始道路网进行了一定程度的简化示意化。其中试验1相比试验2、3的简易程度较低,试验2和3简易度大体一致。而对比两组数据的空间认知度,试验1较复杂,试验2、3更为清晰、明确。其次,在简化程度和认知清晰度相近的情况下,主要对比分析试验2和3的时间效率。本文采用VS2010开发系统,在Windows 8,64位操作系统下对两组数据进行试验,两个试验对于数据1的运行时间分别约为135 s、95 s,数据2为289 s、220 s。试验结果表明试验3的时间效率明显高于试验2。
3.3 定量分析以往研究都是从定性上进行分析评价,本文采用分形维数定量地对试验效果进行评价。无论采用何种方式进行示意化,示意化后的结果空间形态上都具有相似性,因而满足分形的要求。选取相似维数作为本文的研究指标,相似维数D反映原道路网与示意化道路网的相似程度。分维数越大,方格中有公路通过的网络边数越多,新网络与原网络的相似程度越高,网络的覆盖形态越好,曲线的分形维数可用式(3)表示[18-20]
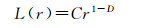 (3)
(3)
由式(3)取对数,则演变为
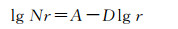 (4)
(4)
利用计盒法进行相似维数的计算,盒子取正方形。利用GIS矢量数据转换栅格数据的过程来模拟用不同尺寸盒子去覆盖曲线的方法,获得不同尺寸r以及方格数Nr,利用最小二乘求线性回归得到相似维数。试验分别计算原始图、试验1、2、3结果图的分形维数,得到数据1的结果值分别为1.011 1、1.014、1.020 5、1.016 9,数据2为1.016 1、1.015、1.018 3、1.014 1。求试验1、2、3与原始图的分形维数差,数据1分别为0.002 9、0.009 4、0.005 8,数据2为0.001 1、0.002 2、0.002。从分形维数差上发现:试验1的分形维数差最小;试验2、3相近,但试验3小于试验2。这表明试验1相较于试验2、3更接近于原始路网,示意化结果复杂;试验2、3示意化程度相近,但试验3与原图的相似度更高些。两组数据的具体分形维数的计算见表 1和表 2,分形维数的结果值见图 13和图 14。
| 特征尺度(ri) | lg ri | 原始图 | 试验1 | 试验2 | 试验3 | |||||||
| 栅格数目(Nri) | lg Nri | 栅格数目(Nri) | lg Nri | 栅格数目(Nri) | lg Nri | 栅格数目(Nri) | lg Nri | |||||
| 2 | 0.693 147 | 5909 | 8.684 232 | 5872 | 8.677 951 | 6152 | 8.724 533 | 5816 | 8.668 368 | |||
| 2.5 | 0.916 291 | 4711 | 8.457 655 | 4687 | 8.452 548 | 4910 | 8.499 029 | 4650 | 8.444 622 | |||
| 3 | 1.098 612 | 3931 | 8.276 649 | 3901 | 8.268 988 | 4068 | 8.310 907 | 3860 | 8.258 422 | |||
| 3.5 | 1.252 763 | 3361 | 8.119 994 | 3338 | 8.113 127 | 3487 | 8.156 797 | 3299 | 8.101 375 | |||
| 4 | 1.386 294 | 2931 | 7.983 099 | 2909 | 7.975 565 | 3053 | 8.023 88 | 2890 | 7.969 012 | |||
| 4.5 | 1.504 077 | 2601 | 7.863 651 | 2579 | 7.855 157 | 2687 | 7.896 181 | 2558 | 7.846 981 | |||
| 5 | 1.609 438 | 2333 | 7.754 91 | 2319 | 7.748 891 | 2417 | 7.790 282 | 2296 | 7.738 924 | |||
| 5.5 | 1.704 748 | 2131 | 7.664 347 | 2109 | 7.653 969 | 2191 | 7.692 113 | 2076 | 7.638 198 | |||
| 特征尺度(ri) | lg ri | 原始图 | 试验1 | 试验2 | 试验3 | |||||||
| 栅格数目(Nr i) | lg Nri | 栅格数目(Nr i) | lg Nri | 栅格数目(Nr i) | lg Nri | 栅格数目(Nr i) | lg Nri | |||||
| 30 | 3.401 197 | 8340 | 9.028 818 | 8343 | 9.029 178 | 8202 | 9.012 133 | 8217 | 9.013 96 | |||
| 35 | 3.555 348 | 7139 | 8.873 328 | 7144 | 8.874 028 | 7024 | 8.857 088 | 7005 | 8.854 379 | |||
| 40 | 3.688 879 | 6229 | 8.736 971 | 6232 | 8.737 453 | 6129 | 8.720 787 | 6130 | 8.720 95 | |||
| 45 | 3.806 662 | 5535 | 8.618 847 | 5546 | 8.620 832 | 5424 | 8.598 589 | 5464 | 8.605 936 | |||
| 50 | 3.912 023 | 4974 | 8.511 98 | 4982 | 8.513 587 | 4876 | 8.492 08 | 4885 | 8.493 925 | |||
| 55 | 4.007 333 | 4513 | 8.414 717 | 4513 | 8.414 717 | 4436 | 8.397 508 | 4451 | 8.400 884 | |||
| 60 | 4.094 345 | 4118 | 8.323 123 | 4124 | 8.324 579 | 4049 | 8.306 225 | 4055 | 8.307 706 | |||
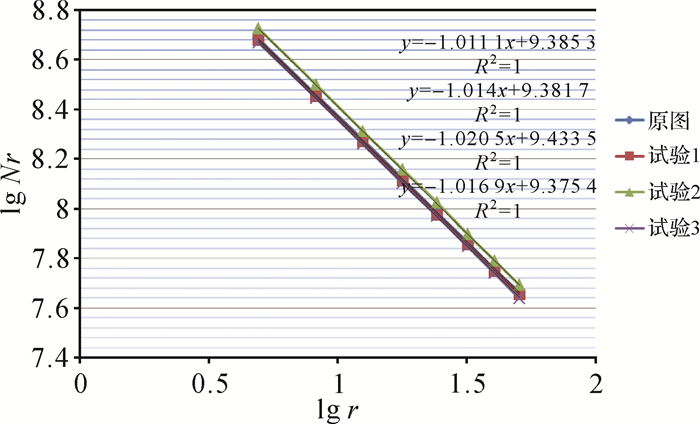
|
| 图 13 分形维数图(数据1) Fig. 13 Fractal dimension chart (data 1) |
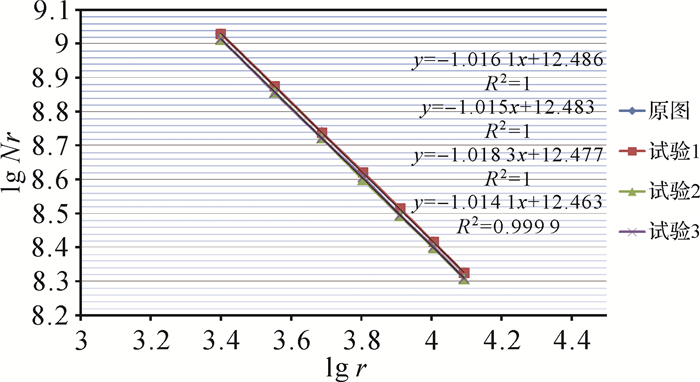
|
| 图 14 分形维数图(数据2) Fig. 14 Fractal dimension chart (data 2) |
4 结论
本文提出了一种新的基于stroke构造、移位一体化的道路网示意化方法,同时还提出利用相似分形维数来定量比较验证不同示意化方法的有效性。试验结果表明,与之前的方法比较,本算法在考虑原始线形的基础上,使示意化过程更为简单,时间效率更高,减少了拓扑冲突问题,保证拓扑一致性及路网的均衡分布,同时又具有很高的空间认知度和清晰度。本文对于相似维数的计算应在一定的无标度区内,而无标度区的计算复杂,将是今后的研究重点。
| [1] | MORRISON A. Public Transport Maps in Western European Cities[J]. The Cartographic Journal , 1996, 33 (2) : 93 –110. DOI:10.1179/caj.1996.33.2.93 |
| [2] | AVELAR S, HURNI L. On the Design of Schematic Transport Maps[J]. Cartographica , 2006, 41 (3) : 217 –228. DOI:10.3138/A477-3202-7876-N514 |
| [3] | AVELAR S. Convergence Analysis and Quality Criteria for an Iterative Schematization of Networks[J]. GeoInformatica , 2007, 11 (4) : 497 –513. DOI:10.1007/s10707-007-0018-z |
| [4] | STOTT J M, RODGERS P. Automatic Metro Map Design Techniques[C]//Proceedings of the XXII International Cartographic Conference. Madrid: [s.n.], 2005. |
| [5] | HONG S H, MERRICK D, DO NOSCIMENTO H A D. Automatic Visualisation of Metro Maps[J]. Journal of Visual Languages & Computing , 2006, 17 (3) : 203 –224. |
| [6] | STOTT J, RODGERS P, MARTINEZ-OVANDO J C, et al. Automatic Metro Map Layout Using Multicriteria Optimization[J]. IEEE Transactions on Visualization and Computer Graphics , 2011, 17 (1) : 101 –114. DOI:10.1109/TVCG.2010.24 |
| [7] | NOLLENBURG M, WOLFF A. Drawing and Labeling High-quality Metro Maps by Mixed-integer Programming[J]. IEEE Transactions on Visualization and Computer Graphics , 2011, 17 (5) : 626 –641. DOI:10.1109/TVCG.2010.81 |
| [8] | AVELAR S, MUELLER M. Generating Topologically Correct Schematic Maps[C]//Proceedings of the 9th International Spatial Data Handling. Beijing: [s.n.], 2000: 28-35. |
| [9] | WARE J M, TAYLOR G E, ANAND S, et al. Automated Production of Schematic Maps for Mobile Applications[J]. Transactions in GIS , 2006, 10 (1) : 25 –42. DOI:10.1111/tgis.2006.10.issue-1 |
| [10] | 董卫华, 李志林, 郭庆胜. 基于动态分段的道路网示意性地图模型综合[J]. 武汉大学学报(信息科学版) , 2010, 35 (8) : 892–895. DONG Weihua, LI Zhilin, GUO Qingsheng. Automated Model Generalization of Schematic Network Maps Based on Dynamic Segmentation[J]. Geomatics and Information Science of Wuhan University , 2010, 35 (8) : 892 –895. |
| [11] | 张蓝, 李佳田, 徐珩, 等. 道路网络示意图的多边形生长算法[J]. 测绘学报 , 2015, 44 (3) : 346–352. ZHANG Lan, LI Jiatian, XU Heng, et al. Polygon Growing Algorithm for Network Schematic Maps[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (3) : 346 –352. DOI:10.11947/j.AGCS.2015.20130724 |
| [12] | LI Zhilin, DONG Weihua. A Stroke-based Method for Automated Generation of Schematic Network Maps[J]. International Journal of Geographical Information Science , 2010, 24 (11) : 1631 –1647. DOI:10.1080/13658811003766936 |
| [13] | 杨敏, 艾廷华, 周启. 顾及道路目标stroke特征保持的路网自动综合方法[J]. 测绘学报 , 2013, 42 (4) : 581–587, 594. YANG Min, AI Tinghua, ZHOU Qi. A Method of Road Network Generalization Considering Stroke Properties of Road Object[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (4) : 581 –587, 594. |
| [14] | 刘彩凤.基于路划功能的城市道路主干网选取方法[D].成都:西南交通大学, 2010. LIU Caifeng. Stroke Function-based Approach to Extracting Backbone of Urban Road Network[D]. Chengdu: Southwest Jiaotong University, 2010. http://cdmd.cnki.com.cn/article/cdmd-10613-2010122525.htm |
| [15] | 徐柱, 刘彩凤, 张红, 等. 基于路划网络功能评价的道路选取方法[J]. 测绘学报 , 2012, 41 (5) : 769–776. XU Zhu, LIU Caifeng, ZHANG Hong, et al. Road Selection Based on Evaluation of Stroke Network Functionality[J]. Acta Geodaetica et Cartographica Sinica , 2012, 41 (5) : 769 –776. |
| [16] | THOMSON R C, RICHARDSON D E. The Good Continuation Principle of Perceptual Organization Applied to the Generalization of Road Networks[C]//Proceedings of the 19th International Cartographic Conference. Vancouver: [s.n.], 1999: 1215-1225. |
| [17] | 董卫华, 郭庆胜, 刘纪平, 等. 道路网示意性地图的渐进式综合研究[J]. 武汉大学学报(信息科学版) , 2007, 32 (9) : 829–832, 837. DONG Weihua, GUO Qingsheng, LIU Jiping, et al. Progressive Generalization Research of Schematic Road Network Maps[J]. Geomatics and Information Science of Wuhan University , 2007, 32 (9) : 829 –832, 837. |
| [18] | 朱洪栓.基于GIS的河南省公路交通网络分形研究[D].开封:河南大学, 2008. ZHU Hongshuan. Study on Fractal Properties of Highway Network in Henan Province Based on GIS[D]. Kaifeng: Henan University, 2008. http://www.oalib.com/references/16485233 |
| [19] | 李雯静, 毋河海. 地图综合中的地图目标自相似性分形衰减研究[J]. 测绘科学 , 2005, 30 (3) : 21–23. LI Wenjing, WU Hehai. Fractal Attenuation Analysis of Cartographic Object on Cartography Generalization[J]. Science of Surveying and Mapping , 2005, 30 (3) : 21 –23. |
| [20] | 陈杰.矢量地图信息定量度量方法研究[D].长沙:中南大学, 2009. CHEN Jie. The Methods of Quantitative Measurement of Geospatial Information in Vector Map[D]. Changsha: Central South University, 2009. http://cdmd.cnki.com.cn/article/cdmd-10533-2009240756.htm |



