2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
极化合成孔径雷达(SAR)能够获得比单极化SAR更全面的目标回波信息,大大提高了目标的识别、分类和图像解译的能力[1-2]。极化目标分解能够综合利用雷达回波中的极化信息提取目标的极化散射特征,是一种有效的极化SAR数据解译的工具。由于基于模型的分解直接与地物真实散射机制相关联,具有一定的物理意义,是近年来极化SAR分解领域的研究重点[3-15]。
Freeman分解是第一个被提出的基于模型的分解,基于此,文献[3-4]结合散射熵、各向异性与Wishart分类器进行了地物分类和图像建筑物提取,并取得了良好效果。然而,原始的基于模型的极化SAR三分量分解中存在两个严重的缺陷,一是散射机制提取模糊问题,二是面和偶次散射存在负功率问题。文献[5]提出修改体散射模型,使其相干矩阵对角线元素为(1, 1, 1),某种程度上降低了体散射功率,但负功率仍然大量存在;文献[12]提出采用去取向以降低体散射功率值,但是由于去取向的局限性使得该方法在某些情况下会失效,而且面和偶次散射模型中的交叉极化分量仍然被假设为零,这导致面或偶次散射提取不充分[12];文献[13]提出的非负特征值分解(NNED)利用数学方法对体散射功率进行限制以消除负功率,但只适用于面和偶次散射为反射对称的情形[13],随后文献[14]对NNED作出改进以适用于非反射对称情形,但其是一种强制性的数学工具,没有从基于模型的角度出发,在某些情况下体散射仍然被过高估计。
本文首先描述了三分量分解中存在的问题,然后深入分析在其改进方法中仍然存在的不足,基于此提出了一种自适应的三分量分解方法。该方法主要包括以下步骤:①确定分解框架,建立更一般化散射模型;②利用散射Alpha角确定除体散射之外剩余散射中的主导散射机制,并得到本文的预分解结果;③采用一种非负特征值法的替代方法对上述结果中存在负功率的像素进行优化,减少负功率像素个数;④当所有散射功率为正值后,再次利用Alpha角确定除体散射之外的剩余主导散射机制,得到本文的最终分解结果。结果表明,本文分解结果能更准确地反映实际地物散射特征,能更好地解决基于模型的分解中存在的问题。
1 基于模型的分解Freeman三分量分解将地物散射分为面散射、偶次散射和体散射,通过对它们建立模型从极化协方差或相干矩阵中提取出各自的散射功率[16]。该分解可以表示成如下形式
 (1)
(1)
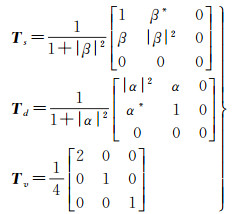 (2)
(2)
式中,|β|≤1;|α|≤1;T为原始数据相干矩阵,元素均为已知数;Ts、Td、Tv为面、二面和体散射模型;Ps、Pd、Pv为其对应的散射功率。然而,在Freeman分解中存在两个严重的缺陷,一是面或偶次散射功率存在负值,也即Ps或Pd可能会出现负数;二是散射机制模糊,这使得Freeman分解在地物分解过程中不具备自适应性。
通过观察可以看到,在三分量分解中,面和偶次散射模型中HV分量均为零,由此可见,HV分量全部分配给了体散射,这不可避免导致体散射被过高估计从而导致负功率和散射机制模糊问题。针对这些问题,文献[12]提出采用去取向处理来降低体散射功率[12],虽然负功率像素个数有所减少,但是仍然大量存在,散射机制提取模糊仍然存在。问题出在去取向本身[17-19],所谓去取向处理就是通过旋转原始相干矩阵使HV分量达到最小,然后将这个最小值分配给体散射,过程可以描述成如下形式
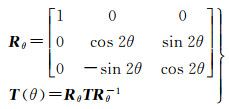 (3)
(3)
式中,Rθ为旋转矩阵,所以θ可以由如下方法解出
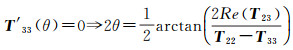 (4)
(4)
可以看到,去取向角2θ的范围为(-π/4, π/4),然而目标的旋转角范围为(-π/2, π/2),所以当目标旋转角比较大时,去取向并不能使HV分量达到最小,此时将HV全部分配给体散射仍然不合理。
另一个典型的改进方法是非负特征值分解(NNED)[13],文献[13]采用非负特征值原理来强制使每个像素中都不可能出现负功率。对于任意一个散射过程,其可以被描述成如下形式
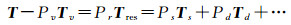 (5)
(5)
式中,Tres为除去体散射外所有剩余散射机制总称;Pr为剩余散射机制功率之和。由于体散射模型中的元素均为常数,所以可以利用这一特点并通过数学手段来强制使剩余各散射机制的功率全为非负数,式(5)中最左边的矩阵必须为非负定矩阵,这样就可以通过|T-PvTv|=0,来解出体散射功率Pv。然而,NNED并没有从基于模型的分解的本质即模型须自适应于极化SAR数据出发,这使得NNED应用于基于模型的分解仍然存在缺陷,这种强制性体现在Pv值的选取上。显然,有无穷多的体散射功率取值都能保证Tres是非负定的,但在NNED中,Pv却选取所有的可能值当中最大的一个,这显然是不合理的。因为当除体散射外剩余散射存在弱去极化情形时,Tres的秩必然为3,但在NNED中,其秩被强制设为2,所以NNED对这种情形下的散射过程提取显然是不充分的,而且体散射仍然被过高估计。
2 自适应的分解 2.1 一般的散射机制由于倾斜的表面和旋转的建筑物均能产生相当大的交叉极化分量,这就需要建立更一般化的散射模型。本文中,该一般化的散射模型具有以下Pauli矢量形式
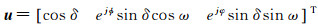 (6)
(6)
式中,δ、ω、Φ、φ为未知实数,再加上其功率系数共有5个自由度,因为任何一种单散射机制其Pauli矢量就是存在5个自由度,所以u表示了一般化的散射向量,因而涵盖了任意可实现的单散射机制[20]。其对应的相干矩阵可表示为
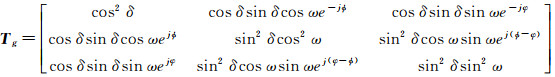 (7)
(7)
本文仍然采用经典的三分量分解中的体散射模型。至此本文提出的分解框架可以表示成如下形式
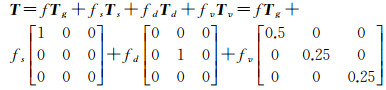 (8)
(8)
式中,f为面或偶次散射功率系数;fs、fd、fv分别为面、偶次和体散射功率系数。由式(8)可看到,除体散射外,剩余散射的主导散射机制为Tg,其类型将由散射Alpha角确定。选取本组模型的依据是:由于散射场景的复杂性,在每个像素对应的场景中可能存在具有不同偏转角的相同散射机制物体,所以式(8)中第1个模型是一般的散射机制模型,在分解中代表像素中较充分的散射机制物体,第2、3个模型为理想情形的面和二面散射机制,因为在本文分解优化过程中,会把场景进行旋转使假设的模型与实际地物散射特征更加匹配,所以在这个新的角度下可以用这种模型来提取实际散射特征。所以相比较于式(1),除体散射外,本文提出的分解能够提取出像素中的具有不同旋转角的两个面或偶次散射目标加上一个偶次散射或面散射目标,即考虑到了除体散射外剩余散射可能存在弱去极化的情形。而且相比较于NNED,本文分解在减去体散射后,剩余相干矩阵的秩仍为3,而不是NNED中为2,因此对于面或偶次散射成分的提取将更充分,同时NNED中的体散射仍被过高估计的问题将得到解决。
2.2.1 未知数提取根据式(8)可以得到各个未知参量,以下列出几个下文会使用到的几个参量
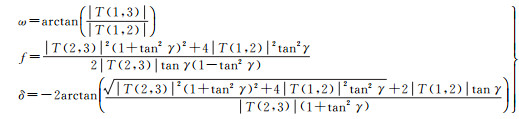 (9)
(9)
式中,假设r=w/2。
2.2.2 确定主导散射机制旋转不变的散射Alpha角参数是一种有效的判别单散射机制类型的工具,其表达形式如下
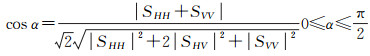 (10)
(10)
首先本文将它改写为以下形式
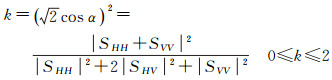 (11)
(11)
通过式(11),可以直观地与相干矩阵中的元素联系起来,所以将它扩展到非相干情形,具有如下形式
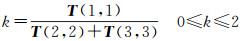 (12)
(12)
由于当α∈[0, π/4]时,主导散射为面散射,此时k∈(1, 2];当α∈(π/4, π/2]时,主导散射为偶次散射,此时k∈[0, 1]。因此,k参数是一种在非相干情形下判别散射机制类型的工具。所以,本文的预分解代码可以归纳为如下。
预分解:通过k参数确定各散射功率系数
1: input: T
2:求解方程:T=fTg+fsTs+fdTd+fvTv;
3: 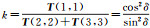
4: if k≤1 then
5: Ps=f+fs, Pd=fd, Pv=fv;
6: else
7: Pd=f+fd, Ps=fs, Pv=fv;
8: end if
9: output: Ps, Pd, Pv
2.3 分解优化本文提出一种新的对负功率像素优化的方法,原理是使极化相干矩阵旋转某一角度来达到所有散射功率系数均为非负的目的,物理意义在于由于相干矩阵的迹是一种旋转不变的量,所以旋转相干矩阵后,一个像素的总的散射功率是不变的,这是本文方法的基础,而且如果直接用假设的散射模型进行提取各自的功率,难免是片面的,本文可以尝试从不同的角度来认识和解释一个像素中的散射成分,这样会更准确,也就是假设雷达以不同的飞行方向照射同样的场景,由于这个实际中很难做到,所以可以旋转相干矩阵至某个角度来达到这样的目的,如果在这个角度下散射模型所提取的功率不存在不一致性,那么表明该分解方法可以真实地解译数据。这样,分解优化实施后没有影响像素中实际散射特征的提取,而且使得所建模型与实际数据更加吻合。最终的分解可以表示成如下形式
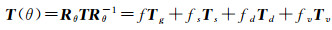 (13)
(13)
下一步是通过设定步进搜索出使f、fs、fd、fv均为非负的θ角,为最终本文要求的相干矩阵旋转角度。需要指出的是,在分解优化过程中,对于θ角的选取是不唯一的,由于只要所有的散射功率均为非负时,散射模型就与实际地物特征是一致的,散射模型就能正确地提取实际散射特征,其次对于一个像素包含的地物场景,我们也确实可以用不同的角度来看待它。至此本文最终的分解代码可以归纳为如下。
分解优化:旋转相干矩阵以适应于散射模型
1: input: T
2: for θ=-π/2 to π/2 do
3:求解方程: T(θ)=fTg+fsTs+fdTd+fvTv
4: if f, fs, fd, fv≤0 then
5: break
6: end if
7: end for
8: output: ω, f, fs, fd, fv, δ
9:执行:预分解步骤3-9
3 试验结果与分析 3.1 AIRSAR数据分解结果比较该数据为美国AIRSAR系统在旧金山地区所采集的全极化数据,数据主要包括海洋、不同旋转角的城区建筑物和森林区域等典型地物。
图 1显示了3种不同分解方法下的RGB合成结果的对比。可以很明显地看到,3幅图像从左到右体散射分量剧烈减弱,如图中左侧的红色椭圆所标注区域所示,即在RGB合成结果中绿色成分明显减弱;同时,城区偶次散射份量显著增强,比较典型的如图中右侧的白色椭圆标注的区域所示。在3幅图像中,本文的分解对于偶次散射成分的提取相比于其他两个分解更为充分,符合该区域的实际散射特征。

|
| 图 1 3种不同分解下的RGB结果对比 Fig. 1 Comparison of the three different decomposition approaches |
需要指出的是,对于本文提出的散射模型,负功率像素个数从优化前的506 323减少到了优化后的18 683,即将负功率像素的比例从优化前66.2%降低到了2.4%,可见负功率问题得到了极大的抑制。
为了更清晰直观地验证本文方法的有效性,截取图 1(a)右侧椭圆区域中一部分来作对比分析。图 2显示了截取区域在3种分解下的比较结果。由椭圆标注区域可见,标注区域为二次散射占主导的城市建筑物区,在本文分解下标注区域的二次散射成分较前两幅明显增强同时体散射也明显减弱。

|
| 图 2 截取区域的分解结果对比分析 Fig. 2 Comparison of the three different decomposition approaches over the selected area |
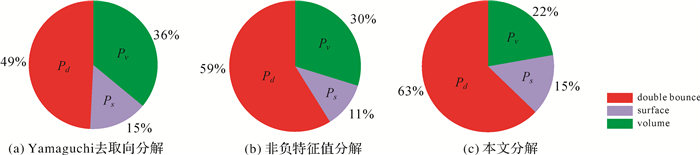
为了定量验证本文分解的有效性,截取了图中矩形所标注的一小块城区以作试验,该区域主导散射为来自建筑物墙壁与地表构成的偶次散射,非主导散射为来自地表或屋顶的面散射以及来自市区树木的体散射。图 3显示了3种分解下的面散射、偶次散射和体散射的功率比例饼图对比。从图 3可看到,体散射功率比例从NNED中的30%降至本文分解中的22%,可知本文分解较NNED进一步抑制了城区的体散射功率,解决了NNED中体散射仍被过高估计的问题。同时可看到,该区域偶次散射比例从NNED中的59%升至本文分解中的63%,符合该区域的实际散射特征。
|
| 图 3 3种分解下的面、偶次和体散射的功率分布 Fig. 3 Power distribution by the three different decomposition approaches |
3.2 E-SAR数据分解结果比较
不失一般性,本文选取了德国E-SAR系统在Oberpfaffenhofen地区采集的全极化数据来进行验证。数据在Yamaguchi分解、非负特征值分解和本文分解下的RGB合成结果如图 4所示。

|
| 图 4 3种不同分解下的RGB结果对比图 Fig. 4 Comparison of the three different decomposition approaches |
首先定性地分析本文分解对于实际散射特征的保持效果,如图 4中左下角的矩形标注的区域,该区域为旋转的建筑物区,偶次散射为主导散射,在Yamaguchi分解中并没有显示出明显的偶次散射占优,说明实际散射特征没有被充分准确地提取出,而在本文分解的RGB结果中,该区域红色调显著增强,说明偶次散射已被更好地抽取出来。相比较于NNED,同样功率均为非负,但在本文分解中体散射分量能被进一步降低,正如上方的矩形标注的区域所示,本文分解的RGB结果中该区域绿色明显减弱。值得一提的是,在经过分解优化后,对于本文的分解模型,该数据中负功率像素比例从优化前的34.7%降至0.1%,负功率像素个数大大减少,可见分解结果将更适应于实际地物散射特征。
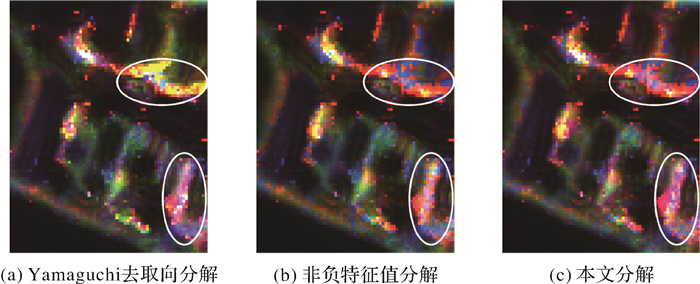
图 5显示了图 4中的左下方矩形区域的分解结果放大图。该区域为旋转的建筑物区,从本文结果中可以更直观地看到更多的像素显示为红色即二次散射占主导,因此对于实际地物散射特征的提取更为充分。
|
| 图 5 截取区域的分解结果对比分析 Fig. 5 Comparison results of the selected area by three different decompositions approaches |
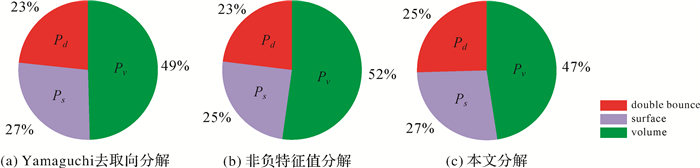
类似的,本文选取图中的上方矩形区域以定量地说明本文分解的准确性。该区域为植被区,主导散射为来自树冠的体散射。3种分解下的面、偶次和体散射功率比例对比如图 6所示。注意到,体散射功率比例从NNED中的52%降低至本文分解中的47%,且面和偶次散射的功率比例从NNED中的25%和23%分别升高至本文分解中的27%和25%,符合该区域实际散射特征。
|
| 图 6 3种分解下的面、偶次和体散射的功率分布 Fig. 6 Power distribution by three different decompositions |
4 结束语
本文提出了一种基于模型的极化SAR自适应三分量分解方法。该分解首次考虑了除体散射外剩余散射可能存在弱去极化的情形,且采用了更一般化的散射模型,该模型涵盖了任何可实现的散射过程,使得像素中的实际散射得到了更充分的保持。从基于模型分解的本质出发,提出了一种能更好地解决基于模型的分解中存在问题的优化措施,使得负功率像素数目大大减少,同时由于负功率的减小使得分解结果与实际地物的不一致性得到缓解,即散射机制模糊问题得到了更好解决。该优化措施是一种非负特征值法的替代方法,不仅大大减少了负功率,且进一步从整体上降低了体散射功率,从而解决了NNED中体散射仍被过高估计的问题。而且,该措施也能应用于其他基于模型的分解方法中。试验结果表明,较现有分解,本文提出的分解是一种稳健的自适应的分解,分解结果更符合实际地物散射特征。
| [1] | 王文光.极化SAR信息处理技术研究[D].北京:北京航空航天大学, 2007. WANG Wenguang. Studies on Information Processing Technique of Polarimetric SAR[D]. Beijing: Beihang University, 2007. http://cdmd.cnki.com.cn/article/cdmd-10006-2008051318.htm |
| [2] | CLOUDE S R, POTTIER E. A Review of Target Decomposition Theorems in Radar Polarimetry[J]. IEEE Transactions on Geoscience and Remote Sensing , 1996, 34 (2) : 498 –518. DOI:10.1109/36.485127 |
| [3] | 郎丰铠, 杨杰, 赵伶俐, 等. 基于Freeman散射熵和各向异性度的极化SAR影像分类算法研究[J]. 测绘学报 , 2012, 41 (4) : 556–562. LANG Fengkai, YANG Jie, ZHAO Lingli, et al. Polarimetric SAR Data Classification with Freeman Entropy and Anisotropy Analysis[J]. Acta Geodaetica et Cartographica Sinica , 2012, 41 (4) : 556 –562. |
| [4] | 刘修国, 姜萍, 陈启浩, 等. 利用改进三分量分解与Wishart分类的极化SAR图像建筑提取方法[J]. 测绘学报 , 2015, 44 (2) : 206–213. LIU Xiuguo, JIANG Ping, CHEN Qihao, et al. Buildings Extraction from Polarimetric SAR Image Using Improved Three-component Decomposition and Wishart Classification[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (2) : 206 –213. DOI:10.11947/j.AGCS.2015.20130535 |
| [5] | AN Wentao, CUI Yi, YANG Jian. Three-component Model-based Decomposition for Polarimetric SAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing , 2010, 48 (6) : 2732 –2739. DOI:10.1109/TGRS.2010.2041242 |
| [6] | CHEN Siwei, SATO M. General Polarimetric Model-based Decomposition for Coherency Matrix[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium. Munich: IEEE, 2012: 99-102. |
| [7] | SINGH G, YAMAGUCHI Y, PARK S E, et al. Hybrid Freeman/Eigenvalue Decomposition Method with Extended Volume Scattering Model[J]. IEEE Geoscience and Remote Sensing Letters , 2013, 10 (1) : 81 –85. DOI:10.1109/LGRS.2012.2193373 |
| [8] | WANG Chunle, YU Weidong, WANG R, et al. Comparison of Nonnegative Eigenvalue Decompositions with and without Reflection Symmetry Assumptions[J]. IEEE Transactions on Geoscience and Remote Sensing , 2013, 52 (4) : 2278 –2287. |
| [9] | LEE J S, AINSWORTH T L, WANG Yanting. Generalized Polarimetric Model-based Decompositions Using Incoherent Scattering Models[J]. IEEE Transactions on Geoscience and Remote Sensing , 2013, 52 (5) : 2474 –2491. |
| [10] | 陈启浩, 刘修国, 黄晓东, 等. 一种极化SAR协方差矩阵综合四分量分解模型[J]. 武汉大学学报(信息科学版) , 2014, 39 (7) : 873–877. CHEN Qihao, LIU Xiuguo, HUANG Xiaodong, et al. An Integrated Four-component Model-based Decomposition of Polarimetric SAR with Covariance Matrix[J]. Geomatics and Information Science of Wuhan University , 2014, 39 (7) : 873 –877. |
| [11] | 张海剑, 杨文, 邹同元, 等. 基于四分量散射模型的多极化SAR图像分类[J]. 武汉大学学报(信息科学版) , 2009, 34 (1) : 122–125. ZHANG Haijian, YANG Wen, ZOU Tongyuan, et al. Classification of Polarimetric SAR Image Based on Four-component Scattering Model[J]. Geomatics and Information Science of Wuhan University , 2009, 34 (1) : 122 –125. |
| [12] | YAMAGUCHI Y, SATO A, BOERNER W M, et al. Four-component Scattering Power Decomposition with Rotation of Coherency Matrix[J]. IEEE Transactions on Geoscience and Remote Sensing , 2011, 49 (6) : 2251 –2258. DOI:10.1109/TGRS.2010.2099124 |
| [13] | VAN ZYL J J, ARII M, KIM Y. Model-based Decomposition of Polarimetric SAR Covariance Matrices Constrained for Nonnegative Eigenvalues[J]. IEEE Transactions on Geoscience and Remote Sensing , 2011, 49 (9) : 3452 –3459. DOI:10.1109/TGRS.2011.2128325 |
| [14] | CUI Yi, YAMAGUCHI Y, YANG Jian, et al. On Complete Model-based Decomposition of Polarimetric SAR Coherency Matrix Data[J]. IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (4) : 1991 –2001. DOI:10.1109/TGRS.2013.2257603 |
| [15] | ARII M, VAN ZYL J J, KIM Y. Adaptive Model-based Decomposition of Polarimetric SAR Covariance Matrices[J]. IEEE Transactions on Geoscience and Remote Sensing , 2011, 49 (3) : 1104 –1113. DOI:10.1109/TGRS.2010.2076285 |
| [16] | FREEMAN A, DURDEN S L. A Three-component Scattering Model for Polarimetric SAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing , 1998, 36 (3) : 963 –973. DOI:10.1109/36.673687 |
| [17] | CHEN Siwei, OHKI M, SHIMADA M, et al. Deorientation Effect Investigation for Model-based Decomposition over Oriented Built-up Areas[J]. IEEE Geoscience and Remote Sensing Letters , 2013, 10 (2) : 273 –277. DOI:10.1109/LGRS.2012.2203577 |
| [18] | LEE J S, AINSWORTH T L. The Effect of Orientation Angle Compensation on Coherency Matrix and Polarimetric Target Decompositions[J]. IEEE Transactions on Geoscience and Remote Sensing , 2011, 49 (1) : 53 –64. DOI:10.1109/TGRS.2010.2048333 |
| [19] | XU Feng, JIN Yaqiu. Deorientation Theory of Polarimetric Scattering Targets and Application to Terrain Surface Classification[J]. IEEE Transactions on Geoscience and Remote Sensing , 2005, 43 (10) : 2351 –2364. DOI:10.1109/TGRS.2005.855064 |
| [20] | CLOUDES R. Polarisation. Applications in Remote Sensing[M]. Oxford: Oxford University Press, 2009 . |


