2. 国家测绘地理信息局卫星测绘应用中心, 北京 100048
2. Satellite Surveying and Mapping Application Center of NASG, Beijing 100048, China
航天遥感技术经过50多年应用与发展,已经形成多角度、全方位、立体式的地球信息获取技术[1-2]。遥感影像空间分辨率不仅是影像质量评价的一项关键性技术指标,更是衡量一个国家卫星遥感水平的重要标志[3-4]。卫星遥感影像的空间分辨率取决于传感器精度,而成像系统性能的提高却伴随着昂贵的制造成本。所以从硬件上改善影像分辨率,在传感器制造工艺、系统成本以及发射载荷限制均存在瓶颈。因此尝试从软件上通过图像处理技术使遥感影像分辨率得以提升,以较小的经济代价改善影像空间分辨率,提高影像利用效益,由此可见超分辨率重建技术研究成果将具有重要的理论意义和实用价值[5-6]。
超分辨率重建是对多幅具有互补信息的低分辨率影像进行处理,获得一幅或多幅高分辨率影像的技术[7]。现有的超分辨率重建方法主要分为基于频域和基于空域的超分辨率重建。基于频域超分辨率重建方法通常为傅里叶变换[8]和小波变换[9-10]的超分辨率重建方法。此类方法优点是运行速度较快、计算相对简单,但因局限于线性空间不变,只包含有限的先验知识,没能成为超分辨率重建技术的主流研究方法。基于空域的超分辨率重建方法主要包括:插值法[11-13]、正则化方法[14-15] (包括L1范数、L2范数及TV正则项)、最大后验概率(maximum a posterior, MAP)方法[16-19]和基于学习的重建方法[1],等等。插值方法因未增加新的高频信息,使得重建结果出现锯齿、模糊等视觉失真的现象;正则化方法中如何恰当地给出保持图像边缘结构的先验条件仍是难点;概率论方法改善重建效果的代价是复杂度较高、计算代价较大;基于学习的方法,往往对单幅遥感影像进行处理,限制了序列遥感影像间差异信息的利用。
综上所述,目前超分辨率重建方法已取得了一定的进展与突破,但遥感影像因覆盖地表范围广、地形起伏大,导致序列遥感影像超分辨率重建增添高频细节信息仍是一个难点。本文对现有超分辨率重建方法进行分析与总结,针对序列遥感影像,以最大限度提升影像纹理细节水平与空间分辨率为目标,提出多尺度细节增强的超分辨率重建模型框架,使得重建影像可以提供更多有益的高频细节信息,同时能够达到兼顾遥感影像微观与宏观信息的目的。
1 多尺度细节增强的超分辨率重建方法原理为使超分辨率重建结果中涵盖更加丰富的地表纹理信息,本文通过三角网优化模型下的小面元遥感影像配准算法实现序列遥感影像的亚像元配准,以具有亚像元配准精度的影像作为试验数据,利用最小二乘滤波方法对影像进行多尺度分解。通过主观判读的方式在序列影像中选取一幅参考影像,以序列影像最大尺度分解结果作为超分辨率重建的冗余信息,冗余信息即为序列影像中均包含的信息。其他观测影像与参考影像相应尺度的分解结果进行差分处理,以获取不同尺度的非冗余信息,非冗余信息即为序列影像间的细节差异信息。利用插值方法对冗余信息和非冗余信息进行插值得到相应的高分辨率影像信息,构造细节增强函数,在细节信息增强的基础上融合细节信息和平滑信息,得到初始的超分辨率重建影像,再通过局部优化模型对初始重建影像质量进一步改善,避免因过度增强而使影像信息灰度值发生改变。本文超分辨率重建方法的总体技术流程如图 1所示。

|
| 图 1 超分辨率重建框架流程 Fig. 1 Flow chart of the super resolution framework |
1.1 基于最小二乘滤波多尺度分解模型及解算
多尺度分解是指通过设置不同的滤波参数将影像分解成一个包含大尺度边缘的平滑层和一个或多个包含中小型尺度纹理的细节层。本文采用文献[20]所提出的最小二乘滤波方法对序列遥感影像进行多尺度分解。最小二乘滤波算法中使用了最优化方法,设目标函数为
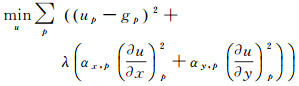 (1)
(1)
式中,u为输入影像;g为输出影像;p为影像上像素点;(up-gp)2表示输出影像和输入影像的相似程度;αx, p(g)和αy, p(g)是平滑权重;λ为权衡两个数据项参数,随着λ值逐渐增大,影像则越趋于平滑。求目标函数最优解,实际上就是求使得目标函数最小的输出影像g,将式(1)转化为矩阵形式
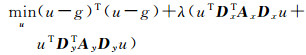 (2)
(2)
式中,Dx、Dy为微分符号组成的对角矩阵;Ax、Ay分别为αx, p(g)和αy, p(g)组成的对角矩阵。欲求式(2)最小值,可得线性方程组如式(3)
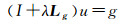 (3)
(3)
式中,Lg=DxTDx+DyTDy,是普通的拉普拉斯矩阵。由此可见,通过设置不同滤波器参数即可得到不同尺度的分解结果uj,要获取大尺度的平滑信息(影像信息中的低频分量),就要设置能使影像更加平滑的滤波参数。
本文利用最小二乘滤波方法对序列遥感影像image1、image2、… 、imagei(i=1,2,…,n)进行多尺度分解,得到一系列渐进平滑的影像信息。假设想要得到m幅渐进平滑的影像信息,则需通过最小二乘滤波方法进行m次分解。更具体地说,如需构造一个j+1级(scalej=0,1,…,m)的多尺度分解结果,以参考影像image1为例,代表输入影像,通过滤波得到一系列渐进平滑影像信息u1、u2、…、uj(j≥1),uj为最大尺度的平滑信息,与此同时可以得到一系列中小型细节信息,即在多尺度分解过程中通过设置不同滤波参数,对多尺度分解的影像信息进行差分处理后所对应的中高频分量,如式(4)所示
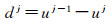 (4)
(4)
式中,j=0, 1, …, m;u0=image1。
本文以序列影像作为试验数据,令u(i, j)代表序列影像通过最小二乘滤波方法多次滤波后得到的不同尺度的平滑信息,d(i, j)代表多尺度分解后通过差分获取的一系列细节信息,为充分利用序列影像间的非冗余信息,通过观测影像与参考影像相应尺度的分解结果进行差分,即d(i, j)=u(i, j-1)-u(1, j)。再通过插值方法得到一系列与之相对应的高分辨率平滑信息U(i, j)和细节信息D(i, j),后续为了便于描述均以参考影像image1为例进行说明。
1.2 纹理信息增强为避免重建影像出现纹理消失等现象,在多尺度分解基础上构建细节增强函数S(β, Dj)。函数S(β, Dj)的目的是为了提升多尺度分解过程的中小型细节的增强幅度,增加重建影像中的高频信息。
 (5)
(5)
式中,细节增强函数S(β, Dj)是双曲正切函数;β*Dj是一个简单的标量乘法。细节增强函数中要求参数β是一个正数,Dj为多尺度分解后通过插值方法获取的高分辨率细节信息,对式(5)求偏导数,可以得到
 (6)
(6)
由此可以证明,当β>0时,S(β, Dj)是关于Dj的增函数,也就是说β越大,中小型细节增强的幅度越大,但同时也面临影像失真的现象,因此在试验过程中结合影像信息熵等客观评价指标,权衡地定义一个细节增强参数β,在保证重建影像不失真的前提下,最大限度地提升影像纹理细节信息。
1.3 信息融合在多尺度分解过程中采取了保持边缘的最小二乘滤波算法。最小二乘滤波虽是对影像平滑与边缘保留一个权衡较好的方法,但对图像中的大尺度细节平滑时却无法做到完全保持边缘结构,因而其细节层中的强边缘(影像信息中的高频分量)可能仍有残留。如果在细节增强过程中,强边缘也被同等尺度的放大,则后续融合过程中整幅影像在高频区域将会出现过饱和的情况。若采取简单拦截,则影像会丢失很多信息;若单纯地归一化,则影像灰度值分布会发生偏移。所以,无论后续采取何种措施都可能使影像信息发生改变。为有效抑制强边缘被过度放大,本文通过函数f来最小化强边缘的锐化程度,式中θ为一个常量,控制强边缘边界被放大的程度。
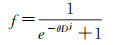 (7)
(7)
在信息增强基础上,基于多尺度分解的影像信息被重构,需要将包含大尺度的平滑信息和中小型尺度的细节信息进行叠加融合,如式(8)所示,即可得到初始的超分辨率重建结果X0。
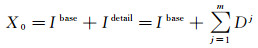 (8)
(8)
式中,Ibase为序列影像的冗余信息;Idetail为序列影像的非冗余信息;Dj为多尺度细节增强后通过插值方法获取的高分辨率影像细节信息。
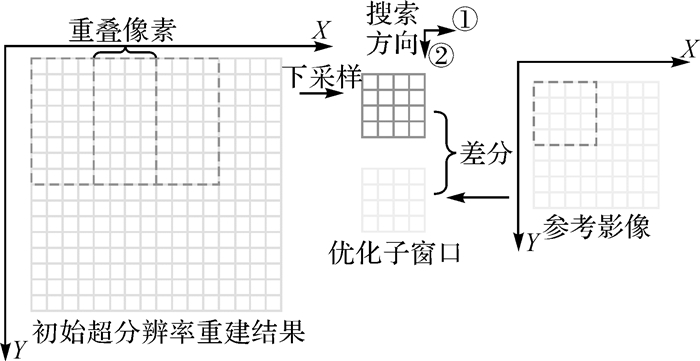
1.4 局部优化模型由于全局约束不能较好地保护重建影像的锐化边缘与高频细节,同时避免细节增强后影像灰度信息及亮度偏离参考影像,论文提出超分辨率重建局部优化模型。假设参考影像大小为l×h,则重建影像大小为2l×2h,选取一个局部优化窗口,对局部优化窗口下采样,将下采样窗口与其对应的参考影像窗口的灰度信息进行差分处理,计算差分处理后影像灰度信息的绝对值之和。若大于预先设定的阈值,则通过局部优化模型进行迭代优化,利用梯度下降方法解决式(9)的最小化问题,依据式(9)进行迭代更新,完成对初始超分辨率重建结果的优化,如图 2所示,目的是使最终结果尽可能地逼近参考影像。
|
| 图 2 局部优化 Fig. 2 Local optimization model |
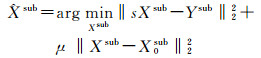 (9)
(9)
式中,Ysub为参考影像image1局部优化子窗口;Xsub为潜在的高分辨率影像局部优化子窗口;X0sub为初始估计的超分辨率重建局部优化子窗口;s为下采样因子;μ为平滑尺度参数。
1.5 超分辨率重建结果质量评价标准本文采取主观与客观相结合方式对重建结果进行定量评价。由于本文选取的试验数据为真实的卫星遥感影像,相应真实的高分辨率影像是不存在的,所以本文利用信息熵[21-22](entropy)和细节增强评价指标[23-24] (enhancement measure evaluation, EME)对遥感影像的超分辨率重建效果作出客观评价。
信息熵是衡量影像信息量一个重要指标,是对影像信息量分布的一种度量。重建影像信息熵的值越大,说明影像灰度信息偏离影像直方图的高峰区越大,即所有灰度值出现的概率趋于相等,表明影像携带的信息量越丰富。二维灰度影像信息熵的数学表达式如式(10)所示,式中Pk代表影像中灰度值为k的像素出现的频率,近似代替概率。
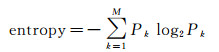 (10)
(10)
影像细节增强评价指标的原理是将影像分为k1×k2块区域,计算子区域中灰度最大值和最小值之比的对数作为细节增强评价结果。EME代表影像局域灰度的变化程度,当影像局域灰度变化越强烈,EME值越大,说明影像涵盖的细节信息越丰富,其表达式如式(11)
 (11)
(11)
式中,Imax; k, jw、Imin; k, jw分别表示影像块wk, l中灰度最大值和最小值。
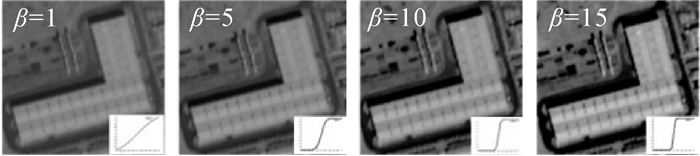
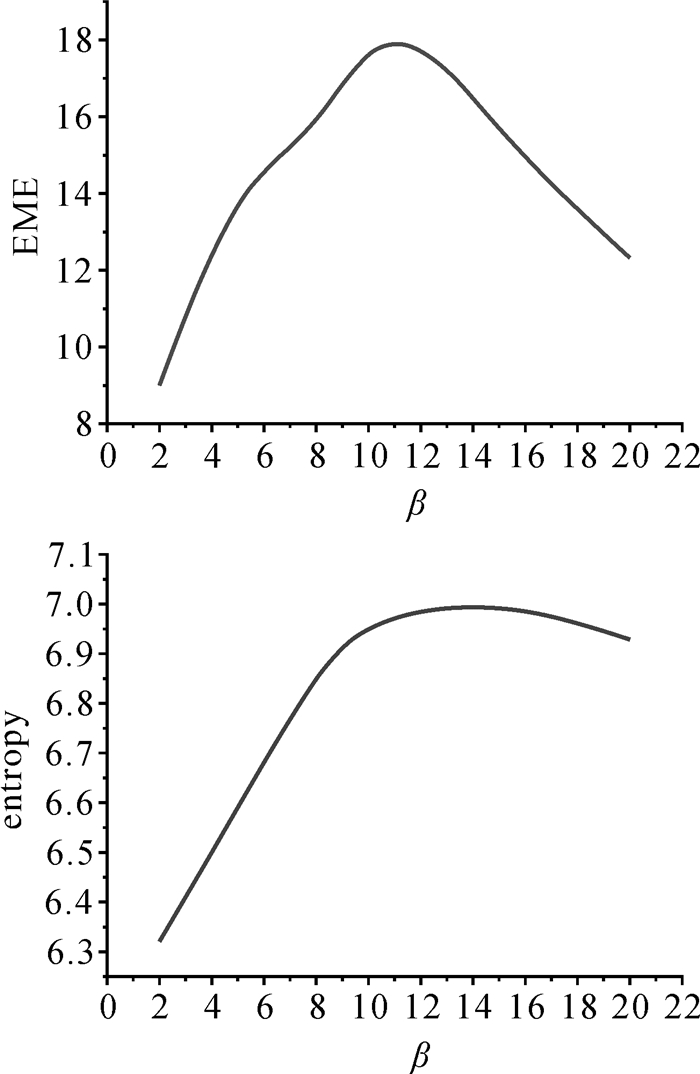
2 试验结果与分析为验证本文提出超分辨率重建方法的有效性,选取资源三号卫星TDI CCD相机获取的遥感影像作为试验数据,在Intel(R) Xeon(R) CPU E21220 @ 3.10 GHz 64位操作系统,Matlab R2011b平台下编程实现。在细节增强过程中,影像中小型细节随着β的增大而增强,但β过大则会导致影像失真,如图 3所示。随着β的增大,影像细节也随之增强,但当β增大到10后,不仅影像细节增强效果的改善已不明显,反而会逐渐失真,而且影像的信息熵和细节增强评价指标上升的趋势已不显著,甚至当β增大到一定程度反而会呈现出下降的趋势,如图 4所示。因此在试验中设置细节增强参数为β=10。而参数θ作为一个抑制大尺度过度增强的常量,防止强边缘过度被放大,试验中通常默认设置为θ=2。
|
| 图 3 不同细节增强参数效果图 Fig. 3 Results of different detail enhancement parameters |
|
| 图 4 客观评价结果 Fig. 4 Evaluation results |
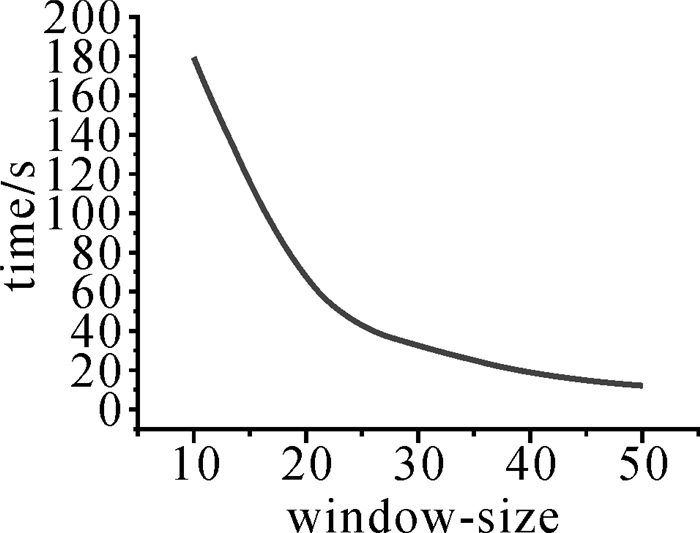
同时在局部优化过程中如何选取合适大小的窗口与窗口间重叠度的设置也非常重要。若窗口太大,可能导致影像中细节信息不能很好地保留,若窗口太小,优化速率会降低。同时还需要考虑优化窗口间的重叠度,若不设置重叠度,影像的边缘可能会出现不连续等问题,若重叠度设置过大,速度反而会变慢。顾及以上因素,本文通过设置不同大小优化窗口进行多次试验,并计算优化时间,如图 5所示。同时与文献[7]提出的全局优化方法进行对比,如图 6所示。虽然局部优化方法用时相对较多,但从重建影像的效果上来看,更好地保护了重建影像的边缘结构及细节信息,而且客观评价指标也有明显提高,可见时间的牺牲是值得的。因此本文根据多次试验,权衡优化速率与优化效果设定局部优化窗口大小为30×30,同时设置重叠度为优化窗口的二分之一时效果较为理想。
|
| 图 5 运行时间测试 Fig. 5 Runtime test graph |

|
| 图 6 全局与局部优化对比结果 Fig. 6 Comparisons of different optimization algorithms |
限于篇幅,本文选取同时相和多时相两组试验进行举例说明,通过多尺度细节增强的超分辨率重建模型框架实现2倍的影像重建,与双三次插值[13]、TV方法[15]、MAP方法[18]进行对比,并通过客观评价方法进行定量分析。
试验1,选取多时相全色遥感影像进行超分辨率重建试验,试验中3张影像分别获取于2015年2月14日、2015年2月19日和2015年4月24日,试验结果如图 7所示。图 7(a)中带框影像为参考影像,图 7(b)为双三次插值结果,图 7(c)为TV方法的超分辨重建结果,图 7(d)为MAP方法的超分辨重建结果,图 7(e)为本文方法重建结果,图 8为4种超分辨率重建方法的合成影像。从图 7、图 8可以看出,相对其他重建影像,本文方法的重建影像较为理想,影像纹理信息明显增强,在主观视觉效果上也取得了较好的改善。

|
| 图 7 不同时相遥感影像的超分辨率重建结果 Fig. 7 Super resolution results based on remote sensing images with different times |

|
| 图 8 不同重建方法的合成影像 Fig. 8 Synthetic image of different reconstruction methods |
试验2,选取同时相三线阵全色遥感影像进行超分辨率重建试验,3张影像获取时间均为2013年7月10日,试验结果如图 9所示。图 9(a)中带框影像为参考影像,图 9(b)-(d)给出不同方法的超分辨率重建影像,图 9(e)为本文方法的超分辨重建影像。图 10为图 9小方框对应区域的局部放大结果,将重建后的影像按照分辨率1:1显示。从图中可以看出,本文方法在纹理信息增强方面有明显优势,重建影像地物纹理突出,同时也较好地保留了影像边缘结构特征。

|
| 图 9 相同时相遥感影像(不同算法)超分辨率重建结果 Fig. 9 Super resolution results based on remote sensing image(different methods) with the same time |
表 1给出图 9中不同重建方法客观评价的量化指标值,本文方法entropy值比双三次插值方法改善了0.74 bits,比TV方法改善了0.87 bits,比MAP方法改善了0.74 bits,可见重建后影像信息量明显增加。同时EME值比双三次插值方法提高了8.54,比TV方法提高了6.62,比MAP方法提高了8.75,表明本文方法在改善局部细节方面具有明显优势。从主观视觉效果上来看,图 10(e)比图 10(b)-(d)明显清晰,说明在提高影像空间分辨率的同时不仅保护了影像的边缘结构信息,同时改善了影像中目标景物的细微程度。
| 影像 | 评价参数 | 参考影像 | 双三次插值方法 | TV方法 | MAP方法 | 本文方法 |
| 试验1 | entropy/bits | 6.275 7 | 6.294 7 | 6.207 0 | 6.334 2 | 7.040 0 |
| EME | 7.455 5 | 4.879 0 | 7.170 0 | 4.774 7 | 11.078 1 | |
| 试验2 | entropy/bits | 6.262 6 | 6.262 3 | 6.133 8 | 6.267 8 | 7.007 0 |
| EME | 9.058 8 | 5.926 3 | 7.850 2 | 5.721 3 | 14.470 6 |

|
| 图 10 局部放大显示 Fig. 10 Display of local amplification |
与试验1的结果相比,试验2的重建影像效果更为理想。可见同时相超分辨率重建效果要好于多时相的超分辨率重建,说明超分辨率重建对具有时间连续性的影像数据可以表现出较好的稳健性。因此在序列影像数据的选择上,要尽量选择时相相同或相近的影像数据,而对于多时相的影像数据,则要尽量选择在同一季节的影像数据,这样影像中地物变化不会太大,重建出的影像才有实际意义和价值。本文通过多尺度增强的超分辨率重建模型框架对不同类型的遥感影像数据进行试验。从表 1中量化的客观评价指标可以得出结论,本文方法在客观评价指标上具有明显的提高,表明影像纹理细节得到了有效改善。而且重建影像中不仅没有出现明显的模糊或锯齿现象,还增加了更多的高频纹理细节信息,重建影像质量的较为理想。与双三次插值方法、TV方法和MAP方法比较,重建影像不仅在视觉效果的改善上有明显优势,而且较好地保护了影像的锐化边缘,丰富了地物纹理信息。
3 总结本文利用资源三号国产卫星遥感影像作为试验数据,针对序列遥感影像,以最大限度提升影像纹理细节水平与空间分辨率为目标,提出多尺度细节增强的遥感影像超分辨率重建模型框架。利用细节增强函数提升影像中小型尺度细节信息,使之生成新的高频细节信息,多尺度分解不仅可以很好地保留细节信息,而且包含较好的边缘结构信息。试验结果表明,本文方法与双三次插值方法、TV方法和MAP方法相比,在客观评价指标上均有提升,表明该方法在抑制噪声的同时具有保护影像边缘结构的能力。可见根据观测影像利用所提出的多尺度细节增强的超分辨率重建方法,可以快速地估计出相应的高分辨率影像,且重建影像中涵盖丰富的地貌纹理信息,体现了该方法的灵活性特点,同时能够重建出更丰富的纹理细节信息,计算量相对减小。但本文针对序列遥感影像只进行了2倍的超分辨率重建试验,对于更大倍数的超分辨率重建试验,如何更好地提供高频信息,还有待于进一步的深入研究。
| [1] | 钟九生, 江南, 胡斌, 等. 一种遥感影像超分辨率重建的稀疏表示建模及算法[J]. 测绘学报 , 2014, 43 (3) : 276–283. ZHONG Jiusheng, JIANG Nan, HU Bin. A Super-resolution Model and Algorithm of Remote Sensing Image Based on Sparse Representation[J]. Acta Geodaetica et Cartographica Sinica , 2014, 43 (3) : 276 –283. DOI:10.13485/j.cnki.11-2089.2014.0040 |
| [2] | ZHANG Kaibing, TAO Dacheng, GAO Xinbo, et al. Learning Multiple Linear Mappings for Efficient Single Image Super-resolution[J]. IEEE Transactions on Image Processing , 2015, 24 (3) : 846 –861. DOI:10.1109/TIP.2015.2389629 |
| [3] | 谭兵, 徐青, 邢帅, 等. 小波超分辨率重建算法及其在SPOT影像中的应用[J]. 测绘学报 , 2004, 33 (3) : 233–238. TAN Bing, XU Qing, XING Shuai, et al. Wavelet Super-resolution Algorithm and Its Application to SPOT Images[J]. Acta Geodaetica et Cartographica Sinica , 2004, 33 (3) : 233 –238. |
| [4] | WANG Shenlong, ZHANG Lei, LIANG Yan, et al. Semi-coupled Dictionary Learning with Applications to Image Super-resolution and Photo-sketch Synthesis[C]//Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI: IEEE, 2012: 2216-2223. |
| [5] | COSSAIRT O, GUPTA M, NAYAR S K. When Does Computational Imaging Improve Performance[J]. IEEE Transactions on Image Processing , 2013, 22 (2) : 447 –458. DOI:10.1109/TIP.2012.2216538 |
| [6] | YANG J, LIN Z, COHEN S. Fast Image Super-resolution Based on In-place Example Regression[C]//IEEE Conference on Computer Vision & Pattern Recognition. [S. l.]: IEEE, 2013:1059-1066. |
| [7] | YANG Jianchao, WRIGHT J, HUANG T S, et al. Image Super-resolution via Sparse Representation[J]. IEEE Transactions on Image Processing , 2010, 19 (11) : 2861 –2873. DOI:10.1109/TIP.2010.2050625 |
| [8] | 钦桂勤, 耿则勋, 徐青. 利用频谱解混叠方法实现超分辨率影像重建[J]. 测绘学报 , 2003, 32 (2) : 143–147. QIN Guiqin, GENG Zexun, XU Qing. Super-resolution Image Restoration by Spectral Dealiasing[J]. Acta Geodaetica et Cartographica Sinica , 2003, 32 (2) : 143 –147. |
| [9] | DOGIWAL S R, SHISHODIA Y S, UPADHYAYA A. Super Resolution Image Reconstruction Using Wavelet Lifting Schemes and Gabor Filters[C]//Proceedings of the 5th International Conference:Confluence the Next Generation Information Technologuser Summit. Noida: IEEE, 2014: 625-630. |
| [10] | BABU P A, PRASAD K V S V R.Binary Plane Technique for Super Resolution Image Reconstruction Using Integer Wavelet Transform[C]//Proceedings of 2013 International Conference on Pattern Recognition, Informatics and Mobile Engineering. Salem: IEEE, 2013: 237-240. |
| [11] | ZHANG Lei, WU Xiaolin. An Edge-guided Image Interpolation Algorithm via Directional Filtering and Data Fusion[J]. IEEE Transactions on Image Processing , 2006, 15 (8) : 2226 –2238. DOI:10.1109/TIP.2006.877407 |
| [12] | 沈焕锋, 李平湘, 张良培. 一种顾及影像纹理特性的自适应分辨率增强算法[J]. 遥感学报 , 2005, 9 (3) : 253–259. SHEN Huanfeng, LI Pingxiang, ZHANG Liangpei. An Adaptive Algorithm for Resolution Enhancement Considering the Texture Attribute of Images[J]. Journal of Remote Sensing , 2005, 9 (3) : 253 –259. |
| [13] | 周登文, 申晓留. 边导向的双三次彩色图像插值[J]. 自动化学报 , 2012, 38 (4) : 525–530. ZHOU Dengwen, SHEN Xiaoliu. Edge-directed Bicubic Color Image Interpolation[J]. Acta Automatica Sinica , 2012, 38 (4) : 525 –530. DOI:10.3724/SP.J.1004.2012.00525 |
| [14] | PARK M K, KANG M G, KATSAGGELOS A K. Regularized High-resolution Image Reconstruction Considering Inaccurate Motion Information[J]. Optical Engineering , 2007, 46 (11) : 117004 . DOI:10.1117/1.2802611 |
| [15] | FADILI J M, PEYRE G. Total Variation Projection with First Order Schemes[J]. IEEE Transactions on Image Processing , 2011, 20 (3) : 657 –669. DOI:10.1109/TIP.2010.2072512 |
| [16] | LIU Ce, SUN Deqing. On Bayesian Adaptive Video Super Resolution[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2014, 36 (2) : 346 –360. DOI:10.1109/TPAMI.2013.127 |
| [17] | FATTAL R, AGRAWALA M, RUSINKIEWICZ S. Multiscale Shape and Detail Enhancement from Multi-light Image Collections[J]. ACM Transactions on Graphics , 2007, 26 (3) : 51 . DOI:10.1145/1276377 |
| [18] | VILLENA S, VEGA M, BABACAN S D, et al. Bayesian Combination of Sparse and Non-sparse Priors in Image Super Resolution[J]. Digital Signal Processing , 2013, 23 (2) : 530 –541. DOI:10.1016/j.dsp.2012.10.002 |
| [19] | 肖创柏, 禹晶, 薛毅. 一种基于MAP的超分辨率图像重建的快速算法[J]. 计算机研究与发展 , 2009, 46 (5) : 872–880. XIAO Chuangbai, YU Jing, XUE Yi. A Novel Fast Algorithm for MAP Super-resolution Image Reconstruction[J]. Journal of Computer Research and Development , 2009, 46 (5) : 872 –880. |
| [20] | 沈焕锋, 李平湘, 张良培. 一种自适应正则MAP超分辨率重建方法[J]. 武汉大学学报(信息科学版) , 2006, 31 (11) : 949–952. SHEN Huanfeng, LI Pingxiang, ZHANG Liangpei. Adaptive Regularized MAP Super-resolution Reconstruction Method[J]. Geomatics and Information Science of Wuhan University , 2006, 31 (11) : 949 –952. |
| [21] | FATTAL R, AGRAWALA M, RUSINKIEWICZ S. Multiscale Shape and Detail Enhancement from Multi-light Image Collections[J]. ACM Transactions on Graphics , 2007, 26 (3) : 51 –59. DOI:10.1145/1276377 |
| [22] | 李弼程, 魏俊, 彭天强. 遥感影像融合效果的客观分析与评价[J]. 计算机工程与科学 , 2004, 26 (1) : 42–46. LI Bicheng, WEI Jun, PENG Tianqiang. Objective Analysis and Evaluation of Remote Sensing Image Fusion Effect[J]. Computer Engineering & Science , 2004, 26 (1) : 42 –46. |
| [23] | AGAIAN S S, PANETTA K A, GRIGORYAN A. Transform-based Image Enhancement Algorithms with Performance Measure[J]. IEEE Transactions on Image Processing , 2001, 10 (3) : 367 –382. DOI:10.1109/83.908502 |
| [24] | AGAIAN S S, SILVER B, PANETTA K. Transform Coefficient Histogram-based Image Enhancement Algorithms Using Contrast Entropy[J]. IEEE Transactions on ImageProcessing , 2007, 16 (3) : 741 –758. DOI:10.1109/TIP.2006.888338 |



