2. 大地测量与地球动力学国家重点实验室, 湖北 武汉 430077 ;
3. 中国科学院大学, 北京 100049
2. State Key Laboratory of Geodesy and Earth's Dynamics, Wuhan 430077, China ;
3. University of Chinese Academy of Science, Beijing 100049, China
基于低轨卫星的导航增强系统是目前国内外研究的热点[1-4]。从美国Iridium系统辅助GPS系统的研究成果来看,利用LEO卫星对导航系统进行性能增强是一种有效的手段[3]。在此增强系统中,LEO卫星具有“源”“端”“中继”3种作用[4]。当LEO卫星作为测距源时,与WAAS系统中GEO卫星类似,需要发布自身的广播星历,而广播星历的生成则需要进行轨道预报。因此,LEO卫星轨道的预报是该导航增强系统需要解决的重要问题之一。
目前,轨道预报方法主要有3种。第1种是分析法[5-6],即在分析获得卫星t时刻平均根数的基础上给出的一种轨道预报方法。该方法在空间环境监测和实时跟踪测量等对预报轨道精度要求不高的领域有着很好的应用效果。第2种是基于多项式拟合的方法,在不考虑卫星的受力情况下,利用多项式拟合卫星的精密轨道得到卫星的速度场,据此进行轨道预报。常用的有最小二乘曲线拟合法、切比雪夫多项式拟合法、拉格朗日多项式拟合法[7-8]。低轨卫星由于轨道较低,受力情况相对于中高轨卫星更为复杂,对于不涉及动力学模型的预报方法而言,只能进行短期(几分钟甚至更短)预报,预报精度为厘米甚至分米级[9-10]。第3种是基于动力学轨道拟合的方法[11-12],用已知的卫星位置坐标采用动力学方法拟合出初始轨道和动力学参数,在此基础上通过积分进行轨道外推。该方法与前两种方法相比,在达到分米级预报精度的前提下,能够实现更长弧长的轨道预报,满足低轨卫星增强导航卫星系统性能的应用[11]。
本文以HY-2A卫星为例进行LEO卫星轨道预报研究,结合动力学拟合及Collocation方法[12-15],重点分析了拟合弧长及预报时长对轨道预报精度的影响。在此基础上,基于超快速星历产品实现HY-2A卫星高精度快速定轨的同时开展轨道预报研究,对进一步研究基于LEO卫星的导航增强系统具有很好的参考价值。
1 动力学拟合方法 1.1 动力学拟合基本原理设LEO卫星初始时刻t0的位置、速度以及动力学参数为(r0, ṙ0, p0),其中,r0、ṙ0分别为LEO卫星的位置及速度,p0则为在径向、沿迹以及法向上的一组经验参数(3个方向上各有一个常数项和两个周期项摄动参数[16-17])。考虑各种摄动力的影响,通过对卫星动力学方程积分可以得到卫星t时刻的位置、速度(r, ṙ),可表示如下
 (1)
(1)
假设在LEO卫星精密星历中,对应t时刻的位置为rt,则采用动力学拟合的观测方程可以表示如下[18]
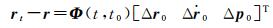 (2)
(2)
式中,Φ(t, t0)=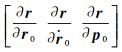
假定在一段弧长[t1, tm]内,LEO卫星精密星历中的ti时刻卫星位置及速度为ri,则可以构建m维观测方程
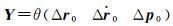 (3)
(3)
式中
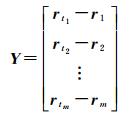 (4)
(4)
 (5)
(5)
对以上方程组进行最小二乘估计,可以得到LEO卫星初始时刻t0的位置、速度以及动力学参数(r0, ṙ0, p0),通过积分可以进行LEO卫星的轨道预报。
1.2 定轨和预报采用的摄动力模型LEO卫星由于轨道高度较低,其受力情况更为复杂。因此,在进行LEO卫星轨道确定及预报过程中需要考虑地球非球形引力、N体摄动、固体潮、海潮、大气阻力、太阳光压、地球辐射压及相对论效应等引起的摄动[19-21]。其中,在采用非差简化动力学法进行快速精密定轨时,大气阻力通过设置伪随机脉冲参数[22]进行补偿(轨道预报过程,没有设置伪随机脉冲参数)。本文在数据处理过程中所采用的动力学模型如表 1所示。
| 模型 | 描述 |
| 地球重力场模型 | EGM2008(120×120) |
| 行星星历 | DE405 |
| 光压模型 | ECOM模型 |
| 固体潮模型 | TIDE2000 |
| 海潮模型 | FES2004(50×50) |
| 章动模型 | IAU2000R06 |
| 半日极移模型 | IERS2010XY |
2 基于事后精密星历的轨道预报精度分析
为分析不同弧长轨道数据的拟合精度以及不同的拟合区间长度对不同弧长的预报影响,本文采用法国国家空间中心(CNES)提供的HY-2A卫星上SLR、DORIS和星载GPS数据联合定轨[23-24]生成的精密星历进行方法测试(径向误差在1 cm左右,沿迹和法向上的误差为2~3 cm,采样间隔60 s)。利用Bernese5.2软件对2014年没有轨道机动情况下的DOY 60-128共计65 d(DOY 73和DOY 106出现轨道机动,暂不处理)的精密星历进行动力学拟合及预报,并统计了轨道拟合及预报结果与参考轨道的位置偏差,预报方案如表 2所示。
| 年积日 | 弧长/h | 拟合区间长度 | 预报弧长长度 |
| N=60, 61, …, 128 | 2 | DOY N天的22-24时 | 预报4 h:从DOY N+1天的0-4时 预报8 h:从DOY N+1天的0-8时 预报12 h:从DOY N+1天的0-12时 预报24 h:从DOY N+1天的0-24时 |
| 4 | DOY N天的20-24时 | ||
| 6 | DOY N天的18-24时 | ||
| 8 | DOY N天的16-24时 | ||
| 12 | DOY N天的12-24时 | ||
| 24 | DOY N天的0-24时 |
2.1 卫星轨道拟合精度分析
根据以上提出的拟合方案,采用动力学拟合法对HY-2A卫星进行相应的轨道拟合与预报数据处理,其不同拟合弧长的拟合精度(3DRMS值)如图 1所示。结果显示:随着拟合弧长的增加,拟合残差逐渐增大。其中,24 h弧长拟合3DRMS值小于8 cm,2 h弧长拟合3DRMS在毫米级水平。

|
| 图 1 HY-2A卫星不同弧长轨道拟合的3DRMS值 Fig. 1 3DRMS of HY-2A satellite different arc length orbit fitting |
2.2 卫星轨道预报结果分析
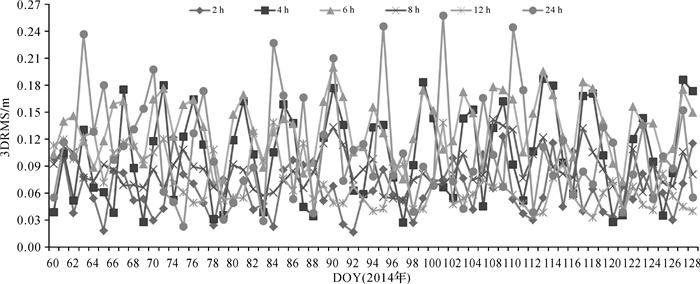
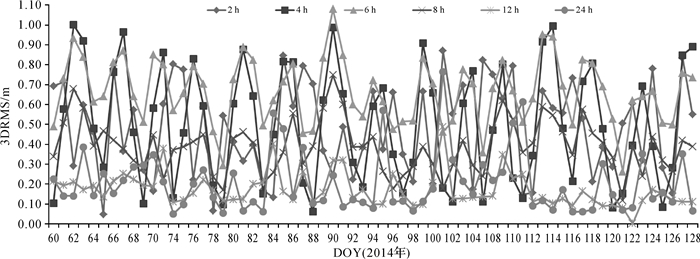
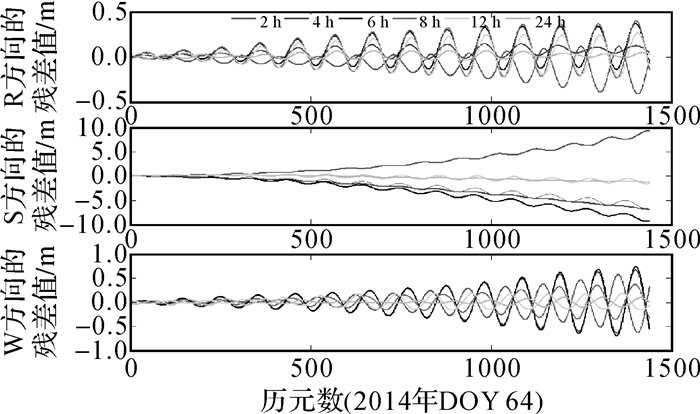
根据2.1节拟合得到相关的动力学参数进行数据处理,分别基于不同拟合区间预报2 h、4 h、8 h、12 h和24 h弧长的HY-2A卫星轨道。在预报过程中采用与轨道拟合时相同的动力学模型及参数,积分步长为3 min,式(4)中多项式阶数q=10。图 2-图 6统计了不同拟合区间分别预报2 h、4 h、8 h、12 h和24 h弧长的轨道预报精度(3DRMS),图 7为2014年DOY 64的不同拟合区间预报24 h弧长在R(径向)、S(沿迹方向)、W(法向)3个方向上的差值时序图。
|
| 图 2 HY-2A不同弧长预报2 h轨道3DRMS Fig. 2 3DRMS of 2 h prediction orbit with HY-2A satellite different arc length |

|
| 图 3 HY-2A不同弧长预报4 h轨道3DRMS Fig. 3 3DRMS of 4 h prediction orbit with HY-2A satellite different arc length |
|
| 图 4 HY-2A不同弧长预报8 h轨道3DRMS Fig. 4 3DRMS of 8 h prediction orbit with HY-2A satellite different arc length |

|
| 图 5 HY-2A不同弧长预报12 h轨道3DRMS Fig. 5 3DRMS of 12 h prediction orbit with HY-2A satellite different arc length |

|
| 图 6 HY-2A不同弧长预报24 h轨道3DRMS Fig. 6 3DRMS of 24 h prediction orbit with HY-2A satellite different arc length |
|
| 图 7 HY-2A不同弧长预报24 h的差值时序图 Fig. 7 Error of 24 h prediction orbit with HY-2A satellite different arc length |
(1) 图 2-图 6表明拟合区间对轨道的预报精度影响较大。当预报2 h弧长时,选择2 h的拟合区间长度较为适宜,其3DRMS可达厘米级;当预报4 h、8 h、12 h和24 h弧长时,采用12 h或者24 h的拟合区间长度进行外推,其预报结果相对比较稳定,精度较好,24 h弧长预报轨道的3DRMS达到分米级,满足高精度应用需求。
(2) 图 7表明当拟合区间长度一定时,随着预报弧长的增加,相比较于R方向及W方向,S方向的预报精度最差,下降最快[25-26]。
3 基于超快速精密定轨结果的轨道预报精度分析由于CNES发布的HY-2A卫星星历是一种事后精密轨道,存在较大时间延迟,在此基础上的轨道预报在实际应用中存在一定限制。因此,需要对HY-2A卫星实现快速精密定轨,以便获得较小延迟下的HY-2A精密轨道。本文采用中科院测量与地球物理研究所(WHIGG)iGMAS数据分析中心提供的GPS超快速产品(时延3~9个小时,星历采样率为15 min,钟差采样率为30 s)对HY-2A卫星进行快速精密定轨及预报。
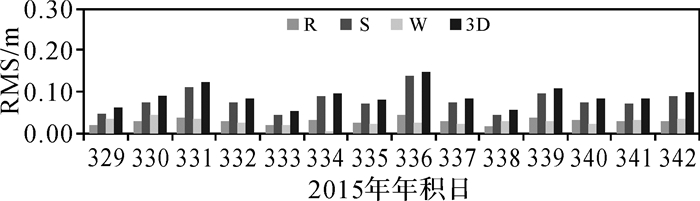
图 8统计的是基于2015年DOY 209-342的快速星历获得HY-2A卫星非差简化动力学轨道与CNES提供的参考轨道在R、S、W和三维位置比较的RMS。从中可以得到,快速精密轨道与参考轨道的差值在径向、沿迹和法向上的平均值分别为1.41 cm、3.30 cm、2.29 cm,3DRMS的平均值为4.27 cm,与文献[27]中结论相一致。
|
| 图 8 采用WHIGG数据分析中心超快速星历定轨结果 Fig. 8 RMS of HY-2A satellite orbit by using WHIGG analysis center GPS ephemeris |
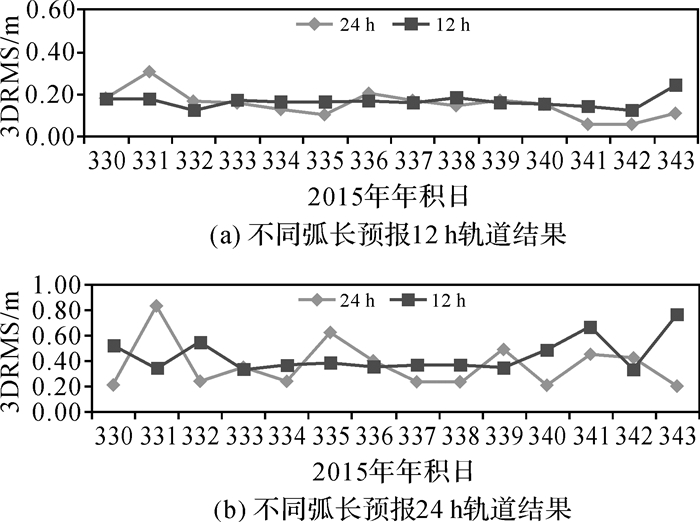
根据2.2节得到的初步结论,本节分别采用HY-2A卫星12 h和24 h弧长的快速定轨结果进行动力学拟合并预报轨道。图 9表示的是两种不同拟合弧长(12 h和24 h)分别进行轨道预报得到2015年DOY 330-343轨道结果与参考轨道的三维位置误差。从图中可以得到,24 h和12 h弧长分别预报12 h轨道时,其3DRMS优于6 dm;当预报24 h轨道时,3DRMS优于1 m。
|
| 图 9 利用iGMAS超快速产品计算的不同弧长精密轨道预报12 h和24 h轨道比较结果 Fig. 9 3DRMS of prediction orbit with 24 h or 12 h rapid precise orbit |
4 结论
本文基于动力学拟合法以HY-2A卫星为例开展了轨道预报研究,分析了不同拟合区间长度对不同弧长预报精度的影响。在此基础上,提出利用GPS超快速产品在实现快速精密定轨的同时,通过采用动力学拟合法可以获得较高精度的预报轨道。研究结果表明:
(1)对于要求预报轨道超过2 h弧长的应用而言,建议采用12 h或者24 h拟合区间进行轨道预报,其预报精度相对较为稳定。
(2)利用WHIGG数据分析中心的超快速产品在实现LEO卫星快速精密定轨后,采用动力学拟合方法进行轨道预报,可以获得与采用事后精密星历进行轨道预报接近的精度,预报12 h弧长轨道时,3DRMS优于6 dm;预报24 h弧长轨道时,3DRMS优于1 m,可以满足较高精度的应用需求。
(3) LEO卫星轨道预报精度很大程度上取决于S方向,且随着预报弧长增加,其预报精度下降很快。因此提高S方向的预报精度,有利于提高低轨卫星的预报精度。
致谢: 感谢中国科学院测量与地球物理研究所iGMAS分析中心提供的GPS超快速产品。
| [1] | 邓琳, 李广侠, 田世伟, 等. 基于LEO增强的COMPASS导航系统抗干扰能力研究[J]. 军事通信技术 , 2012, 33 (2) : 65–69. DENG Lin, LI Guangxia, TIAN Shiwei, et al. Capabilities of LEO Enhanced COMPASS Navigation System for Anti-jamming[J]. Journal of Military Communication Technology , 2012, 33 (2) : 65 –69. |
| [2] | RABINOWITZ M, PARKSINSON B W, SPILKER J J. Some Capabilities of a Joint GPS-LEO Navigation System[C]//Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation. Salt Lake City: ION-GPS, 2000: 255-256. |
| [3] | 赵金峰, 于笑, 冯少栋, 等. 基于LEO增强的COMPASS系统设计及性能分析[J]. 电讯技术 , 2013, 53 (2) : 131–135. ZHAO Jinfeng, YU Xiao, FENG Shaodong, et al. Design and Performance Analysis of LEO Satellites Enhanced COMPASS System[J]. Telecommunication Engineering , 2013, 53 (2) : 131 –135. |
| [4] | 田世伟.从"传统"到"协同:卫星导航增强理论与方法研究[D].南京:中国人民解放军理工大学, 2015. TIAN Shiwei. From "Conventional" to "Cooperative": Research on Theories and Methods on Satellite Navigation Augmentation[D]. Nanjing: PLA University of Science and Technology, 2015. |
| [5] | 刘林, 王彦荣. 卫星轨道预报的一种分析方法[J]. 天文学报 , 2005, 46 (3) : 307–313. LIU Lin, WANG Yanrong. An Analytical Method for Satellite Orbit Forecasting[J]. Acta Astronomica Sinica , 2005, 46 (3) : 307 –313. |
| [6] | 柳青松, 刘峰, 巨涛. 基于GPS的低轨卫星简化解析法轨道预报[J]. 全球定位系统 , 2010, 35 (2) : 1–4. LIU Qingsong, LIU Feng, JU Tao. A Simplified Analytical Method of LEO Satellite Orbit Forecasting Based on GPS[J]. GNSS World of China , 2010, 35 (2) : 1 –4. |
| [7] | 魏二虎, 柴华. GPS精密星历插值方法的比较研究[J]. 全球定位系统 , 2006, 31 (5) : 13–15. WEI Erhu, CHAI Hua. The Comparison Research on GPS Precise Ephemeris Interpolation Methods[J]. GNSS World of China , 2006, 31 (5) : 13 –15. |
| [8] | 张守建, 李建成, 邢乐林, 等. 两种IGS精密星历插值方法的比较分析[J]. 大地测量与地球动力学 , 2007, 27 (2) : 80–83. ZHANG Shoujian, LI Jiancheng, XING Lelin, et al. Comparative Analysis on Two Methods for IGS Precise Ephemeris Interpolation[J]. Journal of Geodesy and Geodynamics , 2007, 27 (2) : 80 –83. |
| [9] | 高鹏, 乔学军, 范城城. HY-2卫星精密轨道拟合与外推的两种方法比较[J]. 海洋测绘 , 2013, 33 (4) : 58–61. GAO Peng, QIAO Xuejun, FAN Chengcheng. Comparison of Two Methods of HY-2 Satellite Precision Orbit Fitting and Extrapolation[J]. Hydrographic Surveying and Charting , 2013, 33 (4) : 58 –61. |
| [10] | 张如伟, 刘根友. 低轨卫星轨道拟合及预报方法研究[J]. 大地测量与地球动力学 , 2008, 28 (4) : 115–120. ZHANG Ruwei, LIU Genyou. Discussion on Orbit Fitting and Orbit Forecasting of Low Earth Orbit Satellites[J]. Journal of Geodesy and Geodynamics , 2008, 28 (4) : 115 –120. |
| [11] | JOERGER M, GRATTON L, PERVAN B, et al. Analysis of Iridium-Augmented GPS for Floating Carrier Phase Positioning[J]. Navigation , 2010, 57 (2) : 137 –160. DOI:10.1002/navi.2010.57.issue-2 |
| [12] | BEUTLER G. Methods of Celestial Mechanics: Physical, Mathematical, and Numerical Principles[M]. Berlin Heidelberg: Springer, 2005 . |
| [13] | 李征航, 龚晓颖, 刘万科. 配置法在卫星轨道积分中的应用[J]. 武汉大学学报(信息科学版) , 2010, 35 (3) : 253–256. LI Zhenghang, GONG Xiaoying, LIU Wanke. Application of Collocation Method to Numerical Integration of Satellite Orbit[J]. Geomatics and Information Science of Wuhan University , 2010, 35 (3) : 253 –256. |
| [14] | BEUTLER G, BOCK H, DACH R, et al. Bernese GPS Software Version 5.0[M]. Bern: Astronomical Institute, University of Bern, 2004 . |
| [15] | 龚晓颖, 蔡诗响, 李征航. 小步长低阶Collocation方法轨道积分性能研究[J]. 宇航学报 , 2013, 34 (5) : 642–648. GONG Xiaoying, CAI Shixiang, LI Zhenghang. Performance Research of Small-Steplength and Low-Order Collocation Method in Orbit Determination[J]. Journal of Astronautics , 2013, 34 (5) : 642 –648. |
| [16] | 宋小勇, 毛悦, 贾小林. BERNESE光压模型参数的统计分析[J]. 测绘科学 , 2009, 34 (3) : 25–27. SONG Xiaoyong, MAO Yue, JIA Xiaolin. Analysis of the Parameter of BERNESE Radiation Force Model by Statistic Method[J]. Science of Surveying and Mapping , 2009, 34 (3) : 25 –27. |
| [17] | 陈俊平, 王解先. GPS定轨中的太阳辐射压模型[J]. 天文学报 , 2006, 47 (3) : 310–319. CHEN Junping, WANG Jiexian. Solar Radiation Pressure Models for the GPS Satellites[J]. Acta Astronomica Sinica , 2006, 47 (3) : 310 –319. |
| [18] | 何仕强, 吴斌, 陈俊平. 利用IGS星历预报GPS卫星轨道[J]. 中国科学院上海天文台年刊 , 2011 (32) : 25–34. HE Shiqiang, WU Bin, CHEN Junping. Orbit Predictions for GPS Satellites Using IGS Ephemeris[J]. Annals of Shanghai Observation Academia Sinica , 2011 (32) : 25 –34. |
| [19] | 李济生. 人造卫星精密轨道确定[M]. 北京: 解放军出版社, 1995 . LI Jisheng. Satellite Precise Orbit Determination[M]. Beijing: The PLA Press, 1995 . |
| [20] | 赵齐乐. GPS导航星座及低轨卫星的精密定轨理论和软件研究[D].武汉:武汉大学, 2004. ZHAO Qile. Research on Precise Orbit Determination Theory and Software of GPS Navigation Constellation and LEO Satellite[D]. Wuhan: Wuhan University, 2004. http://www.cqvip.com/qk/92848A/200504/15333621.html |
| [21] | 周建, 吕志伟. 地球重力场模型对低轨卫星轨道积分的影响[J]. 测绘工程 , 2012, 21 (2) : 14–16. ZHOU Jian, LÜ Zhiwei. The Effects of Earth's Gravity Field Models to LEO Orbit Integration[J]. Engineering of Surveying and Mapping , 2012, 21 (2) : 14 –16. |
| [22] | 韩保民, 朱秀英, 柳林涛, 等. 伪随机脉冲估计及其在简化动力学定轨中的应用[J]. 武汉大学学报(信息科学版) , 2007, 32 (5) : 466–469. HAN Baomin, ZHU Xiuying, LIU Lintao, et al. Estimation of Pseudo-Stochastic Pulses and Their Applications in Reduced-Dynamic Orbit Determination[J]. Geomatics and Information Science of Wuhan University , 2007, 32 (5) : 466 –469. |
| [23] | ZHAO Gang, ZHOU Xuhua, WU Bin. Precise orbit Determination of Haiyang-2 Using Satellite Laser Ranging[J]. Chinese Science Bulletin , 2013, 58 (6) : 589 –597. DOI:10.1007/s11434-012-5564-6 |
| [24] | 郭靖, 赵齐乐, 李敏, 等. 利用星载GPS观测数据确定海洋2A卫星cm级精密轨道[J]. 武汉大学学报(信息科学版) , 2013, 38 (1) : 52–55. GUO Jing, ZHAO Qile, LI Min, et al. Centimeter Level Orbit Determination for HY2A Using GPS Data[J]. Geomatics and Information Science of Wuhan University , 2013, 38 (1) : 52 –55. |
| [25] | 周建华, 杨龙, 徐波, 等. 一种导航卫星中长期轨道预报方法[J]. 测绘学报 , 2011, 40 (S1) : 39–45. ZHOU Jianhua, YANG Long, XU Bo, et al. A Long Duration Orbit Prediction Method for Navigation Satellite[J]. Acta Geodaetica et Catographica Sinica , 2011, 40 (S1) : 39 –45. |
| [26] | JÄGGI A, BOCK H, FLOBERGHAGEN R. GOCE Orbit Predictions for SLR Tracking[J]. GPS Solutions , 2011, 15 (2) : 129 –137. DOI:10.1007/s10291-010-0176-6 |
| [27] | 郭南男, 周旭华, 吴斌. 利用星载GPS数据进行海洋2A卫星快速精密定轨[J]. 宇航学报 , 2015, 36 (7) : 797–803. GUO Nannan, ZHOU Xuhua, WU Bin. Rapid Precise Orbit Determination for Haiyang-2A Using On-board GPS Data[J]. Journal of Astronautics , 2015, 36 (7) : 797 –803. |



