2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
作为大地测量学一个重要的物理量,地球重力场对研究地球形状及其内部构造具有重要的意义,特别是最近几十年,随着专题重力卫星CHAMP、GRACE和GOCE的相继投入使用和卫星测高、重力仪观测技术的不断改善,人们对于求解局部高精度、高分辨率的重力场模型的需求日益迫切。因此,如何充分利用观测数据进行有效地反演地球重力场,成为近年来研究的一个重要课题:如文献[1]研究了卫星测高误差对重力场反演的影响;文献[2]利用两种卫星数据从谱组合法的角度对其展开了讨论等。通常,对于重力场的表示是利用球谐函数将其展开至某些特定阶次,例如EGM08展开至2190阶,EIGEN-GL04S展开至150阶。这种传统的重力场表示方法有着应用上的便利性,但由于其全局紧支撑特性,任何一个球谐系数的变化都会引起整个重力场的改变;另外,它也不能顾及局部数据分布的不均匀性,不适用于局部重力场的精化。由于其本身的局部紧支撑特性,径向基函数能够捕捉到细节的重力场信号,可应用于局部重力场建模。
近些年来,众多学者对于径向基函数表示局部重力场作出了尝试,并在基函数构建以及基函数格网设计算法方面提出了各自的理论。基函数的构建大致可分为以下几类:点质量基函数法[3]、多级小波基函数法[4-5]、Blackman小波基函数法[6-8]、球谐样条核函数法[9]。点质量基函数法在一定程度上可以减少基函数个数,但是该方法实施难度较大,且计算复杂度较其他方法并无改善;小波基函数和球谐样条核函数法由于采用固定类型的基函数格网设计方案,为了捕捉细节信息,需要不断细化基函数格网,进而产生大量的基函数格网点数,这一方面对计算机性能提出了严峻的挑战,另一方面不可避免地对某些区域造成过度参数化,从而加剧了法方程矩阵的病态性,最终达不到较好的建模效果。
在基函数格网设计算法上,由于牵涉基函数位置、数量、带宽等诸多因素,目前还没有一个统一的标准来模型化局部重力场。文献[9]利用多种准则(最小距离、均匀性、灵活性等)分析了多种格网的优劣,结果表明,Reuter格网和三角顶点格网最适合应用于模型化局部重力场。文献[10]研究了不同的径向基函数在不同类型的格网下表示重力场的差异和精度, 所得结论是:Abel-Poisson核、Blackman核和三次多项式核在空域内具有较小的震荡,更适合于局部重力场建模。文献[11]指出径向基函数的数量与研究区域内数据的分辨率及其区域大小有关,并且观测值的数量并不直接影响基函数的数量。文献[8—9]将基函数格网与已知数据的球谐阶次联系起来,认为所选取的基函数格网点数要大于同等阶次的球谐函数系数个数。文献[5]利用多级小波族形成的框架联合模型化局部重力场,并且根据冗余度值(小波个数与产生的Hilbert空间的维度比值)来选定基函数的格网密度参数,这种方法可以提供一个相对稳定的重力场表达,但是所需要的小波基函数数量仍然很大。文献[6]提出了数据自适应精化格网算法,在显著减少基函数个数的同时,还可以灵活地选取与观测信号相适应的基函数位置和带宽。
本文在文献[6]自适应算法的基础上,运用最小均方根误差准则(RMS准则)来求解平均带宽,并采用方差分量估计法,对各个方差因子作出估计。基于此,联合南海地区两种不同的重力场数据,构建该区域高分辨率的径向基函数地球重力场模型。
1 球面径向基函数建模理论及其求解球面径向基函数(spherical radial basis functions,SRBF),简称径向基函数或基函数,是地球向径方向上的局部化对称函数,其函数值大小只与两点间的球面角距有关,它的特点是具有很好的空间局部化特性,即大部分能量集中于基函数点附近的局部区域。图 1绘出了一个空间域正则化Abel-Poisson径向基函数的基本形状。

|
| 图 1 空间域正则化球面径向基函数 Fig. 1 A regularized spherical radial basis function in the spatial domain |
球面上任意一个位置向量x可以表示为
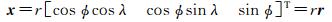 (1)
(1)
式中,ϕ为纬度;λ为经度;r为向径;r为x方向上的单位向量。
考虑两个位置向量x、xi,其中x位于半径为R(Bjerhammar球半径)的球面σR上或外部,xi位于球面上, 则极点位于xi处的外部径向基函数可表示为式(2)
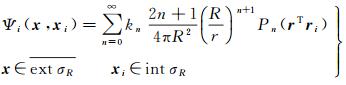 (2)
(2)
式中,Pn为n阶勒让德多项式Pn0;r、ri分别为x、xi方向上的单位向量;kn为基函数核,不同的基函数核会得到不同的径向基函数,笔者取核函数为Abel-Poisson核[10, 15],其具体表达形式为
 (3)
(3)
p为Abel-Poisson核的带宽参数,不同的带宽参数值对应不同的频谱,进而导致径向基函数(SRBF)在空域内不同的空间形状。图 2和图 3给出了Abel-Poisson核在不同带宽参数下的频谱覆盖情况及SRBF的空间形状变化。从图 2可以看出,带宽参数p越大,频谱覆盖范围越小;p越小,频谱覆盖范围越大。图 3中,带宽参数p越大,SRBF越宽阔,能量越分散;p越小,SRBF越狭窄,能量越集中。

|
| 图 2 Abel-Poisson核函数不同带宽参数下的频谱 Fig. 2 Normalized spectrum of Abel-Poisson kernel of different bandwidth |

|
| 图 3 Abel-Poisson正则化基函数不同带宽参数下的空间形状 Fig. 3 The space shape of the Abel-Poisson base function under different bandwidth |
半径为R的球面外调和函数T可以表示为N个径向基函数的和的形式
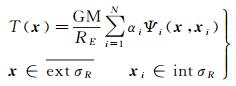 (4)
(4)
式中,αi为径向基函数系数;T(x)为扰动位;GM为地球引力系数;RE为地球平均半径。
地球上同一区域可能有多种类型的重力观测数据,比如重力异常Δg、大地水准面起伏N(或者高程异常),它们都可以表示为扰动位的线性函数[12, 16]
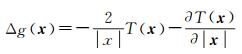 (5)
(5)
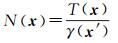 (6)
(6)
与扰动位类似,其他重力观测量同样也可以表示为有限个径向基函数叠加求和的形式,下面直接给出用径向基函数表示的重力异常Δg、大地水准面起伏N公式
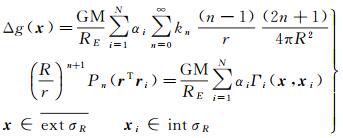 (7)
(7)
 (8)
(8)
式中,Γi(x, xi)、Θi(x, xi)为径向基函数,它们与Ψi(x, xi)的线性关系可由式(5)和式(6)导出,其他符号与前面公式相同。
式(4)、式(7)和式(8)都具有相同的未知基函数系数αi(i=1, 2, …,N),因此,可以利用不同类型的观测数据,共同求解未知系数。
不同类型的重力观测数据可组成如式(9)的线性方程
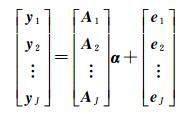 (9)
(9)
式中,Aj为第j组观测值设计矩阵;yj为第j组观测值;α为待求的径向基函数系数;ej为随机观测误差,并服从E{e}=0, D{e}=C。C=diag(C1, C2, …,CJ), 为观测误差的方差-协方差矩阵,并有Cj=σj2Pj-1。式(9)的法方程可写成式(10)
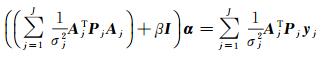 (10)
(10)
式中,σj2为各观测组的方差因子;Pj为第j组观测值权阵;β为正则化参数。之所以要加正则化参数是因为在求解基函数系数过程中,由于卫星数据向下延拓、观测数据分布不均匀、局部模型过度参数化等可能造成法方程矩阵病态的情况。另外,由于观测数据精度可能存在差异,在共同求解基函数系数时要估计各自的权重,方差分量估计法(variance component estimate,VCE)可以一并对各方差因子和正则化参数进行估计[17]。
2 数据自适应精化格网算法(data-adaptive network design,DAND)径向基函数建模,首先需要设置基函数格网,基函数格网有多种选择,如等经纬度格网、等三角形格网或Reuter格网等。本文主要采用Reuter格网[18]。Reuter格网在全球范围可以实现良好的均匀分布,并且格网点的生成比较灵活,Reuter格网的密度由分辨率水平L决定,图 4(a)、(b)绘出了L=20和L=30时的全球Reuter格网分布情况。

|
| 图 4 全球Reuter格网 Fig. 4 Global Reuter grids |
从图 4可以看出,Reuter格网分布呈从赤道到两级递减的趋势,不会因为靠近极点而逐渐变密;L越大,格网点间距越小,分布越密。但是,单一的基函数格网并不能取得良好的建模效果,当观测值分布较不均匀时,基函数格网与观测值之间便不能很好地匹配,往往会导致一些地区过参数化,而另一些地区欠参数化情况的出现;另外,基函数的分布也必须依据重力信号变化的强弱作出调整,单一的Reuter格网并不能满足这一要求。因此,有必要寻求与数据分布、信号变化相适应的基函数格网设计算法。
针对上述问题,文献[6]提出了依赖于观测数据的自适应精化格网算法,它可以明显地改善以往单一格网算法欠参数化的情况,能够与观测信号之间进行良好地匹配,并且可以联合多种数据共同建模,在保证计算精度的基础上,减少了过度拟合现象的发生。另外,为了提高计算速度,本文采用最小均方根误差准则(RMS)替代Klees的广义交叉验证法(GCV)来求解基函数平均带宽,具体步骤如下。
(1)定义球面粗格网,在格网点设置径向基函数,用阻尼最小二乘法求解基函数系数,用最小均方根误差准则(RMS)求解基函数平均带宽
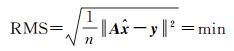 (11)
(11)
RMS准则的判断标准如下。
(a)根据数据频谱信息,估计带宽p的变化范围,并指定适当的步距变化;
(b)对每一个带宽p,建立观测方程,反算基函数系数â,然后按式(11)求解剩余值;
(c)每一个带宽对应一个剩余值,其中最小RMS剩余所对应的带宽即为初始格网最佳带宽。
在数据量较大的情况下,RMS准则相对GCV明显提高了收敛速度。表 1给出了由EGM2008模型计算的南海地区不同阶次的(300、400、500)重力异常数据利用这两种准则判断基函数格网最佳带宽的实例,结果显示:两者得到的最佳带宽基本一致,但是在运算时间上RMS却明显少于GCV。需要说明的是,这里的改进是指在判断精化基函数是否应该存在的准则上,因为减少了计算的循环次数,在计算速度上有很大提高,但在精度方面,由于两者筛选结果基本一致,所得精度也极为相近。
| D/O | N.obs | RMS | GCV | |||
| Opt. p | time/s | Opt.p | time/s | |||
| 300 | 609 | 0.040~0.060 | 69 | 0.040~0.055 | 1768 | |
| 400 | 1862 | 0.017~0.019 | 137 | 0.018~0.020 | 3956 | |
| 500 | 3657 | 0.015~0.018 | 994 | 0.016~0.018 | 13 485 | |
| 注:D/O代表数据阶次;N.obs为观测值个数;Opt.p为最佳带宽。 | ||||||
(2)求解(1)的最小二乘剩余,从最大到最小,依次判定是否其可被选为精化基函数,每选定一个基函数,在局部区域内更新一次“观测值剩余”,直至选不出满足条件的径向基函数为止。
(3)将(1)中的粗格网基函数和(2)中的精化基函数结合起来,作为对该局部重力场的完全参数化,最后利用所有的观测数据,用方差分量估计法(VCE)共同求解基函数系数。
精化基函数算法输入参数对建模结果的好坏起决定性作用,判断准则主要有以下几点。
(1)待定SRBF的剩余值应大于一定的阈值τ1;
(2)待定SRBF的周围(半径为ψc的球盖)应至少存在q个足够大的剩余观测值,足够大意味着q个点的平均值大于另一阈值τ2;
(3)新增加的基函数点与已有的基函数点之间应大于一定的距离(ψmin)。
τ1、τ2、ψc、q、ψmin通常在试验中尝试确定,一般的,τ1、τ2要足够小,依据q和数据分辨率可确定ψc,ψmin不大于初始粗格网间距。
3 实例计算选取南海地区约10°×8°的研究区域作为重力场建模试验对象,具体范围为北纬8°N—18°N,东经108°E—116°E。输入数据有两种,一种是丹麦空间研究所提供的2′×2′的自由空气重力异常数据(DTU13),总共72 000个数据;另一种是由EIGEN-GL04S重力场模型计算得到的大地水准面起伏数据。EIGEN-GL04S由GRACE卫星数据和LAGEOS数据联合解算得到,但是其在高阶精度稍差,因此在建模之前,有必要对其可靠阶次进行分析。图 5绘出了EIGEN-GL04S模型大地水准面阶方差频谱。在2~36阶范围内,大地水准面误差阶方差呈先下降后上升的趋势(蓝线),累计误差阶方差(黑线)缓慢上升,前36阶对应的累计误差方差为0.006 m;在36阶以后,误差阶方差和累计误差阶方差都迅速增大;在125阶左右,累计误差阶方差与信号阶方差(红线)相当,达到0.08 m;此后,累计阶方差开始大于信号阶方差。因此,为了更好地利用EIGEN-GL04S模型的中低阶信息,本文采用“移去-恢复法”,以EIGEN-GL04S模型的前36阶作为参考,而高阶截断至120阶(累计大地水准面误差为0.06 m)。基于此计算了研究区域内6′×6′的高程异常数据,数据总量为8181个。

|
| 图 5 EIGEN-GL04S大地水准面阶方差频谱 Fig. 5 EIGEN-GL04S geoid degree variance spectrum |
EIGEN-GL04S在中低阶波段信号精度较高,但分辨率较低;DTU13重力异常主要由卫星测高数据得到,分辨率较高,包含了丰富的高频信号。因此,联合这两种数据,弥补彼此之间的不足,便可能得到一个高质量、高分辨率的重力场模型。图 6绘制了移去低阶重力场贡献后的两种数据的分布情况。

|
| 图 6 南海部分地区的重力场剩余输入数据 Fig. 6 The input residual gravity data of parts of the South China Sea |
考虑到径向基函数建模普遍出现的“边缘效应”,将基函数格网建模区域四周各扩展1°,即基函数格网覆盖区域为7°N—19°N,107°E—117°E。初始粗格网采用Reuter格网[18],取格网密度参数L=1800,格网总数为11 768。接下来便是精化格网算法输入参数的确定,经过多次尝试,当取τ1=1、τ2=0.5时,此时得到的重力场反演结果与观测值最为相近;另外,为了防止孤立的大剩余观测值的出现(可能不是真实的重力场信号),待定基函数格网点附近应存在若干较大的剩余观测值,本例中取q=3;依据数据分辨率和q的大小,取精化格网点选择半径ψc=0.04°;为了防止SRBF过度集中,任意两个SRBF的球面距应大于一定阈值ψmin,设置为粗格网间距的一半,即ψmin=0.05°。依据上述筛选原则,得到精化基函数点数为2719。最终利用所有选定的基函数(粗+精),共同构建局部重力场。
高分辨率局部重力场基函数系数的精确求解需要足够多的观测量(超定问题),本文中观测值数据量为72 000+8181=80 181,远远多于基函数系数个数14 487,因此能满足求解系数的要求,但同时也可能引起过度拟合;另外,重力异常和高程异常观测点位之间距离可能非常接近,也可能导致所得线形系统存在很强的相关性。上述两种因素综合作用的结果就是所得的法方程矩阵病态化。表 2列出了正则化前后的条件数及其各方差因子。正则化之初,为各方差因子分别赋值为1,此时法方程出现严重的病态性,条件数达到5.85×1012,求解过程提示矩阵奇异,在经过5次迭代之后,方差因子趋于稳定,此时方程条件数为3.73×103,各方差因子分别为σ12=1.694 m2/s4,σ22=0.134 m2,σμ2=7.42×10-2,方差因子比值σ12/σ22=12.64:1,基函数系数可由此解得。
| 方法 | 条件数 | σ12(m2/s4) | σ22/m2 | σμ2 |
| 正则化前 | 5.85×1012 | 1 | 1 | 1 |
| 正则化后 | 3.73×103 | 1.694 | 0.134 | 7.42×10-2 |
本文主要采用Abel-Poisson径向基函数建模(Abel-Poisson basis function modeling,APBF)。图 7绘制出了建模后恢复的重力异常数据的误差分布情况,图 8为该地区对应的SRTM_PLUS30海底地形。

|
| 图 7 APBF模型重力异常数据恢复误差 Fig. 7 Gravity anomaly recovery error of APBF model |

|
| 图 8 南海部分地区海底地形(SRTM_PLUS30) Fig. 8 ubmarine topography of the South China Sea(SRTM_PLUS30) |
从图 7可以看到,绝大部分地区误差值较小,且分布均匀,较大的误差主要集中于区域东南角的南沙群岛、西部的长山山脉和北部的西沙群岛,这主要归因于这些区域复杂的海底地形。南沙群岛由于其岛礁众多、分布较广,且位于海盆的边缘地带,地形最为复杂,建模后拟合误差最大值也出现在这一区域,分别为6.80×10-5 m/s2、-7.54×10-5 m/s2(表 3);区域东部狭长的长山山脉,地质构造复杂,高峰多达1500~2000 m以上,地势崎岖,误差达到5.47×10-5 m/s2;西沙群岛和中沙群岛之间东北向的巨型海槽和群岛东南侧的中央深海海盆,使得该地区的重力异常变化比周围大多数地方都大,因此该地区也有较大的误差;另外,在中沙群岛与南沙群岛的中间地带,海底地形起伏虽小于前3个地区,但仍可以看到明显的剩余误差。除上述几个地区外,绝大部分区域建模误差均小于±1.5×10-5 m/s2,区域整体拟合误差RMS为±0.80×10-5 m/s2(表 3),验证了应用Abel-Poisson径向基函数和数据自适应算法局部构建重力场模型的有效性。
| 10-5m/s2 | |||||
| 模型 | Resol./km | max | min | mean | RMS |
| APBF-DTU13 | ~3.6(2′×2′) | 6.80 | -7.54 | 0.085 | 0.80 |
| APBF-EGM08 | ~9(5′×5′) | 7.70 | -9.56 | -0.076 | 0.75 |
| DTU13-EGM08 | ~9(5′×5′) | 7.48 | -9.98 | -0.011 | 0.74 |
EGM08模型是目前已经得到公认的高阶次重力场模型,可以作为检验新模型质量的参考。但EGM08模型只能展开至2190阶(约5′×5′), 而本文采用的DTU13数据以及APBF模型的分辨率为2′×2′。由于这些数据的空间分辨率不同,因此必须转化为相同的空间尺度,再进行相互比较。表 3列出了EGM08模型与APBF模型以及DTU13数据的偏差统计结果。表 3中,APBF模型与EGM08模型的偏差绝对值不超过9.56×10-5 m/s2,平均值为-0.076×10-5 m/s2,RMS为0.75×10-5 m/s2,两者之间有一定的偏差,但相差不大,进一步证明了APBF模型的有效性和可靠性。
由于兼顾了大地水准面和重力异常不同频谱的影响,建模解得的径向基函数系数

|
| 图 9 APBF模型计算的剩余大地水准面起伏 Fig. 9 Geoid undulation residuals recovered by APBF model |
| m | |||||
| 模型 | Resol./km | max | min | mean | RMS |
| APBF-EIGEN | ~165(1.5°×1.5°) | 0.453 | -0.471 | -0.002 | ±0.066 |
| APBF-EGM08 | ~9(2′×2′) | 0.269 | -0.535 | -0.019 | ±0.115 |
图 9(a)为径向基函数APBF模型恢复的120阶剩余大地水准面起伏,通过与EIGEN-GL04S输入大地水准面起伏数据(图 6(b))比较,两者符合程度较好,偏差最大为0.453 m,最小为-0.471 m,RMS为±0.066 m(表 4),均保持在较低的水平。
图 9(b)为APBF模型得到的高分辨率大地水准面起伏(约3.6 km的空间分辨率),为了评估APBF模型的高阶大地水准面起伏数据的质量,选取EGM08模型作为参考对象,两个模型同时计算至2190(分辨率约9 km),统计结果列于表 4。
由表 4可以看到,APBF模型与EGM08模型的偏差不大,从另一角度表明,APBF模型能够有效地表示高阶、高分辨率的大地水准面。
4 结论本文利用Abel-Poisson径向基函数和改进的数据自适应精化格网算法,联合两种不同类型、不同分辨率的重力场数据,对南海部分地区进行建模。径向基函数模型APBF对原始重力异常数据拟合的符合程度达到了±0.80×10-5 m/s2 (分辨率为2′×2′),绝大部分地区拟合误差值小于±1.5×10-5 m/s2,分布均匀;由于APBF模型兼顾了两种数据的不同频谱特性,不仅能较好地恢复该地区的低阶大地水准面数据,而且还可以得出高阶、高分辨率的大地水准面信息,从而达到了高精度、高分辨率的局部重力场建模的目的。在数据处理中,采用RMS准则相对GCV可以明显提高收敛速度,减少计算量。
与其他建模方法一样,径向基函数建模在一定程度上不可避免地受到复杂地形的影响。但是,应用数据自适应算法,绝大部分误差均可以控制在较小的范围内,从而保证局部重力场建模的有效性。
基函数模型可以融合不同来源、不同分布的重力数据,如GRACE、卫星测高等,从而得到高分辨率、高精度的局部重力场,可以用来精化局部大地水准面;利用径向基函数可以方便地开展重力场多尺度分解方面的研究,结合其他地球物理资料,有助于更好地了解地球的内部构造和动力学变化机制。
致谢: 感谢丹麦技术大学空间研究所提供的DTU自由空气重力异常数据。
| [1] | 彭富清, 陈双军, 金群峰. 卫星测高误差对海洋重力场反演的影响[J]. 测绘学报 , 2014, 43 (4) : 337–340. PENG Fuqing, CHEN Shuangjun, JIN Qunfeng. Influence of Altimetry Errors on Marine Geopotential Recovery[J]. Acta Geodaetica et Cartographica Sinica , 2014, 43 (4) : 337 –340. DOI:10.13485/j.cnki.11-2089.2014.0050 |
| [2] | 钟波, 罗志才, 李建成, 等. 联合高低卫-卫跟踪和卫星重力梯度数据恢复地球重力场的谱组合法[J]. 测绘学报 , 2012, 41 (5) : 735–742. ZHONG Bo, LUO Zhicai, LI Jiancheng, et al. Spectral Combination Method for Recovering the Earth's Gravity Field from High-low SST and SGG Data[J]. Acta Geodaetica et Cartographica Sinica , 2012, 41 (5) : 735 –742. |
| [3] | HEIKKINEN M. Solving the Shape of the Earth by Using Digital Density Models[R]. Helsinki: Finnish Geodetic Institute, 1981. |
| [4] | HOLSCHNEIDER M, CHAMBODUT A, MANDEA M. From Global to Regional Analysis of the Magnetic Field on the Sphere Using Wavelet Frames[J]. Physics of the Earth and Planetary Interiors , 2003, 135 (2-3) : 107 –124. DOI:10.1016/S0031-9201(02)00210-8 |
| [5] | CHAMBODUT A, PANET I, MANDEA M, et al. Wavelet Frames: An Alternative to Spherical Harmonic Representation of Potential Fields[J]. Geophysical Journal International , 2005, 163 (3) : 875 –899. DOI:10.1111/gji.2005.163.issue-3 |
| [6] | SCHMIDT M, FABERT O, HAN S C, et al. Gravity Field Determination Using Multiresolution Techniques[C]//Proceedings of the 2nd International GOCE User Workshop. Frascati: GOCE, 2004. |
| [7] | SCHMIDT M, FABERT O, SHUM C K. On the Estimation of a Multi-resolution Representation of the Gravity Field Based on Spherical Harmonics and Wavelets[J]. Journal of Geodynamics , 2005, 39 (5) : 512 –526. DOI:10.1016/j.jog.2005.04.007 |
| [8] | SCHMIDT M, FENGLER M, MAYER-GÜRR T, et al. Regional Gravity Modeling in Terms of Spherical Base Functions[J]. Journal of Geodesy , 2007, 81 (1) : 17 –38. |
| [9] | EICKER A. Gravity Field Refinement by Radial Basis Functions from In-situ Satellite Data[D]. Bonn: Universität Bonn, 2008. |
| [10] | BENTEL K, SCHMIDT M, GERLACH C. Different Radial Basis Functions and Their Applicability for Regional Gravity Field Representation on the Sphere[J]. GEM-International Journal on Geomathematics , 2013, 4 (1) : 67 –96. DOI:10.1007/s13137-012-0046-1 |
| [11] | WITTWER T B. Regional Gravity Field Modelling with Radial Basis Functions[D]. Delft: Delft University of Technology, 2009. |
| [12] | KLEES R, TENZER R, PRUTKIN I, et al. A Data-driven Approach to Local Gravity Field Modelling Using Spherical Radial Basis Functions[J]. Journal of Geodesy , 2008, 82 (8) : 457 –471. DOI:10.1007/s00190-007-0196-3 |
| [13] | PANET I, KUROISHI Y, HOLSCHNEIDER M. Wavelet Modelling of the Gravity Field by Domain Decomposition Methods: An Example Over Japan[J]. Geophysical Journal International , 2011, 184 (1) : 203 –219. DOI:10.1111/gji.2010.184.issue-1 |
| [14] | FENGLER M J, FREEDEN W, KOHLHAAS A, et al. Wavelet Modeling of Regional and Temporal Variations of the Earth's Gravitational Potential Observed by GRACE[J]. Journal of Geodesy , 2007, 81 (1) : 5 –15. |
| [15] | GRAFAREND E W, KRUMM F. The Abel-Poisson Kernel and the Abel-Poisson Integral in a Moving Tangent Space[J]. Journal of Geodesy , 1998, 72 (7-8) : 404 –410. DOI:10.1007/s001900050179 |
| [16] | TENZER R, KLEES R. The Choice of the Spherical Radial Basis Functions in Local Gravity Field Modeling[J]. Studia Geophysica et Geodaetica , 2008, 52 (3) : 287 –304. DOI:10.1007/s11200-008-0022-2 |
| [17] | KOCH K R, KUSCHE J. Regularization of Geopotential Determination from Satellite Data by Variance Components[J]. Journal of Geodesy , 2002, 76 (5) : 259 –268. DOI:10.1007/s00190-002-0245-x |
| [18] | REUTER R. Über Integralformeln der Einheitssphäre und Harmonische Splinefunktionen[M]. Rheinisch: Hochschule Aachen, 1982 . |
| [19] | SCHMIDT M, HAN S C, KUSCHE J, et al. Regional High-resolution Spatiotemporal Gravity Modeling from GRACE Data Using Spherical Wavelets[J]. Geophysical Research Letters , 2006, 33 (8) . DOI:10.1029/2005GL025509 |
| [20] | KOCH K R. Parameter Estimation and Hypothesis Testing in Linear Models[M]. Berlin Heidelberg: Springer, 2013 . |
| [21] | PANET I, KUROISHI Y, HOLSCHNEIDER M. Flexible Dataset Combination and Modelling by Domain Decomposition Approaches[M]//SNEEUW N, NOVÁK P, CRESPI M, et al. VII Hotine-Marussi Symposium on Mathematical Geodesy. Berlin: Springer, 2012: 67-73. |
| [22] | 汪海洪.小波多尺度分析在地球重力场中的应用研究[D].武汉:武汉大学, 2005. WANG Haihong. Research on Applications of Wavelet Multiscale Analysis in the Earth's Gravity Field[D]. Wuhan: Wuhan University, 2005. http://cdmd.cnki.com.cn/article/cdmd-10486-2006031340.htm |
| [23] | 王虎彪, 王勇, 陆洋, 等. 用卫星测高和船测重力资料联合反演海洋重力异常[J]. 大地测量与地球动力学 , 2005, 25 (1) : 81–85. WANG Hubiao, WANG Yong, LU Yang, et al. Inversion of Marine Gravity Anomalies by Combining Multi-altimeter Data and Shipborne Gravimetric Data[J]. Journal of Geodesy and Geodynamics , 2005, 25 (1) : 81 –85. |


