2. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079 ;
3. 地球空间信息技术协同创新中心, 湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China ;
3. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
与常规RTK技术相比,网络RTK技术扩大了覆盖范围,提高了定位精度,降低了作业成本,减少了用户定位的初始化时间,已经逐渐成为应用最广泛的GNSS精密定位技术。但是,原有的GPS单系统网络RTK技术,高度受制于观测条件,如由于建筑物或者地形的遮挡,可视卫星的数量有限,使得用户在城市、山区等遮挡严重的地区无法获得高精度的定位结果,使其在某些时空条件下的使用受到限制。现今,随着GLONASS系统于2011年12月31日再次实现24颗卫星满星座部署,以及我国独立自主研发的BDS系统于2012年12月27日正式具备向我国及周边地区提供定位服务能力,过去单一的GPS网络RTK正逐步转变为多系统网络RTK。与原有的GPS单系统网络RTK、GPS/BDS/GLONASS 3系统网络相比,RTK将极大地增加可视卫星数,可视卫星数的增加不仅能有效地增强观测卫星的图形强度、提高定位结果精度,更能提高网络RTK系统定位结果的可靠性。因此多系统集成已经成为当前网络RTK技术发展的重要趋势。
目前,已有许多国内外学者对多系统集成网络RTK进行了研究,并取得了丰硕成果[1-14]:文献[2]提出了网络RTK单历元整周模糊度搜索法和综合误差内插法,并通过试验得到了厘米级的定位精度;文献[3]在此基础上进一步提出了BDS网络RTK单历元整周模糊度搜索法,并通过试验进行验证;文献[6]详细介绍了网络RTK的处理策略,并利用悉尼CORS网数据,初步验证了GPS/GLONASS定位精度。文献[7]利用北斗三频数据,使用宽巷组合进行网络RTK定位也取得了厘米级的定位精度; 文献[8]对BDS网络RTK的算法进行了研究,并对比了电离层平静期和电离层活跃期BDS的网络RTK定位精度。然而,这些研究中对于GPS+BDS、BDS+GLONASS、GPS+BDS+GLONASS组合研究较少,特别是GPS/BDS/GLONASS在亚太地区都已具备提供定位服务能力的情况下,网络RTK的相关研究依旧以GPS为主,鲜有不包含GPS系统的研究成果。这并不利于我国的国防建设和BDS系统独立自主的发展。基于此,本文不仅对GPS、GPS+GLONASS网络RTK的定位精度及可靠性进行再次验证,还将对GPS+BDS、GPS+BDS+GLONASS以及不包含GPS系统的BDS、BDS+GLONASS网络RTK进行研究。此外,针对实际作业中,城市建筑物遮挡严重影响测绘作业的情况,专门研究了多系统网络RTK在缺少低高度角卫星状态下的定位精度和性能,为实际测绘作业和相关研究提供参考。
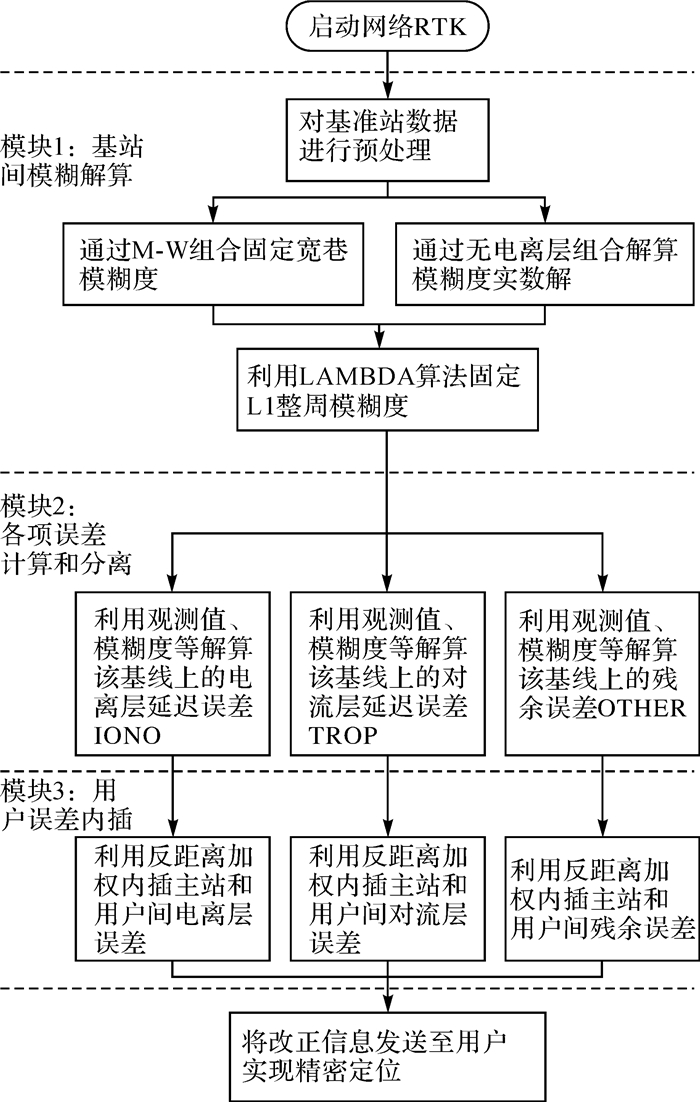
1 GPS/BDS/GLONASS网络RTK定位算法网络RTK的数据处理流程主要分为3个模块:①对GNSS基准站网中的基线进行解算,固定双差整周模糊度;②利用每条基线的GNSS观测值、双差整周模糊度、精确的基准站位置坐标等计算每条基线的电离层延迟、对流层延迟及综合误差;③根据用户发送的概略坐标,插值确定网络RTK用户的差分改正信息,从而为网络RTK用户提供实时厘米级的定位服务。数据处理流程见图 1。
|
| 图 1 网络RTK数据处理流程 Fig. 1 Flow chart of network RTK data processing |
1.1 GPS/BDS/GLONASS网络RTK基站间整周模糊度解算
基站间整周模糊度解算是实现GPS/BDS/GLONASS网络RTK的关键,可分为以下3个步骤[6, 10-12]:
(1)通过载波相位观测值和P码伪距组成Melbourne-Wübbena组合(M-W组合),计算得到宽巷整周模糊度[14]。
(2)将载波相位和伪距观测值进行无电离层组合,解算得到无电离层模糊度的实数解,观测方程如下
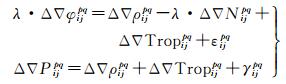 (1)
(1)
式中,ρ为测站到卫星的距离;Trop为对流层延迟误差;ε为载波相位观测值噪声;γ为伪距观测值噪声。
由于GLONASS采用频分多址的信号结构,导致GLONASS双差模糊度在以距离为单位的双差观测方程中,其双差模糊度不为整数,需将其变换为一个双差整周模糊度和一个单差整周模糊度[4, 6],可得观测方程如下
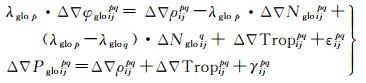 (2)
(2)
式中,λglo、φglo、Pglo、Nglo分别为GLONASS观测值的波长、相位观测值、伪距观测值和整周模糊度;p为观测卫星;q为参考卫星。
(3)利用步骤(1)解算的宽巷整周模糊度、步骤(2)解算的无电离层模糊度实数解和相应的方差协方差阵得到窄巷模糊度的实数解和对应的方差协方差阵[10],并使用LAMBDA算法[15]固定窄巷整周相位模糊度,进而计算得到L1、L2整周相位模糊度。
1.2 GPS/BDS/GLONASS网络RTK误差处理在计算网络RTK误差时,将误差分成电离层延迟、对流层延迟和包含二阶电离层延迟、轨道误差、多路径误差等的综合误差并分别进行计算。在固定各基线的整周模糊度后,即可以根据每条基线的GNSS观测值、双差整周模糊度、精确的基准站位置坐标等计算得到以上3种误差,具体公式如下
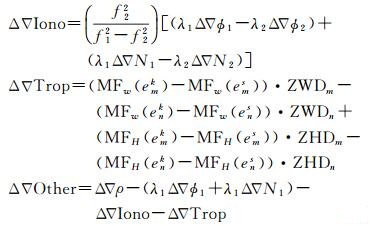 (3)
(3)
式中,MF为对流层映射函数;ZWD为对流层湿延迟,由式(1)估计得到;ZHD为对流层静力学延迟,由GPT2w模型[16]内插得到;Other为综合误差。
在各项误差计算完成后,根据流动站提供的改正坐标即可实时内插流动站的各项误差改正数。由于电离层延迟误差、对流层延迟误差和综合误差具有较强的时空相关性,而流动站和基准站在垂直方向上的距离相较于水平距离要小得多,故本文采用反距离加权法按基线东、北方向矢量分别内插流动站的以上3种误差,进而为用户提供厘米级的定位服务。
2 GPS/BDS/GLONASS网络RTK试验及结果分析按照上述的算法流程,本课题组自主研发了GPS/BDS/GLONASS网络RTK数据综合处理系统DREAMNET(data reserving, editing and managing system of network RTK)和流动站GNSS精密定位软件,详细的数据处理策略如表 1所示。
| 类型 | 参数 | 模型 |
| 观测值 | 观测量 | GPS+BDS+GLONASS相位观测值和伪距观测值 |
| 采样率/s | 1 | |
| 信号 | GPS:L1/L2;BDS:B1/B2;GLONASS:L1/L2 | |
| 截止高度角/(°) | 10 | |
| 观测值定权 | 高度角定权 | |
| 误差改正 | 卫星轨道误差 | GPS:IGV;BDS:BRDC;GLONASS:IGV |
| 电离层延迟误差 | 无电离层组合 | |
| 对流层静力学延迟 | GPT2w模型[16] | |
| 对流层延迟映射函数 | GMF模型[17] | |
| 卫星相位中心偏差 | IGS_08模型 | |
| 接收机相位中心偏差 | GPS:IGS_08模型;BDS:暂无;GLONASS:IGS_08模型 | |
| 参数估计 | 双差整周模糊度 | 估计 |
| 对流层湿延迟 | 估计(随机游走) |
表 1中,IGV为IGS提供的GPS/GLONASS精密预报星历,BRDC为BDS的广播星历。采用实测数据对所研发的软件平台进行了验证。
2.1 试验数据及方案试验使用我国贵阳市连续运行参考站(GYCORS)提供的2015年年积日(DOY)303—317共计15 d(1 s采样率)的GNSS观测数据,基准站点分布图见图 2。由于本文是模拟实时解算,避免了数据延迟、丢失等情况的出现,故与实测精度有些许差别。

|
| 图 2 基准站分布 Fig. 2 The distribution of stations |
为研究卫星导航系统之间不同组合情况下的定位精度,本文共设计以下6种组合模式:
(1)单系统:单GPS、单BDS,简写为G、C;由于GLONASS卫星质量较差且存在频间偏差等误差,导致GLONASS单系统网络RTK定位精度较差且可用性较低[18-20],故本文不对GLONASS单系统网络RTK进行讨论。
(2)双系统组合:GPS+GLONASS、GPS+BDS、BDS+GLONASS,简写为GR、GC、CR。
(3) 3系统组合:GPS+BDS+GLONASS,简写为GCR。
为了研究GPS/BDS/GLONASS网络RTK的定位精度,本文共设计4个试验方案。
2.2 网络RTK误差内插精度分析由于网络RTK主要是对电离层延迟、对流层延迟以及综合误差等进行建模改正,故这些误差内插精度如何就显得十分重要,因此在进行定位精度分析之前,首先要对DREAMNET误差内插精度进行分析。
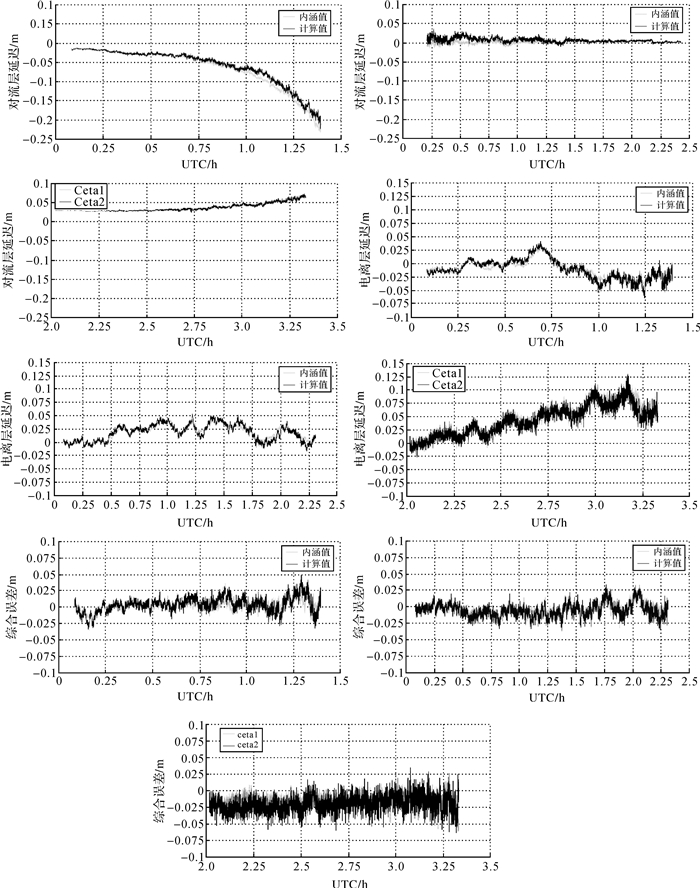
试验1:选用2015年DOY 312 1 s采样率的贵阳市CORS网GNSS观测数据,利用DREAMNET生成的整网误差模型内插QINZ-BAIY基线上的电离层延迟、对流层延迟以及综合误差,并利用QINZ-BAIY基线实际计算的电离层延迟、对流层延迟以及综合误差作为真值进行比较,对DREAMNET误差内插精度进行分析。由图 3可以明显地看出DREAMNET的内插值与实际计算值符合得较好,其中G01的对流层延迟、电离层延迟以及综合误差内插值与计算值的RMS值分别为9.9 mm、7.1 mm、8.5 mm,C06和R22的RMS值分别为7.9 mm、5.4 mm、7.3 mm和2.2 mm、10.7 mm、1.4 mm。试验证明了DREAMNET误差内插的正确性和精度。
|
| 图 3 G01、C06、R22的对流层延迟、对流层延迟和综合误差内插值与计算值对比 Fig. 3 Comparison of interpolation and calculated values in tropospheric delay, tropospheric delay and comprehensive error of G01 C06 and R22 |
2.3 不同组合模式网络RTK定位精度比较
试验2:使用2015年DOY 307 1 s采样率的贵阳市CORS网GNSS观测数据。在数据处理过程中,使用QINZ、XIUW、YONG、QINY、KAIY为基准站,BAIY为流动站。
利用DREAMNET动态确定BAIY站在GPS、BDS、GC、GR、CR、GCR 6种组合模式下的坐标,图 4为BAIY点在6种模式下E、N、U方向坐标差值序列图,表 2为BAIY点在6种模式下的定位精度统计。
| cm | |||||||
| 精度指标 | 方向 | GPS | BDS | GR | CR | GC | GCR |
| 最大偏差 | E | 2.29 | 2.73 | 3.39 | 2.59 | 1.51 | 1.78 |
| N | 3.15 | 2.38 | 4.47 | 3.87 | 1.89 | 2.15 | |
| U | 8.21 | 7.55 | 8.33 | 8.49 | 5.01 | 5.24 | |
| 均值 | E | -0.11 | 0.28 | 0.04 | 0.17 | -0.16 | -0.11 |
| N | 0.13 | 0.01 | 0.03 | 0.16 | 0.21 | 0.14 | |
| U | 0.19 | -0.20 | 0.08 | -0.26 | 0.09 | 0.04 | |
| RMS | E | 0.43 | 0.57 | 0.57 | 0.67 | 0.36 | 0.42 |
| N | 0.53 | 0.60 | 0.84 | 0.91 | 0.41 | 0.52 | |
| U | 1.34 | 1.36 | 1.84 | 1.97 | 0.92 | 1.10 | |

|
| 图 4 BAIY点在6种模式下E、N、U方向坐标差值序列 Fig. 4 Time series of residual error in E, N, U direction of station BAIY in six situations |
图 4显示了DOY 307从UTC 0:00—24:00流动站BAIY在6种不同模式下的东方向(E)、北方向(N)、天顶方向(U)的坐标序列图,可以看出在6种模式下,DREAMNET均可提供稳定的定位服务,其中GC和GCR的坐标误差的离散程度更小,定位精度更高;而BDS和CR组合网络RTK虽然相对其他组合离散程度稍大,但依然能保证绝大部分的定位结果的E、N、U方向偏差是小于0.05 m。
表 2给出了这6种模式的具体定位精度比较,首先从最大、最小值中可以看出,在86 400个历元中定位结果与真值之差都小于0.1 m,故证明了DREAMNET定位稳定性;其次从RMS值可以得到6种组合模式下定位精度皆可以达到水平0.01 m、高程0.025 m,故满足实际作业要求;再次,从最大偏差值和RMS皆可以看出GC和GCR模式定位精度要高于其余4种模式,而GR和CR精度最差,这是因为GLONASS卫星在中低纬度地区卫星数较少且存在频间偏差等误差,使得GR和CR精度相对较差。最后,在不依赖GPS系统的情况下,BDS和CR组合网络RTK的定位精度也达到了水平0.01 m、高程0.025 m,足以满足测绘的日常作业。
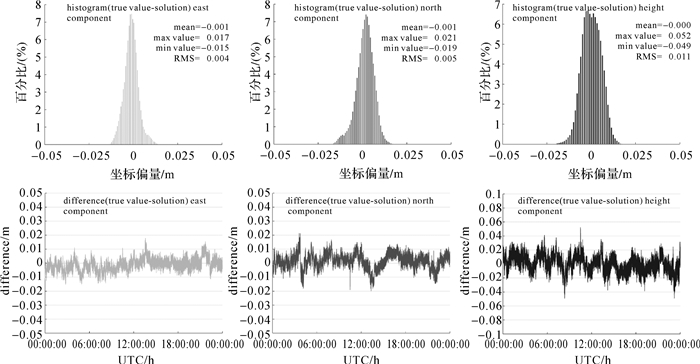
图 4给出了GCR模式下DAIY站分别在E、N、U三维方向的定位精度图。
|
| 图 5 GCR模式下DAIY站三维定位精度 Fig. 5 Positioning accuracy of DAIY provided by GPS/BDS/GLONASS network RTK between UTC 0:00—24:00 |
2.4 高度角变化对网络RTK定位性能的影响
在城市的建设管理过程中,网络RTK技术发挥着重要的作用。然而,由于城市各种楼房建筑的遮挡,可视卫星十分有限,往往使得原有的GPS单系统网络RTK无法进行正常的测绘作业。而GPS/BDS/GLONASS网络RTK由于极大地增加了可视卫星数量,从而有效地克服了这一难题。
试验3:使用2015年DOY 303贵州CORS网数据,利用不同截止高度角模拟不同程度的城市建筑物遮挡,研究GPS网络RTK与GPS/BDS/GLONASS网络RTK在信号受遮挡情况下的定位性能。
由图 4可以看出,GPS网络RTK与GPS/BDS/GLONASS网络RTK在截止高度角为10°时,即无遮挡环境下,两种网络RTK都可以全天候提供正常的定位服务,即可视卫星数大于等于5颗。当截止高度角分别提高到20°、30°、40°时,即信号遮挡逐渐加重时,GPS网络RTK在一天中分别只有96.53%、75.61%和26.1%的时间可以提供定位服务,而GPS/BDS/GLONASS网络RTK由于可视卫星数量较多,在一天中可以提供定位服务的时间分别为99.97%、99.96%和99.84%。且由图 6可知,当高度角为40°时,GPS/BDS/GLONASS网络RTK依然可以提供水平精度0.01 m、高程精度0.025 m的定位服务,保障正常的测绘作业。

|
| 图 6 40°高度角下DAIY站GPS/BDS/GLONASS网络RTK定位精度 Fig. 6 Positioning accuracy of DAIY provided by GPS/BDS/GLONASS network RTK with 40° cut-off elevations |
2.5 DREAMNET 15 d定位结果统计分析
试验4:使用DREAMNET处理2015年DOY 303—317共计15 d的贵州省CORS数据,进一步验证GPS/BDS/GLONASS网络RTK、无GPS系统网络RTK(BDS网络RTK和BDS/GLONASS网络RTK)以及其他组合模式网络RTK的定位精度和DREAMNET的工作性能。
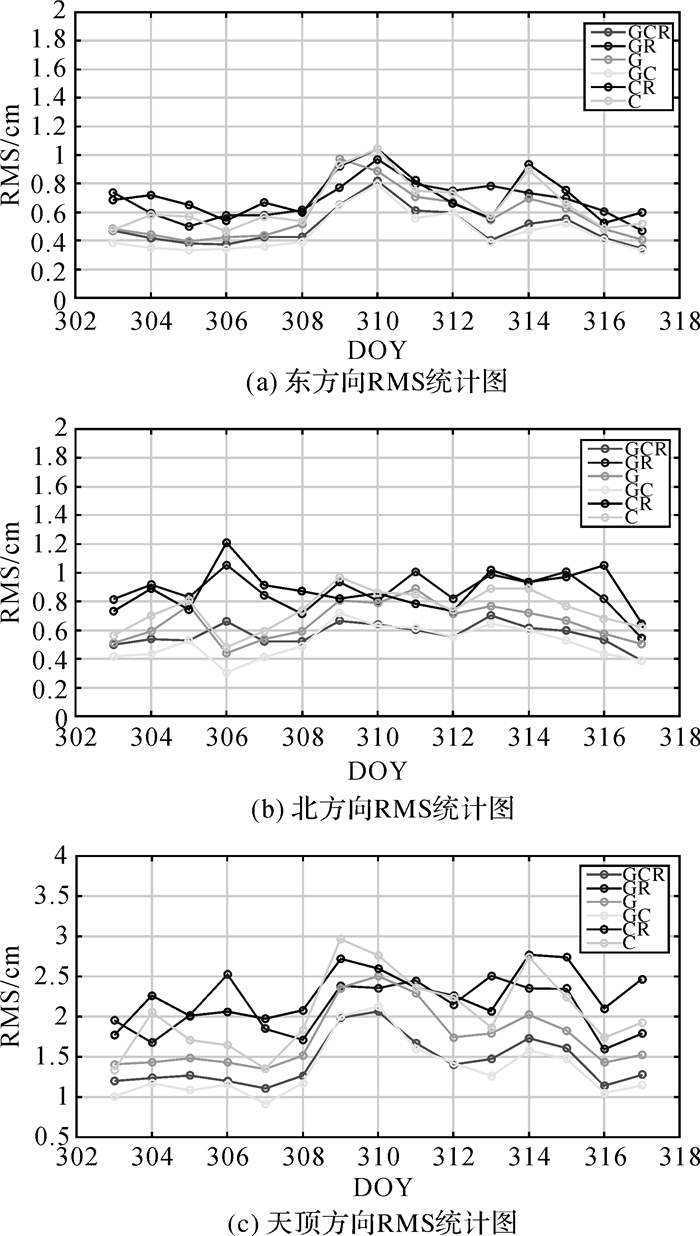
本试验使用DREAMNET计算DOY 303—317共15 d的单天动态解,并统计其单天解RMS值和DOY 303—317的整体RMS值。其中图 7为6种组合模式单天解的E、N、U方向RMS;表 3为6种组合模式在DOY 303—317的整体精度。
|
| 图 7 DOY 303—317 6种组合模式定位精度 Fig. 7 RMS of DAIY in six situations between DOY 303—317 |
| cm | ||||||
| RMS | GPS | BDS | GR | CR | GC | GCR |
| E | 0.60 | 0.67 | 0.69 | 0.72 | 0.47 | 0.50 |
| N | 0.67 | 0.75 | 0.87 | 0.88 | 0.52 | 0.57 |
| U | 1.77 | 2.10 | 2.13 | 2.30 | 1.38 | 1.47 |
由图 7可知,在DOY 303—317期间,6种组合模式的定位精度水平方向皆小于0.015 m,高程方向皆小于0.03 m,且波动不大,进一步证明了DREAMNET的定位结果具有很好的稳定性和较高的精度。对表 3具体分析可得,BDS网络RTK定位精度与GPS网络RTK相比较,在水平方向大致相当,在高程方向上略差,这主要可能是受大气建模误差和低高度角卫星较少的影响[6];GC与GCR组合网络RTK定位精度最高,水平方向上小于0.006 m,高程方向上小于0.015 m;在包括BDS和CR的6种组合模式下DREAMNET皆可达到水平0.01 m、高程0.025 m的定位精度,不仅证明了DREAMNET的定位精度,也证明了BDS系统可以在无GPS情况下满足网络RTK定位需要。其中,GPS/BDS/GLONASS 3系统网络RTK较原有GPS单系统网络RTK在E、N、U方向定位精度分别提高14.16%、15.73%和17.31%,证明了GPS/BDS/GLONASS 3系统网络RTK较GPS单系统网络RTK在精度上有较大提高。
3 结论本文基于贵阳市CORS网15 d数据,使用笔者所在课题组自主开发的网络RTK数据处理系统DREAMNET和流动站GNSS精密定位软件,研究分析了不同组合模式下网络RTK定位精度,以及在不同高度角下不同组合模式的定位性能。得到以下几条结论:
(1)由GPS、BDS、GLONASS 3系统构成的6种组合模式中,GPS网络RTK与BDS网络RTK在水平方向定位精度相当,BDS网络RTK在高程方向略差于GPS网络RTK;GPS/BDS网络RTK与GPS/BDS/GLONASS网络RTK定位精度最高,其中GPS/BDS/GLONASS 3系统网络RTK较GPS单系统网络RTK在E、N、U方向定位精度分别提高14.16%、15.73%和17.31%。
(2)随着高度角的增大,GPS网络RTK的定位性能显著下降,当高度角为40°时,一天中可用时间仅有26.1%,已无法为用户提供正常的定位服务。而GPS/BDS/GLONASS网络RTK由于可视卫星数量较多,即使高度角为40°时,依然可以在99.84%的时间里提供水平方向精度0.01 m、高程方向0.025 m的定位服务。
(3)使用DREAMNET连续解算15 d数据,在6种组合模式下,其结果均非常稳定,皆可以得到水平0.01 m、高程0.025 m的定位精度,证明了DREAMNET的定位精度;其中GPS/BDS/GLONASS网络RTK可以得到水平0.006 m、高程0.015 m的定位精度,足以满足测绘作业的高精度需要。
(4)在不依赖GPS系统情况下,BDS以及CR组合网络RTK均可以达到水平0.01 m、高程0.025 m的定位精度,这证明了在不依赖GPS的情况下,我国的BDS系统足以满足网络RTK定位的需要。
致谢: 感谢贵阳市测绘院地理信息中心为本课题的研究提供的贵阳市连续运行参考站GNSS观测数据;感谢武汉大学卫星导航定位技术研究中心宋伟伟博士提供的宝贵意见。
| [1] | 王世进, 秘金钟, 李得海, 等. GPS/BDS的RTK定位算法研究[J]. 武汉大学学报(信息科学版) , 2014, 39 (5) : 621–625. WANG Shijin, BEI Jinzhong, LI Dehai, et al. Real-time Kinematic Positioning Algorithm of GPS/BDS[J]. Geomatics and Information Science of Wuhan University , 2014, 39 (5) : 621 –625. |
| [2] | 高星伟. GPS/GLONASS网络RTK的算法研究与程序实现[D].武汉:武汉大学, 2002. GAO Xingwei. The Algorithmic Research of GPS/GLONASS Network RTK and Its Program Realization[D]. Wuhan: Wuhan University, 2002. |
| [3] | 祝会忠, 徐爱功, 高猛, 等. BDS网络RTK中距离参考站整周模糊度单历元解算方法[J]. 测绘学报 , 2016, 45 (1) : 50–57. ZHU Huizhong, XU Aigong, GAO Meng, et al. The Algorithm of Single-epoch Integer Ambiguity Resolution between Middle-range BDS Network RTK Reference Stations[J]. Acta Geodaetica et Cartographica Sinica , 2016, 45 (1) : 50 –57. DOI:10.11947/j.AGCS.2016.20140525 |
| [4] | 段举举, 沈云中. GPS/GLONASS组合静态相位相对定位算法[J]. 测绘学报 , 2012, 41 (6) : 825–830. DUAN Juju, SHEN Yunzhong. An Algorithm of Combined GPS/GLONASS Static Relative Positioning[J]. Acta Geodaetica et Cartographica Sinica , 2012, 41 (6) : 825 –830. |
| [5] | 李金龙. 北斗/GPS多频实时精密定位理论与算法[J]. 测绘学报 , 2015, 44 (11) : 1297. LI Jinlong. BDS/GPS Multi-frequency Real-time Kinematic Positioning Theory and Algorithms[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (11) : 1297 . DOI:10.11947/j.AGCS.2015.20150254 |
| [6] | 张绍成.基于GPS/GLONASS集成的CORS网络大气建模与RTK算法实现[D].武汉:武汉大学, 2010. ZHANG Shaocheng. The GPS/GLONASS Integrated CORS Network Atmosphere Modeling and RTK Algorithm Implementation[D]. Wuhan: Wuhan University, 2010. |
| [7] | 高旺, 高成发, 潘树国, 等. 北斗三频宽巷组合网络RTK单历元定位方法[J]. 测绘学报 , 2015, 44 (6) : 641–648. GAO Wang, GAO Chengfa, PAN Shuguo, et al. Single-epoch Positioning Method in Network RTK with BDS Triple-frequency Widelane Combinations[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (6) : 641 –648. DOI:10.11947/j.AGCS.2015.20140308 |
| [8] | 张晶晶. BDS网络RTK虚拟参考站数据生成的算法研究[D].北京:中国测绘科学研究院, 2014. ZHANG Jingjing. Algorithm of Generating VRS Data for Compass Navigation System[D]. Beijing: Chinese Academy of Surveying and Mapping, 2014. |
| [9] | 祝会忠.基于非差误差改正数的长距离单历元GNSS网络RTK算法研究[D].武汉:武汉大学, 2012. ZHU Huizhong. The Study of GNSS Network RTK Algorithm between Long Range at Single Epoch Using Un-difference Error Corrections[D]. Wuhan: Wuhan University, 2012. |
| [10] | 张明, 刘晖, 丁志刚, 等. 基于序贯平差的长距离基准站间模糊度快速固定[J]. 武汉大学学报(信息科学版) , 2015, 40 (3) : 366–371. ZHANG Ming, LIU Hui, DING Zhigang, et al. Fast Ambiguity Resolution between Long-range Base Stations Based on Sequential Adjustment[J]. Geomatics and Information Science of Wuhan University , 2015, 40 (3) : 366 –371. |
| [11] | 唐卫明, 刘经南, 施闯, 等. 三步法确定网络RTK基准站双差模糊度[J]. 武汉大学学报(信息科学版) , 2007, 32 (4) : 305–308. TANG Weiming, LIU Jingnan, SHI Chuang, et al. Three Steps Method to Determine Double Difference Ambiguities Resolution of Network RTK Reference Station[J]. Geomatics and Information Science of Wuhan University , 2007, 32 (4) : 305 –308. |
| [12] | 鄢子平, 丁乐乐, 黄恩兴, 等. 网络RTK参考站间模糊度固定新方法[J]. 武汉大学学报(信息科学版) , 2013, 38 (3) : 295–298. YAN Ziping, DING Lele, HUANG Enxing, et al. A New Method of Ambiguity Resolution in Network RTK between Reference Stations[J]. Geomatics and Information Science of Wuhan University , 2013, 38 (3) : 295 –298. |
| [13] | 高星伟, 陈锐志, 赵春梅. 网络RTK算法研究与实验[J]. 武汉大学学报(信息科学版) , 2009, 34 (11) : 1350–1353. GAO Xingwei, CHEN Ruizhi, ZHAO Chunmei. A Network RTK Algorithm and Its Test[J]. Geomatics and Information Science of Wuhan University , 2009, 34 (11) : 1350 –1353. |
| [14] | LI Bofeng, SHEN Yunzhong, FENG Yanming, et al. GNSS Ambiguity Resolution with Controllable Failure Rate for Long Baseline Network RTK[J]. Journal of Geodesy , 2014, 88 (2) : 99 –112. DOI:10.1007/s00190-013-0670-z |
| [15] | TEUNISSEN P J G. The Least-squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy , 1995, 70 (1-2) : 65 –82. DOI:10.1007/BF00863419 |
| [16] | BÖHM J, MÖLLER G, SCHINDELEGGER M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w)[J]. GPS Solutions , 2015, 19 (3) : 433 –441. DOI:10.1007/s10291-014-0403-7 |
| [17] | BOEHM J, NIELL A, TREGONING P, et al. Global Mapping Function (GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters , 2006, 33 (7) : L07304 . |
| [18] | AL-SHAERY A, ZHANG S, RIZOS C. An Enhanced Calibration Method of GLONASS Inter-channel Bias for GNSS RTK[J]. GPS Solutions , 2013, 17 (2) : 165 –173. DOI:10.1007/s10291-012-0269-5 |
| [19] | WANNINGER L. Carrier-phase Inter-frequency Biases of GLONASS Receivers[J]. Journal of Geodesy , 2012, 86 (2) : 139 –148. DOI:10.1007/s00190-011-0502-y |
| [20] | BANVILLE S, COLLINS P, LAHAYE F. GLONASS Ambiguity Resolution of Mixed Receiver Types without External Calibration[J]. GPS Solutions , 2013, 17 (3) : 275 –282. DOI:10.1007/s10291-013-0319-7 |
| [21] | YAO Yibin, XU Chaoqian, SHI Junbo, et al. ITG: A New Global GNSS Tropospheric Correction Model[J]. Scientific Reports , 2015, 5 : 10273 . DOI:10.1038/srep10273 |
| [22] | YAO Yibin, ZHANG Bao, XU Chaoqian, et al. A Global Empirical Model for Estimating Zenith Tropospheric Delay[J]. Science China Earth Sciences , 2016, 59 (1) : 118 –128. DOI:10.1007/s11430-015-5173-8 |
| [23] | 姚宜斌, 张豹, 严凤, 等. 两种精化的对流层延迟改正模型[J]. 地球物理学报 , 2015, 58 (5) : 1492–1501. YAO Yibin, ZHANG Bao, YAN Feng, et al. Two New Sophisticated Models for Tropospheric Delay Corrections[J]. Chinese Journal of Geophysics , 2015, 58 (5) : 1492 –1501. |


