2. 同济大学测绘与地理信息学院, 上海 200092
2. College of Surveying and Geo-Information of Tongji University, Shanghai 200092, China
GNSS技术的应用使得大尺度的地壳形变监测能力得到了很大的提升[1-4]。然而,由于板内形变与板缘形变存在差异。尤其是我国大陆,因受到印度洋板块、太平洋板块、欧亚板块碰撞、俯冲、挤压联合的共同作用,成为了全球板内地壳运动最为剧烈的地区,形成了复杂的孕震构造环境和地球动力学背景,在广阔分布的活动构造系中有着不同空间尺度的地壳形变特征。研究表明,板内与地震有关的形变和应变积累通常集中在断裂带附近区域几千米至几十千米较窄的范围内[5]。因此,这就需要从不同空间尺度,上千千米大尺度-上百千米中尺度-孕震断层尺度来分析地壳形变特征,进而研究地震的孕育过程。目前应变场的多种解算方法如Delaunay三角网法、高斯距离加权格网法、最小二乘配置法、球谐函数、多面函数法等能够准确得到较大尺度下的地壳运动应变场分布[6],但不利于分析不同空间尺度下发生的地壳形变特征或发现小尺度局部形变的细部特征。小波函数因具有空间和频率局部化的多分辨率分析能力在地球物理领域、信号处理方面得到了广泛应用。然而目前更多是集中在1维和2维小波函数在不同时频域的分解。对于空间小波的研究较少,文献[7-8]首次提出了球面泊松小波(Possion)概念,并用于构建了全球到区域不同尺度的地磁场模型,通过与球谐函数模型比较得出,球面泊松小波可用于表达位于地球内部的多极子磁源产生的磁场;后来,文献[9]探讨了针对观测点位规则分布和不规则分布情况下球面泊松小波磁场和重力场模型的构建。同时,文献[10]提出了高斯差分球面小波(difference of Gaussians,DOG)的概念。后由文献[11]利用DOG球面小波进行了一系列模拟试验,分析了多尺度速度场的特征。文献[12]利用中国陆态网数据采用DOG球面小波建立了中国大陆东方向和北方向多尺度速度场,表示了速度场的大尺度与局部变化特征。鉴于地球外部形状的不规则性及地壳形变的不均匀性,论文基于球面小波理论构建了GNSS多尺度应变场估计模型。利用负位错模型模拟生成数据源,估计了走滑断层闭锁状态下的应变场分布特征;并模拟不同空间影响范围的断层形变,开展了多尺度应变场检测区域地壳形变异常的试验。通过大量的模拟试验验证了球面小波应变场模型的正确性,提出了多尺度应变场在区域地壳形变检测中的优势。
1 模型构建 1.1 球面小波函数 1.1.1 DOG小波设一个半径为1的单位球,球面上任一点x处的DOG球面小波函数表达式为[11-12]
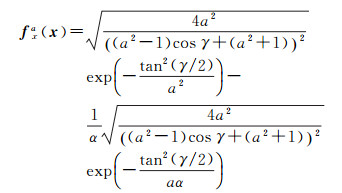 (1)
(1)
式中,γ为球面坐标系下,观测点位矢量x与球面小波中心之间的夹角,取值范围为0≤γ≤180°;a=2-q,q表示尺度,值越大,尺度越小;α取1.25。
1.1.2 Possion小波以||x||=R为半径的球面上任意一点x的Possion球面小波函数表达式为[8-9]
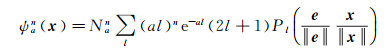 (2)
(2)
式中,Nan表示L2范数正则化;Pl为勒让德多项式,l为勒让德阶数;a为尺度,用来衡量小波所能反映的空间波长;e为小波中心位置;n为小波阶数,反映的是小波波形振荡的剧烈程度。对于x≠0,则有
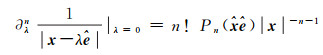 (3)
(3)
式中,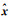
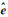
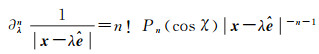 (4)
(4)
式中
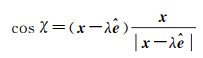 (5)
(5)
定义系数Ckn满足如下方程
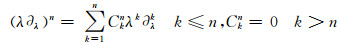 (6)
(6)
Ckn可由如下递推公式进行计算
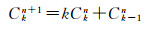 (7)
(7)
设λ=e-a,则球面泊松小波函数可简写为
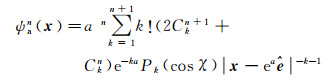 (8)
(8)
由式(1)和式(8)两种球面小波函数,所表示球面小波形状类似,见图 1。图 2所示是不同尺度下球面小波在球面上随纬度变化的经线剖面图。由图 1和图 2可以看出,在尺度相同的情况下,随着与球面小波中心轴的距离变大,小波在球面上的影响逐渐变小。不同尺度相比,尺度较大(即a值较小)的小波更加平缓,在球面上影响面积更大;尺度较小(即a值较大)的小波变化则更加剧烈,在球面上影响范围较小,局域化特征越明显。这说明DOG和Possion球面小波都具有类似的不同分辨率的空间局部化特征,均可以用来反映不同空间尺度下发生的地壳形变特征。通过试验也证实了两种球面小波模型估计结果的一致。
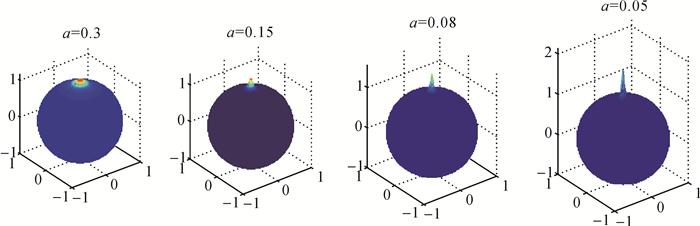
|
| 图 1 不同尺度下的球面小波形状 Fig. 1 Spherical wavelet shape in different scales |
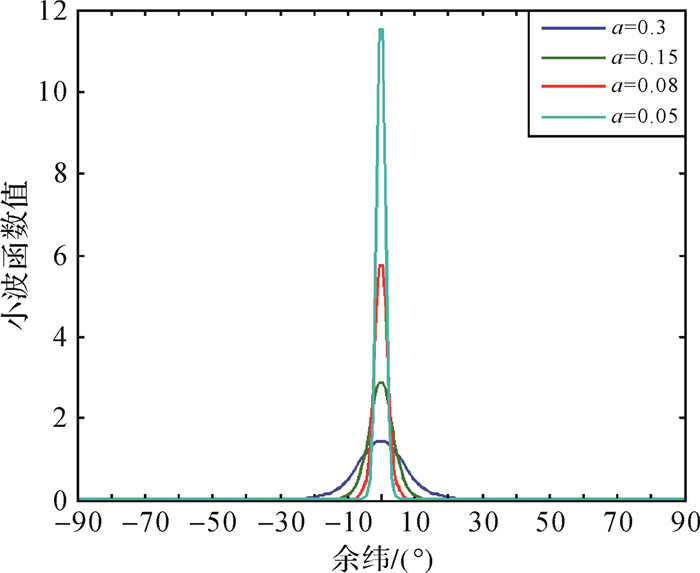
|
| 图 2 不同尺度下的球面小波剖面 Fig. 2 Spherical wavelet profiles in different scales |
1.2 模型参数估计
为构建正确的球面小波框架,首先对球面小波的空间范围和位置按照三角格网规则进行离散化[13],在球面上剖分得到近似相等、均匀分布的格网点,以每个球面网格的顶点作为构建球面小波的中心位置。尺度不同,格网点的密度不同。尺度越小,球面网格的顶点个数越多,所建立的小波基个数也就越多,局域化特征也越突出。在球面小波尺度和位置的确定过程中,并不意味着选取的尺度越多越好。若地壳形变空间尺度较大,这时小波尺度和位置采样过于密集,小波框架就会有冗余。不仅不起作用反而还会因参数过多产生模型的不稳定问题。相反,若地壳形变空间尺度较小,这时采样密度过于稀疏,将不能有效表达小尺度下的形变特征。因此,恰当的小波尺度和位置的确定至关重要。鉴于GNSS测站分布稀疏,且不均匀分布的实际状况,需要结合不同尺度小波的空间影响范围和观测数据的实际分布密度来确定小波中心的位置和尺度。判定依据是,若以某一格网点为中心所建的某一尺度的小波空间影响范围内有不少于3个GNSS测站时,则以此格网点为中心,构建这一尺度的小波函数。仅包含3个测站的尺度作为构建球面小波模型的最小尺度[12]。根据研究区域范围来确定球面小波模型的最大尺度,一般是以两倍的区域范围作为小波的最大尺度[12]。
GPS地壳运动速度场可用各个尺度不同位置的球面小波函数的线性组合来表示。利用N、E、U方向地壳运动速度,建立球面小波函数模型为
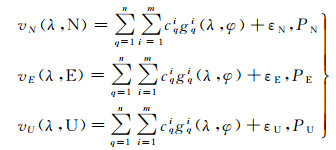 (9)
(9)
式中,n为小波尺度的数量;m为每一尺度相应的小波函数个数;c为待求的小波系数;g为小波基函数;λ、φ为观测站点经纬度;εN、εE、εU为3方向观测噪声;PN、PE、PU为3方向的观测权阵,根据GNSS测站速度估计精度确定。
式(9)简写成矩阵形式为
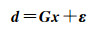 (10)
(10)
采用正则化或附加约束条件进行处理。于是,求取球面小波系数的方程转化为求下列函数最小值的问题。
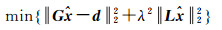 (11)
(11)
式中,λ为正则化参数;L为正则算子。因为上式存在唯一的极小值,相应的解为
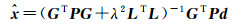 (12)
(12)
因为球面小波反映的是不同空间尺度的变化趋势,球面小波的能量随着尺度的减小而逐渐减少的,较大尺度的小波系数应赋予较大的能量。因此,采用球面上小波函数的标量内积作为L的取值,客观反映了不同尺度形变场空间分布的物理意义。正则化参数λ的求取方法采用了广义交叉验证法[14]。先设置参数λ的一定区间范围,求取GCV函数值,并用高次曲线拟合,求曲线最小值作为参数λ取值,见图 7。
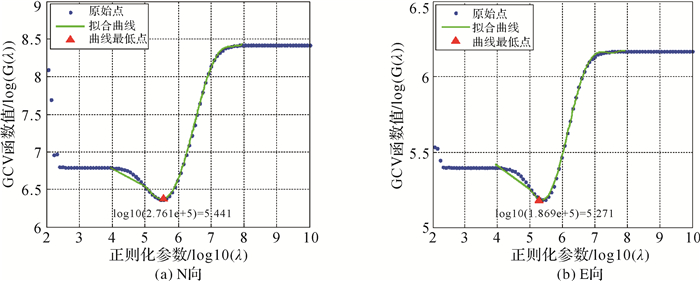
|
| 图 7 正则化参数λ确定 Fig. 7 Calculation of regularization parameter λ |
基于速度场球面小波函数式(9),求取水平速度N、E向的速度梯度为
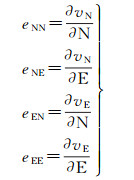 (13)
(13)
由式(13)计算应变率张量为
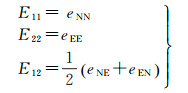 (14)
(14)
由应变率张量解算主应变率、最大剪应变率、最大面膨胀和旋转率[15]。
2 试验分析因为负位错模型是用来表述震间闭锁状态下断层形变的应变积累、闭锁程度和滑动亏损分布[16]。因此,为检验球面小波模型的正确性,利用负位错理论正演闭锁断层区域速度场作为数据源。设地块A和地块B间存在着长趋势的稳定的相对运动vAB。地块A与地块B的边界由断层分割开,在断层面的上部阻碍作用所引起的地壳形变可以用负位错分布来表示
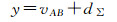 (15)
(15)
式中,y表示地面上任一点位移或速度;d∑表示断层面上负位错分布引起的地壳形变。负位错的方向与断层实际的相对运动方向相反,可以根据断层位错理论来求得[17-18]。
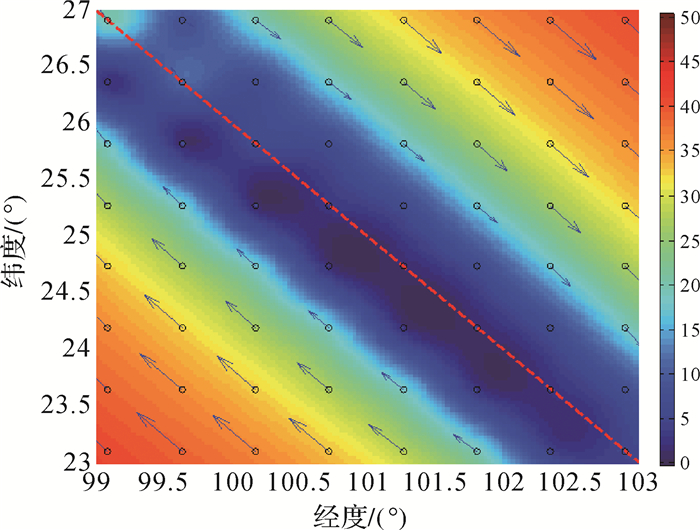
2.1 闭锁走滑断层区域应变场估计为检验球面小波模型估计应变场的正确性,设置震间闭锁状态的走滑断层参数见表 1,在断层区域上方的地表按50 km等间隔模拟布设64个测站。由负位错模型式(15)正演地表闭锁状态下走滑断层区域的速度场,并模拟加入信噪比为10:1的噪声,合成较为真实的地表速度场[19],结果见图 3。可见,离断层远的区域,形变速度较大;离断层越近,受到上覆地表构造运动阻碍作用增大,地表运动速度逐渐衰减。断层带附近运动速度几乎为零,处于闭锁状态。
| 下边缘中心位置 (L,B)/(°) |
方位角 /(°) |
长 /km |
宽 /km |
下边缘深 /km |
倾角 /(°) |
负位错走滑分量 /(mm/a) |
块体相对速度 /(mm/a) |
| (101,25) | 137.16 | 456 | 50 | 60 | 70 | 200 | 118.5 |
|
| 图 3 闭锁走滑断层正演的地表速度场 Fig. 3 Velocity field from locked strike-slip fault |
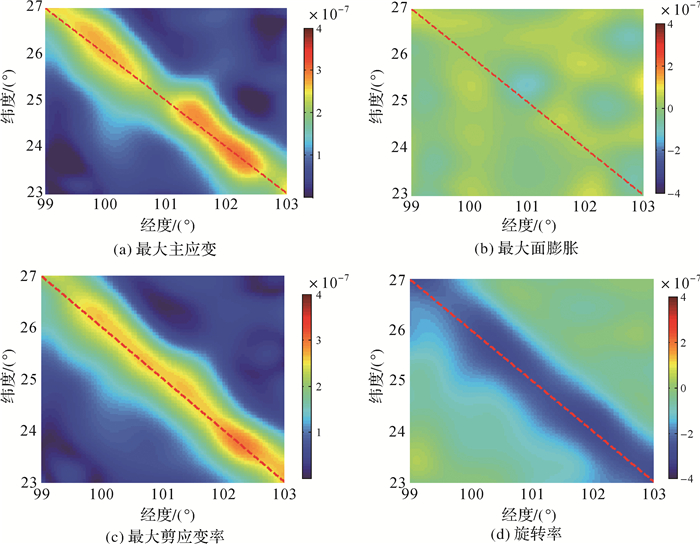
因测区范围约为500 km,故选取构建小波模型的最大尺度为4;因测站分布呈50 km间隔,故确定最小尺度为8。利用球面小波构建了4-8尺度的应变场模型,模型估计残差近似正态分布,中误差为3.2 mm/a,残差值主要集中在-5~+5 mm/a之内。模型估算的最大主应变率、最大剪应变率、最大膨胀率和旋转率见图 4。图中显示,沿断层走向表现出了较强的主应变率和剪应变率、旋转率,见图 4(a)、(c)、(d)。主要是因为闭锁状态导致断层区域速度差异明显,从而产生应变能量的积累;较强的剪应变是因为断层两侧地表位移有明显的方向差异,从而导致产生了一个较强的剪切构造带并发生旋转。旋转率为负值,表示顺时针旋转。由图 4(b),最大面膨胀率几乎为零。分析认为,走滑位错沿断层走向分布,几乎不产生面膨胀。可见,所估计的应变场能够正确反映闭锁状态走滑断层区域的地壳形变特征,验证了球面小波应变场模型的正确性。
|
| 图 4 闭锁走滑断层区域应变场分布 Fig. 4 Strain field distribution in locked strike-slip fault areas |
2.2 多尺度应变场形变异常检测
为检验球面小波多尺度应变场在地壳形变检测中的优势,模拟设置了两个不同空间影响范围的闭锁逆冲断层形变,作为两个形变源。其负位错模型参数见表 2。
| 断层 | 下边缘中心位置 (L,B)/(°) |
方位角 /(°) |
长 /km |
宽 /km |
下边缘深 /km |
倾角 /(°) |
负位错走滑分量 /(mm/a) |
块体相对速度 /(mm/a) |
| 断层1 | (113.6,25) | 0 | 42.6 | 5 | 7 | 50 | 200 | 18 |
| 断层2 | (116.5,25) | 0 | 213.6 | 35 | 57 | 50 | 200 | 22 |
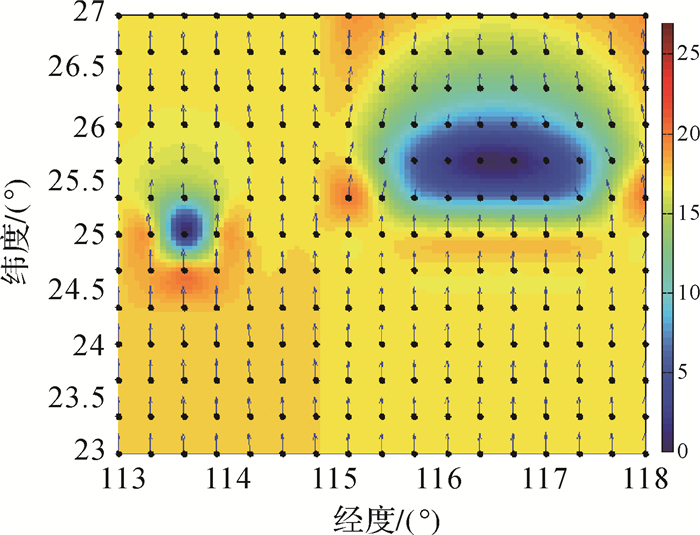
在断层区域上方的地表 113°E-118°E,23°N-27°N范围内,按30 km等间隔模拟布设220个测站。根据负位错理论,正演两个闭锁状态逆冲断层形变地表区域速度场,模拟加入信噪比为10:1的噪声,合成后的速度场见图 5。图中一个断层的形变空间影响范围约为50 km,另一个断层形变空间影响范围约为150 km,显然是两个不同空间尺度的形变源。由图 5可以看出,两个断层附近区域速度较小,远离断层速度较大,断层区域速度梯度较大,积累的应变能量较大,显然是处于闭锁状态的两个断层。两断层北缘均处于拉张状态,具有较强的面膨胀,断层南缘均呈现明显的挤压应变特征。
|
| 图 5 两个闭锁逆冲断层产生的地表水平速度场 Fig. 5 Horizontal velocity from two locked thrust faults |
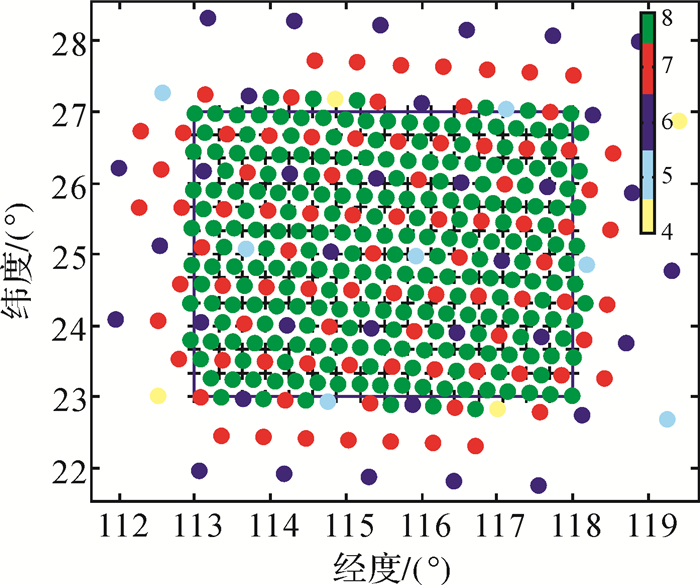
为分析两个不同空间影响范围的形变源在不同尺度应变场中的表现,构建了球面小波的多尺度应变场模型。因为测站间隔为30 km,所以确定小波模型的最小尺度为8,对应的空间分辨率约50 km;因为测区范围约600 km,所以确定球面小波最大尺度为4,对应空间范围约700 km。以球面上研究区域内每一格网点为中心建立不同尺度下的小波函数,若某一尺度的小波函数影响范围内至少有3个测站时,则以此格网点作为构建这一尺度小波函数的中心位置。按照这个原则,经计算在球面上2294个格网点中选取了501个符合条件的格网点作为构建不同尺度小波基的位置。选取的小波基位置分布见图 6。图中的501个小波函数中,其中,4-7尺度中包含的小波基共199个,分别从1至199;8尺度中包含的小波基共302个,分别从200至501。因为测站均匀分布,所以图中不同尺度的小波函数也呈均匀分布。N、E向正则化参数用GCV方法求取,结果见图 7。球面小波模型解算结果残差分布接近正态分布,残差中误差为0.67 mm/a,残差值主要集中分布在-1~+1 mm范围内,残差结果表明,模型拟合度较好,内符合精度较高。
|
| 图 6 球面小波不同尺度下的小波基分布 Fig. 6 Spherical wavelet distribution in different scales |
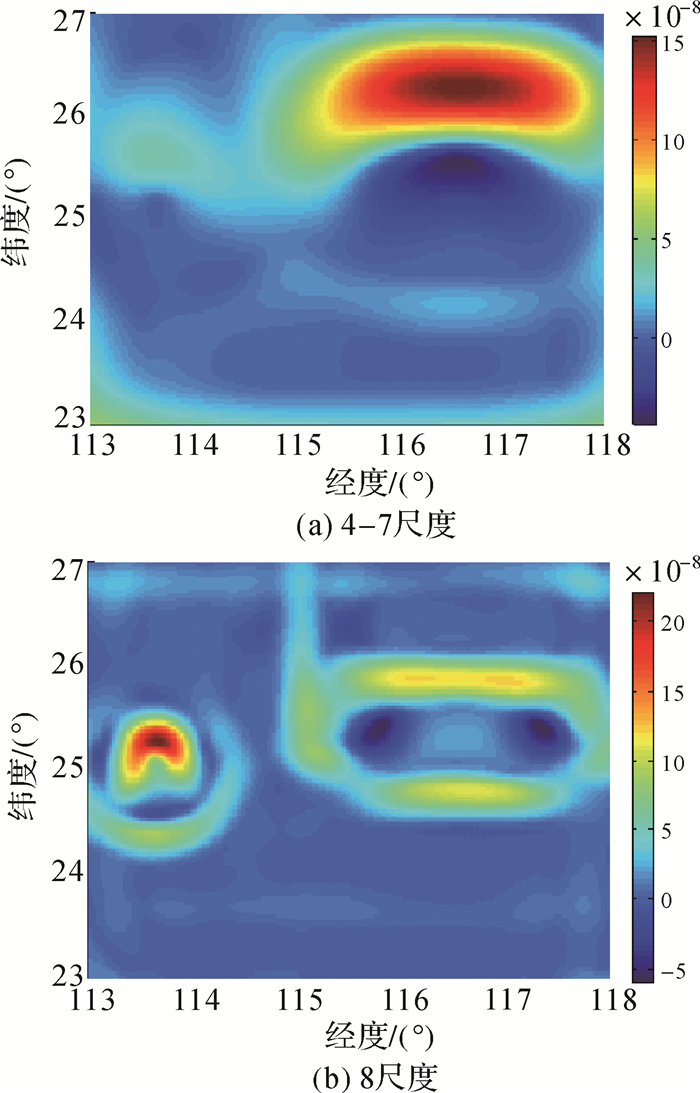
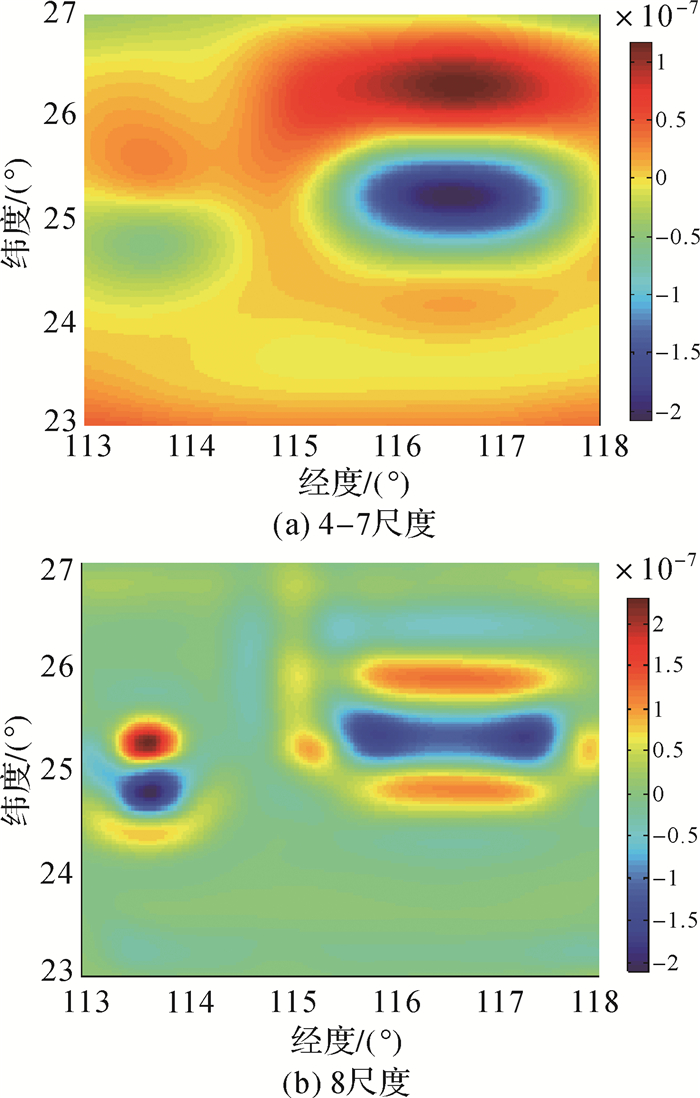
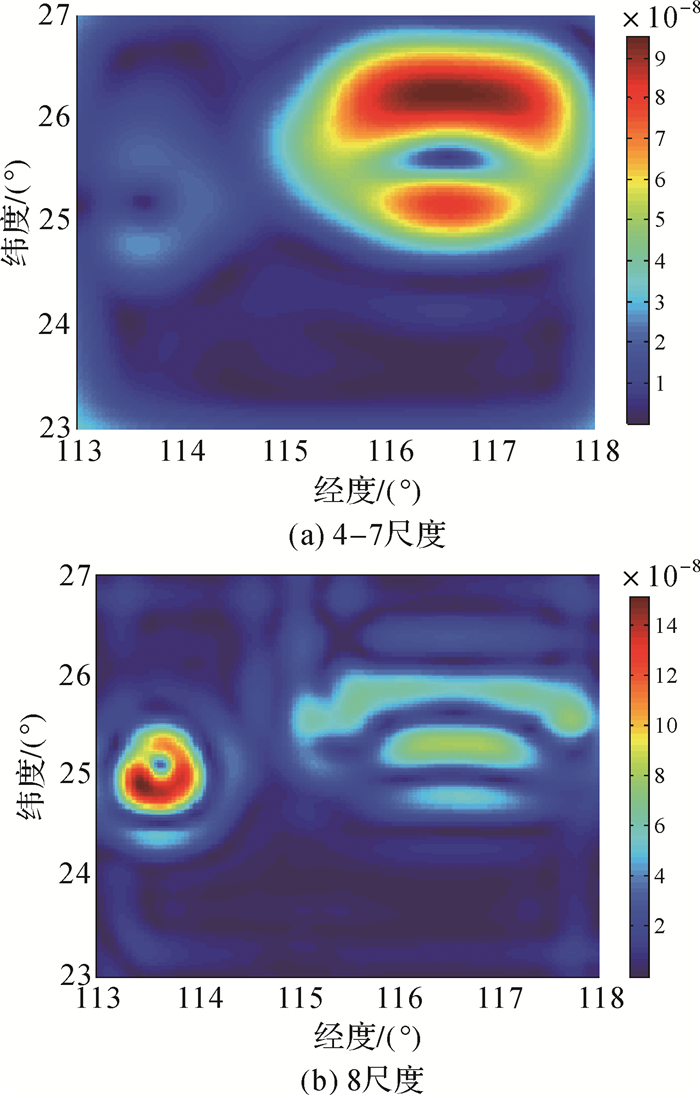
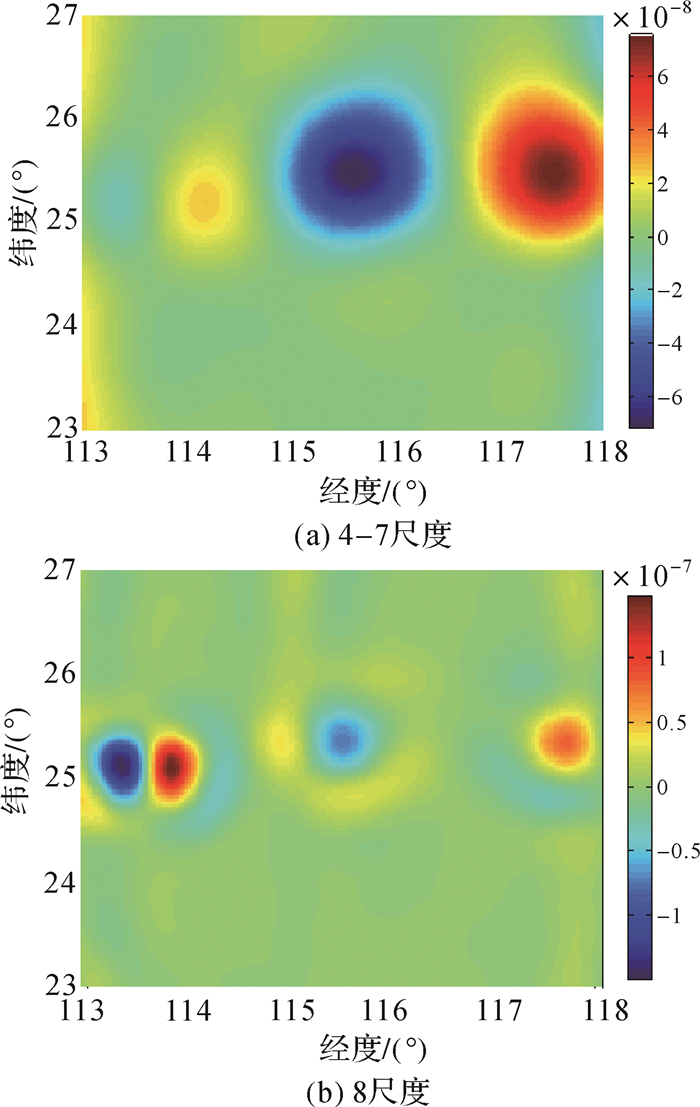
由球面小波模型解算第4-7尺度、第8尺度下的最大主应变率、最大面膨胀率、最大剪应变率和旋转率分别见图 8、 图 9、图 10和图 11。由这4个物理量可以看出,对于50 km影响范围的小断层形变信号,在大尺度(4-7尺度)的应变场中并没有体现,而在小尺度(8尺度)的应变场中表现得非常明显。对于150 km影响范围的大断层形变信号在小尺度即第8尺度中只表现了一小部分信息,而在大尺度(4-7尺度)中的体现得更加完整和明显。可见,不同空间影响范围的地壳形变信息会在相应尺度的应变场中得以体现。150 km形变范围的大断层形变对应4-7尺度的影响范围,唯有在4-7尺度下分析150 km影响范围的大断层形变才会更加有利。同样在8尺度下分析50 km影响范围的小断层形变更有利,因为它可以分离开不相关尺度即4-7尺度信息的影响。可见,多尺度应变场具有检测不同空间尺度地壳形变特征的优势。
|
| 图 8 不同尺度下的最大主应变率 Fig. 8 Maximum principal strain rate in different scales |
|
| 图 9 不同尺度下的最大面膨胀率 Fig. 9 Maximum superficial expansion rate in different scales |
|
| 图 10 不同尺度下的最大剪应变率 Fig. 10 Maximum shear strain rate in different scales |
|
| 图 11 不同尺度下的旋转率 Fig. 11 Rotation rate in different scales |
3 结论
基于球面小波理论构建的多尺度速度场与应变场的估计模型,可从不同空间尺度分析地壳形变的特征。通过负位错理论生成了震间闭锁断层区域地表速度场作为模拟数据,利用球面小波多尺度模型估计并分析了闭锁状态下走滑断层区域应变场分布,结果与实际形变特征吻合,从而验证了模型估计应变场的正确性。模拟两个不同空间影响范围的闭锁逆冲断层形变场,利用模型所估计的多尺度应变场成功检测出了不同空间尺度下发生的地壳形变特征。由此得出,球面小波多尺度应变场模型,可将地壳形变分解表示为不同空间尺度的信息源,获取不同空间尺度下的差异运动的精细图像。不同空间影响范围的地壳形变信息会在相应尺度的应变场中得以体现。对于影响范围较小的局部构造形变信息,只会出现在小尺度应变场中,而在大尺度应变场中无表现。对于大范围地壳形变,虽在小尺度中有所表现,但表现的只是一小部分信息,唯有在相应大尺度应变场中才能体现得更加完整和明显。这充分表明了球面小波多尺度应变场分解的优越性及其在地壳形变检测中的优势所在。球面小波多尺度应变场模型有能力分离不相关尺度信息源或其他背景噪声的影响,从而更有利于地壳运动微形变信息的提取。另外,多尺度应变场还便于分析不同空间尺度形变特征的空间演变过程,为确定断层构造形变与空间响应范围之间的对应关系,帮助认知大陆内部构造变形的运动学特征和动力学过程提供重要的科学依据。
在球面小波多尺度应变场估计模型中,球面上任一个点的值都是由球面上不同尺度所有位置的小波基在这点上共同叠加影响的结果。球面小波的尺度和分布是根据不同尺度小波的空间影响范围和GNSS实际的测站分布密度来决定。因此,当GNSS观测台站分布不均匀时,球面小波也将呈不均匀分布。当没有观测数据或者数据分布稀疏的地方,将不构建球面小波基,同时不会在观测数据区域之外任意产生小波系数。没有构建小波基的地方,受其他小波基的影响较弱。距离球面小波基中心越远,能量衰减越大,受小波影响作用越小。所以,当GNSS测站数据较少或分布不均匀或信噪比较差时,都会影响到球面小波模型的估计效果和精度。随着地壳运动观测网络的不断加密和GNSS观测资料的持续积累,提供的GNSS数据的时空分辨率越来越高,球面小波多尺度模型的估计质量可能会得到极大提高,多尺度应变场在地壳形变检测中的优势将会体现得更加明显。结合更多的实例数据,建立多尺度动态应变场模型,考虑地壳形变的空间分布和时变特征,确定块体与次级地块应变场不同空间分布与活动断层形变之间的对应关系,分析应变场的时空演化过程值得后续进一步研究。
| [1] | 江在森, 马宗晋, 张希, 等. GPS初步结果揭示的中国大陆水平应变场与构造变形[J]. 地球物理学报 , 2003, 46 (3) : 352–358. JIANG Zaisen, MA Zongjin, ZHANG Xi, et al. Horizontal Strain Field and Tectonic Deformation of China Mainland Revealed by Preliminary GPS Result[J]. Chinese Journal of Geophysics , 2003, 46 (3) : 352 –358. |
| [2] | 徐克科, 伍吉仓, 吴伟伟. 基于GNSS时空数据的瞬态无震蠕滑信息检测[J]. 地球物理学报 , 2015, 58 (7) : 2330–2338. XU Keke, WU Jicang, WU Weiwei. Detection of Transient Aseismic Slip of Signals from GNSS Spatial-temporal Data[J]. Chinese Journal of Geophysics , 2015, 58 (7) : 2330 –2338. |
| [3] | 张培震, 邓起东, 张竹琪, 等. 中国大陆的活动断裂、地震灾害及其动力过程[J]. 中国科学:地球科学 , 2013, 43 (10) : 1607–1620. ZHANG Peizhen, DENG Qidong, ZHANG Zhuqi, et al. Active Faults, Earthquake Hazards and Associated Geodynamic Processed in Continental China[J]. Scientia Sinica Terrae , 2013, 43 (10) : 1607 –1620. |
| [4] | 姜卫平, 周晓慧, 刘经南, 等. 青藏高原地壳运动与应变的GPS监测研究[J]. 测绘学报 , 2008, 37 (3) : 285–292. JIANG Weiping, ZHOU Xiaohui, LIU Jingnan, et al. Present-day Crustal Movement and Strain Rate in the Qinghai-Tibetan Plateau from GPS Data[J]. Acta Geodaetica et Cartographica Sinica , 2008, 37 (3) : 285 –292. |
| [5] | 杜方, 闻学泽, 张培震. 鲜水河断裂带炉霍段的震后滑动与形变[J]. 地球物理学报 , 2010, 53 (10) : 2355–2366. DU Fang, WEN Xueze, ZHANG Peizhen. Post-seismic Slip and Deformation on the Luhuo Segment of the Xianshuihe Fault Zone[J]. Chinese Journal of Geophysics , 2010, 53 (10) : 2355 –2366. |
| [6] | 赵丽华, 杨元喜, 王庆良. 考虑区域构造特征的地壳形变分析拟合推估模型[J]. 测绘学报 , 2011, 40 (4) : 435–441. ZHAO Lihua, YANG Yuanxi, WANG Qingliang. Collocation Model Based on Regional Tectonic Features in Crustal Deformation Analysis[J]. Acta Geodaetica et Cartographica Sinica , 2011, 40 (4) : 435 –441. |
| [7] | HOLSCHNEIDER M, CHAMBODUT A, MANDEA M. From Global to Regional Analysis of the Magnetic Field on the Sphere Using Wavelet Frames[J]. Physics of the Earth and Planetary Interiors , 2003, 135 (2-3) : 107 –124. DOI:10.1016/S0031-9201(02)00210-8 |
| [8] | HOLSCHNEIDER M, IGLEWSKA-NOWAK I. Poisson Wavelets on the Sphere[J]. Journal of Fourier Analysis and Applications , 2007, 13 (4) : 405 –419. DOI:10.1007/s00041-006-6909-9 |
| [9] | CHAMBODUT A, PANET I, MANDEA M, et al. Wavelet Frames:An Alternative to Spherical Harmonic Representation of Potential Fields[J]. Geophysical Journal International , 2005, 163 (3) : 875 –899. DOI:10.1111/gji.2005.163.issue-3 |
| [10] | BOGDANOVA I, VANDERGHEYNST P, ANTOINE J P, et al. Stereographic Wavelet Frames on the Sphere[J]. Applied and Computational Harmonic Analysis , 2005, 19 (2) : 223 –252. DOI:10.1016/j.acha.2005.05.001 |
| [11] | TAPE C, MUSé P, SIMONS M, et al. Multiscale Estimation of GPS Velocity Fields[J]. Geophysical Journal International , 2009, 179 (2) : 945 –971. DOI:10.1111/gji.2009.179.issue-2 |
| [12] | 程鹏飞, 文汉江, 孙罗庆, 等. 中国大陆GPS速度场的球面小波模型及多尺度特征分析[J]. 测绘学报 , 2015, 44 (10) : 1063–1070. CHENG Pengfei, WEN Hanjiang, SUN Luoqing, et al. The Spherical Wavelet Model and Multiscale Analysis of Characteristics of GPS Velocity Fields in Mainland China[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (10) : 1063 –1070. DOI:10.11947/j.AGCS.2015.20140141 |
| [13] | KENNER H. Geodesic Math and How to Use It[M]. Berkeley: University of California Press, 1976 . |
| [14] | GOLUB G H, HEATH M, WAHBA G. Generalized Cross-Validation as a Method for Choosing a Good Ridge Parameter[J]. Technometrics , 1979, 21 (2) : 215 –223. DOI:10.1080/00401706.1979.10489751 |
| [15] | 刘序俨, 季颖锋, 黄声明, 等. 地形变应变张量矩阵的不变量分析[J]. 大地测量与地球动力学 , 2011, 31 (4) : 66–70. LIU Xuyan, JI Yingfeng, HUANG Shengming, et al. Analysis of Invariants in Strain Tensor Matrixes of Crustal Deformation[J]. Journal of Geodesy and Geodynamics , 2011, 31 (4) : 66 –70. |
| [16] | 伍吉仓, 许厚泽, 丁晓利, 等. 台湾集集大地震断层非均匀滑动分布的反演[J]. 测绘学报 , 2002, 31 (S1) : 34–38. WU Jicang, XU Houze, DING Xiaoli, et al. Inversion of Variable Fault Slip of Taiwan Chi-Chi Earthquake[J]. Acta Geodaetica et Cartographica Sinica , 2002, 31 (S1) : 34 –38. |
| [17] | 伍吉仓, 邓康伟, 陈永奇. 板块内部层状负位错模型及其反演[J]. 武汉大学学报(信息科学版) , 2003, 28 (6) : 671–674. WU Jicang, DENG Kangwei, CHEN Yongqi. Negative Dislocation Layer for Intraplate Tectonic Movements and Inversion[J]. Geomatics and Information Science of Wuhan University , 2003, 28 (6) : 671 –674. |
| [18] | STEKETEE J A. On Volterra's Dislocations in a Semi-infinite Elastic Medium[J]. Canadian Journal of Physics , 1958, 36 (2) : 192 –205. DOI:10.1139/p58-024 |
| [19] | OKADA Y. Surface Deformation Due to Shear and Tensile Faults in a Half-space[J]. Bulletin of the Seismological Society of America , 1985, 75 (4) : 1135 –1154. |
| [20] | 徐克科, 伍吉仓, 王成. 利用GNSS位移时空序列进行断层无震蠕滑特征分析[J]. 武汉大学学报(信息科学版) , 2015, 40 (9) : 1247–1252. XU Keke, WU Jicang, WANG Cheng. Analysis of Fault Aseismic Slip Feature Based on GNSS Displacement Time-space Series[J]. Geomatics and Information Science of Wuhan University , 2015, 40 (9) : 1247 –1252. |



