2. 中国科学院软件研究所计算机科学国家重点实验室, 北京 100190 ;
3. 北京大学遥感与地理信息系统研究所, 北京100871
2. Institute of Software Chinese Academy of Sciences, Beijing 100190, China ;
3. Institute of Remote Sensing and Geographical Information Systems, Peking University, Beijing 100871, China
Web 2.0环境下,地图制图的服务对象正从测绘相关行业转向公众服务,空间数据采集、地图制图技术、地图发布与传播呈现大众化、网络化和移动化的趋势。目前,Web浏览器、移动客户端出现了大量地图混搭的应用形式:将位置相关信息(如带有地理标签的照片、视频、微博消息等多媒体)以点状符号的形式简单映射到Web地图上。近来出现的基于位置的社交网络(LBSN)[1]也通过地图混搭对朋友圈网络、微博消息等进行时空可视化[2]。然而,混搭地图容易出现图面杂乱、易览性差等制图问题,极大地削弱了地图阅读与信息获取效率[3],这在社交网络、微博、媒体共享服务等大数据环境的制图中显得尤为突出。
本质上,地图混搭是一种专题地图。与传统专题符号不同,混搭地图的符号本身承载丰富信息(如照片、视频、Logo标志等),符号尺寸较大,且数据体量巨大。本文研究“大尺寸”点状符号的实时Web制图,并定义“大尺寸”的内涵为“符号尺寸远大于符号间距”,笔者认为这是大数据环境下混搭制图的一个重要特征。具体有如下特点:①尺寸敏感性,即制图算法需要显式考虑符号大小,因为“大尺寸”符号更容易产生压盖冲突;②海量“大尺寸”符号空间竞争导致的高淘汰率(见3.2.3节);③由于符号本身是信息认知主体,用户更关注符号个体信息的完整表达。
在点状符号可视化方面,本文主要综述3类方法:制图综合、空间变形和表达转换。地图综合中的相关问题是点群综合,采用选取、典型化、聚合、位移等综合算子进行点群化简。典型化、聚合的结果无法表达个体信息[3],因而不太适合本应用;位移虽能保证每个符号可完整识别,却无法高效处理大数据集[3-4]。现有点群化简算法大多为地理相关科学服务,注重保持点群的空间分布规律,采用复杂度高的化简算法[5-8],难以扩展到大规模实时Web制图。此外,这些方法将制图目标作为无大小的点,根据载负量规律[9]减少目标数量,并不保障空间冲突的消解。本文中Web用户强调高效处理,关注个体信息而非整体态势,且无压盖的大尺寸符号是无法保持原始数据的分布模式的,空间分布约束不作为本文的制图目标。另一些算法考虑符号大小,并显式探测空间冲突。如有学者利用数学规划方法寻找点群在尺度轴上的活跃范围,可构建点群在尺度空间的连续表达[10-11],但优化算法的效率使其难以胜任高响应制图任务。当然,可将算法复杂度高的综合结果存储在层次结构中[12-13],如Google通过预存储其海量POI点化简结果来弥补耗时的优化算法[14-15],不足在于难以灵活应对动态语义查询和变化更新。在强调效率的Web和移动制图方面,国内外学者均采用空间剖分结构来加快冲突探测与消解,在小数据量下取得不错的结果[16-18]。
空间变形包括Cartogram、变比例尺表达[19-20]、放大镜等。空间变形能降低放大区域内符号压盖的可能性,但无法控制变形边界区域的空间冲突[4]。表达转换是指通过空间变换(如核密度分析)将离散点群转换为密度图或热图,能够揭示点群分布总体态势与密度差异,但却无法表达个体信息。
综上,地图综合中的选取算子是比较适合本研究的方法,然而针对海量“大尺寸”空间冲突快速消解、符号大小可定制,顾及语义重要性的研究并不多。针对该应用特点和新型用户需求,本文研究了一种高效的“大尺寸”地图符号多尺度可视化方法,旨在满足以下设计原则:
(1) 最小化符号压盖:无压盖的符号有利于用户探索符号本身承载的信息内容,减少干扰。
(2) 语义层次的多尺度表达:利用多尺度结构展现语义重要性,满足重要目标在较小尺度优先出现,次要目标随尺度变大逐级累加的原则[12]。
(3) 平移和缩放一致性:当前缩放级别(或窗口范围)存在的目标在窗口放大(或移动)后须保持,提供图形上下文信息,不迷失方位[15]。
(4) 提高图面空间利用率:利用更多的空间来提高专题信息表达强度。
1 基于偏移Quadtree的多尺度显著性评级 1.1 基本思想:网格单选对于海量点符号的冲突,本文的基本思想是对空间进行划分,每个网格单元选取一个最重要的符号,简称“网格单选法”。采用分治策略处理效率高,且剖分结构能够在较大程度上减少符号的初始压盖。然而,要满足上述设计原则,仍需解决要素重要性评估、网格大小、网格定位等问题。
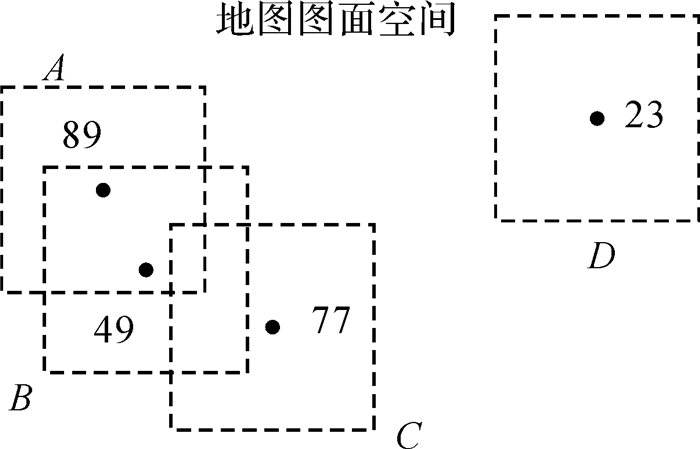
1.2 空间上下文中的相对重要性本文应用场景中的点状符号都具有语义重要性,比如地点口碑、签到数,访问量等。然而,使用这些语义来选取符号并不能满足设计原则(1)和(4)。如图 1所示,选取重要性高于75的点符号,得到的A和C,既没有解决空间冲突,也没有很好地利用图面空闲空间。这里采用相对重要性的概念:相对重要的目标是在空间冲突上下文中重要性最高的目标。在图 1中,A和D的相对重要性较高,因为D的周围没有冲突目标,其较低的重要性依然能够从上下文中凸显出来。相对重要性能够调和语义和空间关系。
|
| 图 1 空间冲突上下文中的相对重要性(图中虚线框代表点符号的覆盖区域) Fig. 1 Relative importance made sense in conflicting context (dashed boxes indicate the extents of point symbols) |
1.3 网格与符号的大小关系
网格单选基本思路中并没有对网格大小进行约定,不同的情况可能会导致“单选法”失效或引入不必要的计算负荷。本文通过制定合理网格划分方案对单选思路进行优化,并规避不必要的空间计算,以达到计算效率最大化。理想的网格单元大小(w)应是符号尺寸(s)的函数:w=f(s),当网格大小使得落入网格内的任意两个符号必然产生压盖时,不需要空间计算就知道只能从中选出一个无压盖符号。据此非严格估算网格与符号的大小关系如下式所述。
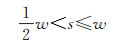 (1)
(1)
式(1)之外有两种情况:①网格过小(小于符号尺寸)将使相邻网格选取的符号必然产生压盖(原则(1)),“单选法”失去意义;②网格过大将降低点符号的空间利用率(原则(4))。若要提高后者的空间利用率,须计算N个点中选M个无压盖且重要性高的点符号(N≫M,M不固定)的组合优化问题,计算复杂度高。下文对“单选法”的优化能够避免该计算过程。
1.4 四叉树层次网格划分与跨网格临近问题本文采用四叉树作为符号选取的空间剖分方案,可根据符号在四叉树中的Morton码判断他们是否落在第z级的同一网格。本文使用二进制Morton码对四叉树网格进行编码,每个层次占2位编码,第z级的编码长度为2z, z∈{1, 2, …, n}。式(2)给出了两个点目标处于四叉树第n层下的Morton码示例(每一层次的编码用中括号分隔),可以看出M1、M2在第1~4级都位于同一个网格,从第5级开始分隔到不同网格。
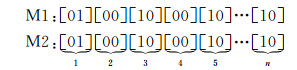 (2)
(2)
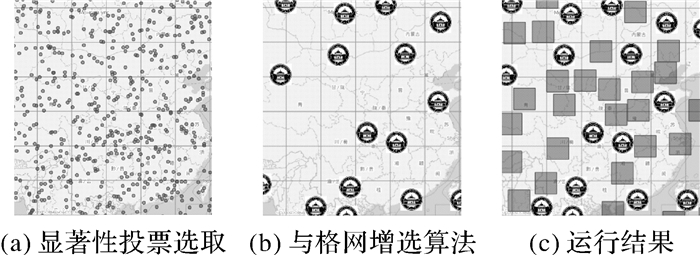
通过四叉树实现基本的网格单选法:①采用递归算法对所有目标进行一次性编码(到第z层),目标的Morton码采用字符数组存储在其属性中,可获得目标在所有缩放级别所在的网格信息;②对编码的前2z位进行子串提取并排序分组,查询特定缩放级别z下位于同一网格中的目标;③对于同一网格内的大量点符号,选取重要性最高的一个作为最终结果(图 6(b));④当地图平移缩放时重复步骤②—③,可实时获得对应缩放级别下点符号的选取结果。
|
| 图 6 模拟点数据 Fig. 6 Random data points |
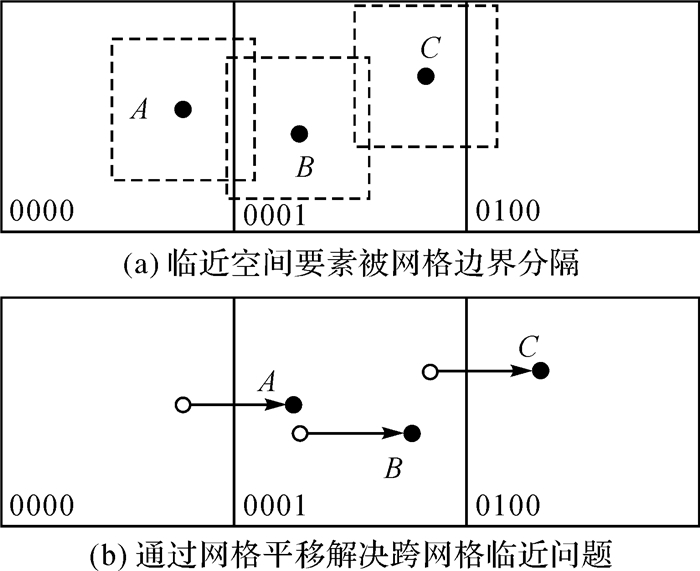
然而,该简单实现有一个明显的缺陷:点符号的临近关系是通过位于同一网格来隐含判定,即位于同一网格认为临近(产生符号压盖),而没有考虑跨网格的临近关系。换言之,相邻网格选出的符号仍然可能产生压盖(图 6(b))。现考查图 2(a)中的3点A、B、C,因为B、C两点被分在了0001网格内,若B比C的重要性高,从中选出B,0000网格选出A点,A、B就会产生的压盖。这是由于网格定位的任意性所致,且无论如何选择网格起点,单一的网格划分无法避免临近关系被网格边界分割。
|
| 图 2 Fig. 2 |
1.5 四叉树多次平移与显著性投票
设想四叉树在不同方向进行多次平移,对每个网格在多次平移中的入选的重要目标进行投票,得票高者作为最终的入选结果。以图 2为例,假设A、B、C的重要性为90、80、20,则图 2(a)中0000网格中A入选,0001网格中B入选,在网格偏移后(图 2(b)),0001网格中A入选,0100网格中C入选,综合两次结果A获得两票,B、C分别获得一票。若A、B、C的重要性为80、90、20,则A、C获得一票,B两票。在多次平移下,得票数高者表明与它周围发生冲突的目标相比其重要性更高。合理的平移次数与方案能把当前目标与其临近目标纳入到相同网格中,并能在多尺度下持续有效。
1.5.1 多尺度结构中的有效平移方案以横向平移为例,将图 2中的点向右进行平移,当偏移量达到一个网格宽度w(或其整数倍)时,A、B、C 3点与网格划分的相对关系复原,因此有效的平移全部发生在w个单位的平移中,其间会出现B、C分在一个网格的偏移区间(图 2a),也会出现A、B分在一个网格的偏移区间(图 2(b))。由于计算中必须把平移过程离散化,不妨考虑将平移分为n个单元,每次的偏移量为w/n,离散偏移量可表示为{0, w/n, 2w/n, …, (n-1)w/n},因为nw/n与0偏移量效果相同,故剔除。
上述偏移仅讨论了一个比例尺下的情况,通常在每个缩放级别下都需要进行该偏移计算,重复计算将极大降低实时处理效率。为了避免在各个缩放级别下都要针对当前网格大小进行单位为w/n的平移,需要找到一种偏移方案,使得在四叉树的上层进行的平移在后续层级中依然是有效的。
现将n分为奇数和偶数情况讨论。首先考虑n为偶数的情况,如图 3(a)所示:n=4,则4次偏移量分别为{0, w/4, w/2, 3w/4}。放大一级后,偏移量长度变成两倍:{0, w/2, w, 3w/2},其中有效的偏移只有{0, w/2}两次平移。如果再放大,偏移量将变为w的整数倍,成了无效平移。由于每次放大操作都使有效平移次数减少一半,偶数偏移次数无法在多尺度结构中保持持续有效。

|
| 图 3 不同偏移次数在四叉树层次中的有效性(w为00网格的宽度) Fig. 3 Effectiveness of offset schemes under even/odd numbers of translation (w: width of the grid with code 00) |
考虑n为奇数的情况,如图 3(b)所示:n=3,3次偏移量为{0, w/3, 2w/3}。放大一级后,3次偏移量为{0, 2w/3, 4w/3},其中4w/3相当于w/3,与放大前的偏移量集合等价。可以证明,n=3的情况下不论放大多少级,偏移量集合均等价于{0, w/3, 2w/3},该性质可以推广至任意奇数n>1。考虑到计算效率,本文选择最小有效平移次数(n=3)。
同理,横向平移原理可扩展到纵向平移,当n=3时,四叉树在二维平面中共有9次平移,平移矩阵由式3表示,其中矩阵元素形如(dx, dy),w为当前网格宽度
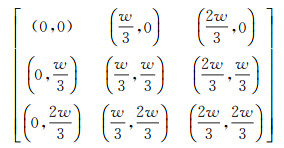 (3)
(3)
式(1)中符号矩形与网格大小关系只是一个初步估计,考虑到网格平移需进行调整。如果平移是连续的,所有的临近目标都会在某个平移阶段落入同一个网格内,但是实际的离散平移下有一个例外,下面进行论述。
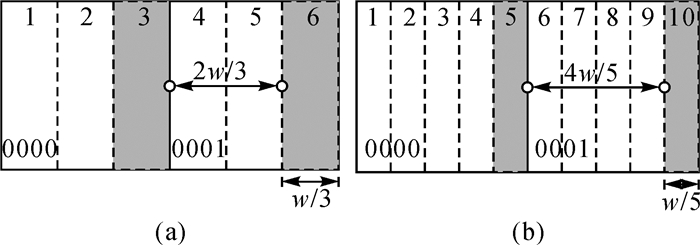
以横向平移3次为例(图 4(a)),将网格按照平移单元w/3进行划分,则落入每个带中的点在一次平移后会落入下一个相邻带中。观察边界情况3、6号带(图 4(a)中灰色区域),位于这两个带的点在平移中不可能落在同一个网格。因为落在3、6号带中任意两点的最小距离为2w/3,如果符号尺寸s=w,还是有可能产生压盖冲突,只是该冲突无法被本文方法探测到。这一情况适用于任何中间间隔两带的带号(如图 4(a)中的1、4号,2、5号)。为了完全解决符号压盖,在3次平移下符号尺寸必须满足:s≤2w/3。同理,当n=5时,符号尺寸须小于4w/5(图 4(b))。可以证明,平移网格下满足无压盖的符号尺寸与一维方向平移次数n(奇数)相关
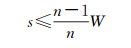 (4)
(4)
|
| 图 4 平移3次和5次下的边界情况及精确符号尺寸上限分析 Fig. 4 Maximum symbol size relative to the selection grid under 3 and 5 translation |
当式(4)中的n→∞,离散偏移趋于连续平移,而最大符号尺寸也趋近网格宽度w,与式(1)相符。当平移次数n较大时,符号与网格的比例相对较大,这样能够提高图面利用率,但同时带来了较大的计算负荷。本文采用符号的最大尺寸为2w/3。
1.5.3 显著性评级的计算流程本文把一个目标在多次四叉树平移中获得的票数作为其显著性评级。显然,在n=3时,能获得的最高显著级别为9,最终可根据需求输出显著性级别高于指定阈值的目标集合。总体计算流程如下。
输入:符号尺寸s;当前地图缩放级别z;指定输出目标的显著性级别SL;查询窗口Q;
输出:缩放级别z对应的选取目标集合P。
步骤1:预处理阶段:按式(3)进行9次平移,每次平移计算所有目标0-zmax级的Morton编码;
步骤2:网格单选与显著性投票(响应地图操作事件,实时计算):
(1) 根据s和z计算网格单选和显著性投票所需的四叉树网格级别k;
(2) 空间查询落入Q中的目标候选集C;
(3) 对9次平移中的每一次:对每个c∈C,提取c的Morton码前2k位子串,进行相同网格分组,每组中重要性c.imp最高的目标其显著性级别c.ds=c.ds+1(投票);
(4) 对每个c∈C,把c加入集合P当且仅当c.ds≥SL。
计算过程中步骤1属于一次性计算,在处理完后步骤2是在每次的放大、缩小和窗口移动的事件中触发,其间不需要重新计算步骤1即可改变s、SL等参数,并实时获得结果;步骤(1)在式(4)后进行了解释;步骤(3)中的显著性级别ds在9次平移网格中进行累加,最高可获得9票;步骤(4)选取满足指定显著性级别的目标作为z级上的最终结果。
2 增大图面利用率的两种扩展从试验结果可以看出,平移四叉树投票算法虽然可有效避免压盖冲突,但还是造成了一定的图面空间浪费。为提高图面利用率(原则(4)),本文提出两种扩展方法。
2.1 格网增选步骤如下所示,格网增选为显著性投票的后续子过程,可利用显著性投票算法记录的信息,如当前窗口Q中的网格,网格中已经选取的目标等。算法通过少量的外接矩形冲突计算,确定是否进行增选,增选多少符号;同时,算法依照显著性评级的顺序对目标进行判断,以保证增选出的目标仍具有较高的显著性。
输入:图面利用率r(缺省值100%);
输出:缩放级别z对应的增选目标集合PS。
步骤1:令增补候选集B=C-P;对B中元素按显著性排序;
步骤2:对每个目标b∈B,根据b的Morton码获取它所在格网及其相邻8个格网(九宫格);
步骤3:获取九宫格中已经选取的目标,判断b是否与他们有压盖关系,若无,则将b加入PS;
步骤4:若点集P+PS的图面利用率超过r,或者窗口Q中所有网格已经增选完毕,则终止循环;否则继续步2。
2.2 多级符号叠加第2种增大图面利用率的方法是采用多级尺寸符号,即在同一个缩放级别中采用不同大小,不同显著性的符号叠加。不同符号尺寸按照表 1分别计算显著性评级,并选取评级为9的点要素,最后将结果进行叠加。在大符号空缺的区域,由小符号填充。不同尺寸的符号位于四叉树的不同层次上,获得某一尺寸符号无冲突表达只需计算相应的四叉树层次,并截取相应长度的Morton码,按1.5.3节中的步骤2进行计算。由于大小不同的符号处于不同四叉树层次,其显著性不同,该扩展方案能够在增大图面利用率的同时提升专题符号的视觉层次(见3.4节)。
| 数据量 | 显著性投票/(%) | 格网增选/(%) |
| 10 | 2.5 | 2.5 |
| 100 | 14.6 | 18.4 |
| 1000 | 17.4 | 39.0 |
| 10 000 | 17.4 | 46.0 |
| 100 000 | 17.4 | 47.9 |
3 试验分析 3.1 原型系统与试验数据
本文试验环境为B/S架构,采用Node.js作为后台服务器,并使用MongoDB数据库存储数据,使用OpenLayers作为客户端软件。试验数据包括两部分:①Flickr网站的真实地理标记照片数据;②全球范围内的随机点数据,试验中点符号的重要性在0~100间随机分配。
3.2 试验结果 3.2.1 算法执行效果图 5(a)为Flickr网站下载的6000个照片位置,可见大量符号聚集压盖,符号尺寸远大于点位间距;图 5(b)为2.4节所述朴素网格单选法的实现结果,可见相邻网格符号仍会产生压盖;图 5(c)的投票选取的结果能够完全避免压盖(显著性级别SL为9)。

|
| 图 5 Fig. 5 |
图 6为随机生成点数据的算法运行结果。图 6(c)中的半透明方框为格网增选算法增选的符号,能够提高显著性评级方法图面利用率,用户可指定图面利用率使增选结果符合预期。
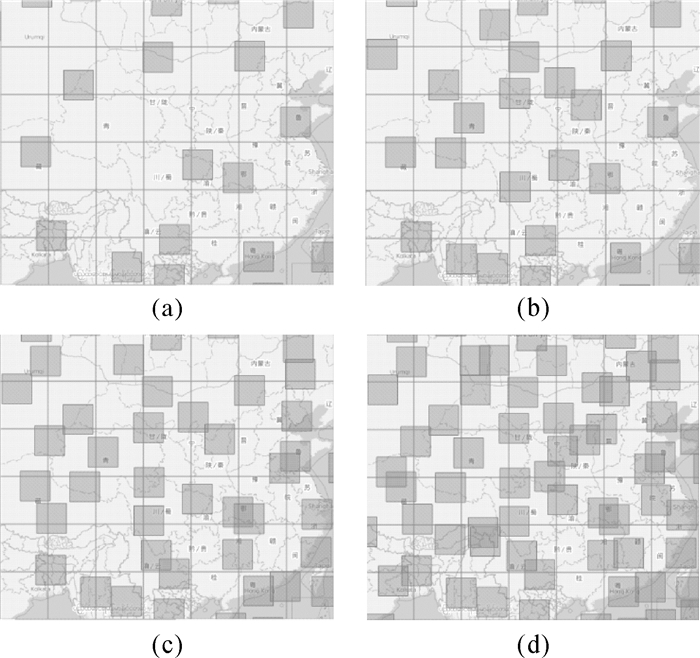
3.2.2 显著性评级对算法影响随着显著性评级参数SL的降低,更多的符号得以表达,但同时压盖冲突逐渐增多(图 7)。在允许部分压盖的应用环境下,降低显著性评级不失为一种增加图面利用率的手段。
|
| 图 7 模拟数据选取结果:显著性评级不小于9(a), 7(b), 5(c), 3(d) Fig. 7 Results of random data points: significance level≥9 (a)、7 (b)、5 (c)、3 (d) |
3.2.3 算法响应实时变化效果
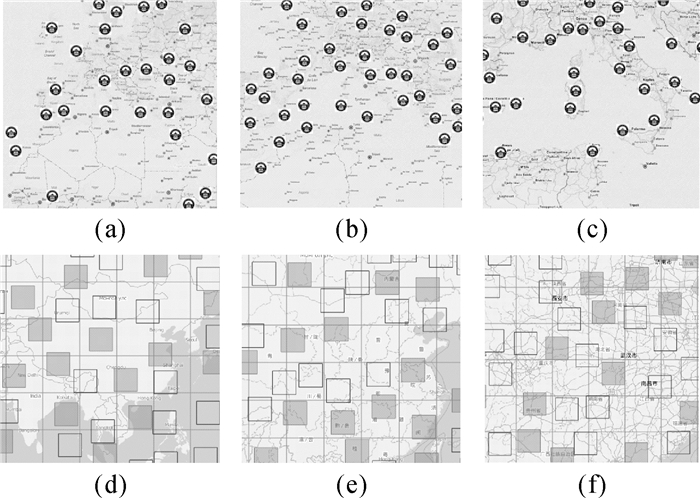
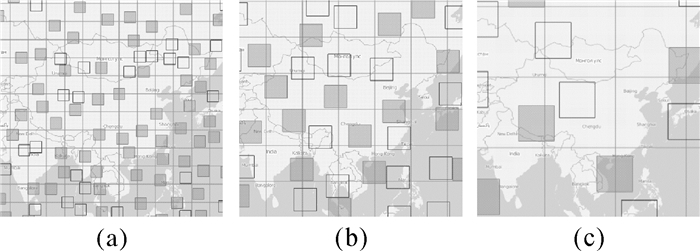
地图缩放和平移时查询窗口Q和缩放级别z发生改变,触发显著性投票(1.5.3节)和格网增选(2.1节)算法运行,实时获得新的结果。随着地图放大,更多的符号显现出来,较小比例尺中符号是较大比例尺符号的子集(原则(3)),较大比例尺中新显现的是(上一缩放级)显著性级别较低的符号(图 8(a)—8(c)),这符合“概览,缩放过滤,按需细节”[17]的信息可视化原则。此外,格网增选在地图操作中能够保证符号无压盖(图 8(d)—8(f))。图 9展示了显著性投票与增选算法可实时响应符号尺寸s变化,符号无压盖,具有良好的鲁棒性;同时,当符号尺寸大于当前选取格网2w/3时,算法将选用上一级格网作为选取依据。试验中选取率在0.5%左右,当符号变大时选取率更低。
|
| 图 8 改变地图缩放级别:Flickr数据结果(a)—(c);模拟数据选取+增选(空心矩形)结果(d)—(f) Fig. 8 Results at varying zoom levels: Flickr data (a)—(c); random data with supplementation (d)—(f) |
|
| 图 9 改变符号尺寸(格网增选的符号为空心矩形):符号宽度21px (a),39px (b),87px (c) Fig. 9 Results of varying symbol sizes: symbol width=21px (a), 39px (b), 87px (c) |
3.3 系统效率
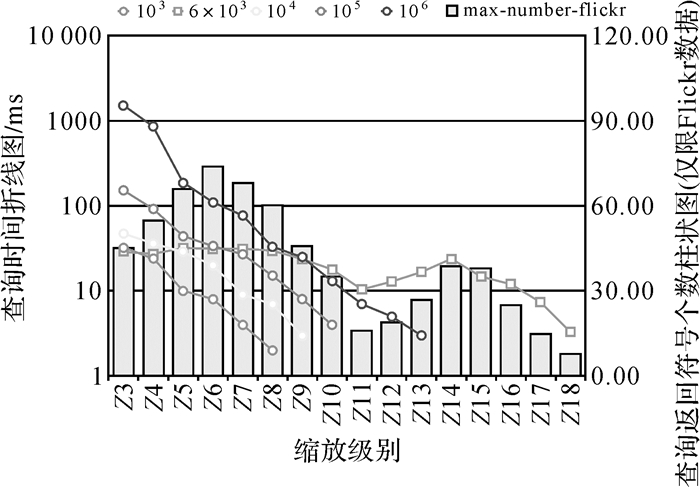
分别考察核心算法(1.5.3节)中预处理(步骤1)和实时查询(步骤2)的运行效率,测试环境为i5-5250U@1.6 GHz笔记本,内存4 GB。对103 、6000(真实Flickr数据)、104、105、106数量级随机分布点的9次平移Quadtree编码耗时分别为0.134 s、0.421 s、0.759 s、5.916 s、33.23 s,该预处理过程在服务器端一次性完成。针对响应地图缩放的实时查询,统计不同数据量从z3(实际最小缩放级别)到z18级的20次试验的耗时均值(图 10)。除了106量级在z3的查询时间为1500 ms,其他均可达到亚秒级的查询效率(105量级的最大查询时间为148 ms;6000量级最大查询时间为31.95 ms)。
|
| 图 10 平移四叉树显著性投票算法在不同数据量和缩放级别下的运算效率 Fig. 10 Performance of our approach under different data volumes and zoom levels |
Flickr数据(6000)在不同缩放级别的测试窗口均选择在目标聚集区符号最多(图 10柱状图)的区域,其查询时间(图 10方形折线图)可视为当前级别的上限,在非聚集区的查询效率更高;同时可见查询时间与检索出的结果数量具有正相关性。与真实数据不同,随机生成点位分布比较平均,在几次放大后数据密度迅速下降,没有聚集中心,使得查询效率快速提高;模拟数据在较大缩放级别下的查询时间在2 ms以内,为清晰起见,图 10中不予表达。
原型系统的显著性投票算法用Javascript实现,已经达到可观的运行效率,采用效率更高的语言或数据库技术可进一步提高系统效率。算法中在同一网格选择重要性最高的要素需要扫描网格中所有数据项,通过对Morton码和显著性属性添加B-Tree索引将大大加快该过程。
3.4 图面空间利用率表 1记录了两种算法处理不同数据量的图面利用效率,试验中考察的区域是固定的,而显著性评级为9,符号大小为45×45。当数据量超过1000时,显著性评级算法的图面利用率稳定在17.4%,因为特定区域内符号数量是有界的(≤格网数量)。格网增选可提升图面利用率,随着数据量增大,格网增选贡献越大,在105量级上基本达到饱和(47.9%)。此外,符号越大空间浪费越大,因而图面利用率也会下降(图 10),具体不再赘述。
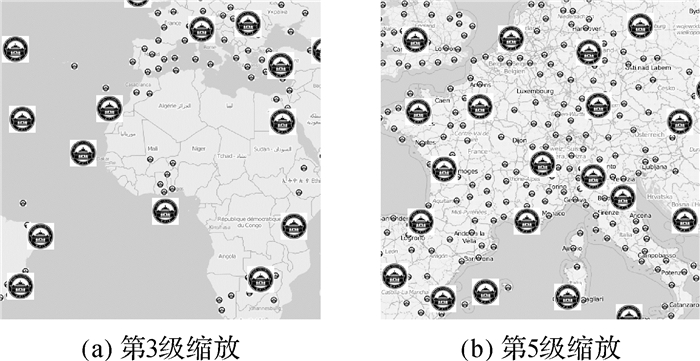
此外,本文在多级符号叠加试验中选用两级符号叠加,小符号尺寸为大符号的1/4,进行选取的网格层级比大符号层级深两级,两级符号的显著性评级均为9,小符号在大符号层级中的显著性低于9,在较深层次被选取出来。图 11展示了真实数据在不同缩放级别下的结果,可见多级符号叠加可以改善图面利用率,具有缩放稳定性。该可视化方案可突出重要目标,弱化次要目标,过滤无关目标,以视觉层次原则区分专题要素的语义重要性。
|
| 图 11 对Flickr数据的多级符号叠加结果 Fig. 11 Increasing map space usage with two-level overlay |
值得注意的是,图面利用率是一个设计问题,并不是越大越好。利用率究竟在多少比较合适,点状符号大小如何选择,选择多少级符号叠加,各级符号大小关系如何,都需要视地图目的用途而定,并需要开展用户试验来评价认知效率。
4 结 论本文研究了一种可高效处理大量符号空间冲突的多尺度可视化方法。该方法可确保任意尺度下符号之间100%无压盖,适用于海量“大尺寸”符号的地图混搭。因为不需空间计算即能完成空间冲突消解,能够达到极高的处理效率,在原型系统中的Javascript非优化实现中可达到105级别数据亚秒级处理效率。同时由于实时进行显著性投票,本方法可支持动态语义过滤:在投票前对数据进行语义过滤,首先选取与用户高度相关的子集(如食品类),再对该子集进行重要性投票,可获得用户相关信息的无冲突表达。显著性投票方法能够体现空间目标的重要性关系,不同显著等级的目标在地图缩放层次中渐进累加,符合信息可视化与空间数据多尺度建模的一般规律[12, 21],并可进一步将结果存储于层次结构用于提高效率或渐进式传输目的。扩展方法可提高Web制图的图面利用率,其中多级符号叠加方法符合视觉层次理论,在同一尺度区分专题符号的语义层次,增加可视化的信息获取效率。进一步的研究将开展定量用户调查,考查该方法的可用性、易用性,为Web地图设计提供依据,并在地图认知理论方面开展相关研究。
| [1] | ROICK O, HEUSER S. Location Based Social Networks:Definition, Current State of the Art and Research Agenda[J]. Transactions in GIS , 2013, 17 (5) : 763 –784. |
| [2] | FIELD K, O'BRIEN J. Cartobiography:Experiments in Using and Organising the Spatial Context of Micro-blogging[J]. Transactions in GIS , 2010, 14 (S1) : 5 –23. |
| [3] | KORPI J, AHONEN-RAINIO P. Clutter Reduction Methods for Point Symbols in Map Mashups[J]. The Cartographic Journal , 2013, 50 (3) : 257 –265. DOI:10.1179/1743277413Y.0000000065 |
| [4] | ELLIS G, DIX A. A Taxonomy of Clutter Reduction for Information Visualisation[J]. IEEE Transactions on Visualization and Computer Graphics , 2007, 13 (6) : 1216 –1223. |
| [5] | 艾廷华, 刘耀林. 保持空间分布特征的群点化简方法[J]. 测绘学报 , 2002, 31 (2) : 175–181. AI Tinghua, LIU Yaolin. A Method of Point Cluster Simplification with Spatial Distribution Properties Preserved[J]. Acta Geodaetica et Cartographica Sinica , 2002, 31 (2) : 175 –181. |
| [6] | 蔡永香, 郭庆胜. 基于Kohonen网络的点群综合研究[J]. 武汉大学学报(信息科学版) , 2007, 32 (7) : 626–629. CAI Yongxiang, GUO Qingsheng. Points Group Generalization Based on Konhonen Net[J]. Geomatics and Information Science of Wuhan University , 2007, 32 (7) : 626 –629. |
| [7] | DE BERG M, BOSE P, CHEONG O, et al. On Simplifying Dot Maps[J]. Computational Geometry , 2004, 27 (1) : 43 –62. DOI:10.1016/j.comgeo.2003.07.005 |
| [8] | 邓红艳, 武芳, 钱海忠, 等. 基于遗传算法的点群目标选取模型[J]. 中国图象图形学报 , 2003, 8 (8) : 970–976. DENG Hongyan, WU Fang, QIAN Haizhong, et al. A Model of Point Cluster Selection Based on Genetic Algorithms[J]. Journal of Image and Graphics , 2003, 8 (8) : 970 –976. |
| [9] | TÖPFER F, PILLEWIZER W. The Principles of Selection[J]. The Cartographic Journal , 1966, 3 (1) : 10 –16. DOI:10.1179/caj.1966.3.1.10 |
| [10] | BEEN K, NÖLLENBURG M, POON S H, et al. Optimizing Active Ranges for Consistent Dynamic Map Labeling[J]. Computational Geometry , 2010, 43 (3) : 312 –328. DOI:10.1016/j.comgeo.2009.03.006 |
| [11] | SCHWARTGES N, ALLERKAMP D, HAUNERT J, et al.Optimizing Active Ranges for Point Selection in Dynamic Maps[C]//Proceedings of the 16th ICA Generalisation Workshop (ICAGW'13).Dresden:Bib Sonomy, 2013. |
| [12] | 艾廷华, 成建国. 对空间数据多尺度表达有关问题的思考[J]. 武汉大学学报(信息科学版) , 2005, 30 (5) : 377–382. AI Tinghua, CHENG Jianguo. Key Issues of Multi-scale Representation of Spatial Data[J]. Geomatics and Information Science of Wuhan University , 2005, 30 (5) : 377 –382. |
| [13] | VAN OOSTEROM, P. Variable-scale Topological Data Structures Suitable for Progressive Data Transfer:The Gap-face Tree and Gap-edge Forest[J]. Cartography and Geographic Information Science , 2005, 32 (4) : 331 –346. DOI:10.1559/152304005775194782 |
| [14] | NUTANONG S, ADELFIO M D, SAMET H.Multiresolution Select-distinct Queries on Large Geographic Point Sets[C]//Proceedings of the 20th International Conference on Advances in Geographic Information Systems.New York, NY:ACM, 2012:159-168. http://cn.bing.com/academic/profile?id=2069779497&encoded=0&v=paper_preview&mkt=zh-cn |
| [15] | SARMA A D, LEE H, GONZALEZ H, et al.Efficient Spatial Sampling of Large Geographical Tables[C]//Proceedings of the 2012 ACM SIGMOD International Conference on Management of Data.New York, NY:ACM, 2012:193-204. http://cn.bing.com/academic/profile?id=2094174879&encoded=0&v=paper_preview&mkt=zh-cn |
| [16] | BEREUTER P, WEIBEL R. Real-time Generalization of Point Data in Mobile and Web Mapping Using Quadtrees[J]. Cartography and Geographic Information Science , 2013, 40 (4) : 271 –281. DOI:10.1080/15230406.2013.779779 |
| [17] | KOVANEN J, SARJAKOSKI L T. Sequential Displacement and Grouping of Point Symbols in a Mobile Context[J]. Journal of Location Based Services , 2013, 7 (2) : 79 –97. DOI:10.1080/17489725.2013.764024 |
| [18] | 杨敏, 艾廷华, 卢威, 等. 自发地理信息兴趣点数据在线综合与多尺度可视化方法[J]. 测绘学报 , 2015, 44 (2) : 228–234. YANG Min, AI Tinghua, LU Wei, et al. A Real-time Generalization and Multi-scale Visualization Method for POI Data in Volunteered Geographic Information[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (2) : 228 –234. DOI:10.11947/j.AGCS.2015.20130564 |
| [19] | HARRIE L, SARJAKOSKI T, LEHTO L. A Mapping Function for Variable-scale Maps in Small-display Cartography[J]. Journal of Geospatial Engineering , 2002, 4 (2) : 111 –123. |
| [20] | HAUNERT J H, SERING L. Drawing Road Networks with Focus Regions[J]. IEEE Transactions on Visualization and Computer Graphics , 2011, 17 (12) : 2555 –2562. DOI:10.1109/TVCG.2011.191 |
| [21] | SHNEIDERMAN B.The Eyes Have It:A Task by Data Type Taxonomy for Information Visualizations[C]//Proceedings of the IEEE Symposium on Visual Languages.Boulder, CO:IEEE, 1996:336-343. |


