高光谱成像是遥感技术的研究热点,被广泛应用于资源探索、矿物识别和环境监测等诸多领域[1-2]。高光谱影像最主要的特点是图谱合一[3],在获取地面图像空间信息的同时,得到每个地物的连续光谱信息,在地物的精细识别与分类中具有很大的优势[4]。然而,光谱波段数的增多在增强不同类别数据差异性的同时,也带来了“维数灾难”问题[5]。因此,如何减少数据维数是实现高光谱影像地物有效分类的关键。
目前,学者们已经提出了一系列的有关高光谱数据的维数简约方法。如主成分分析(principal component analysis,PCA)[6]和线性判别分析(linear discriminant analysis,LDA)[7],它们都是假设高光谱数据满足全局线性的条件,通过不同的判别准则以寻找最优线性模型,但无法揭示出高光谱数据的非线性结构。为此,学者们提出了“流形学习”的概念[8-9],其代表性方法有局部线性嵌入(local linear embedding,LLE)、等距离映射(isometric feature mapping,ISOMAP)和拉普拉斯特征映射(Laplacian eigenmaps,LE)等,这些算法较好地揭示了蕴含在高维空间中的低维流形结构,但都属于非线性降维算法,只在训练样本上有定义,不能学习处理新样本。针对此问题,文献[10—11]分别提出了邻域保持嵌入(neighborhood preserving embedding,NPE)和局部保持投影(locality preserving projection,LPP),这些方法能够快速地处理新样本,但仅利用了影像中的光谱信息,忽略了不同像元在空间位置上的相互关系。
除光谱信息外,高光谱影像中也包含十分丰富的空间信息。从数据本身来看,高光谱数据并不仅仅是由一些相互独立且无序排列的光谱特征向量组成,这些向量在空间位置上是具有一定联系的,空间上距离很近的像元在很大概率上属于同类地物,即地物分布的空间一致性特点[12-14];从图像分布来看,高光谱影像中的同类地物也往往呈现集中性分布或块状分布[15]。因此,为弥补仅利用光谱信息不能有效全面地表征高光谱数据的不足,研究人员开始将影像的空间信息融入到特征提取或分类器设计中。文献[16]在对高光谱影像进行地物分类时,先对数据进行预处理,得到空-谱特征,然后与稀疏表示相结合,有效地解决了影像中的冗余问题。文献[17]提出了一种基于空间一致性的邻域保留嵌入(spatial coherence-neighborhood preserving embedding,SC-NPE)特征提取算法,该算法通过在每个像元周围选取环块,利用环块区域来替代单一像元进行近邻选取,较好地克服了同类地物中差异性较大的噪点的影响,在高光谱影像的地物识别中具有较好的分类效果。
结合高光谱影像的物理特性,本文提出了一种空-谱协同嵌入(spatial-spectral coordination embedding,SSCE)降维算法和空-谱协同最近邻(spatial-spectral coordination nearest neighbor,SSCNN)分类器。该方法通过数据间的空-谱协同距离(spatial-spectral coordination distance,SSCD)度量近邻,并在低维嵌入中融入空间近邻点的光谱信息,最后使用SSCNN分类器分类。该算法在降维过程中综合考虑了高光谱数据中的流形结构以及像元间的空间位置关系,较好地挖掘出数据中的低维嵌入特征。在PaviaU和Salinas高光谱数据集上验证了本文方法的有效性。
1 本文算法 1.1 基于空-谱协同距离的相似性度量算法在高光谱影像中,对于某一特定像元xi(pi, qi),其中pi和qi分别为xi在影像中的行和列,它与其空间位置上相邻的像元不仅是频谱相关的,而且是空间相关的,它们在很大程度上是由相同的地物组成,且距离越近,属于同类点的概率就越大。基于此,本文提出一种新的相似性度量方式并将其应用于流形降维和最近邻分类器。
假设以像元xi为中心的大小为w×w的窗口区域为Ω(xi),其中w为正奇数,Ω(xi)称为近邻空间,其定义为
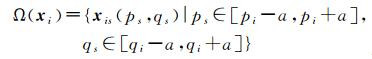 (1)
(1)
式中,a=(w-1)/2;xis(ps, qs)为近邻空间Ω(xi)中的第s个像元;Ω(xi)中共包含w2个像元。对于位于影像边缘位置的像元,由于近邻空间区域不完整,在建立边缘点的近邻空间时,对于缺失的部分使用该像元自身进行填补。
考虑到高光谱影像的空间一致性特点,本算法利用近邻空间Ω(xi)来替代单一像元参与度量。对于影像中的任意两像元xi和xj,其对应的近邻空间分别为Ω(xi)和Ω(xj),定义两者的空-谱协同距离为
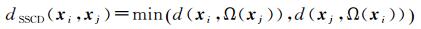 (2)
(2)
式中,d(xi, Ω(xj))为像元xi到以像元xj为中心的近邻空间Ω(xj)的距离,其定义为
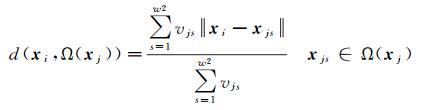 (3)
(3)
式中,vjs表示近邻空间Ω(xj)中任一像元xjs到中心像元xj的权重,采用RBF核函数进行计算,即vjs=exp{-||xj-xjs||2/2σ2},σ为函数宽度,在试验中设置为0.1。该权重的物理意义为:光谱曲线差异性小的像元间的影响程度越大,反之,差异性大的像元间的影响程度越小。此外,当近邻空间中存在与中心像元差别较大的点时,由于该权重的存在,新的度量方式仍然可以较好地表示不同像元间的差异性。
由式(2)和式(3)可以看出,空-谱协同距离有效地利用了高光谱影像中的空间信息,弥补了传统度量方法仅采用单一像元的不足,通过引入空间近邻点的光谱信息参与度量,能更为有效地增大同类地物的相似性和异类地物的差异性,提高了同类地物被选为近邻的概率,改善分类效果。图 1为该相似性度量算法的示意图,其中近邻空间大小为3×3,每一个正方形格子代表一个像元。
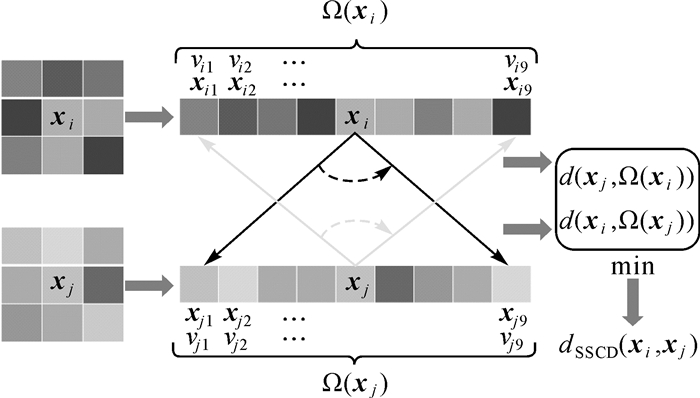
|
| 图 1 高光谱影像中的空-谱协同距离(w=3) Fig. 1 Spatial-spectral coordination distance in hyperspectral image (w=3) |
1.2 SSCE算法
假设含有N个D维数据的高光谱数据集为X={x1, x2, …, xN},其中xi(i=1, 2, …, N)∈RD,对应的低维嵌入为Y={y1, y2, …, yN},yi∈Rd,且d≪D。
结合高光谱影像的空间一致性特点和图嵌入理论[18],本文提出了一种融合空间信息与光谱信息的空-谱协同嵌入(SSCE)算法。该算法采用空-谱协同距离来替代单一像元进行近邻选取,构建空-谱近邻关系图,并在边权值设置阶段进一步利用影像中的空间信息,增大空间近邻点的权重以提升同类数据间的聚集性,实现维数简约。SSCE算法在保持数据间局部邻域关系的同时,又结合了影像的空间信息,使所提取的鉴别特征更为有效,改善地物分类。
SSCE算法的主要步骤如下:
1.2.1 构建空-谱近邻关系图G在高维空间中由式(2)计算每个数据点xi与其他点的空-谱协同距离,选出最近的k个点。若xj为其近邻,则在两者之间设置一条边,否则无边连接。
1.2.2 设置边权值矩阵W在空-谱近邻关系图G中,若xi与xj之间有边连接,则设置边权值为wij,若两者之间无边连接,则边权值设置为0。此外,为进一步挖掘出影像中的空间信息,将近邻空间Ω引入到边权值设置中,当xi与xj之间有边连接且xi∈Ω(xj)或xj∈Ω(xi)时,增大两者之间的权值。点xi与xj间的边权值wij设置为
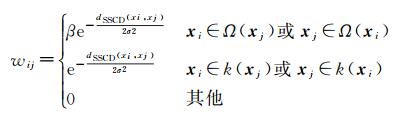 (4)
(4)
式中,k(xi)表示点xi的k个近邻点;β为大于1的常数,用于增强空间近邻点对分类的贡献;e为自然常数。
1.2.3 计算投影矩阵A将数据从高维空间投影到低维空间的过程中,保持数据间的局部邻域关系不变,构建目标函数
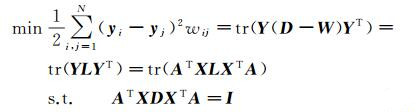 (5)
(5)
式中,W=[wij]N×N为边权值矩阵;D为对角矩阵,且Dii=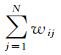
根据约束条件,对式(5)采用拉格朗日乘子法求解可得
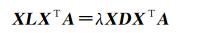 (6)
(6)
求解式(6)的广义特征值和特征向量,可得投影矩阵的最优解为A=[a1, a2, …, ad],其中ai(i=1, 2, …, d)为前d个特征值及其对应的特征向量。
1.3 空-谱协同最近邻分类器分类的另一个关键性问题就是设计合适的分类器。最近邻分类法(K nearest neighbor,KNN)是一种常用地物分类方法,通过寻找训练样本集中的K个已知近邻来判断测试样本的类别。但在近邻选取过程中,仅通过计算单一像元间的欧氏距离进行判别,并没有考虑影像中的空间信息。因此,本文提出了一种空-谱协同最近邻(SSCNN)分类器。该分类器以空-谱协同距离替代欧氏距离进行数据间的相似性度量,得到与测试样本距离最近的K个已知训练样本,并根据训练样本的类别信息计算测试样本属于各类别的权重,将其归为权值最大的一类。由于在分类过程中用到了训练样本的类别信息,因此,SSCNN属于有监督的分类算法,其计算公式如下
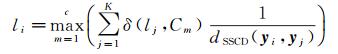 (7)
(7)
式中,li表示测试样本yi的类别;c为高光谱数据中的类别个数;lj为训练样本yj的类别;δ(lj, Cm)为Kronecker delta函数,当lj=Cm成立时,其取值为1,否则取值为0。
2 试验结果及分析 2.1 试验数据集试验中使用具有代表性的PaviaU和Salinas高光谱数据集[19-20]来检验本文算法的分类性能。
(1) PaviaU数据集:该数据集是在2002年由ROSIS传感器获取的位于帕维亚大学区域的高光谱影像。影像的大小为610×340像素,空间分辨率为1.3m,共包含115个光谱波段(波长范围为0.43~0.86μm),去除其中吸水严重的12个波段,将剩余的103个波段用于试验研究。PaviaU数据集中共包含9类地物信息,其假彩色图和真实地物图如图 2所示。

|
| 图 2 PaviaU高光谱影像 Fig. 2 PaviaU hyperspectral image |
(2) Salinas数据集:该数据集是由AVIRIS传感器获取的位于美国加利福尼亚州的Salinas Valley区域的高光谱影像,其大小为512×217像素,含有16类地物信息,空间分辨率为3.7m,去除吸水严重和受噪声影响较大的20(108—112,154—167,224)个波段,将剩余的204个波段用于试验研究。其假彩色图和真实地物信息如图 3所示。

|
| 图 3 Salinas高光谱影像 Fig. 3 Salinas hyperspectral image |
2.2 试验设置
为评估本文算法的分类性能,试验中选取了PCA、LDA、NPE、LPP和SC-NPE算法作为对比,并分别采用最近邻(KNN)分类器和空-谱协同最近邻(SSCNN)分类器两种不同的分类方法进行分类,以验证SSCNN的有效性。本文使用总体分类精度、平均分类精度和Kappa系数作为评价指标。为提高试验的精确度和可靠性,每种试验条件下都进行10次重复试验,每次随机选取一定数量的训练样本,其余为测试样本,将10次试验求取平均值作为最终结果,其中,最优值采用粗体显示。
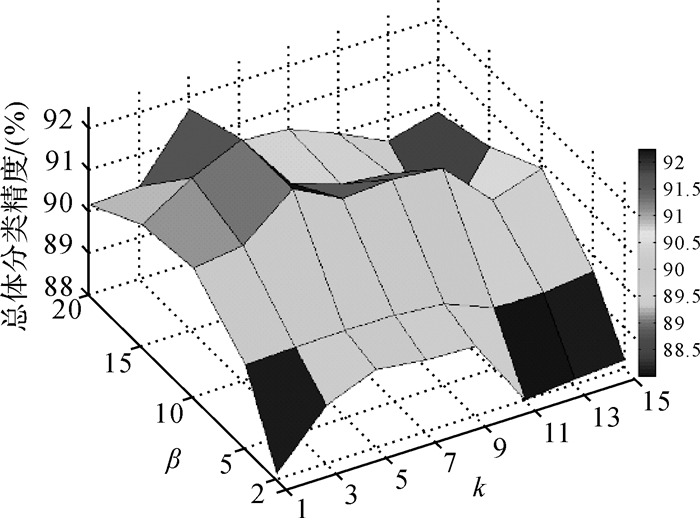
参数设置如下:为研究邻域个数k和参数β的变化对SSCE的影响,文中进行了总体分类精度随两参数值变化的试验,图 4为PaviaU数据集中SSCE在不用邻域个数k和参数β下的总体分类精度。为研究近邻个数K对SSCNN的影响,图 5给出了不同K值下算法的总体分类精度。
|
| 图 4 SSCE在不同k和β下的总体分类精度 Fig. 4 Overall accuracy of SSCE with different k and β |

|
| 图 5 SSCNN在不同K值下的总体分类精度 Fig. 5 Overall accuracy of SSCNN with different K |
由图 4可知,对于PaviaU数据集而言,当k和β分别取5和10时,算法分类精度最高;对于其他取值,分类精度出现起伏,这是由于随着k和β的不断增加,数据间的拟合更加准确,空间近邻点的作用也更为突出,但当两者取值过大时,则会导致过拟合现象,使得算法分类精度降低。对于Salinas数据集,本文也进行了相同的试验分析,设置两参数为:k=5,β=10。由图 5可知,随着K值的增加,SSCNN的分类精度不断降低,且当K=1时,分类效果最为理想。
此外,设置SSCE的窗口大小为5×5,这是由于当w=5时,既可以得到较好的分类效果又保证了算法的运行效率。试验中,各算法的特征提取维数为30,LDA提取c-1维。
2.3 PaviaU试验结果及分析试验中,从PaviaU数据集的每类地物中随机选取50、100、150和200个点为训练样本,剩余为测试样本。表 1为不同算法在不同训练样本数、不同分类器下的总体分类精度、标准差和Kappa系数。
| 分类器 | 算法 | 50 | 100 | 150 | 200 | |||||||||||
| 总体分类 精度/(%) |
标准差 /(%) |
Kappa 系数 |
总体分类 精度/(%) |
标准差 /(%) |
Kappa 系数 |
总体分类 精度/(%) |
标准差 /(%) |
Kappa 系数 |
总体分类 精度/(%) |
标准差 /(%) |
Kappa 系数 |
|||||
| KNN | original | 73.64 | 0.20 | 0.6642 | 76.06 | 0.11 | 0.6937 | 77.78 | 0.07 | 0.7132 | 79.05 | 0.15 | 0.7281 | |||
| PCA | 73.62 | 0.20 | 0.6640 | 76.05 | 0.08 | 0.6936 | 77.73 | 0.12 | 0.7126 | 79.03 | 0.12 | 0.7279 | ||||
| LDA | 73.40 | 0.17 | 0.6604 | 79.51 | 0.11 | 0.7351 | 81.51 | 0.14 | 0.7593 | 82.97 | 0.08 | 0.7768 | ||||
| NPE | 72.06 | 0.26 | 0.6458 | 75.97 | 0.12 | 0.6933 | 78.13 | 0.17 | 0.7182 | 80.00 | 0.16 | 0.7405 | ||||
| LPP | 74.69 | 0.23 | 0.6776 | 77.88 | 0.13 | 0.7163 | 80.01 | 0.15 | 0.7415 | 81.19 | 0.13 | 0.7553 | ||||
| SC-NPE | 72.82 | 0.22 | 0.6545 | 77.31 | 0.14 | 0.7089 | 79.39 | 0.14 | 0.7336 | 82.12 | 0.13 | 0.7664 | ||||
| SSCE | 76.39 | 0.20 | 0.6980 | 81.58 | 0.13 | 0.7621 | 84.81 | 0.11 | 0.8015 | 86.29 | 0.12 | 0.8196 | ||||
| SSCNN | original | 76.74 | 0.18 | 0.7003 | 79.57 | 0.10 | 0.7341 | 81.36 | 0.06 | 0.7549 | 82.66 | 0.11 | 0.7706 | |||
| PCA | 76.73 | 0.19 | 0.7002 | 79.53 | 0.09 | 0.7337 | 81.31 | 0.13 | 0.7542 | 82.61 | 0.10 | 0.7701 | ||||
| LDA | 78.92 | 0.27 | 0.7291 | 84.14 | 0.12 | 0.7935 | 85.33 | 0.19 | 0.8081 | 86.76 | 0.12 | 0.8253 | ||||
| NPE | 75.29 | 0.26 | 0.6833 | 79.09 | 0.12 | 0.7290 | 81.09 | 0.20 | 0.7519 | 82.93 | 0.16 | 0.7750 | ||||
| LPP | 78.18 | 0.21 | 0.7197 | 80.75 | 0.12 | 0.7501 | 82.85 | 0.17 | 0.7750 | 83.74 | 0.11 | 0.7854 | ||||
| SC-NPE | 75.91 | 0.26 | 0.6906 | 80.29 | 0.14 | 0.7436 | 82.54 | 0.15 | 0.7707 | 84.95 | 0.12 | 0.8005 | ||||
| SSCE | 79.81 | 0.19 | 0.7397 | 84.34 | 0.11 | 0.7959 | 87.20 | 0.11 | 0.8311 | 88.45 | 0.13 | 0.8467 | ||||
从表 1可以看出,随着训练样本数量的不断增加,各算法的分类精度和Kappa系数均不断提高,由于训练样本的数量越多,数据中所能提供的具有代表性的先验信息就越多,鉴别性能更为突出,进而提高分类精度。SC-NPE和SSCE算法分别比NPE和LPP算法的分类效果好,这是因为空-谱联合分类方法较好地利用了影像中的空间信息,提高了算法的鉴别能力,更加有利于地物分类。其中,SSCE算法的分类效果最好,由于SSCE算法不仅具有流形降维的优点,在降维过程中较好地保持了数据间的近邻关系;同时,在近邻选取过程中采用空-谱协同距离进行度量,近邻选取更加稳定,并通过增大空间近邻点的权重来提取鉴别信息,改善地物分类。对于各降维算法,在各种训练样本数下,SSCNN的分类效果均比KNN好,通过近邻空间来替代单一像元进行分类,有效地克服了同类地物中差异性较大的孤立点或噪点的影响,增大了这些点在分类过程中正确归类的概率。
为进一步揭示SSCE算法的分类性能,对数据集中的每一类地物进行分类试验。试验中每类地物随机选取5%的样本作为训练样本集,其余为测试样本,并采用SSCNN进行分类,表 2为不同算法下各类地物的分类精度、总体分类精度、平均分类精度和Kappa系数。
| (%) | |||||||||
| 类别 | 训练样本 | 测试样本 | original | PCA | LDA | NPE | LPP | SC-NPE | SSCE |
| Asphalt | 332 | 6299 | 83.25 | 83.27 | 88.14 | 80.68 | 83.68 | 84.36 | 87.33 |
| Meadows | 932 | 17717 | 97.00 | 96.95 | 97.21 | 96.74 | 96.67 | 97.92 | 98.80 |
| Gravel | 105 | 1994 | 75.08 | 74.92 | 67.20 | 66.65 | 74.82 | 72.52 | 82.25 |
| Trees | 153 | 2911 | 79.39 | 79.53 | 83.72 | 78.56 | 80.45 | 82.31 | 83.89 |
| Metal Sheets | 67 | 1278 | 98.83 | 98.83 | 99.84 | 98.59 | 99.30 | 99.30 | 99.37 |
| Soil | 251 | 4778 | 54.08 | 54.00 | 67.31 | 48.77 | 52.68 | 61.66 | 73.29 |
| Bitumen | 67 | 1263 | 87.02 | 86.70 | 79.65 | 85.11 | 85.91 | 89.79 | 90.42 |
| Bricks | 184 | 3498 | 78.50 | 78.22 | 83.99 | 77.04 | 77.99 | 81.39 | 81.65 |
| Shadows | 47 | 900 | 100 | 100 | 99.89 | 99.89 | 100 | 100 | 100 |
| 总体分类精度 | 85.71 | 85.65 | 88.31 | 83.90 | 85.46 | 87.61 | 90.45 | ||
| 平均分类精度 | 83.68 | 83.60 | 85.22 | 81.34 | 83.50 | 85.47 | 88.56 | ||
| Kappa系数 | 0.8064 | 0.8057 | 0.8427 | 0.7816 | 0.8032 | 0.8326 | 0.8716 | ||
由表 2可知,在不同训练样本数目下,采用SSCE进行分类,大多数地物的分类效果都有明显提升,其中,Gravel和Soil这两类地物改善效果尤为突出。同时,SSCE算法的各项评价指标比其他算法都好,这是由于影像中空间信息的利用更有效地表征了高光谱数据的内嵌结构,提取的鉴别特征更加有利于地物分类。
图 6为一次随机试验中各算法的分类结果图及其对应的总体分类精度。从图 6中可以看出,SSCE算法与其他算法相比,得到的分类图大部分区域更加平滑,总体看上去错分点更少,尤其是在Soil的分布区域表现更为突出,且总体分类精度比其他算法更高,可见利用高光谱影像空间一致性特点提出的SSCE算法具有一定的可行性。

|
| 图 6 各算法在PaviaU数据集上的分类结果图及其对应的总体分类精度 Fig. 6 Classification maps and overall accuracy with different methods on PaviaU data set |
2.4 Salinas试验结果及分析
在Salinas数据集中,分别从每类地物中随机抽取40、60、80和100个样本用于训练,其余样本用于测试,表 3为不同算法在不同训练样本数、不同分类器下的总体分类精度、标准差和Kappa系数。
| 分类器 | 算法 | 40 | 60 | 80 | 100 | |||||||||||
| 总体分类 精度/(%) |
标准差 /(%) |
Kappa 系数 |
总体分类 精度/(%) |
标准差 /(%) |
Kappa 系数 |
总体分类 精度/(%) |
标准差 /(%) |
Kappa 系数 |
总体分类 精度/(%) |
标准差 /(%) |
Kappa 系数 |
|||||
| KNN | original | 83.54 | 0.22 | 0.8173 | 84.32 | 0.31 | 0.8260 | 84.96 | 0.24 | 0.8329 | 85.42 | 0.12 | 0.8380 | |||
| PCA | 83.54 | 0.21 | 0.8174 | 84.31 | 0.30 | 0.8258 | 84.94 | 0.24 | 0.8327 | 85.42 | 0.13 | 0.8379 | ||||
| LDA | 83.37 | 0.46 | 0.8154 | 86.53 | 0.24 | 0.8502 | 87.61 | 0.36 | 0.8623 | 87.91 | 0.22 | 0.8656 | ||||
| NPE | 83.76 | 0.37 | 0.8198 | 84.48 | 0.20 | 0.8277 | 85.09 | 0.42 | 0.8344 | 85.39 | 0.25 | 0.8376 | ||||
| LPP | 85.70 | 0.26 | 0.8411 | 85.99 | 0.35 | 0.8444 | 86.53 | 0.27 | 0.8503 | 86.79 | 0.13 | 0.8531 | ||||
| SC-NPE | 85.34 | 0.11 | 0.8352 | 86.37 | 0.17 | 0.8465 | 86.78 | 0.18 | 0.8509 | 87.49 | 0.25 | 0.8587 | ||||
| SSCE | 87.01 | 0.23 | 0.8556 | 87.95 | 0.21 | 0.8661 | 88.94 | 0.20 | 0.8769 | 89.10 | 0.11 | 0.8787 | ||||
| SSCNN | original | 84.82 | 0.25 | 0.8315 | 85.26 | 0.32 | 0.8362 | 85.54 | 0.22 | 0.8392 | 86.12 | 0.13 | 0.8442 | |||
| PCA | 84.82 | 0.25 | 0.8315 | 85.24 | 0.33 | 0.8360 | 85.54 | 0.21 | 0.8392 | 86.11 | 0.15 | 0.8440 | ||||
| LDA | 87.57 | 0.41 | 0.8620 | 88.07 | 0.15 | 0.8685 | 89.07 | 0.15 | 0.8785 | 89.80 | 0.14 | 0.8865 | ||||
| NPE | 85.06 | 0.64 | 0.8340 | 85.34 | 0.36 | 0.8371 | 85.52 | 0.19 | 0.8391 | 85.83 | 0.30 | 0.8426 | ||||
| LPP | 86.67 | 0.19 | 0.8518 | 87.01 | 0.10 | 0.8556 | 87.12 | 0.27 | 0.8567 | 87.26 | 0.41 | 0.8584 | ||||
| SC-NPE | 86.45 | 0.12 | 0.8474 | 86.97 | 0.14 | 0.8530 | 87.53 | 0.25 | 0.8592 | 87.77 | 0.17 | 0.8617 | ||||
| SSCE | 88.77 | 0.14 | 0.8752 | 89.70 | 0.18 | 0.8854 | 90.31 | 0.16 | 0.8921 | 90.75 | 0.20 | 0.8970 | ||||
由表 3可知,随着每类训练样本数量的增加,各算法的分类精度均不断提高,但在各种情况下,SSCE算法的分类效果总是优于其他算法,这是由于SSCE算法在构建数据间局部邻域结构的过程中既保持了流形降维的优点,又结合了影像的空间信息。同时,各算法采用SSCNN分类器的分类效果要优于KNN分类器,通过空-谱协同距离进行数据间的相似性度量,能有效降低同类地物中差异性较大的点的错分概率,进而提高各算法的分类精度。
为验证SSCE算法对每类地物的分类效果,从Salinas数据集的每类地物中随机抽取3%的样本作为训练样本,其余为测试样本,采用SSCNN分类器进行分类。表 4给出了各算法对每类地物的分类结果及其相应的评价指标,图 7为各算法的地物分类图。
| 类别 | 训练样本 | 测试样本 | original | PCA | LDA | NPE | LPP | SC-NPE | SSCE |
| Weeds_1 | 60 | 1989 | 97.49 | 97.38 | 99.79 | 97.23 | 97.59 | 98.99 | 99.44 |
| Weeds_2 | 112 | 3689 | 99.81 | 99.81 | 99.78 | 99.75 | 99.78 | 99.48 | 99.94 |
| Fallow | 59 | 1956 | 99.58 | 99.58 | 98.28 | 99.58 | 99.79 | 99.44 | 99.79 |
| Fallow_P | 42 | 1380 | 99.19 | 99.19 | 99.26 | 98.96 | 99.11 | 99.42 | 99.33 |
| Fallow_S | 80 | 2651 | 95.84 | 95.84 | 98.92 | 96.46 | 97.46 | 98.30 | 98.69 |
| Stubble | 119 | 3919 | 99.87 | 99.87 | 99.69 | 99.74 | 99.90 | 99.80 | 99.95 |
| Celery | 107 | 3543 | 98.93 | 98.93 | 99.97 | 98.91 | 98.91 | 98.76 | 99.45 |
| Grapes | 338 | 11158 | 75.13 | 75.08 | 76.90 | 74.66 | 75.82 | 75.59 | 82.44 |
| Soil | 186 | 6141 | 97.76 | 97.74 | 99.97 | 98.02 | 99.24 | 99.74 | 99.88 |
| Corn | 98 | 3245 | 86.67 | 86.67 | 96.32 | 86.19 | 88.49 | 90.94 | 94.69 |
| Lettuce_4wk | 32 | 1057 | 87.45 | 87.45 | 96.14 | 89.09 | 91.41 | 84.01 | 93.05 |
| Lettuce_5wk | 58 | 1908 | 99.95 | 99.95 | 99.73 | 99.95 | 99.95 | 100 | 100 |
| Lettuce_6wk | 27 | 906 | 97.08 | 97.08 | 98.99 | 97.08 | 97.08 | 98.45 | 97.86 |
| Lettuce_7wk | 32 | 1059 | 93.93 | 93.93 | 96.92 | 93.45 | 94.99 | 92.73 | 97.59 |
| Vinyard_U | 218 | 7195 | 57.05 | 56.79 | 64.31 | 55.13 | 58.60 | 66.67 | 70.82 |
| Vinyard_T | 54 | 1789 | 97.95 | 97.95 | 97.78 | 98.00 | 98.35 | 97.65 | 98.52 |
| 总体分类精度 | 87.07 | 87.02 | 89.75 | 86.75 | 87.90 | 89.01 | 91.67 | ||
| 平均分类精度 | 92.73 | 92.70 | 95.17 | 92.64 | 93.53 | 93.75 | 95.72 | ||
| Kappa系数 | 0.8560 | 0.8555 | 0.8859 | 0.8524 | 0.8652 | 0.8776 | 0.9072 |
由表 4可知,SSCE算法对大部分地物都具有较高的识别率,且其总体分类精度、平均分类精度和Kappa系数均优于其他算法,这表明在高光谱影像的地物分类过程中,SSCE算法能提取出更为有效的鉴别特征,增大同类地物间的聚集性,改善分类效果。同时,由图 7可以看出,SSCE算法的地物分类图中错分点更少,地物分布更加平滑,且相关性较大的地物的分类效果改善尤为突出,如Vinyard_U和Vinyard_T这两类地物,其分类精度在各算法中均为最高,进一步验证了本文算法的有效性。

|
| 图 7 各算法在Salinas数据集上的分类结果图及其对应的总体分类精度 Fig. 7 Classification maps and overall accuracy with different methods on Salinas data set |
3 结论
本文针对传统高光谱影像地物分类算法的不足,结合影像的空间一致性特点,提出了一种空-谱协同嵌入(SSCE)降维算法和空-谱协同最近邻(SSCNN)分类器。为实现更有效的近邻选取,首先提出了一种基于空-谱协同距离的相似性度量方式,提高了同类地物被选为近邻的概率,并在空-谱近邻关系图的构建过程中增大空间近邻点的权重以增强同类地物间的聚集性,提取鉴别特征。同时,在分类器设计阶段再次利用影像中的空间信息,进一步提高了算法的分类精度。在PaviaU和Salinas高光谱数据集上的试验结果表明,本文方法能取得更好的分类效果,其总体分类精度分别达到90.45%和91.67%,有效地改善了高光谱影像的地物分类。
但算法在设计过程中并未考虑高光谱影像的纹理信息,如何融入纹理信息以获取更好的分类效果,这将是下一步研究工作的重点。
| [1] | 田彦平, 陶超, 邹峥嵘, 等. 主动学习与图的半监督相结合的高光谱影像分类[J]. 测绘学报 , 2015, 44 (8) : 919–926. TIAN Yanping, TAO Chao, ZOU Zhengrong, et al. Semi-supervised Graph-based Hyperspectral Image Classification with Active Learning[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (8) : 919 –926. DOI:10.11947/j.AGCS.2015.20140221 |
| [2] | TANG Yuanyan, YUAN Haoliang, LI Luoqing. Manifold-based Sparse Representation for Hyperspectral Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (12) : 7606 –7618. DOI:10.1109/TGRS.2014.2315209 |
| [3] | PU Hanye, CHEN Zhao, WANG Bin, et al. A Novel Spatial-spectral Similarity Measure for Dimensionality Reduction and Classification of Hyperspectral Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (11) : 7008 –7022. DOI:10.1109/TGRS.2014.2306687 |
| [4] | 骆仁波, 皮佑国. 有监督的邻域保留嵌入的高光谱遥感影像特征提取[J]. 测绘学报 , 2014, 43 (5) : 508–513. LUO Renbo, PI Youguo. Supervised Neighborhood Preserving Embedding Feature Extraction of Hyperspectral Imagery[J]. Acta Geodaetica et Cartographica Sinica , 2014, 43 (5) : 508 –513. DOI:10.13485/j.cnki.11-2089.2014.0079 |
| [5] | 黄鸿, 曲焕鹏. 基于半监督稀疏鉴别嵌入的高光谱遥感影像分类[J]. 光学精密工程 , 2014, 22 (2) : 434–442. HUANG Hong, QU Huanpeng. Hyperspectral Remote Sensing Image Classification Based on SSDE[J]. Optics and Precision Engineering , 2014, 22 (2) : 434 –442. DOI:10.3788/OPE. |
| [6] | RODARMEL C, SHAN J. Principal Component Analysis for Hyperspectral Image Classification[J]. Surveying and Land Information Systems , 2002, 62 (2) : 115 –122. |
| [7] | BANDOS T V, BRUZZONE L, CAMPS-VALLS G. Classification of Hyperspectral Images with Regularized Linear Discriminant Analysis[J]. IEEE Transactions on Geoscience and Remote Sensing , 2009, 47 (3) : 862 –873. DOI:10.1109/TGRS.2008.2005729 |
| [8] | QIAN Shenen, CHEN Guanyi.A New Nonlinear Dimensionality Reduction Method with Application to Hyperspectral Image Analysis[C]//Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium.Barcelona:IEEE, 2007:270-273. |
| [9] | LUNGA D, PRASAD S, CRAWFORD M M, et al. Manifold-learning-based Feature Extraction for Classification of Hyperspectral Data:A Review of Advances in Manifold Learning[J]. IEEE Signal Processing Magazine , 2014, 31 (1) : 55 –66. DOI:10.1109/MSP.2013.2279894 |
| [10] | HUANG Ying, SUN Zhuo, WANG Cheng. Neighborhood Preserving Embedding Algorithm for Classification of Hyperspectral Imagery[J]. Advances in Information Sciences and Service Sciences , 2013, 5 (3) : 660 –667. DOI:10.4156/aiss |
| [11] | WANG Zhiyong, HE Binbin.Locality Perserving Projections Algorithm for Hyperspectral Image Dimensionality Reduction[C]//Proceedings of the 19th International Conference on Geoinformatics.Shanghai:IEEE, 2011:1-4. |
| [12] | FAUVEL M, TARABALKA Y, BENEDIKTSSON J A, et al. Advances in Spectral-spatial Classification of Hyperspectral Images[J]. Proceedings of the IEEE , 2013, 101 (3) : 652 –675. DOI:10.1109/JPROC.2012.2197589 |
| [13] | ZHOU Yicong, PENG Jiantao, CHEN C L P. Dimension Reduction Using Spatial and Spectral Regularized Local Discriminant Embedding for Hyperspectral Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing , 2015, 53 (2) : 1082 –1095. DOI:10.1109/TGRS.2014.2333539 |
| [14] | YUAN Haoliang, TANG Yuanyan, LU Yang, et al. Spectral-spatial Classification of Hyperspectral Image Based on Discriminant Analysis[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2014, 7 (6) : 2035 –2043. DOI:10.1109/JSTARS.2013.2290316 |
| [15] | TAN Kun, HU Jun, LI Jun, et al. A Novel Semi-supervised Hyperspectral Image Classification Approach Based on Spatial Neighborhood Information and Classifier Combination[J]. ISPRS Journal of Photogrammetry and Remote Sensing , 2015, 105 : 19 –29. DOI:10.1016/j.isprsjprs.2015.03.006 |
| [16] | 杨钊霞, 邹峥嵘, 陶超, 等. 空-谱信息与稀疏表示相结合的高光谱遥感影像分类[J]. 测绘学报 , 2015, 44 (7) : 775–781. YANG Zhaoxia, ZOU Zhengrong, TAO Chao, et al. Hyperspectral Image Classification Based on the Combination of Spatial-spectral Feature and Sparse Representation[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (7) : 775 –781. DOI:10.11947/j.AGCS.2015.20140207 |
| [17] | 魏峰, 何明一, 梅少辉. 空间一致性邻域保留嵌入的高光谱数据特征提取[J]. 红外与激光工程 , 2012, 41 (5) : 1249–1254. WEI Feng, HE Mingyi, MEI Shaohui. Hyperspectral Data Feature Extraction Using Spatial Coherence Based Neighborhood Preserving Embedding[J]. Infrared and Laser Engineering , 2012, 41 (5) : 1249 –1254. |
| [18] | YAN Shuicheng, XU Dong, ZHANG Benyu, et al. Graph Embedding and Extensions:A General Framework for Dimensionality Reduction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2007, 29 (1) : 40 –51. DOI:10.1109/TPAMI.2007.250598 |
| [19] | FAUVEL M, BENEDIKTSSON J A, CHANUSSOT J, et al. Spectral and Spatial Classification of Hyperspectral Data Using SVMs and Morphological Profiles[J]. IEEE Transactions on Geoscience and Remote Sensing , 2008, 46 (11) : 3804 –3814. DOI:10.1109/TGRS.2008.922034 |
| [20] | KANG Xudong, LI Shutao, BENEDIKTSSON J A. Feature Extraction of Hyperspectral Images with Image Fusion and Recursive Filtering[J]. IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (6) : 3742 –3752. DOI:10.1109/TGRS.2013.2275613 |



