2. 武汉大学动力与机械学院,湖北 武汉430072
2. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China
侧扫声呐(side scan sonar, SSS)图像在沉船、溺水人体、海底热液喷口等水下目标的探测和识别方面具有重要的应用价值[1-3],而图像分割是上述应用的基础,高效、准确的分割算法可确保目标识别的效率和精度。受复杂海洋环境噪声影响,现有算法尚难以满足上述要求,目前SSS图像分割相对困难[4-12]。在诸多分割算法中,基于水平集可实现SSS图像分割,但需选择恰当的初始水平集函数,否则分割精度不高[4-5];基于模糊聚类的SSS图像分割具有较好的抗噪性和准确性,但分割效率较低[6-7];分形理论用于SSS图像分割准确性较高,但分形维特征计算效率偏低[8];当SSS图像目标区、阴影区和海底混响区分别服从简单正比例、威布尔和Gamma分布模型时,利用空间邻域和空间分层马尔可夫随机场(Markov random filed, MRF)可实现上述类别分割[9],MRF图像分割的核心是参数估计,而复杂海洋环境决定了很难用具体分布模型描述SSS图像不同区域和实现普适性的目标分割[10];基于灰度、纹理、形状等特征可实现图像分割[11],但存在多种特征计算的耗时问题;阈值法因具有直观、简单等优点被广泛用于图像分割,如传统二维OTSU法(OTSU2),以最大类间方差为准则,通过穷举法计算分割阈值,实现目标分割[12]。但由于采用了穷举法计算分割阈值,运算效率较低;此外,受拖鱼状态和海洋环境综合影响,OTSU2以原始图像及其邻域均值计算的灰度共生矩阵难以较好地呈现SSS图像的精细纹理;且基于最大类间方差原则难以获得准确的分割阈值[12],导致OTSU2法用于SSS图像分割准确性偏低。上述方法在可靠性和效率上难以兼顾,因此需寻找较优的SSS图像分割算法。
文献[13]从量子行为的角度提出了量子粒子群(quantum-behaved particle swarm optimization, QPSO)算法,QPSO是一种新的智能寻优算法[13],为OTSU2法分割阈值向量的快速计算提供了新的方法。中性集(neutrosophic set, NS)是一种模糊集,为解决不确定性问题提供了一种强大的工具[14],国内外已有学者将其应用于图像分割等领域,如文献[14-16]分别基于NS研究了SAR图像、彩色图像及遥感图像的分割,取得了较好的分割效果。以上两种方法为高噪声污染下的SSS图像模糊区域的快速和准确分割提供了新的思路,为此本文提出了一种结合中性集合(NS)与量子粒子群(QPSO)算法的SSS图像分割方法,以期克服现有方法不足,实现复杂海洋环境噪声影响下SSS图像的高效、准确分割。
1 声呐图像的中性集运算声呐图像转换到中性集由真(T)、不确定(I)和假(F) 3个子集组成。在传统集合中,I=0,T=0(F=1)或T=1(F=0);模糊集合中,I=0,T、F中元素的取值范围均为[0, 1];中性集合中,T、I、F中元素的取值范围均为[0, 1]。若用NS表示中性集,则NS={T(i, j), I(i, j), F(i, j)},T、I、F可由式(1)-式(3)计算[14-16]
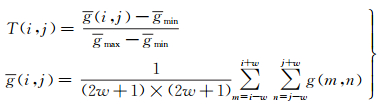 (1)
(1)
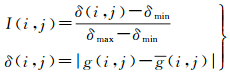 (2)
(2)
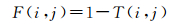 (3)
(3)
式(1)-式(3)中,g(i, j)为原始图像g(i, j)的局域均值,i、j表示原始图像的行列号,m、n为局部邻域内的行列号,当w=1时为3×3邻域,计算时可对图像边缘像素不作处理;gmax、gmin为g(i, j)的最大、最小值;δ(i, j)为g(i, j)与g(i, j)差值的绝对值;δmax、 δmin为δ(i, j)的最大、最小值。
I的分布及其熵值受邻域大小影响较大,常用β增强降低计算过程中的不确定性,计算如下
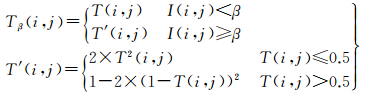 (4)
(4)
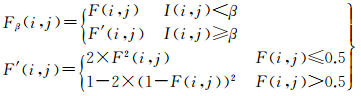 (5)
(5)
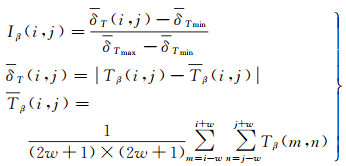 (6)
(6)
式(4)-式(6)中,β可取I集合取值范围的任意值,传统计算时β取常数0.85;Tβ(i, j)为Tβ(i, j)的局域均值,当w=1时为3×3邻域;δT(i, j)为Tβ(i, j)与Tβ(i, j)的差值的绝对值;δTmax、δTmin为δT(i, j)的最大、最小值。
式(4)、式(5)中,β值的选取对后续分割影响较大,可采用式(7)自适应确定[14-15]
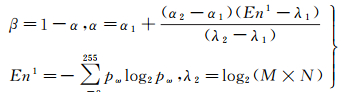 (7)
(7)
式中,M、N为图像高度和宽度;α1、α2为α取值区间内的任意值且有α2 > α1;En1为原始图像的一维熵,pω表示原始图像中灰度值为ω的像素所占的比例;λ1为小于En1的数值;由于I集合中元素的取值范围为[0, 1],α、β的取值范围也应为[0, 1];根据文献[14-15],α1、α2和λ1分别取经验值0.01、0.1和0。
通过β增强后,Tβ集对比度增强且滤除了图像部分噪声,Iβ集包含了SSS图像纹理及目标边缘信息。SSS图像受噪声污染严重,仅基于原始图像和其邻域均值构建灰度共生矩阵难以反映图像的精细纹理;鉴于Tβ、Iβ集的特点,可基于Tβ、Iβ集合构建图像灰度共生矩阵,以期反映精细的SSS图像纹理,提高后续SSS图像分割精度。
2 量子粒子群算法量子粒子群(QPSO)算法以Delta势阱为基础,认为粒子具有量子行为,在寻优过程中,假设第k个粒子在其最优位置Гk=(Гk1, Гk2 , …, ГkD)为中心的Delta势阱中移动,D为粒子维数。Гkd (d∈[1, D])的局部最优位置可按式(8)迭代计算
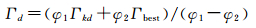 (8)
(8)
式中,φ1和φ2为[0, 1]上任意随机数;Гbest为所有粒子中的最优位置(拥有最佳适应度值);Гkd为第k个粒子的先前的局部最优位置;Гd为第k个粒子进化后的局部最优位置。
在Delta势阱中,量子状态方程为
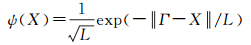 (9)
(9)
式中,X为粒子位置,参数L由势阱的能量强度决定。为了计算粒子的适应度值,需知道粒子的精确位置,而式(9)只给出粒子的概率密度函数Q(X)=|ψ(X)|2=exp(-2‖Г-X‖/L)/L,因此必须使用一种方法来估算粒子位置。若选择Monte Carlo随机模拟,设η是(0, 1/L)上的随机数,即η=u/L,u=rand(0, 1),令η=Q(X),可解得粒子X的位置方程为
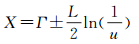 (10)
(10)
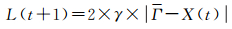 (11)
(11)
式中,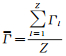
根据式(8)、式(10)和式(11),最后可得QPSO算法的进化方程,即粒子位置的进化方程
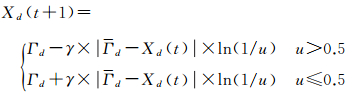 (12)
(12)
式中,γ为收缩扩张系数,可用式(13)计算
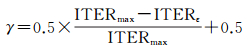 (13)
(13)
式中,ITERmax为最大的迭代次数;ITERε表示第ε次迭代[13, 17-18]。
量子系统是一个复杂的非线性系统,符合状态叠加原理,比线性系统具有更多的状态;系统中的粒子没有确定的轨迹,能够以某一确定的概率出现在搜索空间中的任意位置,提高搜索效率;且QPSO算法中,粒子的状态只有一个控制参数γ,易于控制和实现[17]。
QPSO用于图像分割时,借助基于中性Tβ、Iβ集合构建的灰度共生矩阵,将二维最大熵作为阈值选取准则(即QPSO算法的适应度函数,用来计算粒子进化过程中的Гbest,进而获得所有粒子中的最优位置)。此时式(10)中的X可视为二维分割阈值向量(粒子维数D=2),若为灰度图像,可将粒子的初始位置设置为阈值向量区间[0, 255]内的随机值。因此可基于QPSO计算二维分割阈值向量,解决穷举法计算二维分割阈值向量效率低的缺陷,提高SSS图像分割的效率。
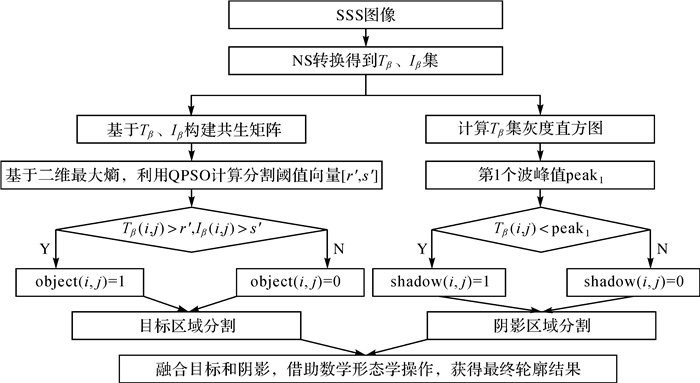
3 侧扫声呐图像分割方法基于以上研究,根据SSS图像的特点,给出了一种基于中性集合与量子粒子群算法相结合的侧扫声呐图像阈值分割方法(NS+QPSO),图 1给出了分割流程,具体计算步骤如下。
|
| 图 1 SSS图像分割流程 Fig. 1 The segmentation process of SSS image |
(1) 原始SSS回波强度多记录为10~16 bit格式,为方便显示需借助式(14)对其量化至256灰阶并形成灰度图像。
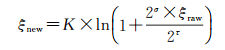 (14)
(14)
式中,K是一个常量,一般取小于100的数值;τ为原始数据的bit记录值;σ为重新量化后的bit值,若σ取8,则将数据量化至0~255;ξnew为量化后的数据;ξraw为原始记录数据,如果原始记录数据成图时已经有很高的对比度,分母也可取为2τ-σ [19]。
然后根据式(1)-式(7)将SSS图像转换到NS集,得到Tβ、Iβ、Fβ集合。
(2) Tβ、Iβ集合包含了利于图像分割的特征,因此可舍弃Fβ集,直接借助Tβ、Iβ集实现灰度共生矩阵[Grs]l1×l2的构建。r、s表示灰度共生矩阵的行、列号,l1×l2表示灰度共生矩阵的大小。Grs即为Tβ(i, j)=r且Iβ(i, j)=s时数值对的个数,其中Tβ(i, j)=r,Iβ(i, j)=s表示中性Tβ、Iβ集合中(i, j)位置处的数值。在这个构建过程中,因SSS图像已量化至256灰阶,则l1=l2=256;此外,由于计算所得Tβ、Iβ取值范围为[0, 1],因此需将Tβ、Iβ转换到[0,255]。灰度共生矩阵的概率密度矩阵可按式(15)计算
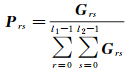 (15)
(15)
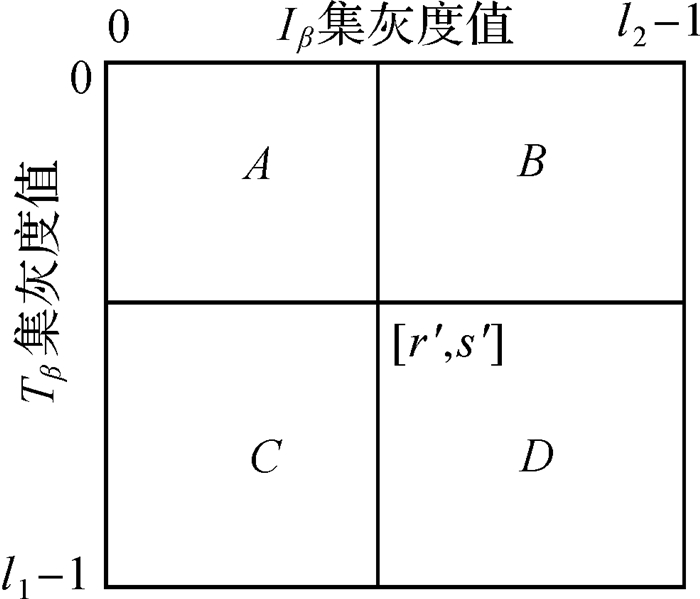
二维阈值向量(即式(10)所述粒子位置)X=[r′, s′]将灰度共生矩阵划分为4个区域(如图 2所示),r′、s′为未知的位置,且r′、s′的取值范围分别为[0, l1-1]、[0, l2-1]。由于Tβ集合代表了SSS图像的整体平滑信息,Iβ集合包含了SSS图像的边缘及纹理信息,因此图 2中A代表了阴影区域,C代表了背景区域,B、D两个区域代表了阴影和目标区域的边缘和纹理特征。熵值可用来评价共生矩阵内元素的分布水平,当背景区域和目标区域熵值的和最大时,[r′, s′]可实现最优的目标分割[14-15]。其中图像二维香农熵可按式(16)、式(17)来计算[14]
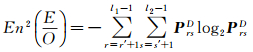 (16)
(16)
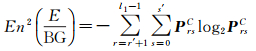 (17)
(17)
|
| 图 2 基于中性Tβ-Iβ集合构建的共生矩阵区域分布 Fig. 2 Quadrants of co-occurrence matrix constructed by neutrosophic Tβ-Iβ subset |
式(16)、式(17)中,En2表示图像二维香农熵;P由式(15)计算,且P的上标C、D与图 2中的区域对应,综合两式,二维香农联合熵可用式(18)计算
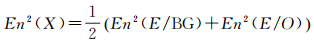 (18)
(18)
式(16)-式(18)中,E代表边缘(Edge);O代表特征目标(Object);BG代表背景区域(Back Ground),X为粒子位置(二维分割阈值向量)。当式(18)最大时,X可实现最优的目标区域分割。因此实现最优的目标区域分割转化为求取最佳X的问题,可用式(19)表述
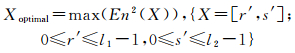 (19)
(19)
(3) 基于QPSO计算分割阈值向量。
①将式(19)作为QPSO算法的适应度函数,基于QPSO算法求取Xoptimal =[r′, s′],当满足Tβ(i, j) > r′且Iβ(i, j) > s′时即可获得目标高亮区分割结果。
②将式(16)替换为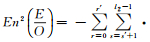
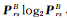
(4) 由于水体或海底目标对声波遮挡造成SSS图像中产生阴影区域,阴影区域的像素灰度值很小,可统计Tβ集灰度直方图,得到第一个波峰值peak1,将Tβ(i, j) < peak1的位置标记为阴影区域,根据目标和阴影成对出现的特征,最终完成阴影区域分割。
(5) 融合SSS图像目标区和阴影区分割结果,利用数学形态学操作对分割结果提取边缘轮廓线,获得最终SSS图像分割轮廓。
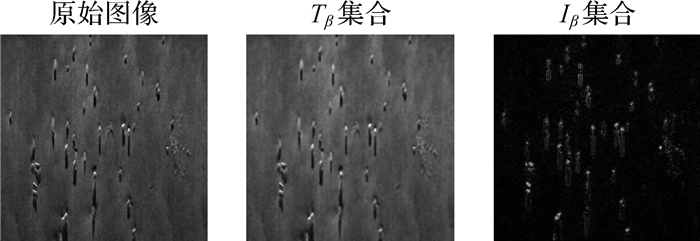
4 试验及分析利用EdgeTech公司的猎雷声呐(littoral mine countermeasure sonar, LMCS)系统实测的多目标似雷物体图像进行试验。计算中性集时,式(1)和式(6)中w取1,式(7)中的α1、α2和λ1分别取0.01、0.1和0。原始图像及其中性集Tβ、Iβ如图 3所示,Tβ集因滤除了部分噪声,较清晰地显示了图像目标及其阴影;Iβ集展现了图像的纹理及边缘信息。因此,可基于Tβ、Iβ集合计算灰度共生矩阵。
|
| 图 3 原始SSS图像及中性Tβ、Iβ集合图像 Fig. 3 The raw SSS image and the image of Neutrosophic Set Tβ and Iβ |
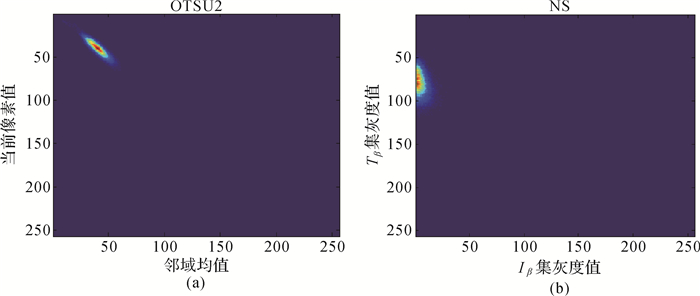
基于OTSU2法和中性Tβ、Iβ集采用式(15)计算共生矩阵的概率密度P如图 4所示(见文后)。由于粗纹理的像素对灰度趋于相同,其高亮区域会集中于主对角线附近,而细纹理的高亮区域会离散分布[20]。图 4中基于NS计算P的高亮区分布离散,而OTSU2法高亮区则集中于图像主对角线,表明基于NS计算的共生矩阵展现了精细的图像纹理,更能体现SSS图像的边缘和纹理信息,利于实现SSS图像的精细分割。
|
| 图 4 基于OTSU2和NS计算灰度共生矩阵的概率密度P的比较 Fig. 4 Comparison of the probability P of the gray level co-occurrence matrix calculated based on OTSU2 and NS |
为验证本文给出的结合中性集合和量子粒子群算法(NS+QPSO)的侧扫声呐图像分割方法的性能,将其与原始OTSU2法进行了比较分析。
OTSU_QPSO:采用原始图像及其邻域均值计算灰度共生矩阵,基于二维最大熵采用QPSO计算分割阈值向量。
NS_OTSU:采用中性集合计算灰度共生矩阵,基于最大类间方差采用穷举法计算分割阈值向量的分割方法。
QPSO算法中,设置粒子数目Z为20,最大迭代次数ITERmax为30,分割阈值向量(粒子位置)X=[r′, s′],r′和s′均为[0,255]内的随机值。4种方法耗时见表 1,可见QPSO算法有效缩短了二维分割阈值向量的计算时间,提高了效率,4种方法多目标高亮区分割结果如图 5所示。为了评估本文方法性能,采用手选方法对图 3原始图像进行目标统计,统计出共含40个特征目标。由图 5可看出,OTSU2和OTSU_QPSO分割出目标数量和形状不正确;NS_OTSU分割出50个特征目标,多处将大目标错分为小目标,但可有效分割出目标形状;本文NS+QPSO方法分割出42个特征目标,目标形状清晰,误将2处大目标物体错分割为小目标,分割结果最优。
| s | |
| 分割方法 | CPU时间 |
| OTSU2 | 4.286 |
| OTSU_QPSO | 1.128 |
| NS_OTSU | 3.782 |
| NS+QPSO | 1.054 |

|
| 图 5 多目标SSS图像目标(高亮区) 4种方法的分割结果 Fig. 5 The segmentation results of target (high-light area) in SSS image of multi-object by the four methods |
对以上结果,分析认为:
(1) OTSU2基于原始图像及其邻域均值计算灰度共生矩阵,用穷举法获取最大类间方差并以此确定阈值和实现目标分割。声呐图像受环境噪声影响显著且目标和阴影差异明显,此特征下OTSU2计算的灰度共生矩阵难以很好地反映图像精细纹理、确定的阈值常会出现偏差,导致目标图像分割结果较差;加之采用穷举法,图像分割耗时较大。
(2) OTSU_QPSO采用了OTSU2法中的灰度共生矩阵计算方法,但基于QPSO实现二维最大香农熵获取及阈值确定,解决OTSU2中最大类间方差在声呐图像目标和阴影差异明显时计算阈值不准问题及穷举法耗时问题,提高了分割效率但对分割精度改善不大。
(3) NS_OTSU采用中性集NS计算灰度共生矩阵,仍以最大类间方差为阈值选取准则。基于NS转换后的声呐图像,Tβ集滤除了图像噪声,Iβ集显示了图像边缘及纹理,据此构建的灰度共生矩阵可反映图像的精细纹理,因此提高了图像分割精度;但由于仍采用穷举法获取最大方差和实现阈值确定,因此分割效率偏低且会对基于NS的图像分割精度造成影响。
(4) NS+QPSO采用了NS和QPSO,因此在分割精度和效率方面均优于前面3种方法。
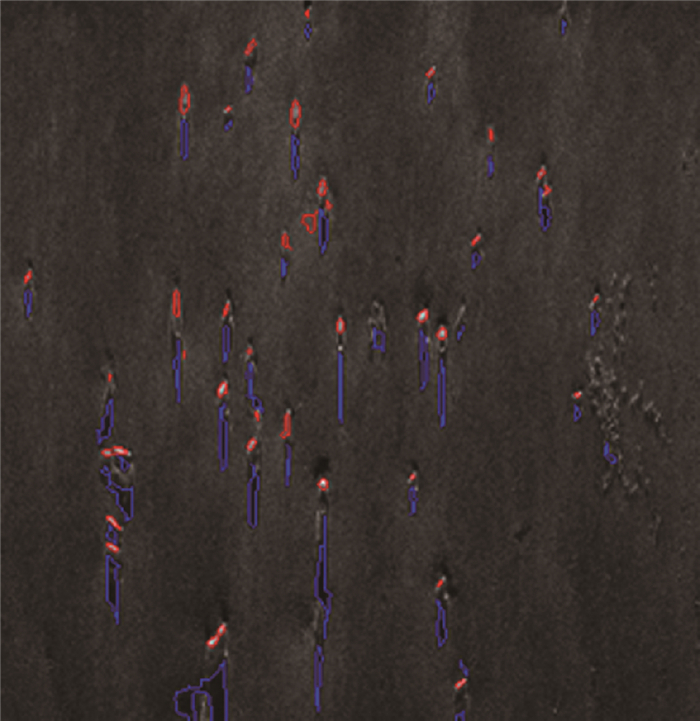
根据SSS图像分割方法步骤(3)中的②,进行阴影区域分割,耗时为1.678 s,由于需重新计算分割阈值,增加了耗时。而根据步骤(4)进行阴影区域分割,分割耗时仅为0.787 s。在分割结果的基础上借助数学形态学开、闭、膨胀、腐蚀运算,得到目标图像最终轮廓如图 6所示。可以看出NS+QPSO方法较好地分割出了SSS图像中的多目标物体及其阴影,能够更好地为后续图像特征提取和似雷物体判别服务。
|
| 图 6 SSS图像最终分割结果 Fig. 6 The segmentation result of SSS image 注:红色为目标轮廓,蓝色为阴影轮廓 |
受测量机理和复杂海洋环境噪声影响,侧扫声呐图像质量往往较低,存在如强随机噪声、对比度偏低、目标图像边缘残缺等问题,加之实际目标尺寸常常缺失,分割结果的定量评估比较困难[9]。为了定量分析本文算法分割低质量SSS图像的性能,根据SSS成像原理模拟了大小为69×101像素的含噪声声呐图像,由于模拟的目标图像及其阴影大小已知,据此可定量评估分割结果的精度。定量客观评价准则一般为真正(true positives, TP),表示分割为目标,实际也为目标的像素数;假正(false positives, FP),表示分割为目标,实际为阴影的像素数;真负(true negatives, TN),表示分割为阴影,实际也为阴影的像素数;假负(false negatives, FN),表示分割为阴影,实际为目标的像素数[21]。基于这4个评价准则,真正率(true positive rate, TPR):指实际目标大小被正确分割的概率;真准确度(true positive accuracy, TPA):指目标分割结果中分割正确的概率;可以用来定量评价声呐图像目标分割精度。上述两个指标可以按式(20)计算
 (20)
(20)
通常借助上述TPR和TPA,采用f作为图像目标分割结果的客观评价指标。其中f=2×TPR×TPA/(TPR+TPA)。如果f的值比较大,则说明分割精度高[21]。采用前述4种方法对模拟声呐图像进行分割,结果如图 7所示;分割耗时及目标分割结果的f值见表 2。可以看出,本文方法的耗时最短,f值最大,分割轮廓效果最好。

|
| 图 7 模拟声呐图像4种方法的分割结果 Fig. 7 The segmentation results of the numerical simulation sonar image by the four methods |
| 分割方法 | f | CPU时间/ s |
| OTSU2 | 0.954 6 | 1.944 |
| OTSU_QPSO | 0.959 1 | 0.924 |
| NS_OTSU | 0.988 7 | 1.771 |
| NS+QPSO | 0.993 2 | 0.627 |
为了进一步验证本文算法的有效性,采用含失事沉船、飞机及溺水人体的SSS图像进行分割试验,结果如图 8所示。可看出本文方法较好地实现了含不同目标的SSS图像分割。

|
| 图 8 本文方法对含有沉船、飞机和溺水人体的SSS图像分割结果 Fig. 8 The segmentation results of SSS image of shipwreck, airplane and drowning victim's body by the proposed method |
5 结论
本文提出的基于中性集合和量子粒子群算法相结合的侧扫声呐图像阈值分割方法,首先借助中性集构建灰度共生矩阵,呈现了SSS图像的精细纹理,提高了分割精度;其次基于二维最大熵理论,借助量子粒子群算法计算二维分割阈值向量,实现了分割阈值向量的快速、准确计算;结合SSS图像特点,基于Tβ集合,采用单阈值进行阴影区域的分割,进一步提高了分割效率。通过对含有不同目标的侧扫声呐图像的分割试验,验证了算法的有效性,为水下侧扫声呐图像提供了一种高效、准确的分割方法。
| [1] | NAKAMURA K, TOKI T, MOCHIZUKI N, et al. Discovery of a New Hydrothermal Vent Based on an Underwater, High-resolution Geophysical Survey[J]. Deep Sea Research Part I:Oceanographic Research Papers , 2013, 74 : 1 –10. DOI:10.1016/j.dsr.2012.12.003 |
| [2] | FLOWERS H J, HIGHTOWER J E. A Novel Approach to Surveying Sturgeon Using Side-scan Sonar and Occupancy Modeling[J]. Marine and Coastal Fisheries , 2013, 5 (1) : 211 –223. DOI:10.1080/19425120.2013.816396 |
| [3] | HEALY C A, SCHULTZ J J, PARKER K, et al. Detecting Submerged Bodies:Controlled Research Using Side-scan Sonar to Detect Submerged Proxy Cadavers[J]. Journal of Forensic Sciences , 2015, 60 (3) : 743 –752. DOI:10.1111/jfo.2015.60.issue-3 |
| [4] | 刘光宇, 卞红雨, 沈郑燕, 等. 基于声呐图像的水平集分割算法研究[J]. 传感器与微系统 , 2012, 31 (1) : 29–31. LIU Guangyu, BIAN Hongyu, SHEN Zhengyan, et al. Research on Level Set Segmentation Algorithm for Sonar Image[J]. Transducer and Microsystem Technologies , 2012, 31 (1) : 29 –31. |
| [5] | KÖHNTOPP D, LEHMANN B, KRAUS D, et al.Segmentation and Classification Using Active Contours Based Superellipse Fitting on Side Scan Sonar Images for Marine Demining[C]//Proceedings of 2015 IEEE International Conference on Robotics and Automation (ICRA).Seattle, WA:IEEE, 2015:3380-3387. |
| [6] | 王雷, 叶秀芬, 王天. 模糊聚类的侧扫声呐图像分割算法[J]. 华中科技大学学报(自然科学版) , 2012, 40 (9) : 25–29. WANG Lei, YE Xiufen, WANG Tian. Segmentation Algorithm of Fuzzy Clustering on Side Scan Sonar Image[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition) , 2012, 40 (9) : 25 –29. |
| [7] | GONG Maoguo, SU Linzhi, JIA Meng, et al. Fuzzy Clustering with a Modified MRF Energy Function for Change Detection in Synthetic Aperture Radar Images[J]. IEEE Transactions on Fuzzy Systems , 2014, 22 (1) : 98 –109. DOI:10.1109/TFUZZ.2013.2249072 |
| [8] | SHAHRIARI H, RANJBAR H, HONARMAND M. Image Segmentation for Hydrothermal Alteration Mapping Using PCA and Concentration:Area Fractal Model[J]. Natural Resources Research , 2013, 22 (3) : 191 –206. DOI:10.1007/s11053-013-9211-y |
| [9] | 叶秀芬, 王兴梅, 张哲会, 等. 改进MRF参数模型的声呐图像分割方法[J]. 哈尔滨工程大学学报 , 2009, 30 (7) : 768–774. YE Xiufen, WANG Xingmei, ZHANG Zhehui, et al. Sonar Imagery Segmentation Algorithm by Improved MRF Parameter Model[J]. Journal of Harbin Engineering University , 2009, 30 (7) : 768 –774. |
| [10] | SONG Sanming, SI Bailu, FENG Xisheng, et al.Prior Parameter Estimation for Ising-MRF-based Sonar Image Segmentation by Local Center-encoding[C]//OCEANS 2015 MTS/IEEE Genova.Genova:IEEE, 2015:1-5. |
| [11] | 巫兆聪, 胡忠文, 张谦, 等. 结合光谱、纹理与形状结构信息的遥感影像分割方法[J]. 测绘学报 , 2013, 42 (1) : 44–50. WU Zhaocong, HU Zhongwen, ZHANG Qian, et al. On Combining Spectral, Textural and Shape Features for Remote Sensing Image Segmentation[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (1) : 44 –50. |
| [12] | VALA H J, BAXI A. A Review on Otsu Image Segmentation Algorithm[J]. International Journal of Advanced Research in Computer Engineering&Technology (IJARCET) , 2013, 2 (2) : 387 –389. |
| [13] | SUN Jun, FENG Bin, XU Wenbo.Particle Swarm Optimization with Particles Having Quantum Behavior[C]//Proceedings of Congress on Evolutionary Computation.Portland, OR:IEEE, 2004, 1:325-331. |
| [14] | HANBAY K, TALU M F. Segmentation of SAR Images Using Improved Artificial Bee Colony Algorithm and Neutrosophic Set[J]. Applied Soft Computing , 2014, 21 : 433 –443. DOI:10.1016/j.asoc.2014.04.008 |
| [15] | SENGUR A, GUO Yanhui. Color Texture Image Segmentation Based on Neutrosophic Set and Wavelet Transformation[J]. Computer Vision and Image Understanding , 2011, 115 (8) : 1134 –1144. DOI:10.1016/j.cviu.2011.04.001 |
| [16] | 于博, 牛铮, 王力, 等. 一种基于中性集和均值漂移的彩色遥感图像非监督建筑物提取方法[J]. 光谱学与光谱分析 , 2013, 33 (4) : 1071–1075. YU Bo, NIU Zheng, WANG Li, et al. An Unsupervised Method of Extracting Constructions from Color Remote Sensed Image Based on Mean Shift and Neutrosophic Set[J]. Spectroscopy and Spectral Analysis , 2013, 33 (4) : 1071 –1075. |
| [17] | 童小念, 施博, 王江晴. 基于量子粒子群算法的双阈值图像分割方法[J]. 四川大学学报(工程科学版) , 2010, 42 (3) : 132–138. TONG Xiaonian, SHI Bo, WANG Jiangqing. Dual-threshold Image Segmentation Method Based on QPSO Algorithm[J]. Journal of Sichuan University (Engineering Science Edition) , 2010, 42 (3) : 132 –138. |
| [18] | OSUNA-ENCISO V, CUEVAS E, SOSSA H. A Comparison of Nature Inspired Algorithms for Multi-threshold Image Segmentation[J]. Expert Systems with Applications , 2013, 40 (4) : 1213 –1219. DOI:10.1016/j.eswa.2012.08.017 |
| [19] | BLONDEL P. The Handbook of Sidescan Sonar[M]. Berlin: Springer Science & Business Media, 2009 . |
| [20] | REGNIERS O, BOMBRUN L, GUYON D, et al. Wavelet-Based Texture Features for the Classification of Age Classes in a Maritime Pine Forest[J]. IEEE Geoscience and Remote Sensing Letters , 2015, 12 (3) : 621 –625. DOI:10.1109/LGRS.2014.2353656 |
| [21] | POWERS D M. Evaluation:From Precision, Recall and F-measure to ROC, Informedness, Markedness and Correlation[J]. Journalof Machine Learning Technologies , 2011, 2 (1) : 37 –63. |



