2. 桂林理工大学广西空间信息与测绘重点实验室,广西 桂林 541004 ;
3. 西华师范大学国土资源学院,四川 南充 637000
2. Guangxi Key Laboratory for Spatial Information and Geomatics, Guilin University of Technology, Guilin 5410043, China ;
3. Land and Resources College, China West Normal University, Nanchong 637000, China
同GPS一样,目前中国的北斗系统(BDS)也发布了多个频率,卫星与接收机通过不同通道发射和接受这些不同频率的导航信号,而这些导航信号在通过不同通道所产生的时间延迟并不完全一致,由此产生的不同频率信号时延之间的差异成为频率偏差,又称为差分码偏差参数DCB,包括卫星DCB和接收机DCB[1-2]。对于GPS系统,二者之和数量级在几纳秒到几十纳秒[3-4],是利用GPS观测数据计算电离层总电子含量的主要误差源[5],同时也是影响单频用户导航定位主要误差源之一。BDS目前已经初步实现了亚太地区PNT功能,获取准确的差分码偏差对于提高利用BDS观测值计算电离层总电子含量以及单频用户定位精度是至关重要的。
传统获取GPS或BDS接收机硬件延迟(DCB)一般通过全球或区域电离层建模来进行估计。这种方法是基于电离层集中在某一特定高度(如350 km)薄壳上的假设,将卫星DCB、接收机DCB和VTEC同时作为待估参数一起求解[6-14]。这种方法获取的DCB精度与选取的电离层模型有较强的相关性,特别是在局部小区域范围内,效果可能会受到电离层模型误差的影响,一些学者研究了不需要复杂电离层模型对卫星和接收机DCB进行估计校准的方法[15-16]。另外一方面由于卫星DCB和接收机DCB本身的强相关性,一般给定卫星DCB一个约束条件(如所有卫星DCB之和为零,也称为“零基准”)才能达到分离二者的目的[17]。“零基准”在分离GPS卫星和接收机DCB时效果较好,因为GPS信号相对较为稳定,而北斗在建设初期很难做到卫星频间偏差稳定性相同,不同轨道高度的卫星所处的外部环境也不尽相同,所以在分离BDS卫星DCB和接收机DCB时,如果采用类似GPS的“零基准”,在某些时刻,如卫星频间偏差出现突变,会影响整体估计的卫星DCB值[18-19]。
基于此,本文提出一种精确估计区域北斗接收机DCB的方法。该方法主要利用在正常情况下电离层延迟和卫星-接收机之间几何距离强相关原理,通过站间单差求取区域其他北斗站相对于参考站的相对DCB值,在已知一个参考站接收机DCB的前提下,便可获取区域内其他站接收机的绝对DCB。该方法不需要复杂的电离层模型,只求取接收机DCB,回避了利用传统电离层建模方法提取接收机DCB对选择的电离层模型依赖的问题,另外也无需考虑在分离卫星和接收机DCB时所采取的基准问题。为了验证本文方法的可行性,选取IGS九峰站作为已知参考站,估计了6个武汉CORS站连续30 d的北斗接收机DCB,并利用GEO实测双频数据扣除估计的接收机DCB和IGS获取的卫星DCB,计算对应穿刺点一天的VTEC量并和GIM格网内插结果进行比对分析,验证了本文提出的方法的可行性。
1 方法介绍 1.1 站间单差电离层延迟与卫星-接收机几何距离关系北斗目前发布了3个频率信号,主要对应载波和伪距观测值。双频无几何组合观测值常用于精确估计TEC和DCB,该组合可以很好地消除一些BDS观测值常见误差,如对流层延迟误差、卫星和接收机钟差等。下面给出BDS双频无几何观测值具体数学表达式
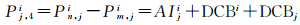 (1)
(1)
式中,Pn, ji和Pm, ji分别表示频道n和频道m对应的伪距观测值,本次选取北斗B2和B3两个频点对应的观测数据进行讨论,即n=2、m=3,频率分别为1 207.140 Hz和1 268.520 Hz;Iji表示Pn, ji对应的电离层延迟量;A是一个常数,大小为1-fn2/fm2;DCBi和DCBj分别表示卫星i和测站j接收机频道n和频道m之间的DCB。
由于伪距观测值噪声相对较高,需要对Pn, ji和Pm, ji进行载波相位平滑处理,通过上式可以发现平滑伪距精度直接影响着DCB估值精度[20]。经过平滑可以得到Pj, 4i[21]。
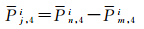 (2)
(2)
假设区域内测站j和测站k同时观测到了卫星i,对这两个站平滑后的无几何组合观测值求差,卫星i的DCB被消除,具体表达式如下
 (3)
(3)
式中,Pjk, 4i表示站间单差平滑无几何组合观测值(SDP4);Ijki表示站间单差电离层延迟(SDI);ΔDCBjk表示两个测站接收机相对DCB。
从式(3)可以看出,SDP4和SDI是相关的(相关系数为常数A)。另外SDP4不可避免地受到单差卫星-接收机几何距离(SDG)的影响。同时结合图 1可以看出,SDG是随时间不断变化的,经过电离层区域的信号路径也随时间在变化,即SDI也是随时间在变化。
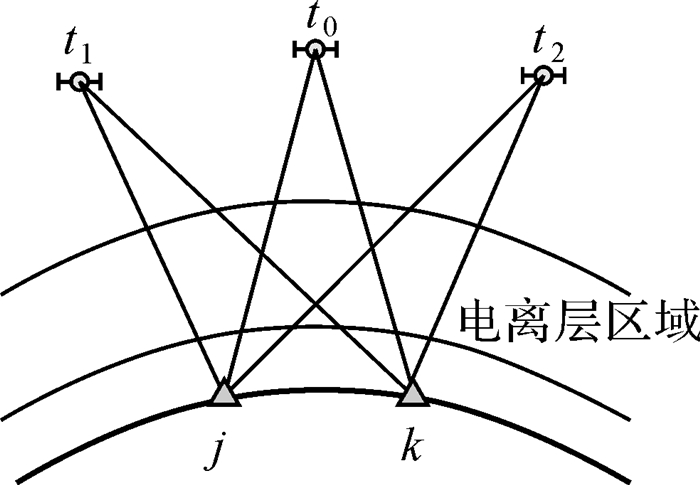
|
| 图 1 单差卫星-接收机几何距离随时间变化图 Fig. 1 SD satellite-receiver geometric ranges changes with respect to time |
通过上面分析可知SDP4同时受到SDI和SDG的影响。因此可以推论SDI和SDG也存在某种相关关系,即此时段内SDG随时间的变化量决定着大部分SDI,剩余部分SDI可以称之为“单差电离层残余变化量”,因此可以用数学表达式表达如下
 (4)
(4)
式(4)描述了SDI和SDG的线性关系,α表示SDI和SDG相关系数;β是一个常量,表示“单差电离层残余变化量”。
1.2 区域BDS接收机DCB的估计区域内必须已知至少一个BDS站接收机DCB,称该站为参考站。该方法首先估计区域内其他北斗站和参考站之间的相对接收机DCB,即单差接收机DCB,然后根据已知参考站的DCB和已求取的单差DCB求取区域内BDS接收机的绝对DCB。在估计单差DCB之前,首先选取满足以下3个条件的卫星和对应的连续观测时段:
(1) 区域内参考站和其他北斗站站距离不能太远,一般说来,基线长度最好不超过100 km。
(2) 一般情况下电离层延迟在较短时间内保持不变,所以连续时段长一般不大于2 h。
(3) 在连续时段内SDG在某个具体时刻存在一个“零点”。
图 2展示了符合以上3个条件的卫星和对应的连续时段的一个实例,实线反映了WHCD站在2014年9月1日一天的北斗卫星可视情况,虚线矩形内的加粗实线则表示满足以上条件的卫星和对应的连续时段。
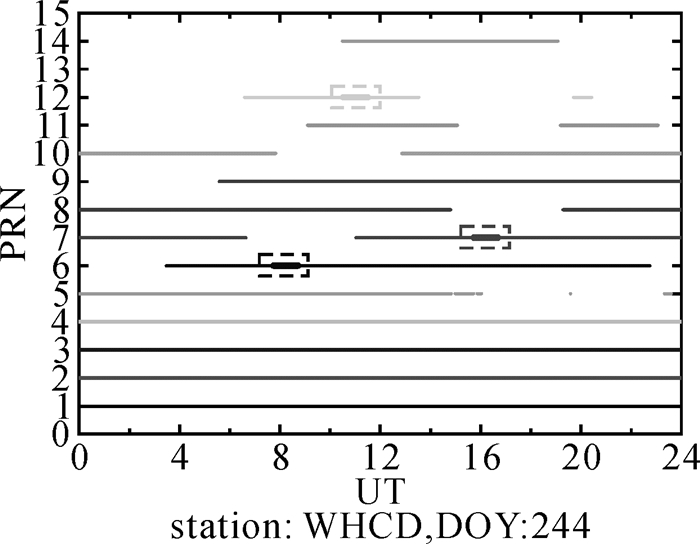
|
| 图 2 满足条件的卫星和连续时段实例 Fig. 2 An example of selected PRNs and continuous periods satisfied the conditions |
以图 2中的12号北斗卫星为例,IGS的JFNG为参考站,图 3展示了12号卫星在10:31至11:31时段内的SDG变化趋势。由图 2可以看出在t0时刻满足SDG为零的条件。需要注意的是在计算SDG时,北斗卫星坐标利用IGS机构(如GFZ)提供的精密轨道星历获取,地面CORS站坐标采用精密单点定位(PPP)获取。
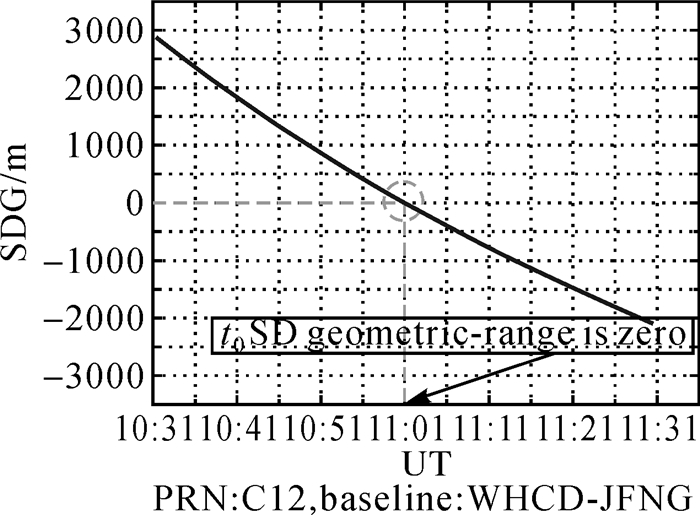
|
| 图 3 SDG变化曲线 Fig. 3 Variation curve of the SD satellite-receiver geometric ranges |
图 4展示了12号卫星对应的SDP4一小时的变化趋势。对比图 3中SDG变化曲线,可以发现它们的变化趋势整体比较相近,经计算二者相关系数为0.862。
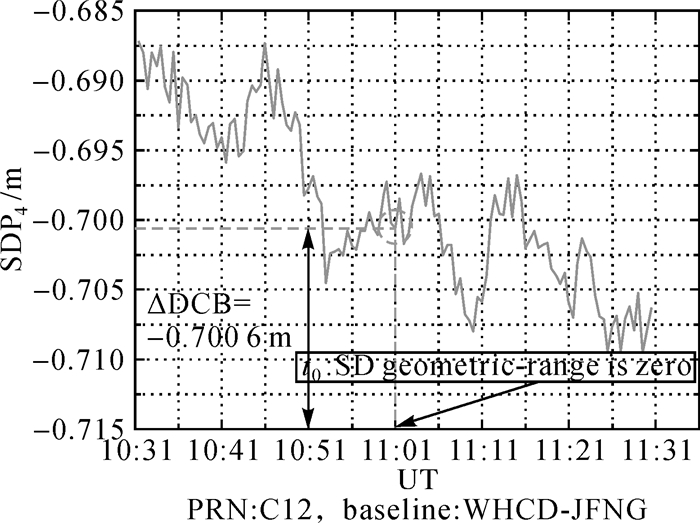
|
| 图 4 SDP4变化曲线 Fig. 4 Variation curve of smoothed SD geometry-free linear observation |
图 3和图 4对应的连续时段满足式(4)的关系。从图 1可以发现在t0时刻(即图 3和图 4对应的t0时刻)SDG为零。因为本文介绍的接收机DCB估计方法是针对小区域,即参考站和其他北斗站距离较近,所以在t0时刻对应的SDI也近似为零。在实际数据处理中,该时段满足
 (5)
(5)
将式(4)和式(5)代入式(3)得到
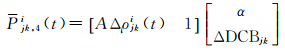 (6)
(6)
式中,α和ΔDCBjk为待估参数。
将t0时刻的观测值带入上式,可以发现待估计的单差DCB即是此时刻对应的单差无几何组合观测值(SDP4),这一特性在图 4中可以反映出来。
在估计完单差DCB之后,根据参考站接收机已知DCB即可求取最终区域内其他北斗站接收机的绝对DCB值,如式(7)
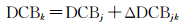 (7)
(7)
式中,下标j表示参考站;下标k表示区域内其他站。
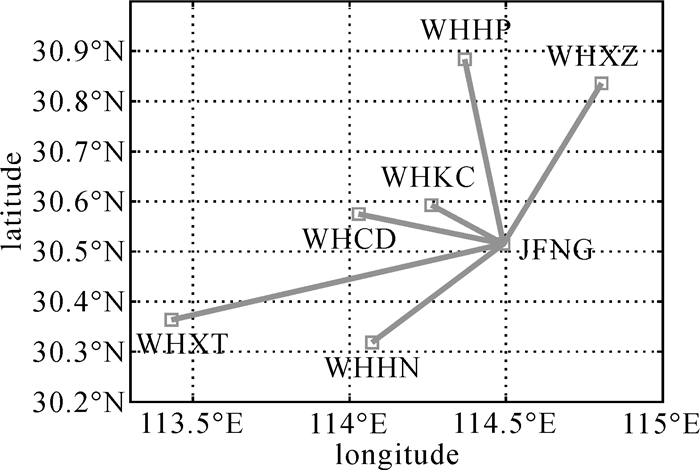
2 试验及分析为了验证本文方法的可行性,选取了IGS九峰站(JFNG)作为已知参考站(通过IGS网站“ftp://cddis.gsfc.nasa.gov/pub/gps/products/mgex/dcb”即可直接获取该参考站BDS接收机DCB值)。本文估计了武汉市内分布较好的6个CORS站BDS接收机DCB,JFNG站和6个CORS站均采用TRIMBLE NETR9接收机。图 5展示了JFNG站和6个CORS站的位置以及它们之间形成基线情况,表 1给出了选取基线的长度。
|
| 图 5 选取的基线情况 Fig. 5 Selected baselines for the estimation of BDS receivers DCBs in Wuhan |
| km | ||||||
| WHCD-JFNG | WHHN-JFNG | WHHP-JFNG | WHKC-JFNG | WHXT-JFNG | WHXZ-JFNG | |
| base line length | 44.8 | 45.8 | 42.4 | 23.6 | 103.1 | 46.4 |
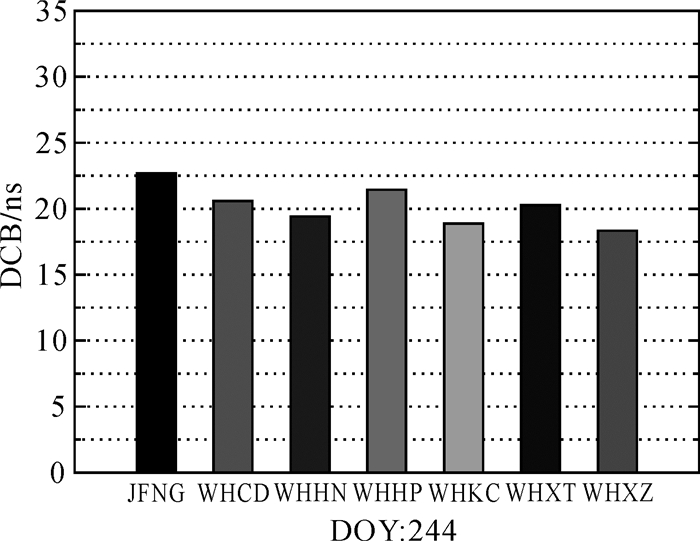
按照第1节介绍的方法,连续估计了图 5中6个CORS站2014年9月份30 d(DOY: 244—273)的北斗接收机DCB。图 6展示了2014年9月1日JGNF站北斗接收机DCB(从IGS机构GFZ获取)以及该方法估计的6个CORS站北斗接收机最终DCB值。表 2为JFNG站以及估计的6个CORS站连续30 d的DCB均方根误差(RMS)。
|
| 图 6 JFNG站及估计的6个CORS站北斗接收机DCB Fig. 6 JFNG station and other estimated CORS stations BDS receivers DCBs |
| ns | |||||||
| station | JFNG | WHCD | WHHN | WHHP | WHKC | WHXT | WHXZ |
| RMS | 0.238 9 | 0.268 0 | 0.309 8 | 0.356 6 | 0.288 9 | 0.321 9 | 0.316 6 |
从图 6可以看出该方法估计的单天北斗接收机DCB主要分布在18~22 ns之间,差距较小,这是因为6个CORS站均采用同一类型接收机。对于GPS系统,一般情况下接收机DCB具有长期的稳定性,均方根误差(RMS)在0.2 ns左右[22]。从表 2可以看出该方法估计的6个CORS站连续30 d北斗接收机DCB均方根误差均在0.3 ns左右,与GPS接收机DCB稳定性相当。
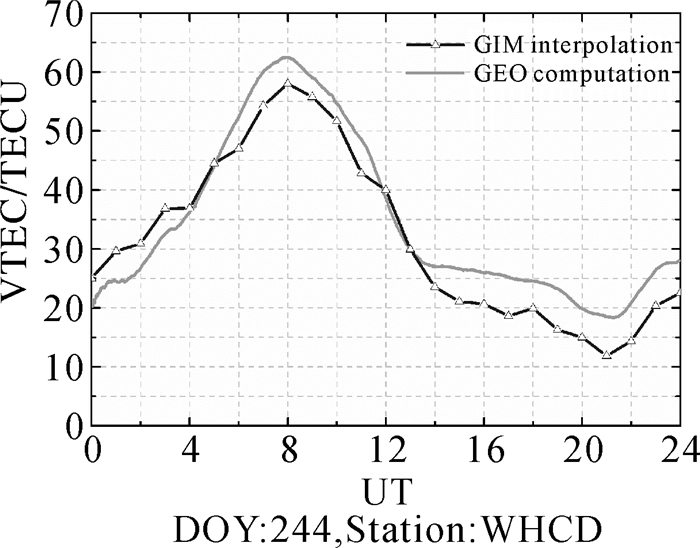
由于北斗GEO卫星在中国区域能够全天可视,并且具有静地性,测站与GEO卫星信号形成的穿刺点位置基本不变,所以观测到的天顶方向电离层总电子含量VTEC(vertical total election content)只随时间变化[23]。利用这一特性,选取2014年9月1日WHCD站观测到1号GEO卫星的双频数据扣除卫星DCB(GFZ获取)和本文估计的接收机DCB,可以得到该GEO卫星穿刺点位置的全天24 h VTEC,并与CODE公布的全球电离层格网内插计算得到的该穿刺点全天24 h的VTEC进行对比分析,结果如图 7所示。
|
| 图 7 GEO双频观测值计算电离层延迟和GIM内插计算电离层延迟量对比 Fig. 7 A comparison of ionosphere delay between GEO computation and GIM interpolation |
从图 7可以看出,由GEO卫星双频实测数据扣除卫星及接收机DCB之后得到的该穿刺点全天VTEC和根据全球电离层格网模型内插得到的VTEC值大小以及变化趋势基本是一致的,间接证明了本文估计的北斗接收机DCB具有可靠性。另外由于全球电离层格网模型经过空间和时间内插,精度会有所损失,无法很好地表现该穿刺点VTEC大小以及随时间细致的变化特征,而由GEO双频实测数据计算VTEC相对随时间变化更平滑,能更细致地表现VTEC随时间的变化趋势。
3 结论本文提出了一种不需要通过传统电离层建模来估计区域北斗接收机DCB的方法。该方法首先构造出单差无几何组合观测值和单差电离层延迟量的线性关系,然后将单差电离层延迟量用单差卫星-接收机几何距离进行线性拟合,常数项即单差电离层变化残余量,在小区域内,当卫星运行至基线中点天顶方向附近连续时段内,忽略该常数项,利用单差卫星-接收机几何距离和单差无几何组合观测值便可估计出单差接收机DCB。该方法只估计区域北斗接收机DCB,无需考虑在分离卫星和接收机DCB时所采取的基准问题,并且在一定程度上避免了利用传统电离层建模方法提取接收机DCB对采用电离层模型依赖的问题。
为了验证本文方法的可行性,选取了IGS的九峰站为参考站,利用本文的方法估计了武汉市6个CORS站连续30 d的北斗接收机硬件延迟,单站估值RMS在0.3 ns左右,具有较好的稳定性。考虑到目前还没有很好的外部检核方法来验证BDS接收机DCB估计精度,本文通过GEO卫星双频实测数据扣除已知卫星DCB和该方法估计的接收机DCB得到该卫星穿刺点全天的VTEC,并与全球电离层格网模型GIM内插得到的穿刺点全天VTEC进行了比较分析,二者无论大小还是变化趋势均有较好的一致性,证明本文方法估计的区域北斗接收机DCB的可靠性。
本文方法针对小区域范围内效果较好。随着区域范围增大,基线长度递增,该方法估计的BDS接收机DCB精度会受到单差电离层变化残余量的影响,因此下一步的工作是通过试验来进一步验证该方法估计BDS接收机DCB的精度和站分布区域大小的具体关系。
| [1] | SARDÓN E, RIUS A, ZARRAOA N. Estimation of the Transmitter and Receiver Differential Biases and the Ionospheric Total Electron Content from Global Positioning System Observations[J]. Radio Science , 1994, 29 (3) : 577 –586. DOI:10.1029/94RS00449 |
| [2] | ARIKAN F, NAYIR H, SEZEN U, et al. Estimation of Single Station Interfrequency Receiver Bias Using GPS-TEC[J]. Radio Science , 2008, 43 (4) . DOI:10.1029/2007RS003785 |
| [3] | CHOI K R, LIGHTSEY E G. Estimation of Total Electron Content (TEC) Using Spaceborne GPS Measurements[J]. The Journal of the Astronautical Sciences , 2008, 56 (3) : 375 –399. DOI:10.1007/BF03256559 |
| [4] | 范国清, 王威, 郗晓宁. 基于广义回归神经网络的电离层VTEC建模[J]. 测绘学报 , 2010, 39 (1) : 16–21. FAN Guoqing, WANG Wei, XI Xiaoning. Modeling of Ionosphere VTEC Using Generalized Regression Neural Network[J]. Acta Geodaetica et Cartographica Sinica , 2010, 39 (1) : 16 –21. |
| [5] | 张小红, 唐龙. COSMIC低轨卫星GPS接收机差分码偏差估计[J]. 地球物理学报 , 2014, 57 (2) : 377–383. ZHANG Xiaohong, TANG Long. Estimation of COSMIC LEO Satellite GPS Receiver Differential Code Bias[J]. Chinese Journal of Geophysics , 2014, 57 (2) : 377 –383. |
| [6] | COCO D S, COKER C, DAHLKE S R, et al. Variability of GPS Satellite Differential Group Delay Biases[J]. IEEE Transactions on Aerospace and Electronic Systems , 1991, 27 (6) : 931 –938. DOI:10.1109/7.104264 |
| [7] | MANNUCCI A J, ⅡJIMA B, SPARKS L, et al. Assessment of Global Tec Mapping Using a Three-dimensional Electron Density Model[J]. Journal of Atmospheric and Solar-Terrestrial Physics , 1999, 61 (16) : 1227 –1236. DOI:10.1016/S1364-6826(99)00053-X |
| [8] | SCHAER S. Mapping and Predicting the Earth's Ionosphere Using the Global Positioning System[J]. Geodätisch-geophys, Arbeiten in der Schweiz , 1999, 59 : 32 –38. |
| [9] | OTSUKA Y, OGAWA T, SAITO A, et al. A New Technique for Mapping of Total Electron Content Using GPS Network in Japan[J]. Earth, Planets and Space , 2002, 54 (1) : 63 –70. DOI:10.1186/BF03352422 |
| [10] | KAO S P, CHEN Y C, NING F S. A MARS-based Method for Estimating Regional 2-D Ionospheric VTEC and Receiver Differential Code Bias[J]. Advances in Space Research , 2014, 53 (2) : 190 –200. DOI:10.1016/j.asr.2013.11.001 |
| [11] | MA Guanyi, GAO Wei, LI Jinghua, et al. Estimation of GPS Instrumental Biases from Small Scale Network[J]. Advances in Space Research , 2014, 54 (5) : 871 –882. DOI:10.1016/j.asr.2013.01.008 |
| [12] | 张东和, 萧佐. 利用GPS计算TEC的方法及其对电离层扰动的观测[J]. 地球物理学报 , 2000, 43 (4) : 451–458. ZHANG Donghe, XIAO Zuo. A Method of Calculating TEC with GPS Data and Its Application to the Ionospheric Disturbances[J]. Chinese Journal of Geophysics , 2000, 43 (4) : 451 –458. |
| [13] | 张小红, 李征航, 蔡昌盛. 用双频GPS观测值建立小区域电离层延迟模型研究[J]. 武汉大学学报(信息科学版) , 2001, 26 (2) : 140–143. ZHANG Xiaohong, LI Zhenghang, CAI Changsheng. Study on Regional Ionospheric Model Using Dual-frequency GPS Measurements[J]. Geomatics and Information Science of Wuhan University , 2001, 26 (2) : 140 –143. |
| [14] | 聂文锋, 胡伍生, 潘树国, 等. 利用GPS双频数据进行区域电离层TEC提取[J]. 武汉大学学报(信息科学版) , 2014, 39 (9) : 1022–1027. NIE Wenfeng, HU Wusheng, PAN Shuguo, et al. Extraction of Regional Ionospheric TEC from GPS Dual Observation[J]. Geomatics and Information Science of Wuhan University , 2014, 39 (9) : 1022 –1027. |
| [15] | HONG C K, GREJNER-BRZEZINSKA D A, KWON J H. Efficient GPS Receiver DCB Estimation for Ionosphere Modeling Using Satellite-receiver Geometry Changes[J]. Earth, Planets and Space , 2008, 60 (11) . |
| [16] | ZHANG Baocheng, TEUNISSEN P J G. Characterization of Multi-GNSS Between-receiver Differential Code Biases Using Zero and Short Baselines[J]. Science Bulletin , 2015, 60 (21) : 1840 –1849. DOI:10.1007/s11434-015-0911-z |
| [17] | JIN Rui, JIN Shuanggen, FENG Guiping. M_DCB:Matlab Code for Estimating GNSS Satellite and Receiver Differential Code Biases[J]. GPS Solutions , 2012, 16 (4) : 541 –548. DOI:10.1007/s10291-012-0279-3 |
| [18] | LI Zishen, YUAN Yunbin, LI Hui, et al. Two-step Method for the Determination of the Differential Code Biases of COMPASS Satellites[J]. Journal of Geodesy , 2012, 86 (11) : 1059 –1076. DOI:10.1007/s00190-012-0565-4 |
| [19] | LI Zishen, YUAN Yunbin, FAN Lei, et al. Determination of the Differential Code Bias for Current BDS Satellites[J]. IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (7) : 3968 –3979. DOI:10.1109/TGRS.2013.2278545 |
| [20] | 张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报 , 2011, 40 (4) : 447–453. ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Calibration of Slant Total Electron Content and Satellite-receiver's Differential Code Biases with Uncombined Precise Point Positioning Technique[J]. Acta Geodaetica et Cartographica Sinica , 2011, 40 (4) : 447 –453. |
| [21] | 张成军, 杨力, 陈军. 提高GPS载波相位平滑伪距定位精度的算法研究[J]. 大地测量与地球动力学 , 2009, 29 (4) : 106–110. ZHANG Chengjun, YANG Li, CHEN Jun. Improving Point Positioning Accuracy Using GPS Carrier Smoothed Pseudorange[J]. Journal of Geodesy and Geodynamics , 2009, 29 (4) : 106 –110. |
| [22] | SARDÓN E, ZARRAOA N. Estimation of Total Electron Content Using GPS Data:How Stable are the Differential Satellite and Receiver Instrumental Biases?[J]. Radio Science , 1997, 32 (5) : 1899 –1910. DOI:10.1029/97RS01457 |
| [23] | 吴晓莉, 韩春好, 平劲松. GEO卫星区域电离层监测分析[J]. 测绘学报 , 2013, 42 (1) : 13–18. WU Xiaoli, HAN Chunhao, PING Jinsong. Monitoring and Analysis of Regional Ionosphere with GEO Satellite Observations[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (1) : 13 –18. |


