2. 中国科学院光电研究院,北京 100094 ;
3. 中国科学院大学,北京 100049
2. Academy of Opto-Electronics, Chinese Academy of Sciences, Beijing 100094, China ;
3. University of Chinese Academy of Sciences, Beijing 100049, China
不同类型的导航信号在卫星和接收机不同通道产生的时间延迟(或硬件延迟)并不完全一致,由此产生的两类导航信号之间的时延差异称为差分码偏差(differential code bias, DCB)[1]。其中,同一频率不同类型测距信号之间的DCB称为频内偏差,不同频率不同类型测距信号之间的DCB称为频间偏差[2-3]。卫星和接收机DCB是GNSS(global navigation satellite system)电离层总电子含量(total electron content, TEC)计算必须扣除的误差[4-8]。同时,由于GNSS卫星钟差参数基准通常定义在某一个指定观测量(如BDS B3I)或某两个频率的消电离层组合观测量(如GPS(P1+P2)与Galileo(E1+E5a))上,使用不同于钟差参数基准的观测量时,需引入DCB参数进行卫星硬件时延偏差改正[9]。
常用的DCB产品可以为两类:一类是IGS(International GNSS Service)提供的高精度后处理产品,另一类是GNSS广播星历实时播发的时间群延迟(timing group delay, TGD)或广播群延迟(broadcast group delay, BGD)参数。IGS提供DCB产品的机构包括以欧洲定轨中心(CODE)为代表的电离层工作组和以德国宇航中心(DLR)为代表的MGEX(multi-GNSS experiment)工作组[10-11]。CODE基于全球分布的IGS基准站采用电离层TEC建模的方式同步处理得到GPS及GLONASS的DCB参数,而DLR基于MGEX观测数据直接采用全球电离层格网(global ionospheric map, GIM)扣除电离层TEC影响,进而估计得到GPS、GLONASS、BDS及Galileo的DCB参数[3, 12]。GPS、BDS及Galileo广播星历中均播发TGD参数,但各导航系统TGD参数的含义并不相同。BDS播发的TGD参数(包括TGD1和TGD2)本质上是B1B3和B1B2频点间的DCB参数,而GPS播发的TGD参数和Galileo播发的BGD(包括BGDE1, E5a和BGDE1, E5b)参数与DCB之间存在一个与频率有关的转换因子[13-14]。与IGS提供的DCB产品相比,TGD参数精度不高且更新频次较低(如GPS TGD参数平均每4个月更新一次[15])。但由于TGD参数能够通过广播星历实时获取,因而能够满足GNSS单/双频导航用户定位的DCB改正需求。
随着GPS的现代化,2005年起发射的GPS Block IIR-M卫星在L2频率上增加了L2C民用信号,2010年起发射的GPS Block IIF卫星新增了L5频率以及L5I5、L5Q5两种民用信号[16]。GPS广播星历的卫星钟差参数以L1P(Y)和L2P(Y)消电离层组合为参考基准,因此单独或联合采用4种民用信号(包括L1C/A、L2C、L5I5及L5Q5)实施标准单点定位(standard point positioning, SPP)时,需要将DCB作为一类改正信息。对GPS导航用户而言,除已有的TGD参数外,民用导航(civil navigation, CNAV)星历中新增了4种ISC(inter-signal correction)参数。目前针对ISC参数使用方法、精度分析及其对GPS导航定位影响的研究较少,文献[17]介绍了ISC参数的使用方法,文献[18]基于CODE及DLR提供的DCB产品初步分析了ISC参数的精度。本文在文献[18]研究的基础上,首先给出并讨论了ISC参数的含义及其在GPS导航定位中的使用方法,进而利用不同机构提供的后处理DCB产品评估了ISC参数的实际精度,最后基于MGEX部分监测站观测数据分析了ISC参数对GPS导航用户单/双频定位精度的影响。
1 GPS ISC参数含义GPS在L1C/A、L2C、L5I5及L5Q5民用信号上相对于L1P(Y)分别定义了一个ISC参数,即ISCC/A、ISCL2C、ISCL5I及ISCL5Q。GPS卫星TGD及ISC参数的定义如下[19]
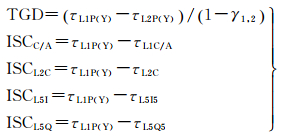 (1)
(1)
式中,τL1P(Y)和τL2P(Y)为L1P(Y)和L2P(Y)信号在卫星端的硬件延迟;τL1CA、τL2C、τL5I5及τL5Q5分别为L1C/A、L2C、L5I5及L5Q5信号在卫星端的硬件延迟;γ1, 2=f12/f22,f1和f2分别为GPS L1和L2信号上的频率。可以看出,ISC参数本质上也是DCB参数。其中,ISCC/A是L1P(Y)与L1C/A信号间的频内偏差参数,ISCL2C、ISCL5I及ISCL5Q分别是L1P(Y)与L2C、L5I5、L5Q5信号间的频间偏差参数。TGD也可以看作是L2P(Y)信号上的ISC参数,不过要乘一个与频率有关的常数进行转换。
表 1进一步给出了GPS广播的TGD、ISC参数与后处理DCB参数之间的对应关系。表中第1列是民用导航星历中定义的TGD及ISC参数类型,第2列是RINEX 3测码数据对应的DCB类型。目前MGEX试验网能够跟踪到C2L、C2S及C2X 3种L2C类型码观测信号,而ISCL2C参数定义并未指定具体的码观测类型,使用时可将ISCL2C参数对应为DCBC1W-C2L、DCBC1W-C2S或DCBC1W-C2X中的任意一种。需要说明的是,第2列中给出的某些DCB类型在实际中无法直接得到,这是因为某些类型的GPS接收机无法同时观测到对应的两类测码信号。如Trimble NETR9接收机只能同时输出C1C、C2W、C2X及C5X 4种码观测量,而Leica GR10/25接收机只能同时输出C1C、C2W、C2S及C5Q 4种码观测量。第3列对应的是中国科学院测量与地球物理研究所(IGG)及DLR基于MGEX观测数据获得的DCB参数,不同于DLR直接采用GIM扣除电离层的影响[3],IGG采用“两步法”逐测站处理得到卫星和接收机的DCB参数[20-21]。第4列对应的是CODE基于IGS全球基准站数据处理得到的DCB参数。分析结果表明,IGG、DLR、CODE提供的GPS卫星DCB产品精度分别可达0.15 ns、0.2 ns及0.1 ns[3, 12, 20-21]。为便于后续对比分析,ISCL2C(对应DCBC1W-C2L或DCBP1-C2)和ISCL5Q(对应DCBC1W-C5Q)参数由不同机构DCB产品的线性组合得到。目前尚无GPS民用接收机能够观测到C5I信号,因此未给出ISCL5I参数实际对应的DCB产品类型。
| CNAV | DCB | IGG/DLR | CODE |
| TGD | 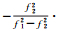 |
 |
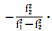 |
| ISCL1C/A | DCBC1W-C1C | -DCBC1W-C1C | DCBP1-C1 |
| ISCL2C | DCBC1W-C2(L/S/X) | DCBC1W-C2W-DCBC2W-C2L | DCBP1-P2+DCBP2-C2 |
| ISCL5I | DCBC1W-C5I | ||
| ISCL5Q | DCBC1W-C5Q | -DCBC1C-C1W+DCBC1C-C5Q |
2 GPS ISC参数改正模型
GPS广播星历中的钟差参数以L1P(Y)+L2P(Y)消电离层组合为参考基准,利用L1(Y)和L2P(Y)实施单点定位时,无需进行TGD参数改正[19]。然而,单独或联合采用L1C/A、L2C、L5I5及L5Q5信号进行单点定位时,需将TGD及ISC参数作为改正信息。本节给出了ISC参数在GPS单/双频导航定位中的改正方法。
GPS卫星与接收机视线方向的伪距观测方程可表示为
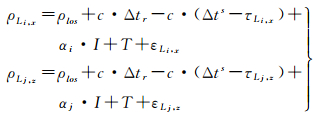 (2)
(2)
式中,ρLi, x为Li频率上的x类型观测值(如L1频率上的P(Y)类型观测值为ρL1, P(Y));ρLj, z为Lj频率上的z类型观测值(单位为m);ρlos为站星视线方向的几何距离(单位为m);Δtr和Δts分别为接收机和卫星钟差(单位为s);τLi, x和τLj, z分别为Li, x和Lj, z信号在卫星端的硬件延迟(单位为s);I为电离层延迟误差(TECu);αi和αj是与频率有关的转换因子(αi=40.28/fi2, αj=40.28/fj2);fi和fj分别为Li和Lj信号上的频率;T为对流层延迟误差(单位为m);εLi, x和εLj, z分别为ρLi, x和ρLj, z上的观测噪声。接收机端硬件延迟在定位中可被接收机钟差参数吸收[22],故式(2)中未将其列出。
GPS卫星钟差是由L1P(Y)+L2P(Y)消电离层组合计算得到,因此,广播星历的卫星钟差参数ΔtSV中含有卫星端L1P(Y)和L2P(Y)的硬件延迟影响
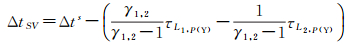 (3)
(3)
由式(1)中TGD及ISC参数定义可知
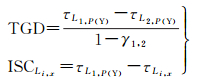 (4)
(4)
式中,ISCLi, x为Li, x测码信号上定义的ISC参数。由式(3)、式(4)可进一步得到
 (5)
(5)
忽略观测噪声的影响,由式(2)、式(5)可以得到新的伪距观测方程
 (6)
(6)
引入γij=fi2/fj2,由ρLi, x和ρLj, z两种观测量构成的消电离层组合观测方程可表示为
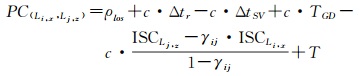 (7)
(7)
将TGD参数表达为TGD=ISCL2, P/1-γ1, 2的形式,由于ISCL1, P=0,式(7)也可以表示为L1P(Y)+L2P(Y)消电离层组合的形式
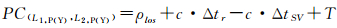 (8)
(8)
GPS民用导航用户可根据式(6)改正TGD及ISC误差后进行单频单点定位,也可根据式(7)选择两种观测量进行双频消电离层组合定位。
3 GPS ISC参数精度分析与TGD参数类似,GPS广播的ISC参数并非每天更新,而是以一定的时间间隔进行更新。本节首先对各GPS卫星ISC参数的更新频次及参数变化进行分析,在此基础上,利用不同机构提供的后处理DCB产品评估GPS ISC参数的实际精度。明确ISC参数的变化规律及其实际精度有利于进一步分析其对GPS导航定位的影响。
选取2014年年积日(day of year, DOY)118 d至2015年112 d GPS民用导航星历的TGD及ISC参数,分析GPS广播的TGD及ISC参数的更新频次及其变化情况。图 1给出了TGD及ISC参数在该时段内的更新时间示意,图中横坐标为GPS卫星SVN(space vehicle number)号,括号内为PRN(pseudo-random noise)号,纵坐标为时间,不同颜色表示TGD或ISC参数的有效时间范围。可以看出,TGD参数并非严格地每4个月更新一次。SVN 57、58、63及64号卫星的TGD参数在近一年的时间内都未更新(后文中的卫星号均指SVN号);48、52及53号卫星的TGD参数2014年10月更新一次后便再未更新;66号卫星的TGD参数2014年10月更新一次后,2015年1月又更新了一次。比较而言,ISC参数的更新频次更有规律:各卫星的ISCC/A、ISCL2C及ISCL5Q参数在2014年6月及2015年2月分别更新了一次。从GPS导航定位对卫星硬件时延偏差的改正需求来看,广播的TGD及ISC参数最好一个月左右更新一次;然而受主控站数据处理策略等因素的影响,TGD及ISC参数可能几个月才更新一次。文献[22]的分析结果表明,由于卫星硬件时延参数稳定性较好,TGD参数数月更新一次能够保持较高的可靠性,但一年或更长时间更新一次则会引入较大的误差[23]。

|
| 图 1 GPS广播的TGD及ISC参数更新时间示意 Fig. 1 GPS broadcast TGD and ISC parameters update time interval |
图 2给出了2014年DOY 118-365天各GPS卫星TGD、ISC参数的变化情况,从上到下4幅子图分别对应TGD、ISCC/A、ISCL2C及ISCL5Q参数,图中竖线左边为GPS Block IIR-M卫星,右边为Block IIF卫星。从图中可以看出:①Block IIR-M与Block IIF卫星TGD参数差异约为20 ns,相同类型卫星TGD之间的差异约为6 ns。②Block IIR-M卫星各ISCL2C参数之间的差异小于2 ns,Block IIF卫星ISCL2C参数的差异小于4 ns,两类卫星ISCL2C参数差异约为13 ns,小于不同类型卫星TGD参数之间的差异。③只有新发射的Block IIF卫星能够播发ISCL5Q参数,各卫星ISCL5Q参数之间的差异最大可达6 ns。④与TGD、ISCL2C及ISCL5Q参数相比,ISCC/A参数的变化范围最小:Block IIR-M卫星ISCC/A参数之间的差异小于0.6 ns,Block IIF卫星的差异小于2.5 ns。总体而言,不同类型卫星TGD、ISC参数差异较大,同一类型卫星TGD、ISC参数差异较小,同时,各卫星ISCC/A参数变化范围明显小于TGD、ISCL2C及ISCL5Q参数。

|
| 图 2 不同GPS卫星的TGD及ISC参数值 Fig. 2 GPS broadcast TGD and ISC values of each individual satellite |
利用IGG、DLR及CODE提供的DCB产品评估GPS广播的TGD及ISC参数精度有以下两点原因:①DCB参数解算时利用了较多的全球基准站观测数据,其精度与可靠性高于广播星历中播发的TGD及ISC参数[14]。②IGG、DLR及CODE提供的DCB产品采用不同处理方法,基本反映了当前DCB参数的最高处理水平[3, 12, 21]。DCB、TGD及ISC参数解算时,卫星和接收机偏差参数是相关的,因此必须引入一个参考基准,才能实现卫星与接收机偏差参数的分离[20]。不同机构提供的DCB产品采用“零均值”基准约束,即所有卫星的DCB之和为零;而TGD及ISC参数采用某台硬件时延偏差标定的接收机为参考基准[3, 21]。由于TGD、ISC参数与各机构DCB产品之间采用的参考基准不同,使用时需将不同的参考基准转换至统一的基准后再进行比较。假设有μ颗卫星,对所有卫星施加“零基准”约束,则有
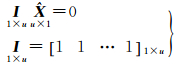 (9)
(9)
式中,
选取其中μ1颗卫星构造新的卫星“零基准”约束
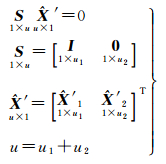 (10)
(10)
式中,S为新的卫星约束基准列向量,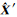
 (11)
(11)
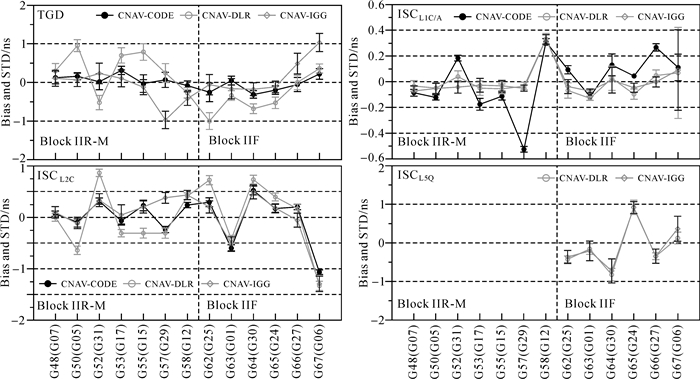
以GPS Block IIF卫星为参考构造新的卫星“零基准”约束,将GPS广播的TGD、ISC参数及后处理DCB参数转换至统一的卫星基准。图 3给出了各GPS卫星TGD、ISC参数相对于IGG、DLR及CODE后处理DCB产品的平均偏差及STD,左上至右下4幅子图分别对应TGD、ISCC/A、ISCL2C及ISCL5Q参数。从图中可以看出,TGD参数与CODE产品之间的偏差为-0.31~0.30 ns,与IGG/DLR产品之间的偏差为-0.97~1.03 ns,与各机构DCB产品之间差异的STD为0.10~0.25 ns。ISCL2C参数与DLR产品之间的偏差较大(-1.32~0.86 ns),与IGG及CODE产品之间的偏差基本相当(-1.16~0.49 ns)。目前CODE尚未提供与ISCL5Q对应的DCB产品,因此仅将ISCL5Q与IGG、DLR产品进行比较。除67号星外,ISCL5Q参数与IGG/DLR产品之间的偏差为-0.89~0.92 ns,STD为0.08~0.21 ns。ISCC/A参数与IGG/DLR产品之间的偏差较小,为-0.13~0.33 ns;与CODE产品之间的偏差为-0.53~0.31 ns。这种差异与IGG、DLR及CODE频内偏差参数的处理策略不同有关:IGG与DLR通过观测值的直接组合处理得到DCBC1C-C1W参数[3, 21],而CODE的DCBP1-C1参数是卫星钟差解算得到的副产品[12]。
|
| 图 3 GPS广播的TGD、ISC参数相对于IGG、DLR及CODE后处理DCB产品的平均偏差及STD Fig. 3 Bias and STD of the GPS broadcast TGD and ISCs relative to the DCB products of IGG, DLR and CODE |
表 2给出了GPS广播的TGD及ISC参数的精度统计情况。表中第2列是各参数的变化范围,后3列是TGD、ISC参数相对于IGG、DLR及CODE对应DCB产品偏差的RMS。从表中可以看出,TGD及ISC参数与不同机构DCB产品的比较结果略有差异;但总体而言,ISCC/A参数精度可以达到0.2 ns,TGD、ISCL2C及ISCL5Q参数精度能够达到0.5 ns。
| 参数范围 | CNAV-IGG | CNAV-DLR | CNAV-CODE | |
| TGD | -9.24~9.85 | 0.41 | 0.56 | 0.23 |
| ISCL1C/A | -1.41~1.01 | 0.10 | 0.12 | 0.18 |
| ISCL2C | -7.17~5.75 | 0.37 | 0.52 | 0.33 |
| ISCL5Q | -3.91~2.05 | 0.55 | 0.49 |
4 GPS ISC参数对单点定位影响分析
从式(6)可以看出,GPS民用导航信号伪距观测方程需同时引入TGD及ISC参数作为改正信息。为分析TGD、ISC参数在定位中的误差项大小,图 4给出了各GPS卫星TGD与ISCC/A、ISCL2C及ISCL5Q参数之间的差异。可以看出,GPS Block IIR-M和Block IIF卫星的TGD与ISCL2C参数之间的差异约为25 ns,与ISCC/A参数的差异约为15 ns。不同类型卫星TGD与ISC参数之间的差异较大,因此这些参数对定位的影响不能忽略。同时可以看出,GPS Block IIR-M卫星TGD与ISCL2C、ISCC/A参数之间的差异分别为5 ns、 2 ns,Block IIF卫星TGD与ISCL2C、ISCC/A及ISCL5Q参数之间的差异分别为6 ns、4 ns及7 ns。同一类型卫星TGD与ISC参数之间的差异较小,仅采用GPS Block IIR-M或Block IIF卫星进行定位时,TGD及ISC参数对单点定位解的影响将会变小,这是因为各卫星相同的卫星硬件延迟误差在定位中会被接收机钟差参数吸收。

|
| 图 4 不同GPS卫星TGD与ISCC/A、ISCL2C及ISCL5Q参数之间的差异 Fig. 4 Differences of ISCC/A, ISCL2C and ISCL5Q with respect to TGD parameters |
由于各监测站能够同时观测到的GPS卫星数量有限,将不再单独利用GPS Block IIR-M或Block IIF卫星进行定位试验。同时,由于能够播发L5Q信号的GPS卫星较少,后续分析中将分别以GPS C2L及C1C+C2L观测量为例,分析ISC参数对GPS单/双频用户导航定位解的影响。
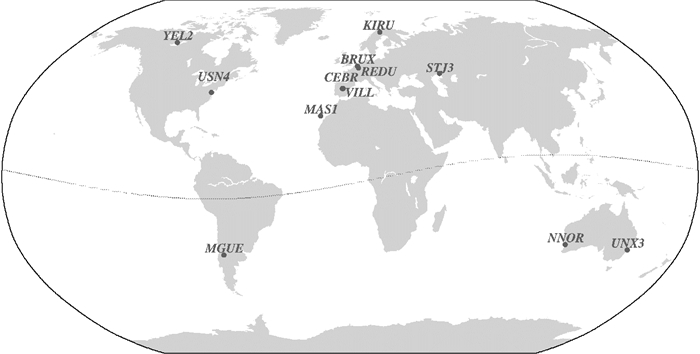
4.1 试验方案选取2014年连续11 d(DOY 300-310)12个MGEX站观测数据、采用单频SPP及双频消电离层组合SPP分析ISC参数对GPS民用导航用户定位精度的影响。试验期间电离层活动较为剧烈:太阳活动指数F10.7在120~188 sfu之间变化,第300及308天的Kp指数大于4。MGEX测试站分布如图 5所示,接收机类型为Septentrio PolaRx4/4TR,能够输出的GPS码观测类型包括C1C、C1W、C2W、C2L及C5Q 5类。以GPS静态精密单点定位(precise point positioning, PPP)的单天解作为坐标参考“真值”,基于动态SPP估计测站坐标及接收机钟差参数。SPP数据处理中,观测数据采样率为60 s,卫星截止高度角为100,卫星轨道及钟差采用广播星历的轨道及钟差参数,对流层误差采用UNB 3 m模型改正[24],单频SPP中电离层误差采用GPS广播星历发播的Klobuchar模型改正。
|
| 图 5 MGEX试验网测试站分布 Fig. 5 Distribution of the selected MGEX stations |
表 3给出了5种不同的SPP定位试验方案。设计这5种试验方案目的有3点:①通过分析C2L观测量采用与不采用ISC参数改正后的位置解精度,分析ISC参数对GPS单频SPP定位的影响。②通过分析C1C+C2L(即L1C/A+L2C)消电离层组合采用与不采用ISC参数改正后的位置解精度,分析ISC参数对GPS双频SPP定位的影响。③通过对比C1C+C2L与C1W+C2W [即L1P(Y)+L2P(Y)]消电离层组合SPP精度,分析GPS普通用户与授权用户定位精度的差异。需要说明的是,利用C1W和C2W进行定位时仅考虑了试验期间能够同时播发L2C民用信号的13颗GPS卫星。
| 定位模式 | 观测量 | ISC改正 | 说明 |
| 单频SPP | C2L | 否 | non_corr:不采用ISC改正 |
| C2L | 是 | ISC_corr:采用ISC改正 | |
| 双频SPP | C1C+C2L | 否 | non_corr:不采用ISC改正 |
| C1C+C2L | 是 | ISC_corr:采用ISC改正 | |
| C1W+C2W |
4.2 结果分析
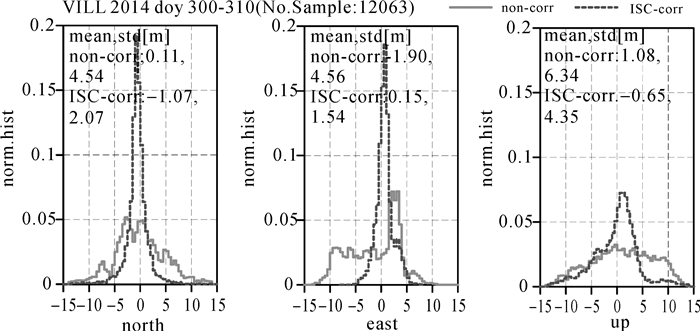
以欧洲地区的VILL站为例,图 6给出了该站2014年DOY 300-310 d C2L单频SPP的定位误差分布,从左至右3幅子图分别对应N、E、U 3个方向的误差分布。可以看出,采用ISC参数改正后,单频SPP的定位误差明显减小。未采用ISC参数改正时,N、E、U 3个方向误差的均值分别为-0.11 m、-1.90 m及-1.08 m,标准差分别为4.54 m、4.56 m及6.34 m;采用ISC参数改正后,N、E、U 3个方向误差的均值分别为-1.07 m、0.15 m及-0.65 m,标准差分别为2.07 m、1.54 m及4.35 m。采用ISC参数改正后,N、E、U 3个方向的定位精度分别提高了2.34 m、3.69 m及2.05 m。
|
| 图 6 VILL站C2L单频SPP N、E、U方向定位误差分布(2014年DOY 300-310) Fig. 6 Normalized histograms of the north, east and up positioning errors of C2L SPP on VILL site (2014 DOY 300-310) |
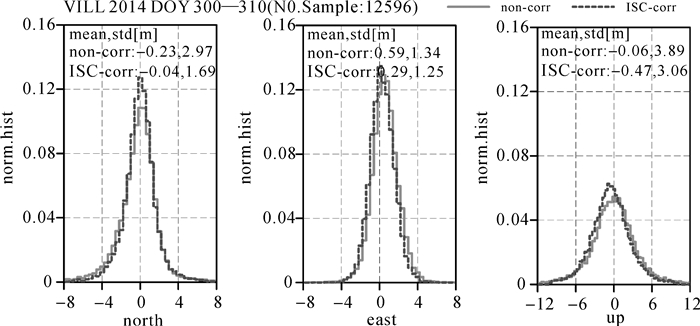
图 7给出了该站2014年DOY 300-310 d C1C+C2L双频SPP的定位误差分布。从图中可以看出,VILL站东方向定位误差最小(-4.0~4.0 m),高程方向定位误差最大(-12.0~12.0 m)。具体而言,未采用ISC参数改正时,N、E、U 3个方向误差的均值分别为-0.23 m、0.59 m及-0.06 m,标准差分别为2.97 m、1.34 m及3.89 m;采用ISC参数改正后,N、E、U 3个方向误差的均值分别为-0.04 m、0.29 m及-0.47 m,标准差分别为1.69 m、1.25 m及3.06 m。采用ISC参数改正后,VILL站N、E、U 3个方向的定位精度分别提高了0.34 m、0.17 m及0.66 m。
|
| 图 7 VILL站C1C+C2L双频SPP N、E、U方向定位误差分布(2014年DOY 300-310) Fig. 7 Normalized histograms of the north, east and up positioning errors of C1C+C2L SPP on VILL site (2014 DOY 300-310) |
表 4给出了试验期间不同试验方案所有测试站的定位误差RMS统计情况。可以看出,利用C2L进行单频SPP未改正ISC参数时,N、E、U 3个方向的误差分别为5.174 m、4.012 m及7.093 m;采用ISC参数改正后,N、E、U 3个方向的定位精度提高了40.1%、46.0%及23.8%,分别达到3.653、2.146及5.284 m。C2L单频SPP三维定位精度提高了30.0%,由改正前的9.765 m提高到6.889 m。利用C1L+C2L进行双频SPP未改正ISC参数时,N、E、U 3个方向的误差分别为1.588 m、1.295 m及3.172 m;采用ISC参数改正后,N、E、U 3个方向的定位精度提高了9.5%、10.2%及13.0%,分别达到1.432 m、1.165 m及2.748 m。C1L+C2L双频SPP三维定位精度提高了12.2%,由改正前的3.786 m提高到3.317 m。单频SPP中除ISC外的其他误差改正项均相同,ISC参数本身的误差影响较小,改正ISC参数能够显著提高单频SPP的定位精度;双频消电离层组合在消除电离层误差的同时也放大了测码伪距观测噪声的影响,双频SPP中ISC参数本身的误差也会被进一步放大,这可能是改正ISC后双频SPP不如单频SPP精度提升的原因之一。此外,C1C与C2L组合定位采用ISC改正后的三维定位精度略高于C1W与C2W消电离层组合的定位精度(3.317 m vs. 3.441 m)。这表明,采用ISC参数改正后,L1C/A+L2C民用信号的双频定位精度与当前L1P(Y)+L2P(Y)消电离层组合定位精度相当。
| 观测量 | ISC改正 | RMS | |||
| N/m | E/m | U/m | 3D/m | ||
| C2L | non_corr | 5.174 | 4.012 | 7.093 | 9.765 |
| C2L | ISC_corr | 3.653 | 2.149 | 5.284 | 6.889 |
| 精度提升/ (%) | - | 40.1 | 46.0 | 23.8 | 30.6 |
| C1C+C2L | non_corr | 1.588 | 1.295 | 3.172 | 3.786 |
| C1C+C2L | ISC_corr | 1.432 | 1.165 | 2.748 | 3.317 |
| 精度提升/(%) | - | 9.5 | 10.2 | 13.0 | 12.2 |
| C1W+C2W | - | 1.505 | 1.203 | 2.830 | 3.441 |
| 注:Imp.=|RMSISC_corr -RMSnon_corr|/RMSnon_corr | |||||
5 结论
针对GPS民用导航星历中新增的ISCC/A、ISCL2C、ISCL5I和ISCL5Q 4种ISC参数,本文给出了GPS ISC参数的含义及其在GPS标准单点定位中的使用方法,利用不同机构(包括IGG、DLR及CODE)提供的后处理DCB产品评估了GPS广播的TGD及ISC参数的实际精度,深入分析了ISC参数对GPS导航用户单/双频定位精度的影响。结果表明:
(1) GPS广播的卫星钟差参数由L1P(Y)和L2P(Y)消电离层组合计算得到,单独或联合采用民用信号实施SPP时,需同时引入TGD及ISC参数作为改正信息。
(2) ISC参数更新频次较有规律,2014年4月至2015年4月期间,各卫星ISC参数在2014年6月及2015年2月分别更新了一次。
(3) TGD及ISC参数与不同机构后处理DCB产品的比较结果略有差异,总体而言,ISCC/A参数精度可以达到0.2 ns,TGD、ISCL2C及ISCL5Q参数精度能够达到0.5 ns。
(4) 同一类型GPS卫星TGD与ISC参数之间的差异较小,不同类型卫星TGD与ISC参数之间的差异较大,TGD及ISC参数对GPS定位影响不能忽略。
(5) 经由TGD及ISC参数改正后,GPS民用导航信号L2C单频SPP精度提升显著,L1C/A+L2C双频SPP精度与L1P(Y)+ L2P(Y)消电离层组合的定位精度相当。
致谢: 感谢Oliver Montenbruck博士在本文研究中提供的帮助。
| [1] | 袁运斌, 欧吉坤. GPS观测数据中的仪器偏差对确定电离层延迟的影响及处理方法[J]. 测绘学报 , 1999, 28 (2) : 19–23. YUAN Yunbin, OU Jikun. The Effects of Instrumental Bias in GPS Observations on Determining Ionospheric Delays and the Methods of Its Calibration[J]. Acta Geodaetica et Cartographica Sinica , 1999, 28 (2) : 19 –23. |
| [2] | LI Zishen, YUAN Yunbin, FAN Lei, et al. Determination of the Differential Code Bias for Current BDS Satellites[J]. IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (7) : 3968 –3979. DOI:10.1109/TGRS.2013.2278545 |
| [3] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P. Differential Code Bias Estimation Using Multi-GNSS Observations and Global Ionosphere Maps[J]. Navigation , 2014, 61 (3) : 191 –201. DOI:10.1002/navi.v61.3 |
| [4] | 常青, 张东和, 萧佐, 等. GPS系统硬件延迟估计方法及其在TEC计算中的应用[J]. 地球物理学报 , 2001, 44 (5) : 596–601. CHANG Qing, ZHANG Donghe, XIAO Zuo, et al. A Method for Estimating GPS Instrumental Biases and Its Application in TEC Calculation[J]. Chinese Journal of Geophysics , 2001, 44 (5) : 596 –601. |
| [5] | 张小红, 李征航, 蔡昌盛. 用双频GPS观测值建立小区域电离层延迟模型研究[J]. 武汉大学学报(信息科学版) , 2001, 26 (2) : 140–143. ZHANG Xiaohong, LI Zhenghang, CAI Changsheng. Study on Regional Ionospheric Model Using Dual-frequency GPS Measurements[J]. Geomatics and Information Science of Wuhan University , 2001, 26 (2) : 140 –143. |
| [6] | 章红平, 施闯, 唐卫明. 地基GPS区域电离层多项式模型与硬件延迟统一解算分析[J]. 武汉大学学报(信息科学版) , 2008, 33 (8) : 805–809. ZHANG Hongping, SHI Chuang, TANG Weiming. United Solution to Polynomial VTEC Modeling and DCB Analysis Using Ground-based GPS Observations[J]. Geomatics and Information Science of Wuhan University , 2008, 33 (8) : 805 –809. |
| [7] | 张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报 , 2011, 40 (4) : 447–453. ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Calibration of Slant Total Electron Content and Satellite-receiver's Differential Code Biases with Uncombined Precise Point Positioning Technique[J]. Acta Geodaetica et Cartographica Sinica , 2011, 40 (4) : 447 –453. |
| [8] | ZHANG Baocheng, TEUNISSEN P J G. Characterization of Multi-GNSS Between-Receiver Differential Code Biases Using Zero and Short Baselines[J]. Science Bulletin , 2015, 60 (21) : 1840 –1849. DOI:10.1007/s11434-015-0911-z |
| [9] | MONTENBRUCK O, HAUSCHILD A.Code Biases in Multi-GNSS Point Positioning[C]//Proceedings of ION ITM 2013.San Diego:Institute of Navigation, 2013:616-628. |
| [10] | DACH R, BROCKMANN E, SCHAER S, et al. GNSS Processing at CODE:Status Report[J]. Journal of Geodesy , 2009, 83 (3-4) : 353 –365. DOI:10.1007/s00190-008-0281-2 |
| [11] | MONTENBRUCK O, STEIGENBERGER P, KHACHIKYAN R, et al.IGS-MGEX:Preparing the Ground for Multi-constellation GNSS Science[C]//Proceedings of the 4th International Colloquium on Scientific and Fundamental Aspects of the Galileo System.Galile:[s.n.], 2013, 9(1):42-49. |
| [12] | SCHAER S.Differential Code Biases (DCB) in GNSS Analysis[C]//Proceedings of IGS Workshop 2008. Miami Beach:Swiss Federal Office of Topography Swisstopo, 2008. |
| [13] | 吴晓莉, 平劲松, 刘利, 等. 区域卫星导航系统硬件延迟解算[J]. 武汉大学学报(信息科学版) , 2011, 36 (10) : 1218–1221. WU Xiaoli, PING Jinsong, LIU Li, et al. Hardware Delay Solution of Regional Satellite Navigation System[J]. Geomatics and Information Science of Wuhan University , 2011, 36 (10) : 1218 –1221. |
| [14] | GUO Fei, ZHANG Xiaohong, WANG Jinling. Timing Group Delay and Differential Code Bias Corrections for BeiDou Positioning[J]. Journal of Geodesy , 2015, 89 (5) : 427 –445. DOI:10.1007/s00190-015-0788-2 |
| [15] | MICHAEL Rivers.The 2 SOPS User Range Accuracy (URA) Improvement and Broadcast Inter-frequency Bias (TGD) Updates[C]//Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2000).Salt Lake City, UT:ION, 2000:2551-2555. |
| [16] | MONTENBRUCK O, LANGLEY R B, STEIGENBERGER P. First Live Broadcast of GPS CNAV Messages[J]. GPS World , 2013, 24 (8) : 14 . |
| [17] | FEESS W, COX J, HOWARD E, et al.GPS Inter-signal Corrections (ISCs) Study[C]//Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2013).Nashville, TN:[s.n.], 2013:951-958. |
| [18] | STEIGENBERGER P, MONTENBRUCK O, HESSELS U.Performance Evaluation of the Early CNAV Navigation Message[C]//Proceedings of the 2015 International Technical Meeting of the Institute of Navigation.Dana Point, California:Laguna Cliffs Marriott, 2015:155-163. |
| [19] | IS-GPS-200 Navstar GPS Space Segment/Navigation User Interfaces[S].Calif, USA:Revision G, GPS Directorate, 2004. |
| [20] | LI Zishen, YUAN Yunbin, LI Hui, et al. Two-step Method for the Determination of the Differential Code Biases of Compass Satellites[J]. Journal of Geodesy , 2012, 86 (11) : 1059 –1076. DOI:10.1007/s00190-012-0565-4 |
| [21] | WANG Ningbo, YUAN Yunbin, LI Zishen, et al. Determination of Differential Code Biases with Multi-GNSS Observations[J]. Journal of Geodesy , 2016, 90 (3) : 209 –228. DOI:10.1007/s00190-015-0867-4 |
| [22] | 张宝成, 欧吉坤, 袁运斌, 等. 基于GPS双频原始观测值的精密单点定位算法及应用[J]. 测绘学报 , 2010, 39 (5) : 478–483. ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Precise Point Positioning Algorithm Based on Original Dual-frequency GPS Code and Carrier-phase Observations and Its Application[J]. Acta Geodaetica et Cartographica Sinica , 2010, 39 (5) : 478 –483. |
| [23] | WILSON B D, YINGER C H, FEESS W A, et al. New and Improved:the Broadcast Inter Frequency Biases[J]. GPS World , 1999, 10 (9) : 56 –66. |
| [24] | LEANDRO R, SANTOS M, LANGLEY R.UNB Neutral Atmosphere Models:Development and Performance[C]//Proceedings of ION NTM 2006. Monterey, CA:Hyatt Regency Hotel, 2006:18-20. |


