美国勇气号和机遇号火星车自2004年登陆火星以来,已在火星表面服役将近12年,高精度的火星车导航定位对安全行驶和科学考察发挥了非常重要的作用[1]。目前,火星车在行进过程中,主要采用航迹推算的方法实时获取位置。其基本原理是利用自身搭载的Pancam相机作为太阳敏感器,在初始位置已知的情况下,观测太阳确定车体的绝对航向,然后融合里程计和惯性导航设备的输出信息,实现载体的位置推算,即进行相对定位。受车轮打滑和惯性导航设备累积误差的影响,航迹推算得到的位置存在累积误差[2-7]。为了消除累积位置误差的影响,地球上的观测者综合运用了无线电测控和地面影像与高精度遥感影像对比两种方法实现绝对定位,前者精度约为百米量级,后者精度可达几米量级。但两种方法都需要在地球上进行解算,无法实现火星车实时、自主绝对定位[8]。
针对火星车实时、自主绝对定位问题,国内外学者开展了广泛的研究,其中采用火星车自身搭载的太阳敏感器实现绝对定位是研究的热点之一。文献[9]在地表对太阳进行了两次时间间隔为26 min的拍摄,得到两个太阳高度角,通过天文位置圆交汇的方法定位,定位经度误差为11′,纬度误差为7′。文献[10]在地表对太阳进行了20 min的跟踪观测,获取了太阳方向矢量的观测序列,采用多矢量定姿算法进行定位,位置误差最大达到200 km。文献[11]进行了3次地表测日定位试验,每次试验对太阳的跟踪观测时长为30 min,采样率为1 min,采用高度法求解得到的位置误差最大值为14.84 km,最小值为4.27 km,平均位置误差为8.546 km。上述测日绝对定位方法精度较低的主要原因是跟踪观测时间较短、太阳在空间的位移量较小、导致位置求解时法方程出现病态。而且长达半个小时的跟踪观测也会影响导航定位的实时性。本文将从病态问题的角度看待测日天文定位问题,研究如何在超短的跟踪观测时间(1~2 min)内,实现测日快速、绝对定位。
1 高度法定位的病态问题 1.1 最小二乘定位模型高度法定位的观测方程为[12]
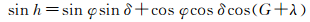 (1)
(1)
式中,h为自然天体高度角,通过观测及大气折射改正得到;δ、G为自然天体的视赤纬和格林尼治时角,可根据天体历表及观测时刻计算得到;λ、φ为测站经度和纬度,为待估参数。设测站天文经纬度的初值为λ0、φ0,对应的改正数为Δλ、Δφ,太阳高度角观测量的改正数为v,则观测方程改写为
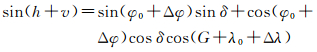 (2)
(2)
令
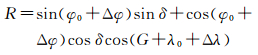 (3)
(3)
则
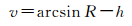 (4)
(4)
对arcsin R进行线性化可得
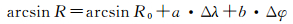 (5)
(5)
式中
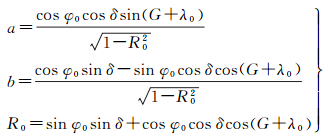 (6)
(6)
令
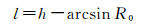 (7)
(7)
则线性化后的观测方程可简写为
 (8)
(8)
若有n组观测方程,则可写成矩阵形式
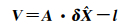 (9)
(9)
式中
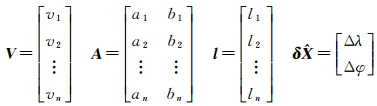 (10)
(10)
此即经典的最小二乘模型,在高度角观测值等权的情况下可按如下公式求解未知参数
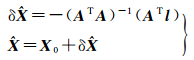 (11)
(11)
当对太阳的跟踪观测时间极短时,由于太阳在空间的位移量极小,导致高度角观测量之间具有很强的相关性。此时,采用式(11)求解位置参数时,法方程表现为病态,较小的观测误差可能造成解算结果的严重失真。对于病态性进行正确诊断和度量,是削弱或克服病态性影响的前提。奇异值分解法是较常用的一种诊断方法。文献[13]给出的一般标准是:λmin > 0.1,认为不存在病态性;0.05 < λmin < 0.1,认为有较弱的病态性;0.01 < λmin < 0.05,认为有中等或较强程度的病态性;若λmin < 0.01,认为病态性较为严重。
以夏至日2014-06-22为例,将测站坐标设为(E 113°37′27.1″,N 34°44′22.7″),采样率为5 s。当太阳在卯酉圈附近(太阳方位角Az≈90°)、介于卯酉圈和子午圈中间(太阳方位角Az≈135°),以及在中天附近(太阳方位角Az≈180°)时,系数矩阵A的奇异值与跟踪观测时间的关系如表 1所示。
| 太阳位置 | 奇异值 | 跟踪观测时长/min | ||||||
| 1 | 2 | 3 | 4 | 5 | 10 | 15 | ||
| Az≈90° | λmax | 2.122 3 | 2.943 2 | 3.580 5 | 4.120 4 | 4.597 3 | 6.474 8 | 7.918 7 |
| λmin | 0.002 0 | 0.005 3 | 0.009 6 | 0.014 7 | 0.020 4 | 0.057 0 | 0.104 2 | |
| Az≈135° | λmax | 0.863 7 | 1.197 8 | 1.457 2 | 1.676 9 | 1.871 0 | 2.635 2 | 3.223 2 |
| λmin | 0.003 1 | 0.008 4 | 0.015 1 | 0.022 9 | 0.031 9 | 0.089 0 | 0.162 9 | |
| Az≈180° | λmax | 0.706 2 | 0.979 3 | 1.191 3 | 1.371 0 | 1.529 6 | 2.154 0 | 2.633 7 |
| λmin | 0.003 7 | 0.009 9 | 0.017 8 | 0.027 1 | 0.037 7 | 0.105 3 | 0.192 7 | |
由表 1可知,当跟踪观测时间小于等于2 min时,最小奇异值λmin < 0.01,系统具有严重的病态性;当跟踪观测时间为3~5 min时,最小奇异值0.01 < λmin < 0.05,系统具有中等或较强程度的病态性;当跟踪观测时间为10 min时,最小奇异值λmin > 0.05,系统有较弱的病态性;当跟踪观测时间为15 min时,最小奇异值λmin > 0.1,认为系统不存在病态性。分析表 1还可以得出以下结论:①太阳在相同的位置附近时,跟踪观测时间越短,系统的病态性越严重;②在相同的跟踪观测时间内,太阳在子午圈附近时的病态程度最轻,其次是卯酉圈和子午圈中间,再次是卯酉圈附近。这是因为太阳在子午圈附近,即中天附近时,其运动速度较快,在相同的时间内具有更大的空间位移量。
1.3 常用有偏估计方法自从20世纪50年代特别是60年代以来,统计学家们作了种种努力,提出了许多类估计,试图改进最小二乘估计。其中,有偏估计就是很重要的一类估计。Tikhonov正则化方法和截断奇异值分解法(truncated singular value decomposition,TSVD)用于直接解算病态观测方程引起了越来越多的关注,并且已经在地球物理反演等领域中得到了成功的应用[14]。
Tikhonov正则化方法的关键是合理确定正则化参数α,TSVD法的关键是合理地确定奇异值的截断水平k,许多文献把k也称之为正则化参数,本文也沿用这一称谓。针对α和k的确定,有两种具有代表性的方法,分别为L曲线法和广义交叉检验法(GCV)[15-16]。
2 不同有偏估计方法的比较事实上,并不存在一种适合所有病态问题的最优有偏估计方法。因此,针对特定的问题,对不同的有偏估计方法及正则化参数确定方法进行比较是一项有意义的工作。本节将Tikhonov正则化方法和TSVD法应用于高度法测日定位的同时,选择L曲线法或GCV法确定正则化参数,通过不同的组合试图找到适用于测日定位的最优有偏估计方法。下面将通过仿真计算进行分析。
依据准确的测站坐标(113°37′27.1″E,34°44′22.7″N),计算夏至日2014-06-22的太阳真高度角,计算程序采用美国海军天文台提供的NOVAS3.0程序包。取太阳敏感器观测太阳的典型精度15″(1σ)[17],采样周期T=5.0 s,跟踪观测时长为2 min,生成仿真观测数据。下面给出4种位置求解方案:
(1) 经典最小二乘:LS。
(2) Tikhonov正则化,GCV法确定正则化参数:Tikhonov & GCV。
(3) Tikhonov正则化,L曲线法确定正则化参数:Tikhonov & L Curve。
(4) TSVD法,GCV法确定正则化参数:TSVD & GCV。
测站经度和纬度初值为λ0=λ+300″,φ0=φ-300″,分别计算太阳在卯酉圈附近(太阳方位角Az≈90°)、介于卯酉和子午圈中间(太阳方位角Az≈135°),以及在中天附近(太阳方位角Az≈180°)时,利用上述4种方法进行计算,每种方法的仿真计算次数为2000次时,均方根误差RMSE统计趋于稳定,结果如表 2所示。
| 求解方案 | Az≈90° | Az≈135° | Az≈180° | |||||
| RMSE(λ) | RMSE(φ) | RMSE(λ) | RMSE(φ) | RMSE(λ) | RMSE(φ) | |||
| 1 | 158.62″ | 5 566.68″ | 947.93″ | 781.36″ | 817.15″ | 12.06″ | ||
| 2 | 5.40″ | 2 321.09″ | 387.42″ | 318.47″ | 397.73″ | 4.72″ | ||
| 3 | 4.98″ | 299.55″ | 36.78″ | 31.41″ | 293.83″ | 4.26″ | ||
| 4 | 4.98″ | 300.25″ | 31.29″ | 27.35″ | 300.69″ | 4.24″ | ||
由表 2可知,利用LS得到的结果具有较大的均方根误差,利用正则化方法及截断奇异值法得到的结果具有明显较小的均方根误差。方案3和4的解算精度最高,结果也比较接近。当太阳方位角Az≈90°时,采用方案3和4求解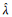
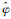
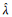
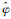
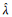
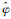
考虑到火星具有与地球相近的自转速度,但半径仅为地球的一半,因此可以估算方案4求解的经度方向最好精度(太阳在卯酉圈附近)约为75 m,纬度方向最好精度(太阳在中天附近)约为63.6 m。从应用角度来看,当早晨太阳处于卯酉圈附近时,通过1~2 min的测日,采用有偏估计方法可以改善火星车在经度方向的位置精度;当中午太阳处于卯酉圈附近时,通过1~2 min的测日,采用有偏估计方法可以改善火星车在纬度方向的位置精度。目前,火星车设计的航迹推算精度约为10%,即每1 km的行进距离产生的航迹推算误差约为100 m。但勇气号在哥伦比亚山上坡时出现过125%的车轮打滑,导致航迹推算误差较大[8]。对比表 2的精度结果,可以考虑在火星车行驶距离达到公里级别或车轮出现严重打滑的情况下,采用有偏估计的方法改善航迹推算的位置精度。
3 初值对有偏估计的影响分析表 2还可以发现,当太阳方位角Az≈90°时,采用方案3或4求解得到的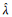
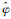
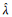
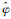
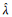
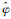
用Δλ和Δφ表示测站位置初值与测站位置真值之差
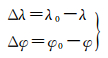 (12)
(12)
则初值相对于真值的位置误差可表示为
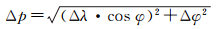 (13)
(13)
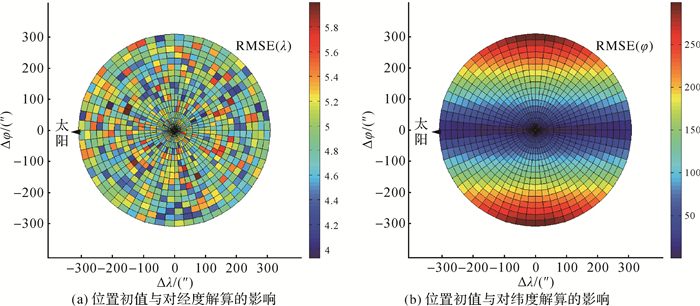
设定不同的Δλ和Δφ,使0″ < Δp < 300″,从而模拟不同的初值条件。其他仿真计算条件同第3节不变,采用方案4(TSVD & GCV,以下统称有偏估计方法)求解,仿真计算次数为2000次时,RMSE值统计趋于稳定。图 1-图 3分别给出了太阳方位角Az≈90°、Az≈135°及Az≈180°时,经纬度的RMSE随测站位置初值的变化情况。图中每一个小颜色块的中心代表一个初值,相应的RMSE值用颜色表示,单位为角秒。
|
| 图 1 太阳方位角Az≈90°时位置初值对有偏估计的影响 Fig. 1 Initial values' impact on bias estimation when Az≈90° |
|
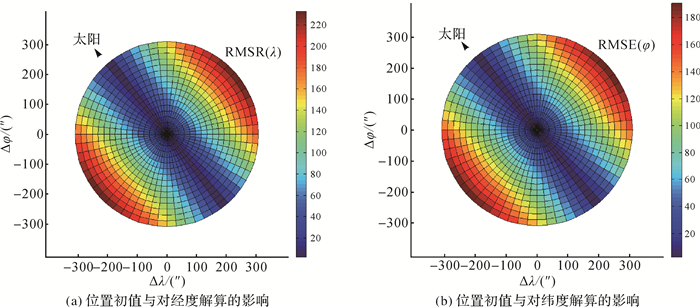
| 图 2 太阳方位角Az≈135°时位置初值对有偏估计的影响 Fig. 2 Initial values' impact on bias estimation when Az≈135° |
|
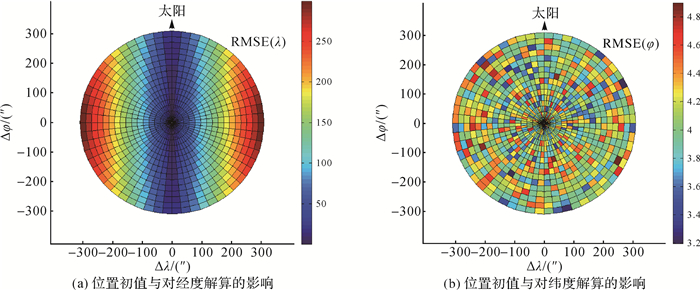
| 图 3 太阳方位角Az≈180°时位置初值对有偏估计的影响 Fig. 3 Initial values' impact on bias estimation when Az≈180° |
如图 1所示,当太阳方位角Az≈90°时,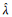
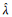
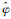
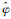
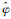
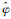
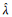
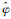
如图 2所示,当太阳方位角A≈135°时,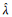
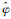
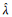
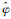
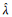
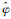
如图 3所示,当太阳方位角A≈180°时,情况恰好与图 1相反。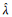
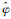
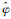

|
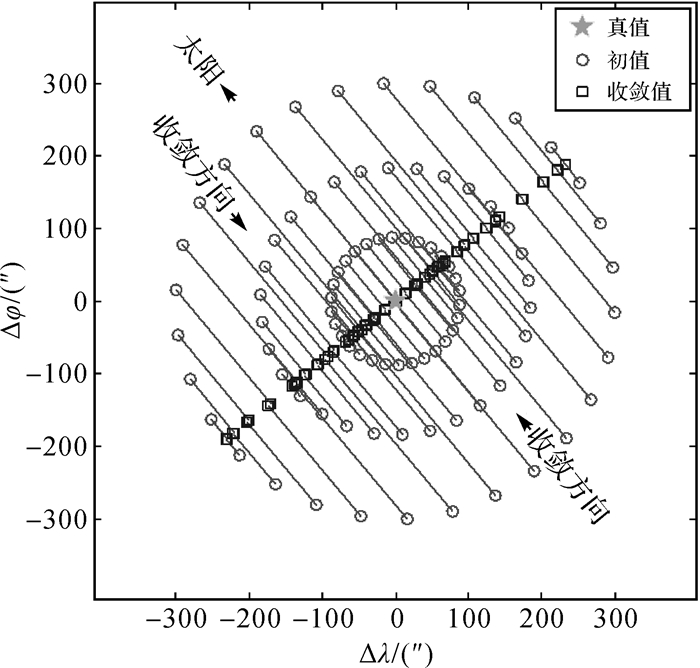
| 图 4 太阳方位角Az≈90°时位置初值的收敛趋势 Fig. 4 Convergence tendency of initial values when Az≈90° |
|
| 图 5 太阳方位角Az≈135°时位置初值的收敛趋势 Fig. 5 Convergence tendency of initial values when Az≈135° |

|
| 图 6 太阳方位角Az≈180°时位置初值的收敛趋势 Fig. 6 Convergence tendency of initial values when Az≈90° |
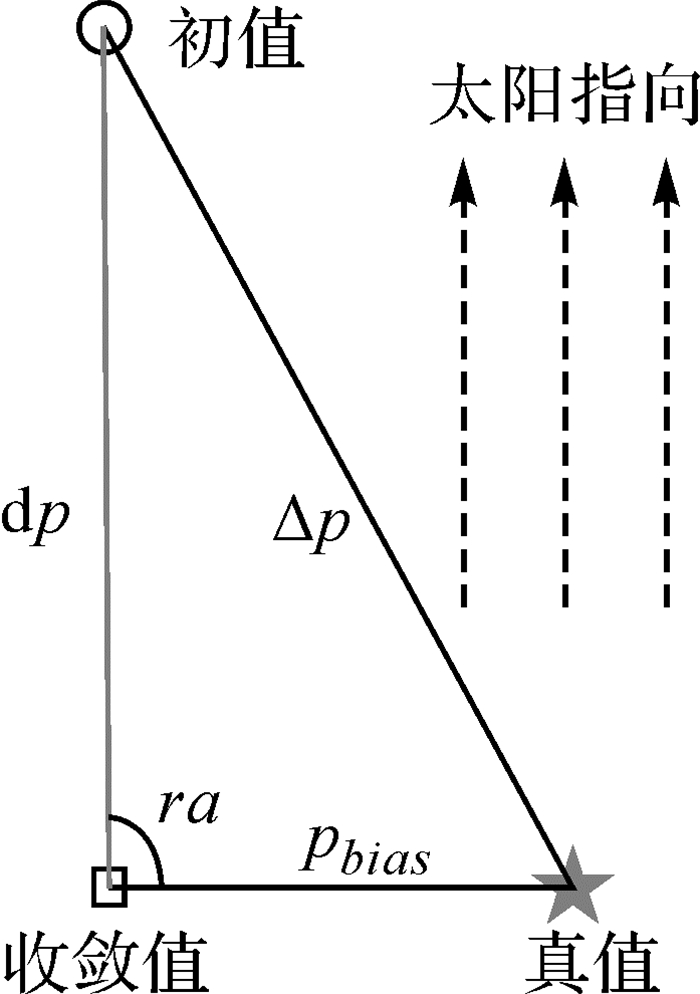
由图 4-图 6可知,有偏估计的作用是将初值沿着太阳的指向稳定收敛到一条线与太阳指向垂直的直线上,且这条直线通过真值。当初值与真值的连线恰好在太阳的指向上时,初值收敛于真值,利用有偏估计求得的位置是无偏的;当初值与真值的连线不在太阳的指向上时,利用有偏估计方法求得的位置是有偏的,这一偏差存在于与太阳的指向垂直的方向。初步猜想,若以初值、初值的收敛值以及真值位置为顶点作三角形,则该三角形在理论上可能为直角三角形或近似直角三角形,如图 7所示。
|
| 图 7 有偏估计对初值的改进效果 Fig. 7 Improved effect of bias estimate on initial value |
在三角形中,初值相对于真值的误差Δp为“斜边”长度,初值与收敛值之间的距离dp,以及收敛值与真值之间的距离pbias为两条“直角边”的长度。为了验证上面关于直角三角形的猜想,下面统计给出了图 4、5和6中90个三角形的“直角”ra的大小,结果如图 7所示。其中ra按如下公式计算
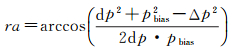 (14)
(14)
由图 8可知,“直角”ra的大小在90°附近上下波动,波动范围不超过±4°。|ra-90°| < 2°的三角形分别占总数的96.7%、100%和96.7%,|ra-90°| < 1°的三角形分别占总数的92.2%、94.4%和90.0%。从统计结果来看,基本可以证实上面关于直角三角形的猜想。显然,在直角三角形中总有pbias < Δp,这就解释了为什么有偏估计总是能够改善初值的精度。

|
| 图 8 “直角”ra的统计结果 Fig. 8 Statistic results of the right angles ra |
在实际应用中,初值的选择往往具有随机性和盲目性,即无法掌控初值、真值及太阳方向之间的关系,也可以认为无法掌控pbias的大小。文献[18]提出了偏改正及部分偏改正理论,其目的就是对有偏估计中参数估值的系统性偏差进行改正,进一步提高解的精度。其提出的理论,在第一类Fredholm积分方程的仿真算例中,使参数估计精度提高了大约11%;在地球重力场恢复的仿真算例中,使参数估计精度提高了大约5%。偏改正理论可以在一定程度上减小参数估值的有偏性,但无法从根本上消除有偏性,这是因为有偏估计的本质是利用参数估值的有偏性换取参数估值较小的方差,使解稳定。
从客观上来讲,快速测日定位中的病态问题是由观测时间过短、太阳在空间位移过小造成的,除非延长观测时间,否则无法改变这一事实。但定位模型也是病态问题产生的原因之一,采用新的定位模型,如矢量法定位模型、航天器姿态算法模型等[19-20],有可能在一定程度上改善单天体定位中的病态问题。
4 结论综合本文分析,可得出以下基本结论:
(1) 有偏估计求解得到的位置相对于初值位置,精度一定有所改善,但改善程度与初值本身有关。
(2) 当初值与真值的连线恰好与太阳方向重合时,有偏估计求得的位置是无偏的,此时位置估值的精度最好,对初值的改善最明显。
(3) 当初值与真值的连线与太阳方向之间存在夹角时,有偏估计求得的位置是有偏的。此时有偏估计对初值的改善程度与夹角有关,夹角越大,改善程度越小。
(4) 当初值与真值的连线垂直于太阳方向时,有偏估计对初值没有改善效果。
本文对快速测日定位中病态问题的研究,以及对有偏估计的应用研究,具有一定的实用价值。例如,月球/火星车长时间漫游活动过程中,一般都会有短暂的静止时间。此时将航迹推算得到的位置作为初值,采用有偏估计的方法改进初值精度,可在一定程度上削弱里程计、惯导等设备累积误差对位置推算的影响,提高定位精度。
| [1] | GONG Weishu. Discussions on Localization Capabilities of MSL and MER Rovers[J]. Annals of GIS , 2015, 21 (1) : 69 –79. DOI:10.1080/19475683.2014.992367 |
| [2] | TREBI-OLLENNU A, HUNTSBERGER T, CHENG Yang, et al. Design and Analysis of a Sun Sensor for Planetary Rover Absolute Heading Detection[J]. IEEE Transactions on Robotics and Automation , 2001, 17 (6) : 939 –947. DOI:10.1109/70.976028 |
| [3] | EISENMAN A R, LIEBE C C, PEREZ R.Sun Sensing on the Mars Exploration Rovers[C]//Aerospace Conference Proceedings.Big Sky, MT:IEEE, 2002, 5:2249-2262. |
| [4] | KURODA Y, KUROSAWA T, TSUCHIYA A, et al.Accurate Localization in Combination with Planet Observation and Dead Reckoning for Lunar Rover[C]//Proceedings of IEEE International Conference on Robotics and Automation.New Orleans, LA:IEEE, 2004, 2:2092-2097. |
| [5] | DEANS M C, WETTERGREEN D, VILLA D.A Sun Tracker for Planetary Analog Rovers[C]//Proceedings of the 8th International Symposium on Artificial Intelligence, Robotics and Automation in Space.Munich:[s.n.], 2005:1-7. |
| [6] | D'AMARIO L A. Mars Exploration Rovers Navigation Results[J]. The Journal of the Astronautical Sciences , 2006, 54 (2) : 129 –173. DOI:10.1007/BF03256481 |
| [7] | FURGALE P, ENRIGHT J, BARFOOT T. Sun Sensor Navigation for Planetary Rovers:Theory and Field Testing[J]. IEEE Transactions on Aerospace and Electronic Systems , 2011, 47 (3) : 1631 –1647. DOI:10.1109/TAES.2011.5937255 |
| [8] | 邸凯昌. 勇气号和机遇号火星车定位方法评述[J]. 航天器工程 , 2009, 18 (5) : 1–5. DI Kaichang. A Review of Spirit and Opportunity Rover Localization Methods[J]. Spacecraft Engineering , 2009, 18 (5) : 1 –5. |
| [9] | COZMAN F, KROTKOV E.Robot Localization Using a Computer Vision Sextant[C]//Proceedings of IEEE International Conference on Robotics and Automation.Nagoya, Aichi:IEEE, 1995, 1:106-111. |
| [10] | ENRIGHT J, FURGALE P, BARFOOT T.Sun Sensing for Planetary Rover Navigation[C]//Proceedings of Aerospace Conference.Big Sky, MT:IEEE, 2009:1-12. |
| [11] | 杨鹏.基于太阳观测图像的月球车天文导航[D].杭州:浙江大学, 2011. YANG Peng.Sun Observation Image Based Celestial Navigation for Lunar Rover[D].Hangzhou:Zhejiang University, 2011. |
| [12] | 李崇辉, 郑勇, 张超, 等. 一种无需精密整平的抗差天文定位方法[J]. 测绘学报 , 2013, 42 (6) : 810–816. LI Chonghui, ZHENG Yong, ZHANG Chao, et al. A Robust Celestial Positioning Method without Precise Leveling[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (6) : 810 –816. |
| [13] | 王斌会. 复共线性诊断方法的比较[J]. 统计与决策 , 2003 (8) : 7–8. WANG Binhui. Comparison of Multiple Linear Diagnostic Methods[J]. Statistics and Decision , 2003 (8) : 7 –8. |
| [14] | KUSCHE J, KLEES R. Regularization of Gravity Field Estimation from Satellite Gravity Gradients[J]. Journal of Geodesy , 2002, 76 (6-7) : 359 –368. DOI:10.1007/s00190-002-0257-6 |
| [15] | HANSEN P C, O'LEARY D P. The Use of the L-curve in the Regularization of Discrete Ill-posed Problems[J]. SIAM Journal on Scientific Computing , 1993, 14 (6) : 1487 –1503. DOI:10.1137/0914086 |
| [16] | GOLUB G H, HEATH M, WAHBA G. Generalized Cross-validation as a Method for Choosing a Good Ridge Parameter[J]. Technometrics , 1979, 21 (2) : 215 –223. DOI:10.1080/00401706.1979.10489751 |
| [17] | 詹银虎, 郑勇, 张超, 等. 超大视场太阳敏感器图像质心提取算法[J]. 测绘学报 , 2015, 44 (10) : 1078–1084. ZHAN Yinhu, ZHENG Yong, ZHANG Chao, et al. Image Centroid Algorithms for Sun Sensors with Super Wide Field of View[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (10) : 1078 –1084. DOI:10.11947/j.AGCS.2015.20150118 |
| [18] | SHEN Yunzhong, XU Peiliang, LI Bofeng. Bias-corrected Regularized Solution to Inverse Ill-posed Models[J]. Journal of Geodesy , 2012, 86 (8) : 597 –608. DOI:10.1007/s00190-012-0542-y |
| [19] | 李崇辉, 李铸洋, 郑勇, 等. 利用多星矢量观测信息进行天文导航定位技术的研究[J]. 导航定位学报 , 2013, 1 (3) : 62–65. LI Chonghui, LI Zhuyang, ZHENG Yong, et al. Celestial Positioning Analysis Based on Multi-star Vector Observation Information[J]. Journal of Navigation and Positioning , 2013, 1 (3) : 62 –65. |
| [20] | 张新帅, 周召发. 航天器姿态算法在地面天文定位中的应用研究[J]. 测绘科学 , 2015, 40 (5) : 139–143. ZHANG Xinshuai, ZHOU Zhaofa. Application of Attitude Determination Algorithms of Spacecraft in Celestial Positioning on Earth[J]. Science of Surveying and Mapping , 2015, 40 (5) : 139 –143. |


